Abstract
Magnetostriction of ferromagnetic materials describes the change of their shape or dimension in response to the reorientation of magnetization under the influence of external magnetic field. Fe100−xGax binary alloys (Galfenol) have large magnetostriction and excellent ductility; and they are very promising rare-earth free materials for applications in sensors, actuators, energy-harvesters and spintronic devices. Here we report results of large-scale ab initio molecular dynamics (AIMD) simulations for Galfenol, especially regarding the mechanism that leads to the sudden drop of tetragonal magnetostriction at x ~ 19, a long-standing puzzle for the community. Based on rigid band analysis, we propose possible ways to further optimize the performance of Galfenol for device applications. For example, we found that the substitution of a small amount of Cu for Ga (1.6%) in certain configuration may double the magnetostriction of Galfenol.
Materials with large magnetostriction are extensively used in sensors, actuators, micro electromechanical systems, and energy-harvesters1,2. One of the most successful magnetostrictive materials hitherto is Terfenol-D that shows large magnetic-field-induced strains up to 2000 ppm (parts per million)3. However, the shortage of rare-earth supplies and the brittleness of rare-earth compounds inspire a new wave of interdisciplinary efforts of searching for more sustainable yet well-performing magnetostrictive materials. As the most promising candidate, binary Fe100−xGax alloys (Galfenol) combine numerous advantages such as large tetragonal magnetostrictive coefficient (λ001 ~ 280 ppm), low saturation magnetic field (about 100 ~ 200 Oe), excellent ductility and low cost4,5,6,7,8. To further optimize the performance of Fe100−xGax alloys for device applications, it is essential to understand the mechanism of its large tetragonal magnetostriction.
Although extrinsic factors were proposed9,10,11, it is believed that the strong magnetostrictive responses of Galfenol result from intrinsic factors, namely, the Ga-induced changes of electronic structures12,13,14. A major goal of the interdisciplinary research of Galfenol is to further enhance their magnetostrictive coefficients for robust performance in devices6,7,8. The abrupt drop of magnetostriction of Galfenol, at x = 17 for slow-cooled (10°C/min) samples or x = 19 for quenched samples, was typically attributed to the development of short- and medium-range orderings of Ga atoms at high Ga concentration in the bcc Fe lattice15,16,17. Therefore, it is crucial to establish the structure-property correlation around x = 17–19 to further improve magnetostrictive response of Galfenol, through synergistic experimental and theoretical efforts8.
Results and Discussion
In this Letter, we report results of large-scale ab initio molecular dynamics (AIMD) simulations for the binary Fe100−xGax alloys, using the Vienna Ab-initio Simulation Package (VASP)18. We successfully reproduced the experimental λ001(x) curve up to x = 21 and explained the decrease of λ001 at x = 19, with the atomic structures produced by AIMD simulations and the Boltzmann statistics. Furthermore, we found that adding a small amount of Cu may extend the ascending trend of λ001(x) of Galfenol. For example, the calculated λ001 of Fe79.7Ga18.7Cu1.6 ternary alloy in a handpicked metastable structure is 550 ppm, significantly higher than the corresponding value of binary Fe100−xGax alloys at the same concentration. This shows a possibility for further enhancing the magnetostriction of Galfenol-based alloys, by introducing a small amount of appropriate elements and also by stabilizing them in benign structures.
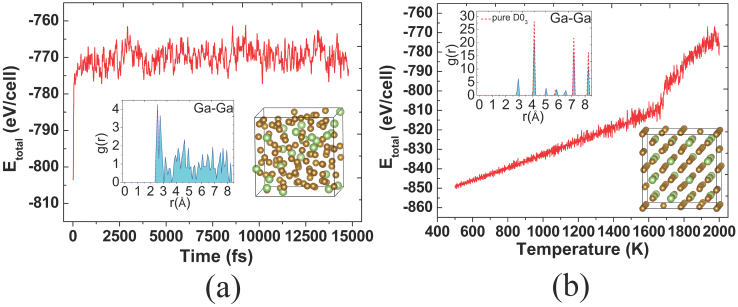
To illustrate the AIMD simulation procedure in the present studies, we use Fe81.25Ga18.75 as an example. We set up ten initial configurations, with chemically random distributions of 104 Fe atoms and 24 Ga atoms on the bcc lattice sites, and first kept them in melting state at 2000 K for 15 picoseconds (ps). As displayed in Fig. 1(a) for one configuration, the free energy of the system quickly converged to about −773 eV/cell after 0.5 picoseconds, indicating its thermal equilibrium. The Ga-Ga radial distribution function [RDF, denoted as g(r)] and the snapshot of atomic arrangement in the insets of Fig. 1(a) exhibit features of the liquid phase at 2000 K. We then cooled the system down from 2000 K to 500 K, with a cooling rate of 1012 K/s around the melting point where the free energy decreases abruptly as shown in Fig. 1(b). The atomic structure at 500 K was further optimized at 0 K, with stringent criteria that require (1) force on each atom less than 0.01 eV/Å; (2) pressure along each axis smaller than 1.0 GPa, and (3) energy convergence better than 10−5 eV.
Figure 1.
(Color online) (a) The AIMD total energy of Fe81.25Ga18.75 during the heating process at 2000 K from its initial configuration. The left and right insets give the radial distribution function (RDF) and the snapshot of crystal structure (SCS) at t = 15.0 ps, respectively. (b) Temperature dependent total energy of Fe81.25Ga18.75 in the simulated annealing process from 2000 K to 500 K. The left and right insets show the RDF and SCS of the fully relaxed structure, and the red dash line in the left inset gives the RDF of bulk D03 structure. The golden and green balls in SCS are for Fe and Ga, respectively.
Note that the calculated Ga-Ga RDF and snapshot of atomic arrangement in the insets in Fig. 1(b) show recrystallization of Galfenol at 500 K. It is important to point out that the number of Ga-Ga first neighbors is negligible in most structures obtained through our AIMD simulations. This is in good agreement with experimental observations that Ga and other metalloid atoms tend not to form first neighbors in the Fe matrix. The sharp peaks in the Ga-Ga RDF curve at 2.85 Å and 4.05 Å correspond to the B2-like and D03 local structures, respectively. For comparison, the Ga-Ga RDF of the bulk D03 structure was also given in the dashed line in the upper-left inset of Fig. 1(b).
To directly compare magnetostrictive coefficients and other quantities with experimental data, we calculated their ensemble averages for each Ga concentration according to
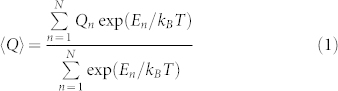 |
Here, N is the number of configurations in the ensemble for each Ga concentration (N = 10 in the present studies) and En and Qn are total energies and the physical quantities of different configurations respectively. As an illustration, the calculated En and Qn (<c′>, <−b1> and <λ001>) for ten different configurations of Fe81.25Ga18.75 were presented in Table S1 in the Supplementary Materials. It is easy to see that the physical quantities are sensitive to the change of atomic structure at this Ga concentration. Since contributions from many configurations that have energies more than 400 meV higher than that of the best configuration are negligible due to their Boltzmann factors, we didn't calculate their magnetoelastic responses.
For the determination of tetragonal magnetostriction coefficient, the supercells were deformed from their optimized geometries along the z-axis with the constant-volume mode (εx = εy = −1/2εz). All atomic positions are further relaxed for each εz. λ001 for each configuration was calculated from the εz-dependent total energy (ETotal) and magnetocrystalline anisotropy energy (EMCA) according to the following formula19,20,
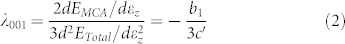 |
Here, the numerator and denominator are directly linked to the magnetoelastic coupling coefficient (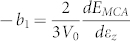 ) and the tetragonal shear modulus (
) and the tetragonal shear modulus (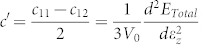 ), respectively. In particular, values of EMCA are calculated by using the torque method, which was recently adapted to VASP21,22.
), respectively. In particular, values of EMCA are calculated by using the torque method, which was recently adapted to VASP21,22.
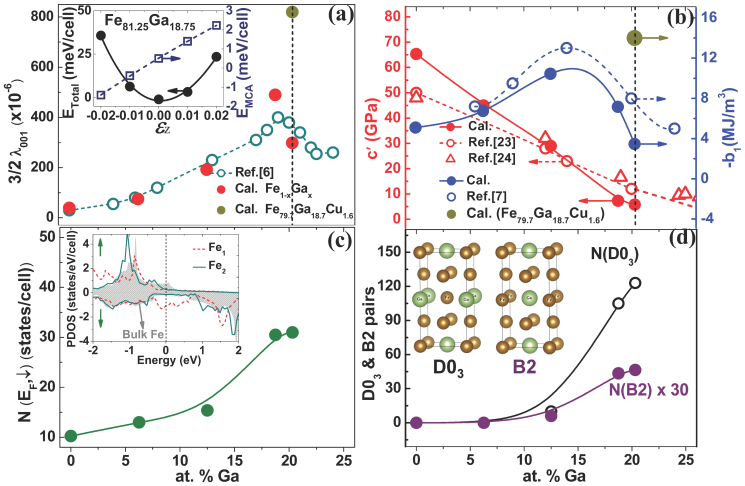
To show the quality of our results, the calculated εz-dependent ETotal and EMCA for a configuration of Fe81.25Ga18.75 are presented in the inset of Fig. 2(a). It is obvious that data points are smooth for high-quality fittings by polynomials of εz (linear function for EMCA and cubic function for ETotal). We determined <b1>, <c′> and <λ001> from the derivatives according to Eqs. (1) and (2) and the curve of <λ001> ~ x (0 ≤ x < 21) is given in Fig. 2(a) (a factor of 3/2 was multiplied for easy comparison with experimental data). As found in experimental results7, <λ001> increases quadratically with x till x = ~19 and decreases abruptly afterward. Fig. 2(b) shows that results of <b1> and <c′> also agree well with their experimental counterparts7: <c′> decreases linearly with x, while <b1> peaks at x ~ 12.5. These good agreements in a broad range of x suggest the validity and predictability of our theoretical approaches and models.
Figure 2.
(Color online) (a) Calculated (red filled circles) x-dependent of 3/2<λ001>, along with the experimental data measured for the quenched samples at room temperature (dark cyan open circle)7. The golden filled circle at x = 20.3 represents result for a metastable structure of Fe79.7Ga18.7Cu1.6. The inset shows the strain-dependent total energy and magnetocrystalline anisotropy energy for one configuration of Fe81.25Ga18.75. (b) Calculated x-dependent <c′> (red filled circles) and <b1> (blue filled circles), along with experimental data of c′ (red open circles and triangles) and b1 (blue open circles)23,24. The golden filled circle represents the calculated b1 of a metastable structure of Fe79.7Ga18.7Cu1.6. (c) Calculated x-dependent number of electronic states at the Fermi level in the minority spin channel, N(EF,↓). The inset shows the projected density of states (PDOS) of Fe1, Fe2 atoms in Fe81.25Ga18.75, along with the shaded region for the PDOS of the bcc bulk Fe. (d) Number of D03 (black open circles) and B2 (×30, purple filled circles) pairs. The insets show Fe (golden balls) and Ga (green balls) atoms in the D03 and B2 structures.
According to Eq. (2), an essential feature of strong magnetostrictive materials is having large EMCA under a small lattice distortion. One factor for the enhancement of magnetoelastic coupling of Galfenol is that Ga atoms produce non-bonding Fe d-states in the minority spin channel. For 3d transition metal systems, the spin-orbit coupling Hamiltonian, HSOC = ξ(σ•L) with σ and L the spin and angular moment operators, is much weaker than their crystal fields (e.g., ξ is about 30 meV for Fe). The value of EMCA can be reasonably estimated through the second order perturbation equation25,
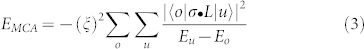 |
where |o> and |u> denote the occupied and unoccupied electronic states; and Eo and Eu are their corresponding energies. For states close to the Fermi level, their SOC interactions with other states are strong because of the small denominators in Eq. (3), and also they are more responsive to lattice strain.
The existence of non-bonding Fe d-states is displayed by the curves of projected density of states (PDOS) in the inset in Fig. 2(c) for two Fe atoms (Fe1 represents the first neighbors of Ga and Fe2 represents the second neighbors of Ga) in Fe81.25Ga18.75. In contrast to the clear separation between the “bonding” and “anti-bonding” states for the bulk Fe (shaded background) and Fe2 in the minority spin channel, high peaks of PDOS can be found around the Fermi level for the Fe1 atom. These states have the dxz,yz feature, with their lobs pointing toward the first neighbors13,19; and they become dangling bonds due to the weak Fe-Ga hybridization. A more clear demonstration for their wave function features can be found in Figure S1 in the Supplementary Materials for Fe81.25Ga18.75. Quantitatively, we give the number of states within ±0.2 eV in the minority spin channel, N(EF,↓), in Fig. 2(c) versus the Ga concentration. It is clear that value of N(EF,↓) increases monotonically with x, corresponding to the availability of Fe dangling bonds around Ga atoms. The trend of N(EF,↓) correlates well to the monotonic increase of <b1> at low Ga concentration in Fig. 2(b).
As the Ga concentration increases beyond x = 12.5, the short- or medium-range chemical orderings become important. Our previous studies revealed that a pure D03 phase has a negative magnetostriction, whereas a B2-like phase has a positive magnetostriction12. In the present study, we calculated the numbers of B2- and D03-pairs by integrating the peak areas in the Ga-Ga RDF curves at 2.85 Å and 4.05 Å. Interestingly, we found a close correlation between the drop of <b1> and the formation of D03 pairs from x = 12.5. While the number of B2-pairs, N(B2), remains small till x ~ 19, the number of D03-pairs, N(D03), increases rapidly after x = 12.5 which has also been observed by experimental detections16. The coincidence between the drop of <b1> and the formation of D03-pairs indicates the detrimental effect of the D03 ordering on magnetostriction. Furthermore, the presence of B2-pairs appears not to have particular role for the enhanced magnetostriction of Galfenol up to x = 19.
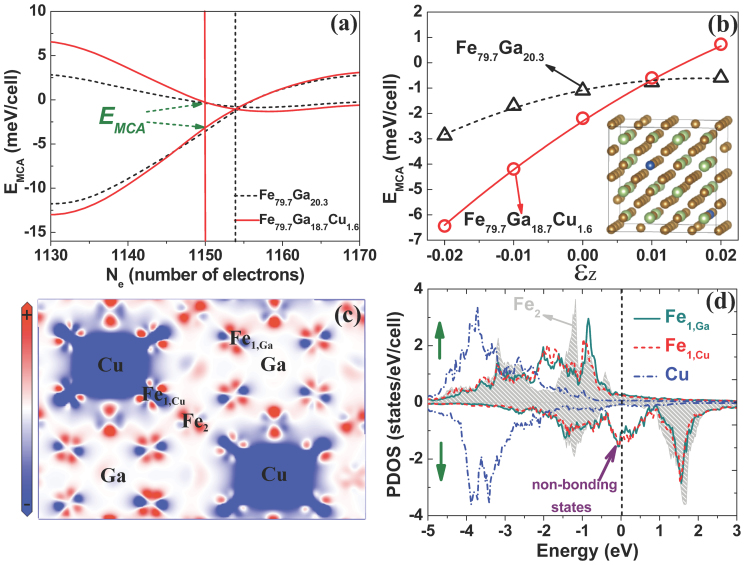
One may use the rigid band model to analyze how λ001 changes with the number of electrons in the unit cell (Ne)13. The EMCA(Ne) curves of Fe79.7Ga20.3 that has a concentration of Ga slightly behind the drop of <λ001> are given in Fig. 3(a) with εz = ±1%. Corresponding to the large decrease of λ001 from x = 19 to x = 20.3, the value of EMCA for either +1% or −1% is small at Ne = 1154 (the number of valence electrons of 102 Fe and 26 Ga atoms). Interestingly, the two EMCA(Ne) curves with εz = ±1% actually cross each other near Ne = 1154. Therefore, one may enhance magnetostriction of Fe79.7Ga20.3 by either decreasing Ne (for positive λ001, by replacing some Ga atoms with Cu or Zn atoms) or increasing Ne (for negative λ001, by replacing some Ga atoms with Ge atoms). Unfortunately, both Cu and Zn have poor solubility with Fe26, so it might be a technical challenge to incorporate them uniformly in the FeGa lattice. For this reason, our AIMD simulations with the 128-atoms supercell indicate that Fe-Ga-Cu compounds don't recrystallize at 500 K after the annealing/quenching procedure. To demonstrate the concept, we calculated magnetostrictive coefficients of three handpicked Fe-Ga-Cu configurations, which cover the most representative local structures. Interestingly, if we replaced two Ga atoms in Fe79.7Ga20.3 by Cu to form a hypothetical Fe79.7Ga18.7Cu1.6 structure as depicted in the inset of Fig. 3(b), the calculated λ001 can be as large as 550 ppm. The corresponding −b1 is also large, 14.5 MJ/m3, as shown by the brown filled circles at x = 20.3 for λ001 in Fig. 2(a) and for −b1 in Fig. 2(b). Accordingly, the slope of strain dependent magnetocrystalline energy for Fe79.7Ga18.7Cu1.6 is significantly larger than that for Fe79.7Ga20.3 in Fig. 3(b). The calculated EMCA(Ne) curves of the hypothetical ternary alloy with εz = ±1% in Fig. 3(a) are similar with those of Fe79.7Ga20.3, indicating that the substitution of 1.6% Cu for Ga doesn't significantly affect the band structure around the Fermi level. These results show the importance of manipulating number of electrons for the design of new generation rare-earth-free magnetostrictive materials.
Figure 3.
(Color online) (a) Calculated EMCA with (εz = ±1% for Fe79.7Ga20.3 (black dash line) and Fe79.9Ga18.7Cu1.6 (red solid line) versus the number of valence electrons in the unit cell. The two vertical lines show positions of their actual Ne, black for Fe79.7Ga20.3 and red for Fe79.9Ga18.7Cu1.6. (b) Strain dependent EMCA of Fe79.7Ga20.3 (black open triangle) and Fe79.9Ga18.7Cu1.6 (red open circle); the inset shows the atomic configuration of Fe79.9Ga18.7Cu1.6, where golden, green and blue balls represent Fe, Ga and Cu atoms, respectively. (c) Charge difference between Fe79.9Ga18.7Cu1.6 and Fe79.7Ga20.3, in a range of ±0.008 eV/Å3. (d) Partial density of states of Fe2, Fe1,Ga, Fe1,Cu and Cu atoms in Fe79.9Ga18.7Cu1.6, the purple arrow highlights the nonbonding states of Fe1,Ga and Fe1,Cu atoms.
To further appreciate the effect of Cu on the electronic structures of Galfenol, the charge density difference, i.e., ρ(Fe79.7Ga18.7Cu1.6)- ρ(Fe79.7Ga20.3), was shown in Fig. 3(c). One may see that the effect of Cu in the Fe-Ga matrix is mainly localized around Cu and Fe1,Cu (the nearest neighboring Fe atom to Cu) atoms. From the PDOS curves of Fe79.7Ga18.7Cu1.6 in Fig. 3(d), we can see that the PDOS of Fe1,Cu is not much different from that of Fe1,Ga. Both of them have fully occupied 3d bands in the majority spin channel and pronounced peaks of non-bonding dxz,yz states near the Fermi level in the minority spin channel, as highlighted by the arrow. This suggests the similarity of Cu and Ga from the point view of their Fe neighbors. The bonding and anti-bonding states of the Fe2 atoms, the second neighbors to Cu and Ga, are well separated in energy in the minority spin channel, as for the binary Fe79.7Ga20.3 alloy. The weak hybridization between d-states of Fe and Cu is also reflected in the curves of PDOS of Cu atoms in Fe79.7Ga18.7Cu1.6. The d-bands of Cu exist in a narrow range from −5 to −3 eV. Nevertheless, small tails of Cu d-states can be found around the Fermi level, which is not found for Ga atoms.
For experimental verifications, one needs to be cautious since the phenomenal enhancement of λ001 relies on an assumption: Cu atoms uniformly substitute Ga atoms. From total energies, we found that Cu atoms actually more prefer to stay together or substitute Fe in the Fe-Ga matrix, as shown in Figures S2 and S3 in the Supplementary Materials. Some of these configurations may not have huge magnetostriction. Therefore, special experimental procedures such as rapid quenching are needed to freeze the metastable structure for the sake of obtaining highly magnetostrictive ternary Fe100−xGax−yCuy samples. Synergistic theoretical and experimental endeavors are necessary to achieve this goal.
In conclusion, ab initio molecular dynamics simulations for Fe100−xGax binary and ternary alloys (0 ≤ x ≤ 21) revealed the mechanism for the drop of tetragonal magnetostriction <λ001> at x = 19 and, more importantly, conceptually provided insights for avoiding the drop. As an example, we demonstrated that uniform substitution of a small amount of Cu for Ga might extend the rising trend of λ001 and double the magnetostriction of Galfenol, if appropriate metastable structures can be stabilized. This shows a new possibility to further optimize the performance of transition metal magnetostrictive alloys for practical applications.
Methods
Density functional simulations were performed with the Vienna Ab-initio Simulation Package. The exchange and correlation interactions among electrons were described at the level of the spin-polarized generalized gradient approximation (GGA), using the Perdew-Burke-Ernzerhof (PBE) functional27. We treated Fe-3d4s4p, Ga-3d4s4p and Cu-3d4s as valence states and adopted the projector-augmented wave (PAW) pseudopotentials to represent the effect of their ionic cores. Self-consistent calculations were performed in the non-collinear mode with the spin-orbit coupling (SOC) term28. The energy cutoff for the plane-wave expansion was 400 eV, sufficient for Fe-Ga systems according to our test calculations. A 4 × 4 × 4 cubic supercell (128 atoms/cell) was used to determine the chemical ordering of Ga in Fe100−xGax alloys. While we used the Γ point to sample the Brillouin zone in the AIMD simulations, all geometries were further optimized with 5 × 5 × 5 Monkhorst-Pack k-points before the determination of electronic and magnetic properties.
Author Contributions
H.W. and Y.N.Z. performed calculations. H.W. prepared the figures. H.W., Y.N.Z., L.Z.S. and R.Q.W. wrote the manuscript. D.S.X. and Z.D.Z. discussed results with others. All authors reviewed the manuscript. R.Q.W. supervised the project.
Supplementary Material
Understanding strong magnetostriction in Fe100-xGax allo
Acknowledgments
We are grateful to Drs. A.E. Clark, M. Wun-Fogle, K.B. Hathaway, and A.B. Flatau for insightful discussions. Work was mainly supported by the ONR in US (Grant No: N00014-08-1-0143, N00014-13-1-0445) and also by the CAS/SAFEA International Partnership Program for Creative Research Teams. L.Z.S. acknowledge the support from NSF (Grant NO: CMMI-0800417), D.S.X. thanks support of the Ministry of Science and Technology of China under Grant No. 2011CB606404, Z.D.Z. thanks support from the National Natural Science Foundation of China (No. 51331006). Calculations were performed on Department of Defense (DOD) supercomputers and on CAS Shenyang Supercomputing Center supported by a grant from Informalization Construction Project of Chinese Academy of Sciences during the 11th Five-Year Plan Period (No.INFO-115-B01).
References
- Clark A. E. in Ferromagnetic Materials Vol. 1, Ch. 3 (ed. Wohlfarth E. P.) (North-Holland, Amsterdam, 1980). [Google Scholar]
- Clark A. E. & Hathaway K. B. in Handbook of Giant Magnetostrictive Materials Chap.1, 1–48 (ed. Engdahl G.) (Academic, San Diego, 2000). [Google Scholar]
- Jerems F., Mac Mahon C., Jenner A. G. & Greenough R. D. Amorphous magnetic materials for transducers. Ferroelectrics 22, 333 (1999). [Google Scholar]
- Clark A. E., Restorff J. B., Wun-Fogle M., Lograsso T. A. & Schlagel D. L. Magnetostrictive properties of body-centered cubic Fe-Ga and Fe-Ga-Al alloys. IEEE Trans. Mag. 36, 3238 (2000). [Google Scholar]
- Guruswamy S., Srisukhumbowornchai N., Clark A. E., Restorff J. B. & Wun-Fogle M. Strong, ductile, and low-field-magnetostrictive alloys based on Fe-Ga. Scripta Mater. 43, 239 (2000). [Google Scholar]
- Atulasimha J. & Flatau A. B. A review of magnetostrictive iron-gallium alloys. Smart Mater. Struct. 20, 043001 (2011). [Google Scholar]
- Clark A. E. et al. Extraordinary magnetoelasticity and lattice softening in bcc Fe-Ga alloys. J. Appl. Phys. 93, 8621–8623 (2003). [Google Scholar]
- Petculescu G., Wu R. Q. & McQueeney R. in Handbook of Magnetic Materials Vol. 20, Chap. 3, 123–223, (ed. Buschow K. H. J.) (Elsevier, 2012). [Google Scholar]
- Cao H. et al. Role of Nanoscale Precipitates on the Enhanced Magnetostriction of Heat-Treated Galfenol (Fe1−xGax) Alloys. Phys. Rev. Lett. 102, 127201 (2009). [DOI] [PubMed] [Google Scholar]
- Laver M. et al. Magnetostriction and Magnetic Heterogeneities in Iron-Gallium. Phys. Rev. Lett. 105, 027202 (2010). [DOI] [PubMed] [Google Scholar]
- Boisse J., Zapolsky H. & Khachaturyan A. G. Atomic-scale modeling of nanostructure formation in Fe-Ga alloys with giant magnetostriction: Cascade ordering and decomposition. Acta Materialia 59, 2656 (2011). [Google Scholar]
- Wu R. Q. Origin of large magnetostriction in FeGa alloys. J. Appl. Phys. 91, 7358 (2002). [Google Scholar]
- Zhang Y. N., Cao J. X. & Wu R. Q. Rigid band model for prediction of magnetostriction of iron-gallium alloys. Appl. Phys. Lett. 96, 062508 (2010). [Google Scholar]
- Du Y., Huang M., Lograsso T. A. & McQueeney R. J. X-ray diffuse scattering measurements of chemical short-range order and lattice strains in a highly magnetostrictive Fe0.813Ga0.187 alloy in an applied magnetic field. Phys. Rev. B 85, 214437 (2012). [Google Scholar]
- Ruffoni M. P. et al. Direct measurement of intrinsic atomic scale magnetostriction. Phys. Rev. Lett. 101, 147202 (2008). [DOI] [PubMed] [Google Scholar]
- Du Y. et al. Relation between Ga ordering and magnetostriction of Fe-Ga alloys studied by x-ray diffuse scattering. Phys. Rev. B 81, 054432 (2010). [Google Scholar]
- Wang H. et al. Ab initio studies of the effect of nanoclusters on magnetostriction of Fe1−xGax alloys. Appl. Phys. Lett. 97, 262505 (2010). [Google Scholar]
- Kresse G. & Hafner J. Ab-Initio Molecular-Dynamics Simulation of the Liquid-Metal Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 49, 14251 (1994). [DOI] [PubMed] [Google Scholar]
- Wu R. Q. & Freeman A. J. Spin-orbit induced magnetic phenomena in bulk metals and their surfaces and interfaces. J. Magn. Magn. Mater. 200, 498 (1999). [Google Scholar]
- Zhang Y. N. & Wu R. Q. Mechanism of Large Magnetostriction of Galfenol. IEEE Tran. Magn. 47, 4044 (2011). [Google Scholar]
- Wang X. D., Wu R. Q., Wang D. S. & Freeman A. J. Torque method for the theoretical determination of magnetocrystalline anisotropy. Phys. Rev. B 54, 61 (1996). [DOI] [PubMed] [Google Scholar]
- Hu J. & Wu R. Q. Control of the Magnetism and Magnetic Anisotropy of a Single-Molecule Magnet with an Electric Field. Phys. Rev. Lett. 110, 097202 (2013). [DOI] [PubMed] [Google Scholar]
- Wuttig M., Dai L. Y. & Cullen J. Elasticity and magnetoelasticity of Fe–Ga solid solutions. Appl. Phys. Lett. 80, 1135 (2002). [Google Scholar]
- Petculescu G., Hathaway K. B., Lograsso T. A., Wun-Fogle M. & Clark A. E. Magnetic field dependence of galfenol elastic properties. J. Appl. Phys. 97, 10M315 (2005). [Google Scholar]
- Wang D. S., Wu R. Q. & Freeman A. J. First Principles Theory of Monolayer Magnetocrystalline Anisotropy and the Diatomic Pair Model. Phys. Rev. B 47, 14 932 (1993). [DOI] [PubMed] [Google Scholar]
- Binary Alloy Phase Diagrams. (2nd edn) Vol. 1 (ed. Massalski T. B.) (ASM International, Metals Park, OH, 1990).
- Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996). [DOI] [PubMed] [Google Scholar]
- Hobbs D., Kresse G. & Hafner J. Fully unconstrained noncollinear magnetism within the projector augmented-wave method. Phys. Rev. B 62, 11556 (2000). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Understanding strong magnetostriction in Fe100-xGax allo