XUV-Exposed, Non-Hydrostatic Hydrogen-Rich Upper Atmospheres of Terrestrial Planets. Part I: Atmospheric Expansion and Thermal Escape

Abstract

The recently discovered low-density “super-Earths” Kepler-11b, Kepler-11f, Kepler-11d, Kepler-11e, and planets such as GJ 1214b represent the most likely known planets that are surrounded by dense H/He envelopes or contain deep H₂O oceans also surrounded by dense hydrogen envelopes. Although these super-Earths are orbiting relatively close to their host stars, they have not lost their captured nebula-based hydrogen-rich or degassed volatile-rich steam protoatmospheres. Thus, it is interesting to estimate the maximum possible amount of atmospheric hydrogen loss from a terrestrial planet orbiting within the habitable zone of late main sequence host stars. For studying the thermosphere structure and escape, we apply a 1-D hydrodynamic upper atmosphere model that solves the equations of mass, momentum, and energy conservation for a planet with the mass and size of Earth and for a super-Earth with a size of 2 R_Earth and a mass of 10 M_Earth. We calculate volume heating rates by the stellar soft X-ray and extreme ultraviolet radiation (XUV) and expansion of the upper atmosphere, its temperature, density, and velocity structure and related thermal escape rates during the planet's lifetime. Moreover, we investigate under which conditions both planets enter the blow-off escape regime and may therefore experience loss rates that are close to the energy-limited escape. Finally, we discuss the results in the context of atmospheric evolution and implications for habitability of terrestrial planets in general. Key Words: Stellar activity—Low-mass stars—Early atmospheres—Earth-like exoplanets—Energetic neutral atoms—Ion escape—Habitability. Astrobiology 13, 1011–1029.

1. Introduction

The evolution of an Earth-like planet, where life on its surface may originate, is strongly related to its formation process, the impact history of the early planetary system, its initial water inventory, the escape of the early protoatmosphere, and the host star–driven evolution of the remaining protoatmosphere or secondary atmosphere (e.g., Halliday, 2003; Lammer et al., 2009, 2012; Lammer, 2013). That the early atmospheres of terrestrial planets contained most likely more hydrogen than they do today or were even hydrogen-dominated was considered decades ago by researchers such as Holland (1962), Walker (1977), Ringwood (1979), Sekiya et al. (1980a, 1980b, 1981), Watson et al. (1981), and Ikoma and Genda (2006).

As illustrated in Fig. 1a, the earliest protoatmosphere of a planet should be a hydrogen-dominated H/He gas envelope that has been captured by the growing protoplanet from the system's nebula gas (e.g., Hayashi et al., 1979). This is a complex process that depends on the formation time of the terrestrial planet, the nebula dissipation time, nebula opacity, the depletion factor of dust grains, the number and orbital parameters of additional planets, the protoplanet's gravity, its orbital location, and the host star's radiation and plasma. Theoretical studies indicate that terrestrial planets may capture tens or even several hundreds of Earth-ocean-equivalent amounts of hydrogen around their rocky cores (e.g., Hayashi et al., 1979; Mizuno, 1980; Wuchterl, 1993; Ikoma et al., 2000; Ikoma and Genda, 2006; Rafikov, 2006).

FIG. 1.

Illustration of the formation of dense hydrogen-rich gas envelopes and coronae around young terrestrial planets (Lammer, 2013). (a) Growing protoplanets can capture huge amounts of nebula-based hydrogen and He, which produce dense gaseous envelopes around the rocky cores. (b) As soon as planetary accretion ends, depending on the interior structure and initial volatile (H₂O, CO₂, CH₄, NH₃, etc.) content of the bodies involved in the formation of a protoplanet, huge amounts of H₂O and CO₂ can be released during the magma ocean solidification into the surrounding environment (e.g., Elkins-Tanton and Seager, 2008; Elkins-Tanton, 2011; Lammer, 2013). The amount of outgassed volatiles depends also on the water and carbon contents of the growing protoplanet as well as on differentiation stages and magma ocean depths. In such an outgassed steam atmosphere, the high X-ray and EUV flux of a young host star dissociates the water molecules, and light H atoms populate the upper atmosphere. (Color graphics available online at www.liebertonline.com/ast)

Additionally, with regard to the captured nebula-based hydrogen envelopes, catastrophically outgassed steam atmospheres that depend on the impact history and the initial volatile content of a planet's interior can also be formed after accretion ends (see Fig. 1b) (Elkins-Tanton and Seager, 2008; Elkins-Tanton, 2011; Hamano et al., 2013). Figure 1b illustrates scenarios where primitive material with added H₂O accretes into a planetary body. The additional water may be sufficient to oxidize all iron in the end member. The second scenario in Fig. 1b illustrates differentiated material where H₂O and volatiles are added during the magma ocean phase. The resulting steam atmospheres depend then on the amount of volatiles that have been delivered or integrated during the growth or magma ocean phase of the planetary bodies (e.g., Elkins-Tanton, 2008).

Elkins-Tanton and Seager (2008) used bulk compositions corresponding to primitive and differentiated meteorite compositions and found that outgassing alone can create a wide range of planetary atmosphere masses that range from ≤1% of the planet's total mass up to ∼6% by mass of hydrogen, ∼20 mass % of H₂O, and/or ∼5 mass % of C compounds. According to their study, hydrogen-rich atmospheres can also be outgassed as a result of oxidizing metallic Fe with H₂O. Depending on the initial volatile inventory and the depth of the magma ocean, during its solidification dense steam atmospheres with surface pressures ranging from ∼10² to 10⁴ bar can be catastrophically outgassed (e.g., Bauer 1978; Abe 1993, 1997; Solomatov, 2000; Elkins-Tanton et al., 2003; Elkins-Tanton, 2008, 2011; Elkins-Tanton and Seager, 2008; Lammer, 2013).

In the case of the Solar System planets, it is also expected that the early accretion stage, which resulted in the formation of planetesimals, most likely occurred in a highly reduced environment that resulted in large iron cores and volatiles of the planetesimals that were later delivered to protoplanets (e.g., Ringwood, 1979; Hunten et al., 1987; Dreibus et al., 1997). Wänke and Dreibus (1988) suggested that H₂O would react with metallic iron in the accreting material to produce FeO or Fe₂O₃ by releasing H into the atmosphere. A more recent study by Rubie et al. (2004) found that during such high-pressure phases, however, iron moves into a metallic state, preferentially to the oxidized phase, leaving H₂O in the magma ocean.

Although different terrestrial planets may accrete from differentiated planetesimals that contain different H₂O and CO₂ contents, both molecules will enter solidifying minerals in small quantities (e.g., Elkins-Tanton, 2008; Elkins-Tanton and Seager, 2008). Elkins-Tanton (2008) showed that an Earth-sized terrestrial planet with a 2000 km deep magma ocean and an initial H₂O and CO₂ content of ∼0.05 and ∼0.01 wt %, respectively, could build up a steam atmosphere of ∼ 250–300 bar surface pressure. Higher initial H₂O and CO₂ contents in the magma ocean of about ∼0.5 and ∼0.1 wt % can result in water-dominated steam atmospheres of ≥3000 bar surface pressure (Elkins-Tanton, 2008, 2011). For an outgassed 300 bar steam atmosphere at early Earth, surface temperatures near the supercritical point of H₂O could have been reached within several to tens of millions of years after the formation of a magma ocean (Elkins-Tanton, 2008; Hamano et al., 2013), while for larger “super-Earths” this timescale may be up to a factor 10 higher (Elkins-Tanton, 2011). After the surface of a young planet cools below the critical point, at an Earth-type planet with a surface pressure of ∼220 bar corresponding to ∼650 K, the supercritical fluid and steam atmosphere collapses into a liquid surface ocean (Elkins-Tanton, 2011; Lammer et al., 2012; Lammer, 2013). It is also possible that huge water oceans and steam atmospheres form directly from progressive solidification of a magma ocean if the initial H₂O inventory is ≥1 wt % or closer to ∼3 wt %, which may be possible for super-Earths (Elkins-Tanton, 2011).

These theoretical findings have become very relevant since the discovery of several exoplanets that fall hypothetically within the rocky planet domain, such as the super-Earths Gliese 876d (7 M_Earth) (Rivera et al., 2005), OGLE-2005-BLG-390Lb (5 M_Earth) (Gould et al., 2006), HD 69830b (10 M_Earth) (Lovis et al., 2006), Gliese 581c (5.6 M_Earth), Gliese 581d (∼8 M_Earth) (Beust et al., 2008), or Kepler-22b (∼2.38 R_Earth) (Borucki et al., 2011). However, by knowing only the mass or the size, it is not possible to characterize a planet as rock-dominated or as a mixed gaseous-rocky or water-rocky-type planet. Fortunately, we know the size and mass of some super-Earths such as GJ 1214b (R_pl=2.678 R_Earth, M=6.55 M_Earth), 55 Cnc e (R_pl=2 R_Earth, M=8.63 M_Earth), CoRoT-7b (R_pl=1.58 R_Earth, M=7.42 M_Earth), Kepler-10b (R_pl=1.4 R_Earth, M=4.56 M_Earth), Kepler-11b (R_pl=1.97 R_Earth, M=4.3 M_Earth), and Kepler-11f (R_pl=2.61 R_Earth, M=2.3 M_Earth), and the hypothesis that all terrestrial exoplanets expected to be rocky can lose their hydrogen or water-rich protoatmospheres becomes testable (Lammer et al., 2011, 2012; Lissauer et al., 2011; Lammer, 2013). Besides very close-in rocky super-Earths, such as CoRoT-7b and Kepler-10b, both of which orbit their Sun-like host stars at about 0.0172 and 0.01684 AU where both planets most likely lost their protoatmospheres completely (e.g., Leitzinger et al., 2011), the other super-Earths are in more distant orbital locations and have lower mean densities, which suggests a presence of substantial envelopes of light gases, such as H/He or H/H₂O.

For instance, GJ 1214b is a transiting super-Earth around an M star and has a mean density of ∼1.9 g cm⁻³, which is much lower than Earth's average density of ∼5.5 g cm⁻³. Because water has a density of about 1 g cm⁻³, the chemical composition of GJ 1214b is most likely a mixture of rocks and H₂O in liquid and gaseous form surrounded by an envelope of hydrogen (e.g., Charbonneau et al., 2009; Nettelmann et al., 2011). This interesting composition is now confirmed by several independent studies (e.g., Miller-Ricci and Fortney, 2010; Croll et al., 2011; Nettelmann et al., 2011). Ikoma and Hori (2012) studied the low-density super-Earths that populate the Kepler-11 system. The results from these authors indicate that indeed a huge amount of hydrogen may have been accumulated around these low-density super-Earths if the planetary disk dissipated slowly or the planets originated in cool environments. For explaining the observed densities of these super-Earths within a mass range between ∼ 2 and 10 M_Earth, they obtained captured hydrogen envelopes of several hundreds to thousands of Earth ocean equivalents (1 EO_H2O∼1.37×10²⁴ g→1 EO_H∼1.5×10²³ g) if a ∼1% mass ratio of atmosphere to the total mass is assumed and up to several 10⁴ EO_H equivalents if a 10% ratio is assumed. Lammer et al. (2013) investigated the blow-off criteria of hydrogen-rich super-Earths, including GJ 1214b, and showed that GJ 1214b would experience hydrogen loss rates on the order of about 9.7×10³² s⁻¹, which are too weak to remove its assumed hydrogen envelope or ocean during the planet's remaining lifetime. It was also shown that, for super-Earths such as GJ 1214b in orbits close to their host star, Roche lobe effects enhance the escape and related mass loss rates of ∼3 times (Lammer et al., 2013). For planets with orbit locations at larger distances similar to the test planets in this study, Roche lobe effects can be neglected. Furthermore, hot super-Earths such as GJ 1214b experience higher temperatures at the mesopause-homopause level, compared to the studied test planets at 1 AU. This will also result in lower thermal escape rates at hydrogen-dominated planets at larger distances. Thus, planets such as GJ 1214b or the low-density super-Earths of the Kepler-11 system indicate that there may be many planets out there that most likely had a different origin than Venus or Earth. These planets are representative of objects that are surrounded by a hydrogen-rich envelope of remaining gas from the protoplanetary nebula or dissociated H₂O vapor.

From our brief discussion, we conclude that terrestrial planetary atmospheres most likely initially originate with more or less dense hydrogen-dominated gaseous envelopes. Because present Venus or Earth is not surrounded by dense hydrogen envelopes and hydrogen is a light atom, it is generally assumed that these protoatmospheres escaped easily from early rocky Solar System planets, so that tectonic-related secondary outgassed atmospheres dominated the evolutionary process during later stages. However, since the discovered low-density super-Earths indicate that conditions may not favor the escape of early protoatmospheres from some planets, it is important to understand whether this is related to the planet's gravity, the stellar soft X-ray and extreme ultraviolet radiation (XUV) flux, the stellar wind plasma flow, or if it depends on the planet's growth time and related initial amount of captured or outgassed volatiles.

Therefore, the aim of the present study was to investigate how such hydrogen-rich atmospheres respond to the high XUV flux of a young and active host star if Earth-type planets orbit inside the habitable zone at 1 AU or corresponding distances of the main sequence stars. We modeled the structure of a hydrogen-dominated upper atmosphere and the related XUV-driven thermal escape rate from a planet with the size and mass of Earth (R_pl=1 R_Earth, M_pl=1 M_Earth) and from a super-Earth with a size R_pl=2 R_Earth and a mass M_pl=10 M_Earth when their thermospheres are exposed to XUV fluxes from 1 to 100 times that of today's Sun, which is the range typical for planets inside the habitable zone (e.g., Ribas et al., 2005; Scalo et al., 2007; Claire et al., 2012). We describe in Section 2 the applied hydrodynamic upper atmosphere model. In Section 3, we present density, velocity, and temperature profiles as well as expected thermal atmospheric escape rates as a function of the stellar XUV flux. We compare our results with previous studies related to a hydrogen-rich early Earth and discuss in Section 4 the implications of our results to habitability aspects of terrestrial planets in general. Finally, this work presents the basic input parameters for part II of these investigations (Kislyakova et al., 2013), in which we study the stellar wind plasma interaction with a hydrogen-rich planetary upper atmosphere within the habitable zone of an M type host star, the formation of extended planetary hydrogen coronae, and the stellar wind plasma-induced nonthermal ion pickup escape process from similar hydrogen-rich test planets.

2. XUV-Induced Hydrodynamic Upper Atmospheric Expansion and Escape

Depending on the host star's energy input into the upper atmosphere of a planet, the atmospheric escape processes can be divided into two categories: thermal and nonthermal escape.

Thermal atmospheric escape can again be divided into the classical Jeans escape and hydrodynamic outflow, which can result in blow-off (e.g., Chamberlain, 1963; Öpik, 1963; Bauer and Lammer, 2004; Tian et al., 2008a, 2008b; Lammer, 2013). In the first case, atmospheric particles that populate the high-energy tail of a Maxwellian distribution at the exobase level, where the mean free path l equals the scale height H

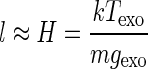(1)

are lost from the exosphere of a planet. Here, k is the Boltzmann constant, T_exo and g_exo the temperature and gravitational acceleration at the exobase level r_exo, and m is the mass of the main atmospheric species at the exobase distance. Under high XUV flux conditions, the thermosphere starts to expand dynamically accompanied by adiabatic cooling so that the exobase location reaches several planetary radii (Watson et al., 1981; Tian et al., 2005b; Lammer et al., 2008, 2012; Tian et al., 2008a, 2008b; Lammer, 2013).

In this second case, which is relevant for the present work, the upper atmosphere is not hydrostatic anymore, so that hydrodynamic blow-off at the exobase level may occur, which results in the evaporation of the whole exosphere. However, under certain XUV conditions and planetary parameters the thermosphere can hydrodynamically expand; but all atoms may not reach escape velocity, in which case the loss results in a strong Jeans-type escape rate from an expanded exobase level.

2.1. Atomic versus molecular hydrogen: breakdown of H₂ molecules

Because we are interested in how the nebula-based hydrogen envelopes or outgassed steam atmospheres respond to and escape thermally due to the XUV flux of a young star, it is important to know whether hydrogen dominates the upper atmosphere in molecular or atomic form. In a previous study related to the dynamics of escaping hydrogen-dominated upper atmospheres from early Earth, Tian et al. (2005b) assumed that H₂ is the main thermospheric species in the upper atmosphere. However, that study focused on ∼5 times higher XUV fluxes compared to today's solar value. Such values are expected for the young Sun at about ∼3.5 Gyr ago when life originated on Earth. According to astrophysical data gathered by multiwavelength satellite observations of solar proxies with younger ages, it is known that the XUV flux of a young Sun-like star is saturated at ∼100 times the average present-time solar value during the first 100 Myr (e.g., Güdel et al., 1997; Ribas et al., 2005; Güdel, 2007) and decreases during the first billion years following a power law to a value that yields XUV flux enhancement values ∼10 times higher than those of today's Sun ∼4 Gyr ago and ∼5 times ∼3.5 Gyr ago (Ribas et al., 2005; Claire et al., 2012). For lower-mass M type stars, this saturation can last longer before the flux of the short-wavelength radiation decreases according to the similar power law as for the Sun-like stars (Scalo et al., 2007). Therefore, at the time when the nebula-based or outgassed hydrogen-rich protoatmospheres originate, the XUV flux values are much higher than applied in the study of early Earth by Tian et al. (2005b). From photochemical studies of hydrogen-dominated “hot Jupiter” thermospheres, it is known that H₂ molecules break down to H atoms if the XUV flux is >25 times that of the present solar value (Yelle, 2004; Koskinen et al., 2010). The H₂ molecules will be dissociated via reaction

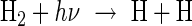(2)

In the case where is a vibrationally excited hydrogen molecule, H atoms can also be produced via reaction

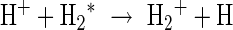(3)

For atmospheric temperatures ≥2000 K, H₂ molecules break thermally into atomic hydrogen (Koskinen et al., 2010)

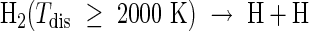(4)

For steam atmospheres, it can be expected that atomic hydrogen dominates the upper atmosphere because the XUV flux dissociates the water molecules in H and OH. Even on present Earth with present-time XUV radiation, the H₂ molecule number density is one order of magnitude lower compared to that of H atoms above 100 km altitude. According to Koskinen et al. (2010), for XUV fluxes >25 times that of the present Sun, a stronger decrease of H₂ in hydrogen-dominated thermospheres and, therefore, a higher amount of H atoms in the upper atmosphere can be expected. Model simulations of hot Jupiters that are exposed to 450 times higher XUV fluxes compared to that of the present solar value indicate that a large fraction of the neutral hydrogen atoms are ionized at distances ≥3 R_pl (Yelle, 2004; García Muñoz, 2007; Koskinen et al., 2013). In the case of the hydrogen-rich gas giant HD 209458b, this distance corresponds to ∼30 Earth radii. Because our test planets are exposed to more than 4.5 times lower XUV flux values compared to that of typical hot Jupiters, it is justified to assume that neutral H atoms dominate over the ionized component up to the exobase level.

Additional possibilities for the production of atomic hydrogen are photochemical reactions between CH₄ and other hydrocarbons below and close to the homopause level (e.g., Atreya, 1986, 1999). Because of these processes, atomic hydrogen populates the upper atmosphere above the homopause level of Jupiter, Saturn, Uranus, and Neptune. Since the studied hydrogen-rich test planets are much hotter compared to the hydrogen-rich Solar System gas and ice giants, are exposed to higher photon fluxes, and may also contain hydrocarbons in their lower atmospheres (Kuchner, 2003), we assume in this particular investigation that atomic hydrogen is most likely the dominant species above the homopause levels of the studied planets.

However, for low XUV fluxes or if it is assumed that IR-cooling molecules such as , CO₂, and so on may decrease the thermospheric temperature and, hence, decrease thermal dissociation of H₂, it is instructive to compare the modeled upper atmosphere structure calculated for pure atomic and molecular hydrogen atmospheres. Therefore, for comparing the difference of a H₂-dominated thermosphere with a H-dominated one, we model both scenarios.

Note that Lammer et al. (2011) and Lammer (2013) showed that, if an outgassed H₂O steam atmosphere results in very high surface pressures such as several ∼ 10³ to 10⁴ bar (Elkins-Tanton, 2011), then the planet might not lose the remaining oxygen in a similar amount compared to the hydrogen. This result agrees with the suggestion of Kasting (1995) and Chassefière (1996a, 1996b), which is that there may be planets, depending on their size, mass, orbital distance, as well as their host star's XUV flux evolution, that could accumulate huge amounts of abiotic oxygen. In this study, we focus only on the escape of hydrogen, either envelopes that remained from captured nebula gas or the part that is lost from a steam atmosphere. In the future, we also plan to study the accompanied thermal and nonthermal escape of oxygen from steam atmospheres.

2.2. Model description and numerical scheme

For studying the response of hydrogen-dominated upper atmospheres of an Earth-like and a super-Earth-type planet within the habitable zone to the stellar XUV flux, we apply a time-dependent 1-D hydrodynamic upper atmosphere model that solves the system of the fluid equations for mass, momentum, and energy conservation in spherical coordinates

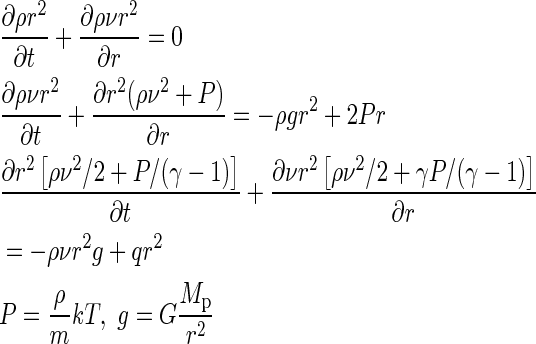(5)

Here, r is the radial distance from the center of the planet; ρ, v, P, T are the mass density, radial velocity, pressure, and temperature, respectively; m is the mass of the particle; k is the Boltzmann constant; G is the gravitational constant; and γ is the polytropic index that corresponds to the ratio of the specific heats. For computational convenience, we introduce the following normalizations

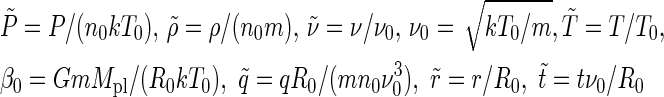(6)

Here, R₀ is the altitude of the lower thermosphere (homopause), which is close to the planetary radius R_pl; n₀, v₀, T₀ are the density, thermal velocity, and temperature at the lower boundary that corresponds to the lower part of the thermosphere around the homopause distance. β₀ is the Jeans escape parameter at the lower boundary. This parameter is ≤1.5 at the corresponding exobase level, if an upper atmosphere reaches blow-off conditions. After introducing these normalizations, we obtain the following system of equations

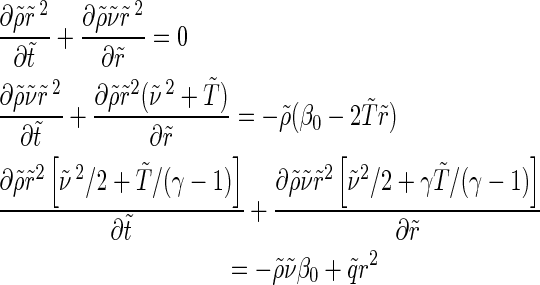(7)

The thermal conductivity can be estimated as c_vV_th/σ. Therefore, the energy flux per one steradian (sr⁻¹) due to the thermal conduction can be estimated as

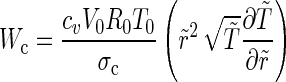(8)

where σ_c is the collisional cross section. Here, the Boltzmann constant is included in the specific heat capacity c_v. If this energy flux W_c is compared with the total energy flux given by the energy-limited formula (see Eq. 29), we find that the ratio of these energies is quite small

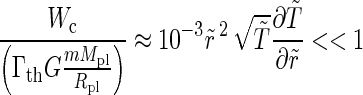(9)

Figure 2 compares the thermal energy flux due to hydrodynamic flow per one steradian of the atmospheric particles with the convective thermal energy flux obtained by our hydrodynamic solutions for a H-dominated upper atmosphere of an Earth-like planet that is exposed to a 10 times higher XUV flux compared to that of today's Sun. The two sudden decreases in the convective thermal energy flux can be explained because it is proportional to the gradient of the temperature; therefore, it decreases in the vicinity of the temperature maximum and minimum. At the first point we have a strong temperature maximum, and at the second point we have a shallow temperature minimum.

FIG. 2.

Comparison of the thermal energy flux per one steradian of the hydrodynamic flow with the thermal energy flux related only to the thermal conductivity. The dashed line shows the thermal energy flux due to hydrodynamic flow of the atmospheric particles. The dot-dashed line shows the thermal energy flux due to the thermal conductivity, which is proportional to the gradient of the temperature.

Therefore, it can be concluded that the influence of the thermal conduction on the atmospheric escape is expected to be rather small so that we can neglect the thermal conduction term in the energy equation in the corresponding Eq. 7. For the description of this numerical scheme, we rewrite our system of equations in vector form

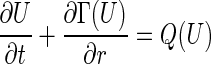(10)

with

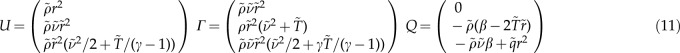
and apply the finite difference numerical scheme of MacCormack (1969), which is of the second order of accuracy. In computational fluid dynamics, this method is widely used as a discretization scheme for the numerical solution of hyperbolic partial differential equations. After we introduce the MacCormack scheme, we obtain the following equations

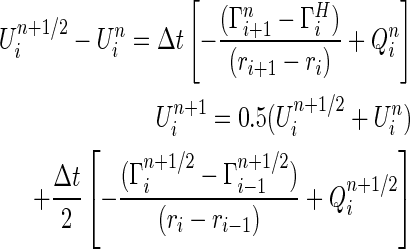(12)

Here, index i numerates grid points along the radial direction, and n is the number of a time step. We use a non-uniform grid: r_i=(r_max)^i/n. The grid size is an increasing function of the radial distance r.

Similar to Tian et al. (2005b), we assume that the lower boundary is fixed at the base of the thermosphere, which corresponds to an altitude distance of ∼100 km. At the lower boundary, we set constant values for density and temperature and a “free” condition for velocity

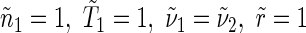(13)

The upper boundary is taken at about 20 R_pl, but the results of our hydrodynamic model are considered as accurate only up to the exobase level, which separates the collision-dominated thermosphere from the collisionless exosphere, because above this distance hydrodynamics is not valid. At the upper boundary, we set free boundary conditions for the velocity, density, and temperature

(14)

As an initial condition for density, we assume the Boltzmann distribution

(15)

The initial temperature is assumed to be constant, T=T₀. For the velocity we introduce the initial flow

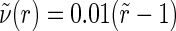(16)

It is worth noting that the final steady-state solution does not depend on the initial conditions. For tests of our numerical code, we compare the calculated velocity profile with the analytical solution of Parker (1958). This comparison is shown in Fig. 3 for a thermal escape parameter β₀ of 5.

FIG. 3.

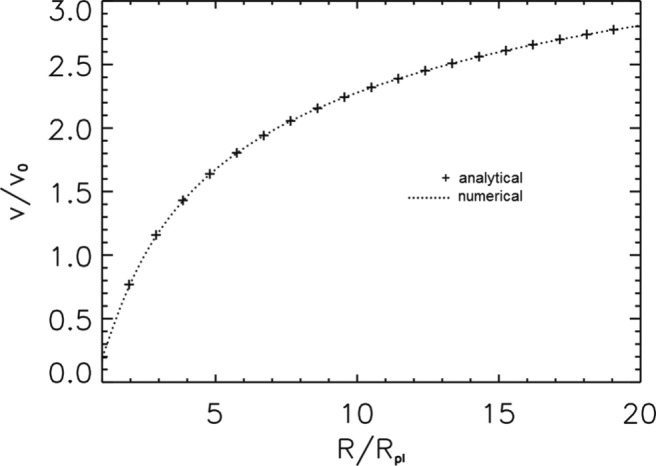
Velocity profile obtained by our code in comparison with the analytical solution of Parker (1958): The solid curve is the numerical solution; the + marks the points corresponding to the analytical solution of Parker for a Jeans escape parameter β₀=5.

2.3. Energy absorption and heating function

The applied energy absorption model and its geometry, which is used for the establishment of a functional dependence between the XUV volume heating rate q(r, θ) and the distance r, is illustrated in Fig. 4.

FIG. 4.

Illustration of the geometrical situation corresponding to our XUV flux absorption model.

The stellar XUV flux outside the planet is illustrated in Fig. 4 by the arrows. The incoming XUV flux decreases due to absorption in the thermosphere, which results in dissociation and ionization and, hence, in heating of the upper atmosphere. The equation for the XUV flux transfer can then be written as

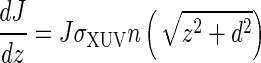(17)

where σ_XUV is the XUV absorption cross section, and J is the XUV flux in units of erg cm⁻² s⁻¹. By integrating Eq. 17 along z, we find

(18)

where J₀ is the XUV flux at the planet's orbit but outside the atmosphere. In spherical coordinates, Eq. 18 can be written as

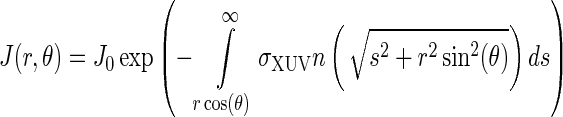(19)

The XUV volume heating rate q(r, θ) is determined by the following equation:

(20)

In the case where θ=0, Eqs. 19 and 20 are similar to those used by Murray-Clay et al. (2009). Here, η is the heating efficiency that defines the percentage of incoming XUV energy that is transferred locally into heating of the gas. Equation 20 can be applied everywhere besides the shadow zone shown in Fig. 4. By averaging the XUV volume heating rate over the planet's dayside, we find

(21)

Finally, we obtain the normalized XUV volume heating rate in the following form:

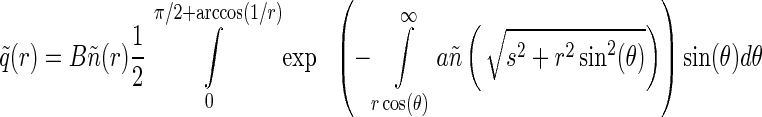(22)

with the coefficient

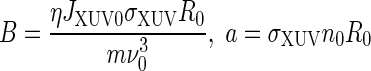(23)

In the present parameter study, we use the integrated XUV flux and do not consider a wavelength dependence of the incoming stellar XUV radiation. For understanding the effect of the spectral dependence on the volume heating rate, the model will be extended in this direction for future studies. By integrating Eq. 22 over the whole domain, we obtain the total energy absorption in normalized units, which is proportional to the incoming stellar XUV flux. The appropriate coefficient B is chosen in order to satisfy Eq. 22 for a given value of J_XUV0. The photoabsorption cross section σ_XUV is ∼5×10⁻¹⁸ cm² and ∼3×10⁻¹⁸ cm² for H atoms and H₂ molecules, respectively. These values are in agreement with experimental and theoretical data of Bates (1963), Cook and Metzger (1964), and Beynon and Cairns (1965). However, Eq. 22 is rather complex, so we introduce the following approximation:

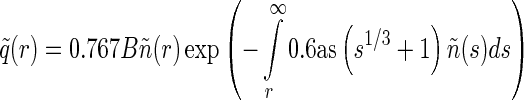(24)

which is more convenient and less time-consuming for the numerical calculations. Figure 5 shows the heating rate normalized to its maximum value q_max, which can be written as

(25)

FIG. 5.

Heating rate as a function of the radial distance in the case of an XUV flux that is 20 times larger than that of today's Sun. The dotted curve is related to Eq. 20, and the dashed curve corresponds to the less complex analytical expression given by Eq. 24.

compared to the function given in Eq. 24. Figure 5 shows that both expressions yield nearly similar results, and Eq. 24 shows a negligible difference from the curve, which results from Eq. 20. Therefore, we apply the less complex formula given by Eq. 24 for the numerical calculations of the hydrodynamic outflow regimes of the hydrogen-rich terrestrial test planets.

Apart from the expansion-related adiabatic cooling of the thermosphere, possible IR-cooling molecules such as CO₂ or may also modify the upper atmosphere structure and the related thermal escape rates. Because it is not known how many IR-cooling species may be available in hydrogen-rich protoatmospheres, we investigate their possible effect on thermospheric cooling by introducing different heating efficiency values. Photochemical models indicate that the heating efficiency η lies for hydrogen-rich atmospheres of hot Jupiters within the range of ∼ 35–60% (Yelle, 2004; Lammer et al., 2009; Koskinen et al., 2013) but may be lower if more IR-cooling molecules that are more stable and abundant in not-so-extreme radiation environments are present in the lower thermosphere.

Because the presence of minor species or IR-cooling molecules in hydrogen-rich protoatmospheres of terrestrial exoplanets is unknown and a detailed photochemical study of hydrogen-rich protoatmospheres of terrestrial planets is beyond the scope of this work, we examine here a possible influence of IR-cooling molecules in H- and H₂-dominated upper atmospheres by applying two η values, a lower value of 15% and a higher one of 40%, which agrees with the calculations of Koskinen et al. (2013) for the hydrogen-rich gas giant HD 209458b.

2.4. Initial conditions and input parameters

Tian et al. (2005b) modeled a hydrogen-rich upper atmosphere of early Earth for solar XUV flux vales that were thought to be true for the Archean era (XUV ∼5 times the present solar value). In the present parameter study, we assumed similar initial input parameters for the hydrogen density (n₀=5×10¹² cm⁻³) and “skin” or equilibrium temperature (T₀=250 K) and the adiabatic index γ=5/3 at the homopause level.

In our calculations, we assume that the upper atmosphere of an Earth-like planet (R_pl=1 R_Earth and M_pl=1 M_Earth) and of a super-Earth (R_pl=2 R_Earth and M_pl=10 M_Earth) are located within the habitable zone at 1 AU of a Sun-like G star or a corresponding orbital distance within K and M star habitable zones and are exposed to XUV flux values in a range between 1 and 100 times that of today's Sun. According to astrophysical observations of young solar proxies, it can be expected that these flux values cover the whole XUV flux range for planets orbiting inside the habitable zone (e.g., Ribas et al., 2005; Güdel, 2007; Scalo et al., 2007; Claire et al., 2012) of their host stars. The chosen lower boundary number density n₀ of 5×10¹² cm⁻³ corresponds to an extremely high H₂O mixing ratio f_H2O at the mesopause or atmospheric cold trap of ∼0.5 but lies also close to the value of Neptune's homopause hydrogen density of ∼10¹³ cm⁻³, which is a remnant of nebula-accumulated gas (e.g., Atreya, 1999). Kasting and Pollack (1983) showed that greenhouse effects in a lower atmosphere can raise the H₂O mixing ratio f_H2O to values that are ≥5×10⁻⁴ near the cold trap so that hydrogen that originates from the dissociation of H₂O molecules will dominate the whole upper atmosphere. Because we did not investigate the hydrogen sources of our upper atmosphere in detail, which can originate from the dissociation of hydrogen-containing volatiles but also from remaining nebula gas, we did not assume different hydrogen mixing ratios in this particular study. However, we note that lower hydrogen content calculations are very important for defining the inner boundary of the habitable zone.

Greenhouse effects near the surface could be related to remnants of nebula-based hydrogen envelopes, the available content of greenhouse gases (CO₂, CH₄, etc.) near the surface, or impacts (e.g., Ikoma and Genda, 2006; Pierrehumbert and Gaidos, 2011; Kopparapu et al., 2013).

The number density n₀ at the base of the thermosphere can never be arbitrarily increased or decreased as much as by an order of magnitude from its real atmospheric value. In fact, the density n₀ is a conservative value and cannot change much even if the surface pressure on a planet varies during its lifetime by many orders of magnitude. The reason for this is that the value of n₀ is strictly determined by the XUV absorption optical depth of the thermosphere above its base level, r₀. Because of this, the base of the thermosphere is conventionally defined as a level r₀ in the upper atmosphere where the bulk of the incident solar XUV radiation averaged over λ in the XUV absorption range, Δλ_XUV, and over zenith angles χ from 0 to π/2 is completely absorbed by the above-lying layers of the atmosphere

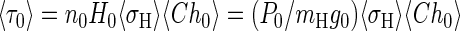(26)

where 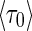is the optical depth of the thermosphere averaged over the XUV wavelength range Δλ_XUV and solar zenith angle χ at which the bulk of the solar XUV radiation is completely absorbed, 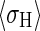is the absorption cross section of H averaged over Δλ_XUV, and H₀ and 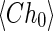are the scale height and a Chapman function at the base r₀. The atmospheric pressure P₀ at the thermosphere base r₀ for any dense atomic hydrogen-dominated atmosphere with a surface pressure P_s≥P₀ should then be a constant value, which is defined by the following equation:

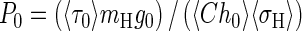(27)

Because of the perfect gas law P=nkT, the base number density n₀ is inversely proportional to the base temperature T₀ so that the variation of the number density at the base of the thermosphere (and the density itself) will always have a limited range of values. These values are determined only by the variation of a skin temperature of a planet, to which the base temperature T₀ is usually quite close. In a denser atmosphere, the base of the thermosphere will simply rise to a higher altitude where the base pressure P₀ retains the same constant value as in a less dense atmosphere.

3. Results

By assuming the previously discussed atmospheric input parameters for the two hydrogen-rich test planets, we modeled for both the volume heating rates, the upper atmosphere structures up to the exobase levels, the exobase temperatures, and finally the thermal escape rates for solar XUV flux values, which are similar to that of the present solar value in 1 AU and for 5, 10, 50, and 100 times higher fluxes compared to that of today's Sun.

3.1. Upper atmosphere heating, expansion, and structure

In the following section, we present results related to the heating of the upper atmosphere, its expansion, and related escape rates for the hydrogen-rich Earth-like planet and the super-Earth that are exposed by stellar XUV fluxes between 1 and 100 times that of today's Sun.

Table 1 shows the exobase temperature T_exo, exobase distance R_exo, and the distance of the transonic point R_s in planetary radii R_pl of the Earth-like planet for a thermosphere that is dominated by hydrogen atoms and molecules. The heating efficiency η is taken to be 15% and 40% for the H-dominated upper atmosphere, which is exposed to various stellar XUV flux values normalized to that of the present solar value in 1 AU. For the H₂-dominated upper atmosphere, the lower value η=15% is chosen.

Table 1.

Comparison of the Exobase Temperature T_exo, Exobase Distance R_exo, and the Distance of the Transonic Point R_s in Planetary Radii R_pl for an Atomic (Heating Efficiency η=15% and 40%) Molecular Hydrogen Thermosphere (Heating Efficiency η=15%) of an Earth-like Planet, Which is Exposed to Various Stellar XUV Flux Values Normalized to That of the Present Solar Value at 1 AU

Earth-like: H atoms [η=15%]	1 XUV	5 XUV	10 XUV	50 XUV	100 XUV
Texo [K]	∼243	∼358	∼485	∼1390	∼2310
Rexo/Rpl	∼7.5	∼9.5	∼10.5	∼16	∼19
Rs/Rpl	∼20	∼16	∼12	∼7.5	∼6.5
Earth-like: H atoms [η=40%]	1 XUV	5 XUV	10 XUV	50 XUV	100 XUV
Texo [K]	∼288	∼575	∼900	∼2950	∼4875
Rexo/Rpl	∼8.5	∼10.5	∼12	∼18.5	∼21.5
Rs/Rpl	∼19	∼11	∼9	∼6	∼5
Earth-like: H2 molecules [η=15%]	1 XUV	5 XUV	10 XUV	50 XUV	100 XUV
Texo [K]	∼463	∼525	∼625	∼1225	∼1875
Rexo/Rpl	∼5.7	∼7	∼7.7	∼11	∼12.5
Rs/Rpl	∼21	∼20	∼15	∼9	∼7

It can be seen that the exobase level for a molecular hydrogen–dominated upper atmosphere expands less if compared to a thermosphere that is dominated by atomic hydrogen, while the exobase temperature for the less-expanded H₂-dominated thermosphere is hotter. The reason for this behavior is that the lighter H atoms experience stronger adiabatic cooling compared to the H₂ molecules. For a higher η of 40%, the exobase level expands farther outward from the planetary surface, and the exobase temperature T_exo becomes hotter compared to the 15% cases. Table 2 shows the similar parameters and modeled results for the more massive and larger super-Earth. It can be seen that the adiabatic cooling and the related expansion of the upper atmosphere is weaker compared to the Earth-like test planet so that T_exo remains hotter. Only for high XUV flux values >50 times that of today's Sun is the XUV heating stronger compared to the adiabatic cooling so that the T_exo of the Earth-like test planet is higher than that of the super-Earth. It can also be seen in Table 2 that T_exo for the “forced” H₂-dominated thermosphere with XUV fluxes ≥50 times compared to that of the present solar value are higher than the dissociation temperature of H₂ molecules. In these cases, dissociated hydrogen atoms would expand the exobase level farther outward so that it may lie between ∼8–11 and ∼10–13 R_pl. For the Earth-like H-dominated planet and a heating efficiency η of 40%, 2000 K is reached for XUV flux values, which are ≥30 times the present solar value, and for the 100 XUV flux value the thermosphere is hotter when compared to the H-dominated more massive super-Earth.

Table 2.

Comparison of the Exobase Temperature T_exo, Exobase Distance R_exo, and the Distance of the Transonic Point R_s in Planetary Radii R_pl for an Atomic (Heating Efficiency η=15% and 40%) and Molecular Hydrogen Thermosphere (Heating Efficiency η=15%) of an Earth-like Planet, Which is Exposed to Various Stellar XUV Flux Values Normalized to That of the Present Solar Value

Super-Earth: H atoms [η=15%]	1 XUV	5 XUV	10 XUV	50 XUV	100 XUV
Texo [K]	∼100	∼625	∼1025	∼1575	∼2075
Rexo/Rpl	∼3.5	∼6.5	∼8.5	∼11	∼13
Rs/Rpl	∼20	∼19	∼18	∼15	∼11
Super-Earth-like: H atoms [η=40%]	1 XUV	5 XUV	10 XUV	50 XUV	100 XUV
Texo [K]	∼500	∼1000	∼1250	∼2625	∼4050
Rexo/Rpl	∼7	∼9	∼10	∼13.7	∼18.5
Rs/Rpl	∼19	∼18	∼17	∼11	∼10
Super-Earth-like: H2 molecules [η=15%]	1 XUV	5 XUV	10 XUV	50 XUV	100 XUV
Rexo/Rpl	∼5	∼6	∼6.5	∼8	∼10
Texo [K]	∼795	∼1130	∼1560	∼2210*	∼2910*
Rs/Rpl	∼22	∼21	∼20	∼19	∼17

^*T_exo values which are ≥2000 K corresponding to the thermal dissociation temperature T_dis of H₂ molecules (see Eq. 4).

The main reason for this unexpected behavior is the following: If an Earth-like planet with its lower gravity is exposed to high XUV fluxes, the number density of the upper atmosphere decreases much slower; and because the XUV volume heating rate is proportional to the atmospheric density, the energy is absorbed over a wider range compared to the more massive super-Earth. Therefore, the XUV heating overcomes the adiabatic cooling and yields for a higher exobase temperature for the lower-mass Earth-like planet. It can be seen from both tables that for high XUV fluxes the exobase levels can also expand to distances that are ≥10 R_pl. In such cases, it can be expected that the super-Earth produces a large exosphere or atomic hydrogen corona that is most likely not protected by an intrinsic magnetosphere; thus the exospheric neutral particles will interact with the stellar wind such that they may be lost by nonthermal ion escape processes such as ion pickup (Kislyakova et al., 2013).

Table 1 shows that, for the H-rich Earth-like planet with a heating efficiency η=15%, the sonic transition point R_s lies about one Earth radius above the exobase level and below for higher XUV cases. For a similar planet with a higher η value of 40%, R_s is reached at the exobase level for XUV flux value >7 times that of today's solar value. For an Earth-like planet with an upper atmosphere that is dominated by H₂ molecules, blow-off is reached for XUV fluxes that are higher than 40 times that of the present Sun. In the case of the hydrogen-rich super-Earth, it can be seen that R_s lies above the exobase level for a heating efficiency η=15% at 100 XUV and for values which are higher than ∼40 times that of the solar value for a higher η of 40%. In the case of a H₂-dominated thermosphere, the super-Earth does not reach blow-off conditions with η=15% within the studied XUV range.

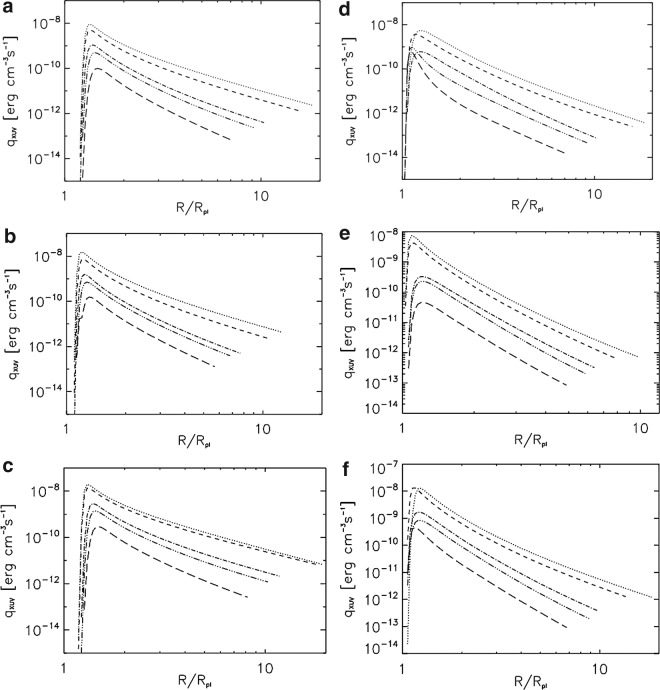
Figure 6 compares the volume heating rate profiles up to the exobase level for 1 XUV (long dashed lines), 5 XUV (dashed-dotted-dotted lines), 10 XUV (dashed-dotted lines), 50 XUV (dashed lines), and 100 XUV (dotted lines) cases between the Earth-like planet (Fig. 5a–5c) and the more massive super-Earth (Fig. 6d–6f). Figures 6a and 6d correspond to profiles of H- and Figs. 6b and 6e to H₂-dominated upper atmospheres and heating efficiencies of 15%. Figures 6c and 6f belong to H-dominated upper atmospheres with 40% heating efficiency.

FIG. 6.

Volume heating rate profiles up to the exobase level for 1 (long dashed lines), 5 (dashed-dotted-dotted lines), 10 (dashed-dotted lines), 50 (dashed lines), and 100 XUV (dotted lines) cases between an Earth-like planet [(a) H atoms, η=15%; (b) H₂ atoms, η=15%; (c) H atoms, η=40%] and the more massive super-Earth [(d) H atoms, η=15%; (e) H₂ atoms, η=15%; (f) H atoms, η=40%].

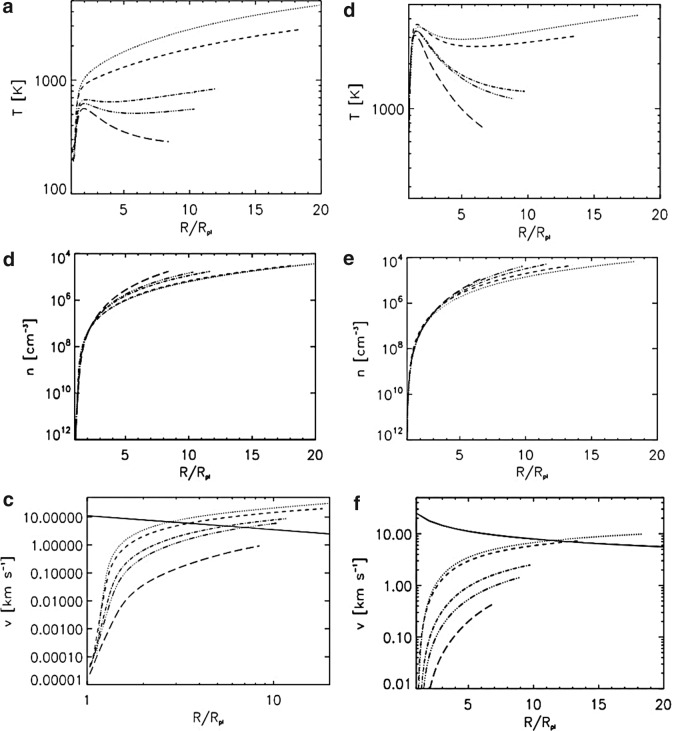
Figure 7 shows the corresponding temperature, density, and velocity structures of the hydrogen-rich non-hydrostatic expanded upper atmosphere from the lower thermosphere up to the exobase level for a heating efficiency η=15% and XUV fluxes, which are 1, 5, 50, and 100 times higher compared to today's solar value for both H-rich test planets.

FIG. 7.

Temperature, density, and velocity profiles up to the exobase level for 1 (long dashed lines), 5 (dashed-dotted-dotted lines), 10 (dashed-dotted lines), 50 (dashed lines), and 100 XUV (dotted lines) flux cases [Earth-like planet (a–c), H atoms, η=15%; super-Earth (d–f), H atoms, η=15%]. The solid lines in (c) and (f) correspond to the escape velocities of the two test planets.

Figure 8 shows the same profiles and upper atmosphere structure for a heating efficiency η=15% and XUV fluxes, which are 1, 5, 50, and 100 times higher compared to today's solar value for both test planets under the assumption that their upper atmospheres are dominated by H₂ molecules. It can be seen that the upper atmosphere does not expand to the same large distances compared to a thermosphere, which would be dominated by atomic hydrogen. The H₂-dominated super-Earth does not reach blow-off conditions, while the Earth-like planet can reach blow-off more or less for XUV flux values that are ≥100 times that of the present Sun.

FIG. 8.

Corresponding temperature, density, and velocity structure of non-hydrostatic expanded upper atmospheres, which are dominated by H₂ molecules from the lower thermosphere up to the exobase level for a heating efficiency η=15% and XUV fluxes that are 1, 5, 50, and 100 times higher compared to today's solar value for both test planets.

However, it should be noted that the modeled profiles correspond to two extreme cases. In reality, it can be expected that there are many upper atmospheres that will consist of H/H₂ mixtures that would produce profiles where the exobase levels will lie somewhere in between those shown in Fig. 7 and Fig. 8. For higher XUV fluxes, the profiles shown in Fig. 7 may be closer to real scenarios, while the profiles shown in Fig. 8 will more likely represent results of lower XUV flux values.

Figure 9 shows the corresponding temperature, density, and velocity structures of the non-hydrostatic expanded upper atmosphere, which is dominated by atomic hydrogen from the lower thermosphere up to the exobase level for a higher heating efficiency value η=40. Compared to Fig. 7, which corresponds to similar parameters but a lower heating efficiency, it can be seen that the exobase levels expand farther out and the Earth-like planet would also experience blow-off for XUV flux values that are ≥5 times that of today's solar value.

FIG. 9.

Temperature, density, and velocity profiles up to the exobase level for 1 (long dashed lines), 5 (dashed-dotted-dotted lines), 10 (dashed-dotted lines), 50 (dashed lines), and 100 XUV (dotted lines) flux cases [Earth-like planet (a–c), H atoms, η=15%; super-Earth (d–f), H atoms, η=40%]. The solid lines in (c) and (f) correspond to the escape velocities of the two test planets.

3.2. Thermal escape rates and atmospheric loss

By analyzing the modeled upper atmosphere response to the stellar XUV flux, we found that, depending on the planet's density, its skin temperature, the possible presence of IR-cooling molecules, and the host star's XUV flux, the upper atmosphere experiences either high Jeans or hydrodynamic blow-off escape at high XUV fluxes, which will influence its evolution during the planet's lifetime. If the dynamically expanding bulk atmosphere does not reach the escape velocity at the exobase level and classical blow-off conditions cannot be achieved, we assume a strong Jeans-type escape. Because the classical Jeans formula is based on the isotropic Maxwellian distribution function, in such a case we have the radial velocity of the outward-flowing bulk atmosphere at the exobase, and thus a distribution function that is not isotropic. Then we calculate the Jeans-type escape rate by using a shifted Maxwellian function that is modified by the radial velocity, obtained from the hydrodynamic code (e.g., Volkov et al., 2011).

Johnson, Volkov, and Erwin (2013) applied a hybrid upper atmosphere model, which combines hydrodynamic and kinetic descriptions for the study of the influence of different boundary conditions at the upper edge of the calculation domain of non-hydrostatic dynamically expanding thermospheres. They considered three cases: (1) matching of fluid and kinetic models, (2) a transonic assumption similar to ours, and (3) a Jeans boundary condition. For all these cases, in spite of differences in the resulting atmospheric profiles, the total escape rates were found to be rather close to each other. This means that the escape rate is not sensitive to the type of boundary condition close to the exobase level.

If we assume a heating efficiency of 15%, we obtain for the 1 XUV case a H₂ outflow rate L_th ∼3.0×10²⁹ s⁻¹ and ∼6×10²⁹ s⁻¹ for atomic hydrogen, which is more or less in agreement with those calculated by Tian et al. (2005a; see Table 2 and Fig. 7, case B). By integrating the XUV heating rate over the computational domain and by taking a product of the escape rate and the potential energy of a particle, we obtain the total energy deposition rate by the following equation

(28)

where M_pl is the planetary mass, m the mass of the atmospheric species, k the Boltzmann constant, and G the gravitational constant. The values obtained in Eq. 28 are somewhat larger than that of Tian et al. (2005a). However, it is important to note that our calculated values shown in Eq. 28 correspond exactly to the energy necessary to move the bulk atmosphere to infinity. Because atomic hydrogen will dominate over H₂ molecules at the exobase level, atomic hydrogen will be the main species that will escape from the planets. In the case where a thermosphere is dominated by molecular hydrogen, the expansion of the thermosphere is less effective, and the escape rate of atomic hydrogen at the exobase level would most likely be lower compared to our values.

Figure 4 illustrates that the irradiated part of the planet is larger than a hemisphere but does not cover the whole sphere. Therefore, we estimate the average hydrogen outflow rate to be between that for the dayside area (2π) and that for the isotropic loss (4π), which for the irradiated part of the planet corresponds to an average geometric factor of ∼3π.

Table 3 compares the thermal H escape rates from the two test planets as a function of the assumed heating efficiency η and XUV fluxes that are normalized to the present mean solar value (1 XUV) in 1 AU. For reasons of comparison, we also included for η of 15% the H₂ escape rates. By analyzing the results of our study according to the occurrence of hydrodynamic blow-off, we found that a hydrogen-rich, Earth-type planet even with a low η of 15% experiences blow-off for XUV flux values that are ≥10 times that of the present Sun if the planet's skin temperature at the base of the thermosphere is about 250 K. It can also be seen in Table 3 that H₂-dominated super-Earths have much lower escape rates compared to similar planets that are dominated by atomic hydrogen. Furthermore, the H₂-dominated super-Earth test planet experiences blow-off only near or above an XUV flux that is ≥100 times higher compared to that of today's solar value in 1 AU. As can be seen in Figs. 7 and 9, in the case of the more massive super-Earth and η=40%, blow-off starts for the XUV fluxes higher than 30 and for η of 15% for the XUV flux values that are ≥100 times that of today's Sun.

Table 3.

Calculated Thermal Escape Rates in Average over an Effective Area of 3π in Units of s⁻¹ for H Atoms and Heating Efficiencies η of 15% and 40% for Various Stellar XUV Flux Values Normalized to the XUV Flux at 1 AU (Habitable Zone) of the Present Sun for an H-Rich Earth Analog Planet and a Super-Earth with a Size of 2 R_Earth and a Mass of 10 M_Earth

	1 XUV	5 XUV	10 XUV	50 XUV	100 XUV
H-rich Earth
Lth [s−1]: η=15%	∼5.7×1029	∼3×1030	∼5×1030	∼1.9×1031	∼3.2×1031
LthJeans-mod [s−1]	∼1.5×1029	∼1.8×1030
LthJeans [s−1]	∼7.8×1028	∼5×1029
Lth [s−1]: η=40%	∼1.4×1030	∼7×1030	∼1.2×1031	∼4×1031	∼6×1031
H2-rich Earth
Lth [s−1]: η=15%	∼3×1029	∼1.3×1030	∼2.0×1030	∼1.0×1031	∼2.0×1031
LthJeans-mod [s−1]	∼1.3×1029	∼5.7×1029
LthJeans [s−1]	∼5×1028	∼2.0×1029
H-rich super-Earth
Lth [s−1]: η=15%	∼2.5×1029	∼1.8×1030	∼4×1030	∼1×1031	∼2.1×1031
LthJeans-mod [s−1]	∼1.4×1028	∼2×1029	∼7×1029	∼9.2×1030
LthJeans [s−1]	∼1.3×1028	∼1.4×1028	∼4×1029	∼2×1029
Lth [s−1]: η=40%	∼1.8×1030	∼5.7×1030	∼1×1031	∼2.5×1031	∼4.8×1031
LthJeans-mod [s−1]	∼1.5×1029	∼1.6×1030	∼5×1030
LthJeans [s−1]	∼1.4×1029	∼6×1029	∼1.3×1030
H2-rich super-Earth
Lth [s−1]: η=15%	∼1.0×1029	∼6×1029	∼2.0×1030	∼7.0×1030	∼1.3×1021
LthJeans-mod [s−1]	∼8×1027	∼3.3×1028	∼1.6×1029	∼1.3×1030
LthJeans [s−1]	∼7×1027	∼2.3×1028	∼9.0×1028	∼4.0×1029

If no blow-off conditions are reached, the most realistic escape rates correspond to L_thJeans-mod.

In the case where the upper atmosphere experiences no blow-off conditions at the exobase level, the more realistic thermal hydrogen escape rate corresponds to high thermal escape rates (L_thJeans-mod) and is based on the previously explained modified shifted Maxwellian distribution function. In such cases, the escape rates are slightly lower compared to the hydrodynamic outflow rate at the exobase, which also contains ballistic particles. However, if we use the classical Jeans formula by neglecting the rapidly upward-flowing atmosphere, which results in the shifted Maxwellian distribution explained above, the result is an underestimate of the escape rate to a great extent. This underestimation depends on the stellar XUV flux, the heating efficiency η, and the mean density of the planet. If blow-off is not reached, the more realistic escape rate in Table 3 is L_thJeans-mod. Compared to the total hydrodynamic outflow rates, however, this more realistic escape rate is lower but higher compared to the traditional Jeans loss, which corresponds to Maxwellian distribution. It can be seen in Table 3 that the more massive super-Earth also experiences for higher XUV fluxes the strong Jeans-type escape L_thJeans-mod compared to the Earth-like planet.

If we assume that our H-rich test planets orbit within the habitable zone of a Sun-like G star, where the XUV flux decreases over time from a factor 100 to the present solar value (1 XUV) during ∼4.5 Gyr [according to the power-law relationship given by Ribas et al. (2005)], we can estimate the total thermal atmospheric hydrogen loss during that time period. Depending on the assumed heating efficiency, we obtain an estimated thermal loss of hydrogen during 4.5 Gyr for the Earth analog planet between ∼5 and 11 Earth ocean (EO_H) amounts (η=15–40%) of hydrogen and for the super-Earth between ∼1.5 and 6.7 EO_H (η=15–40%).

We note that the total hydrogen loss estimations over the lifetime of the two test planets correspond to the XUV flux behavior of Sun-like G type stars. As was discussed in detail by Scalo et al. (2007), lower-mass M type stars remain longer on the XUV saturation phase compared to G or F stars before the flux decreases. Therefore, if the same hydrogen-rich test planets would be located within the orbits of M dwarfs, their upper atmospheres would be longer exposed to higher XUV flux values. For that reason, such planets would lose more hydrogen during their lifetime. From the obtained loss rates, it can be seen that a terrestrial planet within the orbit of the habitable zone of a Sun-like G type star, which does not lose the majority of its hydrogen-rich protoatmospheres during the earliest evolutionary stages, may continue to keep these atmospheric conditions indefinitely.

To get an idea of what the maximum possible hydrogen escape could be, we examine briefly the conditions under which the losses may come close to the energy-limited escape rate. After the discovery of hydrogen-rich hot Jupiters, many authors (e.g., Lammer et al., 2003, 2009, 2012; Vidal-Madjar et al., 2003; Lecavelier des Etangs et al., 2004; Lecavelier des Etangs, 2007; Baraffe et al., 2004; Erkaev et al., 2007; Hubbard et al., 2007a, 2007b; Davis and Wheatley 2009; Leitzinger et al., 2011; Owen and Jackson, 2012) applied the so-called energy-limited (η=100%) escape formula (e.g., Watson et al., 1981; Hunten et al., 1987; Lammer et al., 2003), which can be expressed as

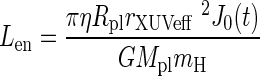(29)

Here J₀(t) is the XUV flux (λ=0.1–120 nm) outside the atmosphere as a function of stellar age at the planet's orbit location, G is the gravitational constant, ρ_pl is the planet's mean density, and r_XUVeff is the effective radius of the XUV energy absorption (Erkaev et al., 2013). This equation can be used to estimate the upper limit of the escape rate if a planetary atmosphere experiences hydrodynamic blow-off at its exobase level (e.g., Watson et al., 1981; Zahnle et al., 1988). For comparing the possible maximum loss rate estimates from Eq. 29 with the modeled thermal escape rates shown in Table 3, we present the estimates for the energy-limited escape rate with η=100% and for the two lower η values 40% and 15% in Table 4. Because Eq. 29 yields the escape rate over the whole sphere (4π), we calculated the escape rates in Table 3 over a more realistic effective area related to 3π the escape rates given in Table 4, which have been corrected by a factor of ¾.

Table 4.

Maximum Possible Atomic Hydrogen Escape Rates Estimated with the Energy-Limited Escape Formula of Eq. 29 as a Function of Heating Efficiency η and Stellar XUV Flux Values Normalized to the XUV Flux at 1 AU (Habitable Zone) of the Present Sun for an H-Rich Earth Analog Planet and a Super-Earth with a Size of 2 R_Earth and a Mass of 10 M_Earth

	1 XUV	5 XUV	10 XUV	50 XUV	100 XUV
H-rich Earth
Len [s−1]: η=15%	∼6.4×1029	∼3.2×1030	∼6.4×1030	∼3.2×1031	∼6.4×1031
Len [s−1]: η=40%	∼1.7×1030	∼8.5×1030	∼1.7×1031	∼8.5×1031	∼1.7×1032
Len [s−1]: η=100%	∼4.3×1030	∼2.1×1031	∼4.3×1031	∼2.1×1032	∼4.3×1032
H-rich super-Earth
Len [s−1]: η=15%	∼5.1×1029	∼2.5×1030	∼5.1×1030	∼2.5×1031	∼5.1×1031
Len [s−1]: η=40%	∼1.3×1030	∼6.5×1030	∼1.4×1031	∼6.5×1031	∼1.4×1032
Len [s−1]: η=100%	∼3.4×1030	∼1.7×1031	∼3.4×1031	∼1.7×1032	∼3.4×1032

If we compare the estimated escape rates from the energy-limited formula with those calculated by the hydrodynamic upper atmosphere model, we see that the energy-limited approach (η=100% in Eq. 29) can overestimate the atmospheric escape rates, especially for lower XUV fluxes and heating efficiencies. The overestimation can be huge, especially if the upper atmosphere does not reach blow-off conditions. If we compare, for example, the escape rate from a hydrogen-rich super-Earth for the 1 and 10 XUV cases with a heating efficiency η=15%, taking into account the modified Jeans escape rate L_thJeans-mod (Table 3: η=15%) with the corresponding escape rates L_en (Table 3: η=15%) estimated from Eq. 29, we obtain overestimation factors of the order of ∼36 and ∼7 times. If Eq. 29 was not modified by a realistic heating efficiency (η=15%), we would obtain an overestimation for η=100% compared to the L_thJeans-mod (Table 3: η=15%) of the two mentioned cases of about ∼243 and ∼49 times. If we compare the super-Earth results of Eq. 29 for an η=15% with that of the hydrodynamic model for 100 XUV and a similar η, we would see an overestimation of ∼2.4 times. So, our results indicate that the energy-limited formula must be very carefully used, even if introducing a less than 100% heating efficiency, Thus, Eq. 29 may only be applied in a very restricted parameter space. This was also pointed out by Lammer et al. (2013).

The main reason for the differences is that the right effective XUV absorption radius r_XUVeff must be known so that the energy-limited formula that is modified by an accurate heating efficiency also yields accurate results. On the other hand, without hydrodynamic simulations in association with the modeling of the stellar XUV absorption, the right values are not obtained. Therefore, if this formula is applied for XUV-exposed low-mass planets, including Earth-like bodies, the equation yields no accurate results if r_XUVeff=R_pl is assumed.

For more massive planets such as hot Jupiters, Eq. 29 with the assumption that r_XUVeff=R_pl yields escape rates that are not so different in comparison to hydrodynamic model results. The reason is that the large gravity of a hot Jupiter prevents the extreme expansion of the thermosphere compared to planets of lower mass and size so that the energy deposition is distributed closer to the planet's visual radius where the assumption r_XUVeff=R_pl provides accurate results. For instance, in the case of the well-studied hydrogen-rich hot gas giant HD 209458b with a skin temperature T₀ ∼ 1350 K and a XUV flux ∼453 times higher compared to that of today's solar value, Eq. 29 leads to a thermal mass loss rate in the order of a few ∼10¹⁰ g s⁻¹ (e.g., Erkaev et al., 2007; Lammer et al., 2009), which is comparable to models solving similar hydrodynamic equations of mass, momentum, and energy conservation as in the present study (e.g., Yelle, 2004; Tian et al., 2005a; García Muñoz, 2007; Penz et al., 2008; Volkov et al., 2011; Koskinen et al., 2013).

Finally, we note that hydrogen-rich planets that are not in the blow-off stage may experience high atmospheric loss rates by nonthermal processes such as stellar wind-induced ion pickup. To understand how efficient this nonthermal escape process could be, we used our modeled thermal escape rates as input parameters in an accompanying article by Kislyakova et al. (2013), who applied a coupled Direct Simulation Monte Carlo stellar wind exosphere interaction model to the upper atmosphere results of the present study.

4. Conclusions

We studied the thermal atmospheric escape of atomic and molecular hydrogen from hydrogen-rich protoatmospheres of an Earth-like planet and a more massive super-Earth with R_pl=2 R_Earth and M_pl=10 M_Earth within the habitable zone of a solar-type G star by applying a 1-D hydrodynamic upper atmosphere model that solves the equations of mass, momentum, and energy conservation. Our results indicate that hydrogen-rich terrestrial exoplanets experience XUV-heated and hydrodynamically expanding non-hydrostatic upper atmospheric conditions during most of their lifetimes. We have found that, depending on the assumed stellar XUV flux values, heating efficiencies, and resulting XUV volume heating rates, hydrogen-rich terrestrial planets expand their exobase level to distances from a few R_pl up to more than 20 R_pl. These expanded upper atmospheres produce huge hydrogen coronae that are most likely not protected by intrinsic magnetospheres. Earth analog planets reach hydrodynamic blow-off escape conditions at the exobase level inside the habitable zone for XUV flux values that are >10 times that of today's solar value even for low heating efficiencies of 15%.

For a higher heating efficiency of 40%, blow-off starts at XUV fluxes that are >5 times compared to the present Sun. Our results also indicate that hydrogen-rich, more massive super-Earths may never reach atmospheric blow-off but experience high Jeans escape rates. For heating efficiencies ≥40%, hydrodynamic blow-off can also start for massive super-Earths within the habitable zones if they are exposed to stellar XUV flux values >50 times that of today's solar value. In the case that the upper atmosphere does not experience hydrodynamic blow-off, nonthermal ion escape processes will become important. The escape rate depends on the planet's gravity and its pressure-related XUV absorption distance. Only during the earliest stages in a planet's evolution when the whole protoatmosphere is much hotter (during the first 100 Myr after the system's origin) and the stellar XUV flux is in its saturation phase, which is about 100 times that of the modern Sun, the hydrogen escape rates of a terrestrial planet within the habitable zone may reach energy-limited values. After the atmosphere cools according to the host star's luminosity at the planet's orbital location, our model calculations yield total losses during 4.5 Gyr of ∼4.5–11 EO_H and ∼1.5–6.7 EO_H for the Earth-like planet and the super-Earth, respectively, by assuming an XUV flux evolution according to Eq. 1 of Ribas et al. (2005). Thus, terrestrial exoplanets in orbits inside the habitable zone, which capture too much H/He nebula gas or degas dense steam atmospheres, most likely keep their hydrogen envelopes and may become sub-Neptune-type planets or low-density super-Earths.

Acknowledgments

M. Güdel, K.G. Kislyakova, M.L. Khodachenko, and H. Lammer acknowledge support by the FWF NFN project S116 601-N16 “Pathways to Habitability: From Disks to Active Stars, Planets and Life” and the related FWF NFN subprojects S116 604-N16 “Radiation & Wind Evolution from T Tauri Phase to ZAMS and Beyond,” S116 606-N16 “Magnetospheric Electrodynamics of Exoplanets,” S116 607-N16 “Particle/Radiative Interactions with Upper Atmospheres of Planetary Bodies under Extreme Stellar Conditions.” K.G. Kislyakova, Yu.N. Kulikov, H. Lammer, and P. Odert thank also the Helmholtz Alliance project “Planetary Evolution and Life.” P. Odert and A. Hanslmeier also acknowledge support from the FWF project P22950-N16. The authors also acknowledge support from the EU FP7 project IMPEx (No. 262863) and the EUROPLANET-RI projects, JRA3/EMDAF and the Na2 science WG5. The authors thank the International Space Science Institute (ISSI) in Bern and the ISSI team “Characterizing stellar and exoplanetary environments.” N.V. Erkaev acknowledges support by the RFBR grant No 12-05-00152-a. Finally, the authors thank referee Tian Feng, from the Tsinghua University, Beijing, China, for suggestions and recommendations that helped to improve the work.

Abbreviation

XUV, soft X-ray and extreme ultraviolet radiation (λ ∼ 0.1–120 nm).