A mixed-effects model approach for estimating the distribution of usual intake of nutrients: The NCI method

Abstract

It is of interest to estimate the distribution of usual nutrient intake for a population from repeat 24-h dietary recall assessments. A mixed effects model and quantile estimation procedure, developed at the National Cancer Institute (NCI), may be used for this purpose. The model incorporates a Box–Cox parameter and covariates to estimate usual daily intake of nutrients; model parameters are estimated via quasi-Newton optimization of a likelihood approximated by the adaptive Gaussian quadrature. The parameter estimates are used in a Monte Carlo approach to generate empirical quantiles; standard errors are estimated by bootstrap. The NCI method is illustrated and compared with current estimation methods, including the individual mean and the semi-parametric method developed at the Iowa State University (ISU), using data from a random sample and computer simulations. Both the NCI and ISU methods for nutrients are superior to the distribution of individual means. For simple (no covariate) models, quantile estimates are similar between the NCI and ISU methods. The bootstrap approach used by the NCI method to estimate standard errors of quantiles appears preferable to Taylor linearization. One major advantage of the NCI method is its ability to provide estimates for subpopulations through the incorporation of covariates into the model. The NCI method may be used for estimating the distribution of usual nutrient intake for populations and subpopulations as part of a unified framework of estimation of usual intake of dietary constituents.

1. Introduction

Nutrients are components of foods, including carbohydrate, fat, protein, vitamins, and minerals. Because many nutrients are found in a wide variety of foods, most nutrients are consumed nearly every day by nearly everyone. There is interest in estimating the distribution of the usual dietary intake of nutrients for a population with regard to establishing population norms, evaluating compliance with dietary recommendations, assessing risk, and making public policy decisions [1].

Usual intake is defined as the long-run average daily intake of a dietary component by an individual. The 24-h recall (24HR) is the standard method of assessing dietary intake in surveillance studies in the U.S. [2]; other methods, such as weighed food records may also be used [3]. Within-individual variability in daily intake is generally large, due to day-to-day variation in diet and other random sources of measurement error, as compared with between-individual variability for most nutrients [4, 5]. Because 24HRs are typically interviewer-administered and collect a large amount of detailed food information that must be coded, it is often impractical to administer more than two recalls per individual, which is the minimum number required to separate within-individual from between-individual variability.

The purpose of this paper is to investigate the use of a model and a quantile estimation procedure, developed at the National Cancer Institute (NCI), for estimating the distribution of usual nutrient intake, using data from two or more 24HRs, and to compare the new estimation procedure (‘NCI method’) to standard methods. Section 2 provides a brief review of the standard methods for estimating nutrient intake. The NCI method is presented in Section 3. Section 4 presents an example comparing the NCI method to other methods using data from a random sample. Simulation studies are presented in Section 5.

2. Standard methods for estimating the distribution of usual nutrient intake

2.1. Methods for estimating the distribution of usual intake for nutrients

In dietary surveillance, it is of interest to estimate the entire distribution of usual intake for a population. Often researchers and policy makers are interested in estimating the area in the tails of the distribution to estimate levels of inadequate or excess intake. Traditionally, one 24HR or the mean of two or more 24HR observations for an individual have been considered as a representative sample of a person’s dietary intake, and the distribution of these values has been used to estimate the proportion of the population or subpopulations having intakes above or below particular dietary standards [6]. Under the assumption that 24HRs yield unbiased estimates of single-day intake, the mean of the distribution of individual means provides an unbiased estimate of mean usual intake. However, because one observation or the mean of a few observations includes a substantial amount of within-individual variability, the spread of the distribution of individual means is substantially larger than the spread of the usual intake distribution. Thus, using the empirical distribution of individual means to estimate usual intake will lead to biased estimates of other moments of the distribution except the mean. To address these limitations, alternative statistical methods have been developed for the problem of excess within-individual variability with two or more 24HRs per person. These methods, described in detail in Dodd et al. [7], separate within-from between-person variation to obtain an estimated distribution that reflects variation in usual intake. The methods are most convenient to apply when the intakes are normally distributed, but this is rarely the case in practice; intake distributions for most dietary components are skewed to the right. Therefore, the statistical methods apply a transformation to the observed intakes to achieve approximate normality, estimate the requisite parameters, and then backtransform the data to the original scale. The methods are described briefly in this section.

For dietary components consumed on an almost daily basis by nearly everyone, such as most nutrients, the distributions of 24HR observations can generally be transformed to approximate normality using power or logarithmic transformations. On the transformed scale, a measurement error model may be used to adjust for within-individual variability. Methods employing this approach for the estimation of frequently consumed nutrients are well-established [8–12]. A 1986 National Research Council (NRC) report [8] and a subsequent algorithm published by the Institute of Medicine (IOM) [12] proposed a measurement error model for the estimation of usual intake:

$$R_{ij}^{\ast }=R_i^{\ast }+e_{ij}$$

where $R_{ij}^{\ast }$ represents the transformed 24HR nutrient intake for individual i at time j, $R_i^{\ast }$ is the usual intake for the individual on the transformed scale, and the e_ij represent within-individual variation. At the population or group level, $R_i^{\ast }$ are assumed to have mean ${\mu }_r^{\ast }$ and variance ${\sigma }_r^2$; the e_ij have mean 0, variance ${\sigma }_e^2$, and are independent of usual intake. The IOM report estimated the distribution of usual intake on the transformed scale by the empirical distribution of ${\stackrel{\sim }{R}}_i^{\ast }$, a shrinkage estimator given by:

$${\stackrel{\sim }{R}}_i^{\ast }={\overline{R}}_{··}^{\ast }+\frac{{\widehat{\sigma }}_r}{\sqrt{{\widehat{\sigma }}_r^2+{\widehat{\sigma }}_e^2/m}}({\overline{R}}_{i·}^{\ast }-{\overline{R}}_{··}^{\ast })=\left(1-\frac{{\widehat{\sigma }}_r}{\sqrt{{\widehat{\sigma }}_r^2+{\widehat{\sigma }}_e^2/m}}\right){\overline{R}}_{··}^{\ast }+\frac{{\widehat{\sigma }}_r}{\sqrt{{\widehat{\sigma }}_r^2+{\widehat{\sigma }}_e^2/m}}{\overline{R}}_{i·}^{\ast },$$ (1)

where ${\overline{R}}_{i·}^{\ast }$ is the individual mean on the transformed scale, ${\overline{R}}_{··}^{\ast }$ is the group mean, and m is the number of recalls per person. This is an intuitively appealing estimator, as the adjusted values are very similar to the individual means ${\overline{R}}_{i·}^{\ast }$ when the within-individual variability ${\widehat{\sigma }}_e^2$ is small or there are a large number of replicates, but are very similar to the grand mean ${\overline{R}}_{··}^{\ast }$ when ${\widehat{\sigma }}_e^2/m$ is large. The IOM algorithm does not clearly address estimation of the distribution on the original scale, but the original NRC reference suggests applying the inverse of the initial transformation to each adjusted value, then constructing the empirical distribution of the backtransformed values.

A method developed at the ISU is an extension of the NRC method for nutrients and uses a semi-parametric transformation of the data to normality followed by a backtransformation to the original scale after adjusting for within-individual variation [9]. In contrast to the NRC method, the ISU method uses a two-stage normality transformation, fitting a grafted cubic polynomial to the normal quantile plot of the data after an initial power or logarithmic transformation. It also allows for heterogeneous within-individual variances in the transformed scale. The backtransformation to the original scale incorporates an adjustment to ensure that the mean of the estimated usual intake distribution in the original scale is essentially equal to the overall mean of the original 24HR data. The latter adjustment reflects the assumption that 24HRs are unbiased for single-day intake on the original scale. The NRC method as implemented in the IOM algorithm, which does not incorporate such an adjustment, implicitly assumes that the unbiasedness applies only on the transformed scale.

The NRC method does not provide guidance for computing standard errors of estimated quantities such as the percentiles of usual intake or the proportion of the usual intake distribution above or below some cutoff values; the ISU method as implemented in the software package C-SIDE [13] (v 1.03, ISU, Ames, IA) produces approximate standard errors based on the Taylor series linearization [13] for data arising from simple random samples, but requires alternative variance estimation techniques if data come from a complex survey.

3. The NCI method for estimating the distribution of usual intake of nutrients

3.1. Model

The NCI method [14, 15] has been proposed for use in estimating the usual intake distributions for episodically-consumed dietary components such as foods, which exhibit a large proportion of zero intakes on any given day. The centerpiece of the NCI method is a two-part model for repeated measures data with correlated random effects. As in the ISU method, the NCI method requires two or more 24HRs on at least a random subset of the population. The model separates usual intake into two parts: the probability to consume a food on a particular day, and given that the food was consumed, the amount eaten on the consumption day. However, nutrient intake may be analyzed as a special case of the two-part model, as we now describe. Because the probability of consumption of a nutrient is close to or equal to 1, only the amount part of the model is needed.

Let T_ij be the true nutrient intake for an individual i (i = 1, …, N) on day j on the original scale. The usual intake for the individual is T_i = E(T_ij|i), the conditional expectation of true single-day intakes (the E(·|i) notation symbolizes that the expectation is conditional on the ith individual). There is no gold standard for measuring nutrient intake; hence, we rely on measures of dietary intake from the 24HR, represented by R_ij. We assume that the 24HR is an unbiased instrument for the consumption day amount, i.e. E(R_ij|i)= T_i. Following the usual assumption in nutrition, as in the ISU method, we assume that the 24HR is unbiased on the original scale. However, a transformation is almost always required for 24HR nutrient data, due to skewed distributions and within-person error that is dependent on the mean intake. A simple, but flexible approach is to apply a Box–Cox transformation, which includes the logarithmic transformation as a limiting case. We define

$$R_{ij}^{\ast }=g(R_{ij},\lambda )$$

to be the Box–Cox transformation of the 24HR data, g(r,λ)= (r^λ−1)λ⁻¹. When λ= 0, the natural log transformation is used. The transformation is chosen such that, on the transformed scale, we have

$$R_{ij}^{\ast }={\mu }_i^{\ast }+e_{ij},e_{ij}~\mathrm{N}(0,{\sigma }_e^2),$$ (2)

where within-person errors e_ij are additive, uncorrelated with the individual mean ${\mu }_i^{\ast }$, and independent of each other. We may also incorporate a vector of covariates X_i that may be associated with ${\mu }_i^{\ast }$ through the model

$${\mu }_i^{\ast }={{\mathbf{X}}^{\prime }}_i\mathbf{\beta }+u_i,u_i~\mathrm{N}(0,{\sigma }_u^2).$$ (3)

Combining (2) and (3) leads to the non-linear mixed effects model for 24HR,

$$g(R_{ij},\lambda )={{\mathbf{X}}^{\prime }}_i\mathbf{\beta }+u_i+e_{ij}.$$

This model may be extended so that the variances of u_i and/or e_ij vary with the level of a specific covariate X_i as long as the covariate is categorical with only a few levels. However, for clarity of exposition, we retain the simpler form of the model here.

3.2. Model fitting

The contribution to the likelihood for the ith subject (j = 1, …,m) is

$$L_i(\lambda ,\mathbf{\beta },{\sigma }_u,{\sigma }_e;r_{i1},\dots ,r_{im})={\int }_{u_i}\prod _{j=1}^{m}g(r_{ij}\mid \lambda ,\mathbf{\beta },u_i,{\sigma }_e)f(u_i\mid {\sigma }_u)\mathrm{d}{u}_i,$$

where

$$g(r_{ij}\mid \lambda ,\mathbf{\beta },u_i,{\sigma }_e)=\frac{1}{\sqrt{2\pi {\sigma }_e^2}}{e}^{-{\left((r_{ij}^{\lambda }-1)/\lambda -{{\mathbf{X}}^{\prime }}_i\mathbf{\beta }-u_i\right)}^2/2{\sigma }_e^2}{r}_{ij}^{\lambda -1}.$$

The full likelihood for the model can be maximized using quasi-Newton optimization of a likelihood approximated by adaptive Gaussian quadrature [16]. This method is implemented in the SAS PROC NLMIXED procedure (SAS Institute, Cary, NC, Version 9.1).

3.3. Estimates of percentiles

Percentiles of the distribution of usual intake of nutrients for the population are estimated by using a Monte Carlo procedure. To generate a distribution of values that reflects the covariate pattern in the population, we use the covariate patterns of the sampled individuals, in combination with the estimates of β and the variance components ${\sigma }_u^2$ and ${\sigma }_e^2$. So that the covariate pattern is proportional to that found in the sample, first we compute X′_i β̂ for each sampled individual i. We simulate k realizations of u_l, a $\mathrm{N}(0,{\widehat{\sigma }}_u^2)$ random variable for each person to form simulated ${\mu }_l^{\ast }={{\mathbf{X}}^{\prime }}_l\widehat{\mathbf{\beta }}+u_l$, where l = 1, …,kN and X_l = X_i for l = i, …,ki. We use k = 100 simulated values per person. The distribution of the 100N values of ${\mu }_l^{\ast }$ reflects a representative sample of transformed usual intakes for the population. The Taylor series expansion may be used to approximate $T_l=E(R_l\mid X_l,u_l)=E(g^{-1}(R_l^{\ast },\lambda )\mid X_l,u_l;\mathbf{\beta })$. For the Box–Cox transformation, this backtransformation is:

$$T_l\cong g^{-1}({\mu }_l^{\ast },\lambda )+\frac{1}{2}{\sigma }_e^2\frac{{\partial }^2\{g^{-1}({\mu }_l^{\ast },\lambda )\}}{\partial {{\mu }_l^{\ast }}^2}={({\mu }_l^{\ast }\lambda +1)}^{1/\lambda }+\frac{1}{2}{\sigma }_e^2(1-\lambda ){({\mu }_l^{\ast }\lambda +1)}^{1/\lambda -2}.$$ (4)

The estimates of λ and ${\sigma }_e^2$ are used to obtain T̃_l.

When the within-person variability is much larger than the between-person variability and the data are highly skewed, the Taylor series approximation may not work well. In these cases, e.g. for vitamin A, we propose the use of the nine-point approximation used by the ISU method [9]. In this approximation, a set of nine points c_k and nine weights w_k are constructed so that the first five moments are the same for the nine-point distribution and the distribution of ${\mu }_l^{\ast }$ given X′_lβ:

$$T_l\cong \sum _{k=1}^9{w}_k{g}^{-1}({\mu }_l^{\ast }+c_k{\sigma }_e)=\sum _{k=1}^9{w}_k{(({\mu }_l^{\ast }+c_k{\sigma }_e)\lambda +1)}^{1/\lambda }.$$

Again, the estimates of λ and ${\sigma }_e^2$ are used to obtain T̄_l.

Sample quantiles computed from the representative sample of the 100N backtransformed values comprise the estimated population quantiles; the sample fractions that fall above or below a given cutoff comprise the estimates of the proportion of the population with usual intake above or below that cutoff.

4. Example

The Eating at America’s Table Study (EATS) was conducted to validate the NCI’s Diet History Questionnaire, a food frequency questionnaire (FFQ) [17]. One thousand men and women aged 20–70 years old from a nationally representative sample completed four 24HRs and the FFQ during 1997 and 1998. The 24HR was telephone-administered by trained interviewers using the U.S. Department of Agriculture’s multiple-pass methodology. Portion size estimation was aided by the use of models and measuring cups. Fours 24HRs were completed, one each season, over a one-year period. Although only the 24HR data are used in this paper, some exclusions based on the FFQ were made in the data cleaning process of the EATS data set: 35 participants were excluded from the analysis for skipping at least two pages of the questionnaire; 79 participants were excluded for reporting implausible energy intake (outside the range of 600 to 3500 kcal per day for women or 800 to 4200 kcal for men).

The model described in Section 3 was applied to the EATS data set for three nutrients, calcium, iron and vitamin A. These were chosen to represent nutrients with a variety of statistical properties. Calcium tends to be a ‘well behaved’ nutrient, with a ratio of within-person to between-person variance that is generally around 1.5, less skewness than other nutrients, and a distribution that can be transformed to approximate normality with a power transformation; vitamin A is the opposite, with a high ratio of within-person to between-person variance (in the order of 4:1), resulting in a distribution that is highly skewed, and more difficult to transform to approximate normality. The distribution of iron generally falls in-between these extremes.

4.1. Estimation of the distribution of usual intake of nutrients

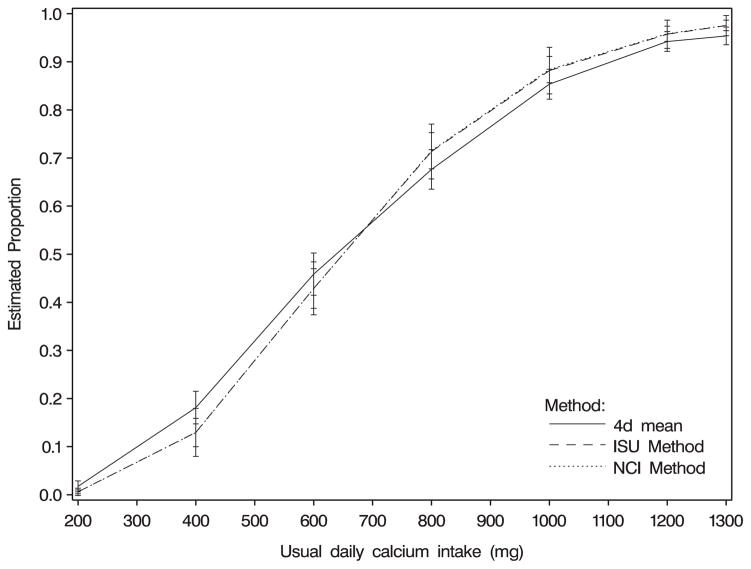
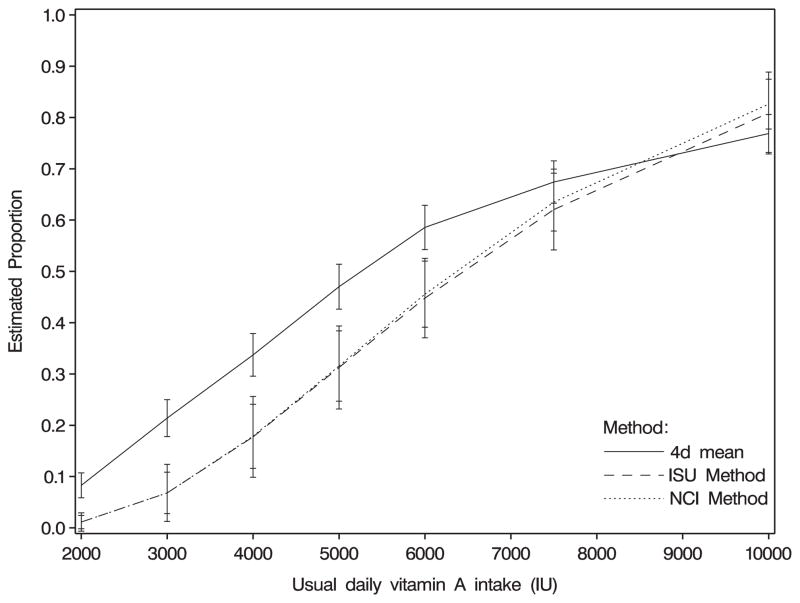
The distributions of usual intakes of calcium, iron, and vitamin A for women and men using 4 days and for only 2 days were estimated using individuals’ means, the NCI method, and the ISU method (Table I). Six recall days had 0 reported intake of vitamin A; these were set to one-half of the lowest non-zero value. Standard errors for the NCI method were estimated using a simple bootstrap with 200 replications; standard errors for the ISU method were computed based on the Taylor linearization method that does not account for variability in the choice of normality [13]. Results indicated that the NCI method was comparable to the ISU method, and both methods greatly differed from the 2d or 4d simple individual mean. The linearization-based estimated standard errors for the ISU method were larger than the bootstrap-based estimates for the NCI method. Graphical representations of the cumulative distributions for calcium and vitamin A are shown in Figures 1 and 2. Estimates for calcium and iron were computed using the Taylor series backtransformation for the NCI method; however, the nine-point approximation was used for vitamin A because we found that the Taylor series backtransformation did not work well for vitamin A in simulations (described in Section 5).

Table I.

Estimated percentages (standard error) of women (N = 519) and men (N = 446) with usual intakes of calcium, iron, and vitamin A below specified levels.

	Calcium			Iron			Vitamin A
	<400mg	<800mg	<1200mg	<12mg	<18mg	<24mg	<1200IU	<5000IU	<7500IU
Women 4d
4d mean	18.1 (1.7)	67.6 (2.1)	94.2 (1.0)	49.3 (2.2)	84.4 (1.6)	94.8 (1.0)	8.3 (1.2)	47.0 (2.2)	67.4 (2.1)
NCI 4d*	12.9 (1.5)	71.5 (1.9)	95.8 (0.8)	44.2 (2.3)	87.6 (1.6)	98.1 (0.5)	1.1 (0.6)	31.6 (3.4)	63.5 (2.8)
ISU 4d†	13.0 (2.5)	71.4 (2.9)	95.7 (1.5)	45.0 (3.0)	86.6 (2.7)	97.2 (1.2)	1.1 (0.9)	31.3 (4.1)	62.1 (4.0)
Women 2d
2d mean	20.6 (1.8)	66.9 (2.1)	90.9 (1.3)	50.7 (2.2)	82.3 (1.7)	93.4 (1.1)	15.8 (1.6)	53.0 (2.2)	68.2 (2.0)
NCI 2d	11.8 (1.9)	69.8 (2.4)	95.4 (1.2)	43.2 (2.7)	85.1 (2.3)	97.3 (1.0)	1.3 (1.2)	33.1 (5.4)	64.4 (3.7)
ISU 2d	12.1 (3.1)	69.8 (3.2)	95.3 (2.1)	44.1 (2.9)	84.7 (3.5)	96.4 (1.9)	1.2 (1.5)	32.0 (5.0)	63.4 (4.6)
Men 4d
4d mean	4.7 (1.0)	42.6 (2.3)	74.0 (2.1)	11.7 (1.5)	46.4 (2.4)	75.1 (2.0)	5.2 (1.0)	35.9 (2.3)	54.3 (2.4)
NCI 4d	2.2 (0.6)	35.8 (2.1)	76.9 (2.1)	7.4 (1.3)	40.9 (2.4)	74.4 (2.4)	1.2 (0.6)	21.6 (2.5)	46.7 (2.5)
ISU 4d	2.1 (1.1)	36.1 (3.2)	76.7 (3.2)	7.6 (2.3)	42.5 (3.2)	74.1 (3.3)	1.1 (0.8)	22.5 (3.7)	47.7 (3.5)
Men 2d
2d mean	6.7 (1.2)	44.4 (2.4)	75.3 (2.0)	14.3 (1.7)	50.2 (2.4)	69.5 (2.2)	9.6 (1.4)	42.4 (2.3)	58.7 (2.3)
NCI 2d	1.3 (0.6)	33.8 (2.9)	77.2 (2.9)	7.3 (1.6)	39.6 (2.7)	71.0 (2.5)	0.9 (0.6)	20.4 (3.5)	44.7 (3.7)
ISU 2d	1.3 (1.1)	33.8 (3.8)	76.8 (4.2)	6.9 (2.8)	39.4 (3.2)	70.4 (3.6)	0.9 (1.0)	20.7 (4.7)	44.3 (3.6)

Source of data: Eating at America’s Table Study [17].

^*Standard errors estimated by bootstrap (n = 200).

^†Standard errors estimated from default Taylor linearization.

Figure 1.

Proportions (+/−2 standard errors) of women with usual calcium intakes below 200–1300 mg per day, estimated using three methods. Data are from the Eating at America’s Table Study [17].

Figure 2.

Proportions (+/−2 standard errors) of women with usual vitamin A intakes below 2000–10 000 IU per day, estimated using three methods. Data are from the Eating at America’s Table Study [17].

4.2. Estimation of the distribution of usual intake of nutrients for subgroups

One advantage of using the NCI method is the ease of performing subgroup analysis by including the subgroup variable of interest as a covariate in the statistical model, rather than doing a stratified analysis as in the ISU method. When all of the model parameters do not vary between subgroups, this method is also more efficient. The efficiency of the modeling subgroup analysis using common variance parameters was studied; results are shown in Tables II(a) and II(b), for women and men, respectively. Models were fit: (1) assuming common variance parameters for the two age groups of interest (20–49 years and 50–70 years), (2) allowing the random effect variance parameter ( ${\sigma }_u^2$) to vary, (3) allowing the within-subject variance parameter ( ${\sigma }_e^2$) to vary, and (4) stratified by subgroup. Because these are nested models, likelihood ratio tests were used to compare each model to the base model, and a ‘best’ model was identified. For women, model (3) was best for calcium, (1) was best for iron, and (2) was best for vitamin A. For men, model (3) was best for calcium, (4) was best for iron, and (2) was best for vitamin A.

Table II.

Comparison of models for subgroup analysis: Model parameters for calcium, iron, and vitamin A for (a) women and (b) men by subgroup.^*

Nutrient	Lambda	Intercept	Age 20–49	${\sigma }_u^2$ 20–49	${\sigma }_u^2$ 50–70	${\sigma }_e^2$ 20–49	${\sigma }_e^2$ 50–70	p†	−2||‡	p-val base§
(a)
Calcium (common)	0.30 (0.03)	19.2 (2.1)	0.66 (0.34)	8.3 (2.8)	8.3 (2.8)	12.0 (3.9)	12.0 (3.9)	5	29 991.0	—
Calcium ( ${\sigma }_u^2$ varies)	0.30 (0.03)	19.2 (2.1)	0.66 (0.34)	8.2 (2.8)	8.6 (3.1)	12.0 (3.9)	12.0 (3.9)	6	29 991.0	0.80
Calcium ( ${\sigma }_e^2$ varies)	0.31 (0.03)	19.5 (2.1)	0.67 (0.34)	8.7 (2.9)	8.7 (2.9)	13.4 (4.4)	10.6 (3.5)	6	29 981.7¶	<0.01
Calcium stratified (sum)								8	29 980.5	0.01
Calcium 20–49	0.32 (0.03)	21.1 (2.7)	—	9.5 (3.7)	—	15.3 (5.9)	—	4	21 159.7	—
Calcium 50–70	0.28 (0.05)	17.0 (3.4)	—	—	6.3 (4.0)	—	7.0 (4.3)	4	8820.8	—
Iron (common)	0.11 (0.02)	2.8 (0.1)	0.03 (0.05)	0.18 (0.03)	0.18 (0.03)	0.36 (0.04)	0.36 (0.04)	5	13 323.8¶	—
Iron ( ${\sigma }_u^2$ varies)	0.11 (0.02)	2.8 (0.1)	0.03 (0.05)	0.19 (0.03)	0.16 (0.03)	0.36 (0.04)	0.36 (0.04)	6	13 323.3	0.49
Iron ( ${\sigma }_e^2$ varies)	0.11 (0.02)	2.8 (0.1)	0.03 (0.05)	0.18 (0.03)	0.18 (0.03)	0.36 (0.04)	0.35 (0.05)	6	13 323.5	0.61
Iron stratified (sum)								8	13 323.1	0.87
Iron 20–49	0.11 (0.03)	2.8 (0.1)	—	0.19 (0.03)	—	0.36 (0.05)	—	4	9379.3	—
Iron 50–70	0.10 (0.04)	2.8 (0.2)	—	—	0.16 (0.05)	—	0.35 (0.08)	4	3943.8	—
Vitamin A (common)	0.05 (0.01)	10.5 (0.6)	−0.26 (0.11)	0.6 (0.2)	0.6 (0.2)	2.4 (0.5)	2.4 (0.5)	5	40 605.8	—
Vitamin A ( ${\sigma }_u^2$ varies)	0.05 (0.01)	10.4 (0.6)	−0.26 (0.10)	0.7 (0.2)	0.3 (0.1)	2.3 (0.5)	2.3 (0.5)	6	40 600.1¶	0.02
Vitamin A ( ${\sigma }_e^2$ varies)	0.05 (0.01)	10.4 (0.6)	−0.26 (0.11)	0.6 (0.1)	0.6 (0.1)	2.4 (0.5)	2.1 (0.5)	6	40 602.1	0.05
Vitamin A stratified (sum)								8	40 597.9	0.09
Vitamin A 20–49	0.05 (0.01)	10.4 (0.7)	—	0.7 (0.2)	—	2.6 (0.6)	—	4	28 397.1	—
Vitamin A 50–70	0.03 (0.03)	9.5 (1.2)	—	—	0.3 (0.2)	—	1.5 (0.7)	4	12 200.8	—
(b)
Calcium (common)	0.24 (0.03)	16.6 (1.9)	0.71 (0.28)	4.0 (1.5)	4.0 (1.5)	6.7 (2.4)	6.7 (2.4)	5	27 015.7
Calcium ( ${\sigma }_u^2$ varies)	0.25 (0.03)	16.8 (1.9)	0.73 (0.28)	4.6 (1.8)	3.1 (1.2)	7.0 (2.5)	7.0 (2.5)	6	27 012.4	0.07
Calcium ( ${\sigma }_e^2$ varies)	0.26 (0.03)	17.6 (2.0)	0.79 (0.30)	4.8 (1.8)	4.8 (1.8)	8.7 (3.2)	6.4 (2.3)	6	27 002.9¶	<0.01
Calcium stratified (sum)								8	26 997.1	<0.01
Calcium 20–49	0.22 (0.03)	15.9 (2.1)	—	3.3 (1.5)	—	5.5 (2.3)	—	4	19 247.2	—
Calcium 50–70	0.32 (0.04)	23.2 (4.6)	—	—	9.1 (5.5)	—	14.8 (8.7)	4	7749.9	—
Iron (common)	0.06 (0.02)	3.0 (0.1)	0.13 (0.05)	0.15 (0.03)	0.15 (0.03)	0.30 (0.04)	0.30 (0.04)	5	13 007.5	—
Iron ( ${\sigma }_u^2$ varies)	0.06 (0.02)	3.0 (0.1)	0.13 (0.05)	0.16 (0.03)	0.14 (0.03)	0.30 (0.04)	0.30 (0.04)	6	13 007.2	0.55
Iron ( ${\sigma }_e^2$ varies)	0.06 (0.02)	3.1 (0.1)	0.13 (0.05)	0.15 (0.03)	0.15 (0.03)	0.32 (0.05)	0.28 (0.04)	6	13 005.2	0.12
Iron stratified (sum)								8	12 997.9¶	0.02
Iron 20–49	0.02 (0.03)	3.0 (0.1)	—	0.12 (0.03)	—	0.25 (0.04)	—	4	9300.2	—
Iron 50–70	0.15 (0.04)	3.5 (0.2)	—	—	0.24 (0.07)	—	0.46 (0.11)	4	3697.7	—
Vitamin A (common)	0.08 (0.01)	12.4 (0.8)	−0.03 (0.16)	1.5 (0.4)	1.5 (0.4)	3.7 (0.8)	3.7 (0.8)	5	35 757.1	—
Vitamin A ( ${\sigma }_u^2$ varies)	0.08 (0.01)	12.4 (0.8)	−0.03 (0.15)	1.7 (0.4)	1.0 (0.3)	3.8 (0.9)	3.8 (0.9)	6	35 752.9¶	0.04
Vitamin A ( ${\sigma }_e^2$ varies)	0.08 (0.01)	12.4 (0.8)	−0.03 (0.16)	1.5 (0.4)	1.5 (0.4)	3.8 (0.9)	3.6 (0.8)	6	35 756.5	0.44
Vitamin A stratified (sum)								8	35 751.7	0.14
Vitamin A 20–49	0.07 (0.02)	11.9 (0.9)	—	1.5 (0.4)	—	3.3 (0.9)	—	4	25 271.3	—
Vitamin A 50–70	0.10 (0.02)	13.8 (1.7)	—	—	1.5 (0.7)	—	5.3 (2.3)	4	10 480.4	—

^*Based on 4 days of data from the Eating at America’s Table Study [17].

^†Number of parameters in model.

^‡−2log likelihood.

^§p-value from the likelihood ratio test compared with model with common variance parameters (base model).

^¶ Indicates the best model based on the likelihood ratio test.

After selecting the best model and obtaining estimates of the distribution of usual intake from the NCI method, these values were compared with subgroup estimates from the ISU method and the 4-d mean (Table III). Estimates from the NCI and ISU methods were generally within one standard error of each other. Both modeling methods produced estimates significantly different than those for the 4-d mean method, except near the mean usual intake, where the NCI, ISU, and 4-d mean methods agree by construction. In most of the cases shown in Table III, the linearization-based standard errors for the ISU method were greater than those estimated by the bootstrap method, suggesting that the default standard error calculations for the ISU method may overestimate the uncertainty of its estimates. To investigate this, bootstrap standard errors were calculated from the ISU method for women 20–49 years for calcium and vitamin A. These standard errors tended to be smaller than the linearization-based ISU method estimates, suggesting that the estimated standard errors from the ISU method may be too large in the tails of the distribution. A simulation study (described below) was undertaken in part to investigate this hypothesis.

Table III.

Estimated percentages of women and men with usual intakes of calcium, iron, and vitamin A below specified levels by age group.

	n	Calcium			Iron			Vitamin A
		<400mg	<800mg	<1200mg	<12mg	<18mg	<24mg	<2000IU	<5000IU	<7500IU
Women
20–49 years	364
4d mean		16.2 (1.9)	65.4 (2.5)	93.7 (1.3)	48.1 (2.6)	82.7 (2.0)	94.5 (1.2)	9.6 (1.5)	50.8 (2.6)	67.3 (2.5)
NCI 4d*,†		11.2 (1.6)	69.0 (2.5)	95.2 (1.0)	43.5 (2.4)	86.7 (1.8)	98.0 (0.6)	5.1 (1.9)	38.7 (3.1)	63.0 (2.5)
ISU 4d‡		10.6 (2.9)	69.0 (3.5)	95.5 (1.9)	44.2 (3.5)	85.8 (3.3)	97.0 (1.5)	1.8 (1.5)	34.8 (4.6)	63.9 (4.6)
ISU 4d bs§		(1.6)	(3.4)	(1.1)				(1.6)	(5.0)	(3.2)
50–70 years	155
4d mean		22.6 (3.4)	72.9 (3.6)	95.5 (1.7)	52.3 (4.0)	88.4 (2.6)	95.5 (1.7)	5.2 (1.8)	38.1 (3.9)	67.7 (3.8)
NCI 4d		17.2 (2.7)	77.4 (3.2)	97.3 (0.9)	45.4 (4.1)	88.0 (2.4)	98.3 (0.7)	0.0 (0.1)	17.5 (6.2)	55.8 (7.2)
ISU 4d		18.9 (4.7)	76.5 (4.8)	96.4 (2.3)	46.7 (5.7)	88.5 (5.0)	97.8 (2.1)	0.1 (0.4)	20.4 (8.9)	57.1 (8.3)
Men
20–49 years	315
4d mean		4.4 (1.2)	40.0 (2.8)	70.2 (2.6)	9.5 (1.7)	43.5 (2.8)	73.3 (2.5)	5.7 (1.3)	35.6 (2.7)	53.7 (2.8)
NCI 4d		1.5 (0.5)	30.8 (2.8)	73.5 (2.6)	5.9 (1.4)	37.3 (2.9)	71.2 (3.0)	4.7 (1.6)	28.3 (2.7)	47.9 (2.3)
ISU 4d		1.7 (1.1)	32.1 (3.8)	72.5 (3.9)	6.1 (2.5)	38.4 (3.9)	70.4 (4.0)	1.5 (1.1)	24.4 (4.3)	47.7 (4.1)
50–70 years	131
4d mean		5.3 (2.0)	48.9 (4.4)	83.2 (3.3)	16.8 (3.3)	53.4 (4.4)	79.4 (3.5)	3.8 (1.7)	36.6 (4.2)	55.7 (4.4)
NCI 4d		4.0 (1.1)	46.6 (3.5)	85.3 (2.2)	11.2 (1.2)	50.9 (2.4)	83.2 (2.2)	0.2 (0.3)	16.6 (4.9)	44.9 (6.2)
ISU 4d		3.0 (2.4)	46.7 (5.6)	87.4 (5.1)	11.0 (5.0)	52.2 (5.8)	82.5 (5.8)	0.4 (0.8)	18.3 (7.4)	44.3 (7.3)

^*‘Best model’ as described in Table II chosen for subgroup (age) analysis for the NCI method.

^†Standard errors estimated by bootstrap (n = 200).

^‡Standard errors estimated from default Taylor linearization.

^§ Bootstrap standard errors for the ISU method.

5. Simulation studies

Two simulation studies were performed based on data from the EATS study; the first was based on calcium intake and the second on vitamin A intake. A goal of both studies was to compare percentile estimates. The first study also compared the accuracy of standard error estimates among the methods of interest.

5.1. Simulation based on calcium

Three hundred data sets were simulated with 500 individuals each. Data were simulated from a normal distribution based on the distribution of transformed calcium in the EATS data, and then transformed using the inverse of the Box–Cox transformation with a lambda of 0.3. Simple means were calculated at the individual level for 2 and 1000 days of intake. Truth was obtained from the percentiles of the 1000-d means for all 300 data sets combined. The ISU method and the NCI method were fit to the two days of data, and the mean of the 5th, 10th, 25th, 50th, 75th, 90th, and 95th percentiles were estimated and compared with truth and with 2-d means. The NCI method was fit using the Taylor series approximation in the backtransformation. Both the NCI method and the ISU method produced results that were very close to truth (Table IV). The mean percentiles for the 2-d means overestimated the percentage of participants in the tails, but were fairly accurate for the 50th and 75th percentiles. Table IV shows that the NCI method produced less variable estimates than the ISU method, most likely due to the latter’s use of a more complex normality transformation.

Table IV.

Selected mean percentiles (standard deviation) from simulation studies.

Estimation method	5th	10th	25th	50th	75th	90th	95th
Simulation I: Calcium (n = 300)
Truth	327	389	511	675	873	1087	1230
2d mean	233 (16)	299 (16)	443 (17)	648 (18)	914 (26)	1210 (43)	1421 (58)
ISU method	327 (23)	389 (22)	510 (19)	674 (19)	873 (28)	1084 (45)	1228 (59)
NCI method	327 (19)	389 (18)	510 (17)	674 (16)	873 (22)	1085 (35)	1227 (46)
Simulation II: Vitamin A (n = 500)
Truth	2208	2752	3974	6001	9056	13 112	16 371
2d mean	1001 (100)	1473 (111)	2702 (159)	5066 (255)	9181 (498)	15 289 (1002)	20 636 (1575)
ISU method	2471 (275)	3078 (278)	4382 (273)	6372 (279)	9108 (434)	12 391 (801)	14 814 (1143)
NCI method	2475 (273)	3082 (278)	4386 (270)	6367 (278)	9074 (428)	12 303 (779)	14 671 (1097)

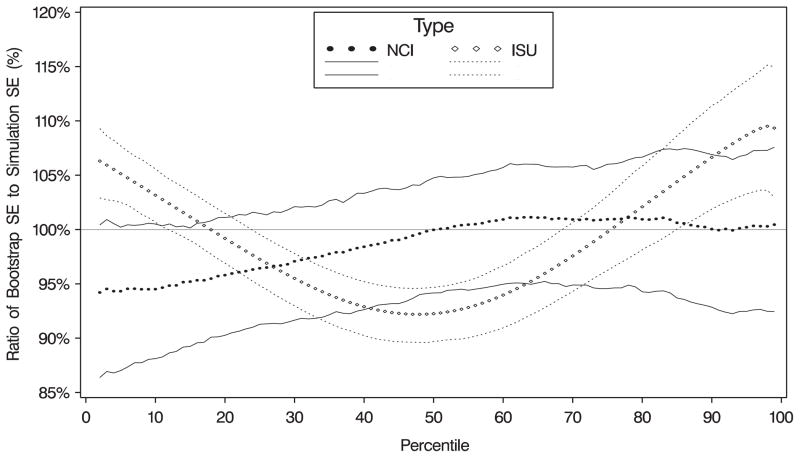
Standard errors of the percentile estimates for the NCI method were derived using the bootstrap with 100 replicates. The values obtained from these methods were compared with the standard deviations of the quantile estimates from the 300 data sets. The simulations indicated that the bootstrap produced estimates that were reasonably close to the estimated standard deviation of the percentile estimates for the simulated data sets (Figure 3). The linearization-based standard errors produced by the ISU method do not show a consistent bias—they were too large in the extreme tails and too small for percentiles near the median. This may explain the small linearization-based standard error for the percentage of women with vitamin A intake below 5000 IU in Table III.

Figure 3.

Simulation results (based on calcium) for estimating standard errors: ratio of standard errors of quantiles to simulated standard errors for two methods (n = 300 simulations). NCI= standard errors from the NCI method; ISU= standard errors (Taylor linearization) from the ISU method. Lines represent the 25th and 75th percentiles of the ratios.

5.2. Simulation results based on vitamin A

Data were simulated from the vitamin A data for women in EATS, using a gamma distribution to simulate data for the model with a log link; the intercept was 8.7, random effect variance 0.37, and scale parameter 1.26. Five hundred data sets of size 500 were simulated. Truth was estimated by 365-d means for all 250 000 simulated individuals. The ISU method and the NCI method were fit to 2 days of data; the nine-point approximation was used for the backtransformation in both methods. The 2-d mean produced mean percentile estimates that were too small for the 5th, 10th, 25th, and 50th percentiles; were close to truth for the 75th percentile; and were inflated for the 90th and 95th percentiles. Both the NCI and the ISU methods produced mean percentile estimates that were above truth for the 5th, 10th, 25th, and 50th percentiles; were close to truth for the 75th percentile; and were below truth for the 90th and 95th percentiles (Table IV).

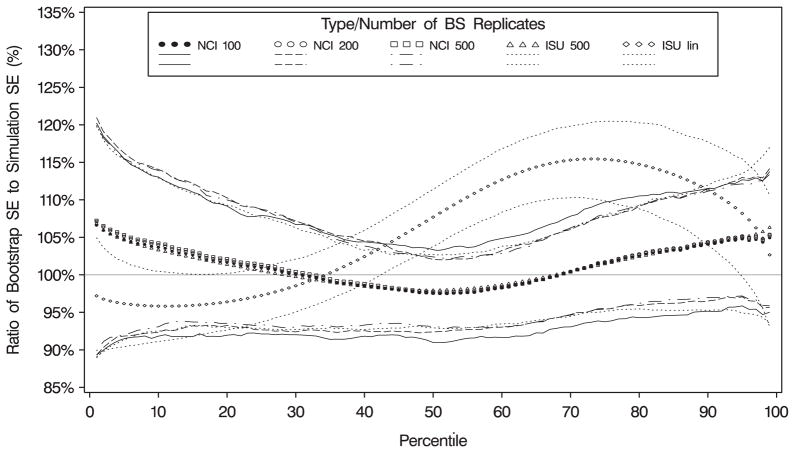
Standard errors of the percentile estimates for the NCI method were derived using the bootstrap with 100, 200, 300, 400, and 500 replicates. Standard errors of the ISU method were obtained using the default linearization method and from bootstrap samples. The values obtained from these methods were compared with the standard deviations of the quantile estimates from the 500 data sets. The simulations indicated that the bootstrap produced estimates that were reasonably close to the estimated standard deviation of the percentile estimates for the simulated data sets (Figure 4). There was not a large difference in the estimated standard errors among the different samples; in particular, there was little additional gain in using more than 200 bootstrap replicates. The ISU linearization method produced standard errors that were biased in the tails; however, bootstrap standard errors from the ISU method were similar to those obtained from the NCI method (Figure 4).

Figure 4.

Simulation results (based on vitamin A) for estimating standard errors: ratio of standard errors of quantiles to simulated standard errors for different methods (n = 500 simulations). ISU= standard errors from the ISU method where 500 indicates the bootstrap method with 500 replicates and lin indicates the Taylor linearization method; NCI= standard errors for the NCI method with 100, 200, or 500 bootstrap samples. Lines represent the 25th and 75th percentiles of the ratios.

6. Discussion

In this paper, the use of the amount part of the NCI method to obtain estimates of the distribution of usual intake of nutrients has been presented and illustrated using examples from the EATS and simulations. The NCI method performs similar to the ISU method for the example nutrients and simulations considered, and both methods are superior to the simple individual mean. Although we used 24HR as the dietary assessment instrument in these analyses, it would be possible to apply this methodology to other dietary assessment tools that meet the model assumptions, such as repeat weighed food records. Additionally, this method requires at least two dietary assessments on at least a subset of individuals. In this paper, we used four days of measurement from the EATS data because it was available and covered a full year of intake; however, we have also illustrated that the method works well with only 2 days of data.

One limitation of the use of the 24HR is the possible violation of the assumption that it is unbiased for the consumption day amount. Validation studies of the 24HR using biomarkers for total energy (doubly labeled water) and protein (urinary nitrogen) have demonstrated biases in 24HRs [18, 19]. Freedman et al. demonstrated that incorporating adjustment for protein intake can reduce the bias in 24HRs for total energy [20]. Yanetz et al. describe how to use doubly labeled water data in a validation study to adjust the estimated distribution of usual energy intake in a national survey [21]. Unfortunately, currently there are no adequate biomarkers that produce unbiased estimates of true intake for nutrients other than energy, protein, and possibly potassium. However, the requirement of unbiasedness is essential for the suggested methodology. Therefore, the degree to which the estimation of the distribution of usual intake may be biased for most nutrients is unknown. In this paper, we have assumed that the 24HR meets the assumption of unbiased estimation for the nutrients we examined; however, this is a potential limitation of this instrument for use with this model.

One advantage of using the NCI method over the ISU method is the efficiency in making estimates for subgroups, by being able to fit common parameters for the subgroups. It is apparent, however, that in some cases fitting different variance parameters by subgroup may be necessary. Even if different variance components are fit, efficiency may be gained by fitting other common parameters, as was demonstrated in the analyses of the EATS data in which a model with some common parameters was superior to a fully stratified model. It is also possible to compare nutrient intake of population subgroups, adjusted for other factors that affect intake if necessary. In addition, the ability to incorporate covariates into the model allows the analyst to make adjustments simultaneously for day of the week, season, and sequence effects, and individual covariates, using a straightforward extension of the model [22].

Standard errors of estimates were calculated for the NCI method using the bootstrap method; they were calculated for the ISU method using Taylor linearization assuming that the transformation is fixed and known [13] and a simple bootstrap in some cases. The assumption of a fixed and known transformation leads to standard errors for the ISU method that ignore the variability due to choosing the normality transformation, which may explain some of the negative bias shown over the percentiles near the median in Figure 1. However, it is important to note that the ISU method’s linearization-based standard errors are intended only for analysis of simple random samples. For analysis of complex survey data, alternative estimation methods, such as the bootstrap and balanced repeated replication methods, will most likely be equally suitable for both the NCI and ISU methods.

The NCI method and ISU method performed similarly in estimating the percent of the sample below a cutoff on the nutrients we examined. However, although this paper provides evidence for the utility of the NCI method for nutrient estimation, further investigation is warranted on the comparison of the NCI method with the ISU method. In particular, further investigation into the impact of sample size, how easily data may be transformed to meet the model assumptions, and estimation of standard errors in the tails is needed. One difference we discovered between the two methods was the type of approximation used in the backtransformation. In the simulations based on calcium, the Taylor series approximation worked well; however, for nutrients with a large amount of within-person variation this method does not appear to work as well as the nine-point approximation. Therefore, the nine-point quadrature approximation is recommended for general use.

The NCI method provides a unified framework for estimating the usual intake of dietary constituents, with application to estimating the distribution of foods [15], nutrients, and applications for relating usual intake to disease [23]. We have shown here that the NCI method, although originally devised to estimate distributions of the usual intake of episodically consumed foods [15], also provides a flexible framework for estimating the distribution of usual intake of nutrients. It thus provides a unified framework for estimating the distribution of usual intakes of any dietary component of interest.