Age-specific Prevalence and Years of Healthy Life in a System with 3 Health States

Abstract

Consider a 3-state system with one absorbing state, such as Healthy, Sick, and Dead. Over time, the prevalence of the Healthy state will approach an “equilibrium” value that is independent of the initial conditions. We derived this equilibrium prevalence (Prev:Equil) as a function of the local transition probabilities. We then used Prev:Equil to estimate the expected number of years spent in the healthy state over time. This estimate is similar to one calculated by multi-state life table methods, and has the advantage of having an associated standard error. In longitudinal data for older adults, the standard error was accurate when a valid survival table was known from other sources, or when the available data were sufficient to estimate survival accurately. Performance was better with fewer waves of data. If validated in other situations, these equilibrium estimates of prevalence and years of healthy life (YHL) and their standard errors may be useful when the goal is to compare YHL for different populations.

1. Introduction

The health of the public may be represented as a 3-state system in which persons can be Healthy, Sick or (eventually) Dead. The transition probabilities among states at different ages may be estimated from longitudinal data. The probabilities may then be used with multi-state life table (MSLT) methods to estimate the expected number of healthy and sick persons at each age, the age-specific prevalence of the Healthy state, and the expected number of person-years spent in the Healthy state. Depending on the definition of “healthy” and “sick”, this last quantity has been referred to as active life expectancy [1, 2, 3, 4] or as years of healthy life (YHL). [5, 6] Both the age-specific prevalence and YHL are standard outputs of multi-state life table calculations, but neither estimate has a convenient associated standard error. Here, we address that need. In section 2 we illustrate the nature of transition probabilities and of multi-state life table calculations. Section 3 develops a new “equilibrium” estimate of the age-specific prevalence, and its approximate variance. In section 4, we use the prevalence estimates to calculate the years of healthy life (YHL) and its standard error, and section 5 illustrates these calculations using longitudinal data from the Cardiovascular Health Study. The summary and discussion are in section 6.

2. Health States, Transition Probabilities, and Multi-state Life Table Estimates

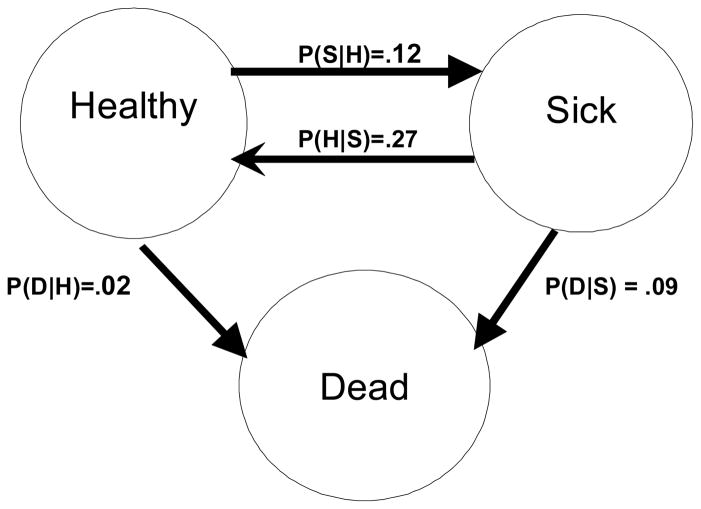
Figure 1 shows the possible transitions among three states of health. Persons who are Healthy have the probability P(H|H) of being Healthy 1 year later, P(S|H) of being Sick 1 year later, and P(D|H) of being dead 1 year later. Similarly, persons who are Sick have the associated probabilities P(H|S), P(S|S), and P(D|S). For this paper we used longitudinal data on self-reported health status, defining Healthy as being in excellent, very good, or good health, and Sick as being in fair or poor health. (Other definitions could have been used). The age-specific probabilities of transition among the three states were estimated from about 40,000 transition pairs (two measures for the same person one year apart) from the Cardiovascular Health Study, as described in section 5.1. The probabilities for age 65 are in Figure 1.

Figure 1. Transitions Among Three Health States.

(Healthy = E/VG/G; Sick = F/P)

Transition probabilities are shown for age 65, estimated from the CHS data.

The transition probabilities can be used to estimate the number of persons who will be in each state at each age, for given initial conditions. Consider an initial population of 65-year-olds of whom 80000 are healthy and 20000 are sick. The transition probabilities in Figure 1 indicate that at age 66, 12% of the healthy will have become sick (9600) and 2% will have died (1600) while 27% of the sick will have become healthy (5400). The number expected to be healthy at age 66 is thus 80000 − 9600 − 1600 +5400 = 73640. Similarly, the expected number sick and dead at age 66 will be 22400 and 3200, respectively. The number in each state at age 67 can be calculated in the same way, but using the transition probabilities for age 66 to 67, which are slightly different from those in Figure 1 because transition probabilities change with age. [7] The multi-state life table calculations (MSLT) were implemented in a spreadsheet for this paper. They could alternatively have been calculated as a product of stochastic matrices multiplied by a vector of initial conditions, or using an on-line Stata program. [8]

If this system satisfied the one-step Markov properties, knowledge of a person’s state at a particular age would completely determine his transition probabilities; that is, all persons in a given state would have the same transition probabilities. That is not the case here. For example, healthy 70-year-olds who were also healthy at age 69 have probability 0.91 of being healthy at age 71, compared to a probability of 0.61 for those who were sick at age 69 and healthy at age 70 (data not shown). However, the MSLT calculations are based on the population-average transition probability for each age-specific state, sometimes known as the cohort (rather than the individual) probability. [9] The average transition probability can be estimated from population data without knowledge of the individual probabilities. For example, suppose the Healthy state at age 70 comprised two sub-states of the same size, one with probability 0.9 of being healthy the following year and one with probability 0.7 of being healthy. The average transition probability is 0.8, and indeed, 80% are expected to remain healthy at age 71 (90% of group 1 and 70% of group 2), even though no person in the population had a transition probability of 0.8. The average transition probability is thus sufficient for this calculation. At age 71, there will no longer be two equal subgroups, but the average transition probabilities may be estimated from a random sample of 71-year-olds. The Cardiovascular Health Study (CHS) population, described in section 5, was positively selected at baseline. However, most of the data used to estimate the transition probabilities were collected long after baseline, when the sample should have been at equilibrium. The life-expectancy calculated from CHS data is reasonably close to national estimates, suggesting that the estimates are valid. [10]

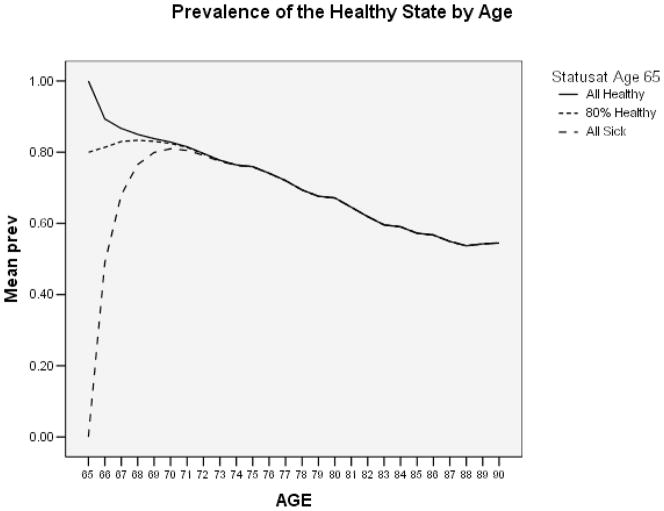
Figure 2 shows the projected prevalence of the Healthy state, calculated for a hypothetical cohort in which all of the 100,000 persons were Healthy at age 65 (solid line), for a second cohort where 80,000 were healthy and 20,000 were sick at age 65 (dotted line), and for a third cohort where the 100,000 persons were Sick at birth (dashed line). Note that after a few years the prevalence is virtually independent of the starting conditions. We will refer to this as the “equilibrium” prevalence (Prev:Equil) at a particular age.

Figure 2. MSLT estimate of Prevalence of Healthy State by Age (All Healthy, 80% Healthy, or None Healthy at 65).

3. Estimating the prevalence of the Healthy state

When longitudinal data are available, the obvious or “natural” prevalence estimate (Prev:Nat) at, say, age 75 would be to collect all persons who were age 75 at any survey wave, and calculate the proportion who were healthy. Prev:Nat is a proportion, and its variance is clear. Alternatively, the prevalence may be taken directly from the multi-state life table (Prev:MSLT), but the variance of Prev:MSLT is not known. As a third approach, we next derive an estimate of the equilibrium prevalence (Prev:Equil) seen in Figure 2, under 3 different assumptions about the transition probabilities. For notational convenience we will estimate “K”, the number who are healthy divided by the number who are sick. The prevalence is then K/(1+K).

3.1 Time-homogeneous probabilities with no deaths

In Figure 1, first assume that the probabilities are the same for everyone in the state and do not change over time (are time homogeneous), and that the probability of death is negligible or zero. This leaves 2 states, Healthy and Sick, which are persistent (reachable from either state) and aperiodic (can be reached in one or more steps), which is the definition of an “ergodic” state. When all states are ergodic, the associated Markov chain is also ergodic, and will converge to a limiting distribution independent of the initial state distribution. [11] This limiting distribution can be determined by inspection. Let H_t be the number who are Healthy at age t and S_t be the number Sick. Each year some persons move from Healthy to Sick, and some move the other way. If the number of persons in the Healthy state is initially large, then a large number will transition to the Sick state in the following year and only a few Sick persons will transition back to the Healthy state, resulting in fewer Healthy persons and more Sick persons in the following year. This transfer would continue until the limiting distribution was reached, where the expected number transitioning from Healthy to Sick (P(S|H)*H_t) was the same as the number moving from Sick to Healthy (P(H|S)*S_t). After that, the number of Sick and Healthy persons would not change. That is, no matter what the initial starting conditions, the system would eventually reach an equilibrium in which P(H|S)*S_t =P(S|H)*H_t, or

$$\text{K}={\text{H}}_{\text{t}}/{\text{S}}_{\text{t}}=\text{P}(\text{H}\mid \text{S})/\text{P}(\text{S}\mid \text{H}).$$ {1}

For the system in Figure 1 (with no deaths), K = 0.27/.12 = 2.25, and the equilibrium prevalence (Prev:Equil) is K / (1+K) = 2.25/3.25 = 0.69, or 69% Healthy.

3.2 Time-homogeneous probabilities and non-negligible death rates

Next, assume that the probabilities are time homogeneous, but the probability of dying is not negligible. Because death is an absorbing state, the Markov process is no longer ergodic, and we drop the Markov assumption from here on. As shown in Figure 2, there is a limiting ratio of the number healthy to the number sick. We solved for the constant, K, such that, for some t, $\frac{H_t}{S_t}=\frac{H_{t+1}}{S_{t+1}}=K$. As shown in Appendix 1,

$$K=\frac{H_t}{S_t}=\frac{P(H\mid H)-P(S\mid S)}{2P(S\mid H)}+\sqrt{\frac{{[P(H\mid H)-P(S\mid S)]}^2}{{[2P(S\mid H)]}^2}+\frac{P(H\mid S)}{P(S\mid H)}}.$$ {2}

That is, no matter what the initial conditions, H_t / S_t will converge to K. Equation {2} reduces to equation {1} if the probability of death is negligible. From the probabilities in Figure 1, K= 2.67; that is, after a few years to overcome any imbalance caused by the initial conditions, there will always be approximately 2.67 times as many Healthy as Sick persons, until eventually all are dead. Prev:Equil = 2.67/(1+2.67) = 0.73.

3.3 Time-inhomogeneous probabilities and non-negligible death rates

Transition probabilities do change with age, as older persons are more likely than younger persons to get sick or die. [6, 7] If, however, the probabilities do not change very rapidly, the relevant equilibrium may have been approximately reached at each age, and equation {2} may hold approximately. This seems to be the case, as shown in the first two columns of Table 1, where Prev:MSLT and Prev:Equil are very similar (this example is explained below).

Table 1.

Prevalence Estimates and Standard Errors by Age (from 1000 bootstrap samples)

	1	2	3	4	5	6	7	8
	Prevalence Estimates			Various Estimated Standard Errors
	MSLT	Equil	Nat	MSLT	Equilibrium		Natural
				Boot	Boot	Derive	Boot	Derive
69	0.845	0.845	0.822	0.016	0.016	0.016	0.008	0.009
70	0.838	0.829	0.809	0.010	0.015	0.015	0.008	0.008
71	0.820	0.797	0.800	0.009	0.016	0.016	0.008	0.008
72	0.811	0.799	0.778	0.008	0.015	0.015	0.008	0.007
73	0.786	0.754	0.760	0.008	0.015	0.015	0.007	0.007
74	0.764	0.731	0.764	0.008	0.016	0.016	0.007	0.007
75	0.766	0.768	0.751	0.008	0.014	0.014	0.008	0.008
76	0.754	0.738	0.737	0.008	0.015	0.015	0.008	0.008
77	0.739	0.720	0.721	0.008	0.016	0.016	0.009	0.009
78	0.720	0.692	0.718	0.009	0.018	0.018	0.009	0.009
79	0.714	0.707	0.712	0.009	0.017	0.017	0.010	0.010
80	0.712	0.709	0.692	0.009	0.019	0.019	0.011	0.010
81	0.696	0.676	0.656	0.011	0.021	0.020	0.012	0.011
82	0.659	0.615	0.657	0.012	0.023	0.023	0.013	0.012
83	0.653	0.647	0.632	0.013	0.023	0.022	0.014	0.013
84	0.627	0.595	0.641	0.013	0.027	0.027	0.014	0.014
85	0.641	0.658	0.645	0.014	0.027	0.028	0.016	0.015
86	0.640	0.638	0.616	0.016	0.027	0.027	0.018	0.018
87	0.610	0.581	0.594	0.018	0.033	0.033	0.021	0.020
mean	0.726	0.710	0.711	0.011	0.020	0.020	0.011	0.011

Columns 1, 2, and 3 are the age-specific prevalences, estimated as noted in the column heading. Prev:MSLT is calculated from the multi-state life table; Prev:Equil is calculated using the equilibrium ratio; Prev:Nat is the proportion of persons at each age who are healthy, combining all waves of data.

Columns 4, 5, and 7 are standard deviation of the prevalence in 1000 bootstrap samples

Column 6 is the mean s.e. calculated from Appendix 2 equations

Column 8 is mean s.e. calculated as Prev:Nat*(1−prevalence)/n

3.4 Variance of prevalence estimates

The variance of Prev:Nat is Prev:Nat*(1−Prev:Nat)/n, and the variance of Prev:MSLT is unknown. We approximated the variance of Prev:Equil by the delta method, as shown in Appendix 2.

4. Years of Healthy Life

Years of Healthy Life (YHL) is the projected number of years that a population with a specified initial distribution will spend in the healthy state. This is a standard output of MSLT calculations. A different estimate of YHL combines a national life table with cross-sectional health data, and is known as the “Sullivan Method”. [12] If the proportion of the life table cohort still alive at age t is A_t, then life expectancy = ΣA_t. (The first and last terms should be divided by 2, to agree with the trapezoidal method for estimating the area under the curve, but we omit this for simplicity). YHL is calculated as:

$$\text{YHL}=\sum {\text{A}}_{\text{t}}\ast {\text{Prev}}_{\text{t}}$$ {3}

where Prev_t is the estimated prevalence at age t. If A_t is known without error, and the prevalence estimate at one age is independent of the prevalence estimates at other ages, the estimate of YHL is merely the weighted sum of independent prevalences and its variance is

$$\text{Var}(\text{YHL})=\sum {{\text{A}}_{\text{t}}}^2\ast \text{Var}({\text{Prev}}_{\text{t}})$$ {4}

Under stationarity assumptions, the estimate of YHL is unbiased and consistent, and the variance estimator is consistent and approximately unbiased. [12]

Prevalence estimates calculated from longitudinal (rather than cross-sectional) data are likely to be correlated across ages, however, because the same person contributes data at different ages (up to 10 times in the example data). Prev:MSLT at, say, age 75 is calculated from all of the transition data up to age 75, and also depends on the initial conditions. Prev:Equil depends on the transition data from age 74 to 75. Prev:Nat depends only on the data at age 75. It seems likely that estimates of Prev:MSLT at various ages would be highly correlated, and that this would also be true for Prev:Nat. The patterns of correlations for Prev:Equil are not immediately obvious, and are explored below.

5. Example

We used longitudinal data from the Cardiovascular Health Study to compare the prevalence and the YHL estimates. We constructed 1000 bootstrap samples to help evaluate the various estimates and their standard errors.

5.1 Data

The Cardiovascular Health Study (CHS) is a population-based longitudinal study of 5,888 adults aged 65 and older at baseline, designed to identify factors related to the occurrence of coronary heart disease and stroke. [13] Subjects were recruited from a random sample of the Medicare eligibility lists in four U.S. counties. Persons not expected to be able to participate for three years, or who were institutionalized, using a wheelchair at home, or under treatment for cancer at baseline were ineligible, and about 59% of those eligible agreed to enroll. [14] Two cohorts were followed, one with 10 annual waves of data (n=5201) and the second (all African American, n=687) with 7 waves. Linear interpolation was used to impute missing data when values were known for interviews before and after the missing value. With this approach, data completeness increased from about 93 to 95 percent. At baseline the mean age was 73 years (range 65 to 100), 58% were women, and 84% were white. Data collection began in about 1990, and follow-up is virtually complete for all surviving subjects in the year 1999. There were 42,453 transition pairs (defined here as two health measures for the same person one year apart, where the person is alive in the first year) in the age range 68 to 87 years, collected from 5764 persons who were in that age range at some time during the study, or an average of 7.4 transition pairs per person. (In this age range there were at least 200 sick persons at each age, permitting reasonable estimates of the associated transition probabilities). We created 1000 bootstrap samples by resampling the 5764 persons with replacement, then creating transition pairs, then calculating transition probabilities, and finally using the probabilities to calculate various estimates of age-specific prevalence and YHL.

5.2 Prevalence estimates and their variances

The first 3 columns of Table 1 present the means (from the 1000 bootstrap samples) of the three prevalence estimates under consideration. (The initial conditions for the MSLT calculation were chosen to make Prev:MSLT = Prev:Equil at age 69). The three estimates agree well, with Prev:MSLT slightly higher than the other two estimates. Columns 4–8 are the standard errors of the prevalence estimates, both the bootstrap and the derived estimates. Among the three bootstrap estimates, the standard error of Prev:Equil (column 5) was about 1.8 times as large as the standard error of Prev:MSLT estimate (column 4) and of Prev:Nat (column 7). The derived standard error of Prev:Equil is very close to the true value (columns 5 and 6), and the derived standard error for Prev:Nat is also appropriate (columns 7 and 8). The derived standard error of Prev:Equil was thus approximately unbiased, but was nearly twice as large as the standard error of the other prevalence estimates.

5.3 Correlations of prevalence estimates over age

The variance of the YHL estimate, in equation {4}, assumes that the prevalences at each age are independent. However, they will be correlated when estimated from the longitudinal data, because the same person will contribute data at up to 9 different ages. As expected, Prev:MSLT at one age was highly positively correlated with Prev:MSLT at ages up to 9 years away, with correlations as high as 0.75 (correlation matrix not shown). The Prev:Nat correlations were also positive and substantial, with a maximum value of 0.59 (not shown). For example, the correlation between Prev:MSLT at ages 75 and 76 was 0.53, and the corresponding correlation for Prev:Nat was 0.48. Table 2 shows the sample correlation coefficients among the Prev:Equil estimates at different ages, which have an unexpected pattern. They are relatively low, die out in fewer than 9 years, and many are negative. The correlation of Prev:Equil at ages 75 and 76 is negative ( = −0.1169), and in general the prevalence estimates at ages t+1 and t−1 are negatively correlated with the prevalence estimate at t. Since the correlations are relatively small and some are negative, it is likely that the variance from equation {4} will be more appropriate for Prev:Equil than for Prev:Nat.

Table 2.

Correlations among Prev:Equil estimates at different ages (from the 1000 bootstrap samples)

	preveq69	preveq70	preveq71	preveq72	preveq73	preveq74	preveq75
preveq69	1.0000
preveq70	−0.1121*	1.0000
preveq71	0.1832*	−0.1215*	1.0000
preveq72	0.1221*	0.1130*	−0.0351	1.0000
preveq73	0.0792*	0.1070*	0.1487*	−0.0394	1.0000
preveq74	0.0794*	0.0947*	0.0833*	0.0407	−0.1237*	1.0000
preveq75	0.0168	0.1054*	0.1160*	0.1431*	0.1410*	−0.1472*	1.0000
preveq76	−0.0059	0.0564	0.0566	0.0199	0.1144*	0.0966*	−0.1169*
preveq77	−0.0006	0.0453	0.0671*	0.0223	0.1262*	0.0888*	0.1911*
preveq78	0.0485	0.0124	−0.0039	0.0644*	0.0752*	0.0207	0.0918*
preveq79	−0.0233	0.1077*	0.0494	0.0839*	0.0735*	0.0023	0.1105*
preveq80	0.0239	−0.0284	0.0211	−0.0014	−0.0109	0.0154	0.0496
preveq81	0.0177	0.0138	0.0079	0.0258	0.0089	−0.0192	0.0670*
preveq82	0.0490	−0.0097	0.0381	0.0396	−0.0412	−0.0149	−0.0365
preveq83	0.0255	−0.0003	0.0107	−0.0226	0.0493	−0.0228	0.0710*
preveq84	−0.0053	0.0375	−0.0078	0.1269*	−0.0122	−0.0403	0.0013
preveq85	0.0324	−0.0359	0.0419	0.0238	−0.0084	0.0105	0.0241
preveq86	0.0161	−0.0024	−0.0210	0.0380	0.0475	0.0090	−0.0591
preveq87	−0.0191	−0.0090	0.0514	−0.0575	0.0296	−0.0178	0.0299

	preveq76	preveq77	preveq78	preveq79	preveq80	preveq81	preveq82
preveq76	1.0000
preveq77	−0.1658*	1.0000
preveq78	0.0514	−0.0734*	1.0000
preveq79	0.0621*	0.1046*	−0.0661*	1.0000
preveq80	0.0541	0.0884*	0.0269	−0.1269*	1.0000
preveq81	0.0313	0.0192	0.2064*	0.1257*	−0.0933*	1.0000
preveq82	0.0373	0.0064	0.0030	0.1091*	0.1049*	−0.0738*	1.0000
preveq83	0.0422	−0.0285	0.0622*	0.0628*	0.0983*	0.0898*	−0.0034
preveq84	0.0004	0.0284	0.0139	0.0557	0.0488	0.0670*	0.0885*
preveq85	0.0080	0.0349	0.0110	−0.0362	0.0549	0.0690*	0.0720*
preveq86	−0.0072	0.0241	0.0051	−0.0199	0.0033	0.0555	0.0697*
preveq87	0.0288	0.0258	0.0320	−0.0261	0.1007*	−0.0121	0.1404*

	preveq83	preveq84	preveq85	preveq86	preveq87
preveq83	1.0000
preveq84	−0.1435*	1.0000
preveq85	0.0646*	−0.0588	1.0000
preveq86	−0.0014	0.0973*	−0.1116*	1.0000
preveq87	0.0224	0.0946*	0.0973*	−0.0867*	1.0000

5.4 Years of Healthy Life (YHL)

Table 3 shows the means and standard errors of different estimates of YHL from age 69 to 87. Column 1 shows the source of the life table used in the Sullivan calculations (equation {3}); column 2 shows the source of the prevalence estimate; column 3 shows how YHL was calculated; then mean YHL, the bootstrap standard error of YHL and the derived standard error and their ratio are shown. Row 1 shows the results of performing a multi-state life table calculation on each of the 1000 bootstrap samples. YHL averaged 11.013 years in the healthy state (YHL), with a bootstrap standard deviation of 0.116. Row 2, using the Sullivan method with both A_t and the prevalences taken from the life table calculated for each bootstrap sample (1000 different life tables) is identical. Row 3, which uses the single life table from the actual data, has a similar mean YHL but a lower standard error. Thus, our dataset was not large enough to justify the Sullivan method assumption that the variability of the life table was negligible.

Table 3.

Years of Healthy Life Calculations (Results from 1000 bootstrap samples)

Type of Calculation for YHL			Mean YHL	Standard Error of YHL
1	2	3	4	5	6	7
life table source	Prevalence Estimate	YHL Calculation		Boot	Sullivan	Ratio
Estimates from 10 waves of data
1-n/a (no separate life table)	MSLT	MSLT	11.013	0.116
2-CHS Boot (1000)	MSLT	Sullivan	11.013	0.116
3-CHS data	MSLT	Sullivan	11.016	0.077
4a- CHS Boot (1000)*	Natural	Sullivan	10.774	0.106	0.034	0.322
4b-CHS data	Natural	Sullivan	10.777	0.071	0.034	0.483
4c-US	Natural	Sullivan	9.980	0.064	0.031	0.481
5a-CHS Boot (1000)*	Equilibrium	Sullivan	10.779	.112	0.063	0.563
5b-CHS data	Equilibrium	Sullivan	10.782	0.077	0.063	0.818
5c-US	Equilibrium	Sullivan	9.989	0.071	0.058	0.816
Estimates from 5 waves of data
6a-CHS Boot (1000)*	Equilibrium	Sullivan	10.305	0.224	0.116	0.531
6b-CHS data	Equilibrium	Sullivan	10.541	0.121	0.119	0.983
6c-US	Equilibrium	Sullivan	9.764	0.115	.0112	0.974

^*”Boot(1000)” means that a different life table was calculated for each bootstrap sample. “CHS data” means that the same life table was used for all calculations. For lines 4c, 5c and 6c, the U.S. life table was used. Standard errors for Sullivan variance came from Table 1. Column 7 is the ratio of the Sullivan standard error to the Bootstrap standard error.

In line 4a we combined the survival from each of the 1000 bootstrap life tables with its associated values of Prev:Nat, to estimate YHL using the Sullivan method (equation {3}). Line 4b used the single life table from the available data, and line 4c used the U.S. life table. Line 5a, 5b and 5c are similar but used Prev:Equil. The bootstrap and Sullivan standard errors for YHL are in columns 5 and 6, and their ratio is in column 7. The Sullivan standard error is much too small in line 4a (only about 32% of the bootstrap standard error) and is still too small in line 4b (about 48% of bootstrap). For Prev:Equil, the standard error was 56% of the bootstrap standard error if 1000 life tables were used and 82% if a single life table was used. The YHL estimate was different when we used the U.S. life table (perhaps because the CHS participants were initially favorably selected), but the standard errors on lines 4c and 5c were comparable to those in lines 4b and 5b, and again the standard errors were underestimated as compared with the bootstrap. The standard error of YHL that used Prev:Equil was better than that using Prev:Nat, but both were biased low.

CHS had 10 waves of data collection, which is an unusually high number. In surveys with fewer waves, the correlation among the ages should attenuate sooner. For example, if we had used only a single wave of data to estimate the prevalence (Prev:Nat), there would be no correlation and equation {4} would be accurate. (If we had done this, the standard error in line 4b would be 0.185, which is considerably larger than the true (bootstrap) s.e. that used all the waves (.071). Discarding the follow-up data to eliminate correlation would thus be inefficient.) If there are only 2 waves, each person contributes a single transition and equation {4} is accurate. If there are 3 waves, all of the correlations among ages are negative, and equation {4} should be conservative. For 4 waves, there will be an approximately equal mix of positive and negative correlations, which might balance out.

To explore the effect of fewer waves of data we repeated the bootstrap calculations using only 5 waves of data, which cut the number of transition pairs approximately in half. As expected there was less correlation of the prevalence estimates among ages than in Table 2. The last 3 rows in Table 3 show the YHL results. The bootstrap standard errors on lines 6 a–c are larger than those on 5 a–c, because there were half as many transition pairs. However, as expected, the derived standard error of YHL based on Prev:Equil (line 6b) was no longer biased low; it averaged 98% of the bootstrap value. Using fewer waves of data did not improve the estimates on lines 6a (compared to line 5a), apparently because the 1000 life tables were estimated with even less precision in the smaller data set.

The bootstrap standard error for the MSLT estimate (Table 3, line 1=.116) is about the same as that for the equilibrium estimate (line 5a=.112). However, when only 5 waves were used, the standard error for the MSLT estimate was 0.303 (not shown) versus 0.224 (line 6a). This suggests that when the sample size is not large, the equilibrium estimate may be less variable than the MSLT estimate. It also suggests that it may be unwise to apply the standard error from the equilibrium estimate to the MSLT estimate, although that would be attractive.

6. Summary and Discussion

6.1 The Equilibrium estimate of the prevalence

The pseudo-equilibrium in equation {2} holds for any 3×3 stochastic matrix with one absorbing state (classified as matrix type “6–d” by Chakraborty and Rao), [15] and may be of theoretical interest in research about this type of matrix. Here, we have concentrated on its practical applications.

6.2 Age-specific prevalence

We compared three estimates of age-specific prevalence from longitudinal data. All estimates were similar, but Prev:Equil was more variable than the other two. Because Prev:Equil easily reproduces Prev:MSLT, it might be preferred to actually performing the multi-state life table calculation if the ultimate goal is to estimate age-specific prevalence. Prev:Equil has an associated variance, which Prev:MSLT does not. Because it is based on transition probabilities rather than on the sample prevalence, and is independent of initial conditions, Prev:Equil may be less biased than Prev:Nat if the data are believed to be biased (for example, in volunteer samples, which are often too healthy at baseline). However, the mean squared error of the estimate would usually be larger for Prev:Equil than for Prev:Nat. Prev:Equil might be useful in sensitivity analyses when the sample is believed to be biased.

6.3 Correlations of prevalence estimates at different ages

The negative correlation between Prev:Equil at t with that at t+1 and t−1 was not expected. This apparently occurred because persons who make transitions in a given year (say, from healthy to sick) contribute to the estimate of the transition probabilities conditional on being healthy in the first year, and to the probabilities conditional on being sick in the following year. In a younger population that had lower probabilities of transition, the correlation pattern might be different. This interesting correlation structure could benefit from further exploration.

6.4 Years of Healthy Life

The YHL estimates based on Prev:Equil and using the Sullivan method were close to the MSLT estimates. The derived standard error of YHL based on Prev:Equil was close to the bootstrap estimate when only a single life table was used (that is, when there was no variability in the life table). It should perform better, and may even be conservative (because of the negative correlations), when the number of waves of data is not large (here, 5 or fewer).

The assumption that variation in the life table is negligible is usually not verifiable. If it makes sense for the scientific question, the problem can be resolved by using national life tables. If, however, no appropriate life is available, then the life table (the A_t) must be estimated from the available data. If the data set is smaller than used here (about 5700 persons, 40,000 transition pairs, and 1800 deaths), it is likely non-conservative to assume that variability of the life table is negligible. Then it would be safest to assess the variability via bootstrap, although the estimates derived here may be useful for preliminary calculations.

6.5 Limitations

These examples used data from the Cardiovascular Health Study for a particular definition of “Healthy”, but findings are likely to be similar for other data. We have not examined a system with more than 3 states in detail, but note that the prevalence in a 6-state system also converges to be independent of the initial conditions, similar to Figure 2. [6] The surprisingly good performance of the Prev:Equil estimate relies on the probabilities changing slowly with age. It may not perform as well in situations with rapid change. The derived variance of YHL depended on the correlation among prevalence estimates at different ages being small and sometimes negative. This might not be in the case in a population that made fewer transitions. The small number of imputed transitions (2%) might have slightly affected the variability of the estimates.

6.6 Conclusion

Estimating the age-specific population prevalence directly from the transition probabilities may be useful in some situations, although in the example the resulting estimate had a larger mean square error than conventional estimates. Applying the Sullivan method to Prev:Equil yielded a good estimate of YHL without requiring calculation of the multi-state life table. When the variability of the appropriate life table was negligible, the derived standard error of the equilibrium YHL was appropriate, and could be used to compare YHL for groups of interest. These results need to be replicated with data from different populations.

Appendix 1

Derivation of K, the “equilibrium” ratio of Healthy to Sick

Let H_t, H_t+1 = the number of Healthy persons at times t and t+1.

Let S_t, S_t+1 = the number of Sick persons at times t and t+1.

If the transition probabilities are time homogeneous (do not change with age), we conjecture that the ratio of the number Healthy to the number Sick approaches a constant; that is, that there is a constant, K, such that eventually, at some time t,

$$\frac{H_t}{S_t}=\frac{H_{t+1}}{S_{t+1}}=K.$$ [a]

H_t+1 and S_t+1 can be calculated from H_t and S_t and the transition probabilities, as follows:

$${\text{H}}_{\text{t}+1}={\text{H}}_{\text{t}}\ast \text{P}(\text{H}\mid \text{H})+{\text{S}}_{\text{t}}\ast \text{P}(\text{H}\mid \text{S})$$ [b]

$${\text{S}}_{\text{t}+1}={\text{H}}_{\text{t}}\ast \text{P}(\text{S}\mid \text{H})+{\text{S}}_{\text{t}}\ast \text{P}(\text{S}\mid \text{S})$$ [c]

From equation a, H_t = K*S_t. Substituting for H_t in equations b and c yields

$${\text{H}}_{\text{t}+1}=\text{K}\ast {\text{S}}_{\text{t}}\ast \text{P}(\text{H}\mid \text{H})+{\text{S}}_{\text{t}}\ast \text{P}(\text{H}\mid \text{S})$$ [d]

$${\text{S}}_{\text{t}+1}=\text{K}\ast {\text{S}}_{\text{t}}\ast \text{P}(\text{S}\mid \text{H})+{\text{S}}_{\text{t}}\ast \text{P}(\text{S}\mid \text{S})$$ [e]

From equation a, the ratio of equation d to e = K, S_t cancels out, and

$$\frac{H_{t+1}}{S_{t+1}}=K=\frac{K\ast P(H\mid H)+P(H\mid S)}{K\ast P(S\mid H)+P(S\mid S)}$$ [f]

This yields a quadratic equation

$${\text{K}}^{2\ast }\text{P}(\text{S}\mid \text{H})+{\text{K}}^{\ast }(\text{P}(\text{S}\mid \text{S})-\text{P}(\text{H}\mid \text{H}))-\text{P}(\text{H}\mid \text{S})=0$$ [g]

Solving equation g for K yields

$$K=\frac{H_t}{S_t}=\frac{P(H\mid H)-P(S\mid S)}{2P(S\mid H)}+\sqrt{\frac{{[P(H\mid H)-P(S\mid S)]}^2}{{[2P(S\mid H)]}^2}+\frac{P(H\mid S)}{P(S\mid H)}}$$

Thus, no matter what the initial conditions, H_t/S_t will converge to K. Because the radix term is ≥ the absolute value of the first term, K ≥ 0. Using the probabilities in Figure 1, the ratio of Healthy to Sick will eventually be constant, in this case 2.67; that is, after a few years to overcome any imbalance caused by the initial conditions, there will always be approximately 2.67 times as many Healthy as Sick persons, until eventually all are dead. Prev:Equil will be 2.67/(1+2.67) = 0.73. In the special case where P(H|S) = 0 and P(H|H)>P(S|S), K is twice the first term. There is thus an equilibrium prevalence even when persons cannot return to health after illness (P(H|S)=0). If P(H|H)<P(S|S), however, that prevalence is 0.

Appendix 2

Derivation of Standard Error for Prev:Equil using the delta method

One-step transition probabilities are

Appendix Table 1.

One step transition probabilities

		Time 1
		Healthy j=1	Sick j=2	Dead j=3
Time 0	Healthy i=1	p11 .89566	p12 .09593	p13 .00841	1.0
	Sick i=2	p21 .35914	p22 .59134	p23 .04952	1.0
	Dead i=3	p31 0.000	p32 0.000	p33 1.000	1.0

where p_ij (i,j = 1,2,3) is the estimated transition probability going from state i at time 0 to state j at time 1, and π_ij = E[p_ij].

For example,

$$\begin{array}{l}\text{E}[p_{11}]={\pi }_{11}=Pr[\text{Healthy}\text{at}\text{time}1\mid \text{Healthy}\text{at}\text{time}0],\\ \text{E}[p_{22}]={\pi }_{22}=Pr[\text{Sick}\text{at}\text{time}1\mid \text{Sick}\text{at}\text{time}0],\\ \text{E}[p_{12}]={\pi }_{12}=Pr[\text{Sick}\text{at}\text{time}1\mid \text{Healthy}\text{at}\text{time}0],\\ \text{E}[p_{21}]={\pi }_{21}=Pr[\text{Healthy}\text{at}\text{time}1\mid \text{Sick}\text{at}\text{time}0].\end{array}$$

Let p = (p₁^t, p₂^t)^t be the random vector of transition probabilities from Appendix Table 1 where p_i = (p_i1, p_i2, p_i3)^t. Each p_i is an independent multinomial random variable with mean E[p_i] = π_i = (π_i1, π_i2, π_i3)^t and variance V[p_i] = Σ_i/n_i, where Σ_i = Diag[π_i] − π_i π_i^t (i=1,2). The variance matrix for p is block diagonal and can be written as

$$V[p]=\mathrm{\sum }=\left(\begin{array}{cc}{\mathrm{\sum }}_1/n_1& 0\\ 0& {\mathrm{\sum }}_2/n_2\end{array}\right).$$

For the function, f, of the random vector, p, we define f(p) as the composite function

$$f(p)=g(k(p))=k(p)/[1+k(p)],$$

where

$$k(p)=\frac{p_{11}-p_{22}}{2p_{12}}+\sqrt{{\left[\frac{p_{11}-p_{22}}{2p_{12}}\right]}^2+\frac{p_{21}}{p_{12}}},$$

we use the delta method and the multivariate Central Limit Theorem of Rao [16] to show that f(p) is asymptotically normal

$$\sqrt{n}(f(p)-f(\pi ))\stackrel{d}{\to }N[0,{(\partial f/\partial \pi )}^t\mathrm{\sum }(\partial f/\partial \pi )],$$

where $n={\sum }_{i=1}^2{n}_i$. The elements of (∂f/∂π) in the asymptotic covariance matrix, V[f(p)], are $\partial f/\partial {\pi }_{ij}=\frac{\partial g}{\partial k}\frac{\partial k}{\partial {\pi }_{ij}}=\frac{1}{{[1+k(\pi )]}^2}\frac{\partial k}{\partial {\pi }_{ij}}$, where

$$\begin{array}{l}\partial k/\partial {\pi }_{11}=\frac{1}{2{\pi }_{12}}+\frac{{\pi }_{11}-{\pi }_{22}}{4{\pi }_{12}^2\sqrt{{\left(\frac{{\pi }_{11}-{\pi }_{22}}{2{\pi }_{12}}\right)}^2+\frac{{\pi }_{21}}{{\pi }_{12}}}},\\ \partial k/\partial {\pi }_{12}=-\left[\frac{{({\pi }_{11}-{\pi }_{22})}^2}{2{{\pi }_{12}}^3}+\frac{{\pi }_{21}}{{\pi }_{12}^2}\right]/\left[2\sqrt{{\left(\frac{{\pi }_{11}-{\pi }_{22}}{2{\pi }_{12}}\right)}^2+\frac{{\pi }_{21}}{{\pi }_{12}}}\right]-\frac{{\pi }_{11}-{\pi }_{22}}{2{\pi }_{12}^2},\\ \partial k/\partial x_{21}=1/\left[2{\pi }_{12}\sqrt{{\left(\frac{{\pi }_{11}-{\pi }_{22}}{2{\pi }_{12}}\right)}^2+\frac{{\pi }_{21}}{{\pi }_{12}}}\right],\\ \partial k/\partial {\pi }_{22}=-\partial k/\partial {\pi }_{11}.\end{array}$$

The remaining elements of (∂f/∂π) are zero, respectively. Because V[p] is block diagonal, the variance V[f(p)] simplifies to

$$\begin{array}{l}v[f(p)]={\left(\partial f/\pi \right)}^t\left(\begin{array}{cc}{\mathrm{\sum }}_1/n_1& 0\\ 0& {\mathrm{\sum }}_2/n_2\end{array}\right)\left(\partial f/\pi \right)\\ ={\sum }_{i=1}^2{\left(\partial f/{\pi }_i\right)}^t({\mathrm{\sum }}_i/n_i)\left(\partial f/{\pi }_i\right)\\ ={\sum }_{i=1}^2{\left(\partial f/{\pi }_i\right)}^t[\mathit{Diag}[{\pi }_i]-{\pi }_i{\pi }_i^t]/n_i\left(\partial f/{\pi }_i\right)\\ ={\sum }_{i=1}^2\left\{{\sum }_{j=1}^3{\left(\partial f/{\pi }_{ij}\right)}^2({\pi }_{ij}/n_i)-{\left[{\sum }_{j=1}^3\left(\partial f/{\pi }_{ij}\right){\pi }_{ij}\right]}^2/n_i\right\}\\ ={\sum }_{i=1}^2\left\{{\sum }_{j=1}^3{\left(\frac{1}{{[1+k(\pi )]}^2}\left(\partial f/{\pi }_{ij}\right)\right)}^2({\pi }_{ij}/n_i)-{\left[{\sum }_{j=1}^3\frac{1}{{[1+k(\pi )]}^2}\left(\partial f/{\pi }_{ij}\right){\pi }_{ij}\right]}^2/n_i\right\}\\ =\frac{1}{{[1+k(\pi )]}^4}{\sum }_{i=1}^2\frac{1}{n_i}\left\{{\sum }_{j=1}^3{\left(\partial k/{\pi }_{ij}\right)}^2{\pi }_{ij}-{\left[{\sum }_{j=1}^3\left(\partial k/{\pi }_{ij}\right){\pi }_{ij}\right]}^2\right\}.\end{array}$$

For this problem, the solution simplifies to:

$$V[f(p)]=\frac{1}{{[1+k(\pi )]}^4}\{\frac{1}{n_1}\left[{\left(\frac{\partial k}{\partial {\pi }_{11}}\right)}^2{\pi }_{11}+{\left(\frac{\partial k}{\partial {\pi }_{12}}\right)}^2{\pi }_{12}-{\left[\left(\frac{\partial k}{\partial {\pi }_{11}}\right){\pi }_{11}+\left(\frac{\partial k}{\partial {\pi }_{12}}\right){\pi }_{12}\right]}^2\right]+\frac{1}{n_2}\left[{\left(\frac{\partial k}{\partial {\pi }_{21}}\right)}^2{\pi }_{21}+{\left(\frac{\partial k}{\partial {\pi }_{22}}\right)}^2{\pi }_{22}-{\left[\left(\frac{\partial k}{\partial {\pi }_{21}}\right){\pi }_{21}+\left(\frac{\partial k}{\partial {\pi }_{22}}\right){\pi }_{22}\right]}^2\right]\}.$$

The asymptotic variance estimate is then obtained by substituting estimates of the probabilities, p_ij (i,j = 1,2), for the parameters π_ij and the sample sizes, n_i, in the formula above. This involves only arithmetic operations and is simple to program.

The variance approximation assumes that the transition probabilities are homogeneous within states. Although heterogeneity is almost surely the case, the close agreement of columns 5 and 6 in Table 1 suggest that the consequences of violating this assumption are small.