Abstract
Surface-tethered biomolecules play key roles in many biological processes and biotechnologies. However, while the physical consequences of such surface attachment have seen significant theoretical study, to date this issue has seen relatively little experimental investigation. In response we present here a quantitative experimental and theoretical study of the extent to which attachment to a charged –but otherwise apparently inert– surface alters the folding free energy of a simple biomolecule. Specifically, we have measured the folding free energy of a DNA stem loop both in solution and when site-specifically attached to a negatively charged, hydroxyl-alkane-coated gold surface. We find that, whereas surface attachment is destabilizing at low ionic strength it becomes stabilizing at ionic strengths above ~130 mM. This behavior presumably reflects two competing mechanisms: excluded volume effects, which stabilize the folded conformation by reducing the entropy of the unfolded state, and electrostatics, which, at lower ionic strengths, destabilizes the more compact folded state via repulsion from the negatively charged surface. To test this hypothesis we have employed existing theories of the electrostatics of surface-bound polyelectrolytes and the entropy of surface-bound polymers to model both effects. Despite lacking any fitted parameters, these theoretical models quantitatively fit our experimental results, suggesting that, for this system, current knowledge of both surface electrostatics and excluded volume effects is reasonably complete and accurate.
Keywords: Thermodynamics, Biosensor, Self Assembled Monolayer
Introduction
Surface-bound biomolecules play key roles in biology, where they participate in cell adhesion,1 biomineralization,2 and neurofilament spacing3 and in biotechnologies, where they serve as the basis for protein4-6 and DNA microarrays7-11 drug delivery vehicles,12 tissue engineering platforms,13 and biocompatible materials.14 Despite the importance of surface-bound biomolecules, however, our understanding of how surface attachment alters, for example, the folding free energies of proteins and nucleic acids remains largely theoretical15,16 (but see work by Zare and co-workers17 and Yi and co-workers18 for rare counterexamples). Indeed, the experimental literature regarding biomolecular-surface interactions has focused almost entirely on the mechanisms by which biomolecules nonspecifically adsorb onto surfaces19,20 or on empirical searches for surfaces that resist such adsorption.21-23 Given the interplay between the folding free energy of biomolecules and their function,24 a better understanding of the effect of surface attachment would likely open the door to the more rational design of, for example, technologies dependent on surface-bound biomolecules.
Theoretical considerations suggest that surface attachment affects the folding free energy of structured biomolecules via several distinct mechanisms.14,25,26 (Fig. 1) Attachment to a non-interacting surface, for example, is predicted to stabilize folded biomolecules due to excluded volume effects, which will reduce the entropy of the unfolded state.27 In contrast, attachment to a charged, but otherwise non-interacting surface should destabilize the folded state.26 Specifically, if the surface and the biomolecule are of the same charge, charge repulsion will stabilize the relatively more expanded unfolded state (although the associated reduction in the entropy of the unfolded state may partially counteract this effect). An oppositely charged surface, however, likely also destabilizes the folded state of surface-bound biomolecules. This is because nonspecific adsorption of the unfolded biopolymer to the surface introduces an alternative, lower energy state.28-30 Finally, attachment to a non-inert surface, i.e., a surface that forms hydrogen bonds, hydrophobic interactions or other specific interactions with the biopolymer, will likely stabilize the unfolded state over the native state because, again, the former more readily supports such interactions.16,31 These theoretical predictions, however, have not seen any detailed experimental investigation. That is, while limited experimental literature confirms that surface attachment alters the folding free energies of biomolecules,17,18 and that surface charge can alter the conformation of biomolecules32 experimentalists have not previously determined the extent to which the effects outlined above contribute to the thermodynamic consequences of surface attachment for any specific biomolecule.
Figure 1.
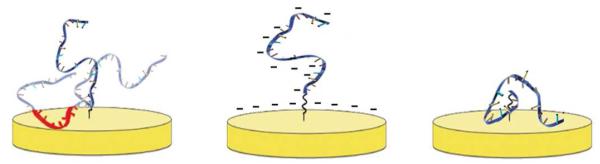
Surface attachment can alter the folding free energies of biopolymers via several mechanisms. (Left) Attachment even to a perfectly inert (non-interacting) surface is expected to stabilize the native state via excluded volume effects that reduce the entropy of the unfolded state.25,27 (Center) In contrast, attachment to a charged, but otherwise non-interacting surface is predicted to stabilize the unfolded state. Specifically, if the surface and the biomolecule are, as shown, of the same charge (which is the case in the study presented here), charge repulsion will destabilized the folded state more than the unfolded state, as the folded state is more compact. An oppositely charged surface, however, likely also stabilizes the unfolded state as nonspecific adsorption of the unfolded biopolymer introduces an alternative, lower energy state.28-30 (Right) Finally, attachment to a surface that is not inert, i.e., a surface that forms specific hydrogen bonding or hydrophobic interactions with the biopolymer, is also expected to stabilize the unfolded state as it accommodates such interactions more readily than the relatively rigid native state. Of note, prior experimental studies have argued that DNA does not form specific interactions with the 6-mercaptohexanol coated gold surface we have employed,31 and thus only the first two effects are expected to contribute significantly to the thermodynamics of the system employed here.
We have recently developed a versatile electrochemical method for monitoring the folding of surface-attached, single-chain biomolecules which we have employed as the signaling mechanism in a broad class of folding-based biosensors.32,33 Here we have used this same method to measure the folding free energy of a simple DNA stem-loop affixed via its 5′ terminus to a 6-mercaptohexanol self-assembled monolayer (SAM) on a gold surface. By comparing the folding free energies of this surface-bound biomolecule with those of the same molecule free in solution over a range of salt concentrations we have quantitatively determined the extent to which electrostatic and excluded volume effects define the stability of the surface-bound biomolecule.
Results
As our model biomolecule we selected a 25-base DNA with self-complementary ends that form a stem-loop structure. Specifically, our construct forms a 6-base stem linked via 13-base, single-stranded loop. For our surface attachment studies we modified the 5′ end of this construct with a thiolterminated six-carbon chain and co-deposited it onto a polycrystalline gold electrode with an excess of 6-mercaptohexanol, which serves as a diluent and allows for precise control of packing density and surface chemistry.34 We selected this biomolecule and this surface for our initial studies because the homogeneous charge and relatively limited chemical complexity of DNA ensures that, in contrast to most proteins,2,20 it refolds reversibly when attached to a hydroxyl-terminated SAM on gold.21 In our studies we have employed a surface packing density of ~1.2 × 1011 DNA molecules/cm2 (determined using ruthenium hexamine binding35) corresponding to a mean DNA-to-DNA distance of 33 nm. As this separation is greater than the 15 nm contour length of a 25-base, single-stranded DNA our experiments were conducted in the dilute regime in which interactions between adjacent DNA molecules are presumably minimal.
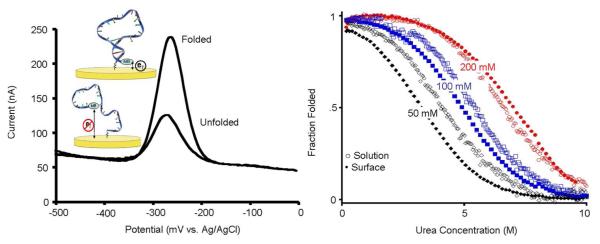
To assess the thermodynamic consequences of surface attachment we have taken advantage of an electrochemical approach previously developed in our laboratory.36 Briefly, this employs an oligonucleotide covalently linked to a redox-active reporter group on one terminus and attached via the opposite terminus to a gold surface via the above-described SAM chemistry. The efficiency of electron transfer from the redox reporter, which is readily measured via square wave voltammetry, depends on the ensemble conformation and flexibility of the oligonucleotide37 and thus reports on conformational changes (Fig. 2, left). Here we have used this to monitor the unfolding of our surface-attached biomolecule and to determine its folding free energy via urea melts (Fig. 2, right), a technique widely employed to characterize the folding free energies of biomolecules in solution.38,39 Briefly, because folding free energy is linearly related to urea concentration the folding equilibrium constant, Kf varies with urea concentration via the relationship
| Eq.1 |
where ΔG0 is the folding free energy in the absence of urea, and m is a constant. If the folded and unfolded states differ in some observable signature (here electron transfer efficiency) the observed signal will change with changing urea concentration in a manner dictated by this relationship, allowing us to extract folding free energies from a fit of this signal as a function of urea.38,39 Using this approach we find that the folding free energy of our surface-bound DNA stem-loop is −3.7±0.3 kJ/mol when measured in 20 mM sodium phosphate (Fig. 2). This value contrasts significantly with the −7.1±0.1 kJ/mol folding free energy we observe in solution (under the same conditions) as determined by monitoring urea melting using circular dichroism spectroscopy. Of note, the solution-phase folding free energy of a DNA oligonucleotide that, like our surface-bound DNA constructs, is terminally modified with a methylene blue is within the margin of error of that observed for the same construct lacking the attached reporter group (Fig. SI1). Therefore we conducted our follow-on solution-phase experiments with constructs lacking this reporter.
Figure 2.
We have employed urea-melts38,39 to determine the folding free energies of a DNA stem loop both in solution (using circular dichroism spectroscopy) and when attached to a gold surface. (Left) We have monitored the latter by measuring electron transfer from a redox tag (methylene blue) on the distal terminus of our stem-loop constructs. Specifically, we used square-wave voltammetry, which is sensitive to the increase in electron transfer efficiency that occurs when the redox tag approaches the surface. (Right) At low ionic strength the stem-loop is more stable in solution than on the surface. At higher ionic strength, conditions under which both solution-phase and surface-attached stem loops are more stable, this trend is reversed.
In order to determine the mechanisms responsible for the large free energy cost associated with surface attachment observed at low ionic strength we followed our initial studies with measurements conducted at higher ionic strengths. In doing so we find that, in solution, the folding free energy of our stem-loop ranges from −7.1 ± 0.1 to −11.7 ± 0.9 kJ/mol as the salt concentration is increased to 250 mM via the addition of sodium chloride (Fig. 3, left). Over these conditions the free energy follows the expected40 square root-dependence on ionic strength. The ionic strength dependence of our surface bound construct is somewhat stronger, varying from −3.7±0.3 to −14.7±0.8 kJ/mol over this same range of conditions (Fig. 3, left). This stronger ionic strength dependence is presumably associated with the negative potential adopted by the surface of our electrode under the conditions we have employed; the potential of zero charge (pzc) for 6-mercaptohexanol-coated gold41 is −0.210 V (vs. Ag/AgCl), 50 mV above the redox potential of methylene blue. (See ref. 42 for a more detailed discussion of potential of zero charge for SAM coated gold surfaces) That is, while inter-strand repulsion destabilizes the stem-loop both in solution and on the surface, the surface-bound biomolecule also experiences repulsion from the negatively charged electrode. This additional repulsion is reduced at higher ionic strengths (it attenuates in synchrony with the characteristic electrostatic screening distance, which is typically approximated by the Debye length), and thus the stability of the surface-bound stem loop increases more rapidly with ionic strength than the stability of the same stem-loop in solution.
Figure 3.
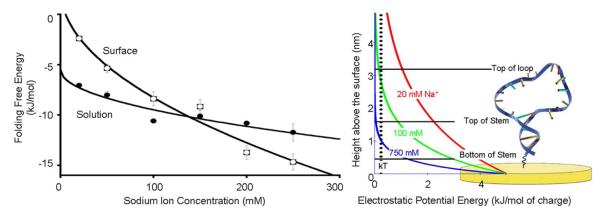
(left) At low ionic strength our DNA stem-loop is less stable on the surface than in solution, presumably due to electrostaticr epulsion from the surface, which is negatively charged at the potential we have employed. At higher ionic strength electrostatic screening increases, negating this effect. Under these conditions the excluded volume effect dominates and the surface-attached molecule becomes more stable than the equivalent molecule in solution. (right) This behavior occurs because the electric field near a charged surface in an electrolyte is a strong function of counterion concentration. At higher sodium ion concentrations the electric field falls to near zero over distances shorter than a single base pair in double-stranded DNA. At lower ionic strengths, in contrast, the electric field remains significant over distances comparable to the size of our DNA stem-loop. The folding free energies observed in solution exhibit the expected40square root dependence on ionic strength. We fitted the surface energies to a square root dependence; this is not theoretically justified but serves as a convenient guide to the eye. The error bars in this and the following plots are standard errors derived from replicate, independent measurements.
While surface attachment destabilizes our construct at low ionic strength, it stabilizes it at high ionic strength, with the two effects canceling at ~130 mM Na+ (Fig. 3, left). This behavior is presumably due to the opposing effects of electrostatics and excluded volume. That is, at low ionic strength, conditions under which the Debye length is long compared to the length of the DNA stem, the negative charge on the surface destabilizes the folded stem-loop relative to its more expanded unfolded state (Fig. 3, right). As the ionic strength increases, however, the electrostatic screening length falls until, ultimately, few if any of the bases in the DNA “feel” a significant electric field from the surface. The excluded volume effect, which is, to a first approximation, independent of ionic strength, thus dominates at higher ionic strengths and surface attachment becomes stabilizing.
To frame the above argument more quantitatively, we have derived a detailed model for the relationship between the change in folding free energy upon surface attachment and the electrostatic properties of the surface and the solution. To do so we have broken the change in folding free energy associated with surface attachment (ΔΔGf) into an enthalpic component (ΔΔHEL) arising due to the above-described electrostatic effects and an entropic effect (ΔΔSEV) associated with the excluded volume of the surface,
| Eq.2 |
under the assumption that, while many factors contribute to folding free energy, only these two effects are appreciably altered by surface attachment. For example, while the translational entropy of the folded and unfolded states change upon surface attachment, they both change identically and thus this effect does not alter relative folding free energies.
Change in enthalpy of folding upon surface attachment
We can estimate ΔΔHEL from the enthalpy changes associated with attaching both the folded (ΔHFSol-Sur) and unfolded (ΔHUSol-Sur) states to an appropriately charged surface:
| Eq.3 |
The two components of this can be calculated from
| Eq.4 |
where ρ(z) is the charge density at height z above the surface associated with the nucleotide monomers and U(z) is the electrostatic energy as functions of z. For an electrolyte above a charged surface U(z) is given by Andelman’s treatment43 of the Poisson-Boltzmann model,
| Eq.5 |
| Eq.6 |
| Eq.7 |
where λD is the Debye length, n0 is the number density of ions, ϕ0 is the potential at the surface of the SAM relative to its potential of zero charge. Given that we are measuring folding the −0.260 V redox potential of methylene blue and that the potential of zero charge of a hydroxyl-terminated six carbon SAM on gold is −0.210 V (both versus Ag/AgCl) ϕ0 is, as noted above, −0.050 V for our system.41 (Of note, while we scan the potential from 0 to −0.5 V during the course of our experiment, the methylene blue only transfers electrons –and thus only reports on the conformation of the biomolecule–over a relatively narrow window around its redox potential).
The enthalpy of surface attachment for the folded state
determine ρF(z), the charge density associated with nucleotide monomers in the folded state, we treat the folded stem-loop as if it forms a uniform B-form DNA rod oriented directly away from the surface. This assumption is based on solution-phase NMR structures of polynucleotide stem-loops indicating that, due to strong base stacking interactions, non-complementary DNA loops of the size we have employed adopt a largely double-helical conformation.44-46 From this, ρF(z) is given by the charge density per unit length of double-stranded, B-form DNA:
| Eq.8 |
The second term here simply denotes the finite length of the DNA helix (LH), beyond which the monomer density is, obviously, zero. Of note, counterion condensation effects are ignored here because counterion condensation theory has been shown to be inaccurate for DNA47 and unnecessary when using a nonlinear Poisson-Boltzmann model rather than a linear Debye-Huckel approximation.48,49
The enthalpy of surface attachment for the unfolded state
To determine ρU(z), the charge density associated with nucleotide monomers in the unfolded state, we define two regimes based on the distance of a given monomer above the surface. For short distances above the surface, (z < z*), the electric field is large enough that the electrostatic energy of the monomer, U(z*), is greater than kT. Under these conditions the DNA is stretched away from the surface due to electrostatic repulsion. For z > z*, in contrast, the DNA adopts a biased random walk under the influence of the excluded volume defined by the electrode and the strong negative electric field at its surface. We have approximated this latter condition by setting a hard-wall repulsion at z = z*. Finally, our expression for ρU effectively takes into account the contour length of the unfolded DNA and thus no explicit third regime (beyond which the monomer density is zero) is required. This two-state regime then gives us:
| Eq.9 |
where ρcoil(z) describes the monomer density at height z above the surface for an end-tethered random coil, as described below, and σ is the length of a single nucleotide in DNA and is taken to be 0.619 nm (refs50-52).
The conformation of a random walk polyelectrolyte, such as single-stranded DNA, tethered to a surface is a function of polymer length and counterion concentration and is described by a Green′s function:53,54
| Eq.10 |
where z1 is the location of the attachment site, usually taken as some small distance above the surface, b is the Kuhn length, and NK is the number of Kuhn segments. The density of the nth monomer as a function of height z above the surface is related to the Green′s function by:
| Eq.11 |
And the overall coil density is the sum of the monomer densities and is given by
| Eq.12 |
While there is no exact analytical solution to ρcoil, the solution is general for polymers of any length if z is expressed in dimensionless unit of magnitude D such that:
| Eq.13 |
An important consideration is that the Kuhn length, b, of a polyelectrolyte such as DNA is dependent on the counterion concentration and varies over our experimental regime. For monovalent salts between 20 mM and 2 M, the counterion concentration dependent Kuhn length b of a single stranded DNA is
| Eq.14 |
where C is the local concentration of counterions in molar units.55,56 An important consideration for our work is that, due to the formation of an electric double layer on a charged surface, C is a function of height, z, above the surface, with C(z) being given by:43
| Eq.15 |
| Eq.16 |
| Eq.17 |
Finally, by combining Eq. 16 and Eq. 17 with Eq. 3 we can calculate the expected change in enthalpy of folding upon surface attachment. For our stem-loop, this estimate varies from 9.6 kJ/mol to 3.9 kJ/mol as the sodium ion concentration varies from 20 to 250 mM (Fig. SI2).
Change in folding entropy and free energy upon surface attachment
Taken in concert with our experimental measurements of the free energy consequences of surface attachment, the above calculations provide the first experimental measure of the excluded volume effect associated with attaching a polymer to a surface. Specifically, significant simulations and theoretical work have demonstrated that the conformational entropy lost by the folded state upon surface attachment is negligible,57 and thus the change in entropy associated with surface attachment arises as a consequence solely of the excluded volume entropy losses of the unfolded state. Using this approach we estimate from our experimental results that the excluded volume entropy of the 25-base unfolded state varies from −16.0 to −22.1 J/mol.K as the sodium ion concentration varies from 20 to 250 mM.
The above estimates of the excluded volume entropy provide a means of testing prior theoretical and simulations-based predictions regarding the magnitude of this effect. Both theory54 and simulation58 suggest that the excluded volume entropic cost of attaching a random coil to surface goes as
| Eq.18 |
Where A≈−1.5kT (ref58) and B is −0.5 kT for a Gaussian chain54 and −0.44 kT for self-avoiding chain.58 Once again, NK, the number of Kuhn segments in the chain, will vary here with counterion concentration as both the persistence length and z* fall as ionic strength rises. For the 25-base construct we have employed, the estimated excluded volume entropy term ranges from −16.9 to −22.2 J/mol.K as the sodium ion concentration varies from 20 to 250 mM (Fig. SI2), estimates that agree quite closely with the semi-empirical values derived in the paragraph above.
When taken in concert with the attachment-associated change in enthalpy calculated above these prior theoretical models of the excluded volume entropy capture what we believe to be the two major components of the free energy change observed upon surface attachment: ΔHEL and ΔSEV. That is, by combining Eq. 2, 3, 16, 17, and 18 we should obtain a complete description of the thermodynamic consequences of such attachment. When we do so we find that, despite lacking any fitted parameters, this simple model reproduces our experimentally observed free energy changes with reasonable accuracy (Fig. 4). This said, the potential of zero charge of a SAM coated surface is generally not well known, and our model depends on the value chosen. If, however, rather than fixing the surface potential, ϕ0 we allow this parameter to float we find that the best fit value is −54 mV, corresponding to a potential of zero charge of 206 mV. This, in turn, corresponds closely to the −210 mV estimate previously reported by Rentsch et al.41
Figure 4.
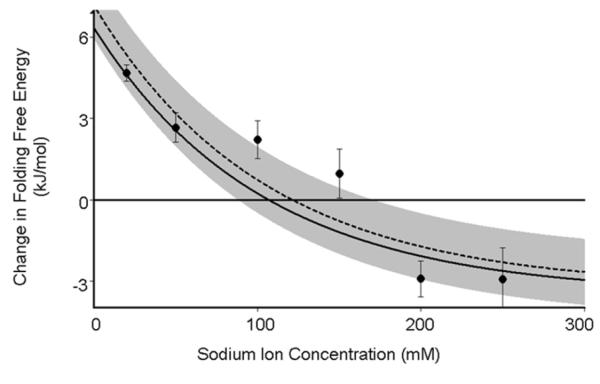
A simple theoretical model, which considers only enthalpic (electrostatic) and entropic (excluded volume) contributions to the folding free energy which contains either no fitted parameters (solid line; see text for model details), or one fitted parameter-the pcz- (dashed line) fits our observations with reasonable accuracy. This, in turn, suggests that our knowledge of these effects (including prior theoretical estimates of the magnitude of the excluded volume effect) is reasonably complete and accurate and that any non-specific interactions between the DNA and our SAM-coated gold surface are negligible. The gre bar, which represents ±1 kT, is shown for scale.
Discussion
Here we have presented a detailed experimental and theoretical description of the thermodynamic consequences of attaching a biopolymer to a surface. Specifically, we find that, at low ionic strength, a simple stem-loop DNA becomes less stable when it is attached to a negatively charged, SAM-coated gold surface. As the ionic strength is increased, however, attachment to this surface becomes stabilizing. We attribute this behavior to two competing mechanisms: electrostatic repulsion from the negatively charged gold surface, which, at lower ionic strengths, destabilizes the more compact folded state, and excluded volume effects, which stabilize the folded conformation by reducing the entropy of the unfolded state. In support of this hypothesis a simple computational model that considers only the electrostatic and excluded volume consequences of surface attachment accurately recapitulates the observed behavior without the use of any fitted parameters.
Its fit to experimental results not withstanding, the model we have presented is not without potentially significant simplifications. For example, the Poisson-Boltzmann distribution we have used to model the electric field over our surface is known to rely on several inaccurate assumptions. Specifically, it assumes the dielectric constant near a surface is constant, and it ignores the discrete volume of ions.43 The model likewise ignores other, potentially important surface-biopolymer interactions including hydrogen bonding and hydrophobic interactions. That it nevertheless accurately fits our observations argues that these effects are minimal for DNA attached to a hydroxyl-terminated SAM, a suggestion that is further supported by the observation that DNA generally does not adsorb to such surfaces.32
Materials and Methods
The DNA oligonucleotides employed were synthesized by Bio-Search Technologies, where they were purified by dual HPLC. The sequence employed is 5′-ACT CTC GAT CGG CGT TTT AGA GAG G-3′. For our surface bound experiments the sequence was modified with a 6-carbon thiol on its 5′ terminus and methylene blue attached via amide bond formation to a 6-carbon amine on its 3′ terminus.
For the surface we employed a polycrystalline gold disk electrodes (2-mm diameter; BAS, West Lafayette, IN). These were polished with a 50 nm alumina slurry (BAS), sonicated in water, and electrochemically cleaned by a series of oxidation and reduction cycling in 1) 0.5 M NaOH (−0.4 to −1.35 V) then 2) 0.5 M H2SO4 (0 to 2 V), then in 3) 0.5M H2SO4 (0 to −0.35 V), in 4) 0.5 M H2SO4 (−0.35 to 1.5 V) and finally in 4) 0.01 M KCl 0.1 M H2SO4 (−0.2 to 1.25 V). To attach the requisite DNA construct this clean gold surface was incubated for 5 min at room temperature in a solution of 50 nM thiol- terminated DNA, 20 μM Tris(2-carboxyethyl)phosphine hydrochloride (to reduce disulfide-bonded dimers), and 180 mM NaCl in 20 mM phosphate buffer (pH 7.0). The resulting DNA-modified surface was washed with the deionized water before being treated with 2 mM 6-mercaptohexanol in water overnight to complete the formation of the SAM.
We determined folding free energies using urea-melts generated with a Hamilton 500C titrator starting at 10 M urea and titrating in buffer. At each urea concentration the system was allowed to equilibrate for 30 s (with stirring) prior to measurement. All solutions were buffered with 20 mM sodium phosphate (pH 7.0) with sodium chloride added to bring the buffer to the desired sodium ion concentration. Surface measurements were conducted using square wave voltammetry from 0 to −0.5 V at a frequency of 60 Hz on a CHI 630 potentiostat (CH Instruments, Austin, TX) in a standard cell with a platinum counter electrode and a Ag/AgCl (saturated with 3 M NaCl) reference electrode. Prior to use each electrode was washed with 10 M urea in buffer, washed again with buffer and then incubated in 10 M urea for 1 hr prior to the start of the titration. To determine folding free energy a plot of peak current (at the −0.260 V potential of methylene blue) versus urea concentration was fitted to a standard two-state unfolding curve with linear, sloping baselines.38,39 Solution phase measurements were conducted on an Aviv Biomedical circular dichroism spectrophotometer. Two solutions were prepared: the first contained 3 μM DNA in the previously described buffer and the second was identical save for the addition of 10 M urea. To determine folding free energy a plot of ellipticity at 275 nm versus urea concentration was fitted to a standard two-state unfolding curve with linear, sloping baselines. The error bars reported for the free energies both in solution and on the surface represent the standard error of the mean of at least three independently measured and fitted titrations.
Supplementary Material
ACKNOWLEDGMENT
The authors thank Adriana Patterson and Ryan White for assistance and advice. A.V.-B. is a Fond Québécois de la Recherche sur la Nature et les Technologies Fellow.
Funding Sources This research was funded by NIH grant R01AI076899.
ABBREVIATIONS
- SAM
Self-Assembled Monolayer
Footnotes
5′ thiol- 3′Methylene blue modified DNA urea denaturation curve in solution and theoretical ΔΔH and TΔΔvs. ionic strength. This material is available free of charge via the Internet at http://pubs.acs.org.
Author Contributions
The manuscript was written through contributions of all authors. / All authors have given approval to the final version of the manuscript
REFERENCES
- (1).Abu-Lail NI, Camesano TA. Biomacromolecules. 2003;4:1000–1012. doi: 10.1021/bm034055f. [DOI] [PubMed] [Google Scholar]
- (2).Gray JJ. Curr. Opin. Struct. Biol. 2004;14:110–115. doi: 10.1016/j.sbi.2003.12.001. [DOI] [PubMed] [Google Scholar]
- (3).Beck R, Deek J, Jones JB, Choi MC, Ikawa T, Watanabe O, Safinya CR. Biophys. J. 2010;98:9a. [Google Scholar]
- (4).Feng J, Wong KY, Lynch GC, Gao X, Pettitt BM. J. Phys. Chem. B. 2007;111:13797. doi: 10.1021/jp075051y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Hartmann M, Roeraade J, Stoll D, Templin MF, Joos TO. Anal. Bioanal. Chem. 2008;393:1407–1416. doi: 10.1007/s00216-008-2379-z. [DOI] [PubMed] [Google Scholar]
- (6).Caiazzo RJ, Jr., Maher AJ, Drummond MP, Lander CI, Tassinari OW, Nelson BP, Liu BC. Proteomics: Clin. Appl. 2009;3:138–147. doi: 10.1002/prca.200800149. [DOI] [PubMed] [Google Scholar]
- (7).Halperin A, Buhot A, Zhulina EB. Biophys. J. 2005;89:796–811. doi: 10.1529/biophysj.105.063479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Fan C, Plaxco KW, Heeger AJ. Proc. Natl. Acad. Sci. U. S. A. 2003;100:9134–9137. doi: 10.1073/pnas.1633515100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Peterson AW, Wolf LK, Georgiadis RM. J. Am. Chem. Soc. 2002;124:14601–14607. doi: 10.1021/ja0279996. [DOI] [PubMed] [Google Scholar]
- (10).Vainrub A, Pettitt BM. Biopolymers. 2003;68:265–270. doi: 10.1002/bip.10271. [DOI] [PubMed] [Google Scholar]
- (11).Seidel M, Niessner R. Anal. Bioanal. Chem. 2008;391:1521–1544. doi: 10.1007/s00216-008-2039-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Mitragotri S, Lahann J. Nat. Mater. 2009;8:15–23. doi: 10.1038/nmat2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Jiao Y-P, Cui F-Z. Biomedical Materials. 2007;2:R24–R37. doi: 10.1088/1748-6041/2/4/R02. [DOI] [PubMed] [Google Scholar]
- (14).Chen H, Yuan L, Song W, Wu Z, Li D. Prog. Polym. Sci. 2008;33:1059–1087. [Google Scholar]
- (15).Eisenriegler E, Kremer K, Binder KJ. Chem. Phys. 1982;77:6296–6320. [Google Scholar]
- (16).Pong B-K, Lee J-Y, Trout BL. Langmuir. 2005;21:11599–11603. doi: 10.1021/la052116k. [DOI] [PubMed] [Google Scholar]
- (17).Chah S, Kumar CV, Hammond MR, Zare RN. Anal. Chem. 2004;76:2112–2117. doi: 10.1021/ac035416k. [DOI] [PubMed] [Google Scholar]
- (18).Kang T, Hong S, Choi I, Sung JJ, Yi J. Bull. Korean Chem. Soc. 2008;29:1451–1458. [Google Scholar]
- (19).Lu JR, Zhao X, Yaseen M. Curr. Opin. Colloid Interface Sci. 2007;12:9–16. [Google Scholar]
- (20).Hlady V, Buijs J. Curr. Opin. Biotechnol. 1996;7:72–77. doi: 10.1016/s0958-1669(96)80098-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Caruso F, Rodda E, Furlong DN, Haring V. Sens. Actuators, B. 1997;41:189–197. [Google Scholar]
- (22).Huang E, Zhou F, Deng L. Langmuir. 2000;16:3272–3280. [Google Scholar]
- (23).Chaki NK. Vijayamohanan, K. Biosens. Bioelectron. 2002;17:1–12. doi: 10.1016/s0956-5663(01)00277-9. [DOI] [PubMed] [Google Scholar]
- (24).Vallée-Bélisle A, Ricci F, Plaxco KW. Proc. Natl. Acad. Sci. U. S. A. 2009;106:13802–13807. doi: 10.1073/pnas.0904005106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Friedel M, Baumketner A, Shea J-E. Proc. Natl. Acad. Sci. U. S. A. 2006;103:8396–8401. doi: 10.1073/pnas.0601210103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Li H, Qian C-J, Sun L-Z, Luo M-B. Polym. J. (Tokyo, Jpn) 2010;42:383–385. [Google Scholar]
- (27).Knotts TA, Rathore N, de Pablo JJ. Biophys. J. 2008;94:4473–4483. doi: 10.1529/biophysj.107.123158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Lai RY, Seferos DS, Heeger AJ, Bazan GC, Plaxco KW. Langmuir. 2006;22:10796–10800. doi: 10.1021/la0611817. [DOI] [PubMed] [Google Scholar]
- (29).White RJ, Phares N, Lubin AA, Xiao Y, Plaxco KW. Langmuir. 2008;24:10513–10518. doi: 10.1021/la800801v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Ricci F, Zari N, Caprio F, Recine S, Amine A, Moscone D, Palleschi G, Plaxco KW. Bioelectrochemistry. 2009;76:208–213. doi: 10.1016/j.bioelechem.2009.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Herne TM, Tarlov MJ. J. Am. Chem. Soc. 1997;119:8916–8920. [Google Scholar]
- (32).Kaiser W, Rant U. J. Am. Chem. Soc. 2010;139:7935–7945. doi: 10.1021/ja908727d. [DOI] [PubMed] [Google Scholar]
- (33).Lubin AA, Plaxco KW. Acc. Chem. Res. 2010;43:496–505. doi: 10.1021/ar900165x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Ricci F, Lai RY, Heegar AJ, Plaxco KW, Sumner JJ. Langmuir. 2007;23:6827–6834. doi: 10.1021/la700328r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Steel AB, Herne TM, Tarlov MJ. Anal. Chem. 1998;70:4670–4677. doi: 10.1021/ac980037q. [DOI] [PubMed] [Google Scholar]
- (36).Xiao Y, Lai RY, Plaxco KW. Nat. Protoc. 2007;2:2875–2880. doi: 10.1038/nprot.2007.413. [DOI] [PubMed] [Google Scholar]
- (37).Uzawa T, Cheng RR, White RJ, Makarov DE, Plaxco KW. J. Am. Chem. Soc. 2010;132:16120–16126. doi: 10.1021/ja106345d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Pace CN. In Enzyme Structure Part L. Vol. 131. Academic Press; 1986. pp. 266–280. [Google Scholar]
- (39).Shelton VM, Sosnick TR, Pan T. Biochemistry. 1999;38:16831–16839. doi: 10.1021/bi991699s. [DOI] [PubMed] [Google Scholar]
- (40).de los Rios MA, Plaxco KW. Biochemistry. 2005;44:1243–1250. doi: 10.1021/bi048444l. [DOI] [PubMed] [Google Scholar]
- (41).Rentsch S, Siegenthaler H, Papastavrou G. Langmuir. 2007;23:9083–9091. doi: 10.1021/la700987u. [DOI] [PubMed] [Google Scholar]
- (42).Becka AM, Miller CJ. J. Phys. Chem. 1992;97:6233–6239. [Google Scholar]
- (43).Poon WCK, Andelman D. Soft and condensed matter physics in molecular and cell biology. CRC Press; 2006. [Google Scholar]
- (44).Marcheschi RJ, Staple DW, Butcher SE. J. Mol. Biol. 2007;373:652–663. doi: 10.1016/j.jmb.2007.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Lin CH, Patei DJ. Chemistry & Biology. 1997;4:817–832. doi: 10.1016/s1074-5521(97)90115-0. [DOI] [PubMed] [Google Scholar]
- (46).Baouendi M, Cognet JAH, Ferreira CSM, Missailidis S, Coutant J, Piotto M, Hantz E, du Penhoat CH. [accessed Dec 21 2011];FEBS Journal. 2011 [Online] DOI: 10.1111/j.1742-4658.2011.08440.x. [Google Scholar]
- (47).Hansen PL, Podgornik R, Parsegian VA. Phys. Rev. E. 2001;64:021907. doi: 10.1103/PhysRevE.64.021907. [DOI] [PubMed] [Google Scholar]
- (48).Lamm G, Pack GR. Biopolymers. 2010;93:619–639. doi: 10.1002/bip.21421. [DOI] [PubMed] [Google Scholar]
- (49).Manning GS. J. Phys. Chem. 2010;114:5435–5440. doi: 10.1021/jp912234x. [DOI] [PubMed] [Google Scholar]
- (50).Robeyns K, Herdewijn P, Van Meervelt L. Artif. DNA. 2010;1:2–8. doi: 10.4161/adna.1.1.10952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Fusetti F, Schröter KH, Steiner RA, van Noort PI, Pijning T, Rozeboom HJ, Kalk KH, Egmond MR, Dijkstra BW. Structure. 2002;10:259–268. doi: 10.1016/s0969-2126(02)00704-9. [DOI] [PubMed] [Google Scholar]
- (52).Chenoweth DM, Dervan PB. Proc. Natl. Acad. Sci. U. S. A. 2009;106:13175–13179. doi: 10.1073/pnas.0906532106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Carslaw HS, Jaeger JC. Conduction of heat in solids. Oxford University Press; USA: 1959. [Google Scholar]
- (54).Dolan AK, Edwards SF. Proc. R. Soc. A. 1974;337:509–516. [Google Scholar]
- (55).Saleh OA, McIntosh DB, Pincus P, Ribeck N. Phys. Rev. Lett. 2009;102:068301. doi: 10.1103/PhysRevLett.102.068301. [DOI] [PubMed] [Google Scholar]
- (56).Tinland B, Pluen A, Sturm J, Weill G. Macromolecules. 1997;30:5763–5765. [Google Scholar]
- (57).Dill KA, Alonso DOV. Colloquim Mosbach Protein Structure and Protein Engineering. 1988;39:51–58. [Google Scholar]
- (58).Chen Y-C. Int. J. Mod. Phys. B. 2007;21:1787. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.