Collective cell streams in epithelial monolayers depend on cell adhesion

Abstract

We report a spontaneously emerging, randomly oriented, collective streaming behavior within a monolayer culture of a human keratinocyte cell line, and explore the effect of modulating cell adhesions by perturbing the function of calcium-dependent cell adhesion molecules. We demonstrate that decreasing cell adhesion induces narrower and more anisotropic cell streams, reminiscent of decreasing the Taylor scale of turbulent liquids. To explain our empirical findings, we propose a cell-based model that represents the dual nature of cell-cell adhesions. Spring-like connections provide mechanical stability, while a cellular Potts model formalism represents surface-tension driven attachment. By changing the relevance and persistence of mechanical links between cells, we are able to explain the experimentally observed changes in emergent flow patterns.

1. Introduction

Collective motility of interacting cells is a poorly understood, but fundamental aspect of several developmental and pathological processes [1, 2]. Groups of cells move together, for example, during gastrulation, tissue vascularization, tumor invasion or wound healing. Multicellular motion can also be recapitulated in cell culture experiments. Studies investigating the motion of kidney epithelial (MDCK, [3, 4]) or endothelial [5, 6] cells, as well as immune cells in explanted lymph nodes [7] indicated an intriguing motion pattern, reminiscent of flow patterns seen in experiments with high density bacterial suspensions [8] or self-propelled inanimate objects [9]. In the absence of directed expansion of the whole monolayer, these cells exhibit a globally undirected, but locally correlated streaming behavior. Thus, in addition to the elastic/glassy behavior of certain monolayers [4], cell sheets can also exhibit a more fluid-like stat in which cell adjacency changes rapidly. Statistical characterization of the spontaneous streaming motion within endothelial monolayers revealed that cells move in locally anisotropic, 50–100 µm wide and 200–300 µm long streams, which form and disappear at random positions [6]. This type of motion is clearly different from both the diffusive movements observed in cell sorting experiments [10, 11] as well as from a motility driven by external chemotactic gradients. Endothelial monolayers also exhibit collective flow patterns in the developing vasculature of the embryo. Studies imaging the vascularization of transgenic quail embryos – in which endothelial cell nuclei express a GFP variant – revealed vigorous motility within the inner lining of major vessels such as the aortae [12]. While statistical characterization of these in vivo motion patterns is not yet available, the reported cell trajectories are in many aspects similar to those observed in monolayer cultures.

To explain the flow that emerges within endothelial monolayers, a suitably extended cellular Potts model (CPM, see, e.g., [13]) was proposed [6, 14]. Individual cells were modelled as fluid-like droplets: their area and perimeter was restricted by a mechanism analogous to surface tension. Such a modeling approach is motivated by the demonstrated fluid-like behavior of simple cell aggregates [15]. The main advantage of the CPM (and a related off lattice [16]) simulations is that cell shapes are explicitly represented. Therefore, the model has the potential to describe dynamics in which controlled cell shape plays an important role [17, 18, 19]. Spontaneous, persistent cell motility was introduced in the CPM through a postulated positive feedback between cell polarity and cell displacements [6]: cell protrusions are assumed to be more likely at the front of the cell than at the back. In turn, the leading edge is stabilized by its continuous advance, a rule that reflects empirical findings such as the contribution of actin polymerization to increased PI3K activity [20, 21]. As model simulations demonstrate, such a mechanism, together with steric constraints resulting from limited cell compressibility, can closely reproduce the observed spontaneous streaming behavior in endothelial monolayers [6] or the increased persistence of invading cells in an ECM environment [22].

While cell-cell adhesion is expected to strongly influence collective flow within a monolayer, its actual role is little understood. Most models that are widely used in multicellular simulations are not sensitive to the relative motion of adjacent cells; for example in the CPM, the “energy” or goal function depends only on the instantaneous configuration and lack temporal persistence or memory. Yet, previous experimental reports indicated altered collective flow when cell-cell adhesion was perturbed [5, 23]. Here we explore the spontaneous streaming movements in epithelial monolayer cultures, and show that when normal cell-cell adhesion is perturbed by calcium chelation, the correlated streams become narrower and the shear between cells is increased. We also suggest a minimalistic self-propelled CPM that is consistent with empirical findings both at the cellular and multicellular scales. The proposed model thus establishes a link between a viscosity-like feature of emergent multicellular motility and subcellular dynamics such as the lifetime of a cell adhesion structures.

2. Results

2.1. Ca-dependent streaming behavior in HaCaT cells

Using time-lapse microscopy, we observed groups of cells moving together in streams within cultured monolayers of the immortalized HaCaT human keratinocyte line (see Fig. 1 and Movies 1 and 2). Cells were grown on a rigid tissue culture plastic. The culture technique provided a high density patch of cohesive cells with a freely moving boundary. Analysis of cell movements were restricted to the center of the patch where no net directional movement was observable. Cells exhibited pronounced spontaneous streaming behavior that was maintained for at least 24 hours after seeding, and it was similar to previously reported streams in MDCK [3] and endothelial [6] cell cultures.

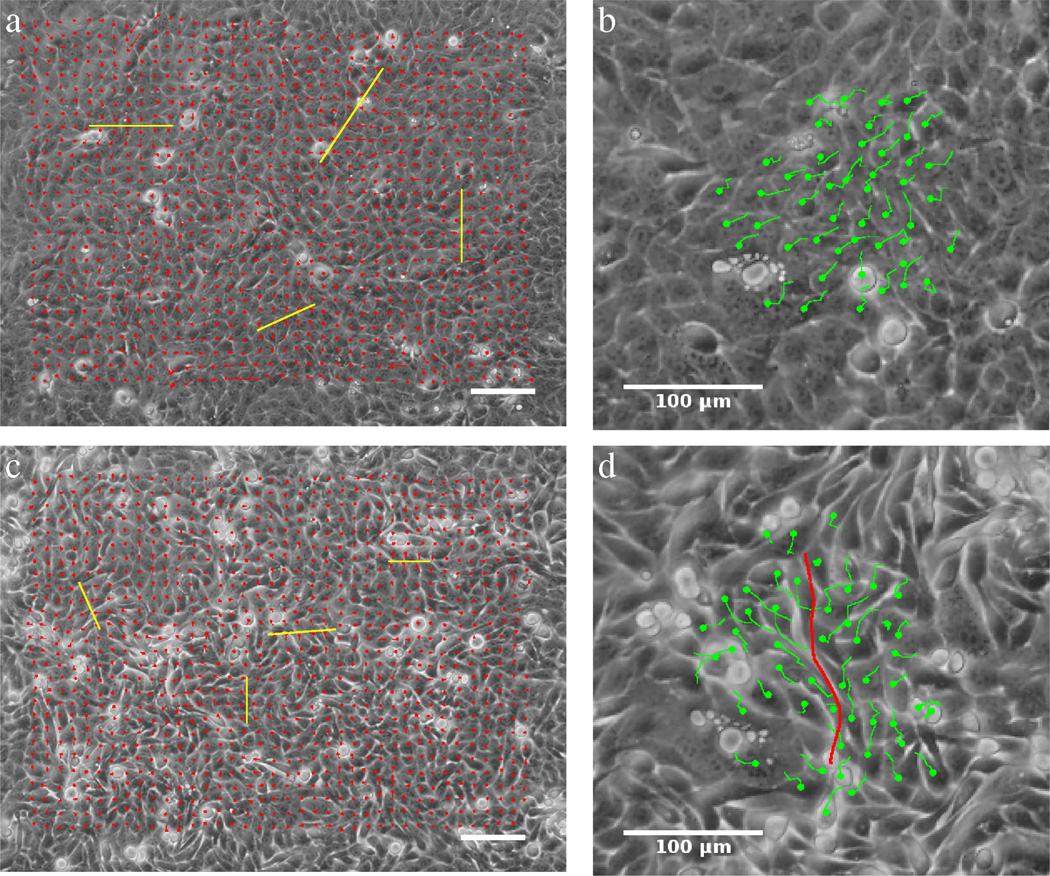
Figure 1.

Collective streaming of HaCaT cells in confluent monolayer cultures, in the absence (a,b) and presence (c,d) of the Ca²⁺ chelator EDTA. The locally prevalent direction of motion was determined by PIV analysis resulting in velocity fields (a,c) and also by manual tracking of cell centroids yielding trajectories of individual cells (b,d). Cells spontaneously form streams, whose widths (yellow bars on a,b) are reduced when free Ca²⁺ is removed from the medium. Adjacent cells moving in opposite directions are readily observed when cell adhesion is compromised (d, red line). Scale bars indicate 100 µm. See also Movies 1 and 3.

To quantitatively characterize the streaming phenomenon, cell displacements were calculated by applying a particle image velocimetry (PIV) technique on image sequences. Images were divided into small segments located in a uniform rectangular grid pattern. For each segment we established the locally prevalent “optical flow” [24, 4], i.e., the movement of various cell constituents visible by phase contrast microscopy. Using the displacements of the PIV field, we construct a sequence of instantaneous velocity fields. To test that the PIV vectors indeed describe actual cell movements, we tracked cells manually on a small sample and found that the two methods resulted in similar velocity fields.

To characterize the correlations in cell movements, we calculated V⃗ (x⃗), the average flow field in a reference frame co-aligned with a typical moving object, similar to the one used to describe streams previously by [6]. This measure is a vector field obtained as the average of velocity vectors found at similar locations x⃗ (e.g., in front, behind, at left and right), but in different reference systems, each co-aligned with the local motion. The vectors V⃗ (x⃗) diminish as averages of uncorrelated random variables when the motion of each object is independent from the rest of the system. As Fig.2a demonstrates, HaCaT cells move by organizing an almost isotropic flow field (the correlation length is similar both along and perpendicular to the flow), a markedly different behavior than the highly anisotropic, narrow flows reported previously for endothelial cells [6]. This result indicates that various cell types exhibit distinct levels of “sheet viscosity” in a multicellular environment, a collective feature that can be characterized by the typical width of co-moving streams or the amount of shear between cells.

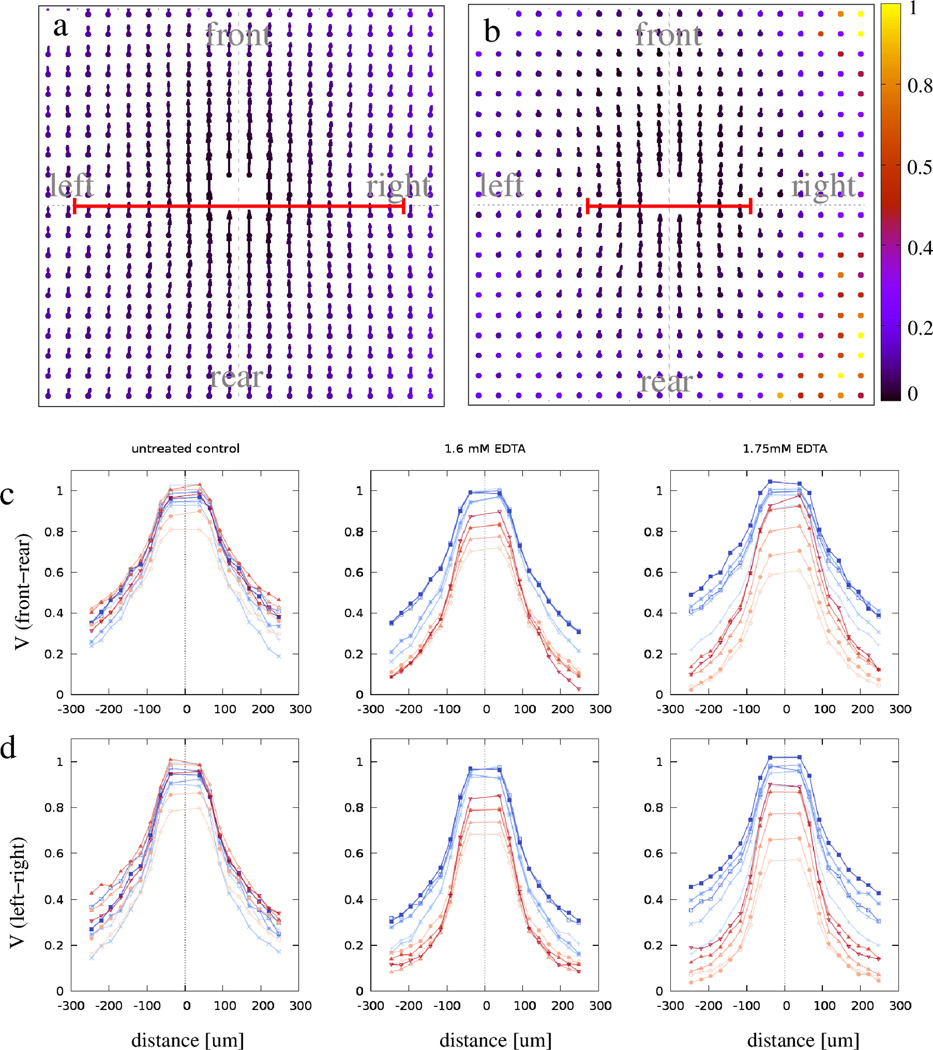
Figure 2.

Average flow fields, V⃗ (x⃗), characterize cell motion around a typical motile cell. The color code indicates the local ratio between the statistical standard error and the magnitude of V⃗. Grid spacing is 25 µm; vectors visualize speeds as displacements extrapolated to a time interval of 100 minutes. In the presence of Ca²⁺, cells move in almost isotropic, wide streams (a). When cell-cell adhesions are perturbed by Ca²⁺ chelation, the flow field becomes more anisotropic as the correlation length is reduced more in the direction perpendicular to the flow (b). The average V⃗ (x⃗) values along the front-rear axis (panel c) and left-right axis (panel d) are plotted for various concentrations of EDTA. Blue and red colors indicate data obtained before and after EDTA treatment, respectively. Color saturation decreases with the time difference between data collection and EDTA perturbation. To compensate for a 20% variation across the cell cultures, values shown are normalized to the maximum of V⃗, obtained immediately before treatment. The red lines in panels a and b indicate stream widths, as obtained by an exponential fit of the velocity profiles shown in panel d.

We hypothesize that “sheet viscosity”, a macroscopic variable, reflects differences within the cell-cell adhesion apparatus of the cells. To test this hypothesis, in a set of experiments we interfered with normal cell adhesion by removing free Ca²⁺ from the culture medium. The decreased extracellular Ca²⁺ concentration results in the disruption of homophilic intercellular bonds between cadherins, the main intercellular adhesion molecules. As Figs. 1 and 2 demonstrate, moderate Ca²⁺ removal transiently alters the spontaneous flow structure, without affecting the speed of individual cell movements (data not shown). When cell adhesions are compromised, adjacent cells moving in opposite directions are also observed (Fig. 1d). Alterations in the V⃗ (x⃗) flow fields can be conveniently compared along lines parallel or perpendicular to the direction of the local motion. As panels c, d in Fig. 2 demonstrate, higher EDTA concentration results in narrower streams up to the concentration of 1.75 mM. For larger concentrations, cell attachment to the coated glass or plastic substrate is also compromised and interferes with the cells’ ability to move.

To estimate the characteristic size of the streams, V_x(x, y = 0) and V_x(x = 0, y) were fitted by exponential functions exp(−|x⃗|/ξ) yielding the correlations lengths ξ_‖ and ξ_⊥, respectively. These correlation lengths decrease in a dose dependent manner, when cadherin function was perturbed. For unperturbed HaCaT monolayers ξ_⊥ = 208 ± 7.8 µm and ξ_‖ = 250 ± 7.8 µm, giving an approximate form factor of F = ξ_‖/ξ_⊥ = 1.2 ± 0.08. The strongest response was elicited by 1.75 mM EDTA, which decreased the stream widths by half, ξ_⊥ = 99 ± 5.2 µm, while the reduction in stream lengths was less: ξ_‖ = 138 ± 5.2 µm. Thus, the stream form factor in the perturbed monolayer increased to F = 1.4 ± 0.1.

2.2. Cellular Potts model with explicit cell adhesion

To test our hypothesis that “sheet viscosity” is an emergent property of cellular adhesion, and to explain our experimental findings with a mechanistic model, we expand the two dimensional self-propelled cellular Potts model (CPM, see Methods) presented by [6]. We introduce explicit cell-cell adhesion, in similar manner as has been recently used by, e.g. in ref [25].

Currently neither the biomechanical nor the biochemical details are known how mechanical linkage with adjacent cells modulates cell motility. We argue that the effects resulted by relative movement of adjacent cells are likely reflect slow establishment or turnover of intercellular adhesion complexes. In particular, it is plausible to assume that relative movement of adjacent cells involves shear deformation of cytoskeletal structures. The continuing deformation of the cytoskeleton builds up mechanical stress which is known to be able to modulate biochemical signals – for example, through eliciting conformational changes at the molecular level. The buildup of mechanical stress, however, is likely limited by breakage and formation of new adhesion complexes at the cell membrane as well as by plastic adaptation of cytoskelatal elements. Thus, the mechanically linked cytoskeletal elements may behave as a Maxwell fluid, where mechanical shear stress reflects the recent history of the local shear rate.

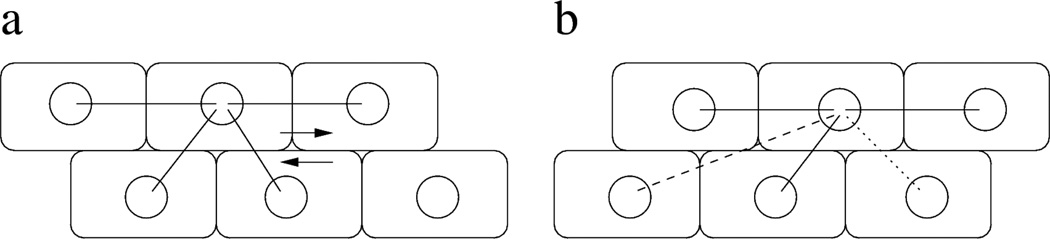
In this work we propose a simplistic model for the plastic dynamics of mechanical contacts linking adjacent cells. We explicitly keep track of connections as “springs” connecting cell centroids (Fig. 3). A minimalistic dynamics of these contacts is set by the following rules. In each time step (MCS) of the simulation

• A two adjacent, but not yet connected cells become connected with a probability p; and

• B a connection of length ℓ, between any connected two cells, is removed with a probability q(ℓ),

where the connection rate/probability 0 < p < 1 is a parameter and the disconnection rate/probability 0 < q(ℓ) < 1 is a monotonic increasing function of the link distance ℓ. As a simple choice of q(ℓ) we use

$$q(\ell )=\text{min}(q_0\ell ,1).$$ (1)

Rule A reflects that the establishment of mechanical connections requires time and spatial proximity of cells. Rule B allows a mechanical connection between cells that are non-adjacent in a 2D approximation. Such contacts may be maintained by means of three dimensional cellular protrusions. Thus, links are preserved with a small, but non-zero probability even after the loss of adjacency as resolved in the CPM. For cells adjacent to a shear-line (a line separating cells that move relative to each other) either rule ensures that cells tend to have more connections rearward than forward. Thus, when these connections are tensile, the net force exerted will act against the relative movement.

Figure 3.

Schematic representation of relative motion within a monolayer. Mechanical connection between cells are indicated by links drawn with solid lines. New connections between adjacent cells (dotted line) form with probability p. Contacts may remain between cells that are no longer adjacent (dashed line), but in each MCS break with a probability q(ℓ), proportional to the distance between the two cell centroids ℓ. This link dynamics results in more rearward connections when adjacent cell layers move in opposite directions.

To couple this mechanical effect to the cell motility apparatus, we first argue that in a monolayer of well attached cells, cells do not passively slide along the substrate driven by external forces. Instead, all cell displacements are thought to result from active cell locomotion. Therefore, mechanical stress likely moves cells only indirectly, through biochemical signals modulating cell polarity. For example, certain epithelial cell types were recently suggested to move against forces exerted on them, hence increasing the mechanical stress in the system [26]. While clearly several interesting and relevant guidance rules are possible, in this work we focus on the one recently proposed by [23]: cells actively minimize the amount of shear within the monolayer. In particular, we assume that active cell motion guidance in Eq. (10) has two components:

$$w=w_p+w_a$$ (2)

where w_p is the bias representing internal polarity (see [6] and Methods) and w_a takes into account the intercellular adhesion links as

$$w_a=\sum _i\mathrm{\Delta }{\mathrm{x⃗}}_i{\mathrm{F⃗}}_i.$$ (3)

In expression (3) Δx⃗_i denotes the displacement of the center of mass of cell i during the elementary step considered. The net mechanical force exerted by the links on cell i is given as

$${\mathrm{F⃗}}_i=\sum _{j\in C_i}f(r_{ij})\frac{{\mathrm{x⃗}}_j-{\mathrm{x⃗}}_i}{r_{ij}},$$ (4)

where C_i denotes the set of cells that are connected to cell i, r_ij denotes the distance between cells i and j and x⃗_i is the center of mass of cell i. Eqs. (3) and (10) express the assumption that cell movement is less likely if it needs to perform mechanical work. The force between two cells is assumed to depend on the distance between them: it is repulsive (or attractive) when representing compressive (or tensile) strain between the cells. For simplicity, we have chosen the functional form of a linear spring for the force-distance relation as

$$f(r)=k(r-r_0).$$ (5)

The spring constant k sets the weight of these interactions relative to the polarity P and CPM parameters: the surface penalty factors α, β and (inverse) compressibility λ. The equilibrium spring length r₀ was chosen as the target cell radius: $r_0=\sqrt{A_0/\pi }$. Thus, the bias (3) makes those elementary steps more likely that move the cells toward the directions of net forces – steps that tend to reduce the total amount of stress between the cells.

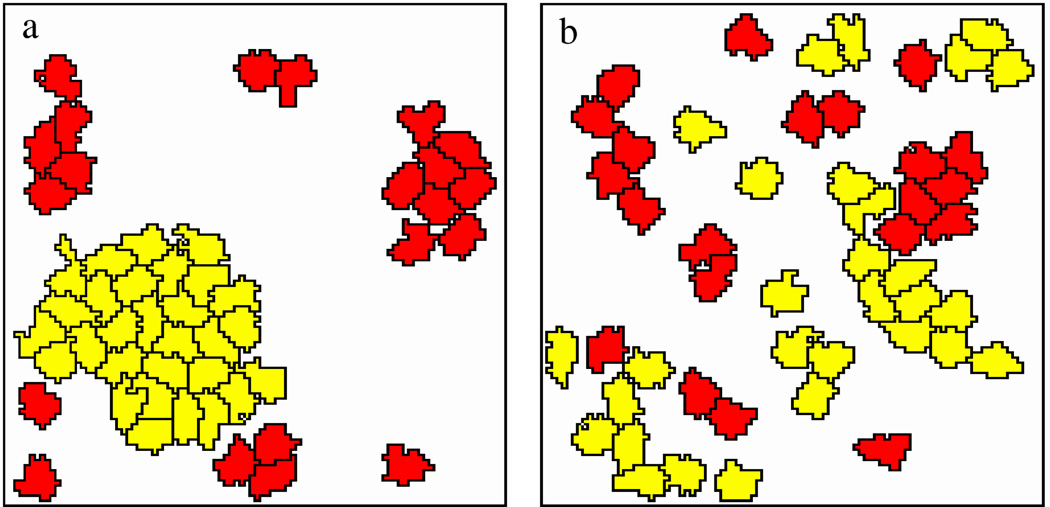
To demonstrate that the proposed rules indeed result in plausible group behavior, model simulations were performed in a closed domain with parameters that are conductive to the formation of stable cell-cell contacts (q₀ ≪ 1). As shown in Fig. 4, adhesive and motile cells aggregate into a single, moving cluster. In contrast, adhesive but not actively moving cells remain scattered in small groups as the diffusive motion of large clusters diminishes.

Figure 4.

Model simulations with (a) and without (b) cell-cell adhesion links. Motile (P = 1) and non-motile (P = 0) cells are represented in yellow and red, respectively. In the presence of cell-cell contacts, adhesive and motile cells aggregate into a single moving cluster. Parameters: α = 1, β = 0.5, p = 0.1, q₀ = 10⁻³, k = 0.2. See also Movie 4.

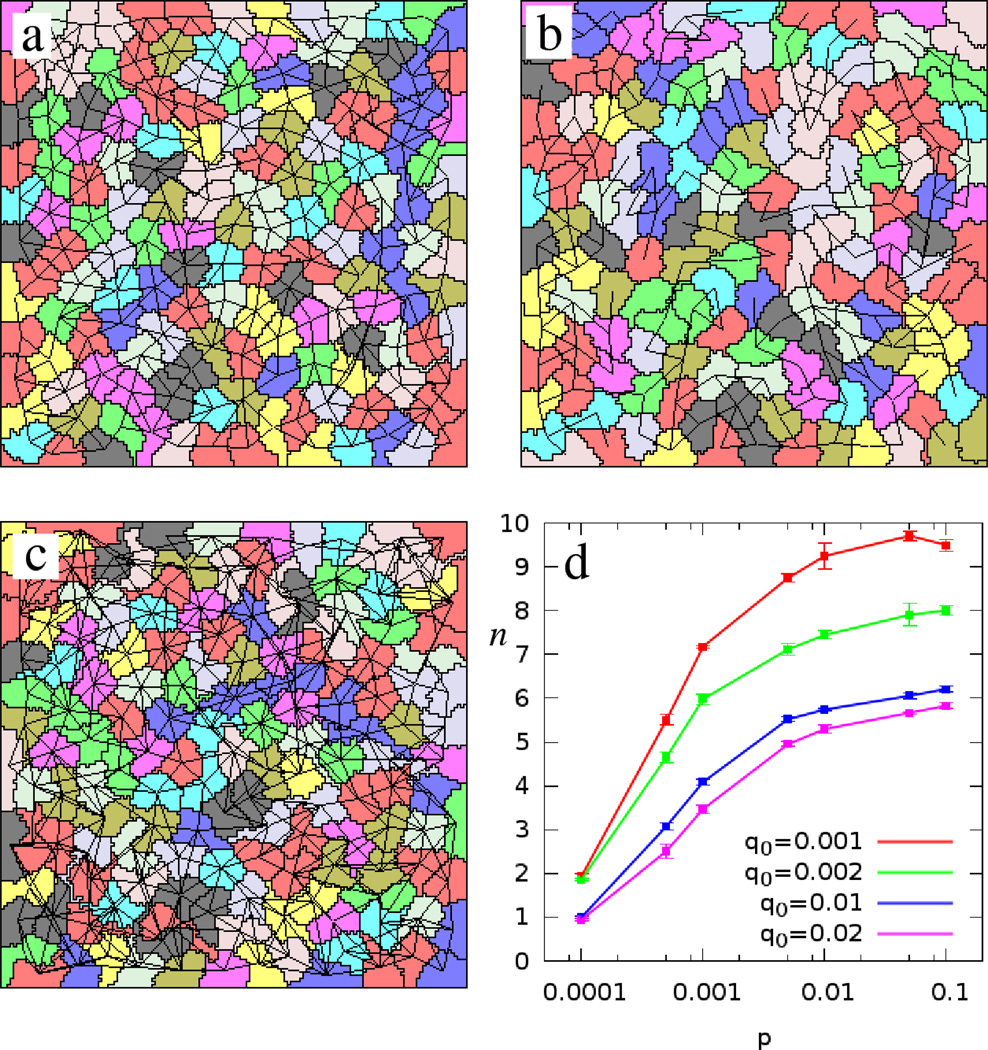
In monolayer simulations, for a given cellular motility, parameters p and q₀ determine the average connectivity of cells (Fig. 5). For small values of p, cells are sparsely connected. In contrast, for large value of p the system saturates as all possible connections are present. The stability of the contacts, q₀, increases the average cellular connectivity and may result in an extensive network of connections between non-adjacent cells. In our simulations we used the values p = 10⁻², 10⁻³ and q₀ = 10⁻² which yield a network in which an average cell is connected to four to six adjacent neighbors.

Figure 5.

Monolayer simulations with various bond dynamics parameters. Panel a shows a typical cell configuration using our standard set of parameter values: p = 10⁻³, q₀ = 10⁻² and k = 0.2. Decreasing p to p = 10⁻⁴ results in sparse connectivity (b). If the connections are maintained longer, such as in the choice of q₀ = 10⁻³, the number of links between non adjacent cells increases (c). The average number of connections per cell (n) saturates with increasing p (d). Red, green, blue and violet colors indicate q₀ values of 0.001, 0.002, 0.01 and 0.02, respectively.

2.3. Cell adhesion determines the width of self-propelled streams

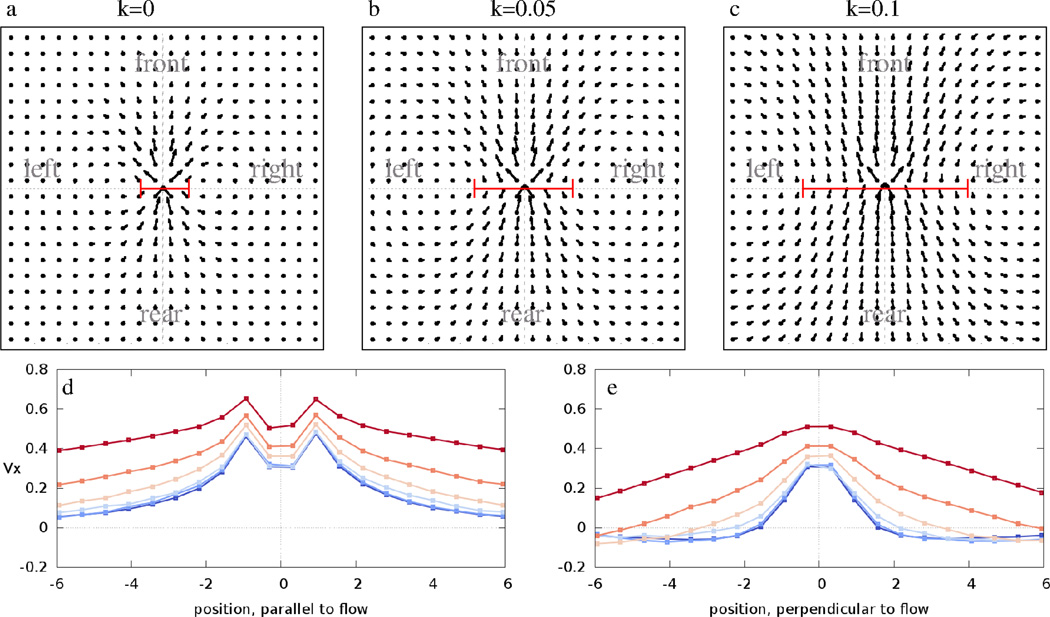
To study the emergent motion in this system and compare it to experimental findings, we calculated the average flow fields V⃗ (x⃗) in systems of 1000 cells both under closed and open boundary conditions – the latter being a patch of cohesive cells surrounded by a cell free area (compare Movies 7 and 8). The results presented below are insensitive to the choice of boundary condition. For values of parameters p and q₀ which result in bonds mostly between adjacent cells, increasing the interaction weight k increases the width of spontaneously developing streams (Fig. 6). The increase in the correlation length parallel to the local direction of flow is smaller, hence the form factor is decreased. Flow field vectors near the focal cell indicate interactions with the immediate neighbors. In the simulations these vectors tend to have a large lateral component reflecting the movement of the neighbors pushed aside during the forward progress of a cell. In the experimental data this regime is missing due to the poor resolution of the PIV velocity fields. However, in Ref [6] where individual cells were tracked, this behavior is also observable (see Fig. 3 of Ref [6]). For large enough k the system organizes into a single rotating vortex. This is indicated in panels 6d and e as a positive asymptotic value of V⃗_x for k = 0.2.

Figure 6.

Average flow fields V⃗ (x⃗) obtained from model simulations performed with p = 10⁻³, q₀ = 10⁻² and various weights, k, assigned to mechanical guidance. The grid spacing corresponds to r₀/2, half of the target cell radius. In the absence of cell-cell contacts (k = 0, panel a) we recover the highly anisotropic, narrow streams reported previously for self-propelled CPM simulations and endothelial cultures [6]. As k increases, the width of the co-moving streams increases, as indicated by bars on panels a, b, and c. The average V⃗_x values along the front-rear and left-right axis are plotted for various values of k in panels d and e, respectively. Distance is given in units of r₀. Blue to red colors indicate k = 0, 0.01, 0.02, 0.05, 0.1 and 0.2, respectively. The red lines in panels a–c indicate stream widths, as obtained by an exponential fit of the velocity profiles shown in panel e. See also Movies 5–9.

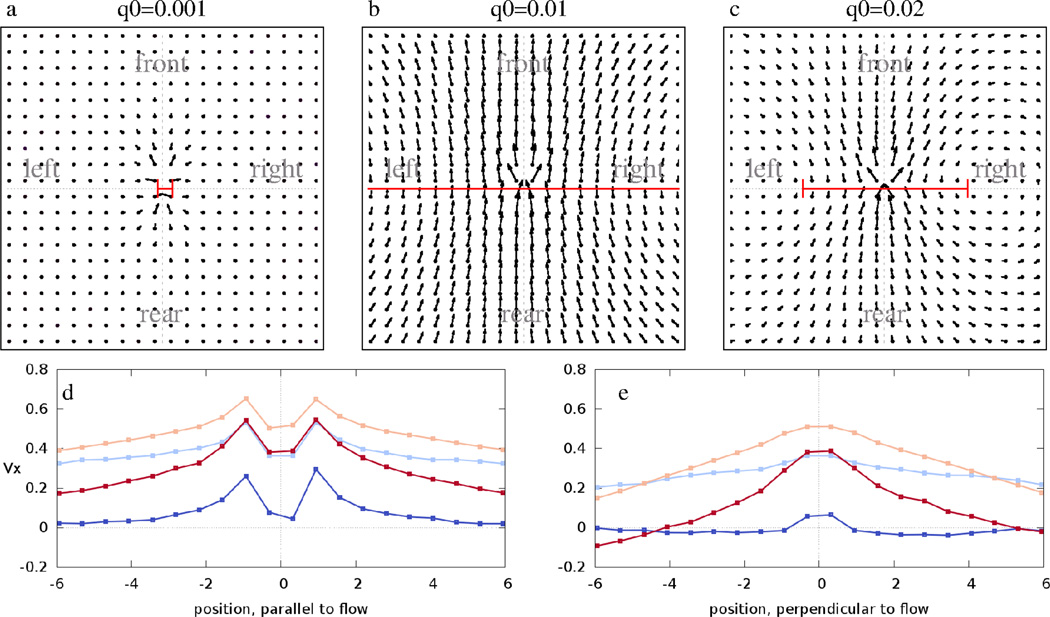
For a given value of k, the parameters p and q₀ also affect the collective flow. As Fig. 7 demonstrates, highly stable adhesion contacts (q₀ ≪ 1) arrest cell motion as cells cannot exchange neighbors. On the other hand, unstable and hence instantaneously adaptive adhesion links do not influence the system’s dynamics, so we recover the narrow-stream behavior seen with k = 0. However, in a regime characterized by intermediate bond stability, co-moving streams can become very wide.

Figure 7.

Average flow fields V⃗ (x⃗) obtained from model simulations performed with p = 10⁻³, k = 0.2 and various values of q₀. Data are presented as in Fig. 6. For long-lived contacts (q₀ = 10⁻³, panel a) the system is frozen. For an intermediate stability of bonds (q₀ = 0.01, panel b) the streams are wide. For faster contact turnover (q₀ = 0.02, panel c) the streams become narrower and similar to the highly anisotropic flows characteristic for k = 0. The average V_x values along the front-rear and left-right axis are plotted for various values of q₀ in panels d and e. Blue, light blue, orange and red colors indicate q₀ = 0.001, 0.002, 0.01 and 0.02, respectively. See also Movies 9–11.

These simulation results compare favorably with our empirical data presented in Fig. 2. In particular, disrupting cell adhesion complexes can be modeled either by decreasing k or p or increasing q₀ – the model predicts a decrease in stream width for any of these changes. Based on these simulations, we conclude that intercellular adhesion kinetics can tune the width of co-moving cell groups – ranging from highly anisotropic, single cell wide to extensive, almost isotropic flow patterns – and thus, delayed formation and turnover of intercellular bonds give rise to an effective “sheet viscosity” within the monolayer.

3. Discussion

3.1. Models of collective cell motion

The ability of coordinated, collective motion is shared by several cell types, both epithelial and mesenchymal [27]. This generic nature of the phenomenon suggests that it is available for understanding using mechanistic approaches such as cell-based models. Out of the few conceivable biological mechanisms, mechanical and biochemical guidance between cells is in the focus of current investigations. On the biochemical aspect, contact inhibition of locomotion has been shown to play a role in the coordination of cell movements [28]. More specifically, the combination of contact inhibition and chemotaxis has been suggested to result in the coordinated motion of endothelial cells [29] and neural crest cells [30].

In this work we have focused on the role of mechanical interactions to guide collective motion. The assumption, that cell-cell connections transfer forces proportional to the distance of connected cells (Eq. 5) is similar to the hypothesis proposing that cell filopodia exert traction forces proportional to their distance from the center of the cell [31]. Several previous studies have been published on the effect of spring-like forces acting between self propelled particles. The proposed models have pairwise interactions acting between units that are close neighbors in addition to a driving force representing active movement. The groundbreaking study of [32] included an alignment interaction – similar to that introduced by [33, 34] – and demonstrated that such systems can behave as self-propelled liquids and crystalline structures, depending on how easily the model units can exchange neighbors.

The alignment interaction, which assumes that the units have some knowledge of the locally prevailing average direction of motion, was substituted in [35] by a rule in which spring-like forces can displace the particles and this displacement is used to update the direction of active movement: the direction of active movement is assumed to align towards the direction of actual cell displacement. This model produced coherent collective motion in a random direction, or a circular motion within a closed simulation domain, yet streaming movements were not reported. In particular, when the noise is increased to destroy the collective flow in the high density (monolayer) regime of the particle model of Ref [35], a jammed (or “glassy” elastic) phase appears [36] instead of a self-propelled fluid-like behavior. The appearance of jammed phases is rather common in self-propelled particle models with excluded volume constrains [37]. Thus the ability of CPM cells to intercalate and relay information like hydrostatic pressure seems to be especially suitable for simulating cellular monolayers.

Streams are, however, readily produced by versions of the cellular Potts model (CPM) in which – just like in the particle model of [35] – the direction of motion is adjusted towards the direction of actual cell displacements [7, 6, 14]. The presence or lack of streams in models may reflect alternative definitions of cell interactions: while the CPM provides cell adjacency relations reminiscent of those within a monolayer, interactions within a fixed radius can introduce a local averaging, akin to increased viscosity.

A further, significant difference between the proposed CPM and most particle models with alignment interaction is that the latter is a polar interaction (when colliding, particles tend to move in a parallel direction) while the interaction between CPM cells is apolar: cells can readily glide in opposite directions, similar to the dynamics of self-propelled rods ([38, 39, 40]). The introduction of springs is designed to penalize relative movement between cells, acting as a kind of friction [41], therefore a polar interaction can be introduced gradually into the proposed model by tuning the parameters of connectivity dynamics. In particular, the appearance of a single vortex behavior seen for stable (low q₀) and sufficiently strong springs is a manifestation of a polar order, similarly to the development of a long range polar order by increasing the friction in the interacting rod model [41]. Our and other related modeling efforts thus suggest that epithelial monolayers are in a globally disordered, but locally nematically ordered state, which can transition into a globally ordered migratory state by slight adjustments of cell adhesiveness.

3.2. Mechanics of cell adhesion

Experimental data on cell aggregates demonstrated that cell adhesion is analogous to surface tension of immiscible liquids [42, 15, 43, 44, 45]. More recent results on zebrafish progenitor cell sorting suggest that the surface tension-like properties of cell-cell adhesion, such as the determination of contact area between adjacent cells, are controlled more by the mechanical stress within the cortical actin cytoskeleton than by the adhesion molecules [46]. The role of adhesion molecules are suggested to provide stability for cell connections, which builds up only after the surface tension driven contact is established [47].

The CPM captures the surface tension-like behavior of cell-cell adhesion through costs associated with free and intercellular cell boundaries. In particular, the simulated cells are more adhesive when the cost of intercellular boundaries is reduced compared to that of free boundaries. A peculiarity of the CPM formalism is that cell movement and cell adhesion are not independent: while differences in costs yield adhesion preferences, the magnitude of costs determines the extent of cell shape fluctuations. Thus, in simulations where costs are decreased along certain cell boundaries to account for stronger adhesion, cell shape fluctuations are increased simultaneously. If cell shape changes are less restricted, it is then easier to move adjacent cells in opposite directions. As discussed in [6], this latter effect is responsible for the observed decrease in stream width in simulations that represent stronger adhesion by decreased surface costs (see Fig. 10 in [6]). This intricate coupling of cell motion and cell adhesion makes the model less accessible to rigorous analysis and renders the model parameters hard to interpret [48].

In the light of the above, we argue that in simulations of epithelia it is worthwhile to decouple cell adhesivity (the force needed to separate two cells) from the freedom of cell membrane fluctuations. Although some cellular Potts models use explicit cell-cell connections for practical purposes such as keeping simulated units in a fixed order [49, 25], or in a certain location [50], to our knowledge, the separation of mechanical and surface-tension driven cell attachments has not yet been studied in detail. The formulation of a central spring connecting mechanically linked cells instead of distributed springs at the cell periphery is a practical simplification. The more realistic setup of mechanical connections distributed at the cellular periphery is more suitable in models where the cell membrane is digitized and each element has a clear identity, like in the Subcellular Element Model [19] or IBCell [51]. In a continuum limit, we expect that the delayed adaptation of cell adhesion can be represented by a Maxwell fluid, where off-diagonal components of the shear stress vanish by exponential relaxation [52]. Controlled stress relaxation within cell layers is an important and still largely unknown process, nevertheless it is a major factor in embryo morphogenesis together with cell-exerted mechanical forces [53].

3.3. Cell sheet viscosity

Here we studied the dynamical (as opposed to static) effects of cell adhesion molecules by experimentally altering the mechanical stability of cell-cell adhesions in epithelial monolayers. Collective flow of epithelial sheets is often investigated on soft, malleable substrates ([3] where the deformation of the substrate can also act as a memory to guide cells [54] as well as allow long-range mechanical communication [4, 55]. In this work we utilized a rigid substrate to eliminate the additional complexities of intercellular communication through substrate deformation. Our results clearly show that cell adhesion molecules can play a role in shaping the spontaneously emerging streams in confluent cultures. In particular, correlations perpendicular to cell movement are significantly decreased as cell adhesion is weakened. Weaker cell adhesion allows the cells to change neighbors more easily, and thus have a larger velocity difference (intercellular shear) between adjacent cells. These findings are in line with recent traction force microscopy studies of epithelial monolayers, which suggest that cells move in a way that minimizes shear stress between them [23].

Our model parameters p and q are in principle directly comparable to the dynamics of cadherin bonds and to the process of establishing mechanical linkage between cytoskeletons. We are unaware of direct empirical estimates for the speed of these processes. Introduction of function blocking peptides can interfere with cadherin function as fast as in 6 minutes [56]. In our experiments, the addition of EDTA markedly changes cell movements after 15 minutes. Both of these values are comparable to the duration of ten MCS, which represent the likely maximal rate of mechanical linkage disassembly. In our simulations the formation of new mechanical connections are rather slow, in a range of 1/p ~ 100 − 1000 MCS ≈ 1 − 10h, comparable to the time needed for two cells moving in opposite directions to pass each other.

We do not believe that our simple model can fully explain the complex movements within a cellular monolayer – thus we did not attempt to find those model parameters which would best fit the experimental data. The overall range of spatial correlations is, however, reasonable: in the experiments here we found correlation values between 150 and 300 µm, while in Ref [6] 200 µm was reported. As the typical cell size (distance between centers of adjacent cells) is 20–30 µm, the correlation length (along the streams) is between 5 and 10 cell diameters. This is the same range as indicated in Figs 6 and 7. The experimental form factor (ratio of correlation length along with and perpendicular to the flow) is in the range of 1.2 to 1.4 (and around 2 for the data shown in Ref [6]). The simulations can yield form factors in a broader range, between around 1 and 2. There are, however, differences in the structure of the flow fields obtained from experiments and simulations. In particular, movement vectors obtained from experiments tend to be parallel with the local direction of motion while in simulations they exhibit a profound radial component, irrespective of the boundary conditions (open or closed, data not shown). This difference may indicate that cells in reality may utilize additional means to synchronize their movement.

In conclusion, we proposed a model for the dual nature of cell-cell adhesion in epithelial monolayers: spring-like connections that provide mechanical stability, and the usual CPM adhesion providing surface-tension driven attachment. By reproducing the experimental velocity-velocity correlations, we show how multicellular streaming behavior can be explained by mechanical cell-cell interactions and spontaneous directed motility. We expect these features also present in more complex problems, such as tumor invasion or wound healing processes.

4. Methods

4.1. Cell culture

Cell cultures were made of commercially available immortalized human keratinocyte cell line HaCaT. Cells were kept in Dulbeccos Modified Eagle Medium (DMEM, Sigma) supplemented with 10% fetal bovine serum (GIBCO), 4 mM L-glutamine, 100 U/ml penicillin, 0.1 mg/ml streptomycin, 0.25 g/ml amphotericin B (Sigma) at 37°C in a humidified incubator with 5% CO₂ atmosphere in tissue culture dishes (Greiner). After brief incubation with 0.5 mg/ml trypsin and 0.2 mg/ml EDTA (Sigma) in PBS (phosphate buffered saline, 0.1M phosphate, 0.9% NaCl, pH 7.4, GIBCO), cells were rinsed and seeded in tissue culture dishes. To achieve a uniformly high cell density, 10⁵ cells/cm², the cell suspension was initially placed in an area limited by a 8 mm diameter cloning ring. This barrier was removed right after the cells attached to the substrate. The resulting confluent monolayer with a freely moving edge was observed by time-lapse videomicroscopy for up to 40 hours.

4.2. Calcium chelation

To decrease the concentration of free extracellular Ca²⁺ ions ethylene diamine tetraacetic acid (EDTA) was added to the medium in concentrations ranging from 1 mM to 2 mM. EDTA forms complex with free calcium and the resultant low [Ca²⁺] results in the disruption of homophilic intercellular bonds between cadherins, the cells calcium-dependent adhesion molecules.

4.3. Automated microscopy

Time-lapse recordings were performed on a computer-controlled Leica DM IRB inverted microscope equipped with a Marzhauser SCAN-IM powered stage and a 10× N-PLAN objective with 0.25 numerical aperture and 17.6 mm working distance. The microscope was coupled to an Olympus DP70 color CCD camera. Imaged cell cultures were kept at 37C in humidified 5% CO₂ atmosphere in tissue culture grade Petri dishes (Greiner). Phase contrast images of cells were collected consecutively every 10 minutes from each of the microscopic fields (n = 16) for various durations ranging from 30 to 40 hours.

4.4. Image Analysis

Cell displacements are estimated for a pair of images by particle image velocimetry (PIV), using the algorithm of [24] implemented in MatLab (Mathworks, Inc.). Briefly, the displacement field is first estimated using large image segments. These estimates are refined in the second step by using smaller image segments which are less specific but allow better spatial resolution.

The local spatial correlations of cell movements are characterized by the average flow field, V⃗ (x⃗), that surrounds moving cells. For a given configuration of cell positions and velocities this measure assigns a reference systems co-aligned with the movement of each cell, and averages the velocity vectors observed at similar locations x⃗ (e.g., immediately in front, behind, left and right). The vectors of V⃗ (x⃗) diminish in a hypothetical ensemble of statistically independent cells, as they are averages of independent random vectors. As described in detail in [6]:

$$\overrightarrow{V}(\overrightarrow{x})={\langle R_{-\phi (\overrightarrow{x}\prime ,t)}\mathrm{\Delta }\overrightarrow{X}(\overrightarrow{x}“,t)\rangle }_{\overrightarrow{x}\prime ,\overrightarrow{x}″,t},$$ (6)

where R_φ is the operator for a 2D rotation with an angle φ, and φ(x⃗, t) denotes the direction of the velocity vector at time t and location x⃗ relative to an arbitrarily chosen reference direction. The 〈…〉_{x⃗0,x⃗“,t} average is calculated over various time points t and all possible location pairs x⃗′, x⃗″ that satisfy

$$\mathrm{x⃗}\prime -\mathrm{x⃗}“\approx R_{\phi (\mathrm{x⃗}\prime ,t)}(\mathrm{x⃗}).$$ (7)

4.5. The Cellular Potts Model

In the CPM approach a non-negative integer value σ is assigned to each lattice site x⃗ of a two-dimensional grid and cells are represented as simply connected domains, i.e., a set of adjacent lattice sites sharing the same label σ. A goal function u (‘energy’) is assigned to each configuration, which guides cell behavior by distinguishing between favorable (low u) and unfavorable (high u) configurations. The simplest choice of u is

$$u=\sum _{<\mathrm{x⃗},\mathrm{x⃗}\prime >}{J}_{\sigma (\mathrm{x⃗}),\sigma (\mathrm{x⃗}\prime )}+\lambda \sum _{i=1}^N\mathrm{\Delta }{A}_i^2,$$ (8)

where the first term enumerates and penalizes cell boundaries and the second term is responsible for maintaining a preferred cell area [57]. The first sum goes over pairs of adjacent lattice sites. For a homogeneous cell population the J_i,j interaction matrix (0 ≤ i, j ≤ N) is given as

$$J_{i,j}=\{\begin{array}{cc}0,\hfill & \text{for}i=j\hfill \\ \alpha ,\hfill & \text{for}ij>0\text{and}i\ne j(\text{intercellular boundary})\hfill \\ \beta ,\hfill & \text{for}ij=0\text{and}i\ne j(\text{free cell boundary}).\hfill \end{array}$$ (9)

The second sum in Eq. (8) goes over the cells. For each cell i the deviation of its area from a pre-set value is denoted by ΔA_i. Parameters α, β and λ are used as weights to tune model behavior such as the smoothness of cell boundaries or variation of cell sizes.

Cell movement is the result of a series of elementary steps. Each step is an attempt to copy the spin value onto a random lattice site b⃗ from a randomly chosen adjacent site a⃗, where σ(a⃗) ≠ σ(b⃗). This elementary step is executed with a probability p(a⃗ → b⃗). If the domains remain simply connected the probability assignment rule ensures the maintenance of a target cell size, adhesion of cells and active cell motion. For convenience and historical reasons p is given as

$$\text{ln}p(\mathrm{a⃗}\to \mathrm{b⃗})=\text{min}[0,-\mathrm{\Delta }u(\mathrm{a⃗}\to \mathrm{b⃗})+w(\mathrm{a⃗}\to \mathrm{b⃗})],$$ (10)

where, as specified below in detail, w represents a bias responsible for the cell-specific active behavior considered, u is the goal function to be minimized, and Δu(a⃗ → b⃗) is its change during the elementary step considered. Since updating each lattice position takes more steps in a larger system, the elementary step cannot be chosen as the measure of time. In a 2D system of linear size L the usual choice for time unit is the Monte Carlo step (MCS), defined as L² elementary steps (irrespective whether executed or not) [58].

While u evaluates configurations, w is assigned directly to the elementary steps and therefore allows the specification of a broader spectrum of cellular behavior. In the model for active cell motility a polarity vector p⃗_k (representing spontaneous cell polarity [59]) is assigned to each cell k and the probability is increased of those elementary conversion steps that advance the cell center in the direction parallel to p⃗_k as

$$w_p(\sigma (\mathrm{a⃗})\to \sigma \prime )=P\sum _k\frac{\mathrm{\Delta }{\mathrm{x⃗}}_k(\sigma (\mathrm{a⃗})\to \sigma \prime ){\mathrm{p⃗}}_k}{|{\mathrm{p⃗}}_k|}.$$ (11)

Parameter P sets the magnitude of the bias and Δx⃗_k represents the displacement of the center of cell k during the elementary step considered. Cell polarity vectors are updated by assuming a spontaneous decay and a positive feedback from cell displacements. In each MCS the change in p⃗_k is

$$\mathrm{\Delta }{\mathrm{p⃗}}_k=-\frac{{\mathrm{p⃗}}_k}{T}+\mathrm{\Delta }{\mathrm{x⃗}}_k,$$ (12)

where parameter T, the polarity decay time, is the characteristic time needed to change cell polarity and Δx⃗_k is the total displacement of the center of cell k over the whole MCS considered.

During model simulations, immutable lattice cells at the periphery of the simulation domain form a closed boundary condition. By utilizing the surface tension-like feature of the CPM, a free boundary condition can also be implemented by using cohesive cells (α = β = 1) and starting the system with a cohesive patch of cells in the center of the simulation domain.