Action Potential Energetics at the Organismal Level Reveal a Trade-Off in Efficiency at High Firing Rates

Abstract

The energetic costs of action potential (AP) production constrain the evolution of neural codes and brain networks. Cellular-level estimates of AP-related costs are typically based on voltage-dependent Na⁺ currents that drive active transport by the Na⁺/K⁺ ATPase to maintain the Na⁺ and K⁺ ion concentration gradients necessary for AP production. However, these estimates of AP cost have not been verified at the organismal level. Electric signaling in the weakly electric fish Eigenmannia virescens requires that specialized cells in an electric organ generate APs with large Na⁺ currents at high rates (200–600 Hz). We measured these currents using a voltage-clamp protocol and then estimated the energetic cost at the cellular level using standard methods. We then used this energy-intensive signaling behavior to measure changes in whole-animal energetics for small changes in electric discharge rate. At low rates, the whole-animal measure of AP cost was similar to our cellular-level estimates. However, AP cost increased nonlinearly with increasing firing rates. We show, with a biophysical model, that this nonlinearity can arise from the increasing cost of maintaining AP amplitude at high rates. Our results confirm that estimates of energetic costs based on Na⁺ influx are appropriate for low baseline firing rates, but that extrapolating to high firing rates may underestimate true costs in cases in which AP amplitude does not decrease. Moreover, the trade-off between energetic cost and firing rate suggests an additional constraint on the evolution of high-frequency signaling in neuronal systems.

Introduction

Action potentials (APs) produced by excitable cells such as neurons and muscle come at an energetic cost. This arises from the ATP required by the Na⁺/K⁺ ATPase to maintain the electrochemical gradients of Na⁺ and K⁺ ions that are necessary for normal resting potentials and ion flow across the membrane (for review, see Attwell and Laughlin, 2001; Niven and Laughlin, 2008; Howarth et al., 2012). Estimates of AP cost in neurons are typically based on measurements of Na⁺ influx, which drives Na⁺/K⁺ ATPase activity. Depending on neuron type, these estimates vary from 10⁷ to 10⁹ ATP molecules per AP (Alle et al., 2009; Sengupta et al., 2010; Hallermann et al., 2012). Further, the consistency of Na⁺ currents over a range of AP firing rates suggests that the ongoing cost of AP production will be proportional to the firing rate (i.e., the cost of increasing AP frequency by 1 Hz is the cost of 1 additional AP per second independent of baseline firing rate). In fly photoreceptors, which do not produce APs, estimates of signaling costs have been verified experimentally (Niven et al., 2007). However, for spiking neurons, measuring the energetic costs of AP production directly at the organismal level has proven more difficult.

In this study, we evaluated the organismal costs of AP production in Eigenmannia virescens, a weakly electric fish that generates a quasi-sinusoidal electric organ discharge (EOD) at frequencies of 200–600 Hz (Hopkins, 1974; Scheich, 1977; Heiligenberg, 1991; Moller, 2005). These fish are nocturnal and rely on their electric sense to navigate, communicate, and capture prey in the dark. The EOD is generated by specialized electrogenic cells (electrocytes) in the electric organ that fire synchronous APs for each EOD cycle (Fig. 1A). Due to the high firing rates and large currents involved, AP production underlying the EOD is thought to involve a large fraction of the whole-animal energy budget (Salazar and Stoddard, 2008; Salazar et al., 2013). Therefore, changes in EOD frequency (EODf) should result in measurable changes in energy consumption. E. virescens behaviorally modulates EODf during encounters with a conspecific of similar frequency: the lower-frequency fish decreases its EODf and the higher-frequency fish increases its EODf such that the frequency difference between fish becomes larger (Heiligenberg, 1991). This so-called jamming avoidance response (JAR) can be elicited using an artificial electrical stimulus to mimic a conspecific's EOD. We used the JAR to measure changes in whole-animal energy consumption for small changes in EOD frequency and, for the first time, were able to compare estimates of AP cost at the cellular and whole-animal levels.

Figure 1.

Cellular basis of the electric organ discharge. A, Illustration of E. virescens showing the location of the electric organ (EO; blue dashed line), and the quasi-sinusoidal EOD waveform (top right). B, Schematic of a single electrocyte from the EO (blue outline, left) showing Na⁺ channels and the electrogenic Na⁺/K⁺ ATPase. Electrophysiological recordings of pharmacologically isolated Na⁺ current (bottom right) were made in voltage clamp with a representative action potential as the voltage command waveform (top right).

Materials and Methods

Animals.

Wild-caught E. virescens purchased from a tropical fish supplier were maintained in community aquaria on a 12 h dark/12 h light photoperiod and fed bloodworms ad libitum three times per week. Water temperature was held at 28 ± 0.5°C. Experimental procedures were approved by the University of Ottawa Animal Care Committee (BL-229) or the University of Oklahoma Institutional Animal Care and Use Committee (R12–025) and conformed to the guidelines of the Canadian Council on Animal Care or the United States Public Health Service for the care and use of laboratory animals.

Electrophysiology.

Procedures for current-clamp and two-electrode voltage clamp of electrocytes have been described and validated previously (Ferrari and Zakon, 1993; Markham et al., 2013). We harvested a 1.5–2 cm section of the tail from fish of either sex, removed the overlying skin, and pinned the exposed electric organ in a Sylgard recording dish containing physiological saline at room temperature (23 ± 1°C). E. virescens electrocytes are cylindrical cells ∼800–1000 μm long and 100–300 μm in diameter, innervated on the posterior face of the cell (Schwartz et al., 1975). The most posterior portion of the electrocyte is the region with voltage-gated ion channels; the anterior portion of the cell exhibits only linear leak. The electric organ comprises two bilateral cylindrical structures with ∼5–6 columns of electrocytes per side (Schwartz et al., 1975). Therefore, for electric organ lengths from 80 to 150 mm, estimates range from 1000 to 2000 electrocytes in total.

Electrophysiological recordings were made with an Axoclamp 900 amplifier and data were acquired with a Digidata 1440 interface (50 kHz sampling rate, no filtering) controlled by pClamp 10 software (Molecular Devices). A two-electrode configuration was used for both current-clamp and voltage-clamp procedures. Membrane potential was recorded with a unity-gain head stage (HS9Ax1; Molecular Devices) and current was injected with a ×10 head stage (HS9Ax10; Molecular Devices) to allow delivery of currents up to 20 μA. Microelectrodes were pulled from thin-wall borosilicate glass to resistances of 0.9–1.2 MΩ when filled with 3 m KCl. The bath was grounded via a chlorided silver wire inserted into a 3 m KCl agar bridge. Both the voltage-monitoring and current-passing electrodes were inserted in the caudal 100 μm of each cell and a grounded shield was placed between the electrodes to prevent capacitive coupling at the required amplifier gains of 10,000–25,000 V/V.

We recorded APs in current-clamp mode by delivering 4 ms depolarizing current steps and increasing current intensity until the step reliably elicited APs. In voltage-clamp mode, we isolated I_Na by addition of 1 mm Ba²⁺ and 5 mm TEA to block all voltage-gated K⁺ currents. In all voltage-clamp procedures, we used a p/6 leak subtraction protocol to subtract linear leak and capacitative currents from the final current record. From a holding potential of −85 mV, we confirmed adequate voltage control and space clamp by standard voltage-clamp recordings of I_Na. For AP-clamp protocols, we used digitized AP waveforms as the voltage-command protocol.

Whole-animal respirometry.

The rate of oxygen consumption (ṀO₂) was measured by intermittent closed-system respirometry (Steffensen, 1989) in 9 fish (1.8 ± 0.3 g). A clear Plexiglas cylinder (∼100 ml volume) thermostatted by immersion in a water bath (28 ± 0.5°C) served as the respirometer. Water PO₂ was recorded continuously by pumping water past a thermostatted O₂ electrode (E-101; Analytical Sensors) and back to the respirometer. The O₂ electrode was connected to a blood gas analyzer (BGM 200; Cameron Instruments) and data acquisition system (Biopac Systems). Fish of either sex were acclimated overnight to the respirometer, and ṀO₂ and EODf were then measured under control conditions. EOD was recorded in 10 s clips using Teflon-coated silver-wire electrodes (0.38 mm diameter, insulated to the tip; WPI) placed at each end of the respirometer. The signal was amplified, filtered with a WPI DAM 50 Differential Amplifier (10× amplification, low- and high-frequency cutoffs of 10 Hz and 3 kHz, respectively), and recorded via a laptop sound card (44 kHz sample rate). The JAR was elicited using a sine-wave signal generated with Labview (National Instruments) and delivered, via the sound card and stimulus isolation unit, across the fish's body using two Teflon-coated silver-wire electrodes. The sine-wave signal was maintained at 3 Hz below the fish's EODf (difference frequency clamped at Df = −3 Hz) to drive EODf upward for 30 min. We defined a JAR as an increase in EODf of >5 Hz. We were not able to reliably measure EOD amplitude during these experiments, so we conducted a separate set of experiments without the respirometry setup using nine additional fish (of either sex); methods for eliciting the JAR were similar except the stimulus duration was 10 min. All data are reported as mean ± SEM unless stated otherwise.

Energetics calculations.

To convert ṀO₂ into units of ATP use, we first assumed that anaerobic processes are not involved and that glucose is the dominant fuel (for review, see Howarth et al., 2012; Salazar et al., 2013). Oxidation of a single molecule of glucose requires 6 molecules of O₂ and yields ∼30 molecules of ATP. We then converted ṀO₂ from μmol g⁻¹ h⁻¹ to O₂ molecules/s and multiplied this value by 5 ATP/O₂, giving the desired units. In the present experiments, resting ṀO₂ was 5.8 ± 1.0 μmolg⁻¹ h⁻¹ (n = 9 fish), which translated to 7.0 × 10¹⁵ ATP/s for resting metabolic rate. For electrocyte calculations, standard methods were used to estimate ATP consumption based on total Na⁺ ion flux during the action potential (Alle et al., 2009; Sengupta et al., 2010).

Electrocyte model.

The biophysical model of an electrocyte was developed and described previously (Markham et al., 2013). Here, we summarize the model equations along with associated parameter values (as in Markham et al., 2013; Table 1). Equation 1 shows the current balance equation relating the transmembrane voltage (V_m) to the dynamic variables representing the transient and persistent Na⁺ currents (I_NaT and I_NaP, where γ is the fraction of I_NaP) and the Na⁺-activated K⁺ current; the inward rectifier (I_R) and leak current (I_L) depend on V_m with no gating dynamics. External current stimuli were represented by I_ext, which in this study comprised single 0.2 ms square pulses of amplitude 20 μA delivered at different frequencies.

The dynamics and voltage-dependent relationships of each current are given by Equations 2–6:

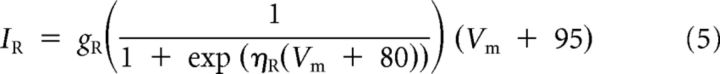The dynamics of the gating variables are given by Equations 7–9, where j = m, n, or h:

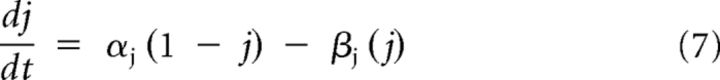The Na dependence of I_KNa was modeled by the gating variable, s, which is a function of the Na⁺ ion concentration [Na] at the cytoplasmic face of the K_Na channels (Equations 10 and 11):

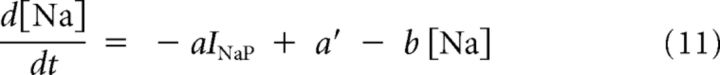Table 1.

Parameter values for the electrocyte model

gNa = 400–1600 μS	gKNa = 2000 μS	a = 2.5 mm ms−1 nA−1
γ =0.1	kαn = 1.209 ms−1	a′ = 12.5 mm ms−1
kαm = 7.6 ms−1	ηαn = 0.00948 mV−1	b = 0.5 ms−1
ηαm = 0.0037 mV−1	kβn = 0.4448 ms−1	kf = 10 mm−1 ms−1
kβm = 0.6894 ms−1	ηβn = −0.01552 mV−1	kb = 2.0 ms−1
ηβm = −0.0763 mV−1	gR = 300 μS
kαh = 0.00165 ms−1	ηR = 0.22 mV−1
ηαh = −0.1656 mV−1	gL = 0.76 μS
kβh = 0.993 ms−1	C = 50 nF
ηβh = −0.0056 mV−1

Results

Cellular-level estimate of action potential cost

To measure the energetic cost of an AP at the single-cell level, we recorded pharmacologically isolated Na⁺ currents (I_Na) from individual electrocytes under voltage-clamp conditions using an AP command waveform (Fig. 1B). Integrating I_Na over the AP duration yields the total Na⁺ ion flux during an AP (10.1 ± 1.0 μA-ms; n = 8 cells). Given that 1 ATP molecule is required by the Na⁺/K⁺ ATPase for every 3 Na⁺ ions transported, we estimated that electrocytes require 2.1 ± 0.2 × 10¹⁰ ATP molecules per AP. This cost is two orders of magnitude more than that estimated for mammalian neurons (for review, see Howarth et al., 2012; Hallermann et al., 2012), much more than the twofold increase expected from a decrease in temperature from 37°C to 23°C (the temperature used in our recordings) (Yu et al., 2012). This confirms the relatively high cost of an electrocyte AP and suggests that increasing EODf will result in a significant and measurable increase in whole-animal energy consumption.

Whole-animal respirometry and the JAR

We used closed-system respirometry to measure the rate of O₂ consumption (Steffensen, 1989) while delivering a sine-wave jamming stimulus at a frequency 3 Hz below the fish's EODf (Heiligenberg, 1991). We were able to elicit JARs in 6 of 9 fish (ΔEODf = 9.2 ± 0.7 Hz) and found that whole animal ṀO₂ increased by 0.18 ± 0.06 μmol g⁻¹ h⁻¹ (2.7 ± 0.4%) for every 1 Hz increase in EODf. We noted, however, that this incremental cost increased exponentially with the baseline EODf of the individual fish [ΔṀO₂ (μmol g⁻¹ h⁻¹/Hz) = 0.003 · exp(0.009 · EODf); R² = 0.88, p = 0.006; n = 6 fish], suggesting that increasing EODf is more costly for fish with higher baseline EODfs (Fig. 2A, note log-linear scale). Indeed, under baseline conditions, we found that resting ṀO₂ increases exponentially with EODf in a manner consistent with incremental costs (ΔṀO₂/Hz). In other words, an exponential relationship with the same rate of rise can explain the effect of baseline EODf on resting ṀO₂ [ṀO₂ = 0.15 · exp(0.009 · EODf); R² = 0.90, p < 0.001; n = 9 fish; compare Fig. 2A,B]. We were not able to reliably measure EOD amplitude during these experiments, so we tested nine additional fish using a standard setup without respirometry. We were able to elicit JARs in 5 of these fish (ΔEODf = 7.2 ± 0.8 Hz). In the baseline condition, there was no relationship between EOD amplitude and EODf (R² = 0.02; p = 0.7), and whereas the EOD amplitude increased slightly during the JAR (4.9 ± 2.6%), the change was not significant (Shapiro–Wilk normality test, p = 0.4; paired t test, p = 0.18).

Figure 2.

AP cost at the whole-animal level depends on baseline frequency. A, Incremental cost: whole-animal oxygen consumption (ṀO₂) measured with respirometry during manipulation of EODf, expressed as incremental change on a log-linear scale. The exponential curve fit (solid black line) is given by ΔṀO₂[μmol g⁻¹ h⁻¹/Hz] = 0.003 · exp(0.009 · EODf); R² = 0.88, p = 0.006, n = 6 fish. B, Baseline cost: Resting ṀO₂ as a function of baseline EODf on a log-linear scale; ṀO₂ = 0.15 · exp(0.009 · EODf); R² = 0.90, p < 0.001, n = 9 fish. Note that the fitted line has the same exponential rate in both A and B. C, Energetic costs in ATP molecules per 1 Hz increase in frequency for different baseline frequencies on a log-linear scale: single cortical neuron (red; based on Hallermann et al., 2012), single electrocyte (green; see text), and entire electric organ (EO, blue; see text) that are assumed to be constant with baseline frequency; whole-animal EOD data from A (open symbols, curve fit in black) are reproduced for comparison.

Assuming that oxidative phosphorylation is the major source of ATP in this context (for review, see Attwell and Laughlin, 2001; Salazar et al., 2013), our data suggest that over the 300–500 Hz range of EOD frequencies in our sample, incremental costs range from 7 × 10¹³ to 4 × 10¹⁴ ATP/s for every 1 Hz increase in EODf (Fig. 2C). Interestingly, with an electric organ composed of 1000–2000 electrocytes (see Materials and Methods), the estimate we obtained for a single electrocyte (2 × 10¹⁰ ATP molecules/AP) suggests that the entire electric organ will consume from 2 × 10¹³ to 4 × 10¹³ ATP molecules for one additional EOD cycle per second (Fig. 2C, compare blue line with mammalian cortical neuron in red and the single electrocyte in green). Extrapolating the relationship derived from whole-animal data (Fig. 2A,C, black line) predicts that this range of costs would occur at baseline EOD frequencies of 180–250 Hz, similar to the low end of reported EOD frequencies in these fish (Hopkins, 1974; Scheich, 1977).

Cost of maintaining AP amplitude at high rates

To explore the possible mechanisms underlying the nonlinear increase in AP cost with firing rate, we considered a recent biophysical model of an E. virescens electrocyte (Markham et al., 2013). Using brief current pulses (20 μA, 0.2 ms) at rates up to 600 Hz, we reliably elicited APs in the model electrocyte, but found that AP amplitude (AP_amp) decreased with increasing firing rate (Fig. 3A, compare left and middle). In contrast, at the whole-animal level, we found that EOD amplitude does not change significantly with increases in frequency during the JAR. In the electrocyte model, this change in AP_amp was due to incomplete deactivation of Na⁺-activated K⁺ channels at high AP rates, leading to net increases in K⁺ current. The original AP_amp was reestablished by increasing the parameter g_Na (equivalent to increasing the number of available Na⁺ channels; Fig. 3A, right). The energetic cost of each AP in these three conditions (as estimated by Na⁺ flux) was 2.20 × 10¹⁰, 2.18 × 10¹⁰, and 2.88 × 10¹⁰ ATP molecules/AP, respectively; this suggests that increasing firing rate alone does little to raise energy demand per AP and may lead to lower costs (Hasenstaub et al., 2010). Conversely, maintaining AP_amp at high firing rate results in higher costs. To illustrate this effect over a range of parameter values, we plotted energetic cost as a function of both firing rate and g_Na (Fig. 3B). Also shown on the color map are contours of constant AP_amp (Fig. 3B); their upward curvature describes the nonlinear increase in cost with firing rate. In addition, maintaining AP_amp at high rate comes with an increasingly high cost as baseline AP_amp increases (Fig. 3B, compare filled symbols with the 121 mV contour at 200 and 500 Hz).

Figure 3.

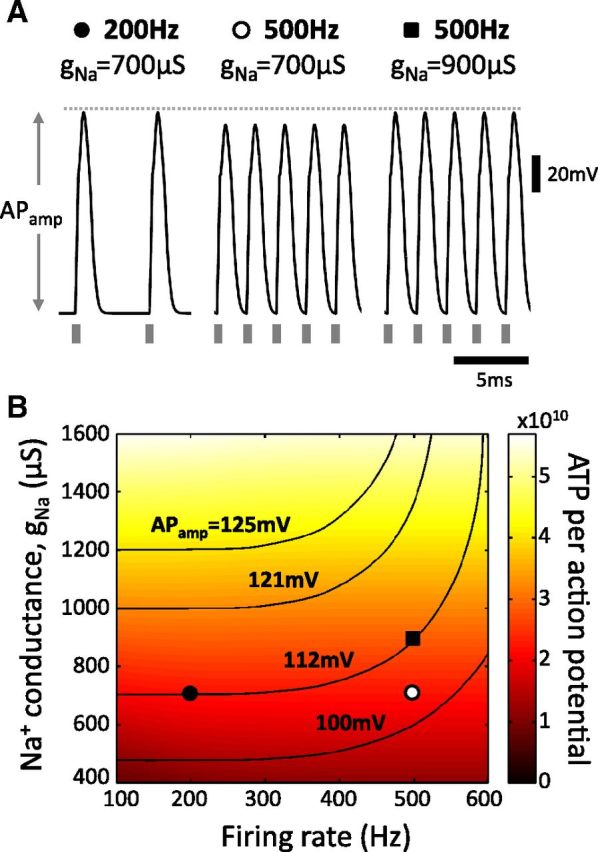
Biophysical model of a single electrocyte shows that increasing cost is due to maintenance of action potential amplitude. A, Membrane potential traces for three different conditions. APs were elicited by current pulses (gray bars; 20 μA, 0.2 ms) at 200 or 500 Hz for two different levels of Na⁺ channel expression (i.e., the parameter g_Na at 700 or 900 μS). Left and middle, Comparison shows a reduction in AP_amp with the increase in stimulus frequency. Right, AP_amp returns to original level when g_Na is increased. Each condition is labeled with a symbol to allow comparison with the survey of parameter space in B. B, Color map of energetic cost in ATP molecules per AP (dark red: low cost; white: high cost; color bar indicates scale) as a function of AP firing rate (Hz) and Na⁺ conductance (g_Na) in the model electrocyte. ATP cost was calculated from Na⁺ currents, as described in the text. Black contours indicate lines of constant AP_amp in the same parameter space. Symbols correspond to the parameter sets from A.

Discussion

The high rates of synchronous APs and the large ionic currents underlying EOD production in the weakly electric fish allowed us to measure the energetic cost of an AP at the whole-animal level. Previously, organismal-level energetics have been used to constrain estimates of AP cost (Attwell and Laughlin, 2001; Lennie, 2003; Sengupta et al., 2010), but the methods involved did not allow the direct and simultaneous comparison of AP firing rates and oxygen consumption. Our results confirm that even small changes in EODf result in measurable changes in whole-animal energy consumption. Moreover, for low EODf, measurements of AP cost at the whole-animal level are in agreement with estimates based on cellular-level experiments. The increased cost at high EODf, however, is not reflected in the cellular estimates. This discrepancy is likely a result of experimental conditions: during electrophysiological recordings, electrocytes are isolated from their normal synaptic inputs and do not fire spontaneously. Nonetheless, if every AP (or EOD cycle) was independent, increasing firing rate (or EODf) should result in a proportional increase in energetic cost (the cost of adding a given number of APs per second). Indeed, in a low-frequency (∼25 Hz) pulse-type weakly electric fish, ṀO₂ increased linearly with EODf (Salazar and Stoddard, 2008). This was not the case in our study of a high-frequency wave-type fish, in which energy consumption increased exponentially with EODf. Our modeling results suggest that constraints on AP_amp can explain this increased cost with firing rate.

Consistent with our model's prediction that increases in g_Na are necessary to maintain AP_amp at high EODf, some species of electric fish, including E. virescens, rapidly regulate electrocyte AP and Na⁺ current amplitudes to produce diurnal and socially induced variations in EOD amplitude (Salazar and Stoddard, 2008; Markham et al., 2009; Salazar et al., 2013). These changes are mediated by the trafficking of Na⁺ channels into the plasma membrane of the electrocyte, a process that can occur in a matter of minutes (Markham et al., 2009, 2013). The same mechanisms are likely involved in maintaining EOD amplitude with increasing EODf during the JAR. Also consistent with our findings, EOD amplitude does not typically vary with EODf across individuals and, in some cases, dominance is communicated by EODf (Fugère et al., 2011). This dominance relationship is also consistent with a strong dependence of energetic cost on EODf (both incremental and baseline; Fig. 2). That said, our modeling results suggest that EOD amplitude should decrease at high EODf unless additional Na⁺ current is available (Fig. 3), which implies that a frequency-dependent energetic cost would be incurred simply to maintain EOD amplitude at a constant level.

Other factors in addition to changes in AP_amp may also underlie increased AP cost at high firing rates. In electric fish, the ion channels underlying AP generation enhance efficiency at high firing rates: the rapid kinetics of Na⁺ channels (Zakon et al., 2008; Hasenstaub et al., 2010) and Na⁺-activated K⁺ channels (Markham et al., 2013) allow fast repolarization and recovery after an AP. For very high frequencies, however, significant trade-offs are likely because both accumulation of extracellular K⁺ and slow kinetics of the persistent Na⁺ currents involved in I_KNa activation may counteract increases in efficiency. In many neural systems, maintaining AP_amp is necessary for reliable information transmission, but we have shown that this becomes increasingly costly at high firing rates. Therefore, the evolution of high-frequency neuronal signaling likely involves similar trade-offs between energetic cost and firing rate.