Abstract
PET imaging is affected by a number of resolution degrading phenomena, including positron range, photon non-collinearity and inter-crystal blurring. An approach to this issue is to model some or all of these effects within the image reconstruction task, referred to as resolution modeling (RM). This approach is commonly observed to yield images of higher resolution and subsequently contrast, and can be thought of as improving the modulation transfer function (MTF). Nonetheless, RM can substantially alter the noise distribution. In this work, we utilize noise propagation models in order to accurately characterize the noise texture of reconstructed images in the presence of RM. Furthermore we consider the task of lesion or defect detection, which is highly determined by the noise distribution as quantified using the noise power spectrum (NPS). Ultimately, we use this framework to demonstrate why conventional trade-off analyses (e.g. contrast vs. noise, using simplistic noise metrics) do not provide a complete picture of the impact of RM and that improved performance of RM according to such analyses does not necessarily translate to the superiority of RM in detection task performance.”
1. Introduction
Positron emission tomography (PET) is a powerful in vivo molecular imaging modality. Nonetheless, PET imaging is affected by a number of resolution degrading factors, including positron range, photon non-collinearity and inter-crystal scattering and penetration, which translate to undesired cross-contamination between adjacent functional regions with distinct activities, referred to as the partial volume effect (PVE) (Soret et al., 2007)(Rahmim and Zaidi, 2008).
This issue has been tackled via a number of post-reconstruction partial volume correction (PVC) methods (Rousset et al., 2007) including (i) region-of-interest (ROI)-based (Mazziotta et al., 1981; Kessler et al., 1984; Rousset et al., 1998a; Du et al., 2005; Labbe et al., 1996; Aston et al., 2002) and (ii) voxel-based techniques, the latter including (a) partition-based (Videen et al., 1988; Muller-Gartner et al., 1992; Rousset et al., 1998b; Meltzer et al., 1996), (b) multi-resolution (Le Pogam et al., 2011; Shidahara et al., 2009; Boussion et al., 2006), or (c) iterative deconvolution methods (Teo et al., 2007) (Kirov et al., 2008)(Boussion et al., 2009). These techniques (with the exception of iterative deconvolution) commonly require access to well-registered anatomic (e.g. MRI) images. In addition, they typically involve a number of simplifying assumptions, and/or can lead to increased noise levels.
A different approach to PVC (that can also reduce image noise) has been to incorporate anatomical information within the PET image reconstruction task, as recently reviewed by Bai et al. (2013). This approach also commonly involves a number of simplifying assumptions such as uniformity of radiopharmaceutical uptake within anatomic regions (e.g. (Lipinski et al., 1997; Comtat et al., 2002)). To this end, more sophisticated approaches (Bowsher et al., 1996; Rangajaran et al., 2000; Nuyts, 2007; Somayajula et al., 2011; Tang and Rahmim, 2009; Tang et al., 2010) have been investigated, though they are often seen introduce a number of additional parameters to be further fine-tuned for particular tasks of interest.
Another possible approach to this problem is so-called resolution modeling (RM), also referred to as point spread function (PSF) modeling, that aims to model the resolution degrading phenomena within the reconstruction algorithm, which we have recently reviewed (Rahmim et al., 2013). These techniques can commonly be divided into (i) image-space (Reader et al., 2002; Reader et al., 2003)(Rahmim et al., 2003)(Rapisarda et al., 2010)(Cloquet et al., 2010)(Kotasidis et al., 2011), or (ii) projection-space methods (Lecomte et al., 1984)(Selivanov et al., 2000; Strul et al., 2003)(Moehrs et al., 2008)(Qi et al., 1998)(Alessio et al., 2006)(Tohme and Qi, 2009)(Panin et al., 2006)(Alessio et al., 2010)(Frese et al., 2003)(Lee et al., 2004)(Rahmim et al., 2008b). Theoretical analysis of differences between these two approaches has also been provided (Cloquet et al., 2010; Rahmim et al., 2013). Majority of works above focused on tracers and scanners with positron range blurring relatively negligible compared to contributions of inter-crystal blurring. However, specific modeling of positron range blurring has also been attempted in the literature: (i) for radioisotopes with highly energetic positron emissions (Bai et al., 2003)(Bai et al., 2005)(Ruangma et al., 2006)(Rahmim et al., 2008b)(Rahmim et al., 2008a)(Alessio and MacDonald, 2008), or (ii) for small animal imaging (Fu and Qi, 2010).
In any case, analysis methodology for the impact of RM varies in the literature, and the present work attempts to provide insight into how they relate to one another. While clearly improved resolution and/or contrast recovery is observed in nearly all past works, it is also the case that the noise distribution is modified, and this issue is often characterized using a range of simplified noise metrics. In Sec. 2 we briefly discuss the commonly invoked metrics in the literature, followed by a discussion of the need for more thorough quantification of the noise distribution. In Sec. 3 we elaborate upon our methodology, including how noise propagation calculations are implemented in the present work, and how they are incorporated within analytic models of detectability. Sec. 4 covers the various results, followed by discussion and summary in sections 5 and 6, respectively.
2. Noise metrics and detectability analysis in the presence of resolution modeling
2.1 Three noise metrics
In the RM literature, noise is most typically quantified using one of the following metrics:
- Spatial variance calculated for an image at a given noise realization with signal values si at any voxel i within a given ROI consisting of N voxels and having a mean m:
This can be thought of as a measure of image roughness, and in the case of multiple noise realization measurements, it can be subsequently averaged.(1) - Ensemble variance of ROI mean uptake mr across multiple noise realizations r=1…R, with the average ROI mean uptake m̅:
The above two metrics are the most commonly invoked, but there exists a third metrics that is sometimes invoked:(2) - Ensemble voxel variance for a given voxel i with values at each noise realization (r=1…R) and ensemble mean s̅i:
The above definition is for a single voxel, thus a variance image can also be generated, and/or the values can be averaged over an ROI.(3)
The above three noise metrics are studied in Sec. 4.3, and their analytic inter-relations are discussed in Sec. 5.1. However, as we discuss and demonstrate in this work, these noise metrics provide a limited picture of the full impact of RM.
2.2 Detection task performance
The above noise metrics are not sufficient to assess detection, e.g. for a defect or lesion, and more thorough analysis and evaluation is required. To see this, let us consider a system with stationary noise, and the noise power spectrum (NPS) as the Fourier transform of the noise covariance. For a task involving detection of a difference signal Δs(r), its Fourier transform denoted by ΔS(p), where r and p respectively denote the spatial- and frequency-domain coordinates, the inter-class (lesion absent vs. present) signal-to-noise ratio (SNR) is given by (e.g. Ref. (Wagner and Brown, 1985)):
| (4) |
The above expression can be derived for an ideal observer with signal- and background-known-exactly (SKE/BKE) having (a) Gaussian noise or (b) Poisson noise in the weak-signal limit, or (c) in the case of the linear Hotelling observer ((Barrett and Myers, 2004), Eqs. 13.238, 13.239, 13.256, respectively).
If we additionally assume an imaging system with shift-invariant resolution, we can go one step further. Consider the modulation transfer function (MTF) as the Fourier transform of the PSF, normalized by the area (volume) A of the PSF. A should ideally be ~1 with proper calibration, but may not be so especially in the case of non-linear reconstruction algorithms. For an original non-blurred difference object Δf(r), its Fourier transform given by ΔF(p), we will then have:
| (5) |
The ratio MTF2 (p) to NPS(p) is referred to as the noise-equivalent quanta (NEQ) which can be thought of as a “window” through which the observer “sees”, and thus the NEQ quantifies how much of the frequency content is transmitted through the imaging and reconstruction.
We also note that under assumption of normality of the observer metric, e.g. a linear observer under Gaussian noise, the area-under-curve (AUC) in ROC analysis is given by (Barrett and Myers, 2004):
| (6) |
where erf(z) is the error function.
Overall, it is clear that detection task performance is not determined by simplistic noise metrics, and more thorough analysis is required.
2.3 Added realism: non-prewhitened matched filtering
RM results in amplified inter-voxel correlations, as studied in this work (Sec. 43), and also previously (Rahmim et al., 2005; Tong et al., 2010; Sureau et al., 2008). In fact, a number of experiments were performed in the past to quantify the impact of correlated noise on human performance (Judy et al., 1981; Guignard, 1982; Burgess, 1984; Myers et al., 1985; Blackwell, 1998): this was due to an interest in the early 1980s to assess the effect of the correlated noise induced by tomographic imaging. Overall, it was observed that human observer task performance was degraded by noise correlations. In fact, prior to these studies, it had been hypothesized by Wagner (1978) that human observers would be inefficient when presented with noise-correlated structure, and that a non-prewhitened matched filter (NPWMF) as an observer for detection might better predict human performance compared to an observer performing prewhitening, which turned out to be true in later studies. In particular, Myers et al. (Myers et al., 1985) found that for a class of noise power spectra of the form pn, n=1,2,3,4 (p is the spatial frequency) modeled such that they yielded the same SNR for an ideal pre-whitened matched filter (PWMF) observer, human efficiency fell as n increased, a pattern that was only properly captured when transitioning to a NPWMF observer.
In the present work, we thus performed assessment of the impact of RM using both PWMF and NPWMF observers. Let us consider a SKE/BKE ideal observer study of an ROI of size n with detected signal-absent s1 and signal-present s2 distributions (which are blurred versions of the original signals f1 and f2), as mathematically put in Sec. 3.1), and with the addition of noise become g1 and g2, respectively. For a given image vector g of size n, not knowing whether it is signal-absent or present, the PWMF operator performs the following:
| (7) |
first applying the inverse of the n by n noise covariance matrix K, followed by the matched filter Δs = s2 − s1 (for an ideal observer, this difference signal is known exactly; otherwise, this can be computed by training, performing averaging and subtraction of a set of signal-present and signal-absent images, arriving at Δg̅). By contrast, NPWMF performs the operation:
| (8) |
For a general linear operator of the form λ(g) = wTg, where w has the same dimensions as the image vector g, the inter-class SNR can be shown to be given by ((Barrett and Myers, 2004), see Eqs. 13.118 and 13.180):
| (9) |
It thus follows for the case of PWMF, that since wT = ΔsTK−1 and w = K−1Δs:
| (10) |
In fact, it can be shown that (9) attains its maximum in this very case ((Barrett and Myers, 2004), Eq. 13.184). By contrast, for the case of NPWMF, where w = Δs, we have:
| (11) |
In the presence of white noise, where K is proportional to the identity matrix, it can be seen that (10) and (11) are equivalent, but not in the general case. Furthermore, in the general case, starting with (10), and moving from the discrete to the continuous limit, and assuming noise stationarity, expression (4) can be derived for the case of PWMF. Going through the same derivation for the case of NPWMF starting with (11), one can show that:
| (12) |
which again is equivalent to (4) in the case of white noise, but not in the general case.
Overall, we attempt to apply the abovementioned general framework to the study of the impact of RM in PET imaging, aiming to provide further insight into the interplay amongst enhanced resolution recovery and the resulting complex noise structure. Such an approach appears especially critical in light of increased investigation and usage of RM in recent years, including its implementation on clinical systems (e.g. Siemens HD PET (Le Meunier et al., 2010, 2011) based on the work by Panin et al. (2006), and GE SharpIR closely based on the work by Alessio et al. (2010) with some modifications), and the variety of metrics used to evaluate performance. To this end, as we discuss in Sec. 3, we have implemented models of noise propagation in iterative reconstruction, and performed comparison with measurements obtained from multiple noise realizations, to better probe the nature of noise propagation and its impact on detection task performance.
3. Experimental design and noise propagation calculations
3.1 Simplified analysis
Let us consider a system response H relating the original signals f to the detected signals s according to s=Hf. It can be seen from (10) and (11) that detection tasks performance depends on three factors: (i) the original difference signal Δf and (ii) its recovery as determined by H (both combine to yield Δs = s2 − s1 = H(f2 − f1) = HΔf), as well as (iii) the covariance matrix K. In the presence of RM, both H and K are modified. Clearly, an improved response H (i.e. reduced degradation; enhanced MTF) as achieved using RM is expected to improve task performance. However, to isolate and study the impact of an RM-modified covariance matrix K, in this part we fixed the system response as constant regardless of RM. We considered a small object of size n=7, and five different signals of increasing width Δs = {0 0 0 1 0 0 0}, {0 0 1 1 0 0 0}, {0 0 1 1 1 0 0}, {0 1 1 1 1 0 0} and {0 1 1 1 1 1 0}. We also considered three covariance matrices:
As elaborately shown and discussed in this work (Sec. 4.3, Sec. 5.1), as well as in past works (Rahmim et al., 2005; Tong et al., 2010; Sureau et al., 2008), RM brings about (i) decreased variance, which the transition from K1 to K2 represents, while (ii) RM also leads to an increase in inter-voxel correlations, as captured by the transition to K3. The detection performance results for the abovementioned signals and covariance matrices are described in Sec. 4.1.
3.2 Noise propagation models
Denoting the system matrix by P = (pij)I×J for a J-dimensional image vector and an I-dimensional projection set, and the sensitivity image by s with its elements given by , the EM algorithm can be written as:
| (13) |
where y is the measured dataset and xm denotes the image estimate at update m. We then write:
| (14) |
| (15) |
where x̅m denotes the mean image for noisy realization of the mean data y̅ (and therefore, em and d are noise vectors for the image and data, respectively). At iteration m, the image covariance matrix is given by , where Cd is the covariance matrix for the data (modeled using independent Poisson statistics; i.e. Cd = diag[y̅]), and Vm is a J-by-I matrix relating data noise to image noise; i.e. em = Vmd.
Qi (2003) developed a unified noise model applicable to a wide range of iterative image reconstruction methods. We next summarize the result for the EM scheme. However, we emphasize that the derivations were based on an assumption of low-noise in the image space (to enable simplifying Taylor expansions), thus implying limitations when having: (1) poor statistics (e.g. first/short frames in a dynamic study), (2) too many iterations. On the other hand, due to the linearity of the gradient of the log-likelihood function with respect to the data, in the case of Poisson distribution in emission tomography, it was noted by Qi (2003) that an assumption of low-noise in the detector-space (e.g. when having numerous crystals) was not needed in addition. For the EM algorithm, it was shown that:
| (16) |
where
| (17) |
| (18) |
In the original treatment by Barrett et al. (1994), an approximation was introduced setting the projection of the mean reconstructed image at iteration m as nearly resembling the noise-free data (i.e. Px̅m ~ y̅, which also effectively implies that x̅m+1 ~ x̅m), from which it follows that:
| (19) |
However, as we demonstrate next, this approximation can lead to incorrect computations at early iterations that in fact carry themselves over to subsequent, later iterations wherein this approximation is more valid.
3.3 Simulation studies
We have in the past implemented (Rahmim et al., 2008b) RM for the geometry of the Discovery RX PET/CT scanner (Kemp et al., 2006), including the presence of septa (2D PET), which we similarly pursue in our analytic simulations in the present work. Due to the extreme computational and memory requirements of the noise propagation computations, transaxial image dimensions were set to 80×80, instead of the usual 128×128. This also resulted in 2D sinograms with dimensions of 117 radial bins and 80 angular bins. The data were reconstructed for up to 70 iterations (single subset), without and with RM.
Two kinds of objects were simulated:
A contrast disc with cold (activity 0.3 of background) and hot (activity 2 times background) regions. This object was utilized to further compare the analytic models to compute noise propagation as discussed in Sec. 3.2.
A myocardial perfusion (MP) study, utilizing the NCAT phantom, and including realistic average counts and noise levels based on clinical studies of five patients with healthy myocardia at the Johns Hopkins PET Center, as we have previously also simulated and optimized (Tang et al., 2009). This also included simulations of a transmural MP defect, spanning 40 degrees over the anterior-lateral region (~1.6 cm in extent). The defect region had an activity that was 10% less than the normal activity. The simulated MP phantom is shown in Figure 1 though the depicted defect has been exaggerated to 40%, solely for better visibility.
Figure 1.
Images of the simulated myocardial perfusion study, (left) without and (right) the perfusion defect, though the intensity of the defect has been exaggerated (40%) for better visibility. Intensities were assigned based on clinical MP studies.
Both studies included simulation of a 2D slice, with a total slice count of 160K in the resulting 2D sinogram, consistent with our real clinical MP studies. We performed 100 noise realizations. To do this, following analytic noise-free simulations, Poisson noise was added to the sinogram data. The simulations included modeling of inter-crystal scattering and penetration, photon non-collinearity and Rb-82 positron range, as elaborated in the past (Rahmim et al., 2008b). Normalization, randoms and scattering were not simulated, but attenuation was modeled in the MP studies. The defect simulated had a spatial extent nearly twice the resolution of the simulated scanner.
3.4 Observer task performance
The MP study was utilized in the proposed context of detection AUC analysis, including MTF and NPS computations. This analysis was used to shed light on the various resolution and noise structures introduced in the context of RM, and how this can modify detectability task performance, as obtained using (4) and (6).
Furthermore, a channelized Hotelling observer (CHO) study was additionally performed, as motivated and discussed in Sec. 5.3. Four octave-wide rotationally symmetric frequency channels were applied to the reconstructed images. The start frequency and width of the first channel were both 1/64 cycles per pixel and the size of the channels was 32×32. This channel model was previously found to give good prediction of a human observer performance in myocardial defect detection (Wollenweber et al., 1999; Wollenweber et al., 1998).
The reconstructed images were cropped to the channel template size, with the centroid voxel of the defect region at the center of the cropped image. The pixel values in the cropped short-axis images were then windowed by scaling the image so the maximum value in the heart was mapped to 255 and the resulting floating values were rounded to integers. This scaling and rounding was performed to duplicate what should be done to images used in a human observer study.
The leave-one-out strategy was applied in training and testing the observer (Metz, 1986). One-hundred noise realizations were utilized. For each pair of normal/abnormal image noise realization, the other noise realizations were used in training the CHO. This process was repeated for all the noise realizations in each testing ensemble. The resulting ratings acquired from the CHO were used to estimate ROC curves with the LABROC4 program (Metz et al., 1990; Metz et al., 1991).
3.5 Dual metric trade-off analysis
We compared observer studies employing conventional dual-metric resolution (FWHM) vs. noise trade-off curves as generated with increasing number of iterations. Simplified noise metrics utilized included the spatial roughness σspatial, ensemble standard deviation of ROI mean σensemble, and ensemble voxel standard deviation σ0, as defined in (1), (2) and (3), respectively.
As for the measure of resolution, we note that imaging of a point source with no background to extract the PSF is an idealistic measure, which may not fully capture the ‘effective resolution’ of the scanner when utilizing non-linear reconstruction algorithm such as EM. A more realistic solution is to consider a known phantom, and to extract the effective resolution from knowledge of the original object and from the measured blurred image (Lodge et al., 2009). In the present work, to estimate the effective resolution of the system, we performed reconstructions of noise-free MP images without and with the defect, followed by calculation of the difference image (representing the blurred object), then estimating the FWHM width of a symmetric Gaussian needed to convolve with the known object to best match the blurred image. Unconstrained nonlinear optimization using the Nelder-Mean simplex search method (Lagarias et al., 1998) was used to this end to estimate the effective PSF FWHM.
4. Results
4.1 Simplified analysis
As elaborated in Sec. 3.1, we considered a simplified analysis involving an object of size n=7, and five different signals of increasing widths. We fixed the system response to single out the impact of the RM-modified covariance matrix K and its interaction with the signal Δs. In particular, we considered three different covariance matrices, as defined in Sec. 3.1, where a decrease in voxel variances was captured by K2, while an additional increase in inter-voxel correlations was captured by K3, both effects encountered in RM as we show in Sec. 4.3.
The resulting SNR2 values are shown in Table 1, as computed using (10) and (11) for the cases of PWMF and NPWMF, respectively. Increasing SNR2 values indicate increasing unlikelihood that the measured signal is purely due to noise. In the case of K1, SNR2 continues to grow with increasing signal widths as it becomes more unlikely that the measured signal is due to noise. A similar pattern is found in the case of K2, while the SNR values are even larger, since signal variance is modeled to be smaller (as is the case in RM). However, the growth with increasing widths is slowed down in the case of K3, due to the interplay between the signal and the covariance matrix. In fact, for the PWMF, while SNR values increase for narrower signals as one transitions from K1 and K2 to K3, one instead observes decreased SNR values for the wider signals: this is because increased inter-voxel correlations within a wide signal can make it relatively more likely that the signal is due to noise in comparison to the case where such positive correlations are absent. Moreover, for the NPWMF, further decreases are observed in observer task performance with respect to the PWMF used as the observer. As discussed in Sec. 2.3, the NPWMF was used to better capture human task performance in the presence of correlated noise, removing the ability of the ideal observer to perform noise prewhitening.
Table 1.
SNR2 as computed using (10) and (11) for a range of signals Δs and covariance matrices K for two observers: PWMF and NPWMF. Results are equivalent for K1 and K2, as they are proportional to the identity matrix.
| {0 0 0 1 0 0 0} | {0 0 1 1 0 0 0} | {0 0 1 1 1 0 0} | {0 1 1 1 1 0 0} | {0 1 1 1 1 1 0} | |
|---|---|---|---|---|---|
| K1 (PWMF/NPWMF) | 1 | 2 | 3 | 4 | 5 |
| K2 (PWMF/NPWMF) | 1.25 | 2.5 | 3.75 | 5.0 | 6.25 |
| K3 (PWMF) | 3.04 | 3.54 | 3.23 | 3.42 | 4.21 |
| K3 (NPWMF) | 1.25 | 1.54 | 1.80 | 2.11 | 2.45 |
Overall, it is observed that while decreased variances, as encountered in RM, can lead to increased SNR, and thus improved detectability, increased inter-voxel correlations as also encountered in RM (Sec. 4.3) complicate this picture, and can even result in decreased detectability especially for extended objects.
4.2 Noise propagation models
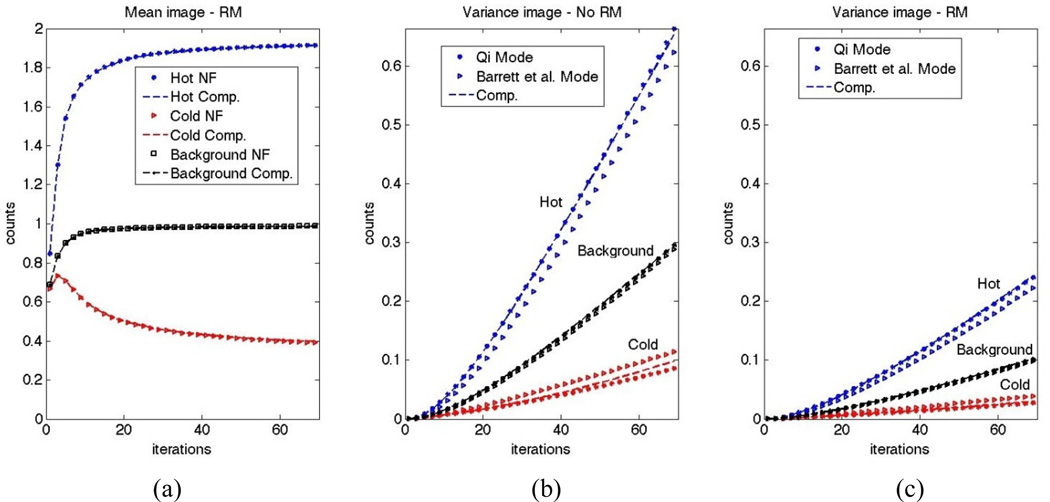
We compared the analytical results derived by Qi (2003) and Barrett et al. (1994), as described in Sec. 3.2 for the contrast phantom including hot, cold and background regions, as described in Sec. 3.3. Figure 2a plots the mean counts in the three regions as obtained utilizing noise-free (NF) simulations as well as those computed from reconstructed images from 100 noisy realizations, for the case of RM. Excellent matches are observed. Similar results were observed for the case of no RM (not shown).
Figure 2.
(a) Mean image counts in the case of RM as obtained from noise-free (NF) calculations and average reconstructed images computed from 100 noise realizations. Similar curves where obtained for the case of no RM (not shown). Variance image as obtained using the analytic models of Qi vs. Barrett et al., and as computed from 100 noise realizations, are also shown for reconstructions (b) without and (c) with RM.
Figure 2b,c plots counts from variance images as obtained using analytic models of Qi vs. Barrett et al., as well as computed form noisy realizations, for the cases without and with RM. Inconsistencies are observed between the two analytic model, while it can be seen that the computed variance plots depict better match with the model by Qi. To explain this, we note that the mean values in the three regions, as depicted in Figure 2a, converge in different directions. In other words, in early iterations, it is the case that x̅m+1/x̅m > 1 for voxels in the hot region, x̅m+1/x̅m ~ 1 for the background region, and x̅m+1/x̅m < 1 for the cold region. Subsequently, the term diag [x̅m+1/x̅m] in (18) (dropped in (19)) accounts for underestimated and overestimated variance values for the hot and cold regions, respectively, when using the additional approximation leading to (19). Furthermore, we observe that the incorrect noise calculations at early iterations carry themselves over to subsequent, later iterations.
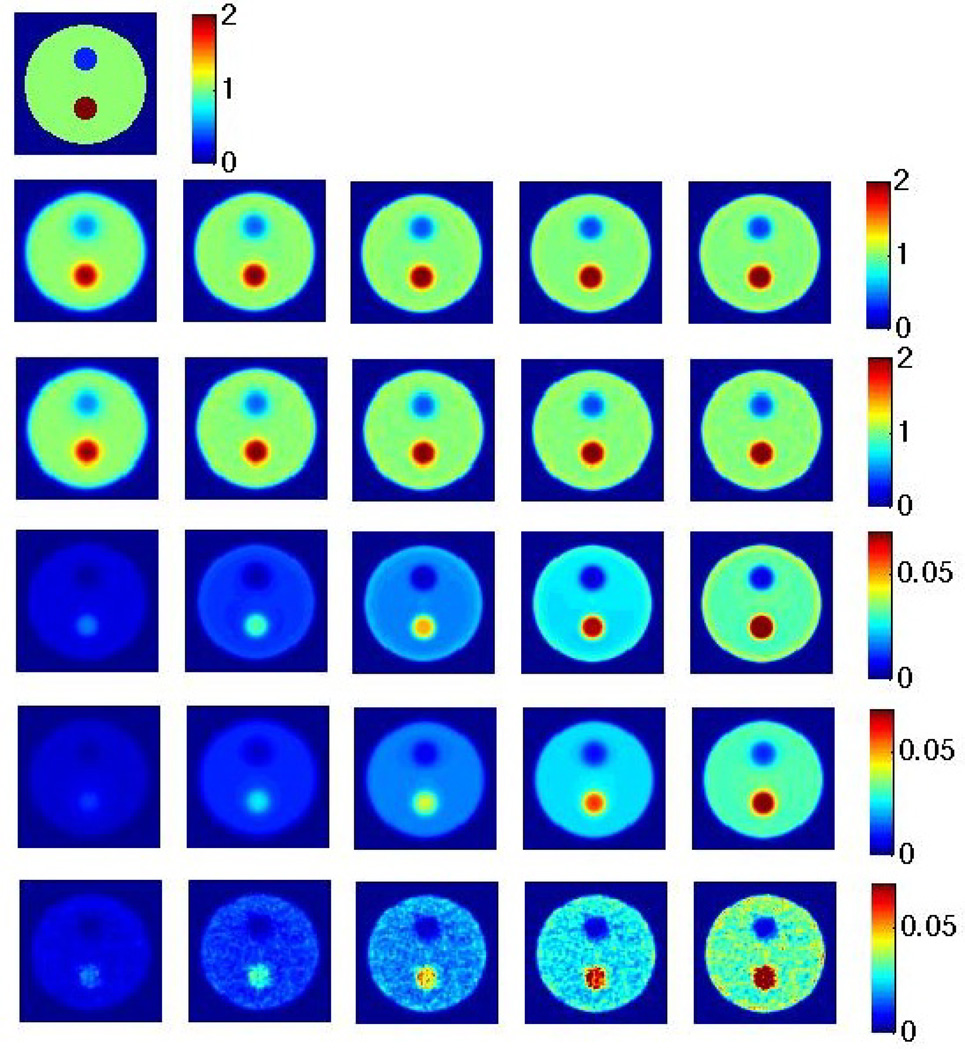
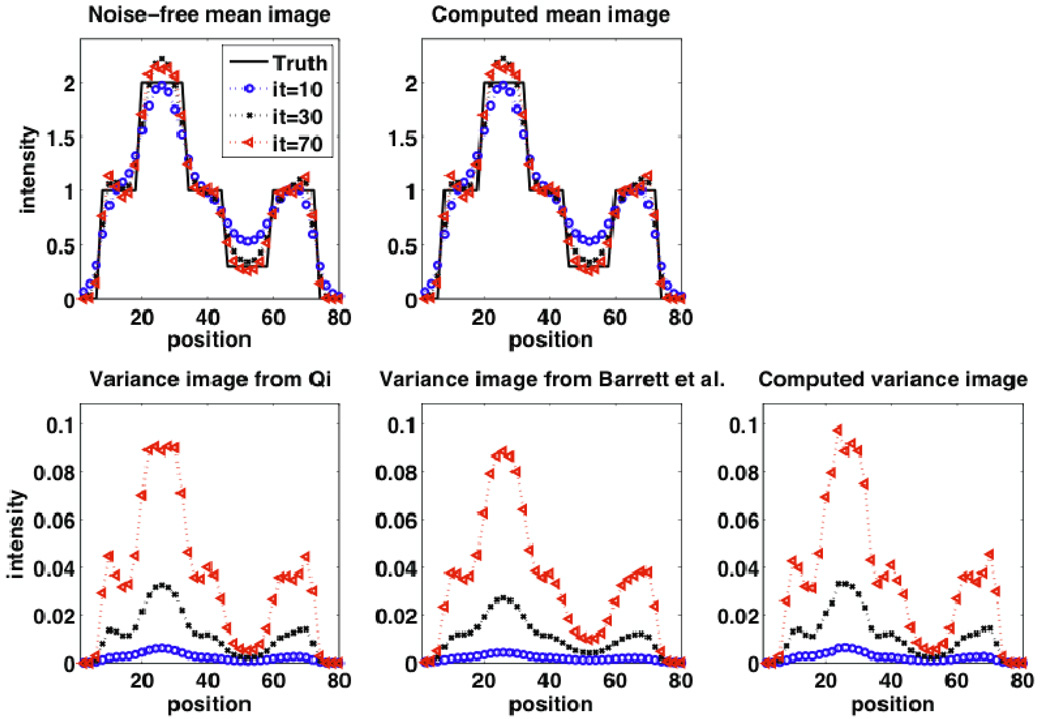
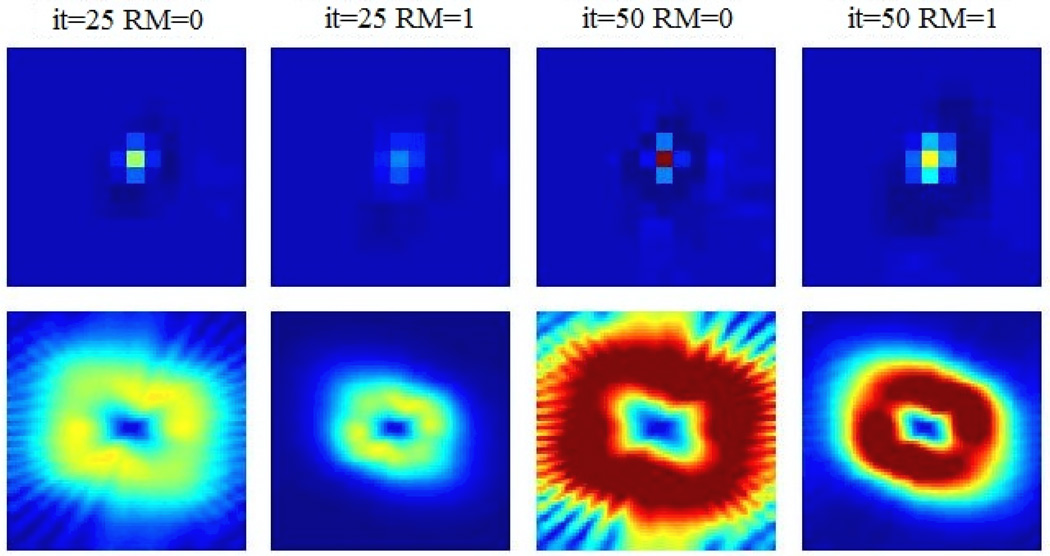
The corresponding images to above plots can be seen in Figure 3 as shown for different iterations in the case of RM. Again, visually, better matches to the computed variance image can be observed when the analytic model by Qi is utilized. Clearly, also, it is seen that the variance increases with increasing iterations. Vertical profiles through the images passing through all three regions (background, hot and cold) are shown in Figure 4, for the case of RM. Similar observations as above can be made. In addition, one observes edge artifacts, reminiscent of the Gibbs phenomenon (as elaborately reviewed elsewhere (Rahmim et al., 2013)), which become more prominent with increasing iterations. This is true in the mean images (whether from noise-free images or as computed from noisy realizations), and interestingly, also in the computed variance image. In particular, the analytic model by Qi is seen to properly capture the presence of edge artifacts in the variance image, while the one by Barrett et al. does not capture this real effect. This is an interesting and new observation, to our knowledge, and confirms modified variability for the edges in the case of RM. However, one ought to remember that voxel variance is overall reduced when switching from no RM to RM (as seen in Figure 2).
Figure 3.
(row 1) Original image; (row 2) Noise-free reconstructions, iterations 10, 15, 20, 25 and 30 from left to right (and similarly for images below); (row 3) Mean images computed from 100 noise realizations; (row 4) Analytic variance image based on the method of Qi; (row 5) Analytic variance image based on the method of Barrett et al.; (row 6) Variance image computed from 100 noise realizations. All reconstructed images shown are for the case of RM.
Figure 4.
(row 1): (left) Noise-free reconstructions, and (right) mean images computed from noise realizations; (row 2): Analytic variance image based on the method of (left) Qi and (center) Barrett et al., as well as (right) the variance image computed from noise realizations (to obtain these plots with very good quality, 1000 noise realizations were generated). Results are shown for iterations 10, 30 and 70. All reconstructed images shown are for the case of RM. The observed edge artifacts were not seen in the case without RM (not shown).
Finally, we wish to note that as emphasized in the paragraph preceding Eq. (16) Qi’s model was derived based on an assumption of low-noise in the image space (as a Taylor series expansion was invoked). As such, poorer-statistic frames may not reveal the very good agreements with the computed variance from noisy realizations as seen in Fig. 2. This would be especially the case in cold regions were the image non-negativity constraint implicit in the EM algorithm can create considerable noise-induced bias in low-statistic studies. Furthermore, we witnessed that even in our case, when too many iterations were utilized (>100 iterations), mismatches become very apparent. Nonetheless, the model is clearly very successful in capturing the overall computed variance especially at earlier iterations. As a consequence, we have used this more accurate formulation, including expression (18), in the rest of this work.
4.3 Detectability analysis
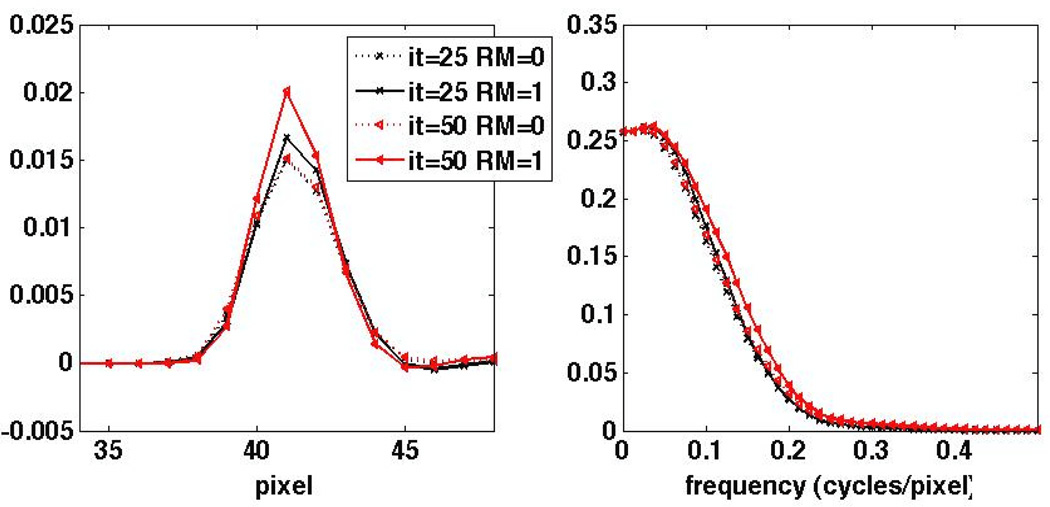
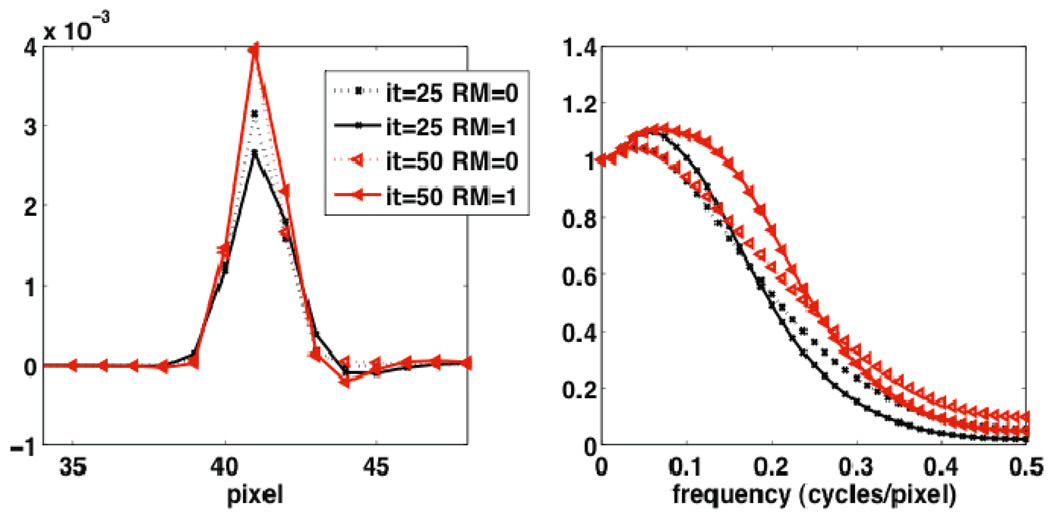
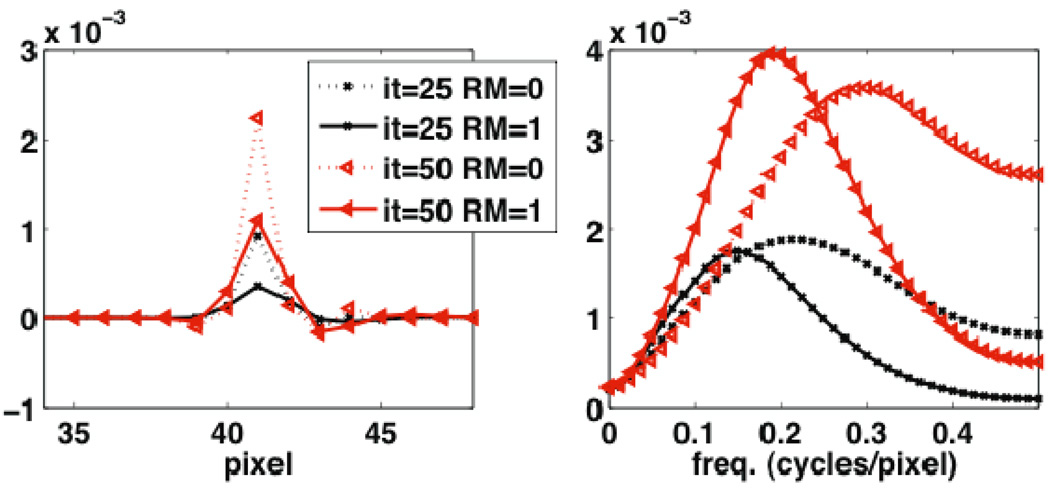
Utilizing the MP study elaborated in Sec. 3.3 for the rest of this work, Figure 5 depicts the difference signal Δs as obtained from reconstructions without and with a perfusion defect (in the noise-free case). The corresponding Fourier-domain representation ΔS is also shown. Some enhanced recovery is observed at mid frequencies. This is not entirely obvious, however, because the signal includes contributions due to the PSF as well as the shape of the defect. To better separate these effects. Figure 6 plots the measured difference signal due to a point siurce defect (single voxel of regular size with 10% less activity than normal myocardial uptake), and the corresponding normalized Fourier transform, i.e. the MTF. Enhancements in MTF frequency recovery due to RM are more conveniently observed.
Figure 5.
1D profiles through (left) the difference signal Δs as obtained by subtraction reconstructions with and without the MP defect and (right) the resulting Fourier transform ΔS. The results are shown for the 25th and 50th iterations.
Figure 6.
1D profiles through the reconstructed PSF for an original point source defect instead of the extended perfusion defect shown in Figure 5, (left) as obtained by subtracting reconstructions with and without the point defect, and (right) the resulting MTF. The results are shown for the 25th and 50th iterations.
Figure 7 shows images of the covariance structure at the MP defect location without and with RM for two different iterations of 25 and 50. The corresponding Fourier transform. i.e. the NPS, are shown in the second row. Figure 8 depicts horizontal 1D profiles through the abovementioned covariance and NPS images, also for two different iterations of 25 and 50. It cab be seen in both figures that RM results in reduced variance, but increased covariance with nearby voxels. This is attributed to the less sparse nature of the system matrix in the presence of RM; e.g. back-projection of counts detected along a particular line-of-response (LOR) effectively span a wider range of voxels. In the frequency domain, the resulting NPS in the case of RM is seen to depict values that are amplified in the mid-frequency domain, while exhibiting smaller values at higher frequencies. In the context of detection task SNR (e.g. Eq. (4)), which we quantify next, the observed amplified mid-frequency NPS levels are expected to diminish performance of RM, as would not be purely expected based on an enhanced MTF for RM.
Figure 7.
Images of (top) noise covariance (spanning up to 8 voxels in each direction) with respect to a point source at the center of the defect, and (bottom) the corresponding Fourier transform, i.e. the NPS (spanning up to 0.5 cycles/pixel in each direction). The results are shown for the 25th and 50th iterations. Intensity scales are matched for images in each row.
Figure 8.
1D horizontal plots through (left) the noise covariance and (right) the NPS as shown in Figure 7. The results depicted are for the 25th and 50th iterations.
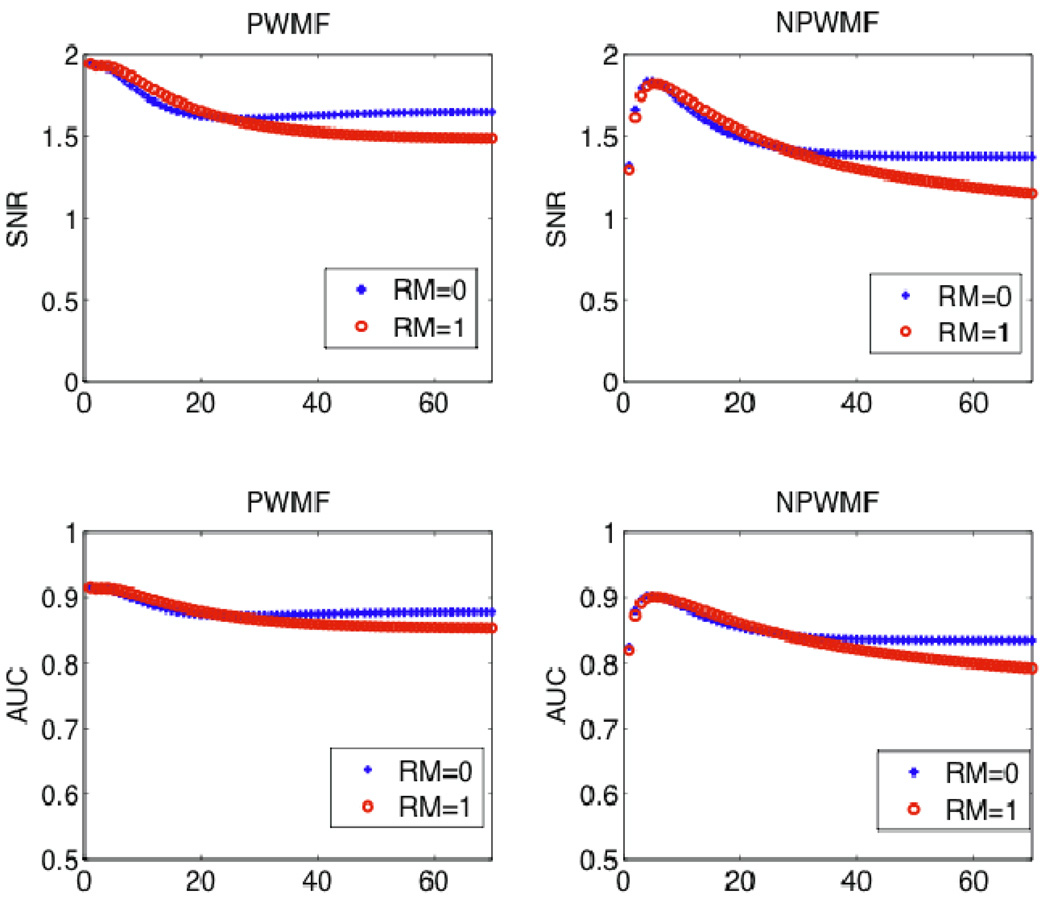
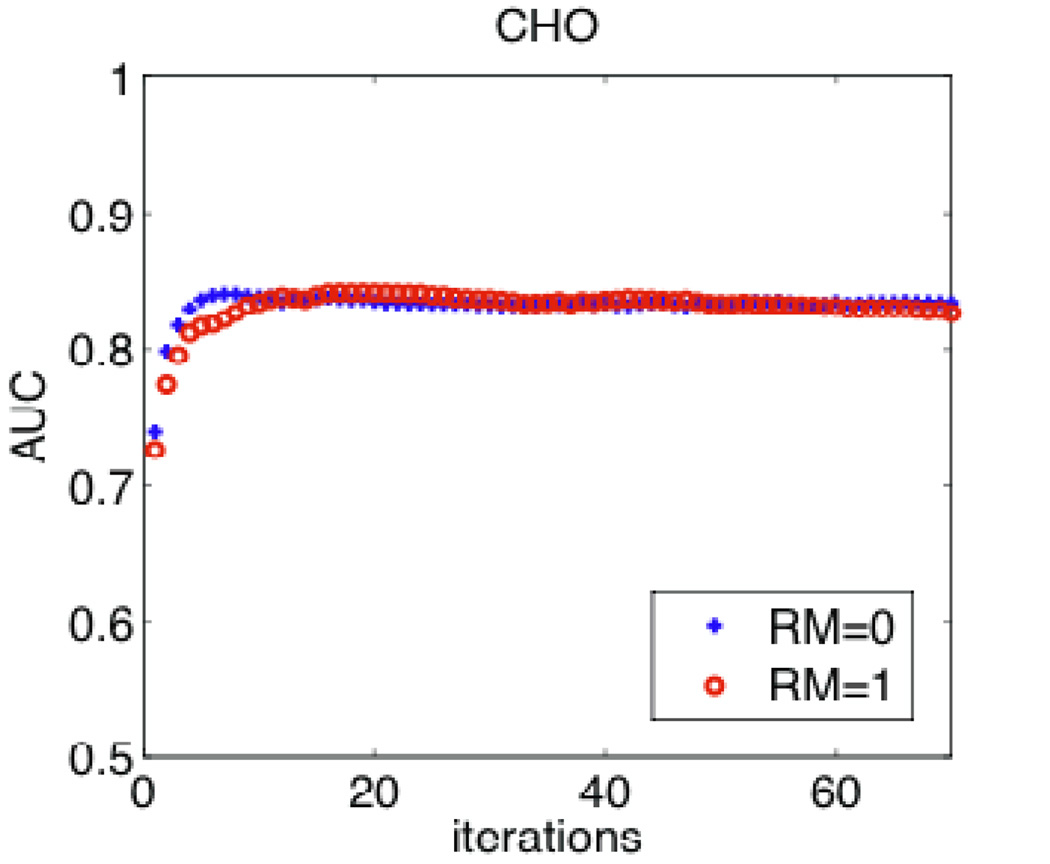
Figure 9 shows the resulting SNR calculations, for the cases of PWMF and NPWMF, according to (4) and (12) respectively (note that utilizing (4) instead of (5) has the advantage of not requiring assumption of shift-invariant resolution, and the effect of blurring is implicit in the difference signal ΔS(p)). The resulting AUC calculations according to (6) are also shown. The figure also demonstrates comparisons using the CHO study as obtained from 100 noise realizations. It is clearly seen that the NPWMF and CHO both results in smaller AUC values compared to the PWMF observer. Furthermore, their performances at lower iterations are especially degraded: this is because of noise correlations, which are more extensive at earlier iterations, and the NPWMF and CHO (which are more consistent with human observers) are especially challenged by the correlated structure. In any case, in all these analyses, it is seen that RM does not pose enhanced detectability.
Figure 9.
(top) Plots of SNR without and with RM for iterations up to 70, for the cases of PWMF and NPWMF as computed used (4) and (12) respectively. (Middle) Resulting AUC values for the cases of PWMF and NPWMF as obtained using (6). (Bottom) AUC values as obtained using CHO analysis (error bars, now shown, were ~0.03).
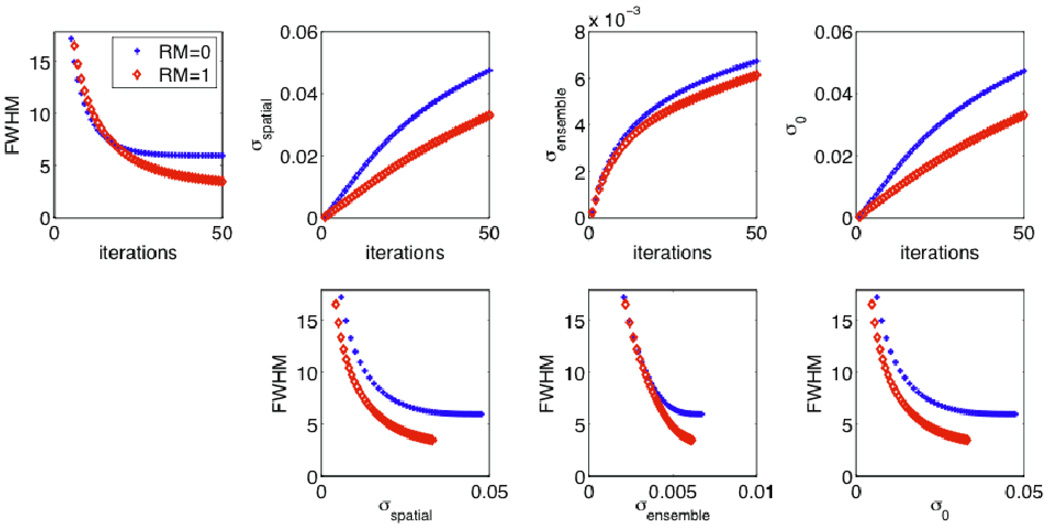
By comparison, different results are obtained when utilizing conventional trade-off curve analysis. Figure 10 depicts resolution vs. iteration, noise vs. iteration, as well as resolution vs. noise trade-off curves as generated using increasing iterations. The effective image resolution (FWHM) was extracted as elaborated at the end of Sec. 3.5. Noise was quantified (MP defect used as the ROI) using measures of spatial roughness σspatial standard deviation of ROI mean uptake σensemble, and voxel standard deviation σ0, as defined by (1), (2) and (3) respectively. The results depict improved performance for RM, though the improvement is reduced for the case of σensemble. This can be understood because increased inter-voxel correlations will reduce noise as measured this way, as we discuss elaborately in Sec. 5.1. In any case, it is clearly seen that all three noise metrics lead to enhanced dual-metric quantitative performance for RM, whereas in the context of actual observer task performance in the present work, RM does not outperform its counterpart, underlining the need not to make any conclusions of detection enhancement for RM based on dual-metric trade-off analysis.
Figure 10.
Plots of (top) FWHM and various noise metrics vs. iterations, as well as (bottom) dual-metric effective resolution vs. noise trade-off curves as generated with increasing iterations.
5. Discussion
5.1 Comparison of simplified noise metrics
The two dominant noise metrics in the literature as defined in (1) and (2), namely spatial roughness σspatial and ensemble standard deviation of ROI mean σensemble, are affected differently in the presence of RM. To better understand the differences, we note that for a uniform region with voxel variance and inter-voxel covariance covi, j between any two voxels i and j, the expectations of the above two statistics are given by (Tong et al., 2010):
| (20) |
| (21) |
Next, we note that RM can result in (i) diminished voxel variance and (ii) increased covariance covi, j for a given iteration number, as we have demonstrated in this work (Sec. 4.3), and as observed in some past studies (Rahmim et al., 2005; Tong et al., 2010; Sureau et al., 2008). Both these effects are related to reduced sparsity of the system matrix in the presence of RM, leading to inclusion and thus inter-relation of more voxels in relation to detected events along a particular LOR. The former effect, i.e. reduced voxel variability as a result of RM, can explain reductions in SUVmax variability as quantified by Armstrong et al. (2011). It also follows according to (20) and (21) that the abovementioned two effects combine to a reduced measure of spatial noise or image roughness, while they work against one another for ensemble variance of mean ROI values. As such, noise when measured spatially can be significantly reduced due to RM for a given iteration number, contrary to the ensemble measure of noise which could be improved less, as we have shown in our simulations (Figure 10), or remain nearly unchanged (Tong et al., 2010) or even increase (Blinder et al., 2012). Note that the size of the ROI (N) clearly modifies the relative contributions of the first and second terms in (21), and smaller ROIs are expected to amplify the contribution of the second term.
This can also explain why dual-metric contrast (or resolution) vs. noise trade-off analysis in the literature can be observed to depict greater improvements when noise is defined as σspatial ; e.g. (Reader et al., 2003; Rahmim et al., 2008b; Rapisarda et al., 2010; Kotasidis et al., 2011; Cloquet et al., 2010; Le Meunier et al., 2010), compared to when σensemble is utilized; e.g. (Alessio et al., 2010; Alessio et al., 2006; Cloquet et al., 2010; Sureau et al., 2008)). In a retrospective analysis of clinical FDG PET/CT studies by Akamatsu et al. (Akamatsu et al., 2012), liver SNR assessment was performed, where noise was quantified as standard deviation of mean values of multiple ROIs in the liver, which can be thought of an attempt to capture σensemble without having access to multiple noise realizations. Their analysis revealed significant improvements only when RM was paired with the TOF capability, but not without it.
In any case, what the present work emphasizes is that inference of detection task performance for RM vs. no RM based on dual-metric trade-off analyses involving simplistic noise metrics (which should not be made anyways) may be especially faulty when σspatial is utilized, and to a lesser extent when using σensemble. We add that σspatial has an additional issue in that it is sensitive to inherent noise-free non-uniformities, e.g. due to background structure or PVE blurring of the ROI edges. In fact, expression (20) for σspatial was derived (Tong et al., 2010) based on an assumption of noise-free uniformity for the ROI. Otherwise, we can show that:
| (22) |
where the added last term is the noise-free image roughness, i.e. variance of ensemble averaged voxel values s̅i around the overall ROI mean m̅. An alternative approach to removing this issue and yet not requiring numerous noise realizations is to perform only a single repeat measurement and to calculate the difference image, followed by computation of σspatial on the difference image (Lodge et al., 2010). The result is mathematically equivalent to computing σspatial on a single, uniform image (only offset by a factor of due to computing the difference) but has the advantage of being applicable to images that are non-uniform in the noise-free case. This also allows use a very large ROI, well beyond the correlation lengths, making the second term in (20) negligible compared to the first term, and thus feasibly allowing computation of the overall σ0. Nonetheless, this approach does not allow computation of σensemble which is an important metric on its own.
5.2 NPS characterization
By analogy to the Fourier transform of a Gaussian distribution, one may at first expect the increased inter-voxel correlations due to RM to lead to a narrower NPS. Subsequently, one could imagine that the enhanced MTF performance at higher frequencies would be complemented by the narrower NPS, the latter appearing in the denominator of (3) and (4), enhancing overall performance. However, the above analogy is invalid as the NPS in tomography resembles a high-pass filter, not a low-pass (e.g. Gaussian) filter (Myers et al., 1985). In any case, as demonstrated in Sec. 4.3, RM resulted in increased mid-frequency components for the NPS, while exhibiting diminished values at highfrequency components.
In fact, the PWMF framework (4) and (5) as utilized in this work was pursued in a dissertation by Wilson (1994) to investigate detector response compensation in SPECT imaging. Similar observations were made in that the enhanced MTF performance was countered by increased NPS values at mid frequencies, resulting in NEQ and SNR metrics that were not improved upon the inclusion of RM.
5.3 PWMF vs. NPWMF vs. CHO
The ideal observer poses an upper limit on performance for a binary classification task and is a useful tool for assessing imaging systems (He et al., 2008). This observer and the linear Hotelling observer (i.e. the PWMF) are identical in the case of Gaussian noise, and require knowledge/computation of (i) the covariance matrix K and (ii) its inverse (as seen in (7)). The first issue can be tackled using analytic noise propagation computations or generation of multiple noise realizations, both of which were pursued in the present work. The second issue can be prevented upon assumption of noise stationarity, leading to the NPS in the denominator, as seen in (4), and as also pursued in the present work. However, the stationarity assumption may not be valid, and thus inversion of a very large covariance matrix may need special attention (Barrett et al., 2001). By contrast, the NPWMF operation (8) (which better correlates with human performance, as discussed in Sec. 2.3) does not require knowledge of the covariance matrix, considerably simplifying this problem, while analytic computation of the SNR requires knowledge of K only (not its inverse) as seen in (11). A simplification of this problem, also implemented in this work, is to consider channelization, namely in the context of the CHO, which significantly reduces the entire image; e.g. to a 4-dimensional vector when 4 channels are utilized, as discussed in Sec. 3.4. The CHO model is consistent with a known mechanism of the visual system, and has shown very good prediction of human observer performance over a broad range of detection tasks, including in the context of MP defect detection (Wollenweber et al., 1998; Wollenweber et al., 1999).
5.4 Observer studies of RM
PET imaging
A number of numerical and/or human observer studies of RM in PET imaging have been performed. Kadrmas et al. (Kadrmas et al., 2009a; Kadrmas et al., 2009b) performed numeric channelized non-prewhitened (CNPW) (discussed below) as well as human observer studies of tumour detection using a multi-component whole-body phantom with realistic FDG uptake and including “shell-less”68Ge silicone gel lesions. Inclusion of RM led to statistically significant improvements in the context of localization ROC (LROC) analysis. Similar patterns were observed in ROC/LROC analysis of numeric (CNPW and CHO) and human observer studies by Schaefferkoetter et al. (2013) involving addition of separately scanned small spheres to the lung or the liver in clinical patient scans. However, in the case of TOF absent, RM improvements were limited to lung lesions, and liver lesions exhibited no improvements. Our own ROC observer analysis in Sec. 4.3 (Rb-82 PET) revealed non-enhanced perfusion defect detectability performance upon inclusion of RM, whereas recent phantom studies (F-18 PET) by Managa et al. (2013) showed improvements in defect detection upon inclusion of RM (we discuss below the potentials impacts of different types of analyses as well as contrast/noise environments on task performance).
SPECT imaging
Studies were also performed in the context of SPECT imaging to assess RM, more commonly referred to as (collimator)-detector response compensation (DRC) in the literature (Frey and Tsui, 2006). These included MP SPECT simulations using ROC analysis involving (i) CHO by Frey et al. (2002) and (ii) human observers by Sankaran et al. (2002). The CHO studies revealed statistically significant improvements (p=0.001) when DRC was performed in addition to attenuation compensation only (AC), but the statistical significance dropped when performed in addition to both attenuation and scatter compensation (ASC) (p=0.049). The human observer study also revealed some improvements, but they were not statistically significant (p=0.084 for DRC+AC vs. AC; p=0.79 for DRC+ASC vs. ASC). (iii) In a clinical MP study by Narayanan et al. (2003) involving human observer ROC analysis, the three territories: left anterior descending coronary artery (LAD), left circumflex coronary (LCx) and right coronary artery (RCA) were individually considered. In addition, the maximum score of any given observer for the three territories was taken as the overall score representing performance for the overall detection of coronary artery disease (CAD). Inclusion of DRC in addition to ASC was seen to improve AUC values for LAD, LCx, and also the overall CAD, but it degraded performance for the RCA. In any case, statistical comparisons of DRS+ASC were only performed in comparison to FBP and AC, and did not appear to be significance when compared with ASC. (iv) In a notable study by Gifford et al. (2000), however, considerable and statistically significant improvements due to DRS were demonstrated. We discuss sources of such differences next. Two things were different about this study: (1) it was in a different context of simulated Ga-67 tumor imaging, and (2) it involved LROC analysis, thus involving both detection and localization, unlike the other three SPECT studies which involved ROC analysis only, which takes us to our next observation.
ROC vs. LROC analysis
Review of abovementioned observer studies can suggest enhanced performance of RM relative to no RM when LROC analysis (as opposed to ROC) is performed. Technically, one cannot make such a definitive conclusion based on the abovementioned SPECT studies, because the LROC study was performed in a different context of tumor imaging, as compared to MP defect detection in the other three studies. It is in fact entirely plausible that RM can enhance tumor imaging whereas its impact on defect detection may be limited. In other words, while RM can complicate the noise structure, its enhancement of lesion contrast may be considerably significant to ultimately enhance tasks performance, whereas improvements in cold contrast may be relatively limited.
By contrast, LROC vs. ROC analyses were performed within a consistent environment in the PET studies by Schaefferkoetter et al. (2013): the resulting (AUCROC, AUCLROC) pairs for the different reconstruction methods were as follows: baseline (0.57 ± 0.01; 0.13 ± 0.03), RM (0.61 ± 0.02; 0.22 ± 0.04), TOF (0.68 ± 0.02; 0.37 ± 0.05), and TOF+RM (0.78 ± 0.04; 0.55 ± 0.07). Individual analysis of statistical significance were not performed for LROC vs. ROC analyses; however, clearly enhanced separations are observed in the case of LROC.
Two explanations are possible as to why LROC studies may depict enhanced performance when RM is introduced: (1) the trade-off provided by RM, namely enhanced contrast and reduced voxel variance at the cost of more correlated noise structure, may perform more favorably in the context of LROC than ROC analysis. ROC analysis considers the SKE scenario where the location of the signal (e.g. tumor) to be detected is known in advance, and the task is merely that of detection. However, the clinical reality is often more complex, and the task involves both detection and localization. When image noise is stationary, these two tasks can be correlated (Swensson et al., 1997), but noise may not be stationary particularly due to presence of background structure, and localization task performance can be degraded due to confusion with features within this structure (Seltzer et al., 1991). This latter issue is important due to the presence of background variability which is not the case in the BKE assumption (Kupinski et al., 2003).
(2) LROC analysis, by its very nature, provides a wider dynamic range of values, thus providing a greater ability to detect statistically significant differences. A way to see this is that ROC analysis (in studies where presumed signal location is not indicated; e.g. oncologic studies) can be thought of as performing LROC analysis while additionally suppressing the localization information, and the resulting loss of information can therefore result in a degradation of statistical power.
In any case, additional emphasis on LROC analysis, as opposed to ROC analysis, appears appropriate, and as such, the ROC analysis and findings in the present work should be put in such a context, suggesting a need for future extension to that domain, and of not making definitive conclusions about superiority of performance (or lack thereof) for RM when assessed using ROC analysis only. LROC analysis could be performed using human observer studies, or numerical observers that have shown good prediction of human performance. In fact, conventional numeric observer ROC analysis was not found to depict good correlation with human LROC analysis in assessment of RM (Gifford et al., 1999). By contrast, good quantitative agreements were observed for the multiclass CNPW observer in SPECT (Gifford et al., 2005) and PET (Gifford et al., 2007). Multiclass observers are one way to extend numerical ROC analysis to LROC analysis, involving perception analysis at every voxel and finding the location with maximum rating. Overall, the CNPW observer (a handicapped version of CHO) when used in the multiclass context was shown by Gifford et al. (2005; 2007) to be a reasonable substitute to multiclass CHO for iterative reconstruction strategies, especially as it involves smaller training requirements in the computationally-intense context of numeric LROC analysis. Subsequently, this observer was used in the LROC studies of RM in PET as mentioned in the beginning of this section.
Impact of the contrast and noise environments on RM
We note that incorporation of RM may or may not pose an additional benefit in observer task performance depending on the environment. As outlined previously, in the absence of TOF, improvements were not observed in the detection of liver lesions as studies by Schaefferkoetter et al. (2013), in comparison to the detection of lung lesions. What is additionally interesting is that the picture changed completely in the presence of TOF, i.e. significant improvements were observed in liver tumor detection when using TOF+RM in relation to the use of TOF only. Overall performance was seen to improve considerably in both ROC and LROC analyses, though more so in the latter (the numbers were reported above). Interestingly, in the LROC study by Kadrmas (2009b), somewhat similar pattern were also observed for the resulting AUC values: baseline (0.418 ± 0.051), RM (0.516 ± 0.052), TOF (0.673 ± 0.054) and TOF+RM (0.813 ± 0.046).
These observations point to the fact that the contrast as well as noise environments both may play key roles as to whether, and to what extent, RM can enhance task performance, an issue that is of importance in general and for different tasks (Karakatsanis et al., 2013a; Karakatsanis et al., 2013b), and one that needs to be more thoroughly studied and understood in the specific context of RM. Last but not least, it is worth emphasizing that statistical significance may not translate to clinical significance, and that most above studies are designed (e.g. number of lesions, sizes, contrast, etc.) so as to capture the former, and not necessarily the latter, and as such, careful considerations need to be made to ultimately assess whether RM enhanced task performance significantly in a clinical sense.
6. Summary
The present work has provided a framework to demonstrate why conventional quantitative analysis involving dual-metric trade-off curves, e.g. resolution vs. noise (where noise is defined using metrics such as image roughness or ensemble standard deviation of ROI mean) may reveal enhanced quantitative performance for PET image reconstruction methods invoking RM, while actual observer task performance may not show a similar pattern. This was attributed to the complex structure of the noise distribution in the presence of RM, as specially captured by the noise power spectrum, and its interaction with the signal to be detected; while RM can clearly result in enhanced resolution recovery at mid-frequencies, it also results in increased NPS values at these frequencies. We have shown that the extent of the abovementioned differences in performance using conventional dual-metric analyses vs. observer tasks is reduced when the former utilize the ensemble standard deviation of ROI mean, as opposed to image roughness, and that in any case, observer studies are required to carefully assess performance of a given RM technique under evaluation. Finally we have noted that whether or not RM results in enhanced observer studies can depend on the imaging environment (e.g. background structure as modified in different organs; background noise as modified with time-of-flight imaging) as well as whether ROC vs. LROC analysis is performed.
Acknowledgment
This work was in part supported by the NIH grant 1S10RR023623 and the NSF grant ECCS1228091. We wish to thank Eric Frey, Dan Kadrmas, Nicolas Karakatsanis and Saeed Ashrafinia for helpful discussions. We also wish to thank both reviewers, one to recommend consideration of past works on the impact of correlated noise on detection (as now discussed in Sec. 2.3), and another for various useful suggestions including addition of Fig. 4 demonstrating the presence of edge artifacts, not only in the mean image, but also in the variance image.
References
- Akamatsu G, Ishikawa K, Mitsumoto K, Taniguchi T, Ohya N, Baba S, Abe K, Sasaki M. Improvement in PET/CT Image Quality with a Combination of Point-Spread Function and Time-of-Flight in Relation to Reconstruction Parameters. Journal of Nuclear Medicine. 2012;53:1716–1722. doi: 10.2967/jnumed.112.103861. [DOI] [PubMed] [Google Scholar]
- Alessio A, MacDonald L. Spatially Variant Positron Range Modeling Derived from CT for PET Image Reconstruction; IEEE NSS/MIC Conf. Proceed; 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alessio AM, Kinahan PE, Lewellen TK. Modeling and incorporation of system response functions in 3-D whole body PET. Medical Imaging, IEEE Transactions on. 2006;25:828–837. doi: 10.1109/tmi.2006.873222. [DOI] [PubMed] [Google Scholar]
- Alessio AM, Stearns CW, Shan T, Ross SG, Kohlmyer S, Ganin A, Kinahan PE. Application and Evaluation of a Measured Spatially Variant System Model for PET Image Reconstruction. IEEE Trans Med Imag. 2010;29:938–949. doi: 10.1109/TMI.2010.2040188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong IS, Williams HA, Matthews JC. Accuracy and variability of quantitative measurements using PET with time-of-flight information and resolution modelling; 2011 Ieee Nuclear Science Symposium and Medical Imaging Conference (Nss/Mic); 2011. pp. 4167–4170. [Google Scholar]
- Aston JA, Cunningham VJ, Asselin MC, Hammers A, Evans AC, Gunn RN. Positron emission tomography partial volume correction: estimation and algorithms. J Cereb Blood Flow Metab. 2002;22:1019–1034. doi: 10.1097/00004647-200208000-00014. [DOI] [PubMed] [Google Scholar]
- Bai B, Laforest R, Smith AM, Leahy RM. Evaluation of MAP image reconstruction with positron range modeling for 3D PET; Nuclear Science Symposium Conference Record, 2005 IEEE; 2005. pp. 2686–2689. [Google Scholar]
- Bai B, Li QZ, Leahy RM. Magnetic Resonance-Guided Positron Emission Tomography Image Reconstruction. Seminars in Nuclear Medicine. 2013;43:30–44. doi: 10.1053/j.semnuclmed.2012.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai B, Ruangma A, Laforest R, Tai YC, Leahy RM. Positron range modeling for statistical PET image reconstruction. Nuclear Science Symposium Conference Record, 2003 IEEE. 2003;Vol.4:2501–2505. [Google Scholar]
- Barrett HH, Myers KJ. Foundations of Image Science. Hoboken, New Jersey: Wiley & Sons, Inc.; 2004. [Google Scholar]
- Barrett HH, Myers KJ, Gallas B, Clarkson E, Zhang HB. Megalopinakophobia: Its symptoms and cures. Medical Imaging 2001: Physics of Medical Imaging. 2001;2:299–307. [Google Scholar]
- Barrett HH, Wilson DW, Tsui BMW. Noise properties of the EM algorithm. I. Theory. Phys Med Biol. 1994;39:833–846. doi: 10.1088/0031-9155/39/5/004. [DOI] [PubMed] [Google Scholar]
- Blackwell KT. The effect of white and filtered noise on contrast detection thresholds. Vision Res. 1998;38:267–280. doi: 10.1016/s0042-6989(97)00130-2. [DOI] [PubMed] [Google Scholar]
- Blinder SA, Dinelle K, Sossi V. Scanning rats on the high resolution research tomograph (HRRT): a comparison study with a dedicated micro-PET. Med Phys. 2012;39:5073–5083. doi: 10.1118/1.4736802. [DOI] [PubMed] [Google Scholar]
- Boussion N, Hatt M, Lamare F, Bizais Y, Turzo A, Cheze-Le Rest C, Visvikis D. A multiresolution image based approach for correction of partial volume effects in emission tomography. Phys Med Biol. 2006;51:1857–1876. doi: 10.1088/0031-9155/51/7/016. [DOI] [PubMed] [Google Scholar]
- Boussion N, Le Rest CC, Hatt M, Visvikis D. Incorporation of wavelet-based denoising in iterative deconvolution for partial volume correction in whole-body PET imaging. Anglais. 2009;36:1064–1075. doi: 10.1007/s00259-009-1065-5. [DOI] [PubMed] [Google Scholar]
- Bowsher JE, Johnson VE, Turkington TG, Jaszczak RJ, Floyd CR, Coleman RE. Bayesian reconstruction and use of anatomical a priori information for emission tomography. Medical Imaging, IEEE Transactions on. 1996;15:673–686. doi: 10.1109/42.538945. [DOI] [PubMed] [Google Scholar]
- Burgess AE. Statistical Efficiency of Perceptual Decisions. P Soc Photo-Opt Inst. 1984;454:18–26. [Google Scholar]
- Cloquet C, Sureau FC, Defrise M, Van Simaeys G, Trotta N, Goldman S. Non-Gaussian space-variant resolution modelling for list-mode reconstruction. Phys Med Biol. 2010;55:5045–5066. doi: 10.1088/0031-9155/55/17/011. [DOI] [PubMed] [Google Scholar]
- Comtat C, Kinahan PE, Fessler JA, Beyer T, Townsend DW, Defrise M, Michel C. Clinically feasible reconstruction of 3D whole-body PET/CT data using blurred anatomical labels. Phys Med Biol. 2002;47:1–20. doi: 10.1088/0031-9155/47/1/301. [DOI] [PubMed] [Google Scholar]
- Du Y, Tsui BMW, Frey EC. Partial volume effect compensation for quantitative brain SPECT imaging. Medical Imaging, IEEE Transactions on. 2005;24:969–976. doi: 10.1109/TMI.2005.850547. [DOI] [PubMed] [Google Scholar]
- Frese T, Rouze NC, Bouman CA, Sauer K, Hutchins GD. Quantitative comparison of FBP, EM, and Bayesian reconstruction algorithms for the IndyPET scanner. Medical Imaging, IEEE Transactions on. 2003;22:258–276. doi: 10.1109/TMI.2002.808353. [DOI] [PubMed] [Google Scholar]
- Frey EC, Gilland KL, Tsui BMW. Application of task-based measures of image quality to optimization and evaluation of three-dimensional reconstruction-based compensation methods in myocardial perfusion SPECT. IEEE Trans. Med. Imaging. 2002;21:1040–1050. doi: 10.1109/TMI.2002.804437. [DOI] [PubMed] [Google Scholar]
- Frey EC, Tsui BMW, editors. Collimator-Detector Response Compensation in SPECT. New York, NY: Springer Science+Business Media, Inc.; 2006. [Google Scholar]
- Fu L, Qi J. A residual correction method for high-resolution PET reconstruction with application to on-the-fly Monte Carlo based model of positron range. Medical Physics. 2010;37:704–713. doi: 10.1118/1.3284980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gifford HC, Kinahan PE, Lartizien C, King MA. Evaluation of multiclass model observers in PET LROC studies. IEEE Trans Nuc Sci. 2007;54:116–123. doi: 10.1109/TNS.2006.889163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gifford HC, King MA, Pretorius PH, Wells RG. A comparison of human and model observers in multislice LROC studies. IEEE Trans Med Imaging. 2005;24:160–169. doi: 10.1109/tmi.2004.839362. [DOI] [PubMed] [Google Scholar]
- Gifford HC, King MA, Wells RG, Hawkins WG, Narayanan MV, Pretorius PH. LROC analysis of detector-response compensation in SPECT. IEEE Trans Med Imaging. 2000;19:463–473. doi: 10.1109/42.870256. [DOI] [PubMed] [Google Scholar]
- Gifford HC, Soares EJ, Wells RG, King MA. Evaluating detector resolution compensation methods in SPECT imaging through numerical observer ROC and human observer LROC. Nuclear Science Symposium, 1999. Conference Record. 1999 IEEE. 1999;vol.3:1418–1422. [Google Scholar]
- Guignard PA. A Comparative Method Based on Roc Analysis for the Quantitation of Observer Performance in Scintigraphy. Physics in Medicine and Biology. 1982;27:1163–1176. doi: 10.1088/0031-9155/27/9/006. [DOI] [PubMed] [Google Scholar]
- He X, Caffo BS, Frey EC. Toward realistic and practical ideal observer (IO) estimation for the optimization of medical imaging systems. IEEE Trans. Med. Imaging. 2008;27:1535–1543. doi: 10.1109/TMI.2008.924641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judy PF, Swensson RG, Szulc M. Lesion Detection and Signal-to-Noise Ratio in Ct Images. Med. Phys. 1981;8:13–23. doi: 10.1118/1.594903. [DOI] [PubMed] [Google Scholar]
- Kadrmas DJ, Casey ME, Black NF, Hamill JJ, Panin VY, Conti M. Experimental Comparison of Lesion Detectability for Four Fully-3D PET Reconstruction Schemes. Ieee T Med Imaging. 2009a;28:523–534. doi: 10.1109/TMI.2008.2006520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadrmas DJ, Casey ME, Conti M, Jakoby BW, Lois C, Townsend DW. Impact of Time-of-Flight on PET Tumor Detection. J Nucl Med. 2009b;50:1315–1323. doi: 10.2967/jnumed.109.063016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karakatsanis NA, Lodge MA, Tahari AK, Zhou Y, Wahl RL, Rahmim A. Dynamic whole body PET parametric imaging: I. Concept, acquisition protocol optimization and clinical application. Phys. Med. Bio. 2013a doi: 10.1088/0031-9155/58/20/7391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karakatsanis NA, Lodge MA, Zhou Y, Wahl RL, Rahmim A. Dynamic whole body PET parametric imaging: II. Task- oriented statistical estimation. Phys. Med. Bio. 2013b doi: 10.1088/0031-9155/58/20/7419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kemp BJ, Kim C, Williams JJ, Ganin A, Lowe VJ. NEMA NU 2–2001 performance measurements of an LYSO-based PET/CT system in 2D and 3D acquisition modes. J Nucl Med. 2006;47:1960–1967. [PubMed] [Google Scholar]
- Kessler RM, Ellis JR, Eden M. Analysis of emission tomographic scan data: limitations imposed by resolution and background. J Comput Assist Tomogr. 1984;8:514–522. doi: 10.1097/00004728-198406000-00028. [DOI] [PubMed] [Google Scholar]
- Kirov AS, Piao JZ, Schmidtlein CR. Partial volume effect correction in PET using regularized iterative deconvolution with variance control based on local topology. Phys Med Biol. 2008;53:2577–2591. doi: 10.1088/0031-9155/53/10/009. [DOI] [PubMed] [Google Scholar]
- Kotasidis FA, Matthews JC, Angelis GI, Noonan PJ, Jackson A, Price P, Lionheart WR, Reader AJ. Single scan parameterization of space-variant point spread functions in image space via a printed array: the impact for two PET/CT scanners. Phys Med Biol. 2011;56:2917–2942. doi: 10.1088/0031-9155/56/10/003. [DOI] [PubMed] [Google Scholar]
- Kupinski MA, Hoppin JW, Clarkson E, Barrett HH. Ideal-observer computation in medical imaging with use of Markov-chain Monte Carlo techniques. J Opt Soc Am A Opt Image Sci Vis. 2003;20:430–438. doi: 10.1364/josaa.20.000430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Labbe C, Froment JC, Kennedy A, Ashburner J, Cinotti L. Positron emission tomography metabolic data corrected for cortical atrophy using magnetic resonance imaging. Alzheimer Disease and Associated Disorders. 1996;10:141–170. doi: 10.1097/00002093-199601030-00005. [DOI] [PubMed] [Google Scholar]
- Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence properties of the Nelder-Mead simplex method in low dimensions. Siam Journal on Optimization. 1998;9:112–147. [Google Scholar]
- Le Meunier L, Slomka PJ, Dey D, Ramesh A, Thomson LEJ, Hayes SW, Friedman JD, Cheng V, Germano G, Berman DS. Enhanced definition PET for cardiac imaging. J Nucl Cardiol. 2010;17:414–426. doi: 10.1007/s12350-010-9193-7. [DOI] [PubMed] [Google Scholar]
- Le Meunier L, Slomka PJ, Dey D, Ramesh A, Thomson LEJ, Hayes SW, Friedman JD, Cheng V, Germano G, Berman DS. Motion frozen F-18-FDG cardiac PET. J Nucl Cardiol. 2011;18:259–266. doi: 10.1007/s12350-010-9322-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Pogam A, Hatt M, Descourt P, Boussion N, Tsoumpas C, Turkheimer FE, Prunier-Aesch C, Baulieu JL, Guilloteau D, Visvikis D. Evaluation of a 3D local multiresolution algorithm for the correction of partial volume effects in positron emission tomography. Med. Phys. 2011;38:4920–4933. doi: 10.1118/1.3608907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lecomte R, Schmitt D, Lamoureux G. Geometry Study of a High Resolution PET Detection System Using Small Detectors. Nuclear Science, IEEE Transactions on. 1984;31:556–561. [Google Scholar]
- Lee K, Kinahan PE, Fessler JA, Miyaoka RS, Janes M, Lewellen TK. Pragmatic fully 3D image reconstruction for the MiCES mouse imaging PET scanner. Phys Med Biol. 2004;49:4563–4578. doi: 10.1088/0031-9155/49/19/008. [DOI] [PubMed] [Google Scholar]
- Lipinski B, Herzog H, Rota Kops E, Oberschelp W, Muller-Gartner HW. Expectation maximization reconstruction of positron emission tomography images using anatomical magnetic resonance information. Medical Imaging, IEEE Transactions on. 1997;16:129–136. doi: 10.1109/42.563658. [DOI] [PubMed] [Google Scholar]
- Lodge MA, Rahmim A, Wahl RL. A Practical, Automated Quality Assurance Method for Measuring Spatial Resolution in PET. Journal of Nuclear Medicine. 2009;50:1307–1314. doi: 10.2967/jnumed.108.060079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lodge MA, Rahmim A, Wahl RL. Simultaneous measurement of noise and spatial resolution in PET phantom images. Physics in Medicine and Biology. 2010;55:1069–1081. doi: 10.1088/0031-9155/55/4/011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mananga E, El Fakhri G, Bonab A, Ouyang J. Assessment of myocardial defect detectability with PET-CT. J NUCL MED MEETING ABSTRACTS. 2013;54:98. [Google Scholar]
- Mazziotta JC, Phelps ME, Plummer D, Kuhl DE. Quantitation in positron emission computed tomography: 5. Physical-anatomical effects. J Comput Assist Tomogr. 1981;5:734–743. doi: 10.1097/00004728-198110000-00029. [DOI] [PubMed] [Google Scholar]
- Meltzer CC, Zubieta JK, Links JM, Brakeman P, Stumpf MJ, Frost JJ. MR-based correction of brain PET measurements for heterogeneous gray matter radioactivity distribution. J Cereb Blood Flow Metab. 1996;16:650–658. doi: 10.1097/00004647-199607000-00016. [DOI] [PubMed] [Google Scholar]
- Metz CE. ROC methodology in radiologic imaging. Invest Radiol. 1986;21:720–733. doi: 10.1097/00004424-198609000-00009. [DOI] [PubMed] [Google Scholar]
- Metz CE, Shen J-H, Herman BA. Annual Meeting of the American Statistical Association. Anaheim, CA: 1990. New Methods for Estimating a Binormal ROC Curve From Continuously-distributed Test Results. [Google Scholar]
- Metz CE, Shen JH, Kronman HB, Wang P-L. CLABROC. Chicago: University of Chicago Press; 1991. [Google Scholar]
- Moehrs S, Defrise M, Belcari N, Del Guerra A, Bartoli A, Fabbri S, Zanetti G. Multi-ray-based system matrix generation for 3D PET reconstruction. Phys Med Biol. 2008;53:6925–6945. doi: 10.1088/0031-9155/53/23/018. [DOI] [PubMed] [Google Scholar]
- Muller-Gartner HW, Links JM, Prince JL, Bryan RN, McVeigh E, Leal JP, Davatzikos C, Frost JJ. Measurement of radiotracer concentration in brain gray matter using positron emission tomography: MRI-based correction for partial volume effects. J Cereb Blood Flow Metab. 1992;12:571–583. doi: 10.1038/jcbfm.1992.81. [DOI] [PubMed] [Google Scholar]
- Myers KJ, Barrett HH, Borgstrom MC. Effect of noise correlation on detectability of disk signals in medical imaging. J. Opt. Soc. Am. 1985;2:1752–1759. doi: 10.1364/josaa.2.001752. [DOI] [PubMed] [Google Scholar]
- Narayanan MV, King MA, Pretorius PH, Dahlberg ST, Spencer F, Simon E, Ewald E, Healy E, MacNaught K, Leppo JA. Human-observer receiver-operating-characteristic evaluation of attenuation, scatter, and resolution compensation strategies for Tc-99m myocardial perfusion imaging. J Nucl Med. 2003;44:1725–1734. [PubMed] [Google Scholar]
- Nuyts J. The use of mutual information and joint entropy for anatomical priors in emission tomography. IEEE Nucl. Sci. Symp. Conference Record. 2007;6:4149–4154. [Google Scholar]
- Panin VY, Kehren F, Michel C, Casey M. Fully 3-D PET reconstruction with system matrix derived from point source measurements. IEEE Trans Med Imaging. 2006;25:907–921. doi: 10.1109/tmi.2006.876171. [DOI] [PubMed] [Google Scholar]
- Qi J. A unified noise analysis for iterative image estimation. Phys Med Biol. 2003;48:3505–3519. doi: 10.1088/0031-9155/48/21/004. [DOI] [PubMed] [Google Scholar]
- Qi J, Leahy RM, Cherry SR, Chatziioannou A, Farquhar TH. High-resolution 3D Bayesian image reconstruction using the microPET small-animal scanner. Phys Med Biol. 1998;43:1001–1013. doi: 10.1088/0031-9155/43/4/027. [DOI] [PubMed] [Google Scholar]
- Rahmim A, Cheng J-C, Sossi V. Improved noise propagation in statistical image reconstruction with resolution modeling; Nuclear Science Symposium Conference Record, 2005 IEEE; 2005. pp. 2576–2578. [Google Scholar]
- Rahmim A, Lenox M, Michel C, Reader AJ, Sossi V. Space-variant and anisotropic resolution modeling in list-mode EM reconstruction. IEEE Nucl. Sci. Symp. Conf. Record. 2003;5:3074–3077. [Google Scholar]
- Rahmim A, Qi J, Sossi V. Resolution modeling in PET imaging: Theory, practice, benefits and pitfalls. Med Phys. 2013;vol.40:064301. doi: 10.1118/1.4800806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahmim A, Tang J, Lodge MA, Lashkari S, Ay MR, Bengel FM. Resolution modeled PET image reconstruction incorporating space-variance of positron range: Rubidium-82 cardiac PET imaging; IEEE Nucl. Sci. Symp. Conf. Record; 2008a. pp. 3643–3650. [Google Scholar]
- Rahmim A, Tang J, Lodge MA, Lashkari S, Ay MR, Lautamaki R, Tsui BM, Bengel FM. Analytic system matrix resolution modeling in PET: an application to Rb-2 cardiac imaging. Phys Med Biol. 2008b;53:5947–5965. doi: 10.1088/0031-9155/53/21/004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahmim A, Zaidi H. PET versus SPECT: strengths, limitations and challenges. Nuclear medicine communications. 2008;29:193–207. doi: 10.1097/MNM.0b013e3282f3a515. [DOI] [PubMed] [Google Scholar]
- Rangajaran A, Hsiao I-T, Gindi G. A Bayesian joint mixture framework for the integration of anatomical information in functional image reconstruction. J Math Imaging Vis. 2000;12:199–217. [Google Scholar]
- Rapisarda E, Bettinardi V, Thielemans K, Gilardi MC. Image-based point spread function implementation in a fully 3D OSEM reconstruction algorithm for PET. Phys Med Biol. 2010;55:4131–4151. doi: 10.1088/0031-9155/55/14/012. [DOI] [PubMed] [Google Scholar]
- Reader AJ, Ally S, Bakatselos F, Manavaki R, Walledge RJ, Jeavons AP, Julyan PJ, Zhao S, Hastings DL, Zweit J. One-pass list-mode EM algorithm for high-resolution 3-D PET image reconstruction into large arrays. Nuclear Science, IEEE Transactions on. 2002;49:693–699. [Google Scholar]
- Reader AJ, Julyan PJ, Williams H, Hastings DL, Zweit J. EM algorithm system modeling by image-space techniques for PET reconstruction. Nuclear Science, IEEE Transactions on. 2003;50:1392–1397. [Google Scholar]
- Rousset OG, Ma Y, Evans AC. Correction for partial volume effects in PET: principle and validation. J Nucl Med. 1998a;39:904–911. [PubMed] [Google Scholar]
- Rousset OG, Ma Y, Wong DF, Evans AC. In: Quantitative Functional Imaging with Positron Emission Tomography. Carson R, Daube-Witherspoon ME, Herscovitch P, editors. San Diego: Academic Press; 1998b. pp. 67–75. [Google Scholar]
- Rousset OG, Rahmim A, Alavi A, Zaidi H. Partial volume correction strategies in PET. PET Clinics. 2007;2:235–249. doi: 10.1016/j.cpet.2007.10.005. [DOI] [PubMed] [Google Scholar]
- Ruangma A, Bai B, Lewis JS, Sun X, Welch MJ, Leahy R, Laforest R. Three-dimensional maximum a posteriori (MAP) imaging with radiopharmaceuticals labeled with three Cu radionuclides. Nuclear medicine and biology. 2006;33:217–226. doi: 10.1016/j.nucmedbio.2005.11.001. [DOI] [PubMed] [Google Scholar]
- Sankaran S, Frey EC, Gilland KL, Tsui BMW. Optimum compensation method and filter cutoff frequency in myocardial SPECT: A human observer study. Journal of Nuclear Medicine. 2002;43:432–438. [PubMed] [Google Scholar]
- Schaefferkoetter J, Casey M, Townsend D, El Fakhri G. Clinical impact of time-of-flight and point response modeling in PET reconstructions: a lesion detection study. Phys Med Biol. 2013;58:1465–1478. doi: 10.1088/0031-9155/58/5/1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selivanov V, Picard Y, Cadorette J, Rodrigue S, Lecomte R. Detector response models for statistical iterative image reconstruction in high resolution PET. IEEE Trans. Nuclear Science. 2000;47:1168–1175. [Google Scholar]
- Seltzer SE, Swensson RG, Nawfel RD, Lentini JF, Kazda I, Judy PF. Visualization and Detection-Localization on Computed Tomographic-Images. Investigative Radiology. 1991;26:285–294. doi: 10.1097/00004424-199104000-00001. [DOI] [PubMed] [Google Scholar]
- Shidahara M, Tsoumpas C, Hammers A, Boussion N, Visvikis D, Suhara T, Kanno I, Turkheimer FE. Functional and structural synergy for resolution recovery and partial volume correction in brain PET. Neuroimage. 2009;44:340–348. doi: 10.1016/j.neuroimage.2008.09.012. [DOI] [PubMed] [Google Scholar]
- Somayajula S, Panagiotou C, Rangarajan A, Li QZ, Arridge SR, Leahy RM. PET Image Reconstruction Using Information Theoretic Anatomical Priors. Ieee T Med Imaging. 2011;30:537–549. doi: 10.1109/TMI.2010.2076827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soret M, Bacharach SL, Buvat I. Partial-volume effect in PET tumor imaging. J Nucl Med. 2007;48:932–945. doi: 10.2967/jnumed.106.035774. [DOI] [PubMed] [Google Scholar]
- Strul D, Slates RB, Dahlbom M, Cherry SR, Marsden PK. An improved analytical detector response function model for multilayer small-diameter PET scanners. Phys Med Biol. 2003;48:979–994. doi: 10.1088/0031-9155/48/8/302. [DOI] [PubMed] [Google Scholar]
- Sureau FC, Reader AJ, Comtat C, Leroy C, Ribeiro M-J, Buvat I, Trebossen R. Impact of image-space resolution modeling for studies with the High-Resolution Research Tomograph. J Nucl Med. 2008;49:1000–1008. doi: 10.2967/jnumed.107.045351. [DOI] [PubMed] [Google Scholar]
- Swensson RG, Judy PF, Wester C, Seltzer SE. Nodule polarity effects on detection and localization performance in liver CT images. P Soc Photo-Opt Ins. 1997;3036:85–93. [Google Scholar]
- Tang J, Kuwabara H, Wong DF, Rahmim A. Direct 4D reconstruction of parametric images incorporating anato-functional joint entropy. Phys. Med. Bio. 2010;55:1–12. doi: 10.1088/0031-9155/55/15/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang J, Rahmim A. Bayesian PET image reconstruction incorporating anato-functional joint entropy. Phys. Med. Bio. 2009;54:7063–7075. doi: 10.1088/0031-9155/54/23/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang J, Rahmim A, Lautamaki R, Lodge MA, Bengel FM, Tsui BM. Optimization of Rb-82 PET acquisition and reconstruction protocols for myocardial perfusion defect detection. Phys Med Biol. 2009;54:3161–3171. doi: 10.1088/0031-9155/54/10/013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teo BK, Seo Y, Bacharach SL, Carrasquillo JA, Libutti SK, Shukla H, Hasegawa BH, Hawkins RA, Franc BL. Partial-volume correction in PET: Validation of an iterative postreconstruction method with phantom and patient data. J Nucl Med. 2007;48:802–810. doi: 10.2967/jnumed.106.035576. [DOI] [PubMed] [Google Scholar]
- Tohme MS, Qi J. Iterative image reconstruction for positron emission tomography based on a detector response function estimated from point source measurements. Phys Med Biol. 2009;54:3709–3725. doi: 10.1088/0031-9155/54/12/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong S, Alessio AM, Kinahan PE. Noise and signal properties in PSF-based fully 3D PET image reconstruction: an experimental evaluation. Phys Med Biol. 2010;55:1453–1473. doi: 10.1088/0031-9155/55/5/013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Videen TO, Perlmutter JS, Mintun MA, Raichle ME. Regional correction of positron emission tomography data for the effects of cerebral atrophy. J Cereb Blood Flow Metab. 1988;8:662–670. doi: 10.1038/jcbfm.1988.113. [DOI] [PubMed] [Google Scholar]
- Wagner RF. Decision theory and the detail signal-to-noise ratio of Otto Schade. Photogr. Sci. Eng. 1978;22:41–46. [Google Scholar]
- Wagner RF, Brown DG. Unified Snr Analysis of Medical Imaging-Systems. Physics in medicine and biology. 1985;30:489–518. doi: 10.1088/0031-9155/30/6/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson DW. Noise and Resolution Properties of FB and ML-EM Reconstructed SPECT Images. University of North Carolina at Chapel Hill; 1994. [Google Scholar]
- Wollenweber SD, Tsui BMW, Frey EC, Lalush DS, LaCroix KJ. Comparison of human and channelized Hotelling observers in myocardial defect detection in SPECT. Journal of Nuclear Medicine. 1998;39:771A. [Google Scholar]
- Wollenweber SD, Tsui BMW, Lalush DS, Frey EC, LaCroix KJ, Gullberg GT. Comparison of Hotelling observer models and human observers in defect detection from myocardial SPECT imaging. IEEE Trans Nuc Sci. 1999;46:2098–2103. [Google Scholar]