An Amino Acid Packing Code for α-helical Structure and Protein Design

Abstract

This work demonstrates that all packing in α-helices can be simplified to repetitive patterns of a single motif: the knob-socket. Using the precision of Voronoi Polyhedra/Deluaney Tessellations to identify contacts, the knob-socket is a 4 residue tetrahedral motif: a knob residue on one α-helix packs into the 3 residue socket on another α-helix. The principle of the knob-socket model relates the packing between levels of protein structure: the intra-helical packing arrangements within secondary structure that permit inter-helix tertiary packing interactions. Within an α-helix, the 3 residue sockets arrange residues into a uniform packing lattice. Inter-helix packing results from a definable pattern of interdigitated knob-socket motifs between 2 α-helices. Furthermore, the knob-socket model classifies 3 types of sockets: 1) free: favoring only intra-helical packing, 2) filled: favoring inter-helical interactions and 3) non: disfavoring α-helical structure. The amino acid propensities in these 3 socket classes essentially represent an amino acid code for structure in α-helical packing. Using this code, a novel yet straightforward approach for the design of α-helical structure was used to validate the knob-socket model. Unique sequences for 3 peptides were created to produce a predicted amount of α-helical structure: mostly helical, some helical, and no-helix. These 3 peptides were synthesized and helical content assessed using CD spectroscopy. The measured α-helicity of each peptide was consistent with the expected predictions. These results and analysis demonstrate that the knob-socket motif functions as the basic unit of packing and presents an intuitive tool to decipher the rules governing packing in protein structure.

While protein primary and secondary structure are well characterized, the exact manner by which residues pack to form higher order protein structure remains largely a challenge to describe. To better approach this problem, we previously developed a novel construct called the relative packing clique (RPC) that provides a natural vocabulary to describe packing.¹ Using Voronoi Polyhedra²/Delauney Tesselations,³ the RPC precisely defines a set of residues that all contact each other and classifies them based on contact order.⁴ In an extensive RPC analysis of packing between α-helices, this work demonstrates how simple combinations of a tetrahedral packing unit called the knob-socket can represent all α-helical packing. Just as the arrangement of hydrogen bonds defines secondary structure,^5;6 the knob-socket motif explains how side-chain packing arrangements at the secondary structure level allow higher order packing between α-helices. The knob-socket motif not only provides a clear method to describe side-chain packing between α-helices, but also presents a new paradigm for investigating protein packing to improve protein structure prediction and design.

Generally, the major difficulty in developing a useful characterization of protein tertiary structure has been in discovering an effective construct that produces order from non-specificity of packing interactions. The simplest approach has been to investigate pair-wise contacts,^7–17 which has shown success in finding amino acid correlations. However, a pair-wise treatment of residue interactions is too simplistic and cannot capture the 3-dimensional complexity of packing.¹⁸ More elaborate analyses of protein packing, including our own, consider multi-body arrangements of residues.^1;18–33 While these studies have generally found side-chain interactions to be broadly regular and tetrahedral, none so far has been able to develop a coherent description of protein packing. Another approach employs graph theory to organize protein interactions in hopes of identifying some common patterns across fold types. As the graphs are quite fold specific, this strategy has difficulty in finding common motifs across fold families^34–37 and is therefore more suited to distinguishing between protein families.^38;39 As a new perspective on protein packing, we show in this work that the knob-socket motif addresses the multi-body residue interactions and simplifies packing to uncomplicated pattern representations.

In the well-studied system of side-chain interactions between α-helices,^{27;28;30;31;40–42} this work extends the classic analyses of α-helical packing: Crick’s knobs-into-holes⁴³ and Chothia et al.’s ridges-into-grooves. ^44;45 Similarly to the analysis of tertiary structure discussed above, recent investigations of α-helix packing have characterized amino acid propensities^{7;8;24;38;46–48} and energetics,^49–56 but have not significantly advanced the insight into α-helical packing beyond the initial knob-into-hole and ridge-into-groove models. The knobs-into-holes translates to primary structure as the well-known heptad repeat,⁵⁷ but this pattern is limited to helix coiled-coils.^58;59 To describe other types of helical packing, an elegant implementation of knobs-into-holes has been developed recently that computationally assesses helical packing.^60;61 As an alternative, the helical lattice superposition model views packing as side-chain interlacing at Cα positions.⁶² In conjunction with the helical wheel,⁶³ these approaches have been used to dissect helix-helix packing interfaces,^64–68 yet only a few examples of designed α-helices have been successful. From the pioneering work on redesigning α-helical packing^69–71 and modulating helix oligomerization state^72–74 to more recent design of α-helix oligomers,^75–83 the designed proteins in these studies have been largely built from known scaffolds and sequences. Even with such advances in design, the understanding of α-helix packing remains primarily the residue repeats indicated on a helical wheel by the canonical knob-into-hole coiled-coil or ridge-into-groove packing. The simplification of α-helical packing by the knob-socket motif into discrete patterns presents an entirely new approach to interpreting and designing interactions to produce new α-helical oligomers and even unique α-helical folds.

The underlying approach taken in this work has its roots in the studies interrogating protein packing^84–90 using Voronoi Polyhedra.² By grouping residues based on graph theory cliques and sorting the cliques using contact order,⁴ we demonstrate that the complexity of helical packing can be simplified to combinations of a single 4-residue motif called the ‘knob-socket’. While this motif can be thought of as a refinement of Crick’s knob-into-hole,⁴³ the knob-socket motif represents a significant improvement not only to the analysis of protein tertiary structure but also protein design and prediction. The knob-socket construct allows an intelligible dissection of protein packing into the specific contributions from the various levels of protein structure. Beginning with secondary structure, the knob-socket motif characterizes the fundamental arrangement and propensities of residues that favor as well as disfavor α-helical structure. For higher order structure, the knob-socket motif identifies patterns within the α-helix packing that determines the specific interaction between α-helices. The packing patterns are identified for all α-helix packing not only in classical coiled-coil structures but also in globular proteins. To reiterate, in all of these classifications the only motif needed to describe inter-helix interactions is the knob-socket. The simplicity of reducing α-helix packing to patterns of knob-socket motifs provides a natural approach for the rational and de novo design of stable α-helix sequences. In practical application, a knob-socket based method was used to design sequences of varying α-helicity. The synthesis and subsequent characterization further demonstrated the validity of the knob-socket approach.

Results

RPC motif distribution in α-helix packing

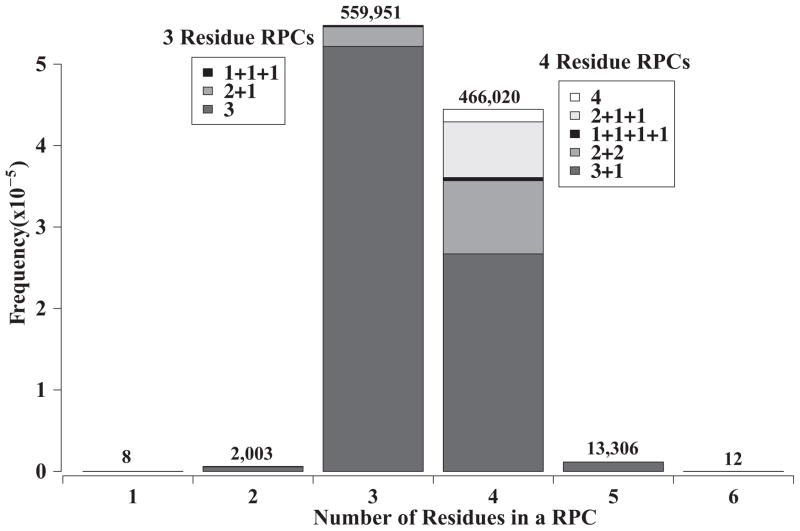
A relative packing clique (RPC) classification¹ was performed on a comprehensive set of interacting α-helices taken from the Protein Data Bank⁹¹ (for more detail, see Materials and Methods). An inspection of the resulting RPC patterns indicated certain RPC types consistently occurred across all packing patterns. To quantify this regularity, a histogram of RPC size and type was compiled from the analysis and is shown in Figure 1. Although RPCs of 1 and 2 residues were expected to display high counts, the cliques composed of 3 and 4 residues dominate the distribution with 54% and 45% of the total RPCs, respectively, which adds up to 99% of all the 1,041,300 RPCs in α-helices. Because the classification of RPCs is based on residue contact order, the analysis indicates whether the RPCs involve residues all packing from a single α-helix versus those packing between two or more α-helices. As a brief guide to our nomenclature, residues close in sequence are summed together. Those belonging to the same secondary structure element but not contiguous in sequence are separated by a colon “:” and are usually hydrogen bonded. Non-local residue contacts are denoted with a plus sign “+”. For example, the 4 residue RPC, 2:1+1 consists of 2 local residues hydrogen bonded to 1 residue, and 1 non-local residue. As an RPC, all the residues of this clique contact each other.

Figure 1. Distribution of Relative Packing Cliques (RPCs).

A histrogram divides the 1,041,300 α-helix RPCs into the six classes based on the number of residues involved in the clique. Values on top of each column indicate the number of members. The two most prevalent clique sizes are 3 and 4 residues that represent ~99% RPCs and are further sub-divided based on the number of secondary structural elements contributing to the RPC. For nomenclature, a “+” between numbers indicate the residues are separated on different α-helices, and no “+” means all the residues reside on the same α-helix. Numbers in parentheses are the percentage of the counts for that class. The 3 residue RPCs fall into three major classes: 3 – all residues from a single α-helix (96.9%), 2+1 – the residues split between two α-helices (2.8%), and 1+1+1 – three residues from three separate α-helices (0.3%). RPC class designated as 3 has three subclasses which include ‘2:1’ (97.9%) – the most dominant motif forming a socket, ‘3’ (2.0%) and ‘:3’ (< 0.1%). Similarly, 4 residue RPCs are grouped into 5 major classes: 4 – all four residues from the same helix (3.7%), 3+1 and 2+2 – the residues split between two α-helices (60.9% and 19.8%, respectively), 2+1+1 – the residues from three α-helices (14.8%), and 1+1+1+1 – all four residues from four separate α-helices (0.8%). The RPCs of the type ‘3+1’ is classified further as; ‘2:1+1’ (98.7%) – the most prevalent knob-socket interaction motif between two helices, and two other rarely fond patterns are ‘3+1’ (0.5%), and ‘:3+1’ (0.8%).

Figure 1 shows that the 3 and 4 residue RPCs break down into specific types. Out of the 559,951 RPCs of 3 residues, a 97% majority fall into one type designated the 2:1 motif, where all 3 residues originate from the same α-helix. As shown in Figure 2a, the 2:1 indicates 2 residues are contacting neighbors or near neighbors in sequence that are packed to another hydrogen bonded residue in the same α-helix. The remaining 3% of 3 residue RPCs involve packing between α-helices and are split between 2 types and these all occur toward the α-helical termini. A little less than 3% are 2+1 RPCs that occur between 2 α-helices, and the remaining less than 0.5% are 1+1+1 RPCs involving residues from 3 separate α-helices. Similarly, all of the 4 residue RPCs except for 1 type involve packing between at least 2 α-helices. Percentages are from the total of 466,020 RPCs that are 4 residue. At 61%, the most common 4 residue RPC is the 2:1+1 between two α-helices, which is basically 1 residue from another helix packed into a 3 residue 2:1 intrahelical packing clique (Figure 2d). The next most prevalent at 20% is the 2+2 RPC also between 2 α-helices, and this type is followed by the 2+1+1 RPC involving 3 α-helices at 15%. The final two contributing types of RPCs do not occur often. The 4 (all local residues contacting) RPC occur slightly below 4% under special circumstances and are observed at the ends of distorted α-helices. Lastly, 1+1+1+1 RPC within four α-helices is quite rare at just under 1%.

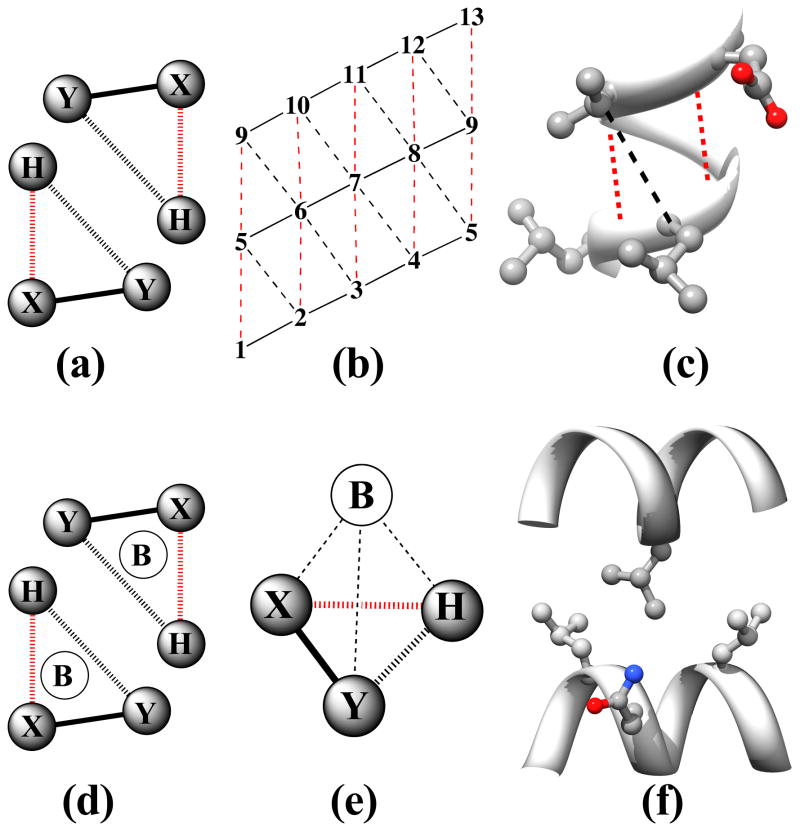
Figure 2. The Knob-Socket Motif.

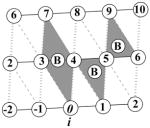
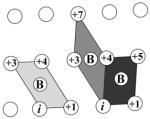
Based on the original definition from previous work,¹ a knob-socket RPC involves 4 residues from 2 α-helices, where all side chains pack against each other in a 3+1 configuration. The 2:1+1 indicates that a 3 residue socket local to one α-helix pack with the 1 residue knob on the other α-helix. Helix representations were created using Chimera.¹²³ (a) A two-dimensional representation of the RPC socket shows the 3 residues X, Y, and H. While the residues’ side-chains all pack against each other, the main-chain interactions differ as indicated by the lines. The i to i+4 α-helical hydrogen bond (broken red line) connects X and H. Consecutive residues X and Y share a peptide bond (solid black line). Residues Y and H only pack with their side-chains (broken black line). (b) The modified version of Crick’s⁴³ α-helical lattice showing the 2 types of socket RPCs on the α-helix surface. Residues on the edge wrap to display all possible sockets of the α-helix. The first in the lower left corner is a low X or XY:H socket, where the X residue is the lowest position in the sequence. The next socket is a high X or H:YX socket, where the X residue is the highest position in the sequence. In helix there is always an alternating pattern of these 2 sockets. (c) The low and high X sockets are shown on an α-helix structure from kinase 2ra7.⁹⁵ The low X consists of LL:V and the high X consists of D:LV. In this case the covalent bonds are replaced by the ribbon trace, but the other bonds are the same. Residues i and i+5 clearly cannot contact as they face away from each other. (d) A two-dimensional representation of the knob-socket motif shows the 3 residues in the socket are all packed against a knob residue B from the other helix. (e) The tetrahedral arrangement of the 4 residue knob-socket motif is shown, where residues are reduced to spheres for clarity. The knob residue B contacts all the 3 socket residues only through side-chain interactions (broken black lines). (f) The knob-socket motif shown between 2 α-helices.⁹⁵ On one α-helix, a low X socket of LQ:L packs against the knob B residue L from the other α-helix.

Comprising only 2% of the total interactions, the remaining RPC groups (1, 2, 5, and 6 residue RPCs) do not contribute significantly to α-helix packing. For the two types of RPCs with less than 3 residues, the common theme between the 1 and 2 residue RPCs is the involvement of a Gly residue. Of the over 1 million RPCs categorized, only 8 residues are isolated singletons. These occur at helical termini as a Gly or next to a Gly. At 0.2%, the 2 residue RPCs include intra-helical pairs of neighboring or hydrogen bonded and inter-helical pairs, yet in all cases, the pair is usually a long residue like an Arg or Leu packing into the space opened by a Gly. For the two sizes above 4 residue RPCs, the common theme for these larger RPCs is that all the interactions include the 3 residue, 2:1 intra-helical RPC as part of the larger RPC. With just a little over 1%, the 5 residue RPCs usually consist of 2 residues from 1 or 2 helices packed into a 3 residue 2:1 RPC on the other helix, where the residues are a combination of usually larger amino acids Leu, Ile, Val, Phe and Tyr. This 5 residue RPC is more often found towards the helix termini where short turns allows flexibility for 5 side chains to pack against each other, and sometimes they occur at the crossing of two or more α-helices. Surprisingly, no kinks or bulges are needed to accommodate the 5 large residues in this RPC. The 6 residue RPCs are also quite rare, as only 12 cases were found out of over 1 million RPCs. In all, the 6 residues form a triangular prism with the 2:1 intra-helical RPC on one end and another set of 3 residues that is either 2:1 intra-helical RPC from 1 helix or the RPC with similar arrangement from 2 or 3 α-helices.

From complexities of side-chain interactions, this RPC analysis reveals an elegant simplicity to α-helix packing: the single type 2:1+1 RPC accounts for all the packing in α-helices. This 4 residue packing construct consists of the 2:1 RPC acting as a socket that accepts a “+1” knob residue from another α-helix (Figure 2d,e). As it is an extension from previous α-helix packing models, this construct is designated the knob-socket motif. Within α-helices, the 3-residue socket is the primary packing arrangement of residues, since all other intra-helical RPCs occur rather infrequently at <2% and under special circumstances. Between α-helices, the inter-helical RPCs (those designated with a “+”) primarily consist of the 4 residue knob-socket arrangement in 2:1+1 fashion. The next most prevalent RPCs are of the 2+2 and 2+1+1 types, while the remaining inter-helical RPCs make up a minor, ~2% of overall interactions. These two other major inter-helical RPC types can be considered as deriving from the knob-socket RPC. The 2+2 RPCs result from 2 consecutive knob-socket RPCs between the two α-helices, while the 2+1+1 RPCs result from neighboring knob-socket RPCs in the packing of the three α-helices. The elegance of the knob-socket model is that it relates the socket packing arrangement formed within α-helical secondary structure as the determinant to the higher order packing of knob-sockets between α-helices. It is natural to view the knob-socket as derivative of Crick’s knobs-into-holes^{43;58;60–62} or other models of α-helix packing^{27;28;30;31;44;45;63;72–74} (see Table 1), as elements of the knob-socket model have been previously identified. However, the knob-socket represents a significant improvement in revealing the repetitive structure of α-helical packing. In particular, the knob-socket model reduces the complexity of all α-helical packing to simple patterns of single motif. In so doing, the packing structure of an α-helix is more akin to an array of sockets rather than true holes, and this model extends beyond descriptions of canonical patterns to non-canonical ones as well. Moreover, unlike previous models that focus primarily on intra-helical interactions, the knob-socket model discovers the contribution of packing at the level of intra-helical 2° structure, and as shown below, brings new insight in the identification of a specific packing code. In the next sections, the socket and the knob-socket motif are described in more detail as well as this model’s insights into α-helical packing and application to α-helical design.

Table I.

Models of Helix Packing

Model	Motif	Application
Knob-Socket intra-helical packing: 3 residue X,Y,H socket, 2 types i,i+1,i+4 (low X socket) i,i-1,i-4 (high X socket) inter-helical packing: 4 residue tetrahedral knob B in X,Y,H socket sockets can share a knob		1 simple motif The model recognizes importance of intra-helical packing as well as inter-helical packing Able to describe all canonical (Fig. 4) and non-canonical packing (Fig. 5) at any α-helical crossing angle (Ω) Provides specificity to packing (Figs. 6 & 7)
Knobs-into-Holes43;58;60–62;66;78;108 5 residue inter-helical packing a knob B residue packs into a 4 residue hole 3 types of 4 residue holes: i,i+1,i+3,i+4 (light grey) i,i+3,i+4,i+7 (medium grey) i,i+1,i+4,i+5 (dark grey)		1 simple motif Describes only inter-helical packing Best depicts canonical heptad repeat coiled coils at Ω = −160° and 30° Describes other canonical and non-canonical packing less well, Misses 4 residue packing
Helical Wheel63;66;72–74;78;124 pairwise interactions from particular repetitions in sequence residue i (filled square) with residue i+n (open square)		Describes only inter-helical packing Represents only pairwise packing of canonical sequence repeats heptad (7mer) coiled-coils, where Ω = −165° and 25°, and n = 3 undecamer (11mer) coiled-coil, where Ω = 175° and n=3 and 7.
Ridges-into-Grooves44;45 i±n residues form ridges shown by lines that pack into grooves created by 2 parallel i±n ridges ridges formed by i±n, where n=1,3 or 4.		Describes only inter-helical packing Represents canonical α-helix packing at Ω = −50° and 130° the best Non-canonical and remaining 3 canonical packing requires complicated combinations.
Close Packed19;30–33 hexagonal/face-centered close packing of layers layers between residue interfaces of +3 and +4		Describes only inter-helical packing Identifies packed residue groups as layers between sets of α-helices Layers identify super-secondary structures Close packed layers a general and non-specific description of packing
Puzzle Pieces24;27–29 pair and triplet elements combinations of these elements describe hydrophobic core packing		Identification of only hydrophobic amino acid propensities in motifs Although suggested by motifs, does not explicitly differentiate between intra and inter α-helical packing Combinations of pairs and triplets used to characterize the hydrophobic core packing between α-helices

Knob-Socket Model of α-helical Packing

As demonstrated above, the knob-socket motif is the dominant arrangement involved in helical packing and could be considered the fundamental packing unit in α-helices. Essentially, the model reveals the intra-helical packing at the secondary structure level that promotes inter-helical packing at the tertiary structure level. For this reason, we detail the intra-helical and inter-helical parts of this motif and the intrinsic dependency of the knob-socket on the patterns of sockets in an α-helix. In addition, as depicted in Figure 2, the knob-socket allows a simplified and clear representation that retains the essential information about α-helical packing without overwhelming complexity.

For intra-helical packing, all residues pack against each other in 3 residue RPCs. These 3 residue 2:1 RPCs result from side-chain packing at the level of secondary structure, deriving only from intra-helical interactions. By RPC definition, all of the residues’ side-chains pack against each other,¹ and the two orientations of the 2:1 motif share the same organization of residues. The 2:1 describes main-chain interactions of “2” neighboring residues X and Y sharing the covalent peptide bond, where the X residue shares the “:1”, helical i to i+4 hydrogen bond with residue H. The H and Y residues share only side-chain packing interactions between them and are separated by three residues in the sequence. Altogether, the three residues X, Y, and H form the RPC socket motif. With a few exceptions, these cliques all exhibit the same connectivity but in two orientations (Figure 2a). When residue X is at the lowest sequence position in the clique, the hydrogen bonded residue H and the covalent residue Y are higher in sequence by 4 and 1 position, respectively. To indicate the sequence and structure relationships, this low X socket is designated as the XY:H socket, where the “:” indicates that residue H is hydrogen bonded. When residue X is the highest sequence position in the clique, the hydrogen bonded residue H and the covalent residue Y are lower in sequence by 4 and 1 position, respectively. This high X socket is designated as the H:YX socket to indicate the sequence and structure relationships. As an extension of the α-helical grid of residues used by Crick,⁴³ we incorporate the bonding interactions of the two socket orientations to create the lattice shown in Figure 2b. This modified lattice representation clearly depicts the repetitive pattern of intra-helical packing of the two XY:H and H:YX sockets. Examples of XY:H sockets in the α-helix lattice (Figure 2b) include residues 1-2-5 and 2-3-6. Examples of H:YX sockets in the α-helix lattice (Figure 2b) include residues 2-5-6 and 3-6-7. The lattice also clearly demonstrates how the α-helix presents a regular socket pattern along the entire α-helical surface. Besides the covalent peptide bonds and hydrogen bonding, the packing between i and i+3 residues also contributes to the regularity of the socket pattern. As depicted by the 2 sockets on an α-helical face in Figure 2c, alternative packing arrangements such as interactions between residues’ side-chains at i and i+5 positions never occur for 2 reasons. These residues point in almost opposite directions on an α-helix and are always occluded by the i,i+3 packing.

In our continued analysis, it is at times clearer to discuss these 3 residue RPC sockets as one of a set of hierarchical groupings. At the basic level, the order of the residues indicates position in sequence and structure as in XY:H and H:YX described above. Combining these two into a single group, XY•H implies either low or high X orientation. For example, the AL•V socket represents both the low X AL:V and high X V:LA sockets. The final grouping XYH only indicates amino acid content without any implication of order. As a convention, the residues in XYH are ordered alphabetically by amino acid single letter code. As an example, stating ALV includes 12 sockets (or 6 XY•H socket groups): AL:V and V:LA (or AL•V), VA:L and L:AV (or VA•L), LV:A and A:VL (or LV•A), LA:V and V:LA (or LA•V), VL:A and AL:V (or VL•A), AV:L and L:VA (or AV•L). Each of these socket groupings will be used to clarify the following explanations of the knob-socket model.

For inter-helical packing, the 4 residue RPC, 2:1+1 builds off of the 3 residue sockets described above by simply packing the 2:1 RPC on one α-helix together with a “+1” knob B residue from another α-helix (Figure 2d–f). This 2:1+1 or knob-socket RPC motif describes all of inter-helical packing at the level of tertiary and quaternary structure. As presented schematically in two dimensions by Figure 2d, the knob-socket motif consists of 4 residues from two α-helices whose side-chains all contact each other by RPC definition.¹ The knob-socket motif interacts in a tetrahedral configuration as a single packing unit (Figure 2e). The knob B on one α-helix packs into the 3 residue XY•H socket presented by another α-helix. As an example of knob-socket packing across 2 α-helices, Figure 2f shows a more appropriate description of the inter-helical packing, where the knob B residue rests in the socket formed by the X, Y and H residues. By combining Figures 2b and 2d, patterns of these knob-socket motifs can be easily represented on the modified lattice by placing the knobs into the appropriate low and/or high X sockets. Of course, these designations are relative as a residue can participate in more than one role in different RPCs. So, a residue may act as a knob B in one knob-socket motif and also as part of a socket in another. Therefore, to be complete, packing patterns for both α-helices involved in the interaction need to be shown on a modified lattice. This is done in the following section for the major canonical patterns of α-helical packing.

Canonical Packing Patterns Between α-helices

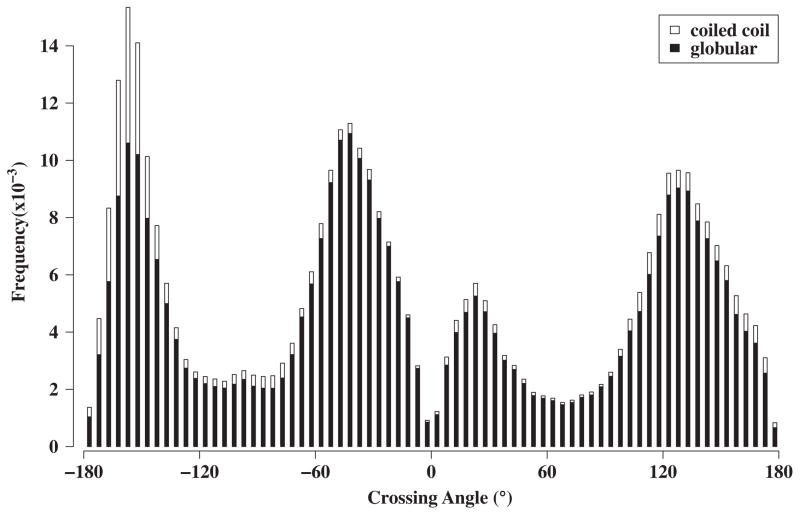
Figure 3 plots the distribution of the α-helix crossing angles across the knob-socket motifs. Like previous analyses of helix crossing angles,^62;92;93 the 4 major peaks can be seen at −150°, −45°, 25°, and 130°. Closer inspection of the curve indicates a shoulder due to a 5^th peak at 175° for the anti-parallel undecatad (11mer) repeat coiled-coil.^73;94 Each peak is centered around a certain canonical packing pattern between the two α-helices: −150° anti-parallel heptad repeat coiled-coil, −45° parallel ridge into groove, 25° parallel heptad repeat coiled-coil, and 130° anti-parallel ridge-into-groove. The knob-socket model provides a physical explanation to the various features of the distribution. First, the low counts of packing at 0° and 180° can be discerned from the modified lattice shown in Figure 2b. The skew caused by the orientations of the 3 residue sockets disfavors head on 0° or 180° packing between α-helices. For the peaks, the higher frequency of knob-sockets at these angles is due to the longer stretches of α-helix interactions. This is especially true for the large increase around −150° due to longer runs of knob-socket in anti-parallel coiled-coils. The valleys are due to the smaller interaction surface between α-helices crossing at ±90°. It is interesting that if the coiled-coil proteins are removed, the 3 major peaks of −150°, −45°, and 130° are just about equal. The smallest peak of the parallel 25° heptad repeat may be due to the longer contact order needed to bring two α-helices into a parallel orientation. Also, the orientation having all of the Cβ pointing in the same direction may make packing less favorable, which is the same relationship found to a lesser extent between the anti-parallel −150° the parallel −45° and ridge-into-groove peaks. The unfavorable packing due to the direction of side-chain Cβ also explains why the 175° anti-parallel undecatad repeat coiled-coil has no corresponding parallel form around a α-helical crossing angle −5°.

Figure 3. Crossing Angles Dependency of RPCs cliques.

Instantaneous crossing angles between two α-helices for each RPC was computed using HELANAL¹²¹ (see Materials and Methods), and the frequency distribution of helix RPCs is shown against the crossing angle. The black is from α-helices in globular proteins and the white are from coiled-coils. It is interesting to note that the distributions would be about equal if the coiled-coils were removed. Each peak corresponds to a canonical packing pattern depicted in Figure 4. The well-known peaks of coiled coils are found for anti-parallel at −165° and 25°. The other peaks occur at −30° and 150°, which also includes the shoulder at 175°.

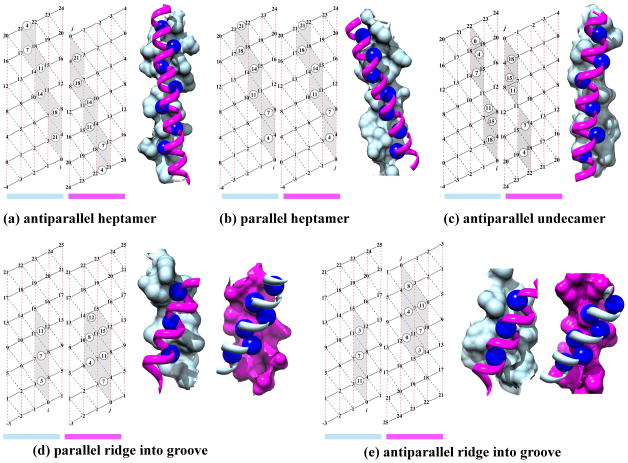
As an improvement over previous descriptions of α-helical packing^{43–45;58;60–63;72–74}, the knob-socket model provides a simplified representation of the complexities of packing as well as a straightforward vocabulary to describe it. Moreover, the knob-socket model is able to intuitively describe any type of canonical packing instead of performing well for just a few of the patterns. Figure 4 illustrates these abilities by clearly depicting the canonical patterns for each of the 5 peaks on modified α-helical lattices. Essentially, packing between the two α-helices forms a series of interlocking knob-sockets along the interface. On the modified α-helix lattice, the grey area represents the sockets on one helix and the circled numbers are the packed knob residues from the other helix. Using the knob-socket model, the paths of sockets defines the exact surface area contact on an α-helix that a knob residue from another α-helix packs against. Across all the patterns shown in Figure 4, the most common is one knob residue shared between 2 sockets: a low XY:H socket on top of a high H:YX socket or classically Crick’s knobs-into-holes motif.⁴³ As shown in bottom of the right α-helical lattice around residue 22 of Figure 4a and in the top of the middle α-helical lattice around residues 4 and 8 of Figure 4c, the other possible configurations (neighboring low XY:H and high H:YX sockets) of shared knob-sockets exist, but these are more found as deviations from the canonical patterns depicted in Figure 4. Previous models of α-helix packing could not account for such variations. In addition, the canonical packing patterns clearly illustrate that the 2+2 RPC is not a determinant of packing but rather is a product of 2 consecutive shared knob-sockets. Because of this dependency, the 2+2 does not directly contribute to packing. This descriptive accuracy reveals that only the knob-socket motif is required to comprehensively describe all of α-helical packing, including alternate canonical patterns and variations from regularity.

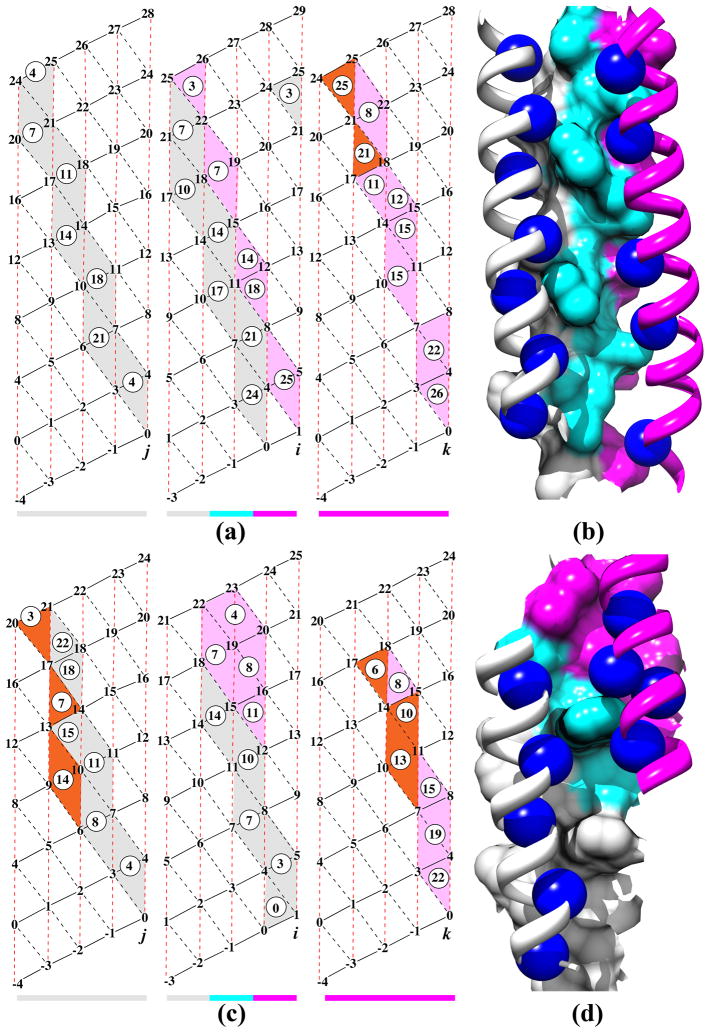
Figure 4. Canonical Helix-Helix Packing Patterns.

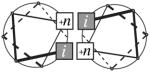
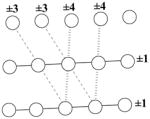
For an α-helical pair, the interaction pattern is shown using a modified version of Crick’s⁴³ α-helical lattice along with a structural representation of the packing. The numbers in the lattices are the residue numbers relative to the earliest residues i and j in the packing interface. The color bar under each lattice corresponds to the color of the α-helix in the depicted interaction pair. Grey sockets are involved in inter-helical knob-socket interactions, whereas white sockets are only intra-helical secondary structure packing. Circled numbers are knob residues corresponding to positions on the other helix packing into their respective sockets. For the depiction of the packing interface, the surface of one helix is shown in torquoise while the other helix is shown in magenta ribbon with the knob residues in blue spheres. Depiction was performed using Chimera¹²³. Helix angle was calculated with HELANAL¹²¹. (a) Canonical packing pattern for left-handed anti-parallel α-helix dimer with a crossing angle of −165°⁹⁵. In this canonical packing, the same regular packing pattern appears on both sides of helices in the shared knob-socket motif or classic knobs-into-holes packing⁴³ of the heptad repeat⁵⁷. (b) Left handed parallel coiled-coil pattern of helix packing with crossing angle of 25°. Similar to pattern in (a), both helices shows identical knob-socket patterns at interface. (c) An example of right handed anti-parallel packing pattern with a crossing angle of 175°⁹⁶. Instead of a heptad or 7mer repeat, the repetition occurs every 11 residues^73;94. This causes a α-helix packing angle change from −165° to 175°. (d) Canonical pattern for right-handed parallel helix dimer on helix lattice with a crossing angle of −50°⁹⁷. Most clearly shown are the singular knob-sockets. This is also representative example of a 4-4 packing in the ridge into groove interaction^44;45. (e) Right handed ridge into grove with helices running antiparallel to each other with crossing angle of +135°. Both patterns in (d) and (e) shows the ±4n ridge along the residues 3-7-11 packs against the ±4n groove between the ridges formed along the residues 0-4-8-12 and 3-7-11-15. The ridges forming the groove on one α-helix pack into corresponding grooves on the other α-helix formed by three ±4n ridges: 0-4-8-12, 3-7-11-15, and 6-10-14. The pattern of knob sequences follow along the i+4 ridge, which packs into the sockets formed along the i+4’s.

The parallel and anti-parallel coiled-coils exhibit the same pattern of shared-knob sockets that corresponds to the heptad repeat⁹⁵ as shown in Figure 4a and 4b. The heptad sequence repeat is defined on the α-helix lattice by the residues surrounding the combined low and high X sockets or the hole in Crick’s model. The knob-socket analysis also reveals certain dependencies due to regularity of coiled-coil packing pattern. All knob residues have the same unique characteristic of also being a residue at the intersection of 4 packing sockets. Because these packing sockets overlap and in sum include all residues in the packing surface, knowing the pattern of knob residues on an α-helix also provides the pattern of packing sockets on that α-helix, and conversely, knowing pattern of packing sockets identifies the pattern of knob residues. For a canonical coiled-coil, this dependency can be made even simpler, since the knob-socket follows a regular pattern. Knowing any 2 consecutive knob residues or 4 consecutive packing sockets provides enough information to define the remaining packing interface. Also, the pseudo heptad repeat of the knob residues provides a unique identifier of this coiled-coil conformation. In this way, the knob-socket helps in modeling as well as analyzing protein structure.

As can be seen in Figures 4c, 4d, and 4e, the knob-socket motif describes the patterns of the other 3 canonical packing patterns that contain a knob participating with a single socket. Figure 4c shows the packing pattern of an anti-parallel right handed coiled-coil with a crossing angle of 175°.⁹⁶ This pattern elongates the classic coiled-coil pattern. From a knob-socket analysis, the orientation of α-helices results from a pattern of a shared knob-socket followed by a pair of single knob-sockets. The residues involved in this packing pattern produce a pseudo undecatad residue repeat at the sequence level.^73;94 Because of the simplified and clear rendition of the repetitive packing element by the knob-socket motif, characterization of the complete interface requires only identification of the knob residues. The pseudo undecatad or 11mer periodicity of the knobs’ residue positions acts as a simple way to identify this type of helix packing in a protein structure.

As shown in Figures 4d and 4e, respectively, the knob-socket motif readily accounts for the parallel and anti-parallel ridge into groove packing.⁴⁴ For these 3 patterns shown in Figure 4c, 4d, and 4e, the packing includes single knob-socket elements in the patterns to complete the packing pattern. For the −45° and 130° ridge into groove packing, the red dashed lines are ±4n ridges, black dashed lines are ±3n ridges, and black solid lines are ±1n ridges. The grooves are between any two parallel lines. This packing results in shorter but wider stretches of α-helical packing. Figure 4d shows the canonical packing pattern for a parallel helix-helix⁹⁷ interaction with a crossing angle of −50°, while Figure 4e shows the canonical packing pattern for an anti-parallel helix-helix interaction. For both, the packing includes one instance of a single knob-socket: knob B on one α-helix packing into a high H:YX socket on the other α-helix. A ridges-into-grooves approach defines these as a class 4–4 packing pattern.⁴⁴ As seen on the modified α-helix lattice, the knob-socket motif presents a straightforward diagram of the ridges and grooves, which does not translate well to a repetitive primary sequence. Again, because of the regularity of the pattern, knowing which residues interacted across the α-helix interface would again be enough to define the socket packing surfaces on each α-helix. Also, the 4 residue repeat of the interacting knob residues functions as a signature for this type of α-helical packing.

As defined by the knob-socket model, packing of higher numbers of α-helices can be simply thought of as combination of the above pairwise canonical patterns, yet the patterns can be quite non-canonical also. To demonstrate this, Figure 5 shows the knob-socket packing patterns for two sets of 3 α-helix bundles on the modified α-helical lattices next to structural representations. Consistent with earlier studies,^{44;45;98–100} the knob-socket analysis demonstrates that a maximum number of 3 α-helices can concurrently interact with each other. Even when higher numbers of α-helices exist in a structure, the larger α-helical bundles are simply combinations of 3 α-helix bundles. The patterns shown in Figure 5 present an easily digestible representation of the α-helical packing complexity not found in the corresponding structural representations. The portrayal allows clear insight into the manner of packing in these bundles. First, in addition to the 2+2 dependency found in the pair of α-helix interactions, the 2+1+1 RPC derives from the knob-socket patterns. Next, an analysis of these 3 α-helix bundles using the knob-socket motif reveals an order to the interactions. A pair of α-helices usually forms a stable foundation by packing in a canonical pattern with each other. In the first bundle in Figure 5a, α-helices i and j pack as an anti-parallel coiled-coil, while in the second bundle in Figure 5c, α-helices i and j pack as a parallel coiled-coil. The third α-helix packs less regularly against the first, but more regularly against one of the two α-helices. In Figure 5a, α-helix k packs well with α-helix i in a parallel coiled-coil pattern and significantly less well with α-helix j with only 2 contacts. In Figure 5c, α-helix k packs more regularly with α-helix j in a distorted anti-parallel coiled-coil configuration, but makes more contact with α-helix i but in a non-canonical patterns. Clear characterization of these deviations is another strength of the knob-socket model as pointed out above. In particular, Figure 5c shows all 3 residues in a socket from α-helix k (the high X socket of 4, 7, and 8) packs into 6 sockets on the C-terminal end of α-helix i. Each of the residues from α-helix k pack into shared sockets. Only residue 7 displays the typical low on top of high socket pattern, and the remaining 2 residues exhibit atypical neighboring sockets patterns. As this packing is clearly not knob-into-hole⁴³ and violates ridges-into-grooves rules,⁴⁴ the pattern is indescribable by previous methods, yet it is clear in knob-socket representation.

Figure 5. Patterns of Knob-Socket motif for packing of three helices.

Panels (a) and (c) shows the packing patterns of knob-socket motifs on the helical lattice between three helices. There are three pairs of packing surfaces that are shown by shaded socket patterns of the same color on the helical lattices. Packing surface between helix pairs i–j is grey, i–k is light magenta and j–k is shown by orange triangles on the helical lattice. Color bars at the bottom of each helical lattice indicate the color of helix in the structural models shown on the right in panels (b) and (d). Helix j and k are represented by grey and magenta ribbons respectively and helix i is surface representation in structural model. Knobs from the helices j and k are shown as dark blue spheres that are packed against the sockets on helix i that are represented by light grey and magenta surfaces respectively. The teal (light blue) surface on helix i represents the interface between the packing surfaces of i–j and i–k helices. The panel (a) is canonical pattern, where two pairs ( i–j, and i–k) of helices pack against each other with coiled–coil topology and panel (b) is example of mixed coiled-coil (i–j) and ridge-into-grove (i–k) packing pattern between three helices. From both the examples it can be observed that there is strong packing between two pairs of helices (i–j and i–k) in each helical bundles and the third pair (j–k) is weaker interaction.

Propensity of Socket Composition Defines α-helix Structure

In addition to the clear depiction of α-helix packing interactions, the knob-socket model provides a completely new and non-linear view of α-helix packing and moreover, α-helix propensity. In particular, the knob-socket model defines 3 classes of structures involved in determining α-helix packing. The first two are directly evident from modified α-helix lattices in Figures 4 and 5 and indicate packing state: sockets are either filled (colored triangles) or free (white triangles). As part of a 4 residue knob-socket RPC, filled sockets are packed with a knob residue and are involved in inter-helical packing. Free sockets disfavor packing with knob residues and are involved only in intra-helical packing. Common to both of these sockets is that they favor α-helical structure based on the XYH packing, which is non-linear in its approach to α-helix formation. The third class is implied inverse set of the first two: sockets that do not favor α-helical structure or non-sockets. So, the three classes are 1) filled sockets, 2) free sockets, and 3) non-sockets. For each, socket amino acid composition can be queried for frequency. This analysis categorizes sockets not only on their preference for inter-helical packing, but moreover on their propensity to form intra-helical packing that is a socket’s propensity to form an α-helix. As a code representing protein structure, these propensities refer to a code that defines packing between α-helices.

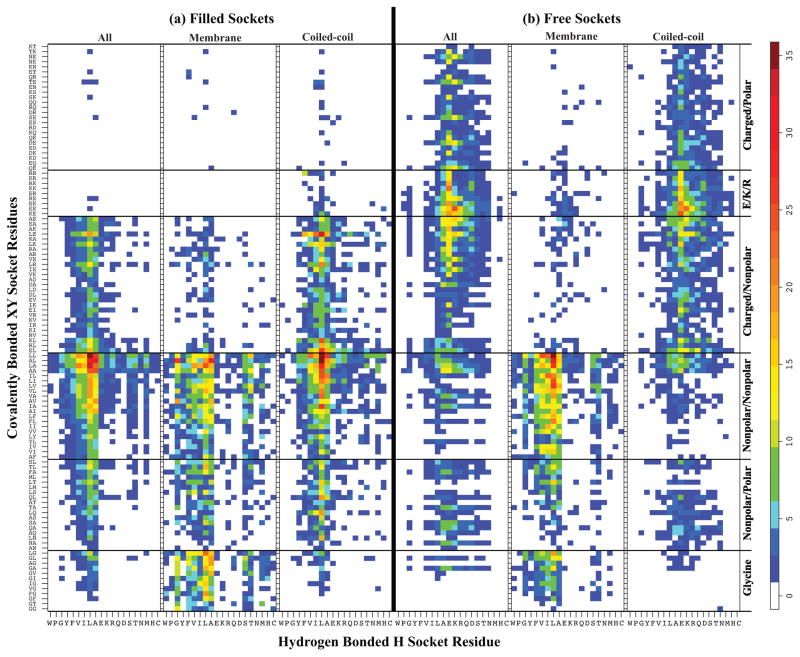
Figure 6 displays relative probability histograms of 2,240 combined XY•H sockets from an 8,000 possible combinations that are either filled (Figure 6a) or free (Figure 6b) for all proteins in SCOP family (All), membrane proteins (Membrane) and coiled-coil proteins (Coiled-coil). To properly portray the distribution of socket propensities, the sample in Figure 6 includes the top 100 most frequent XY•H sockets for both filled and free types and 12 most frequent sockets involving glycine in membrane proteins, and these are plotted with XY residues on the y-axis versus H residues on the x-axis. Frequency of the socket is displayed in the z-axis. For direct comparison, Figure 6a and 6b show the same sample in the same ordering. The ordering was developed to provide the most contrast and insight into the composition of sockets that prefer to be filled, free, and non. The XY pairs are arranged according to the amino acid type (non-polar, polar, and charged) with non-polar groups towards the bottom, charged towards the top middle, and polar at the ends. The XY pairs with glycine are located at the very bottom of the Y axis and are shown to highlight the socket differences due to a membrane environment. The H residue is ordered with the amino acids generating the highest frequency in the middle descending to those with the least on the sides, where non-polar amino acids are on the left and the charged/polar are on the right.

Figure 6. XY•H amino acid preferences.

Heat map showing the residue preferences for filled and empty sockets in helix packing. Relative probability (see Materials and Methods section for details) of socket forming H and XY residues are represented in heat map. Two parts in the figure represent the frequency distributions of socket forming residues that favor to be filled with knob in panel (a) Filled Sockets and those that prefer to be free in panel (b) Free Sockets. Heat maps for membrane proteins (Membrane) and coiled-coil proteins (Coiled-coil) are given for comparison along with those from all SCOP family proteins (All). For each filled and free sockets, residue pair XY is plotted on Y-axis where XY residue pairs are divided in six groups. From bottom, the first block contains XY pairs with glycine, the second block contains nonpolar/polar residue pairs, the third block shows a nonpolar residue pair, the fourth block is pair of residues that are charged/nonpolar, and the top one is pair of charged/polar residues. Small block of charged residues that are E/R/K is indicated separately. Residue H is plotted on X-axis where residues are arranged as hydrophobic, charged and polar from left. The color ramp on the right side shows the normalized frequency values ranging from low (blue) to high (dark red). Comparison of high frequency regions in both (a) and (b) clearly shows that combination of small nonpolar residue at H and pair of small nonpolar residues at XY positions favors the sockets that like to be filled by packing with the knob and hence these types of sockets usually occur at helix interfaces. Similarly the region where combination of E/R/K at XY position and small nonpolar (L/A) or charged (E/K) is most favored for the sockets that prefer to be empty and hence can be found on the surface of helix which does not pack with other helices. Also, difference in amino acid’s socket preferences between the protein families can be seen. The socket preferences in membrane protein are very different from those in coiled-coil protein. The high frequency of Gly in membrane proteins tells that Gly plays an important role in membrane protein packing.

Overall, a comparison of Figure 6a and 6b shows distinct preferences of amino acids for filled, free, and non-socket composition. While each socket type exhibits certain tendencies, there are deviations and some interesting findings, especially for non-sockets. As expected, the filled sockets prefer the non-polar amino acids in the following order: Leu, Ala, Ile, Val, and Phe, and usually consist of at least 2 of these amino acids. As a corollary, filled sockets distinctly disfavor 2 or more charged or polar residues, especially in the X and Y positions. The most prevalent filled sockets that exhibit over 20 times higher probability than average are LL•L, LA•L, LL•A, AL•A, and LL•A. Somewhat surprising are the inclusion of Glu, Lys, and Arg in certain higher frequency filled sockets with 2 other Leu residues like LE•L, LR•L, and LK•L. Most of the filled sockets display weak to no tendencies to be free sockets, except for AA•A, AL•A, LA•L and LA•A. Besides these, free sockets prefer combinations that include one or more Glu, Lys, and Arg charged amino acids and sometimes with single non-polar amino acid. The most prevalent free sockets over 20 times higher probability than average are EE•K, KE•E, and KK•E, which all include the i to i+4 salt-bridge and the most prevalent EE•K opposes the α-helical dipole.¹⁰¹ Of the non-polar amino acids, Leu and Ala are involved in many free sockets. Also, many free non-polar sockets are those that are found in membrane proteins. Overall, the distribution of the free sockets’ amino acid composition is more diverse than the filled sockets’ including combinations of non-polar, polar, and charged groups, but there is little uniformity over the distribution.

Across the different protein families, the membrane proteins and coiled-coil proteins are separately analyzed. The socket distribution in coiled-coil proteins follows very closely what is found across all protein families for both filled and free sockets. By contrast, membrane proteins exhibit expected socket distributions favoring primarily combinations hydrophobic amino acid types. Both filled and free sockets with charged or polar amino acids show very low probability in membrane proteins. Even the free sockets with high probabilities such as EE•K, KE•E, and KK•E, show only the probabilities of random distribution. As in All protein families, Leu and Ala are the most frequently observed amino acids in sockets in membrane protein families, but there also the prevalence of Ile and Val (amino acids with branching at the Cβ side-chain atom). The primary difference between filled and free sockets is the use of residues Ile and Val branched at their Cβ side-chain atom. As interesting, contributions of Gly to sockets in membrane protein are noticeably high compared to those in other families of proteins. Among the sockets with one Gly, LG•L, GL•A, AL•G and AV•G, and FG•L are most frequently observed sockets in the packing interfaces of membrane proteins. The well-known GxxxG motif in packing interfaces of transmembrane proteins^102–105 and extremophiles^106;107 is represented as a GX•G socket in the knob-socket model, where X is any of the 20 amino acids. Among these, GL•G, GA•G, GV•G, and GG•G sockets appear in high frequency. Although these packing motifs have been identified in previous studies¹⁰⁸, they were considered more 1° sequence motifs characteristic of a membrane protein rather than 3º structural motifs. Our analyses demonstrate the difference between membrane and coiled-coil proteins in socket frequencies as well as amino acid content.

While both filled and free sockets promote helix formation, non-sockets are combinations of amino acids with low propensity to form a socket and therefore disfavor α-helix formation. In Figure 6, the non-sockets are those that display whitespace in both parts of Figure 6 as well as many of the 6,000 low count XY•H combinations not shown. From the plots, a few generalizations can be made. The most well known residues that break α-helix structure are Gly and Pro. Surprisingly, many residues in addition to Gly and Pro do not favor α-helical structure in globular proteins. Non-sockets include the aromatic residues Tyr and Trp as well as the polar Gln, Asp, Ser, Thr, Asn, Met, His, and Cys. It is surprising that this many polar groups disfavor α-helix socket formation, and this list does not follow the standard rules about residues with branching at the Cβ.

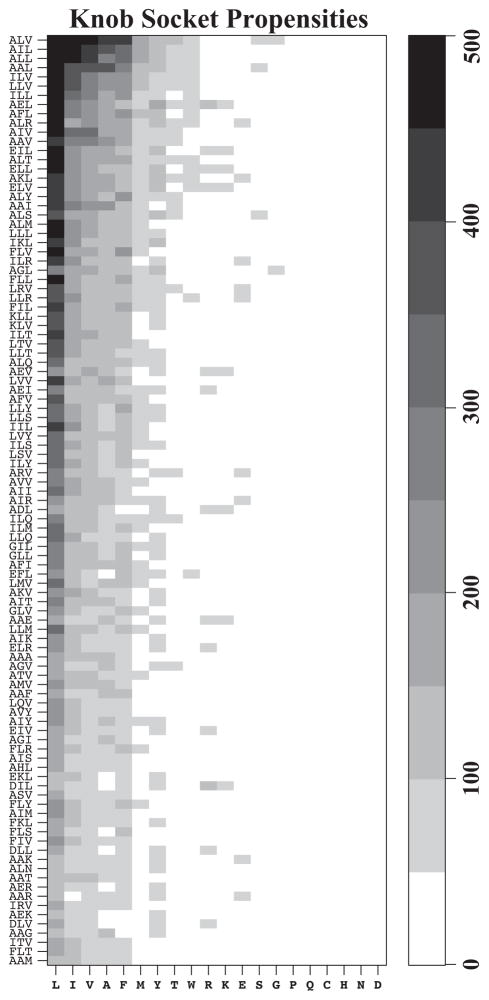
To complete an analysis of the knob-socket model’s packing code, Figure 7 investigates the propensity of the 20 amino acids to be knob B residues and the XYH composition of the top 100 filled sockets that each knob B favors. Because the XYH represents 12 combinations of sockets, the top 5 filled sockets of ALV, AIL, ALL, AAL and ILV are a little different than the more specific XY•H sockets in Figure 6. In general, the knob B residues can be loosely organized into 4 groups. As the primary mediator of packing between α-helices, the residues that have a high likelihood of packing as a knob B residue into a filled socket are all the non-polar amino acids in the following order: Leu, Ile, Val and Ala. While all these non-polar amino acids pack as knob B residues with some frequency into all of the top 100 filled sockets, Leu is by far the most frequent knob B residue with a steep drop off for the frequency of the remaining 3 non-polar residues. The next grouping includes Phe, Met, and Tyr that are somewhat favored as knob B residues. While Phe is occasionally found in α-helix forming sockets, Met and Tyr are interesting as these residues appear infrequently in sockets (Figure 6). With few counts to any consistent socket type, Thr, Trp, Arg, Glu, and Ser rarely act as knob B residues. The remaining residues of Gly, Pro, Gln, Cys, His, Asn, and Glu are hardly found as knob B residues and could be thought of as disfavoring inter-helical interactions.

Figure 7. Knob propensities for most preferred sockets.

The heat map shows the propensities for 20 amino acid knobs B that pack with 100 most preferred XYH sockets on helical interface. The groups of three residues that make the sockets are arranged on the Y-axis from top to bottom with decreasing frequencies. Knob residues are displayed on X-axis with sequence order from left to right with high propensity knobs on left most side of the plot. Grey scaled color ramp shows the frequencies of knob residues from light (least preferred) to dark (most preferred). Non-polar beta branched residues; Leu, Ile and Val as well as small non-polar side chain Ala are most favored knobs in helix packing motifs. Amongst the bigger hydrophobic side chains, Phe is preferred over Tyr and Trp in most helix-helix interaction interfaces. Not surprisingly, most of the polar and charged residues occur with very low frequencies.

Protein Design Based on the Knob-Socket Model

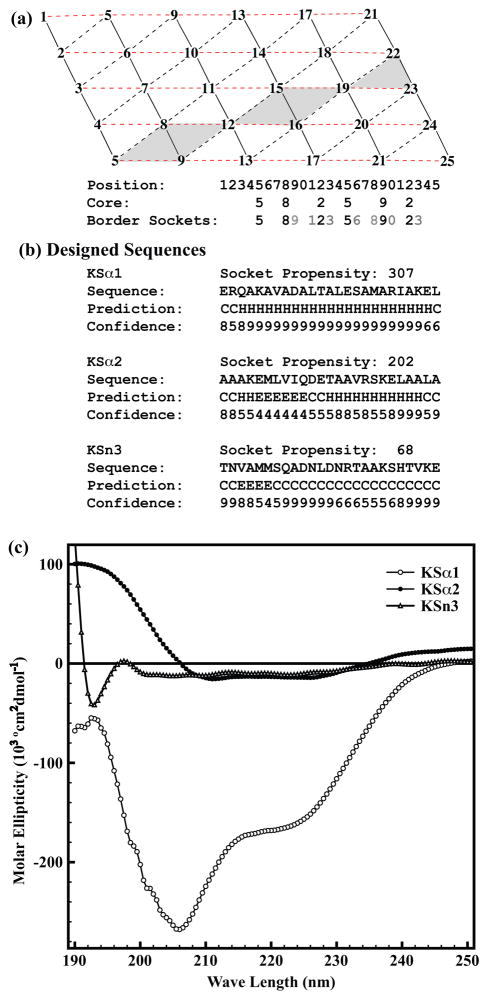
Because the knob-socket model reveals residue propensities that underly packing in α-helices, the analysis performed above provides a novel approach to the rational and de novo design of α-helix structure. Amino acid composition and configuration are now defined in a non-linear fashion for sockets that will form or inhibit α-helix formation and furthermore, the socket patterns that promote specific orientations of α-helix oligomerization. While proving oligomerization is outside the scope of this study, successful design of α-helices can be readily measured. Figure 8a shows the stepwise rational, de novo design of two α-helix sequences of residue length 25 that form different levels of α-helical structure as determined by the average frequency of sockets. The design principle is simple: the sequence is guided by the socket packing pattern on the modified α-helix lattice. However, the patterning of sockets makes the order non-linear. First, the core residues along the path of alternating i+3 and i+4 residue position are selected (i.e. 5-8-12-15-19-22). Then, positions 9, 16, and 23 are filled with a residues that create sockets favoring α-helix formation. This is repeated for over the remaining positions to produce a sequence with sockets that prefer α-helix structure. As can be seen in Figure 8a, this procedure follows a non-sequential progression through the peptide sequence that is determined by the three-dimensional packing arrangement of the XY•H sockets.

Figure 8. Knob-Socket Procedure for.

α-helix Design.

(a) The basic principle is driven by arrangement of packing on the modified α-helix lattice. First, the core residues along the path of alternating i+3 and i+4 residue position are selected (i.e. 5-8-12-15-19-22). Next, fill the positions with the amino acids to form the border sockets with desired socket propensities. For example, fill the position 9 with a residue that forms socket with residues at 5 and 8 and at 8 and 12. Repeat this for the position 16 and 23, then expand socket region gradually by choosing residues for the positions 11, 13, 18, and 20. Repeat the same procedure until all the lattice points are filled. The sequence is checked to insure sockets are created with desired socket propensities. (b) The three 25 residue sequences designed using above mentioned design strategy followed by their consensus secondary structure predictions^110–115 and confidence level of predictions. For each designed sequence, helicity is shown by the calculated socket propensities. (c) Overlay of the far-UV circular dichroism (CD) spectra for the three synthesized peptides on normalized molar ellipticity scale. Two minima at 215nm and 225nm in CD spectrum are indicative of strong helicity of KSα1, which was predicted to be strongly helical with high socket propensity of 307. Although KSα2 is same as KSα1 in amino acid composition it shows very low helicity due to rearrangement of the residues in socket motif. Spectral pattern for KSn3 suggests a completely random coil conformation of the peptide that was designed with low socket propensity residues.

Figure 8a shows the novel sequence design steps applying knob-socket motif. Each peptide sequence was evaluated for its uniqueness using Psi-Blast¹⁰⁹ within the threshold E-values, and no similar sequence was found. In addition, each sequence was run against several secondary structure prediction servers^110–115 and the consensus prediction along with average confidence level are shown. For the first peptide named KSα1, high frequency sockets were chosen for an average socket propensity of 307 over the whole sequence. With very low sequence identity to any known structure, KSα1 is a novel sequence, yet has a high likelihood of folding into the predicted α-helix conformation based on the knob-socket model. To further demonstrate the predictive ability of the knob-socket model a positive control peptide designated KSα2 uses essentially the same amino acid content as KSα1. The sockets for KSα2 were chosen to produce the lowest possible α-helix propensity and came out to be 202. When ran against the respective sequence and secondary structure prediction servers, the KSα2 peptide is unique and is predicted to exhibit low α-helical content as expected. As a negative control, the third peptide KSn3 was designed from non-sockets, which produced an average socket propensity of 68. For each of these unique sequences, peptides KSα1, KSα2 and KSn1 were synthesized and secondary structural features were validated by CD spectroscopy.

Figure 8b shows the CD spectra of the 3 synthesized peptides. For KSα1, the curve exhibits the classic α-helix signature of minima at λ= 208nm and 222nm.¹¹⁶ The intensities of these minima indicate high α-helical content. With the same amino acid content as the KSα1 sequence rearranged to favor less α-helical structure, KSα2 produces a CD spectrum with the α-helical minima at λ=210nm and 226nm, but the intensities are extremely weaker in comparison with KSα1. For the KSn3 - the negative control peptide, the CD spectrum displays strong random coil conformation rather than α-helical structure. These results point out that the packing rules defined by the knob-socket model allows a direct manipulation of α-helical content within a peptide. Not only can we de novo generate a sequence with α-helical content, but we can modulate the extent to which the sequence forms α-helical structure. As a direct example, KSα1 and KSα2 possess essentially the same amino acid content, but the different socket patterns change the amount of α-helical structure each peptide produces. As another example, the KSn3 sequence was designed not to form α-helical sockets and the result produces an unfolded peptide. Therefore, the arrangement of the amino acids based on the socket portion of the knob-socket model determines how well the sequence can form α-helical structure.

Discussion

Comparison of the Knob-Socket Model to Current Models of Helix Packing

Table 1 provides a direct comparison of the knob-socket model to 5 other models of helix packing. While it seems that aspects of the knob-socket model are captured in these other models, there is 1 similarity and 3 major differences between these models and the knob-socket model. In general, all of the models in Table 1 account for packing between α-helices. Yet, each is somewhat limited and only performs well for subsets of the 5 canonical types of α-helix packing (see Figure 4)^{43–45;58;60–63;72–74} or for describing α-helix core packing for secondary^27;28 and super-secondary structure identification.^30;31 The most successfully used approach has been surprisingly the helical wheel in protein design,^72–74 but this approach has been limited to the canonical coiled-coil structures of 7 residue^72;74 and 11 residue⁷³ sequence repeats. As the first major difference, the single motif of the knob-socket model is able to simply and intuitively describe all canonical α-helical packing types (Figure 4) as well as non-canonical packing of α-helices (Figure 5). So, while the knob-socket model reproduces the knobs-into-holes^{43;58;60– 62} as a shared knob-socket, the knob-socket describes all of α-helical packing, including intra-helical packing. This is the second major difference: identifying the importance of packing within an α-helix. The XY•H socket characterizes not only the packing innate to α-helical structure, but also the role that packing at the level of 2° structure has in establishing higher order 3° and 4° interactions. Although the XY•H socket motif is found in other models^{19;24;29;32;33} as far back as Efimov^30;31 and notably Lim^27;28, neither recognizes the socket as the primary motif to protein packing, but rather complicate the description of packing with more general combinations of other motifs. Because we had developed a precise vocabulary that exactly describes packing¹, we could eliminate dependent packing groups that were redundant to the description of packing and derive that the single knob-socket motif describes α-helical packing. As the third major difference, the knob-socket model identifies specificity in protein packing not provided by any other model. The amino acids distributions of socket and knob preferences in Figure 6 and 7, respectively, essentially characterizes a code for packing of α-helical 2°, 3°, and 4° structure, which represents a step forward in understanding protein structure.

A Simple, Spatial Representation of Protein Packing

By identifying the fundamental unit of protein packing, the knob-socket model is able to characterize the structural patterns and define the rules that govern α-helix packing. In precisely calculating cliques of interacting residues and classifying them with contact order,⁴ the analysis proves that α-helical packing results from a single 4 residue motif: 2:1+1 RPC or knob-socket. As the basic descriptor of packing in α-helices, the knob-socket model improves on previous approaches to classify α-helix packing^7;8;24;38 by producing an intuitive representation of packing based on knob-socket patterns. This knob-socket representation simplifies α-helical residue packing into clear and intuitive patterns for helical dimers (Figure 4) as well as higher order structures (Figure 5). For example, previous ground-breaking work changed an α-helix anti-parallel heptamer coiled coil (Figure 4a) into an anti-parallel undecamer coiled coil (Figure 4c)⁷³. The patterns shown in Figure 4 clearly explain the packing pattern change caused by the sequence change. Moreover, the knob-socket model provides a construct to intelligently interrogate α-helical packing based on amino acid preferences in sockets and knobs (Figure 6 and 7, respectively). The amino acid preferences are effectively a code to generate packing at the 2°, 3°, and 4° levels of α-helical structure from soluble to membrane proteins. In this way, the knob-socket model produces fresh insight into a field that is commonly thought of as already saturated in packing structure^{5;27;28;31;43;44;57;58;60–62} and design.^{69;70;72–79} As a result of these analyses, the knob-socket model also provides a new approach for the de novo design of α-helical structure. The structure of an α-helix can be simply designed using the modified α-helical lattice (Figure 2b) and the favored socket propensities of amino acids (Figure 6). Packing between α-helices is governed by the pattern of filled sockets (Figure 4 and 5) as well as the propensity of knobs for those sockets (Figure 7). As a simple demonstration of this design approach, the socket propensities were used to design peptides with varying amounts of helical content, which was verified by CD spectroscopy (Figure 8).

By successfully characterizing α-helical packing, the knob-socket model represents a new paradigm to understand and investigate the structure of protein packing based on two simple principles. First, the complexity of packing can be reduced to arrangements of a single motif. Just as covalent bonds define primary structure and hydrogen bonds define secondary structure,^5;6 higher order protein structure is described by the knob-socket motif. The other fundamental concept is that the knob-socket model defines the packing relationship between secondary structure and higher levels of protein structure. It is the pattern and composition of intra-helical socket packing at the level of secondary structure that determines the packing interactions at the level of tertiary/quaternary structure. Because these principles are easily generalized, the knob-socket model provides a clear path to characterization of packing’s contribution to protein structure.

Materials and Methods

Relative Packing Clique Analysis

A relative packing clique (RPC) is a set of residues that all contact with each other through non-bonded contacts. Contacts were calculated from a Voronoi polyhedra analysis^2;117 of all non-bonded, heavy atoms in a protein fold, which included side-chain to side-chain contacts and side-chain to main-chain contacts for all residues. In addition, contacts were considered for main-chain to main-chain contacts for all non-neighboring residues. The resulting Delaunay tessellation³ defines a contact graph between residues. A clique within this graph identifies a RPC and found using the maximal clique detection method of Bron and Kerbosch.¹¹⁸

Knob-Socket Identification

In the development of the knob-socket model, RPCs were identified in all 15,273 domains in the ASTRAL SCOP 1.75 set of structures filtered at 95% sequence identity¹¹⁹ only between residues that are defined α-helical by DSSP.¹²⁰ All the RPCs are first classified depending upon the number of residues in the cliques, which produced 6 classes of 1 to 6 residue cliques. Both 3-body RPCs and 4-body RPCs make up to 98.3% of total 1,041,300 cliques in the helices. These two classes were analyzed further in greater detail. In each class, a contact order analysis⁴ was performed based on residue number to classify individual RPCs.¹ The 3-body RPCs are mostly local and are named sockets in our model. 93.1% cliques are found to be cliques involving the residues i, i+1, and i+4 (Low X socket) or i, i+3, and i+4 (high X socket). The 4-body RPCs involve local and non-local residues. In our classification scheme, local residues are grouped together. A colon are residue belonging to the same secondary structure but non-contiguous in sequence. A plus sign “+” indicates a non-local separation between the residues in a clique. For instance, 3 local residues packing against a non-local residue would be a 3+1 RPC. 80.3% 4-body RPCs occur between two helices and only 3.5% account for the interactions within one helix. The remaining 16.2% account for the RPCs describing the packing between three or four α-helices. The packing cliques between two α-helices can be grouped into 3+1 and 2+2 RPCs, where 75% are the 3+1 and the rest are the 2+2. In analyzing the patterns of RPCs, all other classes were found to be dependent on 3+1 packing. Therefore, these are named knob-socket motifs: a single residue “knob” packing into a 3 residue “socket”. For each knob-socket RPC, instantaneous crossing angles between two interacting helices were calculated using the algorithm found in HELANAL.¹²¹ In an effort to establish the packing patterns between two helices, all the knob-socket motifs between two helices are identified and renumbered starting from earliest residues for both helices. By putting the renumbered residues of the cliques on the modified helical lattice, packing patterns depending on the crossing angles were characterized (Figure 3, 4 and 5).

Conversion of frequencies into relative probabilities

To compare the filled and free socket frequencies on the same scale between the different families of proteins in Figure 6, we converted the raw frequencies into relative probabilities, where 1 is equal to random distribution. There are 8000 possible XY•H socket combinations from the 20 amino acids. Therefore, each XY•H socket has probability of 1 out of 8000. For the total observed frequency in a class of sockets of a protein family, the probability of the random distribution (average probability: P̃_r) and the each socket’s relative probability (P_i) over a random distribution can be calculated using following equations.

$$\stackrel{\sim }{\text{P}}\text{r}=\frac{1}{8000}\times \mathit{Total}\mathit{number}of\mathit{Sockets}$$ (1)

$$P_i=\frac{{\nu }_i}{\stackrel{\sim }{\text{P}}\text{r}}$$ (2)

In equation (2), ν_i is the frequency of socket i. In all the proteins, the total number of free sockets is 527,303 and filled sockets is 278,772. In membrane proteins, the total number of free sockets is 20,442 and filled sockets is 11,610. In coiled-coil proteins, the total number of free sockets is 38,619 and filled sockets is 20,706.

Peptide Synthesis and Characterization

All three peptides (KSα1, KSα2, and KSn3) were synthesized using a CS Bio Co. automated solid-phase peptide synthesizer.¹²² Five fold concentrations of f-moc amino acids and rink amide resin were used, respectively. Following synthesis, the peptide was cleaved from the resin using a cocktail consisting of 5mL TFA, 250μL Thioanisole, 125μL EDTA, 250μL deionized H₂O and 0.375g of distilled phenol. The product was precipitated and washed with diethylether and resuspended in 1mL of 10% acetic acid for overnight lyophilization. A 3mg/mL solution was prepared by dissolving the dry peptide in 80:20 water to methanol and purified using a Waters HPLC equipped with a C18 column. The run was performed using an acetonitrile gradient in which the detector was set to λ=220nm. KSα1 eluted at approximately 67% acetonitrile. The molecular mass of each peptide was confirmed using an Accu-TOF mass spectrometer equipped with an electrospray ionizer. The molecular mass for the KSα1 and KSα2 was determined to be 2655.46 g/mol and 2899.40 g/mol for KSn3. Secondary structure of each peptide was analyzed by circular dichroism (CD) using a 10μM solution in a 10mM phosphate buffer at pH 7. KSα1 and KSn3 were fairly soluble in phosphate buffer, however vortexing was required to dissolve KSα2 due to its limited solubility. Spectra were generated on JS810 CD spectrophotometer (Jasco) using 1cm quartz cuvette containing 1mL of each 10μM peptide solution. The wavelength scan was performed in far-UV region in the range of 190nm to 250nm.

Highlights.

• Knob-socket model provides a specific code for α-helical packing structure

• Knob-socket motif forms the basic unit of protein packing

• Knob-socket model offers new paradigm to approach α-helix tertiary structure

• Defines the packing at the 2° structure level that allows 3° and 4° interactions

• Simple patterns of knob-socket describe all α-helix packing

• New robust approach to design of α-helix structures