Bayesian Model Selection in High-Dimensional Settings

Abstract

Standard assumptions incorporated into Bayesian model selection procedures result in procedures that are not competitive with commonly used penalized likelihood methods. We propose modifications of these methods by imposing nonlocal prior densities on model parameters. We show that the resulting model selection procedures are consistent in linear model settings when the number of possible covariates p is bounded by the number of observations n, a property that has not been extended to other model selection procedures. In addition to consistently identifying the true model, the proposed procedures provide accurate estimates of the posterior probability that each identified model is correct. Through simulation studies, we demonstrate that these model selection procedures perform as well or better than commonly used penalized likelihood methods in a range of simulation settings. Proofs of the primary theorems are provided in the Supplementary Material that is available online.

1. INTRODUCTION

We propose a new class of Bayesian model selection procedures by imposing nonlocal prior densities (Johnson and Rossell 2010) on model parameters. Nonlocal prior densities are density functions that are identically zero whenever a model parameter is equal to its null value, which is typically 0 in model selection settings. Conversely, local prior densities are positive at null parameter values; most current Bayesian model selection procedures employ local prior densities. We demonstrate that model selection procedures based on nonlocal prior densities assign a posterior probability of 1 to the true model as the sample size n increases when the number of possible covariates p is bounded by n and certain regularity conditions on the design matrix pertain. Under the same conditions, we show that standard Bayesian approaches based on local prior specifications result in the asymptotic assignment of a posterior probability of 0 to the true model. Among the Bayesian model selection procedures that share this deficiency are procedures based on intrinsic Bayes factors (Berger and Pericchi 1996), fractional Bayes factors (O’Hagan 1995), and g-priors (Liang et al. 2008).

We also compare the proposed selection procedures to related frequentist methods. Previous research has demonstrated that the smoothly clipped absolute deviation (SCAD) algorithm (Fan and Li 2001), the adaptive LASSO (Zou 2006), the nonnegative garotte (Breiman 1995), the elastic net algorithm (Zou and Hastie 2005), and the Dantzig selector (Candes and Tao 2007) consistently identify the correct model when the number of possible covariates is fixed a priori. Fan and Peng (2004) extended this consistency property to certain penalized-likelihood-based model selection procedures by showing that they achieve oracle properties when p < O(n^1/3). We show that the proposed classes of Bayesian model selection procedures have a similar consistency property even when p = O(n). Numerical comparisons between several model selection procedures and Bayesian procedures based on nonlocal priors are presented in Section 4. In large sample settings, these comparisons demonstrate that model selection procedures based on nonlocal prior densities are often better able to identify the correct model and have smaller prediction errors than competing methods.

In practice, it is usually important to identify not only the most probable model for a given set of data, but also the probability that the identified model is correct. An important advantage of the model selection procedures proposed in this article is that they naturally provide an estimate of the posterior probability that each model is correct. In simulation studies, we show that these posterior probabilities closely approximate the empirical probabilities that the selected model is true. In contrast, most common frequentist algorithms identify only the model that maximizes a penalized version of the likelihood function, whereas most Bayesian algorithms provide posterior model probabilities that cannot reasonably be interpreted as posterior probabilities at all. For instance, common Bayesian procedures assign vanishingly small posterior probabilities to all models in high-dimensional settings, even when the maximum probability model assigns relatively high probability to the true model. It is for this reason that articles describing Bayesian model selection algorithms usually do not report the posterior probability assigned to the most probable model, often opting instead to report the marginal probabilities that individual covariates were included in models sampled from the posterior distribution.

The primary innovation of this article is the manner in which prior densities are defined on regression coefficients. Although our methodology can be extended to more general model selection settings, we restrict attention herein to the study of linear models. We also make the assumption that the true model is an element of the model space. Letting Y_n = (y₁, …, y_n)′ denote a random vector, X_n an n × p matrix of real numbers, and β a p × 1 regression vector having ith component β_i, we examine linear models of the form

$${\mathbf{Y}}_n~N({\mathbf{X}}_n\mathit{\beta },{\sigma }^2{\mathbf{I}}_n).$$ (1)

We consider two classes of nonlocal prior densities. The first class of prior densities for β consists of product moment (pMOM) densities, which we define as

$$\pi (\mathit{\beta }\mid \tau ,{\sigma }^2,r)=d_p{(2\pi )}^{-p/2}{(\tau {\sigma }^2)}^{-rp-p/2}{\mid {\mathbf{A}}_p\mid }^{1/2}\times exp\left[-\frac{1}{2\tau {\sigma }^2}{\mathit{\beta }}^{\prime }{\mathbf{A}}_p\mathit{\beta }\right]\prod _{i=1}^p{\mathit{\beta }}_i^{2r},$$ (2)

for τ > 0, A_p a p × p nonsingular scale matrix, and r = 1, 2, …. The normalizing constant d_p is independent of σ² and τ. The parameter r is called the order of the density. Consonni and La Rocca (2010) proposed a similar class of prior densities for application to graphical models, though in their proposal the densities corresponding to Equation (2) are not proper.

The second class of prior densities we examine are product inverse moment (piMOM) densities, which we define to have the general form

$$\pi (\mathit{\beta }\mid \tau ,{\sigma }^2,r)=\frac{{(\tau {\sigma }^2)}^{rp/2}}{\mathrm{\Gamma }{(r/2)}^p}\prod _{i=1}^p{\mid {\mathit{\beta }}_i\mid }^{-(r+1)}exp\left(-\frac{\tau {\sigma }^2}{{\mathit{\beta }}_i^2}\right),$$ (3)

for τ > 0 and r = 1, 2, …. When r = 1, this class of densities possesses Cauchy-like tails.

The parameter τ in both the pMOM and piMOM densities represents a scale parameter that determines the dispersion of the prior densities on β around 0. In setting the value of this hyperparameter, it is critical to consider the scale of the corresponding columns of X_n. For simplicity, we have assumed that the columns of X_n have been standardized so that a single value of τ is appropriate for each component of β. If this assumption is not valid, then separate hyperparameters τ_i should be introduced to reflect the anticipated effect of each component of β on the expected value of Y_n.

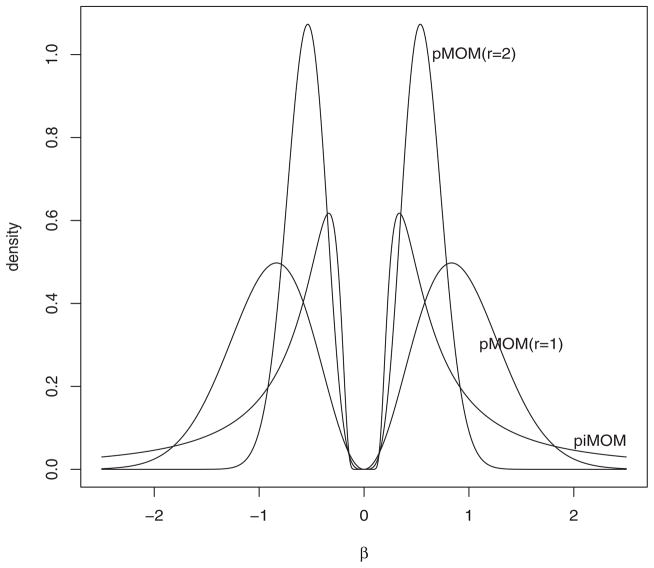
The densities in Equations (2) and (3) are nonlocal densities at 0 because they are identically 0 when any component of β is 0. This feature of the densities is illustrated in the univariate setting in Figure 1. It is this property that permits model selection procedures based on these nonlocal prior densities to efficiently eliminate regression models that contain unnecessary explanatory variables. In contrast, Bayesian model selection procedures based on local prior densities assign positive density values to regression coefficient vectors that contain components that are equal to 0.

Figure 1.

Nonlocal prior densities for a single regression coefficient. These densities correspond to the default nonlocal priors used in the simulation study in Section 4.

The nonlocal prior densities specified in Equations (2) and (3) differ in a crucial way from the multivariate MOM and iMOM densities proposed by Johnson and Rossell (2010; JR10) for hypothesis testing. The multivariate MOM and iMOM densities proposed in JR10 are 0 only when all components of the parameter vector are 0. As a result, those densities may impose little or no penalty on models that contain many parameters that have estimates that are close to 0, provided only that one or more of the included model parameters are not 0. In contrast pMOM and piMOM densities arise as the independent products of the MOM and iMOM prior densities proposed in JR10, and are 0 if any component of the parameter vector is 0. This property represents a much stronger penalty on the regression vector when any one of its components is close to 0. As we demonstrate in Section 2, this stronger penalty is necessary to achieve consistency of posterior model probabilities when the number of potential covariates p increases linearly with n.

In the next section, we describe the properties of our proposed model selection procedures and contrast these properties to those obtained using standard Bayesian methods. In Section 3, we describe simulation algorithms to explore the posterior distribution on the model space. In Section 4, we report simulation studies that compare the finite sampling performance of several model selection procedures in situations in which the number of potential covariates is of the same order of magnitude as the number of observations. Section 5 provides several new insights into the connections between commonly used penalized likelihood procedures and related Bayesian model selection algorithms, paying particular attention to extensions of penalized likelihood methods that follow from the Bayesian models proposed in this article.

2. MAIN RESULTS

Let Y_n = (y₁, …, y_n)′ denote a random vector, X_n an n × p matrix of real numbers, and β a p × 1 regression vector. The goal of the model selection procedures proposed in this article is to select the nonzero components of β when it is assumed that Y_n ~ N (X_nβ, σ²I_n) and p < n. Bayesian model selection is based on the comparison of the posterior model probabilities for each possible model. To fix the terminology, we assume that a component of β is excluded from the true model if its value is 0, and denote a model by j = {j₁, …, j_k} (1 ≤ j₁ < · · · < j_k ≤ p) if and only if β_j1≠ 0, …, β_jk ≠ 0 and all other elements of β are 0. We write k ⊆ j to indicate that model j contains all components of β present in model k, with ⊂ denoting a proper subset. The cardinality of model j is denoted by |j|, or more simply by j when there is no risk of confusion. We let t denote the true model with t = |t|. The dimension of the true model is regarded as fixed. The regression coefficient for model j is denoted by β_j = (β_j1, …, β_j|j|)′, and the set of 2^p possible models that can be defined from the p components of β is denoted by 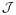. Ignoring dependence on n, we let X_j denote the design matrix formed from the columns of X_n corresponding to model j, and we denote the eigenvalues of an arbitrary positive definite matrix B of rank m by λ₁(B) ≥ · · · ≥ λ_m(B). Finally, we denote the regression coefficient for the true model by ${\mathit{\beta }}_{\mathbf{t}}^0={({\beta }_{t_1}^0,\dots ,{\beta }_{t_t}^0)}^{\prime }$, and we define $\mathrm{\Delta }=2{max}_i(\mid {\beta }_{t_i}^0\mid )$ and $\delta =0.5{min}_i(\mid {\beta }_{t_i}^0\mid )$. Under each model k, the sampling density for the data is assumed to be

$${\mathbf{Y}}_n\mid {\mathit{\beta }}_{\mathbf{k}},{\sigma }^2~N({\mathbf{X}}_{\mathbf{k}}{\mathit{\beta }}_{\mathbf{k}},{\sigma }^2{\mathbf{I}}_n).$$ (4)

The sampling properties of posterior probabilities based on nonlocal prior densities in linear model settings are easiest to study in the known variance case and for pMOM priors. Therefore, we examine the known variance case first, and then extend these properties to situations in which the variance is not known a priori, and then to models where piMOM prior densities are specified on the regression parameters.

From Equations (1) and (2), it follows that the marginal density of the data under a pMOM prior density on β_k can be expressed as

$$m_{\mathbf{k}}({\mathbf{y}}_n)=d_k{(2\pi )}^{-n/2}{\tau }^{-k/2-rk}{({\sigma }^2)}^{-n/2-rk}{\left[\frac{\mid {\mathbf{A}}_{\mathbf{k}}\mid }{\mid {\mathbf{C}}_{\mathbf{k}}\mid }\right]}^{1/2}\times exp\left[-\frac{R_{\mathbf{k}}}{2{\sigma }^2}\right]{\mathbf{E}}_{\mathbf{k}}\left(\prod _{i=1}^k{\beta }_{k_i}^{2r}\right),$$ (5)

where

$$\begin{array}{l}{\mathbf{C}}_{\mathbf{k}}={\mathbf{X}}_{\mathbf{k}}^{\prime }{\mathbf{X}}_{\mathbf{k}}+\frac{1}{\tau }{\mathbf{A}}_{\mathbf{k}},{\stackrel{\sim }{\mathit{\beta }}}_{\mathbf{k}}={\mathbf{C}}_{\mathbf{k}}^{-1}{\mathbf{X}}_{\mathbf{k}}^{\prime }{\mathbf{y}}_n,\\ R_{\mathbf{k}}={\mathbf{y}}_n^{\prime }({\mathbf{I}}_n-{\mathbf{X}}_{\mathbf{k}}{\mathbf{C}}_{\mathbf{k}}^{-1}{\mathbf{X}}_{\mathbf{k}}^{\prime }){\mathbf{y}}_n,\end{array}$$

and E_k(·) denotes expectation with respect to a multivariate normal distribution with mean β̃_k and covariance matrix σ² C_k⁻¹. It follows that the posterior probability of model t, p(t | y_n), is defined by

$$p(\mathbf{t}\mid {\mathbf{y}}_n)=\frac{p(\mathbf{t})m_{\mathbf{t}}({\mathbf{y}}_n)}{{\sum }_{\mathbf{k}\in \mathcal{J}}p(\mathbf{k})m_{\mathbf{k}}({\mathbf{y}}_n)},$$

where p(k), k ∈ 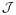, denotes the prior probability assigned to model k. Based on these expressions, the asymptotic sampling properties of p(t | y_n) obtained under pMOM priors imposed on regression coefficients are characterized in the following theorem.

Theorem 1

Suppose there exists ε > 0 such that p(t)/p(k) > ε for all k ∈ 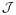. Assume further that p ≤ n and that there exist M > c > 0 and N such that ${\lambda }_1({\mathbf{X}}_n^{\prime }{\mathbf{X}}_n)<nM$ and ${\lambda }_p({\mathbf{X}}_n^{\prime }{\mathbf{X}}_n)>nc$ for all n > N, and that there exist constants a₁ and a₂ such that λ₁(A_k) < a₁ and λ_k (A_k) > a₂ for all k ∈ 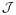. If the prior density on the regression vector β_k under each model is specified by Equation (2) and r ≥ 2, then

$$p(\mathbf{t}\mid {\mathbf{y}}_n)\stackrel{p}{\to }1.$$

The proofs of the theorems and the corollaries that follow appear in the online Supplementary Material. Heuristically, consistency under pMOM priors of order r ≥ 2 can be understood by examining the form of their marginal densities in Equation (5). When t ⊂ k, each component of β_k not in t reduces ${\mathbf{E}}_{\mathbf{k}}({\prod }_{i=1}^k{\beta }_{k_i}^{2r})$ by a factor that is O_p(n^−r), which is enough to overcome the potential addition of p ≤ n covariates to the model. (Note that this factor does not arise from the multivariate generalizations of the MOM and iMOM densities proposed in JR10.) When t ⊄ k and |k| is moderate in size, the factor exp(−R_k/2σ²) drives the ratio of the marginal density of the data under model k to model t to 0 exponentially fast. For large |k| and t ⊄ k, a balance of these effects drives the ratio of the marginal densities to 0.

Next, we consider the case in which σ² is not known. In this setting, a common inverse gamma density with shape and scale parameters (α, ψ) is assumed for the value of σ² under all models k ∈ 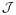. Then, the marginal density of the data under model k ∈ 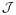is

$$m_{\mathbf{k}}({\mathbf{y}}_n)=d_k{(2\pi )}^{-\frac{n}{2}}{2}^{\frac{\nu }{2}}{\tau }^{-rk-\frac{k}{2}}{\left[\frac{\mid {\mathbf{A}}_{\mathbf{k}}\mid }{\mid {\mathbf{C}}_{\mathbf{k}}\mid }\right]}^{\frac{1}{2}}\times \frac{{\psi }^{\alpha }}{\mathrm{\Gamma }(\alpha )}{\left({\nu }_{\mathbf{k}}{\mathbf{s}}_{\mathbf{k}}^2\right)}^{-\frac{{\nu }_k}{2}}\mathrm{\Gamma }\left(\frac{{\nu }_{\mathbf{k}}}{2}\right){\text{E}}_{\mathbf{k}}^T\left(\prod _{i\in \mathbf{k}}{\beta }_i^{2r}\right),$$ (6)

where

$$\begin{array}{l}{\nu }_{\mathbf{k}}=n+2rk+2\alpha ,s_{\mathbf{k}}^2=\frac{2\psi +R_{\mathbf{k}}}{{\nu }_{\mathbf{k}}},\\ d_k={\left[{\int }_{{\mathcal{R}}^k}{(2\pi )}^{-k/2}{\mid {\mathbf{A}}_{\mathbf{k}}\mid }^{1/2}exp\left(-\frac{1}{2}{\mathit{\gamma }}^{\prime }{\mathbf{A}}_{\mathbf{k}}\mathit{\gamma }\right)\prod _i^k{\gamma }_i^{2r}d\mathit{\gamma }\right]}^{-1},\end{array}$$

and $E_{\mathbf{k}}^T$ denotes the expectation taken with respect to a multivariate t-density with mean β̃_k, scale matrix $s_{\mathbf{k}}^2{({\mathbf{C}}_{\mathbf{k}})}^{-1}$, and ν_k degrees of freedom.

Corollary 1

Assume that the conditions of Theorem 1 apply, except that the value of σ² under all models k ∈ 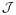is assumed to be drawn from a common inverse gamma density with shape and scale parameters (α, ψ). If the number of possible covariates p is further restricted so that p < bn for some b < 1 as n → ∞ and r ≥ 2, then

$$p(\mathbf{t}\mid {\mathbf{y}}_n)\stackrel{p}{\to }1.$$

Analytic expressions are not available for the marginal densities of the data when piMOM priors are imposed on the regression coefficients. However, we know that the posterior model probability assigned to the true model possesses the same consistency property as that under pMOM densities of order r ≥ 2, as indicated in the next corollary.

Corollary 2

Assume the conditions of Corollary 1 hold, except that the prior density on the regression vector β_k under each model is now specified according to Equation (3). Then,

$$p(\mathbf{t}\mid {\mathbf{y}}_n)\stackrel{p}{\to }1.$$

These results show that Bayesian model selection procedures based on either the specification of piMOM prior densities or pMOM prior densities of order r ≥ 2 on regression coefficients result in consistent estimation of the true model as p increases with n. The next theorem demonstrates that this property may not hold when local prior densities are specified on regression coefficients. This lack of consistency provides theoretical insight into the well-known fact that in high-dimensional settings, common Bayesian model selection procedures assign negligible posterior probability to any given model.

Theorem 2

Define 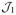= {k ∈ 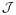: t ⊂ k, |k| − |t| = 1}, that is, models k that contain the true model plus one additional covariate. For each k ∈ 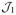, suppose that the prior density imposed on β_k, say ${\pi }_{\mathbf{k}}^L({\mathit{\beta }}_{\mathbf{k}})$, is a continuous local prior; that is, that there exist constants δ, c_L > 0 such that

$$\frac{{\pi }_{\mathbf{k}}^L({\mathit{\gamma }}_{\mathbf{k}})}{{\pi }_{\mathbf{t}}^L({\mathit{\beta }}_{\mathbf{t}})}>c_L,\{{\mathit{\gamma }}_{\mathbf{k}}:\mid {\gamma }_{k_j}-{\beta }_{t_i}^0\mid <\delta ,k_j=t_i\in \mathbf{t};\mid {\gamma }_{k_j}\mid <\delta ,k_j\notin \mathbf{t}\}.$$ (7)

Suppose further that the conditions of Theorem 1 apply, and that the sampling density for the data is described by Equation (4). If the prior densities assumed for model t and k ∈ 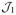satisfy p(k)/p(t) > δ > 0, and there exists an N such that p > n^1/2+ε for some δ, ε > 0 and all n > N, then $p(\mathbf{t}\mid {\mathbf{y}}_n)\stackrel{\text{a}.\text{s}.}{\to }0$.

Theorem 2 states that the posterior probability of the true model goes to 0 whenever the following conditions apply: (1) the number of possible covariates is greater than $O(\sqrt{n})$, (2) local prior densities are imposed on the regression coefficients in each model, and (3) the relative prior probabilities assigned to all models are bounded away from 0.

Because the conclusion of this theorem differs dramatically from the consistency results reported by other authors (e.g., Moreno, Giron, and Casella 2010), it is important to distinguish between our notion of consistency and the pairwise consistency reported elsewhere. The conclusions of Theorems 1 and 2 concern the asymptotic behavior of the posterior probability of the true model t as the sample size increases. Other authors have focused on what might be called pairwise consistency, which refers to the Bayes factor between the true model and any single model k ∈ 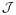becoming large as n increases. It is important to note that pairwise consistency is a much weaker property than model consistency since it is possible to achieve pairwise consistency even when the posterior probability of the true model approaches 0. Indeed, it is not necessarily the case that pairwise consistency is enough to guarantee even the convergence to 1 of the probability that the maximum a posteriori model equals the true model.

Using this weaker notion of pairwise consistency, Moreno, Giron, and Casella (2010) proved that intrinsic Bayes factors in favor of the true model compared to any other model become unbounded as n increases when p = O(n), and that a similar result holds for model selection based on the Bayesian information criterion (BIC; Schwarz 1978) when p = O(n^α) and α < 1. However, it is our view that pairwise consistency is of limited practical importance. For instance, pairwise consistency provides no advantage for those interested in Bayesian prediction or inferential procedures that require model averaging. If a modeling procedure obtains only pairwise consistency, then the number of possible models that must be averaged for valid Bayesian inference increases rapidly with increasing p. This fact may preclude the use of such models in ultrahigh-dimensional settings (i.e., p ≫ n.) From a more philosophical perspective, the assignment of decreasingly small probabilities to the true model as the sample size increases raises questions regarding the interpretation of posterior model probabilities.

3. COMPUTATIONAL STRATEGIES

Identifying high posterior probability models is computationally challenging for two reasons. First, the model space has 2^p dimensions, which often makes it impossible to compute the marginal densities for all possible models. Second, the evaluation of the marginal density for each model may require the numerical evaluation of a potentially high-dimensional integral.

We might address the high-dimension problem by adapting one of the search algorithms proposed for classical model selection (e.g., least angle regression, Efron et al. 2004; local quadratic approximation, Fan and Li 2001). However, in addition to identifying the most probable model, we are interested in assessing its probability and perhaps the probability of other high-probability models. For this reason, we propose a Markov chain Monte Carlo (MCMC) scheme to obtain posterior samples from the model space.

The computational difficulties associated with evaluating the marginal density of the data under each model vary according to the choice of nonlocal prior imposed on the regression coefficients. In the case of pMOM prior densities, exact expressions for the moments appearing in Equations (5) and (6) are available in the literature, for example, by Kan (2008). However, the computational effort associated with these expressions increases exponentially with increasing model size. In addition, if A_k is not an identity matrix, the prior normalization constant d_k can also be difficult to evaluate. For piMOM prior densities, analytic expressions are not available for the marginal densities. To address these problems, we propose setting A_k = I_k whenever there is no subjective information regarding the prior correlation between regression coefficients in model k. We also recommend the use of Laplace approximations (Tierney and Kadane 1986) to approximate the marginal likelihood of the data under each model.

For pMOM densities with unknown variance and A_k = I_k, the normalization constant d_k is given by

$$d_k={[(2r-1)!!]}^{-k},$$

and the Laplace approximation to the marginal likelihood function under model k can be expressed as

$$\frac{\mathrm{\Gamma }(\frac{{\nu }_{\mathbf{k}}}{2}){\psi }^{\alpha }{2}^{\frac{{\nu }_{\mathbf{k}}}{2}}{(2\psi +{\mathbf{y}}^{\prime }\mathbf{y}-{\stackrel{\sim }{\mathit{\beta }}}_{\mathbf{k}}^{\prime }{\mathbf{C}}_{\mathbf{k}}{\stackrel{\sim }{\mathit{\beta }}}_{\mathbf{k}})}^{-\frac{{\nu }_{\mathbf{k}}}{2}}}{\mathrm{\Gamma }(\alpha ){[(2r-1)!!]}^k{(2\pi )}^{\frac{n}{2}}{\tau }^{\frac{k}{2}+rk}}\times \frac{\left({\prod }_{i\in \mathbf{k}}{({\beta }_i^{\ast })}^{2r}\right)exp\left\{-\frac{{\nu }_{\mathbf{k}}-2}{2{\nu }_{\mathbf{k}}}{\left({\mathit{\beta }}_{\mathbf{k}}^{\ast }-{\stackrel{\sim }{\mathit{\beta }}}_{\mathbf{k}}\right)}^{\prime }\frac{{\mathbf{C}}_{\mathbf{k}}}{s_{\mathbf{k}}^2}\left({\mathit{\beta }}_{\mathbf{k}}^{\ast }-{\stackrel{\sim }{\mathit{\beta }}}_{\mathbf{k}}\right)\right\}}{{\mid {\mathbf{C}}_{\mathbf{k}}+2r\frac{{\nu }_{\mathbf{k}}{s}_{\mathbf{k}}^2}{({\nu }_{\mathbf{k}}-2)}D({\mathit{\beta }}_{\mathbf{k}}^{\ast })\mid }^{\frac{1}{2}}},$$ (8)

where $D({\mathit{\beta }}_{\mathbf{k}}^{\ast })$ is the diagonal matrix with entry (i, i) given by $1/{({\beta }_i^{\ast })}^2$ and

$${\mathit{\beta }}_{\mathbf{k}}^{\ast }={\text{argmax}}_{{\mathit{\beta }}_{\mathbf{k}}}\left\{N\left({\mathit{\beta }}_{\mathbf{k}};{\stackrel{\sim }{\mathit{\beta }}}_{\mathbf{k}},\frac{{\nu }_{\mathbf{k}}}{{\nu }_{\mathbf{k}}-2}{s}_{\mathbf{k}}^2{\mathbf{C}}_{\mathbf{k}}^{-1}\right)\prod _{i\in \mathbf{k}}{\beta }_i^{2r}\right\}.$$

Equation (8) is obtained by approximating the multivariate t density in Equation (6) by its limiting normal distribution and using a standard Laplace approximation.

For piMOM densities and unknown variance, the corresponding Laplace approximation to the marginal density of the data under model k is

$$\frac{{\psi }^{\alpha }{(2\tau )}^{\frac{k}{2}}}{{(2\pi )}^{\frac{n}{2}}\mathrm{\Gamma }(\alpha )}\frac{e^{f({\mathit{\beta }}_{\mathbf{k}}^{\ast },{\eta }^{\ast })}}{{\mid V({\mathit{\beta }}_{\mathbf{k}}^{\ast },{\eta }^{\ast })\mid }^{\frac{1}{2}}},$$ (9)

where

$$\begin{array}{l}({\mathit{\beta }}_{\mathbf{k}}^{\ast },{\eta }^{\ast })={\text{argmax}}_{({\mathit{\beta }}_{\mathbf{k}},\eta )}f({\mathit{\beta }}_{\mathbf{k}},\eta ),\eta =log({\sigma }^2),\\ f({\mathit{\beta }}_{\mathbf{k}},\eta )=-\frac{2\psi +{({\mathbf{y}}_n-{\mathbf{X}}_{\mathbf{k}}{\mathit{\beta }}_{\mathbf{k}})}^{\prime }{\mathbf{X}}_{\mathbf{k}}^{\prime }{\mathbf{X}}_{\mathbf{k}}({\mathbf{y}}_n-{\mathbf{X}}_{\mathbf{k}}{\mathit{\beta }}_{\mathbf{k}})}{2e^{\eta }}-\frac{\eta (n-k+2\alpha )}{2}-\sum _{i\in \mathbf{k}}\frac{\tau e^{\eta }}{{\beta }_i^2}+log({\beta }_i^2),\end{array}$$ (10)

and V (β_k, η) is a (k + 1) × (k + 1) matrix with the following blocks:

$$\begin{array}{l}{V}_{11}=-e^{-\eta }{\mathbf{X}}_{\mathbf{k}}^{\prime }{\mathbf{X}}_{\mathbf{k}}-\text{diag}\left(6\tau e^{\eta }{\mathit{\beta }}_{\mathbf{k}}^{-4}-2{\mathit{\beta }}_{\mathbf{k}}^{-2}\right)\\ V_{12}=\frac{2\tau e^{\eta }}{{\mathit{\beta }}_{\mathbf{k}}^3}+e^{-\eta }({\mathbf{X}}_{\mathbf{k}}^{\prime }{\mathbf{X}}_{\mathbf{k}}{\mathit{\beta }}_{\mathbf{k}}-{\mathbf{X}}_{\mathbf{k}}^{\prime }{\mathbf{y}}_n)\\ V_{22}=-\frac{2\psi +{({\mathbf{y}}_n-{\mathbf{X}}_{\mathbf{k}}{\mathit{\beta }}_{\mathbf{k}})}^{\prime }{\mathbf{X}}_{\mathbf{k}}^{\prime }{\mathbf{X}}_{\mathbf{k}}({\mathbf{y}}_n-{\mathbf{X}}_{\mathbf{k}}{\mathit{\beta }}_{\mathbf{k}})}{2e^{-\eta }}-\sum _{i\in \mathbf{k}}\frac{\tau e^{\eta }}{{\beta }_i^2}.\end{array}$$ (11)

The quantity ${\mathit{\beta }}_{\mathbf{k}}^{-a}$ in Equation (11) denotes the vector with components ${\beta }_i^{-a}$. These Laplace approximations have been implemented in the R software package mombf, by Rossell.

Based on these approximations to the marginal likelihoods of the data, we propose the following MCMC algorithm for exploring the model space.

1. Choose an initial model k^curr

2. For i = 1, …, p,

   1. Define model k^cand by excluding or including β_i from model k^curr, according to whether β_i is currently included or excluded from k^curr.

   2. Compute

      $$r=\frac{m_{{\mathbf{k}}^{\text{cand}}}(y)p({\mathbf{k}}^{\text{cand}})}{m_{{\mathbf{k}}^{\text{cand}}}(y)p({\mathbf{k}}^{\text{cand}})+m_{{\mathbf{k}}^{\text{curr}}}(y)p({\mathbf{k}}^{\text{curr}})}$$ (12)

      using either Equation (8) or (9).

   3. Draw u ~ U (0, 1). If r > u, define k^curr = k^cand.

3. Repeat Step 2 until a sufficiently long chain is acquired.

The sequence of sampled models obtained from the chain produced by this algorithm can be used to identify the maximum a posteriori (MAP) model, as well as to estimate the posterior probabilities of the MAP and other high-probability models.

To choose an initial model, we recommend starting at the null model (k = 0) and making several passes (a)–(c), deterministically moving to k^cand when r > 0.5 in Equation (12). The process stops when no movements are made in a complete pass (a)–(c), that is, a local maximum is found.

4. SIMULATION STUDIES

In this section, we assess the sampling properties of p(t|y_n) for local and nonlocal priors in several simulation experiments, and we compare these properties to the corresponding properties of two penalized likelihood procedures, SCAD and LASSO. We determined regularization parameters for SCAD and LASSO using 10-fold cross-validation, as implemented in the R software packages ncvreg, by Breheny, and parcor, by Kraemer and Schaefer (available at http://cran.r-project.org/web/packages).

We implemented the Metropolis-Hastings algorithm described in Section 3 to estimate p(t|y_n). Because this algorithm had to be implemented for a large number of simulated datasets (rather than a single application), we did not attempt to sample extensively from each posterior distribution. For each simulated dataset, we performed 500 burn-in iterations and 5000 subsequent updates for posterior inference.

The MCMC algorithm was initialized as described in Section 3. The truly nonzero regression coefficients were the last variables to be considered for inclusion in the initial model to avoid bias in the initial updates of the chain toward the true model. The MAP model was typically visited in fewer than 50 updates in all simulation settings. Coupling diagnostics proposed by Johnson (1996, 1998) were applied to the resulting chains, which led to the following two findings: (1) iterates in the MCMC algorithms based on the nonlocal prior densities differed in total variation distance from the stationary distribution by less than 0.1 within 100 iterations under all simulation settings; and (2) the total variation distance between two independent draws from the posterior distribution and iterates separated by more than 100 iterations in a chain also differed by less than 0.1 under all simulation scenarios.

We considered σ² = 1.0, 1.5, and 2.0 and generated the components of the design matrix X from a multivariate normal distribution. In each simulation, the variance of each column of X was set to 1, and the correlations between columns were set to either ρ = 0 or 0.25. That is, we set X = ZC^1/2, where Z was an n × p matrix of independent standard normal deviates and C was a p × p matrix with diagonal elements 1 and off-diagonal elements ρ. To determine a practically relevant range for correlations between the columns of X, we relied on our experience in analyzing microarray data. For example, in the GSE5206 and GSE2109 datasets (available from the Gene Expression Omnibus, http://www.ncbi.nlm.nih.gov/geo), the mean absolute pairwise correlations between gene expression values are, respectively, 0.16 and 0.18 (75th percentiles = 0.23 and 0.18). Based on these values, we set the mean correlation between columns in our experiments to be either ρ = 0 or ρ = 0.25. When ρ = 0.25, the maximum sample correlation between any pair of columns of X typically exceeded 0.5 for p = 100 and 0.4 for p = 500. We assumed a vague I G(0.001, 0.001) prior for σ² in all procedures based on the nonlocal priors. Posterior model probabilities were insensitive to the choice of the inverse gamma density parameters provided only that both parameters were much smaller than the minimum of 1 and the residual sums of squares R_k for all models.

We tested three classes of nonlocal prior models: pMOM densities of the first order (r = 1), pMOM densities of the second order (r = 2), and piMOM densities. We note that pMOM densities of the first order are not guaranteed to provide consistent model selection under the assumptions of Theorem 1. However, these densities are less spiked around their prior modes than are higher-order pMOM densities, which often leads to better finite sample properties. We also tested the local, intrinsic prior model proposed by Casella et al. (2009) and the Bayesian information criterion (BIC; Schwarz 1978), which was suggested by Moreno, Giron, and Casella (2010) as an asymptotic approximation to the intrinsic prior.

To set the value of the hyperparameter τ for the nonlocal priors, we adopted the default recommendations proposed in JR10. When all columns of X_n have been standardized, the default value for the first-order pMOM prior is τ = 0.348; for the second-order pMOM prior, it is τ = 0.072, and for the pi-MOM prior, the default value is τ = 0.113. At these values of τ, the nonlocal priors assign 0.99 marginal prior probability to |β_i|/≥ 0.2σ, which is an approximate range of interest in many applications. In actual applications, the choice of τ should be determined after a subjective evaluation of the magnitude of substantively important effect sizes. Together with the sample size, the choice of τ implicitly determines the magnitude of the regression coefficients that will be shrunk to 0; the marginal prior density for each regression coefficient should thus be carefully considered when setting the value of τ for application of our method to real datasets. The marginal density assigned to each component of β_k by the default priors is depicted in Figure 1.

For each class of prior densities, we adopted the beta-binomial prior model proposed by Scott and Berger (2010) on the model space. Letting γ denote a value between 0 and 1, this prior is obtained by assuming that the prior probability assigned to model k is specified as

$$p(\mathbf{k}\mid \gamma )={\gamma }^k{(1-\gamma )}^{n-k},\gamma ~\text{Beta}({\zeta }_0,{\zeta }_1).$$ (13)

We further assumed that ζ₀ = ζ₁ = 1. As Scott and Berger noted, this prior imposes a strong penalty on model size, which is an important feature when it is used in model selection algorithms that do not otherwise impose such penalties through the priors specified on model parameters. For sparse models, the effect of this prior is to add a penalty on the addition of spurious covariates that is approximately O(p⁻¹), which, according to the heuristic justification of the proof of Theorem 1 in Section 2, is enough to provide consistency of the pMOM priors of order r = 1. Extending this logic to Theorem 2, the beta-binomial prior combines with local priors to impose a penalty of order O(n^−3/2) for the addition of spurious covariates, which is $O(\sqrt{n})$ too small to make model selection based on local priors consistent when p = O(n).

4.1 Comparison of Bayesian Model Selection Procedures

We first compared the posterior probability assigned to the true model obtained under the first- and second-order pMOM, piMOM, intrinsic prior densities, and the BIC. We simulated data from linear models for values of n between 10 and 500, in each case setting p = n, ρ = 0, and σ² = 1.0, 1.5, 2.0. We set five components of the regression coefficient to the values 0.6, 1.2, 1.8, 2.4, and 3; all remaining components were set to 0.

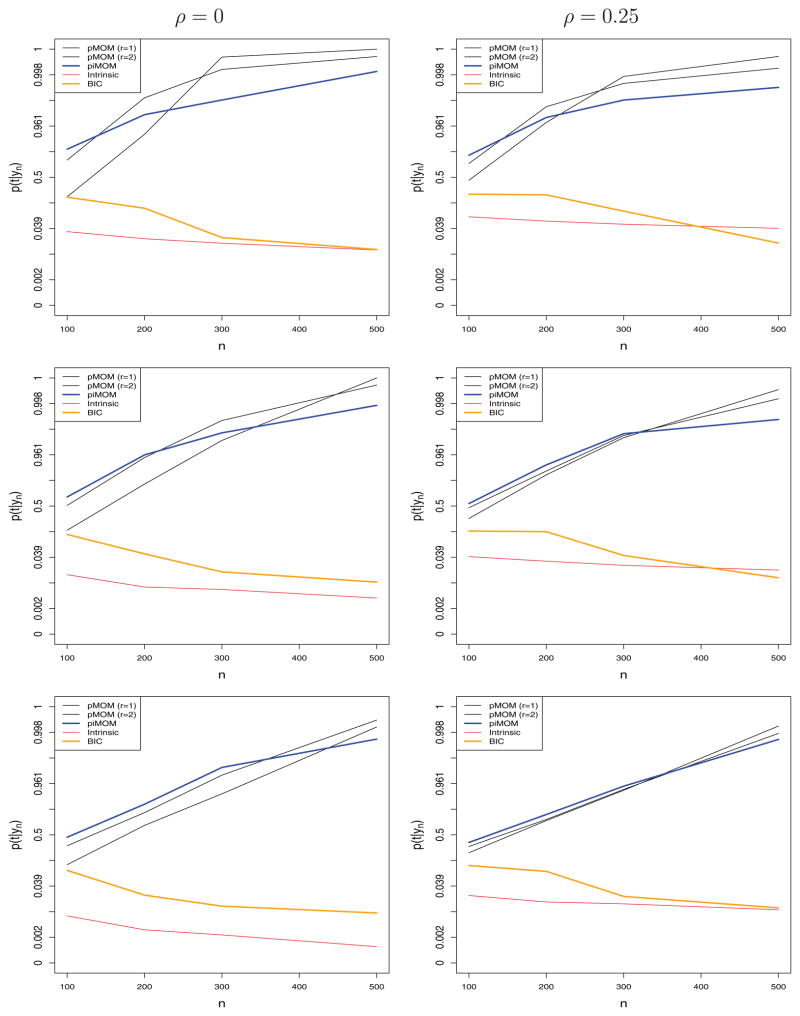
Figure 2 displays, on the logit scale, the average of the posterior model probability p(t|y_n) as a function of n from the pMOM, piMOM, intrinsic prior, and BIC-based selection procedures. As suggested by theory, the average posterior probability assigned to the true model increases with n under the nonlocal prior specifications, whereas it decreases to 0 under the intrinsic prior specification and its BIC approximation. For instance, the average value of p(t|y_n) typically exceeds 0.5 when n ≈ 100 under the nonlocal priors. At the same value of n, the average posterior probability of the true model under the intrinsic prior and BIC specifications is less than 0.05. When n = 500, the average posterior probability assigned to the true model is essentially 1 under the nonlocal priors, whereas it is approximately 0.01 under the local priors.

Figure 2.

p(t|y_n) versus n. Top: σ² = 1; middle: σ² = 1.5; bottom: σ² = 2.

4.2 Comparison to Penalized Likelihood Selection Procedures

In practice, most model selection procedures are tackled using penalized likelihood methods. In the following simulation study, we compare Bayesian model selection procedures based on nonlocal priors to two common frequentist procedures, SCAD and LASSO.

We considered the six simulation scenarios described in Section 4.1. In each scenario, we obtained 10,000 simulations for SCAD and LASSO. Due to the computationally intensive nature of our MCMC algorithm, in the Bayesian approaches we simulated 1000 datasets for the nonlocal priors and BIC, and 500 datasets for the intrinsic priors. (For n = 500, it took approximately 7 min to obtain the results for one dataset on a cluster machine with 12-core CPUs and 32 GB RAM for each of the Bayesian methods.)

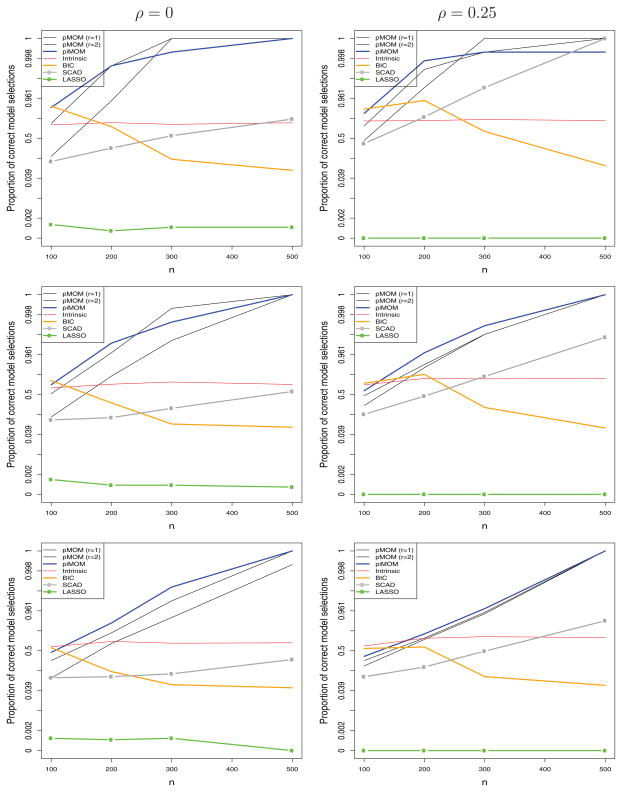
We denote by t̂ the model selected by a procedure for a simulated dataset. For Bayesian methods, t̂ is defined as the posterior mode, whereas for SCAD and LASSO it is defined from coefficients that are estimated to be nonzero. Figure 3 shows, on the logit scale, the average of P(t̂ = t) obtained under each of the scenarios for each of the model selection procedures. From these plots, it is clear that model selection procedures based on the nonlocal priors provided substantially higher empirical probabilities of identifying the true model for sample sizes of 200 or greater.

Figure 3.

P(t̂ = t) versus n. Top: σ² = 1; middle: σ² = 1.5; bottom: σ² = 2.

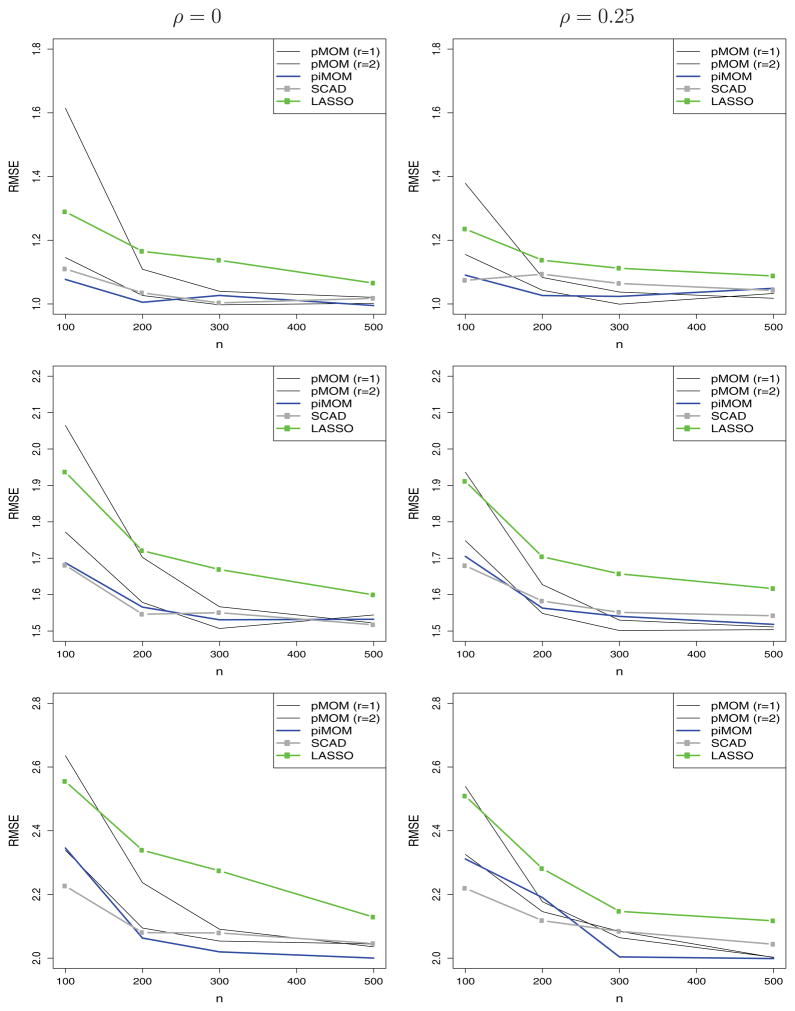
Out-of-sample prediction root mean square errors (RMSE) are displayed in Figure 4. To make the comparison of the prediction errors commensurate, the values displayed in Figure 4 were based on the MAP estimates of the regression parameters obtained under the MAP model for the nonlocal priors, and were based on the maximum penalized likelihood estimates for SCAD and LASSO. Prediction errors are not presented for the BIC and intrinsic prior procedures owing to the formal lack of a prior density for the BIC and the difficulty in obtaining the MAP estimate for the intrinsic prior. As the panels in Figure 4 indicate, the piMOM procedure’s prediction errors were typically slightly smaller than those obtained under SCAD; SCAD had slightly smaller prediction errors than the pMOM procedures when r = 1 and n < 200; and the pMOM procedure with r = 1 usually outperformed SCAD for n ≥ 200. The pMOM procedure with r = 2 was generally not competitive with any procedure except the LASSO for sample sizes smaller than 300.

Figure 4.

Out-of-sample RMSE versus n. Top: σ² = 1; middle: σ² = 1.5; bottom: σ² = 2.

The results in Figure 4 can be explained by noting that the true model provides the most accurate out-of-sample predictions. Thus, model selection algorithms that identify the “true” predictors are also likely to provide the best predictions, provided that the biases of the associated regression coefficients are small. For Bayesian procedures that employ proper priors, these biases are known to be of order O(1/n), so in large samples it follows that Bayesian procedures that provide the highest probability of selecting the true model are likely to also provide optimal, or nearly optimal, out-of-sample prediction errors. For this reason, the default piMOM prior (which has the heaviest tails and so the smallest biases) tends to provide the smallest prediction error.

The performance of the selection procedure based on the second-order pMOM prior densities was less impressive. We attribute its poor performance in both identifying the correct model and in out-of-sample prediction to the choice of τ and the lighter tails of the pMOM density at larger values of β. This problem is illustrated in Figure 1, which shows that this density assigns little weight to values of regression coefficients greater than about 1.2.

The similarities of the curves in Figures 2 and 3 warrant additional emphasis. From these figures, we see that the Bayesian procedures based on nonlocal priors provide estimates of p(t|y_n) that correlate well with P(t̂ = t). That is, the posterior probability assigned to the maximum a posteriori model provides a bona fide estimate of the probability (in the frequentist sense) that the chosen model is correct. This is an important feature of our model selection procedures that is not shared by other methods. For example, this property does not hold for model selection based on the intrinsic priors. Even though the maximum a posteriori model obtained under the intrinsic prior specification is generally around 70% for large values of n, it assigns to the true model an average posterior probability that is always close to 0.

Further details concerning the simulation studies, including marginal probabilities of inclusion for nonzero and zero coefficients, false discovery rates, and the numerical values of points displayed in the figures (Tables S1–S7), can be found in the online Supplementary Material.

5. DISCUSSION

The Bayesian model selection procedures described in Section 2 provide consistent estimation of the true regression model in the sense that the Bayesian posterior probability of the true model converges to 1 in probability when the conditions of Theorem 1 are satisfied. In stating this finding, we also note that most Bayesian model selection procedures, including those based on local priors, provide consistent estimation of the true model under the conditions of Theorem 1 for fixed p as n → ∞. This fact follows from the consistency of the Bayes factor when the number of covariates is fixed a priori (e.g., Casella et al. 2009) and the posterior normality conditions cited by Walker (1969).

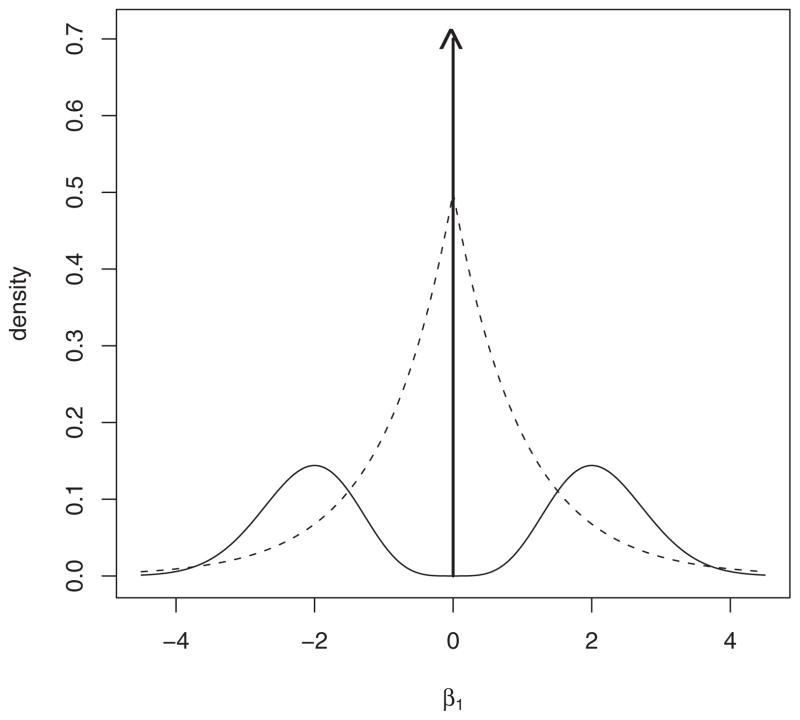
An explanation of how the proposed Bayesian model selection procedures are able to achieve consistency for p = O(n) can be found by comparing nonlocal prior densities to the double exponential prior distribution implicit to the Bayesian LASSO procedure (Park and Casella 2008). To simplify matters, we consider the test of whether a single regression coefficient β₁ is equal to 0. If the prior probability that β₁ = 0 is 0.5, and there is a 0.5 probability that it is drawn from a pMOM prior, then the marginal prior on β₁ can be depicted by the solid curve in Figure 5. This prior density is an equal mixture of a point mass at 0 and a pMOM density. In contrast, the double exponential prior associated with the LASSO is depicted as a dashed line in Figure 5.

Figure 5.

Nonlocal prior density versus LASSO prior density. The density depicted by the solid line represents an equal mixture of a one-dimensional pMOM density and a point mass at 0. The density illustrated by the dashed line represents the double exponential prior density associated with the LASSO procedure.

The most salient differences between the prior densities pictured in Figure 5 are seen in their behavior near the value β₁ = 0. Although the double exponential prior peaks at 0, it also places substantial mass in neighborhoods around 0. Small but nonzero values of the parameter can thereby be assigned high probability under the LASSO prior. On the other hand, the marginal prior obtained from the mixture of the pMOM density and point mass prior assigns negligible probability to small, nonzero values of β₁. As a consequence, the pMOM mixture provides more shrinkage toward 0 for regression coefficients that are not supported by the data.

To extend the analogy between the LASSO and Bayesian procedures based on double exponential priors to other classical and Bayesian model selection methods, note that the LASSO and SCAD procedures select models by minimizing |L₁| objective functions of the general form

$$l(\widehat{\mathit{\beta }})-\sum _i{w}_i\mid {\widehat{\mathit{\beta }}}_i\mid ,$$ (14)

where l(β̂) denotes the log-likelihood function evaluated at an optimal value of β̂, and {w_i } denotes weights. Ridge regression and related L₂ estimation procedures determine regression coefficients that maximize objective functions of the form

$$l(\widehat{\mathit{\beta }})-\sum _i{w}_i{\widehat{\mathit{\beta }}}_i^2,$$ (15)

which, from a Bayesian perspective, correspond to imposing a (local) Gaussian prior on the regression parameter β. By maximizing rather than integrating, the BIC can be justified as an approximation to Bayes factors obtained by imposing Gaussian (or other local) priors on the regression coefficients included in each model (e.g., Kass and Raftery 1995). The objective function associated with model selection using the BIC can be expressed as

$$l(\widehat{\mathit{\beta }})-\mathit{cp}log(n)$$ (16)

for some positive constant c.

Using similar reasoning, an objective function that might be associated with pMOM priors can be expressed as

$$l(\mathit{\beta })-\mathit{cp}log(n)+d\sum _{i}log\left[{\left(\frac{{\mathit{\beta }}_i^2}{\tau {\sigma }^2}\right)}^r\right],$$ (17)

for some d > 0, whereas the objective function associated with the piMOM priors might be expressed as

$$l(\mathit{\beta })-\mathit{cp}log(n)-d\sum _i{\left(\frac{\tau {\sigma }^2}{{\mathit{\beta }}_i^2}\right)}^r.$$ (18)

In both cases, the model that maximizes the objective function over all components of β included in the model is selected as the best model. By comparing Equations (17) and (18) with Equation (16), we see that the effect of the nonlocal objective functions is to add to the standard BIC a penalty term that can become arbitrarily large in models that contain regression coefficients that are close to 0.

It is important to note, however, that Equations (17) and (18) do not add an additional penalty to models that contain coefficients that are large in magnitude. This feature makes it possible to avoid stiff prior penalties on models that contain many parameters. In contrast, Theorem 2 shows that severe prior penalties are required on the model space to obtain consistent results when local priors are imposed on regression coefficients.

With regard to the choice between maximizing an objective function or integrating over a prior density to obtain a Bayes factor, we feel that the Bayesian approach offers two advantages. First, the specification of normalized prior densities provides an automatic guide to the selection of the constants c and d that appear in the objective functions in Equations (17) and (18). Second, as discussed previously, posing the model selection problem within the Bayesian context facilitates inference regarding the posterior probability that each model is true.

Extensions of the results from our simulation study to the p ≫ n setting will require substantial reformulation of the model selection problem. In such settings, the columns of the design matrix X cannot be independent, which means that the definition of a true model will generally be ambiguous. This implies that further constraints are needed to define the true model, or that an alternative formulation of the inferential problem must be posited. We are currently investigating such extensions using alternative Bayesian interpretations of model selection procedures combined with screening techniques suggested by, for example, Fan and Lv (2008).

In practice, we find that the pMOM priors of order r = 1 and piMOM priors perform well in applications, although we recommend that the former be used only in conjunction with beta-binomial priors on the model space. The pMOM priors offer some advantage in computational speed over piMOM priors, particularly if A_k is chosen to be the identity matrix (thus eliminating the need to compute the prior normalization constant). This choice of A_k also stabilizes the posterior covariance matrix of β_k when the columns of X_k are highly correlated. However, the piMOM prior introduces a smaller bias in the estimation of large components of β. We recommend that τ be chosen based on scientific considerations whenever possible, but have found that the default values recommended in JR10 work well in a variety of simulation settings, provided that the columns of X_n have been standardized so as to have unit variance (see Section 4).

The model selection procedures described in this article have been implemented in the R package mombf. The R code based on this package that was used to obtain the simulation results in Section 4 is included in the article’s online Supplementary Material. Instructions for implementing these model selection procedures for an arbitrary dataset using R can be obtained by typing vignette(“mombf”) in the R command line (http://cran.r-project.org/web/packages/mombf/index.html).