Modeling Local Control After Hypofractionated Stereotactic Body Radiation Therapy for Stage I Non-Small Cell Lung Cancer: A Report From the Elekta Collaborative Lung Research Group

Abstract

Purpose

Hypofractionated stereotactic body radiation therapy (SBRT) has emerged as an effective treatment option for early-stage non-small cell lung cancer (NSCLC). Using data collected by the Elekta Lung Research Group, we generated a tumor control probability (TCP) model that predicts 2-year local control after SBRT as a function of biologically effective dose (BED) and tumor size.

Methods and Materials

We formulated our TCP model as follows: TCP =e^{[BED10 – c * L – TCD50]/k} ÷ (1 + e^{[BED10 – c * L – TCD50]/k}), where BED10 is the biologically effective SBRT dose, c is a constant, L is the maximal tumor diameter, and TCD50 and k are parameters that define the shape of the TCP curve. Least-squares optimization with a bootstrap resampling approach was used to identify the values of c, TCD50, and k that provided the best fit with observed actuarial 2-year local control rates.

Results

Data from 504 NSCLC tumors treated with a variety of SBRT schedules were available. The mean follow-up time was 18.4 months, and 26 local recurrences were observed. The optimal values for c, TCD50, and k were 10 Gy/cm, 0 Gy, and 31 Gy, respectively. Thus, size-adjusted BED (sBED) may be defined as BED minus 10 times the tumor diameter (in centimeters). Our TCP model indicates that sBED values of 44 Gy, 69 Gy, and 93 Gy provide 80%, 90%, and 95% chances of tumor control at 2 years, respectively. When patients were grouped by sBED, the model accurately characterized the relationship between sBED and actuarial 2-year local control (r=0.847, P=.008).

Conclusion

We have developed a TCP model that predicts 2-year local control rate after hypofractionated SBRT for early-stage NSCLC as a function of biologically effective dose and tumor diameter. Further testing of this model with additional datasets is warranted.

Introduction

In recent years, hypofractionated stereotactic body radiation therapy (SBRT) has emerged as an effective treatment option for medically inoperable stage I non-small cell lung cancer (NSCLC) patients. SBRT in this setting has demonstrated excellent local control rates (1) and has been linked to improvements in overall survival (2). Compared with radiation therapy (RT) delivered via traditional techniques, SBRT uses highly conformal dose distributions, large daily fraction sizes, and shortened overall treatment courses. All of these characteristics contribute to the appeal of SBRT as a safe, effective, and convenient treatment option for medically inoperable stage I NSCLC patients.

The Elekta Collaborative Lung Research Group consists of 5 international institutions that use advanced treatment techniques, including online image guided RT (IGRT) to deliver SBRT for stage I NSCLC. Data from this group have already been presented, and several predictors of local control have been identified (3). The most significant predictor of local control is biologically effective dose (BED), calculated by use of the linear quadratic model with an α/β ratio of 10 Gy. Among patients treated with a relatively low BED, other factors such as tumor size and treatment duration seem to affect outcome.

Here we attempted to generate a robust tumor control probability (TCP) model using data from the Elekta Lung Research Group.

Methods and Materials

Study population and treatment techniques

The study population consisted of patients who underwent image-guided lung SBRT for stage T1-3 N0 M0 NSCLC between 1998 and 2010 at 1 of 5 international institutions participating as members of the Elekta Lung Research Group. Details regarding the staging workup, treatment techniques, and follow-up evaluation of these patients have been reported previously (4). Briefly, patients were treated with volumetrically prescribed, image guided hypofractionated SBRT. Starting in 2005, cone beam computed tomography (CT) was available. Density correction was used in treatment planning for all patients. A variety of treatment schedules was used, with total doses of 24–64 Gy delivered in 1–15 fractions.

Follow-up examinations were performed according to local guidelines in each institution. At the minimum, patients were followed up with CT scans performed at regular time intervals. 18F-fluorodeoxyglucose/positron emission tomography scanning was performed for response assessment and/or when clinically indicated based on CT findings suggesting local, regional, or distant recurrence. Biopsy confirmation of local recurrence was not required; local recurrence could also be diagnosed on the basis of anatomic and functional imaging findings at the discretion of the treating physicians. Local recurrence was qualitatively defined as disease progression in the treated lung parenchyma. Fusion of pretreatment and posttreatment imaging studies was not attempted because SBRT is known to cause morphologic changes in lung tissue (5).

TCP model

Our model was based on a standard TCP model:

$$\mathit{TCP}=e^{[d-\mathit{TCD}50]/k}÷(1+e^{[d-\mathit{TCD}50]/k})$$ (1)

where d is treatment dose, TCD50 is the dose required to achieve 50% tumor control, and k is a fitting constant that is equal to 25 divided by the slope of the TCP curve at a dose equal to the TCD50 (6). Based on previous reports that local control rates after SBRT for stage I NSCLC decrease with tumor size, we hypothesized that effective dose decreases approximately linearly with increasing tumor diameter. Thus, the TCP model used for this analysis was:

$$\mathit{sBED}=\mathit{BED}10-c\ast L$$ (2)

Combining (1) and (2), where d = sBED:

$$\mathit{TCP}=e^{[\mathit{BED}10-c\ast L-\mathit{TCD}50]/k}÷\left(1+e^{[\mathit{BED}10-c\ast L-\mathit{TCD}50]/k}\right)$$ (3)

where sBED is the size-adjusted BED, BED10 is the BED (calculated using the Linear Quadratic Model with α/β = 10 Gy) prescribed to the planning target volume, c is a constant, L is tumor diameter, and TCD50 and k are as defined above.

We used a bootstrap resampling method to identify optimal model parameters and to characterize their distributions, as suggested by Deasy et al (7). For each bootstrap iteration, one-half of the patient cohort was selected at random and evaluated using a wide range of values for c, TCD50, and k. For each combination of variables, patients were divided into 8 bins of equal size by sBED. Least-squares optimization was used to select the values of c, TCD50, and k that provided the best fit between the predicted and observed 2-year actuarial local control rates for each bin. This process was repeated for 500 iterations. Mean values and 95% confidence intervals (CI) were calculated for each parameter.

Evaluating the TCP model

Kaplan-Meier curves were generated for patients with TCP values above 95%, for patients with TCP values between 85% and 95%, and for patients with TCP values below 85%. Log-rank testing was used to test the separation between each pair of curves.

To test the robustness of the TCP model, patients were grouped by tumor stage (T1a, T1b, or T2, using the American Joint Committee on Cancer version 7). A 2-tailed χ² test was performed to compare the 2-year actuarial rate of local recurrence in each tumor stage group with that predicted by the TCP model after adjustment for follow-up. This process was repeated after patients were grouped by SBRT course duration.

To evaluate the importance of tumor size in our model, a second optimization was performed with the value of c fixed at 0 Gy/cm. Patients were again grouped by tumor stage, and χ² tests were used to compare the observed local recurrence rates in each group with that predicted by the new TCP model.

Results

At the time of this analysis, data for 504 tumors from 482 patients treated with definitive hypofractionated SBRT were available. The median tumor size was 2.6 cm (range, 0.9–8.5 cm). The median prescription dose was 54 Gy (range, 26–64 Gy) delivered in a median of 3 fractions (range, 1–15 fractions) over a median duration of 8 days (range, 1–27 days). The most common fractionation schedules were 18 Gy in 3 fractions (n=208), 12 Gy in 4 fractions (n=128), 12 Gy in 5 fractions (n=40), and 12.5 Gy in 3 fractions (n=34). Ninety-five percent of patients were treated with 3–8 fractions, and 95% were treated over a duration of 3–16 days. The mean follow-up time after the completion of SBRT was 18.4 months (range, 0.3–87.1 months). Follow-up was often limited by patient mortality; the 2-year and 3-year overall survival (OS) rates were 60% and 48%, respectively. Twenty-six local recurrences were observed, with a median time to local recurrence of 12.0 months (range, 1.8–53.0 months).

The optimal model parameters were as follows: TCD50 =0 Gy (95% CI, −30 to 30), k =31 Gy (95% CI, 19–43), and c =10 Gy/cm (95% CI, 2–18). The k value of 31 Gy corresponds to a slope of 0.8% per Gy for the TCP curve at the TCD50. Using these parameters, sBED ranged from −10.5 Gy (for a 7.0-cm tumor treated with 35 Gy in 5 fractions) to 169.0 Gy (for a 1.1-cm tumor treated with 60 Gy in 3 fractions). Only 33 of 504 tumors (6.6%), however, received an sBED of less than 50 Gy, which equates to a TCP of 83%.

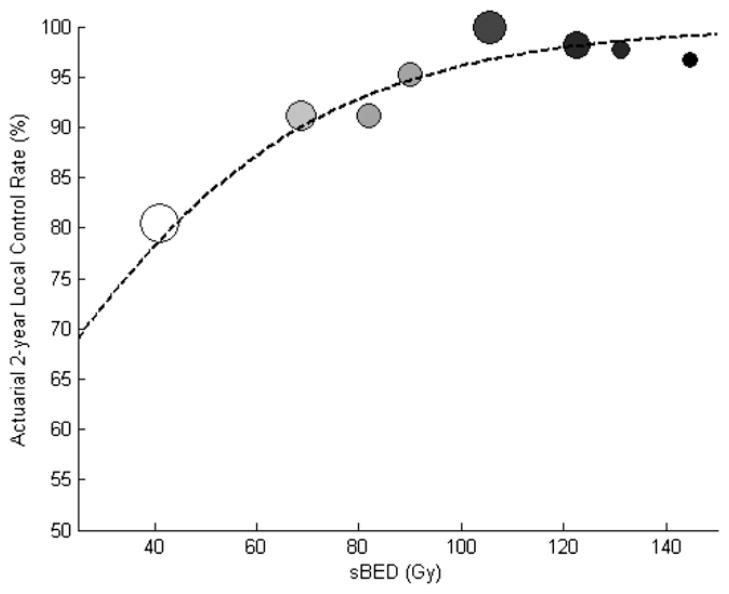
The TCP modeling results are displayed graphically in Fig. 1. There was a highly significant correlation (Pearson’s correlation coefficient = 0.847, P=.008) between the predicted and observed actuarial 2-year local control rates when patients were sorted by sBED into 8 groups. The sBED values required to provide 80%, 90%, and 95% chances of tumor control at 2 years were 44 Gy, 69 Gy, and 93 Gy, respectively.

Fig. 1.

Actuarial 2-year local control vs size-adjusted biologically effective dose (sBED). Each circle represents the outcomes in 60–66 patients after sorting by sBED. sBED is defined as biologically effective dose (calculated using the linear quadratic model with α/β = 10 Gy) minus 10 times the tumor diameter in centimeters. The size of each circle is proportional to the mean tumor diameter. Darker circles indicate a higher biologically effective dose. Dotted line depicts the optimal tumor control probability model (TCD50 = 0 Gy, k = 31 Gy).

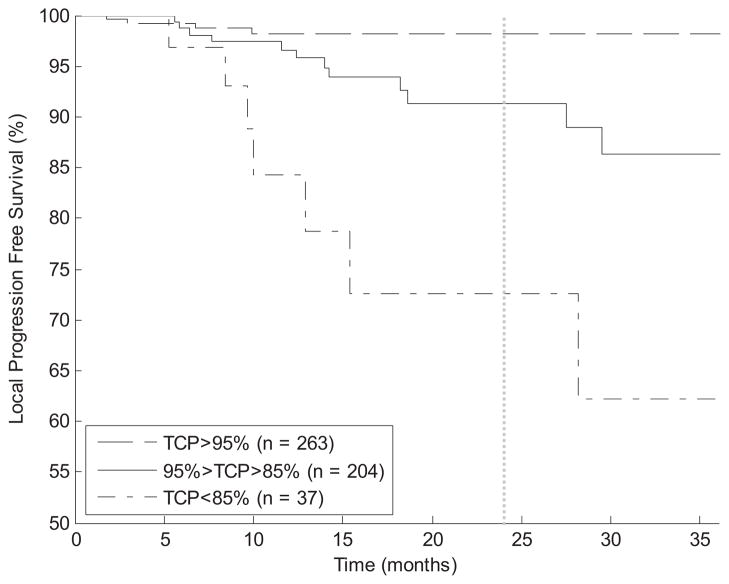
Kaplan-Meier curves for local progression-free survival after dividing patients by TCP into 3 groups (>95%, 85%–95%, and <85%) are shown in Fig. 2. Log-rank testing demonstrates a statistically significant (P<.01) difference between every pair of curves.

Fig. 2.

Kaplan-Meier curves for local progression-free survival. Patients are sorted by 2-year tumor control probability (TCP) into 3 groups. Log-rank test demonstrates a statistically significant (P<.01) separation between each curve.

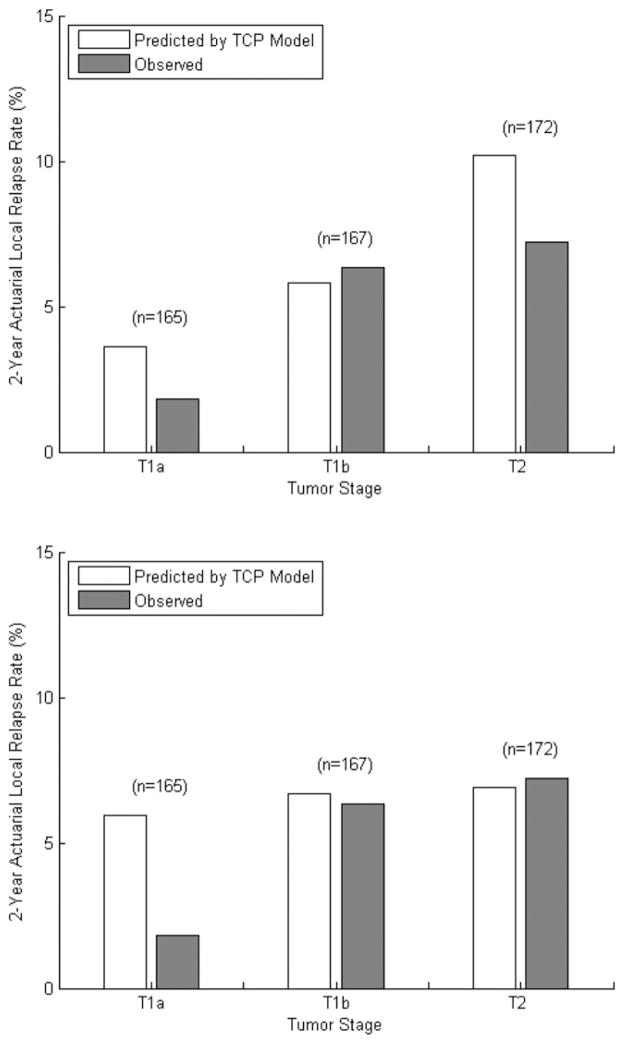
Comparison of the expected and observed 2-year rates of local control after grouping patients by tumor stage is shown in Fig. 3. Two-tailed χ² testing revealed no significant difference (P>.05) between the frequency of local recurrences and that predicted by the TCP model in each stage group. When the tumor size was removed from the TCP model (c = 0 Gy/cm), optimal model parameters were as follows: TCD50 = 10 Gy, k = 40 Gy. In that case, the TCP model significantly overestimated the risk of local recurrence among patients with tumors smaller than 2 cm (predicted, 5.9%; observed, 1.8%, P=.025).

Fig. 3.

Predicted and observed 2-year actuarial local relapse rates after grouping patients by T stage, with (top) and without (bottom) inclusion of tumor size in the tumor control probability (TCP) model. With tumor size included (c = 10 Gy/cm, top), 2-tailed χ² testing revealed no significant difference between the rates of local recurrences and those predicted by the tumor control probability (TCP) model, with P values of .211, .766, and .199 for T1a, T1b, and T2 tumors, respectively. When tumor size is excluded from the model (c = 0 Gy/cm, bottom), the optimal TCP model significantly overestimates the frequency of local relapse (P=.025) for T1a tumors.

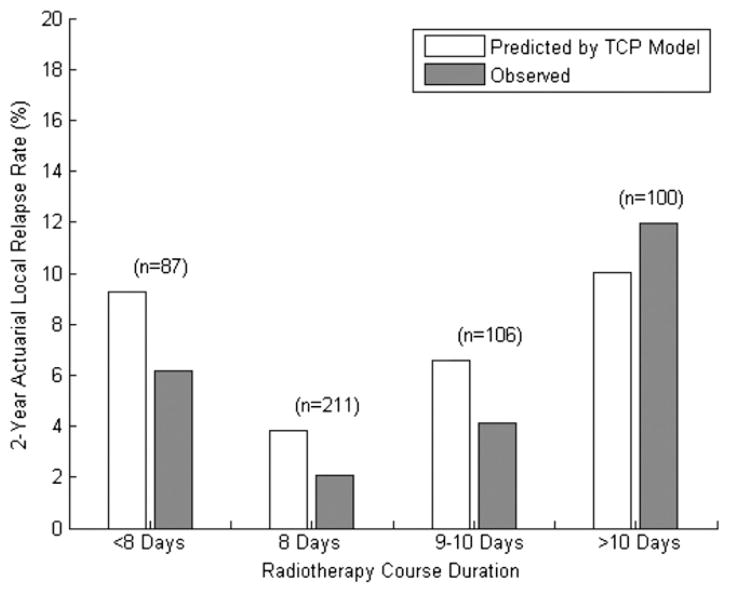
The expected and observed 2-year local recurrence rates after grouping patients by treatment duration are shown in Fig. 4. The incidence of local recurrence varied significantly with treatment duration. The 2-year local recurrence rates in each group, however, did not differ statistically from those predicted by the TCP model (P>.10, using a 2-tailed χ² test).

Fig. 4.

Predicted and observed 2-year actuarial local relapse rates after grouping patients by radiotherapy course duration. Two-tailed χ² testing revealed no significant difference between the rates of local recurrences and those predicted by the tumor control probability (TCP) model, with P values of .315, .178, .307, and .530 for <8 days, 8 days, 9–10 days, and >10 days, respectively.

Discussion

In this analysis, we used clinical data from more than 500 cases of early-stage NSCLC treated with SBRT to generate a TCP model. Our model, which is fairly simple, can be used to predict the 2-year probability of local control as a function of BED prescribed to the PTV and tumor diameter. The importance of including tumor size in the model was demonstrated by the fact that its exclusion led to an overestimation of the local failure rate in patients with small tumors. Additional analyses indicate that the model would not be improved by the addition of other variables such as treatment duration.

The form of our TCP model suggests that as BED increases, the effect of tumor size on predicted outcome diminishes. A fractionation schedule of 50 Gy in 5 fractions, for example, would yield predicted 2-year local control rates of 93%, 90%, and 83% for 1-cm, 3-cm, and 5-cm tumors, respectively. When a more aggressive regimen such as 54 Gy in 3 fractions is used, those TCP values increase to 99%, 98%, and 96%. This principle is consistent with previous findings from our group and from other reports (1, 3, 8, 9). A review of published experiences suggests that the influence of tumor size on local control seems to decrease with the intensity of the SBRT regimen used. In a study where 45 Gy was delivered to the isocenter in 3 fractions (PTV BED ≈ 95 Gy), the 3-year rate of local control was 78% for T1 patients and only 40% for T2 patients (8). In Radiation Therapy Oncology Group (RTOG) 0236, where a BED of 151 Gy was delivered to the PTV, the 3-year rate of local control was 100% for T1 tumors and 91% for T2 lesions (1).

It might seem unusual that the value of TCD50 in our model is 0 Gy. This should not be taken to indicate that an sBED of 0 Gy would provide a 50% chance of tumor control. As mentioned earlier, the vast majority of tumors in our dataset were treated with an sBED of at least 50 Gy. Our TCP model is not intended to be accurate outside that range. The values for k and TCD50 obtained in this report simply describe the steepness and location (left-to-right) of our S-shaped TCP curve. Other TCP modeling methods were tested on this dataset, including a classical model incorporating tumor volume and interpatient variations in tumor cell radiosensitivity (10). Although the performance of that model was identical to that of the sBED model, we favor the sBED model because of the ease with which it may be implemented by clinicians.

Only 10 out of 504 (2%) tumors used for this analysis were treated with SBRT delivered in a single fraction. Thus, it would be inappropriate to use our TCP model to predict outcomes using this approach. Published reports describe moderate local control rates after single-fraction SBRT for stage I NSCLC, with a suggestion that local control may vary with RT dose and tumor size (11–13). The RTOG is currently investigating single-fraction treatment with a dose of 34 Gy. Similarly, this model should not be used to predict outcomes after RT courses with fraction sizes less than 8 Gy or with treatment durations longer than 2 weeks. Although an earlier report from this group indicated that RT courses longer than 11 days were associated with inferior local control, we found no evidence that the accuracy of our model varied systematically with treatment length (Fig. 4). The incorporation of accelerated repopulation into our model did not improve its performance (data not shown). This is consistent with the hypothesis that the “kickoff time” for accelerated repopulation of NSCLC cells is approximately 3 weeks after the initiation of cytotoxic therapy (14).

In this analysis, BED and sBED were calculated using the linear quadratic equation with an α/β ratio of 10 Gy. This is consistent with the manner in which fractionation schedules are commonly evaluated in existing SBRT literature. As an exploratory analysis, we repeated our method using a range of values for α/β (data not shown). With an α/β ratio of 5 Gy, the “optimal” TCP model significantly overestimated 2-year local control with fraction sizes of 18 Gy or higher and underestimated local control after SBRT using fraction sizes of less than 18 Gy (P<.001). By contrast, when a higher α/β ratio of 25 Gy was used, the “optimal” TCP model significantly overestimated local control for lesions treated with daily fraction sizes of less than 12 Gy (P<.001). Thus, we found no reason to deviate from the α/β ratio of 10 Gy that is typically used. Novel cell survival models, such as the universal survival curve (15) and the generalized linear quadratic model (16), may be more useful than the linear quadratic model for reconciling outcomes after conventional RT and hypofractionated SBRT. Comparison of these approaches was beyond the scope of this analysis.

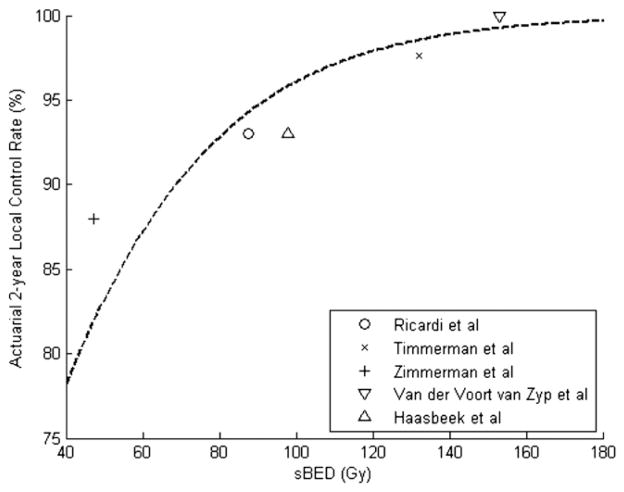
Our TCP model clearly must be validated using other datasets. As an exploratory measure, we performed a literature search to identify published SBRT experiences against which our model could be tested. We identified 5 published series (excluding 1 from the institution leading this collaboration) in which relatively consistent treatment schedules were used, sample size was at least 50 patients, and 2-year local control rates were reported (1, 17–19). Figure 5 compares the local control rates in those series, plotted against sBED, with those predicted by our TCP model. For each series, the reported 2-year local control rate was within 6% of that predicted by our TCP model (Pearson’s correlation coefficient = 0.906, P=.034).

Fig. 5.

Reported 2-year local control rates for 5 published series, plotted against size-adjusted biologically effective dose (sBED, defined as mean biologically effective dose −10 × mean tumor diameter, in centimeters). The dotted line represents the tumor control probability model proposed in this report. (Pear-son’s correlation coefficient = 0.906, P=.034).

Numerous reports indicate that treatment of early-stage NSCLC with an aggressive SBRT regimen such as 18–22 Gy in 3 fractions provides an excellent chance of tumor control (1, 20). When the target lesion is near central structures or the chest wall, however, SBRT may be associated with significant toxicity (21–23). Dosimetric predictors of skin, chest wall, and rib complications have been suggested (21, 23). In difficult cases where the target volume is close to 1 or more organs at risk, an understanding of the likelihood of tumor control and treatment-related toxicity associated with various SBRT schedules would help clinicians select the optimal treatment regimen. It is in these situations where TCP modeling will be most clinically relevant.

There are several limitations to this analysis that should be considered. Although the overall sample size of 504 was quite large, only 26 local recurrences were observed. Thus, there is a range of TCP parameters that would produce models that fit the observed failure patterns. We did not require pathologic confirmation of local failures, adding further uncertainty to our findings. Based on our patient population, this model may not be useful for predicting outcomes after treatment with single-fraction SBRT or with fraction sizes of less than 8 Gy. As mentioned earlier, this TCP model requires validation using additional SBRT datasets. Because follow-up time was limited, we were not able to model local control at time points beyond 2 years. Late recurrence of NSCLC after SBRT can occur, however, so additional study of long-term outcomes is warranted (24). This will be especially important if SBRT is to be explored as a treatment option for patients who are medically fit for surgical resection. Finally, nodal or distant disease progression could potentially obscure the detection of local recurrence in NSCLC patients treated with SBRT. Although competing risks regression was beyond the scope of this study, such analyses are under way.

Conclusion

We have developed a simple TCP model that predicts 2-year local control after hypofractionated SBRT for early-stage NSCLC as a function of biologically effective dose and tumor diameter. Its predictions are compatible with existing SBRT literature. Further testing of this model with additional datasets is warranted.

Summary.

We used a multi-institutional database of more than 500 non-small cell lung cancer tumors treated with stereo-tactic body radiation therapy to generate a model for tumor control probability. We introduce the term size-adjusted BED (sBED = biologically effective dose minus 10 times the tumor diameter in centimeters). We found that sBED values of 44 Gy, 69 Gy, and 93 Gy provided, respectively, 80%, 90%, and 95% chances of tumor control at 2 years. Validation of this model with additional datasets is underway.