PIRPLE: A Penalized-Likelihood Framework for Incorporation of Prior Images in CT Reconstruction

Abstract

Over the course of diagnosis and treatment, it is common for a number of imaging studies to be acquired. Such imaging sequences can provide substantial patient-specific prior knowledge about the anatomy that can be incorporated into a prior-image-based tomographic reconstruction for improved image quality and better dose utilization. We present a general methodology using a model-based reconstruction approach including formulations of the measurement noise that also integrates prior images. This penalized-likelihood technique adopts a sparsity enforcing penalty that incorporates prior information yet allows for change between the current reconstruction and the prior image. Moreover, since prior images are generally not registered with the current image volume, we present a modified model-based approach that seeks a joint registration of the prior image in addition to the reconstruction of projection data. We demonstrate that the combined prior-image- and model-based technique outperforms methods that ignore the prior data or lack a noise model. Moreover, we demonstrate the importance of registration for prior-image-based reconstruction methods and show that the prior-image-registered penalized-likelihood estimation (PIRPLE) approach can maintain a high level of image-quality in the presence of noisy and undersampled projection data.

1. Introduction

X-ray computed tomography (CT) is a prevalent modality for diagnostic and interventional imaging with high spatial resolution and relatively short acquisition time. However, ionizing radiation associated with this modality is a concern, particularly for patients that undergo a sequence of CT studies over the course of diagnosis, treatment, and follow-up. Dose reduction strategies play an important role in limiting potential risks and can be categorized into two general groups: 1) modification of the x-ray technique (e.g., lower mA); and 2) reduction in the data acquired (e.g., sparse projection views). The first approach is applicable to nearly any tomographic system, whereas the second is more appropriate to systems employing a pulsed x-ray source, as common with 3D capable interventional C-arms. (Siewerdsen et al., 2005; Fahrig et al., 2006; Schafer et al., 2011) Without some form of compensation, both dose reduction methods decrease the overall data fidelity and consequently suffer a reduction in image quality. Reconstruction techniques that seek to preserve image quality therefore stand to benefit by using the available data more effectively and/or injecting additional information into the reconstruction process to overcome the loss in data fidelity.

Model-based reconstruction approaches have attempted to use the available data more effectively through the incorporation of sophisticated forward models that include so-called x-ray optics including an extended source and detector footprints/blur (Long et al., 2010; Feng et al., 2006; Yu et al., 2000; De Man and Basu, 2004), spectral effects (De Man et al., 2001; Elbakri and Fessler, 2002, 2003; Lasio et al., 2007), complex geometries including data redundancy and missing data (Snyder et al., 2006), as well as measurement noise models. (Snyder et al., 1993; Xu and Tsui, 2009; Whiting et al., 2006) Moreover, because model-based approaches are often defined as the implicit solution to an objective function, the objective may be modified to include additional sources of information. Examples include penalized-likelihood objectives with various roughness penalties that encourage smoothness and edge-preservation (Lange, 1990; Nikolova et al., 1998; Vogel and Oman, 1996; Sidky and Pan, 2008). Such model-based approaches have demonstrated significant improvement in the trade-off between dose and image quality (Thibault et al., 2007; Evans et al., 2011) and are now available on commercial multi-detector CT systems in the clinical setting. (Yoon et al., 2012; Schabel et al., 2013)

While such model-based approaches improve dose utilization, they typically neglect a potential wealth of patient-specific anatomical information found in previously acquired scans of the same patient. Techniques that incorporate such prior information in the reconstruction process offer a promising advance – for example, the prior-image-constrained compressed sensing (PICCS) technique (Chen et al., 2008), which introduces an objective function that integrates previously acquired images. The original formulation of the PICCS objective does not integrate measurement noise and assumes that data consistency can be enforced through a linearized measurement model, most commonly accomplished through an equality constraint on the projection of the volume estimate and line integrals estimated from the data (e.g., through gain correction, logarithmic transformation, and other data corrections). Recent modifications to PICCS allow the introduction of statistical weights within a heteroscedatic Gaussian noise model (Lauzier and Chen, 2013, 2012), but a linearized model is still assumed, making it difficult to include certain nonlinear effects (e.g., a polyenergetic forward model) within the framework.

A critical aspect of effectively using previously acquired anatomical information is that the prior image should be accurately registered to the current data. While such integration has been conducted in the past without registration (e.g., in cardiac imaging where a “prior image” is derived from the current data (Chen et al., 2009), or in the dose reduction (DR) PICCS variant (Tang et al., 2011) which operates on a single dataset), there are many situations including interventional imaging, treatment monitoring, and cancer screening which would benefit from registration of prior information – for example, the staged registration-then-reconstruction approach incorporated in the PICCS framework in (Nett et al., 2009). Moreover, recent cardiac studies (Bergner et al., 2010) note that even in cases where prior images are derived from the current data residual motion artifacts are still observed suggesting the need for registration.

In this paper, we present a model-based approach that integrates both a (Poisson) noise model and prior images in the reconstruction process. This approach, called PIRPLE – prior image (with) registration penalized-likelihood estimation, poses the problem as a joint registration and reconstruction. A preliminary introduction of PIRPLE was presented in (Stayman et al., 2011), and an initial evaluation of the methodology without registration was reported in (Ding et al., 2012). In this work, we present a detailed description of the algorithm, an investigation of the reconstruction parameter space, and a quantitative evaluation of the approach as compared with other model-based, prior-image-based, and traditional reconstruction methods. In particular, we consider scenarios that push dose reduction to its limits using both reduction in x-ray fluence and sparse sampling.

2. Methods

2.1. Forward Model and Likelihood-based Objective Function

We seek a model-based reconstruction approach that incorporates both measurement noise and prior image information. Toward this end, we adopt the following forward model, written in a matrix-vector form, where the mean measurements, ȳ, are given by

$$\overline{y}=\mathbf{D}\{g\}exp(-l),l=\mathbf{A}\mu$$ (1)

where D is an operator converting a vector to a diagonal matrix, g is a vector of measurement dependent gains (including x-ray fluence, detector sensitivity, etc.), l denotes a vector of all the line integrals associated with an acquisition, μ is the vector of attenuation values representing the imaging volume, and the matrix A is the linear projection operator. We note that, as with other model-based approaches, the simple model in (1) can be adapted to more sophisticated forward models – for example, the polyenergetic form proposed in (Elbakri and Fessler, 2002).

Choosing a Poisson model for the expected variations in y allows one to form a likelihood-based objective function with the log-likelihood written as

$$logL(y;\mu )=\sum _{i=1}^N{h}_i\left({\left[\mathbf{A}\mu \right]}_i\right)h_i\left(l_i\right)=\sum _{i=1}^N{y}_{i}log\left(g_{i}exp\left(-l_i\right)\right)-g_{i}exp\left(-l_i\right)$$ (2)

where inconsequential constant terms have been dropped, the subscript ¹ i denotes the i^th measurement, h_i represents a marginal log-likelihood for each measurement, and y is a vector representing the N (noisy) measurements. A general roughness-penalized, likelihood-based estimator may be formed from (2) as the implicit maximizer of an objective:

$$\widehat{y}=\underset{\mu }{argmax}logL(y;\mu )-R(\mu )=\underset{\mu }{argmax}logL(y;\mu )-{\beta }_R{\Vert {\mathbf{\Psi }}_R\mu \Vert }_{p_R}^{p_R}$$ (3)

where R(μ) denotes an arbitrary regularizer, and we have chosen a specific roughness penalty in the second line which incorporates the image gradient operator, Ψ_R, a p-norm operator, and a scalar control parameter β_R, which allows one to tune the estimator for a specific noise-resolution tradeoff. When p_R = 2, for example, a quadratically regularized estimator is formed which tends to apply a blur somewhat uniformly throughout the volume. On the other hand, taking p_R = 1 amounts to a total variation (TV) style regularization (Vogel and Oman, 1996) which allows larger differences between voxels and can exhibit highly nonuniform smoothing with strong edge-preservation.

2.2. Prior-Image Penalized-Likelihood-based Objective Functions

We choose to modify this penalized-likelihood objective with the addition of another penalty term that encourages similarity with a previously acquired prior image, μ_P, such that

$$\widehat{y}=\underset{\mu }{argmax}logL(y;\mu )-{\beta }_P{\Vert {\mathbf{\Psi }}_P(\mu -{\mu }_P)\Vert }_{p_P}^{p_P}-{\beta }_R{\Vert {\mathbf{\Psi }}_R\mu \Vert }_{p_R}^{p_R}$$ (4)

where we have allowed for independent control of the strength of this prior image penalty through the parameter, β_P, and for independent choices of the p-norm and transformation, Ψ_P. We refer to (4) as the prior-image penalized-likelihood estimator (PIPLE). As with the roughness penalty, particular selections for the norm in the prior image penalty can have a dramatic effect on image reconstruction. Whereas p_P = 2 tends to blend (or average) features found in the measurement data with those in the prior, lower p_P values tend to enforce similarity between the reconstruction and the prior up to a point, allowing for larger differences and anatomical change.

While the PIPLE approach can integrate information from the prior image while accommodating anatomical change, it is important to recognize that some changes between the prior image and the current anatomy can arise from motion between scans. Thus, more effective use of prior anatomical information may be facilitated with proper registration of the prior image. We propose a modified estimator, referred to as PIRPLE, that seeks a joint solution to the registration and reconstruction as follows:

$$\{\widehat{y},\widehat{\lambda }\}=\underset{\mu ,\lambda }{argmax}logL(y;\mu )-{\beta }_P{\Vert {\mathbf{\Psi }}_P(\mu -\mathbf{W}(\lambda ){\mu }_P)\Vert }_{p_P}^{p_P}-{\beta }_R{\Vert {\mathbf{\Psi }}_R\mu \Vert }_{p_R}^{p_R}$$ (5)

where W denotes a transformation operator parameterized by the vector λ (e.g., for a rigid transformation, a vector of six translations and rotations). Details of the registration operator are discussed below. We reiterate that (5) represents a joint optimization, rather than a staged approach with a single registration followed by reconstruction.

2.3. Relation to PICCS

The PIPLE objective in (4) is closely related to a PICCS objective, typically expressed as:

$$\widehat{y}=\underset{\mu }{argmin}\left[\alpha {\Vert {\mathbf{\Psi }}_P(\mu -{\mu }_P)\Vert }_1+(1-\alpha ){\Vert {\mathbf{\Psi }}_R\mu \Vert }_1\right]s.t.\mathbf{A}\mu =\widehat{l}(y)$$ (6)

In this case, the relative strengths of the prior image and roughness terms are controlled through a single parameter, α, and consistency of the reconstruction with the measurements is enforced through an linear equality constraint where projections of the reconstruction must match estimates of the line integrals, l̂, which are, in turn, based on the measurements. Thus, application of (6) involves a linearization of the forward model and an approach for forming line integral estimates. This process is straightforward for the simple model in (1); however, more sophisticated forward models such as the polyenergetic models proposed in (Elbakri and Fessler, 2002; De Man et al., 2001) do not generally have a invertible closed-form solution that would permit a linear constraint. The PICCS objective also enforces an equality in the data consistency constraint, thereby attempting to match estimated line integrals exactly, including noise that might corrupt those estimates. In contrast, the model-based penalized likelihood estimation in PIPLE and PIRPLE do not enforce strict equality with measurements, instead balancing the data fit with the prior image and roughness penalties. An unconstrained form of (6) can be expressed as

$$\begin{array}{l}\widehat{y}=\underset{\mu }{argmin}\alpha {\Vert {\mathbf{\Psi }}_P(\mu -{\mu }_P)\Vert }_1+(1-\alpha ){\Vert {\mathbf{\Psi }}_R\mu \Vert }_1+\gamma \Vert \mathbf{A}\mu -\widehat{l}(y)\Vert \\ =\underset{\mu }{argmax}-\Vert \mathbf{A}\mu -\widehat{l}(y)\Vert -\frac{\alpha }{\gamma }{\Vert {\mathbf{\Psi }}_P(\mu -{\mu }_P)\Vert }_1-\frac{(1-\alpha )}{\gamma }{\Vert {\mathbf{\Psi }}_R\mu \Vert }_1\end{array}$$ (7)

where γ is a weighting on the data fit term. One may consider arbitrarily large values of γ to approximate the PICCS objective while better illustrating the relationship with the PIPLE objective in (4). Therefore, the unconstrained PICCS formulation in (7) is a special case of the PIPLE formulation in (4) with a specific choice of data fit terms and norms and a different parameterization of penalty strengths. Note also that the first term in (7) can be modified to a weighted norm yielding a penalized weighted least-squares estimator analogous to that in (Sauer and Bouman, 1993) as presented in (Lauzier and Chen, 2012, 2013).

2.4. Optimization Approach - PIPLE

While the previous sections introduced a general class of prior-image-based reconstruction methods, the optimization algorithm to solve those objectives must also be defined. The formulations in (4) and (5) use p-norms traditionally defined as follows

$${\Vert x\Vert }_p={\left(\sum _i{\left|x_i\right|}^p\right)}^{\frac{1}{p}}\to {\Vert x\Vert }_p^p=\sum _i{\left|x_i\right|}^p$$ (8)

where p is denoted generally and could refer to either the prior image or roughness terms, p_P or p_R, respectively, in (3) – (5). The form in (8) can be difficult to use in gradient-based optimization due to nondifferentiability at the origin. As such, we invoke a modified p-norm:

$${\Vert x\Vert }_p^p\cong \sum _{i}f\left(x_i\right)f\left(x_i\right)=\{\begin{array}{ccc}a{x}_i^2& \left|x_i\right|<\delta & a={\left(2\delta \right)}^{-p}{\left({\delta }^{2}p\right)}^{p-1}\\ \frac{1}{p}{\left|x_i-bsgn\left(x_i\right)\right|}^p& \left|x_i\right|\ge \delta & b=\delta \left(1-\frac{p}{2}\right)\end{array}$$ (9)

that ensures differentiability near the origin by replacing a δ-neighborhood around the origin with a quadratic function. The original function is shifted away from the origin, and the function value and derivative match at δ and −δ. This modified p-norm and its derivative are shown in Figure 1, though we have eliminated the analytic expressions of derivative for brevity. For p = 1, f (x_i) is equivalent to the Huber loss function (Huber, 1981). For p<1, f (x_i) is nonconvex which can also lead to difficulties in optimization, although graduated nonconvexity approaches (Blake and Zisserman, 1987) may be applied to find solutions. While p values less than one are not a focus in this paper, they may be useful. One motivation for the use of p = 1 in PICCS is that it encourages sparse solutions in a space dependent on the transform Ψ for the linearly constrained objective function. Since the data fit term in (4) and (5) is nonlinear, it is possible that sparseness could be is better enforced through such low p values.

Figure 1.

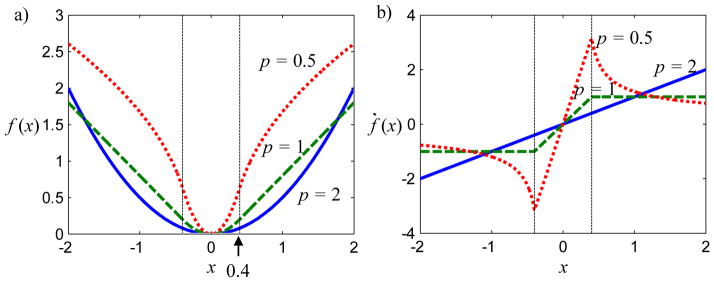
Illustration of (a) the modified p-norm and (b) its derivative for p = 0.5, 1.0, and 2.0 with δ = 0.4. Note that the function is differentiable everywhere and that p < 1 is nonconvex.

The PIPLE objective in (4) solves only for the attenuation volume (without registration). For this estimator we may leverage previous advances in algorithm development, such as the separable paraboloidal surrogates (SPS) approach outlined in (Erdogan and Fessler, 1999a, b). In this case, the likelihood part of the objective function is identical to that in (Erdogan and Fessler, 1999a), but the penalty functions are different. Fortunately, both the roughness penalty and prior image penalty (for p ≥ 1) meet the five criteria in (Erdogan and Fessler, 1999a; Huber, 1981) for finding paraboloidal surrogates. Thus, it is straightforward to derive the following SPS simultaneous update equation:

$${\widehat{\mu }}_j={\left[{\widehat{\mu }}_j+\frac{{\displaystyle \sum _{i=1}^N}{\mathbf{A}}_{ij}{\stackrel{.}{h}}_i\left({\left[\mathbf{A}\widehat{\mu }\right]}_i\right)-{\beta }_R{\displaystyle \sum _{k=1}^K}{\left[{\mathbf{\Psi }}_R\right]}_{kj}{\stackrel{.}{f}}_R\left({\left[{\mathbf{\Psi }}_R\widehat{\mu }\right]}_k\right)-{\beta }_P{\displaystyle \sum _{k=1}^K}{\left[{\mathbf{\Psi }}_P\right]}_{kj}{\stackrel{.}{f}}_P\left({\left[{\mathbf{\Psi }}_P\left(\widehat{\mu }-{\mu }_P\right)\right]}_k\right)}{{\displaystyle \sum _{i=1}^N}{\mathbf{A}}_{ij}^2{c}_i\left({\left[\mathbf{A}\widehat{\mu }\right]}_i\right)+{\beta }_R{\displaystyle \sum _{k=1}^K}{\left[{\mathbf{\Psi }}_R\right]}_{kj}^2{\omega }_{f_R}\left({\left[{\mathbf{\Psi }}_R\widehat{\mu }\right]}_k\right)+{\beta }_P{\displaystyle \sum _{k=1}^K}{\left[{\mathbf{\Psi }}_P\right]}_{kj}^2{\omega }_{f_P}\left({\left[{\mathbf{\Psi }}_P\left(\widehat{\mu }-{\mu }_P\right)\right]}_k\right)}\right]}_{+}$$ (10)

which is defined in terms of derivatives of the marginal log-likelihoods, ḣ_i, derivatives of the modified p-norm function, ḟ, and optimal curvatures, c_i, as derived in (Erdogan and Fessler, 1999a). Curvatures of the penalty function rely on the definition ω_f(t) = ḟ(t)/ t and [·]₊ denotes the application of a nonnegativity constraint. This simultaneous update function is expected to be monotonically convergent since it fits within the theoretical framework given in (Erdogan and Fessler, 1999a) and is easily parallelized for efficient computation on graphical processing units (GPUs).

2.5. Optimization Approach - PIRPLE

The PIRPLE objective in (5) is a joint optimization of both attenuation and registration parameters. Like many registration problems, one should not expect the objective function to be convex, and care must be taken with respect to local maxima. We solved the objective using an alternating maximization approach between SPS updates for the attenuation parameters with fixed registration and Broyden-Fletcher-Gordfarb-Shanno (BFGS) Quasi-Newton updates (Luenberger, 2007) for the registration parameters with fixed attenuation. A BFGS approach was implemented using a line search and a step length that satisfies the Wolfe conditions (Wolfe, 1969) to ensure sufficient increases in objective function value.

These registration updates require function and gradient evaluations for the following objective (eliminating constant factors dependent only on attenuation):

$$\mathrm{\Theta }(\lambda ;\mu )=-{\Vert {\mathbf{\Psi }}_P\left(\mu -\mathbf{W}(\lambda ){\mu }_P\right)\Vert }_{p_P}^{p_P}=-{\displaystyle \sum _{k=1}^K}f\left({\left[{\mathbf{\Psi }}_P\left(\mu -\mathbf{W}(\lambda ){\mu }_P\right)\right]}_k\right)$$ (11)

Given a differentiable registration operator W, one may write elements of the gradient as

$${\left[{\nabla }_{\lambda }\mathrm{\Theta }(\lambda ;\mu )\right]}_i=\frac{\partial }{\partial {\lambda }_i}\mathrm{\Theta }(\lambda ;\mu )={\left[{\mathbf{\Psi }}_P{\stackrel{.}{\mathbf{W}}}_i(\lambda ){\mu }_P\right]}^T\stackrel{.}{f}\left({\mathbf{\Psi }}_P\left(\mu -\mathbf{W}(\lambda ){\mu }_P\right)\right)$$ (12)

where the notation ḟ denotes a derivative operating on each element of the operand, and Ẇ_i(λ) denotes the derivative of the registration operator with respect to the i^th parameter. Together (11) and (12) are used within BFGS updates to the registration parameters.

It remains to select a specific differentiable registration operator. For the initial work detailed below, we chose a simple 3D rigid registration for which λ is a vector of three rotations and three translations defining the location and pose of the prior image. Note that the underlying PIRPLE framework is unchanged and allows for W to represent a deformable registration operator. (Stayman et al., 2012b) As the number of parameters specifying the W transform grows, a limited memory variant of BFGS (Liu and Nocedal, 1989) may be more appropriate. For the simple case of rigid registration, we implemented a registration operator (and its derivative) that uses kernel-based interpolation as in (Stayman et al., 2012a) with various differentiable kernels, including separable B-splines and tricubic kernels (Thevenaz et al., 2000).

Table 1 presents pseudocode for the alternating maximization procedure. An outer iteration loop cycles between registration updates and image updates whereby improved registration estimates are used to improve attenuation estimates, which in turn improve the registration values, and so on. Superscripts with square brackets indicate the outer loop (or outer and inner loop) indices. Note that the estimated inverse Hessian (H) from the previous outer loop iteration is reused in the subsequent iteration as an initial estimate. A modified form of (10) that includes a transformed prior with fixed λ is applied within the image update block.

Table 1.

Pseudocode for iterative solution of the PIRPLE objective

μ[0] = Initial reconstruction (e.g., FBP)

λ[0,0] = Initial guess of registration parameters

H[0,0] = σI, Initial guess for inverse Hessian

for n = 0 to max_iterations−1

% Registration Update Block

for r= 1 to R

Compute ∇λ Θ (λ[n, r −1]; μ[n,0])

H[n, r] = BFGS update based on {∇λ Θ (λ[n, r −1]), H[n, r −1]}

φ̂ = line search in λ[n, r −1] + φH[n, r]∇λ Θ(λ[n, r −1])

λ[n, r] = λ[n, r −1] + φ̂H[n, r]∇λ Θ(λ[n, r−1])

end

λ[n+1,0 ] = λ[ n, R]; H[n+1,0] = H[n, R]

% Image Update Block

for j = 1 to number_of_voxels

$${\mu }_j^{[n+1]}={\left[{\mu }_j^{[n]}+\frac{\left(\begin{array}{l}\sum _{i=1}^N{\mathbf{A}}_{ij}{\stackrel{.}{h}}_i\left({\left[\mathbf{A}{\mu }^{[n]}\right]}_i\right)-{\beta }_R\sum _{k=1}^K{\left[{\mathbf{\Psi }}_R\right]}_{kj}{\stackrel{.}{f}}_R\left({\left[{\mathbf{\Psi }}_R{\mu }^{[n]}\right]}_k\right)\\ -{\beta }_P\sum _{k=1}^K{\left[{\mathbf{\Psi }}_P\right]}_{kj}{\stackrel{.}{f}}_P\left({\left[{\mathbf{\Psi }}_P\left({\mu }^{[n]}-\mathbf{W}\left({\lambda }^{[n,R]}\right){\mu }_P\right)\right]}_k\right)\end{array}\right)}{\left(\begin{array}{l}\sum _{i=1}^N{\mathbf{A}}_{ij}^2{c}_i\left({\left[\mathbf{A}{\mu }^{[n]}\right]}_i\right)+{\beta }_R\sum _{k=1}^K{\left[{\mathbf{\Psi }}_R\right]}_{kj}^2{\omega }_{f_R}\left({\left[{\mathbf{\Psi }}_R{\mu }^{[n]}\right]}_k\right)\\ -{\beta }_P\sum _{k=1}^K{\left[{\mathbf{\Psi }}_P\right]}_{kj}^2{\omega }_{f_P}\left({\left[{\mathbf{\Psi }}_P\left({\mu }^{[n]}-\mathbf{W}\left({\lambda }^{[n,R]}\right){\mu }_P\right)\right]}_k\right)\end{array}\right)}\right]}_{+}$$

end

end

2.6. Simulation and Testbench Experiments

To investigate the performance of the proposed algorithms, we simulated a lung nodule surveillance scenario in which a patient who has received a thoracic CT scan (e.g., for lung cancer screening or other purposes) has presented with a suspicious lesion. A common surveillance strategy is to conduct a follow-up scan at a later time to determine if there is abnormal growth (e.g., measurement of nodule volume and doubling time). The follow-up CT shares a great deal of patient-specific anatomical information with the initial screening scan. Thus, we propose to use the initial CT volume as the previously acquired prior image, μ_P, in PICCS (6,7), PIPLE (4), and PIRPLE (5) reconstructions. Figure 2 illustrates the digital phantom used for these simulation experiments.

Figure 2.

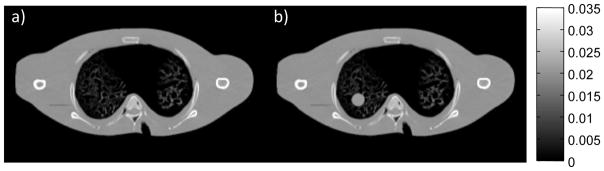
Illustration of digital phantoms used in the lung nodule surveillance scenario. Both phantoms were derived from real CT images of a custom anthropomorphic phantom with simulated lung materials. (a) The prior image anatomy is free of nodules whereas, (b) the current anatomy contains a spherical nodule in the right lung.

For all simulations, we used a system geometry with a 1200 mm source-to-detector distance and 600 mm source-to-axis distance. The detector comprised 760 pixels at 1.552 mm pitch. A separable footprints projector (Long et al., 2010) was used to model the projection of 2 mm isotropic voxels on the detector. We assumed a monoenergetic x-ray model (60 keV) and Poisson noise in the measurements. The detector gain vector, g, in (1) was selected as uniform with a value of I₀, equal to the expected number of photons in the unattenuated beam. We considered both “fully sampled” data with 360 projections acquired over 360° as well as sparse short-scan data over 206°. While we focus predominantly on a relatively high sparsity using only 20 projections, we also consider a second case of moderate sparsity using 100 angles over this short scan range. (Unless otherwise indicated simulations used the high sparsity scenario.)

Two different kinds of simulation experiments using prior images were conducted. The first set of studies, which focused on parameter selection and performance of PIPLE, used the perfectly registered prior image in Figure 2a. The second set of experiments focused on PIRPLE and the importance of registration considered an unregistered prior image - in this case, a 2D rigid transformation of the phantom in Figure 2a.

In addition to the simulations, physical experiments were also conducted on a cone-beam CT (CBCT) testbench to compare reconstruction methods. These studies reproduced a similar lung nodule surveillance scenario with an anthropomorphic chest phantom. The system geometry used a 1500 mm source-to-detector distance and 1220 mm source-to-axis distance, a Varian PaxScan 4343CB flat panel detector with 768² binned pixels at 0.556 pitch. A 100 kVp x-ray technique was used. For prior images and reference scans, 450 mAs acquisitions using 360 projections over 360° were performed. For follow-up scans, low exposure sparse acquisitions were conducted using 49 angles over 196° using 4.9 mAs total. The phantom for these experiments is shown in Figure 11a–c.

Figure 11.

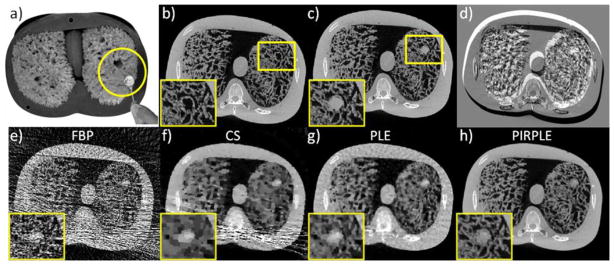
CBCT phantom experiments using a) an anthropomorphic chest phantom with natural sponges simulating lung tissue and a 0.5 inch removal acrylic sphere to simulate a lung nodule. Fully sampled CBCT acquisitions (450 mAs) in two scenarios (no nodule vs. nodule) we collected to reconstruct a) a prior image (no nodule); and b) a fully sampled reference image (with nodule). Rigid motion of the phantom between the two data acquisitions was induced and is apparent in the difference image in d). Sparse current data acquisitions (4.9 mAs) in the second scenario were used to produce reconstructions e–h) using FBP, CS, PLE, and PIRPLE.

2.7. Algorithms and Implementation Specifics

We compared the proposed PIPLE and PIRPLE reconstruction approaches with a number of other methods including filtered-backprojection (FBP), Huber penalized-likelihood estimation (PLE), PICCS as formulated in (6), and compressed sensing (CS) reconstruction (without using a prior image). While FBP uses a voxel-driven interpolating backprojector, the other approaches are iterative and employed matched separable footprint projectors and backprojectors. Each algorithm was written in Matlab with external calls for projection operations implemented in optimized CUDA/C++ routines executed on GPUs (nVidia GTX-580).

PLE was implemented using separable paraboloidal surrogates (Erdogan and Fessler, 1999a) and a Huber penalty (9). We applied 500 (single subset) iterations to achieve a nearly converged solution. For PICCS, we adopted an alternating optimization approach where the PICCS objective was optimized via coordinate descent (with a line search that checked for sufficient decrease), and the PICCS constraint was applied via simultaneous arithmetic reconstruction technique (SART) (Andersen and Kak, 1984) updates. We applied 3000 such iterations to ensure an accurate approximation of the converged solution. The CS reconstruction was produced using the same technique as PICCS, except the parameter, α, in (6) was set to zero, thereby removing the prior image term from the PICCS objective and reducing the estimator to a standard CS estimation form. PIPLE and PIRPLE were implemented as discussed in the previous section, and unless otherwise noted, 500 iterations were applied in estimating the solution. Moreover, the number of BFGS iterations in the registration block (R in Table 1) was set to five for simulation studies and two for the testbench studies. For all PIRPLE runs, the initial registration estimate was zero translation and zero rotation.

2.8. Parameter Selection

All of the iterative approaches possess various parameters that must be specified prior to reconstruction. This includes the regularization parameters, β_R, β_P, and δ, in PLE, PIPLE, and PIRPLE, and the control parameter, α, in PICCS. Proper selection of these parameters is important to achieve optimal performance of each approach and to make fair comparisons between the various approaches.

For the investigations in this paper, we tried to maximize performance of each approach by performing an explicit parameter sweep. For example, for PLE we performed a two-dimensional sweep over β_R and δ to find the parameter set that produced the minimum root mean-squared error (RMSE) between the reconstruction and the true anatomy. For PICCS, a sweep over α was performed, with both Ψ_P and Ψ_P chosen to be the traditional spatial gradient operator. For PIPLE and PIRPLE, we conducted a sweep over β_R, β_P, and δ. In the current investigations, the parameter p associated with the p-norm in both penalties in (8) was fixed at p = 1. Moreover, we observed a slight increase in performance in PIPLE and PIRPLE using Ψ_P = I, instead of the spatial gradient operator as used for Ψ_R.

Not only did these parameter sweeps allow fair performance comparisons, they also provided a great deal of insight into how one might select such parameters in real application scenarios, where performance can be sensitive to parameter selection, but the computation time associated with freely varying such parameters could be prohibitive. This is especially important for the approaches where there are three main parameters (β_R, β_P, and δ) that control reconstruction performance. For each parameter sweep, we reconstructed noisy sparse short-scan projection data (20 angles over 206° and I₀ = 10³) of the digital phantom with nodule, using a prior image penalty incorporating the nodule-free phantom volume data.

3. Results

Investigations of PIPLE and PIRPLE are presented in following four subsections and include the results on the sensitivity of PIPLE to parameter selection, the performance of PIPLE relative to other approaches using a perfectly registered prior image, a simulation study of the importance of prior image registration and the performance of the joint registration-reconstruction approach used by PIRPLE, and finally an application of PIRPLE to experimental testbench data.

3.1. Sensitivity to Parameter Selection

A summary of the RMSE (computed over the entire volume of the phantom) for different parameter choices in PIPLE is shown in Figure 3. A number of important trends are evident in analysis of RMSE(β_P, β_R, δ). First, for sufficiently small δ, both the shape of the RMSE surface and the location and value of its minimum do not vary greatly. For large δ (e.g., δ values approaching the tissue-air or tissue-bone attenuation differences), the penalties become more quadratic, with additional smoothing and averaging of prior information (as opposed to sparse inclusion), and there is a detrimental effect on the RMSE of the reconstruction. This suggests keeping δ values small relative to the expected attenuation differences in the reconstruction and optimizing over β_R and β_P. In the β_R-β_P plane, one sees a distinct plateau (the flat gray region on the right of each plot) for high β_P corresponding to an excessive prior image penalty, where too much information is incorporated from the prior image and the reconstruction is nearly identical to the prior image. Similarly, when β_R is too large (white region at the top) reconstructions have high RMSE due to the excessive blur induced by the roughness penalty. When both β_R and β_P are low (lower left white region) reconstructions are noisy or exhibit significant streaks due to undersampling. Interestingly, for low β_R the RMSE surface appears to follow a nearly separable form. That is, one could find the optimal parameters with individual one-dimensional sweeps in β_P and then β_R, rather than an exhaustive two-dimensional parameter sweep. For example, starting with a small β_R, first compute the optimal β_P for inclusion of prior image information (black arrow in Figure 3) and then increase β_R to balance noise and blur (white arrow Figure 3).

Figure 3.

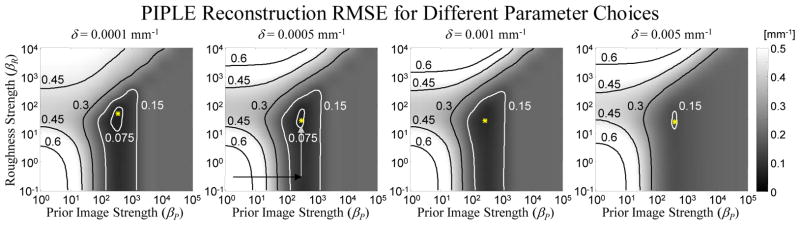
A summary of the β_R, β_P, and δ parameter sweep for the simulated lung nodule surveillance problem for I₀=10³. RMSE for PIPLE reconstruction as compared with the true anatomy is computed for each parameter set and is represented in grayscale with specific contours showing equal RMSE solutions. The minimum RMSE in each image is labeled with an asterisk. Note that choice of δ has little influence on the optimal β_R and β_P. Moreover, below a certain value (δ = 0.001), there is little change in the shape of the RMSE surface and minimum RMSE value. The second plot shows two arrows illustrating the proposed 1D trajectory (from low β_R and β_P to an optimal β_P, followed by an optimization of β_R.) for selecting optimal regularization parameters avoiding the need for an exhaustive 2D optimization.

The same parameter sweep was conducted over a range of incident fluence (I₀) as summarized in Figures 4 and 5. Because we have observed that sufficiently small δ yielded similar RMSE, Figure 4 concentrates on β_R and β_P for a fixed δ = 10⁻⁴ mm⁻¹. The RMSE surface has similar overall structure for various levels of I₀, including the gray plateau for high β_P and white peaks (high error) for high β_R and for the under-regularized lower left quadrant (low β_P and β_R). Interestingly, the valley of low RMSE is shallower for the high noise scenario and deeper for the high signal scenario, and the position of the minimum RMSE does vary in β_R and β_P. Not surprisingly, the minimum RMSE rises for the higher noise cases and is lower for the high signal regime. To further justify the choice of δ = 10⁻⁴, Figure 5 illustrates the minimum RMSE (i.e., at the optimal choice of β_R and β_P) as a function of δ and I₀. Again, while there is a distinct falloff in RMSE below δ ~10⁻³ mm⁻¹, the RMSE quickly plateaus at all levels of I₀. Figure 5 also shows the optimal β_R and β_P (i.e., values minimizing RMSE) as a function of I₀. A 2^nd-order polynomial (in log-log space) approximately captures the relationship between incident fluence and optimal settings for both of the regularization parameters.

Figure 4.

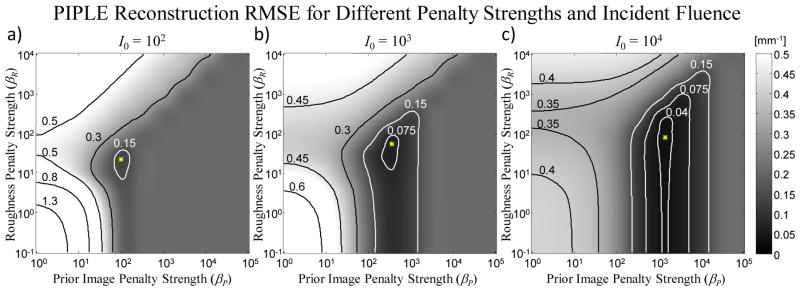
RMSE in reconstructions of the lung nodule image [Figure 2(b)] from sparse projections over a range of prior image penalty strengths (β_P) and roughness penalty strengths (β_R) for three levels of incident fluence: (a) 10², (b) 10³, and (c) 10⁴ photons / pixel. In this case, δ is fixed at 10⁻⁴ mm⁻¹. The optimum (minimum RMSE) is marked with an asterisk.

Figure 5.

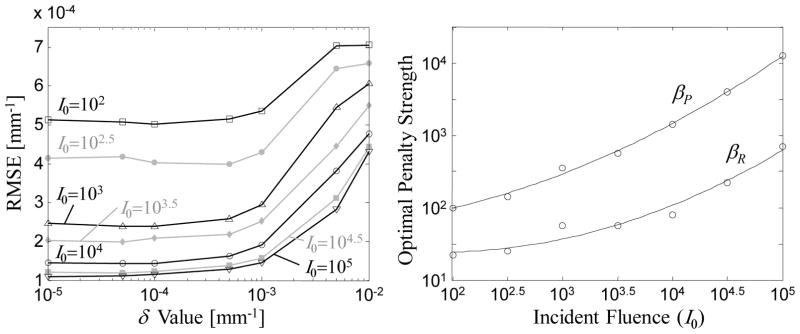
(a) Illustration of RMSE with optimal choices of β_R and β_P for different values of δ, over a range of exposure levels (I₀). Note that RMSE quickly plateaus near δ ~10⁻³ mm⁻¹. (b) Optimal values of β_P and β_R evaluated as a function of incident fluence and fit with a 2^nd-order polynomial.

Together, these studies suggest a favorable situation for predictability and selection of PIPLE parameters. Rather than necessitating a computationally intense survey of a broad three-dimensional parameter space, a fairly straightforward search can be accomplished by first computing the optimal β_P (with a fixed, small value of δ and β_R) and then computing the optimal β_R (at the optimal value of β_P). Alternatively, Figure 5(b) suggests a low-order parameterization by which the optimal β_P and β_R can be estimated for a given exposure level. Of course, the particular optima and the low-order parameterization in Figure 5(b) are specific to the object and system model detailed above, and the extent to which the nearly separable behavior in Figures 4 and 5 holds in general is the subject of future investigation.

3.2. PIPLE Reconstructions – Simulated Data

A comparison of methods for reconstruction of noisy, sparse, short-scan data is shown in Figure 6. For reference, FBP reconstruction of fully sampled data is also presented. Each column represents a different level of incident fluence, with I₀ increasing from left to right by powers of 10. Each row shows results for a given reconstruction method: FBP, CS, PICCS, PLE, and PIPLE. Particularly, at low I₀, we noticed a slight difference in optimal β_P and β_R values between a global RMSE optimization (i.e., minimization of RMSE computed over the entire image) and a local RMSE optimization (minimization in a small region immediately about the nodule), PIPLE results are shown for both optimization scenarios for comparison.

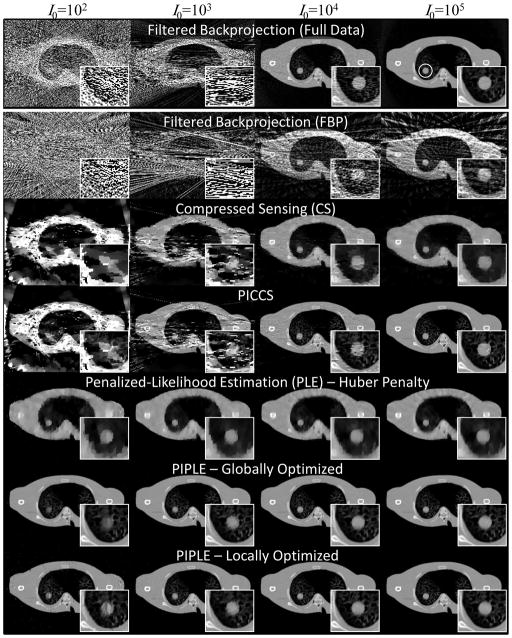
Figure 6.

Qualitative comparison of various reconstruction methods at different levels of incident x-ray fluence (I₀, with units photons / pixel). All reconstructions used a highly sparse data acquisition of 20 projections over 200° except for the filtered-backprojection case in the top row, which used 360 projections over 360°. Zoomed images of the nodule are shown for each case. The region-of-interest used for local RMSE computation in proximity to the nodule is shown as a white circle in the upper right image.

Qualitative assessment of the results in Figure 6 reveals several trends. Fully sampled FBP suffers from dramatically increased noise and streaking at low I₀. This is also true for the sparse data case; however, FBP additionally exhibits significant view sampling artifacts even at the highest levels of I₀. CS, on the other hand, does an excellent job of eliminating view sampling artifacts in the high signal regime, although spatial resolution is significantly less than in the fully sampled scenario. Moreover, as noise increases, there are substantial artifacts throughout the CS reconstructions. PICCS is able to incorporate fine detail structures from the prior image to preserve high spatial resolution; however, it too finds difficulty at low levels of incident fluence. These methods (FBP, CS, and PICCS) lack an explicit noise model as part of the reconstruction algorithm and appear to have difficulty at increasing levels of noise in the projection data. PLE, on the other hand, incorporates a model of measurement noise and does not exhibit the same kind of streaking or artifacts at low I₀. A reduction in spatial resolution is observed at lower exposure levels, and even at high levels PLE is unable to attain the fine structure details found in PICCS. Finally, PIPLE, which incorporates both a noise model and a prior image is able to mitigate both the noise at low fluence and incorporate high resolution details throughout the range of exposure levels. At the lowest photon levels, there is visible degradation in the image quality about the nodule, but PIPLE generally appears to perform best in the low fluence, sparse data regime. Optimization based on local RMSE appears to improve the imaging performance in proximity to the nodule at very low exposure levels at the cost of increased artifacts and noise elsewhere in the image.

Figure 7 presents a quantitative assessment of the reconstructions illustrated in Figure 6 in terms of both the global and local RMSE. The results support similar conclusions as in the qualitative assessment above. Specifically, PIPLE achieves the highest performance, and although the performance for all methods degrades at lower levels of I₀, those incorporating a statistical noise model tend to exhibit better performance in the low fluence regime; furthermore, the prior image methods trend toward equivalent (high) performance at high signal levels. In addition, it is interesting to note that at high signal levels, PLE and CS appear to perform comparably, using edge preservation to overcome view sampling effects. For low fluence levels, the local RMSE is similar for PIPLE and PLE, suggesting that the additional information provided by the prior does little to improve image quality for the nodule at such severely reduced photon levels. The apparent increase in performance (i.e., decrease in local RMSE) for PICCS and CS at low exposure levels in Figure 7(b) arises from sensitivity to the particular noise realization and the associated artifacts around the nodule. For example, the local RMSE varies greatly when a particular noise realization produces or does not produce a streak going through the local region-of-interest.

Figure 7.

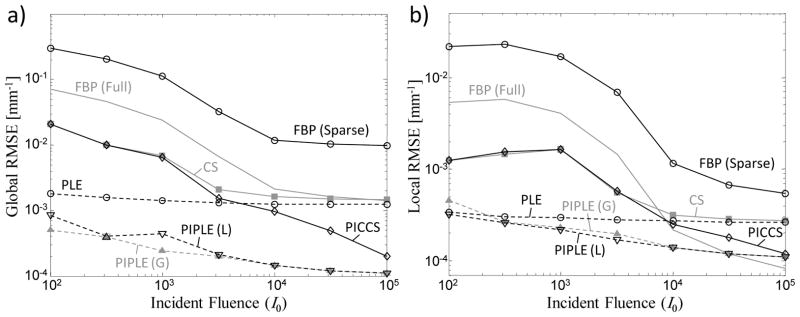
(a) Global and (b) local RMSE computed for various reconstruction methods for a perfectly registered prior image. Methods incorporating a statistical model are shown as dashed lines, whereas nonstatistical methods are plotted with solid lines. PIPLE(G) and PIPLE(L) denote parameter selection based on global and local RMSE optimization, respectively.

In (Yan et al., 2012), it was suggested that a moderate number of projections is preferable for some algorithms. As such, we conducted a second brief simulation study using moderate sparsity with 100 projections over 206°. Qualitative results of this experiment for I₀=10³ is shown in Figure 8. With additional projections, we see that higher spatial resolution images can be produced by CS and PLE, but both CS and PICCS suffer from noise streaks which arise from their strict equality constraints and fitting to noise in the projections. In contrast, the noise model in PLE and PIPLE allows for elimination of these streaks, and PIPLE is able to produce a higher resolution result with its incorporation of prior information. As in the high sparsity case, in moving to higher fluence (reducing projection noise) shows similar performance of CS and PLE and similar performance of PICCS and PIPLE.

Figure 8.

Qualitative comparison of reconstruction methods in the same lung nodule surveillance but in the case of moderate sparsity (100 projections over 206°) with I₀ = 10³.

3.3. PIRPLE Reconstructions - Simulated Data

The previous experiments illustrate the ability of PIPLE to handle data that is simultaneously noisy and undersampled in the scenario of a perfectly registered prior image. Such images are not always available, of course, so it is important to consider the case of an unregistered prior image. The following study evaluates the performance of various algorithms with a mild misregistration of the prior image – viz., a rigid translation of (−3.1, 2.1) voxels in the (x,y) domain and a rotation of 2.865°. Three reconstruction methods (PICCS, PIPLE, and PIRPLE) were considered in the presence of such misregistration, and qualitative results over a range of I₀ are shown in Figure 9.

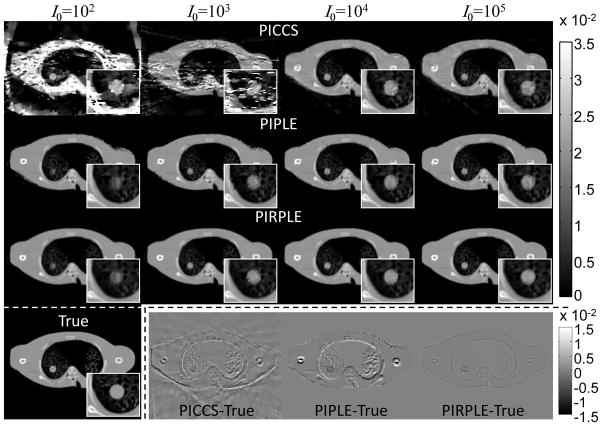
Figure 9.

PICCS, PIPLE, and PIRPLE reconstructions using a misregistered prior image. For reference, both the true image and difference images for the I₀=10⁵ case are shown in the bottom row.

The overall trends as a function of I₀ are similar to the perfect registration scenario in Figure 6, with increased noise and streaking for PICCS at low exposure levels, and we observe additional artifacts for PICCS and PIPLE even at the highest levels. Specifically, the misregistered prior image yields false structures both in the nodule and in the background anatomy, including an apparent double-image at the edges of the phantom and in the humerus. In contrast, PIRPLE, which integrates registration as part of the reconstruction, does not exhibit such a double-image or false structures, although a small amount of blur resulting from interpolation in registration of the prior is apparent when compared to the true image. These features are particularly apparent in the difference images of Figure 9. Degradation at the lowest exposure levels is similar for PIRPLE as for PIPLE in the perfectly registered scenario (Figures 6–7). In all cases, PIRPLE provided registration accuracy to within 1 voxel (giving translation and rotation error less than 0.25 pixels and 0.022°.

A quantitative comparison of these results is shown in Figure 10. For comparison, the case of PIPLE with perfect registration is also shown. The importance of registration is reflected in these RMSE plots, with PIRPLE achieving the lowest RMSE (both locally and globally) among all methods using a misregistered prior. Moreover, the performance approaches that of PIPLE with a perfectly registered prior. (The separation in global RMSE between PIRPLE and perfectly-registered PIPLE is somewhat exaggerated on a logarithmic plot. This small residual arises from slight blurring due to interpolation in the rigid transformation used in PIRPLE.) The analysis also demonstrates that use of a misregistered prior image can result in poorer performance than if no prior image were used at all: compare, for example, unregistered PIPLE and PICCS versus PLE. As in Figure 7, trends in local RMSE at the lowest fluence levels should be interpreted with some caution, since the particular noise realization and streaking can dominate the RMSE. At high fluence levels, it is only with proper registration of the prior image (i.e., PIRPLE) that the local RMSE is improved through incorporation of the prior image. The other methods – i.e., PLE (which makes no use of a no prior) and PICCS and PIPLE (each without registration) – perform comparably in local RMSE at high exposure levels.

Figure 10.

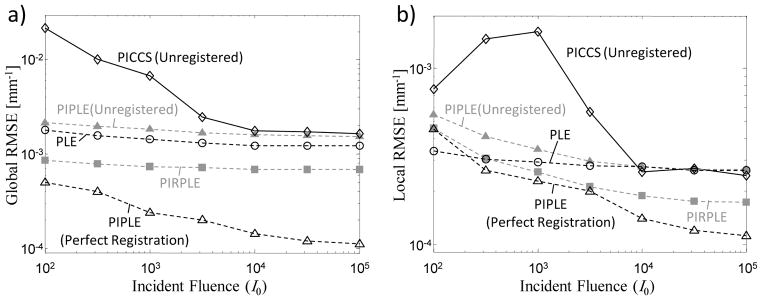
Comparison of (a) global and (b) local RMSE for various reconstruction methods when an unregistered prior image is available.

3.4. PIRPLE Reconstructions- CBCT Testbench Data

In addition to the previous simulation studies, CBCT data were also collected on a CBCT testbench outfitted with a flat-panel detector. This investigation used an anthropomorphic chest phantom (Figure 11a) and was designed to reproduce the same lung nodule surveillance scenario as the simulation studies - i.e., sparse, low exposure follow-up data with a nodule and a high-quality prior image without a nodule. Specifically, a prior image was formed by collection CBCT using a fully sampled acquisition protocol with 360 projections over 360° at 450mAs (1.25 mAs/frame) and 100 kVp and reconstructing using PLE onto a 2 mm voxel grid. Sparse short-scan “current” data were acquired with 49 angles over 196° at 4.9 mAs (0.1 mAs/frame) at 100 kVp. Rigid 2D motion was induced between scans and was estimated to be a (6.4,23.5) mm translation and a 1.7° rotation.

Figure 11e–f shows reconstructions of the sparse data with FBP, CS, PL, and PIRPLE. Parameter selection for all approaches was optimized using RMSE relative to the fully sampled follow-up reference. In this case, the optimization yielded the following reconstruction parameters for PLE: β_R=10³, δ=10⁻³ and PIRPLE: β_R=10³, β_P=10³, δ=10⁻⁴. Qualitatively, the relative performance between these reconstruction methods was similar to simulations studies with a highly streaked FBP image, a CS image with modest spatial resolution and some residual streaks, an essentially streak-free PLE reconstruction with similar (or perhaps slightly better) spatial resolution than CS, and the PIRPLE reconstruction that has no streaks and that reproduces the highest resolution features. These qualitative results are reflected in quantitative RMSE values as compared to the reference image with 0.0192 mm⁻¹ (FBP), 0.0062 mm⁻¹ (CS), 0.0022 mm⁻¹ (PLE), and 0.0011 mm⁻¹ (PIRPLE).

In addition to the reconstruction comparisons above, convergence plots were generated for the PIRPLE as applied to the testbench data. Specifically, two plots were computed. For the first plot that illustrates convergence of the algorithm, 1000 iterations of PIRPLE were applied to estimate Φ^∞, the value of the objective function at the solution. We plot then the value of the objective at the n^th iteration, Φ^[n], subtracted from Φ^∞ in Figure 12A. Moreover, to illustrate the relative actions of each update in the alternating optimization, the objective function differences immediately after an image update are plotted at n=0.5, 1.5, 2.5, etc., whereas, the differences immediately after a registration update are plotted at n=1, 2, 3, etc. A zoomed plot of the first few iterations is also included for clarity. A second plot, Figure 12B, was also computed to illustrate convergence toward the “true” solution that shows the RMSE (relative to a fully sampled reference image) as a function of iterations. In this case, only image updates are shown since registration estimates don’t influence the image-based RMSE metric.

Figure 12.

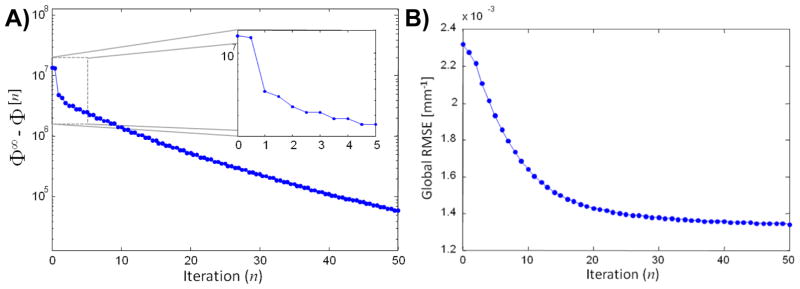
Illustration of PIRPLE convergence properties on the CBCT phantom data example. A) Objective function value as a function of iteration. Each full iteration is comprised of an image update followed by a registration update. The differences between the objective function value at each iteration, Φ^[n], and its value at the solution, Φ^∞. Values are shown immediately after an image update at n=0.5, 1.5, 2.5, etc. and immediately after a registration updates at n=1,2,3, etc. B) Global RMSE (relative to a fully sampled PLE reconstruction) as a function of iteration (image updates only).

The objective function convergence plot suggests that the registration updates are particularly important in the early iterations of the algorithm. Though there continues to be small changes in the registration values at later iterations, objective function value improvements in later iterations are principally driven by the image update. The convergence is monotonic and yields a registration estimate that is within one-half voxel translation and 0.12° rotation when compared to a registration between fully sampled prior and current data reconstructions. The objective function plot suggests steady improvements toward a particular local solution. Similar monotonic behavior is seen in the RMSE convergence plot further suggesting good convergence properties. However, in general, poor local minima may exist (in particular due to the registration aspects of the objective function). While this particular example is particularly well-behaved in terms of convergence, more periodic anatomical structures and lower contrast situations may be more challenging.

4. Discussion

This paper introduced a novel framework for integration of prior images into model-based reconstruction of sparse and noisy projection data. The methodology leverages a statistical model of image noise and integrates prior images using a sparsity enforcing penalty that combines prior information while allowing for differences due to anatomical change. Moreover, to differentiate between change arising from physical change in image content versus change associated with anatomical motion, we introduced a variant of the penalized-likelihood approach, PIRPLE, to perform a joint registration of the prior image and a reconstruction of the current data. The model-based framework does not require an explicit linearization of the forward model, which allows for future variations that accommodate additional physical effects like beam-hardening without pre-corrections to projection data.

The importance of registration in prior-image-based reconstruction was also investigated. While such approaches appear to provide improved image quality even with misregistered priors, there is potential for the introduction of false structures and details when a prior image is incorrectly registered. The joint approach undertaken in PIRPLE allows for iterative refinement of both the registration and the reconstruction to eliminate false structures. While the investigation in this paper was limited to the simple case of rigid registration, deformable registration methodologies have been explored and successfully applied to match the current and prior anatomy (Ren et al., 2012; Wang and Gu, 2013). The PIRPLE framework is general and allows for this kind of nonrigid registration to be accommodated and is the subject of ongoing work (Dang et al., 2013). While the potential issue of false structures can be mitigated with improved registration, the question of determining what image features are attributable to the projection data (and which are derived solely from the prior image) is an important consideration, also the subject of ongoing studies (Stayman et al., 2012c).

The studies detailed above also elucidate the manner in which optimal algorithm parameters (e.g., the regularization strength β_P and β_R) can be reliably selected in a simple manner, rather than an exhaustive, computationally intense exploration of the full parameter space. Specifically, we found that the RMSE presents a relatively well-behaved optimization character (i.e., presents a separable form free of local minima) and that a pair of one-dimensional trajectories through the parameter space can suffice in determining the optimal (or near optimal) parameters. Moreover, once parameters are found for a particular object, there is a predictable, low-order scaling that may be applied for different levels of incident fluence. The sensitivity of such behavior to the degree of angular sampling and other forms of sparse data acquisition were not investigated here, and are the subject of future work.

While the registration aspect of PIRPLE generally leads to a nonconvex objective function, we have found that the proposed alternating optimization approach can converge to the correct solution given a sufficiently close initial guess. (All the scenarios investigated in this paper used an initial guess within a few voxels of translation and rotation angles of less than five degrees.) We expect that initial conditions far from the solution will confound the alternating optimization and it will be subject to local minima. Thus, a relatively good initial registration may be critical to the performance of PIRPLE. Future studies will need to be conducted to determine how close the initial guess needs to be to avoid local optima.

This work presented in this paper demonstrates the potential improvement in CT image quality to be gained by integrating statistical modeling and prior information within the reconstruction process. A lung nodule surveillance scenario simulating repeat imaging in the presence of a growing lesion showed that the proposed methodology can maintain image quality even at very low exposure levels. We expect that PIPLE and PIRPLE can be applied to other situations, such as interventional imaging where prior CT studies are typically available and dynamic imaging scenarios whereby a “prior image” may be derived by other means (e.g., a time-averaged volume as in (Chen et al., 2009; Chen et al., 2012)).