Bayesian Evaluation of inequality-constrained Hypotheses in SEM Models using Mplus

Abstract

Researchers in the behavioural and social sciences often have expectations that can be expressed in the form of inequality constraints among the parameters of a structural equation model resulting in an informative hypothesis. The question they would like an answer to is “Is the Hypothesis Correct” or “Is the hypothesis incorrect?”. We demonstrate a Bayesian approach to compare an inequality-constrained hypothesis with its complement in an SEM framework. The method is introduced and its utility is illustrated by means of an example. Furthermore, the influence of the specification of the prior distribution is examined. Finally, it is shown how the approach proposed can be implemented using Mplus.

Many researchers in the behavioural and social sciences have expectations that can be expressed in the form of inequality constraints among the parameters of a Structural Equation Model (SEM). Based on previous research, literature reviews, and the current academic debate, they formulate order restrictions among, for example, regression coefficients. For example, in health psychology research, an important distinction is the distinctiveness of symptoms of complicated grief (CG) and uncomplicated grief (UG)(Boelen & van den Bout, 2008). As we will discuss in more details later, CG symptoms should be expected to be more strongly associated with symptoms of depression and anxiety than responses of UG. The question they would like an answer to is “Is the Hypothesis Correct” or “Is the hypothesis incorrect?”. The evaluation of inequality-constrained hypotheses has been studied within the SEM framework (Gonzalez & Griffin, 2001; Stoel, Galindo-Garre, Dolan, & Van den Wittenboer, 2006; Van de Schoot, Hoijtink, & Deković, 2010; Van de Schoot & Strohmeier, 2011) as well as outside the SEM framework (Barlow, Bartholomew, Bremner, & Brunk, 1972; Hoijtink, Klugkist, & Boelen, 2008; Klugkist, Laudy, & Hoijtink, 2005; Robertson, Wright, & Dykstra, 1988; Silvapulle & Sen, 2004; Van de Schoot, Hoijtink, et al., 2011; Van de Schoot, Mulder, et al., 2011). The procedures described in these studies tested an inequality-constrained hypothesis against the classical null hypothesis (i.e., “Nothing is going on”), against an unconstrained hypothesis (i.e., “Something is going on, but not the null hypothesis”), or against other inequality-constrained hypotheses (i.e., CG symptoms are expected to be more strongly associated with symptoms of depression than responses of UG, but the opposite holds for anxiety). For an overview of literature see Van de Schoot, Romeijn, and Hoijtink (2011). A comparison of an inequality-constrained hypothesis with its complement received hardly any attention in literature, but only this latter comparison would provide an answer to the question of interest: “Is the Hypothesis Correct” or “Is the hypothesis incorrect?”. One exception is the study of van Rossum, Van de Schoot, and Hoijtink (2011) (see also Hoijtink, 2012), in the context of analysis of variance. In the current paper we propose a method for the evaluation of an inequality constrained-hypothesis with respect to its complement using Bayesian statistics available in the software Mplus (Muthén & Muthén, 2007).

In what follows we first introduce Bayesian SEM, followed by the formulation of inequality-constrained hypotheses in Bayesian SEM models, and the use of Bayes factors to evaluate such hypotheses. Then we discuss specification of the prior distribution for the evaluation of inequality-constrained hypotheses and finally we apply the proposed methodology to a real-life data set from clinical and health psychology.

Bayesian SEM Models

For an introduction to Bayesian estimation see Lynch (2007), for more technical details see Gelman, Carlin, Stern, and Rubin (2004), for Bayesian model selection see Hoijtink et al. (2008) and Hoijtink (2012), for Bayesian structural equation modelling see Lee (2004). There is a variety of software packages available for Bayesian analyses: R packages (e.g., mcmc), WinBUGS, AMOS, OpenBUGS, MlwiN, Mplus v6.x. For the current paper we use Mplus (1998–2010) because of its popularity among applied researchers. Bayesian estimation first became available in Mplus in version 6, which was relesed in the summer of 2010. For a technical implementation of Bayesian statistics in Mplus, see Asparouhov and Muthen (2010b), Asparouhov and Muthen (2010a) and the website of Mplus: www.statmodel.com.

Let y_i = (y₁, …, y_p) be a p × 1 vector of observed variables for person i, and let ω_i = (ω₁, …, ω_q) be a q × 1 vector of latent variables for person i. The measurement model is then given by

$${\mathit{y}}_i=\mathbf{\Lambda }{\mathit{\omega }}_i+{\mathit{\epsilon }}_i,$$ (1)

where Λ is a p × q matrix of factor loadings, and ε is a p × 1 vector of measurement errors with ε ~ N(0, Ψ_ε), and Ψ_ε being a diagonal matrix.

For the structural model, let ω_i = {η_i, ξ_i} with η = (η₁, …, η_q1) being a q₁ × 1 vector of outcomes variables and ξ = (ξ₁, …, ξ_q2 ) being a q₂(= p - q₁) × 1 vector of explanatory latent variables, then

$${\mathit{\eta }}_i=\mathbf{\Pi }{\mathit{\eta }}_i+\mathbf{\Gamma }{\mathit{\xi }}_i+{\mathit{\delta }}_i,$$ (2)

where Π and Γ are matrices of unknown regression coefficients. Furthermore, δ ~ N(0, Ψ_δ) and ξ ~ N(0, Φ). It is assumed that ε and δ are independent. Equations (1) and (2) describe the general SEM framework.

Let θ = {θ¹, θ²} which consist of unknown parameters with θ¹ = vec{Π, Γ} and θ² = {Λ, Ψ_ε, Ψ_δ, Φ}, and let Y be the observed data set with sample size n. In a Bayesian SEM model θ is considered to be random. The behavior of θ given Y in such a Bayesian model can be described by g(θ|Y) ∝ h(θ)× f(Y |θ), where f(Y |θ) is the likelihood function, h(θ) is the prior distribution, and g(θ|Y ) is the posterior distribution.

Using the posterior distribution the mean, mode or median of the desired parameters can be estimated. Bayesian estimation uses Markov Chain Monte Carlo (MCMC) algorithms to obtain a sample from g(θ|Y ). The idea behind MCMC is that the conditional distribution of one set of parameters given other sets can be used to make random draws of parameter values, ultimately resulting in an approximation of the joint distribution of all the parameters. The default MCMC sequence used in Mplus is a Gibbs sampler where t iterations (t = 1, …, T ) are used to obtain new values for θ in each step drawing from a conditional posterior parameter distribution. The Gibbs sampler has three steps:

• Step 1: Sample η_i and ξ_i given Y, Π, Γ, Λ, Φ, Ψ_ε, Ψ_δ

• Step 2: Sample Π, Γ, Λ, Φ given Y, η_i, ξ_i, Ψ_ε, Ψ_δ

• Step 3: Sample Ψ_ε and Ψ_δ given Y, η_i, ξ_i, Π, Γ, Λ, Φ

These three conditional distributions have been derived in Lee (2004) and for the implementation in Mplus see Asparouhov and Muthen (2010a). In Mplus it is easy to sample from these conditional distributions. Typically, several MCMC chains are used (default in Mplus is two chains) and some part of each chain is discarded as a burn-in phase (in Mplus by default the first half). Mplus automatically monitors convergence using the Gelman-Rubin convergence criterion which considers within and between chain variability of the parameter estimates (Gelman et al., 2004; Asparouhov & Muthen, 2010b). In Mplus it is possible to first estimate the SEM model using maximum likelihood estimation and use these parameter estimates as starting values in the Bayesian analysis.

The default prior specification in Mplus is

$$h({\mathit{\theta }}^1)=\prod _{k=1}^{K}h({\theta }_k^1),$$ (3)

where $h({\theta }_k^1)=\mathcal{N}({\theta }_0,{\tau }_0^2)$ with θ₀ = 0 and ${\tau }_0^2=\infty$. In Mplus this prior distribution is used for means and intercepts of observed and latent continuous variables, thresholds of observed categorical dependent variables, factor loadings, and regression coefficients. For the prior distribution of θ² Mplus uses non-informative inverse Gamma distributions for variances and residual variances of observed and latent parameters, an inverse Wishart distribution if more than one latent variable is estimated and a Dirichlet distribution for categorical latent variable parameters. Below it will be shown that the default prior distribution used by Mplus is suited for the evaluation of inequality-constrained hypotheses by means of the Bayes factor (which will be elaborated in the next section). This is because the default prior distribution leads to an adequacy quantification of the complexity of inequality-constrained hypotheses (elaborated in the section after the next).

inequality-constrained hypotheses

In SEM, researchers have typically expectations about θ¹ and not about θ². Hence, we will focus on inequality constraints imposed on the Π or Γ matrix. If M is the number of inequality constraints imposed on θ¹, and K the number of parameters involved, then let A be an M × K matrix of full rank with known constants. Now, an inequality-constrained hypothesis can be specified as follows:

$$H_i:\mathbf{A}{\mathit{\theta }}^1>\mathit{d},$$ (4)

where d is an m × 1 vector of known constants.

Lets consider a hypothetical example and say, based on some theory, we expect the following ordering of four regression coefficients $H_i:{\theta }_1^1>{\theta }_2^1>{\theta }_3^1>{\theta }_4^1$, then

$$\mathit{A}=\left[\begin{array}{ccccc}1& -1& 0& 0& 0\\ 0& 1& -1& 0& 0\\ 0& 0& 1& -1& 0\\ 0& 0& 0& 1& -1\end{array}\right],{\mathit{\theta }}^1=\left[\begin{array}{c}{\theta }_1^1\\ {\theta }_2^1\\ {\theta }_3^1\\ {\theta }_1^4\end{array}\right]\text{and}\mathit{d}=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],$$ (5)

which renders

$$H_i=\left[\begin{array}{c}{\theta }_1^1-{\theta }_2^1>0\\ {\theta }_2^1-{\theta }_3^1>0\\ {\theta }_3^1-{\theta }_4^1>0\end{array}\right],$$ (6)

which is equivalent to $H_i:{\theta }_1^1>{\theta }_2^1>{\theta }_3^1>{\theta }_4^1$.

Another example is $H_i:{\theta }_2^1-{\theta }_1^1>{\theta }_3^1-{\theta }_2^1>0.10$, where the difference between the first two regression coefficients is larger than the difference between the last two regression coefficients. Moreover, the difference between the coefficients is expected to be larger than 0.10. This hypothesis can be constructed using:

$$\mathit{A}=\left[\begin{array}{ccc}-1& 2& -1\\ 0& -1& 1\end{array}\right],{\mathit{\theta }}^1=\left[\begin{array}{c}{\theta }_1^1\\ {\theta }_2^1\\ {\theta }_3^1\end{array}\right]\text{and}\mathit{d}=\left[\begin{array}{c}0\\ 0.10\end{array}\right].$$ (7)

Note that, the requirement that A is of full rank requirement excludes about equality constraints like $\mid {\theta }_1^1-{\theta }_2^1\mid <d$ which could be constructed using

$$\mathit{A}=\left[\begin{array}{cc}1& -1\\ -1& 1\end{array}\right]$$ (8)

and

$$\mathit{d}=[-d,-d].$$ (9)

Bayes Factors for the evaluation of H_i

Typically applied researchers test the hypothesis

$$H_0:{\mathit{\theta }}^1=0,$$ (10)

or,

$$H_0:{\theta }_1^1={\theta }_2^1=\dots ={\theta }_K^1,$$ (11)

for K parameters against the alternative hypothesis

$$H_1:\text{not}{H}_0.$$ (12)

We argue, however, that researchers are not really interested in such a test (Hoijtink et al., 2008; Klugkist et al., 2005; Van de Schoot, Hoijtink, et al., 2011; Van de Schoot, Romeijn, & Hoijtink, 2011; Wagenmakers, 2007). Rather, they are interested in the evaluation of their expectations directly. These expectations are about the expected ordering of, for example, regression coefficients and are based on previous research or a literature study. Therefore we propose to evaluate the inequality-constrained hypothesis presented in (4) instead of the null hypotheses in (10) or (11).

The evaluation of H_i versus either H₀ or H₁ using p-values has been described by, for example Silvapulle and Sen (2004); Van de Schoot, Hoijtink, et al. (2011); Van de Schoot, Mulder, et al. (2011). However, H_i is contained in H₁ which might be considered logically inconsistent. Moreover, we argue that many applied researchers are interested in the question “Is the Hypothesis Correct” or “Is the hypothesis incorrect?”. Therefore we will explore the comparison of H_i versus its complement,

$$H_{\neg i}:\text{not}{H}_i.$$ (13)

As was shown by, Mulder et al. (2009) and Mulder, Hoijtink, and Klugkist (2010) the Bayes factor of H_i versus an unconstrained hypothesis, H_u, can be written as

$${BF}_{iu}=\frac{f_i}{c_i},$$ (14)

where f_i can be interpreted as model fit, or the proportion of the posterior distribution of H_u in agreement with the inequality-constrained hypothesis H_i. Furthermore, c_i can be interpreted as the complexity of H_i or as the proportion of the prior distribution of H_u in agreement with the constraints of H_i. Using f_¬i = 1 - f_i and c_¬i = 1 - c_i,

$${BF}_{\neg iu}=\frac{f_{\neg i}}{c_{\neg i}}=\frac{1-f_i}{1-c_i}.$$ (15)

Combining Equations (14) and (15) leads to

$${BF}_{i\neg i}=\frac{{BF}_{iu}}{{BF}_{\neg iu}}=\frac{f_i/c_i}{(1-f_i)/(1-c_i)}.$$ (16)

The resulting Bayes factor can be interpreted as a relative measure of support for the research question “Is the Hypothesis Correct” or “Is the hypothesis incorrect?”. If BF_i¬i > 1, H_i is more supported by the data than H_¬i. If BF_i¬i ≈1, none of the two hypotheses is preferred by the data. For BF_i¬i < 1, H_¬i is more supported by the data than H_i. See Kass and Raftery (1995) for more information about the Bayes factor and its interpretation and for the interpretation in the context of inequality-constrained hypotheses Van de Schoot, Mulder, et al. (2011).

Complexity

In this section we will focus on the prior distribution, h(θ¹) and we will show that the default prior specification, i.e. (3), that is used in Mplus is suitable for the computation of the Bayes factor (16). This is because this default specification results in an adequate quantification of the complexity of inequality-constrained hypotheses.

Hoijtink (2012) defines the complexity of inequality-constrained hypotheses using an argument based on equivalent sets of hypotheses. Consider, for example, the hypothesis $H_{iz}:{\theta }_1^1>{\theta }_2^1>{\theta }_3^1$. There are z = 1, …, 3! permutations of the θ¹’s rendering hypotheses that have an equivalent structure. A logical implication is to consider these hypotheses to be of the same complexity. This leads to the following definition:

Definition 1

An Equivalent Set consist of equivalent hypotheses H_i1, …, H_iZ for which H_i1 ∪ … ∪ H_iZ encompasses 100% of the parameter space.

With 3!=6 equivalent hypotheses, 16.6% of the parameter space is in agreement with each hypothesis, with Z equivalent hypotheses the proportion of the parameter space in agreement with each is 1/Z. This leads to the following definition of complexity:

Definition 2

The Complexity of an inequality-constrained Hypothesis is the proportion of the parameter space in agreement with H_iz.

Let A_m = {A_m1, …, A_mK } denote the m-th row from A. The following restrictions on A render an hypothesis that is a member of an equivalent set:

1. Each A_mk ∈ {−1, 0, 1}.

2. For m = 1, …, M, Σ_k A_mk = 0.

3. A₁ can be divided into D subsets of the same size, such that for m = 2, …, M, A_m is a permutation of these subsets.

The number of elements in an equivalent set can be determined as follows:

1. Obtain all D! permutations of the D subsets in θ¹, that is divide ${\theta }_1^1,\dots ,{\theta }_K^1$ in the same subsets as A₁₁, …, A_1K.

2. Denote the number of permutations for which Aθ¹ > 0 is in agreement with H_i by B.

3. Then Z = D!/B.

The following theorem shows that prior distributions of the form Equation (16) render a complexity measure in agreement with Definitions 1 and 2 for hypotheses that belong to an equivalent set:

Theorem 1

(for the proof see Appendix A). Let

$$h({\mathit{\theta }}^1,{\mathit{\theta }}^2)=h({\mathit{\theta }}^1)h({\mathit{\theta }}^2).$$ (17)

For prior distributions with the property that $h({\theta }_1^1,\dots ,{\theta }_K^1)=h({\theta }_{(1)}^1,\dots ,{\theta }_{(K)}^1)$ for all permutations (1), …, (K) of 1, …, K, it holds that c_i = 1/Z for each hypothesis in an equivalent set.

Note that the default prior used by Mplus, see (3), is in agreement with the requirements specified in Theorem 1.

Not all inequality-constrained hypotheses belong to an equivalent set. Consider, for example,

$$H_{i1}:\begin{array}{c}{\theta }_1^1-{\theta }_2^1>{\theta }_3^1-{\theta }_4^1\\ {\theta }_1^1>{\theta }_2^1\\ {\theta }_3^1>{\theta }_4^1.\end{array}$$ (18)

Each element of H_i1 can be permuted in two ways, however, although all 2 × 2 × 2 permutations cover 100% of the parameter space, not each permutation is equally complex. For example, 0% of the parameter space is in agreement with

$$H_{i2}:\begin{array}{c}{\theta }_1^1-{\theta }_2^1>{\theta }_3^1-{\theta }_4^1\\ {\theta }_2^1>{\theta }_1^1\\ {\theta }_3^1>{\theta }_4^1\end{array}.$$ (19)

Consider also $H_{i1}:{\theta }_1^1>0,{\theta }_2^1>0$. If the ordinate (0,0) is treated as the natural midpoint of the parameter space. The permutation argument renders four hypotheses (another is $H_{i2}:{\theta }_1^1<0,{\theta }_2^1<0$) that are of equal complexity. Note that, Jeffreys (1961) (Chapters 5 and 6) and Berger and Mortera (2006) in the univariate counterpart of H_i1 use 0 as the mean of the prior distribution and thus as the natural midpoint of the parameter space.

It can be proven that for hypotheses of the form (4), and thus also for hypotheses belonging to equivalent sets, that the complexity of an hypothesis is independent of the mean and variance of the prior distribution in Mplus.

Theorem 2

(for the proof see Appendix B) If $h({\theta }_k^1)=\mathcal{N}({\theta }_0,{\tau }_0^2)$ for k = 1, …, K and A is of full rank, c_i is independent of θ₀ for ${\tau }_0^2\to \infty$.

An implication of Theorem 2 for hypotheses of the form H_i : Aθ¹ > d can be illustrated using the hypothesis $H_i:{\theta }_1^1>{\theta }_2^1+1>{\theta }_3^1+4$. Using the prior distribution from Theorem 2, it can be seen that c_i = 1/6, that is, the complexity of the hypothesis $H_i:{\theta }_1^{\ast }>{\theta }_2^{\ast }>{\theta }_3^{\ast }$ where ${\theta }_1^{\ast }={\theta }_1,{\theta }_2^{\ast }={\theta }_2+1$ and ${\theta }_3^{\ast }={\theta }_3+4$. Similarly, the complexity of H_i : θ¹ > 2 is 1/2, that is the complexity of the hypothesis H_i : θ* > 0, where θ*= θ − 2. Stated otherwise, application of Theorem 2 to hypotheses of the form (4) implies that the parameter space is centered around d instead of 0.

As was illustrated above, the complexity c_i of an informative hypothesis is independent of the prior distribution for the nuisance parameters. Furthermore, since the prior distribution for the nuisance parameter is specified to be vague, the posterior distribution and consequently the fit f_i of an informative hypothesis are virtually independent of the prior distribution for the nuisance parameters.

The overall conclusion is that the Bayes factor for the comparison of an informative hypothesis with its complement is independent of the prior distribution, that is, independent of subjective decisions that have to be made by a researcher, and thus, in this sense, objective. Moreover, the default prior specification in Mplus are suitable for computation of the Bayes factor in Equation (16).

Estimation of c_i and f_i

According to Definition 2, complexity can be computed by the proportion of parameter space in agreement with the inequality-constrained hypothesis. For simple hypotheses, one can use Z = D!/B. However, if more complex hypotheses are used c_i can be obtained using sampling from the prior distribution h(θ¹). In this situation, c_i can be obtained using two steps for t = 1, …, T :

1. Sample ${\theta }_{tk}^1$ from $\mathcal{N}({\theta }_k^1\mid {\theta }_0,{\tau }_0)$ for k = 1, …, K and t = 1, …, T;

2. Estimate c_i by the proportion of ${\mathit{\theta }}_t^1$ for t = 1, …, T in agreement with H_i.

The fit of the model, f_i, can be estimated using a sample from the posterior distribution, g(θ¹|Y):

1. Sample θ_tk from the posterior distribution for k = 1, …, K;

2. Estimate f_i by the proportion of θ_t for t = 1, …, T in agreement with H_i.

Samples from g(θ¹|Y ) can be obtained using Mplus using the option ANALYSIS: ESTIMATOR = BAYES in combination with the option SAVEDATA: BPARAMETERS ARE. These statements result in a file where all the parameters of the statistical model are saved for each iteration of the Gibbs sampler after omission of the burn-in phase. The second step of the computation of f_i is to count the number of iterations where the inequality constraints are satisfied. One could do this by hand, but there is also an R package called MplusAutomation (Hallquist, 2003) that provides functions to compute these calculations based on Mplus output. For simple order restrictions c_i can be computed by hand using Theorem 1, or it can be sampled using the procedure described above. Unfortunately, it is not yet possible to sample from the prior distribution in Mplus. The final step is to compute the BF_i¬i using Equation (16), and this can easily be done when the estimates for c_i and f_i are computed.

Precision of c_i and f_i

In this section we will evaluate the precision of the Bayes factor when evaluating inequality constraint hypotheses. As was shown in the previous section three steps have to be executed in order to compute the required BF:

• Obtain a sample of size T from the unconstrained prior and posterior distribution.

• Use this sample to determine c_i and f_i for the informative hypothesis under consideration, that is, determine the proportion of the sample from the unconstrained prior and posterior distribution in agreement with the hypotheses under consideration.

• Compute the required Bayes factors.

This procedure will work fine if the number of parameters K and the number of constraints M are relatively small. For larger values of K and M the size of T, needed to obtain accurate estimates of c_i and f_i, becomes so large that the procedure may no longer be of practical value. The question how large K and M may be such that simply sampling from the prior and posterior of the unconstrained model will render accurate estimates of c_i and f_i will now be considered.

The larger M the smaller c_i and the larger the sample that is needed in order to be able to accurately estimate c_i. Therefore the elaboration below is based on a complete ordering of the K parameters, that is M = K − 1 with $H_i:{\theta }_1^1>\dots >{\theta }_K^1$. If T is large enough to accurately estimate c_i for this hypothesis, it will also be large enough to estimate c_i for informative hypotheses based on fewer inequality constraints. In Table 1 the sizes T of the sample from the prior distribution needed in order to be able to accurately estimate c_i for K = 2, …, 8 are displayed. Note that, by accurately it is meant that the difference between the true c_i and the lower bound and upper bound of a 95% central credibility interval for the estimate of c_i is less than 10%. Assuming that f_i is exactly known, this implies that BF_iu = f_i/c_i is never off by more than 10%.

Table 1.

K versus T

K	2	3	4	5	6	7	8
True ci	1/2 =.5	1/6 =.166	1/24 =.042	1/120 = .008	1/720 =.0014	1/5040 = .0002	1/40320 =.000025
T	1000	3000	9600	120,000	360,000	2,520,000	20,160,000
LB-95%	.47	.154	.038	.0078	.00127	.000182	.000023
UB-95%	.53	.180	.046	.0089	.00152	.000217	.000027

The following can be concluded from Table 1. The complexity c_i can accurately be evaluated for a complete ordering of 6 parameters using a sample of T = 360, 000 from the prior distribution. The implication is that c_i can almost exactly be computed for any inequality-constrained hypothesis based on K = 6 parameters using a sample of T = 1, 000, 000 from the prior distribution. Accurate computation of complexity for a complete ordering of 7 parameters can be achieved using a sample of, 5,000,000. For more than 7 parameters accurate computation of c_i for a complete ordering may not always be possible. Note that not always a complete ordering of parameters is of interest. Consider, for example, ${\theta }_1^1>{\theta }_2^1>{\theta }_3^1>{\theta }_4^1,{\theta }_5^1>{\theta }_6^1>{\theta }_7^1>{\theta }_8^1$, the combination of two independent sets of constraints. The complexity of this hypothesis is 1/24 × 1/24 = .0017. According to Table 1 a complexity of about .0017 can accurately be estimated using T = 360, 000 and virtually exactly using T = 1, 000, 000. As exemplified in the previous bullet, Table 1 does not only apply to hypotheses in which the parameters at hand are completely ordered. As long as there is an idea of the size of the complexity to be estimated, Table 1 gives an indication of the sample sizes needed in order to be able to obtain an accurate estimate.

Now the T rendering accurate estimates of c_i has been discussed, the implications for f_i can be elaborated. If the sample from the prior is of size T, use also a sample from the posterior of size T. If the fit of a hypothesis is really bad, irrespective of the size of T, the number of parameter vectors sampled from the posterior distribution that are in agreement with H_i will be very small. This is not a problem if one only wants to compare the hypothesis at hand to its complement. The conclusion will simple be that H_i is not supported by the data.

Real-life Example

To illustrate the Bayesian procedure of evaluating an inequality-constrained hypothesis versus its complement, we re-evaluate the data of Boelen and van den Bout (2008) (see also, Boelen, Van de Schoot, de Keijser, & van den Bout, 2010). The authors collected data to examine the distinctiveness of symptoms of complicated grief (CG) and uncomplicated grief (UG). Symptoms of CG represent distressing and disabling responses to bereavement, including persistent yearning, feeling that life is empty, and numbness. Symptoms of UG represent relatively benign grief reactions, including missing the lost person, crying, and having emotional recollections related to the death. To examine the distinctiveness of CG and UG, Boelen and van den Bout (2008) used data from 130 mourners who all received mental help after their loss. They were recruited via grief counselors, therapists, and other caretakers.

Symptoms of CG were assessed using the Dutch version of the Inventory of Complicated Grief (ICG Boelen, van den Bout, de Keijser, & Hoijtink, 2003). This is a 30-item questionnaire tapping potentially problematic grief reactions. Respondents rate the presence of symptoms in the preceding month on 5-point scales ranging from ”never” to ”all the time”. Items representing UG were taken from the ”Present Feelings” subscale of the Texas Revised Inventory of Grief. Respondents rate the presence of grief reactions on 5-point scales ranging from ”completely true” to ”completely false”. For the purpose of the present illustrative analyses we selected only three items of both questionnaires with the highest explained variance in the original factor analysis. Symptoms of depression were assessed using the Beck Depression Inventory. Anxiety was assessed with the state version of the State-Trait Anxiety Inventory.

There is evidence that symptoms of CG are phenomenologically and qualitatively distinguishable from reactions representing UG with symptoms of CG but not UG being associated with concomitant mental health problems (Boelen et al., 2003; Dillen, Fontaine, & Verhofstadt-Denve, 2008). This is relevant, as it suggests that CG represents a clinical condition worthy of being included in psychiatric classification systems, such as the Diagnostic and Statistical Manual of mental disorders. Notably, CG is not yet included in these systems.

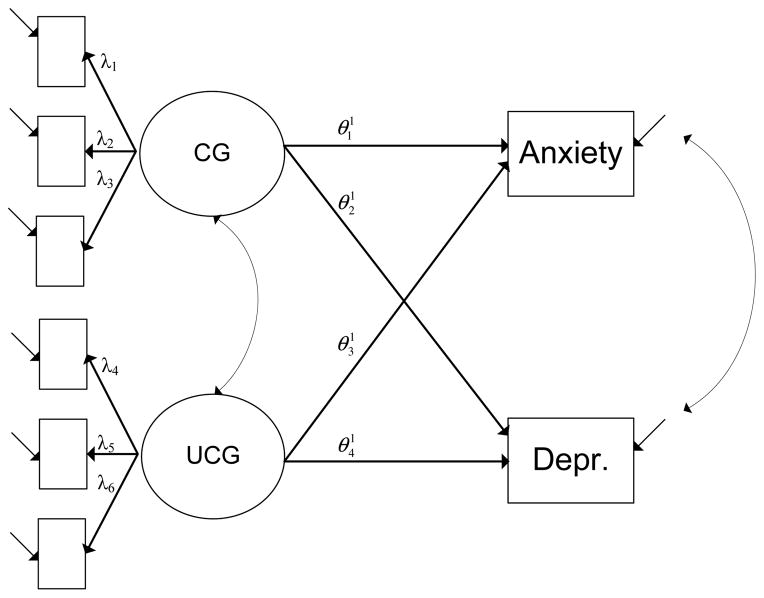
We re-analysed these data, testing the prediction that, if CG symptoms are indeed more debilitating than symptoms of UG as prior research has shown, CG symptoms should be expected to be more strongly associated with symptoms of depression and anxiety than responses of UG. See Figure 1 for a graphical representation of the model where the indicators of the latent constructs are defined as categorical variables. For the Mplus syntax see Appendix C. The inequality-constrained hypothesis can be written as

Figure 1.

Path model between symptoms of complicated grief (CG), uncomplicated grief (UG), anxiety and depression.

$$\mathit{A}=\left[\begin{array}{cccc}1& 0& -1& 0\\ 0& 1& 0& -1\end{array}\right],\mathit{\mu }=\left[\begin{array}{c}{\theta }_1^1\\ {\theta }_2^1\\ {\theta }_3^1\\ {\theta }_4^1\end{array}\right]\text{and}\mathbf{0}=\left[\begin{array}{c}0\\ 0\end{array}\right],$$ (20)

which renders:

$$H_i=\left[\begin{array}{c}{\theta }_1^1-{\theta }_3^1>0\\ {\theta }_2^1-{\mu }_4>0\end{array}\right],$$ (21)

which is equivalent to $H_i:{\theta }_1^1>{\theta }_3^1$ and ${\theta }_2^1>{\theta }_4^1$.

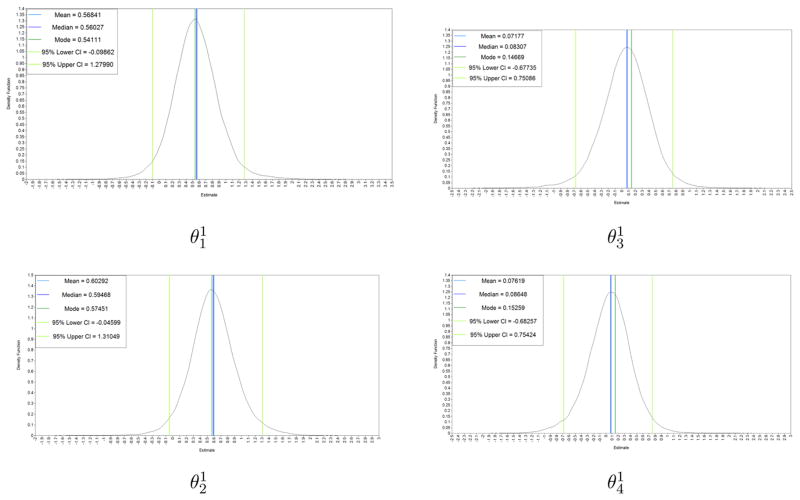
Mplus v6.11 was used to estimate the model shown in Figure 1, using four chains, maximum likelihood estimates as starting values and a Gelman-Rubin convergence criterion of .01 (see Appendix C). The default prior distributions of Mplus were used. The posterior results are shown in Table 2 (note that for reason of space we did not include all thresholds) and the posterior distributions of ${\theta }_1^1\dots {\theta }_4^1$ are shown in Figure 2. For description purposes it can be interesting to inspect the credibility intervals. In the table it can be seen that the 95% credibility interval of the four parameters of interest does contain zero. Moreover, it can be seen that the correlations between the independent and between the dependent variables are substantial. It is easy to show that c_i = .25 because H_i consist of four equivalent hypotheses:

Table 2.

Posterior parameter estimates with in boldface the parameters of interest. Note that we left out the information about the thresholds for reasons of space.

	Est.	SD	95% C.I.
Anxiety ON
$\text{CG}({\theta }_1^1)$	0.560	0.343	−0.099–1.280
$\text{UCG}({\theta }_3^1)$	0.083	0.356	−0.677–0.751
Depr. ON
$\text{CG}({\theta }_2^1)$	0.595	0.334	−0.046–1.310
$\text{UCG}({\theta }_4^1)$	0.086	0.354	−0.683–0.754
CG WITH
UCG	0.821	0.069	0.654–0.919
Anxiety WITH
Depr.	0.700	0.081	0.514–0.804
Intercepts
Anxiety	3.472	0.237	3.011–3.943
Depr.	3.535	0.242	3.071–4.020
Res. Var.
Anxiety	0.572	0.104	0.349–0.754
Depr.	0.522	0.099	0.312–0.703
Factor loadings
λ1	0.669	0.064	0.533–0.780
λ2	0.830	0.066	0.679–0.939
λ3	0.598	0.081	0.421–0.739
λ4	0.569	0.079	0.416–0.725
λ5	0.550	0.095	0.345–0.716
λ6	0.679	0.099	0.456–0.840

Figure 2.

Posterior distributions with posterior mean, mode, median and 95% C.I. for ${\theta }_1^1\dots {\theta }_4^1$.

1. $H_1:{\theta }_1^1>{\theta }_3^1$ and ${\theta }_2^1>{\theta }_4^1$;

2. $H_2:{\theta }_1^1<{\theta }_3^1$ and ${\theta }_2^1>{\theta }_4^1$;

3. $H_3:{\theta }_1^1>{\theta }_3^1$ and ${\theta }_2^1<{\theta }_4^1$;

4. $H_4:{\theta }_1^1<{\theta }_3^1$ and ${\theta }_2^1<{\theta }_4^1$

Furthermore, for f_i the proportion of iterations of the Gibbs sampler where the parameter estimates are in line with the inequality constraints can be computed using MplusAutomation. For our model, in total 82,800 iterations were performed and 57,934 of these iterations met the constraints, which renders an estimate for f_i of .699. Using these results

$${BF}_{i\neg i}=\frac{f_i/c_i}{(1-f_i)/(1-c_i)}=\frac{.699/.25}{(1-.699)/(1-.25)}=\mathrm{6.97.}$$ (22)

In conclusion, H_i is 6.97 times more likely then H_¬i. This finding indicates that the evidence for complicated grief being a stronger predictor of depressive and anxious symptoms than uncomplicated is approximately 7 times greater than the converse (i.e., uncomplicated grief is a stronger correlate of negative emotional symptoms).

Conclusion

Traditional hypotheses tests are not equipped to deal with informative hypotheses formulated in terms of inequality constraints among the parameters of a structural equation model. Also, the statistical tools that are available to evaluate an inequality-constrained hypothesis test it against the classical null hypothesis, against an unconstrained hypothesis, or “Is the hypothesis incorrect?”, but tools to evaluate this hypothesis in SEM were not yet available. In the current paper we presented a solution for this problem using Mplus.

Bayesian estimation was first made available in Mplus in 2010 which makes it possible for applied researchers to switch to Bayesian statistics easily. Also, the Bayesian toolkit in Mplus allows for the computation of a Bayes factor for the comparison of an informative hypothesis against its complement. The prior specifications are an important aspect of this comparison, but the defaults in Mplus are specified in such a way that the prior distributions are specified correctly. A next step would be to include the computation of the Bayes factor in the syntax Mplus so that researchers do not have to switch to other software to compute the Bayes factor. On the other hand, the computation is very simple and the R package MplusAutomation can compute the necessary estimates.

Appendix A. Proof of Theorem 1

Proof of Theorem 1

If A₁ is divided in D subsets of the same size, θ¹ = [θ₁, …, θ_D], where each subset of θ contains the same number of elements, there are D! permutations of θ: θ¹, …, θ^D!.

If the number of equivalent hypotheses is Z, D!/Z = B of these permutations are in agreement with each equivalent hypothesis, that is, [θ¹, …, θ^D!] = […, θ^z1, …, θ^zB, …], leading to H_iz : H_iz1 ∪… ∪ H_izB.

Because each θ ∈ H_iz can be permuted to a θ′ ∈ H_iz′ for which it holds that h(θ) = h(θ′) it holds that

$$c_{iz}={\int }_{\mathit{\theta }\in H_{iz}}h(\mathit{\theta })d\mathit{\theta }={\int }_{{\mathit{\theta }}^{\prime }\in H_{{iz}^{\prime }}}h({\mathit{\theta }}^{\prime })d{\mathit{\theta }}^{\prime }=c_{{iz}^{\prime }}.$$ (23)

Since Σ_z c_iz = 1 this implies that c_iz = 1/Z for z = 1, …, Z.

Appendix B. Proof of Theorem 2

Proof of Theorem 2

Let de rows of A be denoted by A₁, …, A_M, A_m = [A_m1, …, A_mK] and d = [d₁, …, d_M]. Then

$$c_i=P({\mathit{A}}_1\mathit{\theta }-d_1>0,\dots ,{\mathit{A}}_M\mathit{\theta }-d_M>0\mid \left[\begin{array}{c}{\mathit{A}}_1\mathit{\theta }-d_1\\ \dots \\ {\mathit{A}}_M\mathit{\theta }-d_M\end{array}\right]~\mathcal{N}(\mathit{V}{\theta }_0-\mathit{d},\mathit{W}{\tau }_0^2)),$$ (24)

where

$$\mathit{V}=\left[\begin{array}{c}{\sum }_k{A}_{1}k\\ \dots \\ {\sum }_k{A}_{Mk}\end{array}\right],$$ (25)

and

$$\mathit{W}=\left[\begin{array}{ccc}{\sum }_k{A}_{1k}^2& \dots & {\sum }_k{A}_{Mk}{A}_{1k}\\ \dots & \dots & \dots \\ {\sum }_k{A}_{1k}{A}_{Mk}& \dots & {\sum }_k{A}_{Mk}^2\end{array}\right].$$ (26)

Since ${lim}_{{\tau }_0^2\to \infty }P(\mathit{Z}>\mathbf{0}\mid \mathit{Z}~\mathcal{N}(\mathit{V}{\theta }_0-\mathit{d},\mathit{W}{\tau }_0^2))=P(\mathit{Z}>\mathbf{0}\mid \mathit{Z}~\mathcal{N}(\mathbf{0},\mathit{W}{\tau }_0^2))=P(\mathit{Z}>\mathbf{0}\mid \mathit{Z}~\mathcal{N}(\mathbf{0},\mathit{W}))$, where Z is a vector of length M containing [A₁θ − d₁, …, A_Mθ − d_M], the ${lim}_{{\tau }_0^2\to \infty }{c}_i$ reduces to

$$c_i=P({\mathit{A}}_1\mathit{\theta }-d_1>0,\dots ,{\mathit{A}}_M\mathit{\theta }-d_m>0\mid [\begin{array}{c}{\mathit{A}}_1\mathit{\theta }-d_1\\ \dots \\ {\mathit{A}}_M\mathit{\theta }-d_M\end{array}]~\mathcal{N}(\mathbf{0},\mathit{W})),$$ (27)

that is, independent of θ₀.

Appendix C. Mplus syntax

DATA: FILE = data.dat;
VARIABLE:
NAMES ARE TRIG4 TRIG5 TRIG9 ITG4 ITG5 ITG10 STAITOT BDIM;
CATEGORICAL ARE TRIG4 TRIG5 TRIG9 ITG4 ITG5 ITG10;
MISSING ARE ALL ( −999);
ANALYSIS:
ESTIMATOR = bayes; !here you select the Bayesian estimator
CHAINS = 4; !change the number of chains
PROCESSOR= 4 (starts); !increase computation speed
BCONVERGENCE = .01; !select a smaller convergence criterium
STVALUES = ml; !use maximum likelihood estimates as starting values
MODEL:
STAITOT BDIM on CG UCG;
UCG by TRIG4 TRIG5 TRIG9;
CG BY ITG4 ITG5 ITG10;
SAVEDATA: BPARAMETERS ARE c:/Bresults2.dat; !save the parameter estimates for each iteration after burn-in