Single cell Hi-C reveals cell-to-cell variability in chromosome structure

Abstract

Large-scale chromosome structure and spatial nuclear arrangement have been linked to control of gene expression and DNA replication and repair. Genomic techniques based on chromosome conformation capture assess contacts for millions of loci simultaneously, but do so by averaging chromosome conformations from millions of nuclei. Here we introduce single cell Hi-C, combined with genome-wide statistical analysis and structural modeling of single copy X chromosomes, to show that individual chromosomes maintain domain organisation at the megabase scale, but show variable cell-to-cell chromosome territory structures at larger scales. Despite this structural stochasticity, localisation of active gene domains to boundaries of territories is a hallmark of chromosomal conformation. Single cell Hi-C data bridge current gaps between genomics and microscopy studies of chromosomes, demonstrating how modular organisation underlies dynamic chromosome structure, and how this structure is probabilistically linked with genome activity patterns.

Chromosome conformation capture¹ (3C) and derivative methods (4C, 5C and Hi-C)^2-6 have enabled the detection of chromosome organisation in the 3D space of the nucleus. These methods assess millions of cells and are increasingly used to calculate conformations of a range of genomic regions, from individual loci to whole genomes^3,7-11. However, fluorescence in situ hybridisation (FISH) analyses show that genotypically and phenotypically identical cells have non-random, but highly variable genome and chromosome conformations^4,12,13 probably due to the dynamic and stochastic nature of chromosomal structures^14-16. Therefore, whilst 3C-based analyses can be used to estimate an average conformation, it cannot be assumed to represent one simple and recurrent chromosomal structure. To move from probabilistic chromosome conformations averaged from millions of cells towards determination of chromosome and genome structure in individual cells, we developed single cell Hi-C, which has the power to detect thousands of simultaneous chromatin contacts in a single cell.

Single cell Hi-C

We modified the conventional or “ensemble” Hi-C protocol³ to create a method to determine the contacts in an individual nucleus (Fig. 1a, Supplementary Information). We used male, mouse, spleenic CD4⁺ T cells, differentiated in vitro to T helper (Th1) cells to produce a population of cells (>95% CD4⁺), of which 69% have 2n genome content, reflecting mature cell withdrawal from the cell cycle. Chromatin cross-linking, restriction enzyme (Bgl II or Dpn II) digestion, biotin fill-in and ligation were performed in nuclei (Fig. 1a and Extended Data Fig. 1a) as opposed to ensemble Hi-C where ligation is performed after nuclear lysis and dilution of chromatin complexes³. We then selected individual nuclei under the microscope, placed them in individual tubes, reversed cross-links, and purified biotinylated Hi-C ligation junctions on streptavidin-coated beads. The captured ligation junctions were then digested with a second restiction enzyme (Alu I) to fragment the DNA, and ligated to customized Illumina adapters with unique 3 bp identification tags. Single cell Hi-C libraries were then PCR amplified, size selected and characterized by multiplexed, paired-end sequencing.

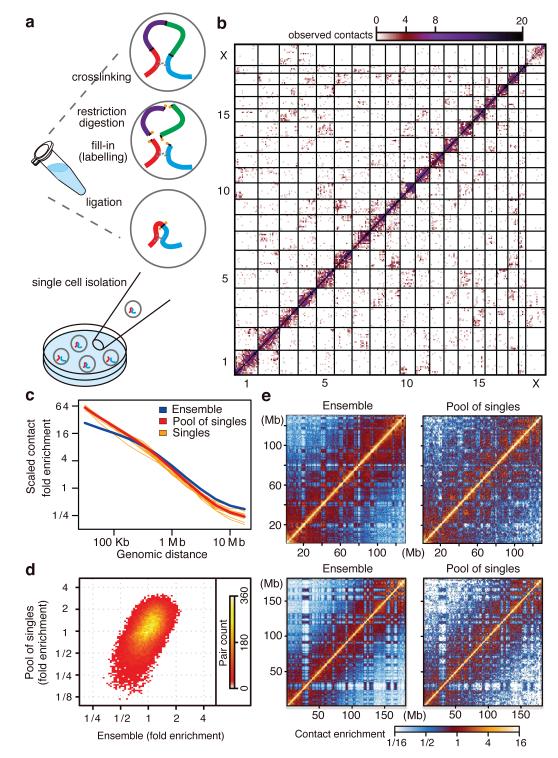
Figure 1. Single cell and ensemble Hi-C.

a, Single cell Hi-C method. b, Single cell Hi-C heatmap (cell-5), coverage for 10 Mb bins. c, Contact enrichment versus genomic distance, from ensemble Hi-C, pool of 60 single cells and 10 individual cells, scaled to normalise sequencing depths. d, Normalising by the trends in c, intra-chromosomal contact enrichments for 1 Mb square bins, comparing ensemble and pooled single cell Hi-C (Spearman correlation = 0.56). e, Intra-chromosomal contact enrichment maps of ensemble and pooled single cell Hi-C, for chromosome 10 (top) and chromosome 2 (bottom), using variable bin sizes.

De-multiplexed single cell Hi-C libraries were next filtered thoroughly to systematically remove several sources of noise (Extended Data Fig. 1b-f, Supplementary Information). Hi-C in male diploid cells can theoretically give rise to at most two ligation products per autosomal restriction fragment end, and one product per fragment end from the single X chromosome. Using Bgl II, the total number of distinct mappable fragment-end pairs per single cell cannot therefore exceed 1,201,870 (Extended Data Fig. 1g, Supplementary Information). In practice, deep sequencing of the single cell Hi-C libraries demonstrated that following stringent filtering our current scheme allows recovery of up to 2.5% of this theoretical potential, and has identified at least 1000 distinct Hi-C pairings in half (37/74) of the cells. Deep sequencing confirmed saturation of the libraries’ complexity, and allowed elimination of spurious flow cell read pairings and additional biases (Extended Data Tables 1-3). Based on additional quality metrics we selected ten single cell datasets, containing 11,159-30,671 distinct fragment-end pairs for subsequent in-depth analysis (Extended Data Fig. 1h-l). Visualization of the single cell maps suggested that despite their inherent sparseness, they clearly reflect hallmarks of chromosomal organization, including frequent cis-contacts along the matrix diagonal and notably, highly clustered trans-chromosomal contacts between specific chromosomes (Fig. 1b).

Single cell and ensemble Hi-C similarity

We used the same population of CD4⁺ Th1 cells to generate an ensemble Hi-C library. Sequencing and analysis¹⁷ of 190 million read pairs produced a contact map representing the mean contact enrichments within approximately 10 million nuclei. The probability of observing a contact between two chromosomal elements decays with linear distance following a power law regime for distances larger than 100 kb^3,18. We found similar regimes for the ensemble, individual cells and a pool of 60 single cells (Fig. 1c). Moreover, after normalizing the matrices given this canonical trend, comparison of intra-chromosomal interaction intensities for the pool and ensemble, by global correlation analysis of contact enrichment values at 1 Mb resolution generates a highly significant correspondence (Fig. 1d). This is emphasized by the high similarity observed in comparisons of individual chromosomes from ensemble and pooled Hi-C maps (Fig. 1e). In summary, despite different experimental procedures and sparse nature of the single cell matrices, the pooled matrix retains the most prominent properties of the ensemble map, confirming the validity of the approach and prompting us to further explore the similarities and differences among the individual cell chromosomal conformations.

Intra- and inter-domain contacts

A key architectural feature of ensemble Hi-C datasets is their topological domain structure^18-20. As expected 1403 domains were identified in the Th1 cell ensemble Hi-C map¹⁸ (Supplementary Information Table 1, and Supplementary Information). We used the ensemble domains to ask whether the same domain structure can be observed at the single cell level. Visual inspection of the domain structure overlaid on individual intra-chromosomal contact maps (Fig. 2a), and global statistical analysis of the ratios between intra- and inter-domain contact intensities in individual cells (approximately 2-fold enrichment on scales of 100 Kb to 1 Mb, Fig. 2b and Extended Data Fig. 2a), both supported the idea that domains are observed consistently in the single cell maps. To test whether domain structures are variable between individual cells, we estimated the distributions of intra-domain contact enrichments across cells and compared it to the distributions derived from reshuffled maps. We reasoned that cell-to-cell variation in intra-domain contact intensities would result in an increase of the variance of this distribution compared to the expected variance resulting from sampling contacts in uniformly (shuffled) intra-domain contacts. The data however (Fig. 2c), showed that the distributions for the intra-domain enrichments in real cells are not more varied than expected (Kolmogorov-Smirnov p < 0.52). A similar observation was derived by comparison of the correlations between intra-domain contact enrichments for pairs of real and pairs of reshuffled maps (Extended Data Fig. 2b). While this analysis cannot quantify variability in the high-resolution internal structure of domains, the data suggests that domain intactness is generally conserved at the single cell level.

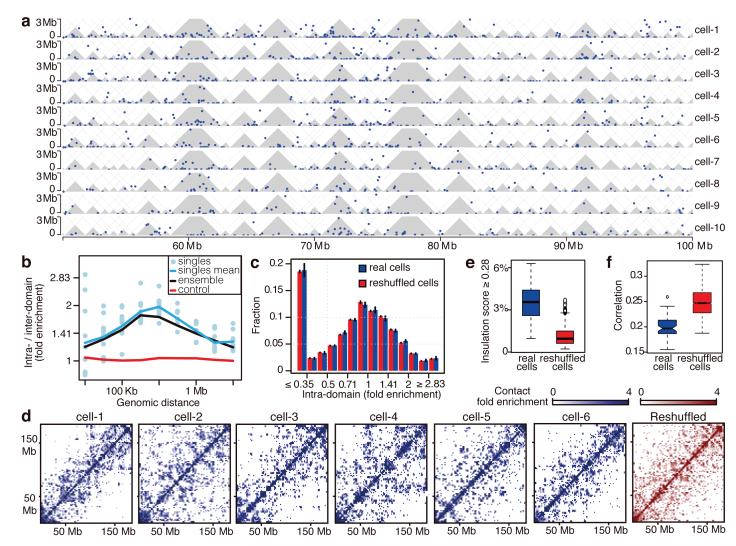
Figure 2. Conserved intra-domain, but not inter-domain structure in single cells.

a, Individual intra-chromosomal contacts of 50 Mb region of chromosome 2 up to 3 Mb distance (blue dots), domains (grey). b, Ratios between intra-domain and inter-domain contact enrichments over genomic distance. Control is combined trend of 10 single cells calculated by repeatedly shifting the domains randomly. c, Distribution of intra-domain contact enrichments per domain from 9 cells (where Bgl II was used) and reshuffled datasets (black bars, standard errors). d, Maps of inter-domain contacts intensities for chromosome 2 from individual cells and reshuffled controls using variable bin sizes. e, Distribution of percentage of loci with high insulation scores in single vs. reshuffled cells. f, For all pairs of single cells, the correlations between inter-domain contact numbers of all pairs of domains within the same chromosome were computed. Shown are the distributions of these correlations in the real and reshuffled cells.

Visual comparison of whole chromosome contact maps (Fig. 2d) suggested that unlike intra-domain interactions, inter-domain contacts within single cell chromosomes are structured non-uniformly. The maps showed large-scale structures as indicated, for example, by specific insulation points separating chromosomes into two or more mega-domains in a cell-specific fashion. To rule out the possibility that this can be explained by sparse sampling of contacts in each single cell map we again used reshuffled controls. In each map (real or randomized) we quantified the frequency of loci that strongly polarize the matrix into two weakly connected submatrices (using an insulation score; Supplementary Methods). We confirmed that single cell maps indeed show many more such loci than reshuffled maps (Fig. 2e and Extended Data Fig. 2c). The reshuffled controls made by mixing contacts from different single cell maps, are in fact similar to sparse versions of the ensemble map, which do not show specific structure at the intra-domain level. Along similar lines, the correlation in contact intensities between domains on the same chromosome in pairs of single cell maps is lower compared to reshuffled controls (Fig 2f). Taken together, these data show that domains form a robust and recurrent conformational basis that is evident in each of the single cells. However, inter-domain contacts are highly variable between individual cells, suggesting large-scale differences in higher-order chromosome folding that are obscured in ensemble maps, averaged over millions of such structures²¹.

3D structural modeling of X chromosomes

To determine whether the single cell Hi-C data is consistent with unique chromosome conformations we developed a modeling approach to reconstruct the conformations of the single-copy, male X chromosome. We used intra-chromosomal contacts as distance restraints and calculated structural models using a simulated annealing protocol to condense a particle-on-a-string representation of individual chromosomes from random initial conformations (Supplementary Information), to produce both fine-scale and low-resolution models, with backbone particles representing either 50 or 500 kb of the chromosome, respectively. For fine-scale calculations, each intra-chromosomal contact restrained its precise position on the chromosome, while low-resolution calculations combined contacts into larger bins. Tests of our simulation protocol demonstrated that restraint density was the most important parameter for modeling (Extended Data Fig. 3a, b). Hence, from the ten high-quality single cell datasets, we selected six with the largest numbers of intra-chromosomal X contacts, plus one with a lower number of contacts (cell-9) for contrast.

Repeat calculations starting from random positions generated 200 X chromosome models for each cell at both scales. The fine-scale models displayed very low numbers of restraint violations (Extended Data Fig. 3c). We introduced an estimated average unit DNA distance length²² to approximate packaging of chromatin fibers (~0.15 μm/50 kb) (Supplementary Information). This resulted in models with a mean X chromosome territory diameter of 4.3 μm (range 3.3-5.9 μm), in good agreement with X chromosome paint FISH in Th1 cells (Fig. 3a; mean diameter 3.7 μm) and chromosome territory sizes in live cells²³. We confirmed that the restrained points in a single cell are indeed close in the structures calculated from them (Extended Data Fig. 3c, d). Interestingly, the single cell distance matrix demonstrates how the network of contacts in a model imparts further structural information beyond the directly observed contacts (Extended Data Fig. 3d).

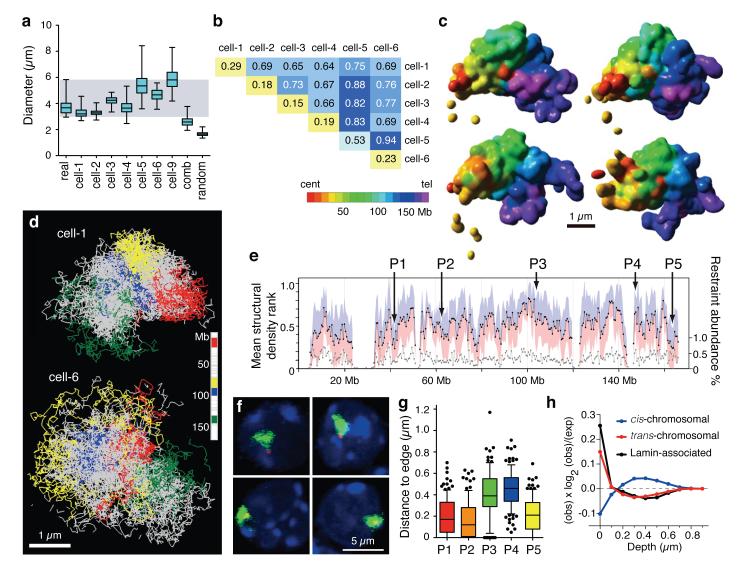
Figure 3. Structural modeling of X chromosomes.

a, Distribution of longest diameter of X chromosome paint DNA FISH signals in 62 male Th1 cells (real), 200 structural models calculated for each single cell (cell-1 to -9), 200 structures from combined dataset (cell-1 and -2; comb) and 200 structures from 20 randomised cell-1 datasets (random; 10 calculations per dataset). Whiskers denote minimum and maximum. b, Average coordinate root-mean-square deviation (RMSD) values in microns comparing 200 low-resolution structural models for each cell and between cells. c, Four surface-rendered models of the X chromosome from cell-1, which are most representative of the data based on hierarchical clustering of pair-wise RMSD values (Supplementary Information). Scale bar, 1 μm. d, Structural ensembles of the four most representative fine-scale models for cell-1 and cell-6, with four large regions coloured. Scale bar, 1 μm. e, Mean structural density rank for 500 kb regions (black) from 6 × 200 fine-scale models from cell-1 to -6. Standard deviation (blue/pink). Abundance of intra-chromosomal restraints (grey, right axis). DNA FISH probes (P1-P5) are indicated. f, DNA FISH on Th1 cells. X chromosome paint (green) and specific locus signals (red). g, Distribution of DNA FISH distance measurements between signal centres for probes P1 - P5 and edge of the X chromosome territory in Th1 cells (n = 114, 113, 105, 115, 108 for P1-P5). Whiskers denote 10 and 90 percentiles. h, Enrichment of cis-, trans-contacts and Lamin-B1 associated domains at various depths on the chromosome models relative to null hypothesis of random positions.

Comparison of the low-resolution models demonstrated convergence toward a single conformation for each single cell dataset (Fig. 3b and Extended Data Fig. 3e). For fine-scale models, hierarchical clustering revealed 4-5 that were most representative of the data (Fig. 3c). In all cases models from a single cell were significantly more similar to each other than to models from different cells. (Extended Data Fig. 4a, b).

Highlighting four regions of the X chromosome showed large-scale conformational differences between cells (Fig. 3d), supporting the finding of highly variable inter-domain contacts. Models created by shuffling Hi-C contacts, or combining contacts from two cells resulted in structures smaller and more compact than observed chromosome territories (Extended Data Fig. 4c, d) with many restraints stretched toward or exceeding their upper bounds (Extended Data Fig. 3c). These results reaffirm that the variation in single cell contacts is not the result of partial sampling of a single underlying structure.

We next asked whether despite their cell-to-cell variability, X chromosome structures share common folding properties that could be tested in real cells. One such important property, which is often consistent within a cell population, and with multiple potential functional implications, is localisation within the chromosomal territory relative to its surface. To predict loci with consistent positions within their chromosome territory we calculated the structural density along the X chromosome (Supplementary Information) and identified regions with consistently high or low structural density (Fig. 3e). We chose five such regions (P1-P5) with predicted positions near the surface (P1, P2, P5; low structural density) or inside (P3, P4; high structural density) the model X chromosome territories using the 1200 models from the six cells (Extended Data Fig. 4e). We then performed double label DNA FISH with X chromosome paints and P1-P5 BAC probes (Fig. 3f) to directly test these predictions. The distances between DNA FISH signals and edge of the chromosome territory in over one hundred Th1 cells showed that probes P1, P2 and P5 were indeed found predominantly outside or toward the edge of the chromosome territory, whereas signals for probes P3 and P4 were found at internal positions (Fig. 3g). These data show that despite highly variable inter-domain structure of the X chromosomal territory, some of its key organisational properties are robustly observed across the cell population.

Domains at the interface

Overlaying data from trans-chromosomal contacts on the X chromosome models demonstrates that trans-chromosomal contacting regions are strongly enriched toward the inferred surface of the models (Fig. 3h), providing further validation. These observations prompted us to further explore the structural characteristics of interfaces between chromosomal territories, and the relationships between such interfaces and the domain structure of the territory itself. We found that trans-chromosomal contact enrichments of domains vary across cells (Fig. 4a), showing a significant difference between the mean contact enrichment per domain in the real and reshuffled maps (p < 1.2e-9, Kolmogorov-Smirnov test). The higher variance of the distribution for the real data suggests some domains are more likely to contact elements on other chromosomes. Previous work has suggested that active genomic regions on the sub-domain scale often loop out of their chromosome territories²⁴, which might imply less defined local domain structures and disassociation from their chromosome territory. However, our analysis shows that trans-contacting domains retain domain organisation, as demonstrated by the intra-domain contact probabilities within them (Fig. 4b and Extended Data Fig. 5a, b). On the other hand, trans-contacting domains show slightly reduced contact intensity to other domains on the same chromosome (Fig. 4c and Extended Data Fig. 5c, d), consistent with localisation on the interfaces of their territories rather than dissociation from them.

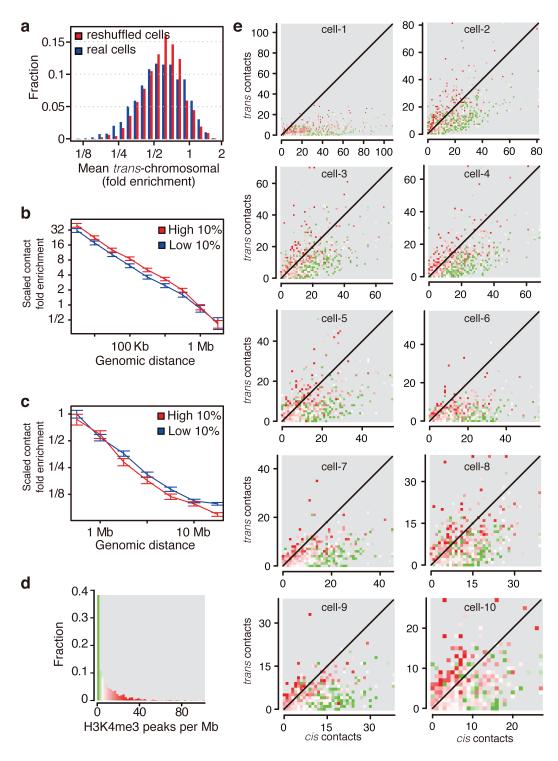
Figure 4. Active domains localise to territory interfaces.

a, Distribution of trans-chromosomal contact enrichments of each domain averaged across real and reshuffled cells. Reshuffling maintains the number of cis and trans contacts within each cell and chromosome. b, Intra-domain contact enrichment over genomic distance for high vs. low trans-chromosomal contacting domains selected independently in each cell, with 95% confidence intervals. c, Same sets as in b but plotting the enrichment of inter-domain contacts. d, Distribution of H3K4me3 peak density in domains (number of peaks divided by size), color-coded according to density. e, Domains plotted according to number of trans- and cis-chromosomal (excluding intra-domain) contacts, color coded for H3K4me3 density as in d.

Analyses of ensemble Hi-C data have previously shown that active marks correlate with enrichment of trans-chromosomal contacts^3,17. Using the single cell maps combined with annotation of domains based on their enrichment for histone H3 lysine 4 tri-methylation (H3K4me3) hotspots²⁵ (Fig. 4d), we tested whether this correlation is the result of low frequency re-localisation of active domains to other chromosome territories (looping out), or from frequent localisation of active domains on territory interfaces. As shown in Fig. 4e, domains with high trans- to cis-chromosomal contact ratios (excluding intra-domain) are highly correlated with H3K4me3 enrichment in all cells. However, the data show that domains (including active ones) retain their association with the territory in almost all cases. Very few domains with strong trans-contacts were found to lack association with their own territory (i.e., upper left points in graphs in Fig. 4e). Some of this lack of perfect territory re-localisation can be explained by having two copies of each autosomal domain, but the overall reduction with territory association for trans-contacting domains is much smaller than the 50% expected by this explanation (reduction estimated at 15-20% and 10% for contacts across 1-5 Mb and 10 Mb, respectively, Fig. 4c). Comparison of active domain localization shows that different active domains are highly trans-contacting in each cell (Extended Data Fig. 5e). Together, these data show that preferential localisation of active domains to territory interfaces is a hallmark of chromosome organisation in all cells. Active domains maintain their intra-domain organisation, and only partially lose intra-chromosomal contacts with other domains. Our data are consistent with the concept that chromosomal territories are maintained robustly despite the trans-chromosomal contacts between active domains.

Interestingly, domains associated with Lamin-B1²⁶, which are thought to be primarily inactive regions, are also found toward the surface of the models (Fig. 3h). However, these domains are highly anti-correlated with H3K4me3 domains (Spearman’s correlation = −0.73) and typically depleted of trans-chromosomal contacts (Extended Data Fig. 5f-i). Superposition of H3K4me3, Lamin-B1 enriched domains and trans-chromosomal contacts on the X chromosome models illustrates spatial partitioning of the active, trans-contacting regions from those that are Lamin-associated, although both types of domains tend toward the surface of the chromosome territory, supporting the above descriptions of differential positioning of domains (Extended Data Fig. 5j and Supplementary Videos 1 and 2).

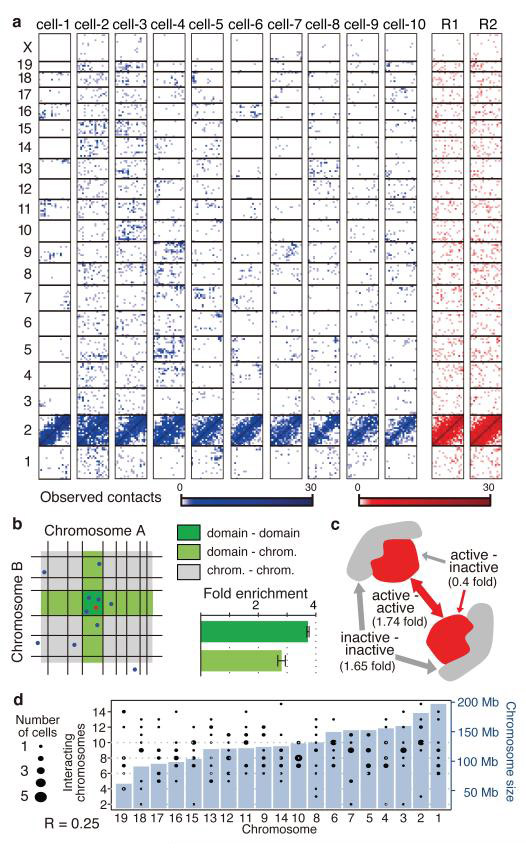
Ensemble Hi-C maps generate a highly complex view of chromosomal contacts, including low intensity contacts between all possible chromosomal pairings^3,8,17,19. In contrast, years of single cell analyses by microscopy have suggested that individual cells have much simpler and discrete chromosome structures involving a limited number of interfaces between spatially constrained chromosomal territories^27,28. Our single cell maps bridge the gap between the genomic and imaging techniques, showing cell-specific clusters of trans-chromosomal contacts associating some pairs of chromosomes, and a lack of contacts between other chromosome pairs (Fig. 5a, blue). Such organisation is completely lacking in reshuffled maps (Fig. 5a, red) confirming it is not a consequence of sparse contact sampling (Extended Data Fig. 6a, b). Trans-chromosomal contact clusters bring pairs of domains together, as shown by comparing the enrichment in trans-contacts between pairs of elements connecting the same two domains and pairs connecting one domain with two different domains (Fig. 5b). Such synergistic contacting preferentially brings together pairs of active domains, with interaction between active and inactive domains being underrepresented (Fig. 5c and Extended Data Fig. 6c). Although inactive domains are depleted as a group from trans-chromosomal interactions (Fig. 4e), inactive domains that engage in trans-contacts are more likely to interact with other inactive domains. Interestingly, analysis of interacting pairs of domains suggests that the number of chromosomes contacted by each chromosome is relatively constant (less than 30% difference) despite the >3-fold change in chromosome size, the total number of trans-chromosomal contacts in the map, or a number of other factors (Fig. 5d and Extended Data Fig. 7a-e). We note that even though the total number of chromosome-chromosome interfaces per single cell is bounded, the detailed interface between chromosome pairs can involve multiple domain-domain contacts reflecting higher order organization (Extended Data Fig. 7f).

Figure 5. Chromosomal interfaces.

a, All trans-chromosomal contacts formed by chromosome 2 in real cells (blue) and reshuffled (red). b, Schematic diagram of a chromosomal interface between linearly adjacent domains, their borders marked in black on two chromosomes, A and B. We considered each of the two contacting fragments of every trans-chromosomal contact and classified every nearby trans-chromosomal contact as domain-domain, domain-chromosome and chromosome-chromosome, the latter being used as background for normalisation (Supplementary Information). Contact under consideration (red), nearby contacts (blue). Fold enrichments shown for each group type (error bars, standard deviation). c, Trans-chromosomal contacts are highly significantly enriched between active domains (H3K4me3 enriched) or between inactive domains, but not mixed interaction (chi-square test; p = 5.8e-18; even after taking account of the generally higher connectivity of active domains). d, Bar graph depicting mouse autosomes ordered by size with number of interacting chromosomes per single cell (black circles depict the distribution over individual cells). Mean number of interacting chromosomes changes modestly (30%) with chromosome size, suggesting a highly organized territory structure with surface that is not scaling with chromosome length.

Overall, these results indicate that each chromosome contacts a discrete and fairly constant number of other chromosomes in a single cell, with little dependency on the chromosome size. At the single cell level both the microscopic and genomic observations therefore indicate highly defined territory structures, which can be hypothesised to harbor much of the chromosome within the territory, and expose a limited, relatively constant surface area engaged in chromosome-to-chromosome interfaces. Since these interfaces are highly variable among different cells, their averaging by ensemble Hi-C contributes toward the relatively uniform trans-chromosomal contact matrices previously reported.

We have presented a new experimental strategy to create Hi-C contact maps from single cells. The approach allows for characterization of thousands of simultaneous contacts occurring in individual cells, and provides unique insights into Hi-C technology and 3D chromosomal architecture (Supplementary Videos 3 and 4). Single cell contact maps reflect conservation of domain structure that was recently characterized^18-20, but show that inter-domain and trans-chromosomal contact structure is highly variable between individual cells. Genome-wide statistical analysis and reconstruction of the single copy X chromosome models gave us the opportunity to quantify key features of chromosomal architecture. For example, active domains tend to locate on the boundaries of their chromosomal territories in the majority of nuclei, while maintaining associations with other domains on the same chromosome. Our results do not exclude chromosome territory intermingling²⁹, but argue against domains becoming completely immersed in other territories. Coupled with previous observations of small and large-scale chromatin mobility^30-32 a highly dynamic view of chromosomal organization ermerges, where territories are continuously being remodeled, while maintaining some key local (domain) and global (depth from surface) organisational features.

Online Methods

Male Th1 cells were fixed and subjected to modified Hi-C, in which nuclei were maintained through restriction enzyme digestion, biotin fill-in labelling and ligation. Single nuclei were isolated and processed to prepare single cell Hi-C libraries for paired-end sequencing.

Sequences were mapped to the mouse genome, and abnormal read pairs were discarded. Read pairs that occurred only once (without duplication) in the library sequencing were removed. We chose 10 single cell datasets for further in-depth analyses based on several quality criteria (see Supplementary Information). To validate the single cell Hi-C procedure, we pooled the single cell Hi-C datasets and compared them to ensemble Hi-C dataset prepared from approximately 10 million cells essentially as described³. We created reshuffled datasets by randomly redistributing contacts of the analyzed single cells to create the same number of cells with the same number of contacts in each cell as a control to statistically analyse the variation among single cell datasets.

We reconstructed three-dimensional X chromosome structure models using restrained molecular dynamics calculations employing a simulated annealing protocol. A combination of unambiguous distance restraints from the X intra-chromosomal contacts in the single cell Hi-C dataset and anti-distance restraints between regions that were found not to contact each other in the ensemble Hi-C dataset was used. To assess the precision and accuracy of the structure generation process we used the protocol to generate synthetic Hilbert curve structures, and explored the impact of varying the number of restraints. For pair-wise comparison of the structures, we calculated the root-mean-square deviation (RMSD). To compare the X chromosome models to X chromosome structure in vivo, we selected five loci with consistently high or low structural density in the models, and compared distances between the loci and the X chromosome territory surface in cells (DNA FISH).

Full description of the methods can be found in the Supplementary Information.

Supplementary Material

Extended Data Table 1. Testing sequencing saturation.

Several single-cell libraries were massively re-sequenced. a, Shown are the numbers of read-pairs in the original and re-sequenced runs, the number of fend-pairs in the original one, the number of fend-pairs when combining the sequences of the two runs, and the addition to fend-pairs the re-sequencing contributed. %valid non-amplified are the percentages of singly covered fend-pairs in the original sample that were supported by more read-pairs in the re-sequenced one. These fend-pairs were discarded as potential spurious pairs in the original run, but proved by the re-sequencing to be valid pairs. This gives a sense of the fraction of valid pairs we discard when removing the read-pairs suspected to be sequencing pairing errors. b, Shown are fend-pair coverage contingency tables of the original and the re-sequenced runs for the five single-cells.

Extended Data Table 2. Testing inter-cellular spurious ligations.

Mouse and human nuclei or single cell Hi-C samples were mixed in different stages of the experiment (group A, before fixation; group B, before library construction [so all the mouse and human samples in each library have the same identification tag]; group C, before library amplification [so mouse and human samples in each library have different identification tags]). We created single cell (for group A) or human/mouse two cell (for groups B and C) Hi-C libraries and analysed them. The table shows the percentages of the three possible read-pairs: mouse-mouse (mm9-mm9), human-human (hg18-hg18) and human-mouse (hg18-mm9). The expected pair type in each library is marked in blue. Mean percentage of unexpected read-pairs per lane are also shown. For group A, we selected mouse cells based on morphology.

In Group A, all six libraries contain almost exclusively mouse-mouse read-pairs with insignificant human-human or mouse-human pairs. Each group B library has both human-human and mouse-mouse read-pairs as expected, and the number of spurious human-mouse read-pairs is extremely low. In each group C library, which was created by amplifying the distinctly tagged human (C1-C6) and mouse (C7-C12) single cell samples in the same tube (e.g., C1 and C7, C2 and C8, etc.), the fractions of foreign pairs (human reads with a mouse tag and vice versa) and of spurious pairs (human-mouse) were consistently extremely low.

To estimate the fraction of foreign and spurious pairs that could have originated simply from mapping a truly pure mouse library to a concatenated human-mouse genome, libraries from pure mouse cells (group D) were mapped to such a genome. The mean percentages of both foreign and spurious fend-pairs in this lane are the same as those found in the different human-mouse mixed lanes, suggesting there is no inter-cellular contamination.

Extended Data Table 3. Sequencing pairing errors.

PhiX174 DNA library was added to four lanes of single cell Hi-C multiplexed libraries. In theory, no mixed mouse-phiX174 read-pair is expected, but in fact a small number were detected. Shown are the fraction of phiX174 DNA loaded to each lane capacity, the percentage of phiX174 read-ends in the lane, and the observed number of read-pairs by type. The pairing probability was crudely estimated from these figures, and from it the number of expected spurious mouse-mouse read-pairs was calculated. Most of these spurious pairs are discarded when the unique identification tags at the beginning of each read-end are matched. Shown is the estimated number of spurious mouse pairs that coincidently have matching identification tag and are therefore not detected and removed.

Extended Data Figure 1. Single cell Hi-C quality controls.

a, Efficiency of biotin labelling at Hi-C ligation junctions for two Hi-C ligation products, showing 90 - 95% efficiency (Supplementary Information). b, Read-pair classification. c, Discarding the missed RE2 read-pairs removes a uniform “blanket” of non-specific contacts from the map. d, Estimating numbers of multiple covered fends. Shown is the dependency between the number of fend-pairs in a sample and the estimated number of autosomal fends covered by more than two fend-pairs under different models. The binomial model (grey line) distributes fend-pairs to fends randomly without any constraint, as if sampling fend-pairs from an infinite number of chromosomes. e, Single-cell Hi-C fragments coverage. Number of fends in each 250 kb genomic bin for Bgl II or Dpn II as RE1. Tail of bins with few fends is for bins of low mappability and near the chromosomes edges. f, Median fend length (distance from RE1 to the first upstream RE2) in each 250 kb genomic bin for Bgl II or Dpn II as RE1. Values larger than 300 bp are of poorly mappabale bins. g, Information on the two restriction enzymes we used for RE1, Bgl II (6 cutter, which we used predominantly) and Dpn II (4 cutter, only used for cell-8). Blind fends do not have a RE2 site in their fragment. Fends in which their first RE2 site starts a non-unique 36 bp sequence are marked as non-unique fends. We discarded both blind and non-unique fends and used only the unique fends. The number of actual fends in a male mouse genome, which have two copies of each autosome and a single X chromosome are shown as well as the median fragment length (chromosomes Y and mitochondrial genome were ignored throughout the analysis). h, Information on the ten single-cell datasets that successfully passed the quality control filters. p-value of the number of autosomal fends with more than two covering fend-pairs was calculated from the binomial model (panel d and Supplementary Information). i, Percentages of read-pair types. j, Percentage of fend-pair types. k, Distribution of fend-pair coverage (number of read-pairs that support each fend-pair) in the ten single-cell datasets. l, Distribution of mean contacts per fend calculated for each mappable 1 Mbp, normalized by the mean value in each cell, and averaged across autosomal or X chromosomes from the ten single-cells.

Extended Data Figure 2. Chromosomal domains.

a, Ratios between intra-domain and inter-domain contact enrichments over genomic distance. The mean single cell trend is shown in black. Chromosomes are grouped into four groups: group 1 (chromosomes 1, 8, 15, 16 and X), group 2 (chromosomes 2, 6, 10, 13 and 18), group 3 (chromosomes 3, 5, 11, 14 and 17) and group 4 (chromosomes 4, 7, 9, 12, 19). The intra- over inter- domain enrichment is persistent in all chromosome groups and does not seem to stem from peculiar chromosomes. b, Distribution of correlations between intra-domain contact numbers of all domains from pairs of real and reshuffled controls. c, Distribution of the insulation score at each fend in nine single cell Hi-C datasets (where RE1 is Bgl II; real cells) is shown in red. Fifty sets of reshuffled cells were produced (see Supplementary Methods) and their insulation score distribution is shown in black. Real cells have a heavier tail of highly insulating loci, which is indicative of non-uniform and cell-specific inter-domain contact structure.

Extended Data Figure 3. Modeling protocol quality controls.

a, Results of structure calculations using restraints from a space-filling Hilbert curve test structure with 4096 particles and four typical results of structure modelling using different numbers of restraints are shown (upper panels). Structure calculations of the Hilbert curve from random positions using different sets of 1024 restraints (lower panel). b, Comparison of RMSD values from Hilbert curve and single cell X chromosome models. Structure calculations for Hilbert curves were repeated 100 times with variable numbers of restraints as shown. The root mean square deviation (RMSD) values between 100 models (precision) using the indicated number of restrains (mean +/− SD) are plotted in blue. The RMSD values between the original Hilbert curve and each of the 100 models (accuracy) for the same numbers of restraints are plotted in green (mean +/− SD). RMSD values from 100 repeated calculations of fine-scale (50 kb backbone) X chromosome structure from the seven single cell datasets are also plotted (red; mean +/− SD). c, Restraint violation analysis. The distances between directly restrained positions in fine-scale (50 kb backbone) X chromosome models are shown. Models for the six single cell datasets (cell-1 to cell-6; red) show no values exceeding the upper bound (dashed line). Calculations with six shuffled interaction maps (created from cell-1 dataset; blue) show significant violations. Structure calculations performed on merged pairs of datasets (yellow; all possible combination of cell-1 to cell-4) have a few violations and are significantly closer to the upper limit. d, Comparison of structure-derived distance matrix from 200 fine-scale X chromosome models from cell-1 (orange) and its single cell Hi-C contacts (black crosses). The orange colour indicates the minimum distance between backbone particles. e, Comparison or X chromosome structural models for six cells computed using low-resolution (500 kb binned) single-cell Hi-C interaction data. The bundles shown represent minimised structural alignments of five models from repeat calculations for each cell. Colours indicate chromosomal positions as shown. Scale bar, 1 μm.

Extended Data Figure 4. Comparison and investigation of models.

a, Pair-wise comparison of fine-scale X chromosome structural models by RMSD analysis. Each pixel represents an RMSD value for a pair-wise comparison of two models. Lighter pixels indicate structures of higher similarity (low RMSD). Diagonal elements have been excluded. The order of 200 models in each panel was determined by hierarchical clustering of the RMSD values. Numbers shown are the mean RMSD values and the standard deviations for all the comparisons for each cell calculated by comparing the Hi-C contact particles. b, Cell-to-cell comparison of 200 fine-scale X chromosome structural models by RMSD analysis. Each pixel represents an RMSD value for a pair-wise comparison of two models. c, Fine-scale X chromosome structures calculated from cell-1 and cell-3 datasets, and a structure from the combined dataset. Colours indicate chromosomal positions as shown. Scale bar, 1 μm. d, Typical structure calculated using a randomised dataset, where the interacting points for cell-1 have been shuffled with a pairing probability proportional to one over the square root of the sequence separation. Colours and scale as shown in c. e, Distribution of measurements of depth from the surface for five loci P1 - P5 (Fig. 3e) in 1200 X chromosome models (200 fine-scale models for each of the six cells). Whiskers on box plots define 10th and 90th percentiles and the outliers are shown as individual dots.

Extended Data Figure 5. Epigenomic landscape of chromosomes

a, Intra-domain contact enrichment for each quartile of trans-chromosomal contacting domains. b, Same as a but subtracting the mean quartile enrichment in each genomic distance emphasizing the differences shown in a. c, Using the same sets as in a but plotting the enrichment of inter-domain contacts within the same chromosome. d, Same as c but subtracting the mean quartile enrichment in each genomic distance. e, Percentage of cells in which high and low H3K4me3 enriched domains are trans-interacting. For each cell the domains with top 10th percentile trans intensity were defined as trans-interacting in that cell. We then counted for each domain the fraction of cells in which that domain was trans-interacting. Shown are the distributions of these fractions for H3K4me3 enriched and non-enriched domains (the top and bottom 25th percentiles, respectively). f, Distribution of the average LaminB1-DamID enrichment in chromosomal domains, color coded according to the enrichment value. g, Domains plotted according to their number of trans- and cis-chromosomal (but excluding intra-domain) contacts, color-coded as in f. The domain LaminB1-DamID enrichment and H3K4me3 peak density are highly anti-correlated (Spearman’s correlation = −0.73). h, Intra-domain contact enrichment for high vs. low quartile of domains stratified by their mean LaminB1-DamID enrichment. Error bars indicate 95% confidence intervals. i, Using the same sets as in h but plotting the enrichment of inter-domain contacts within the same chromosome. Error bars as in h. j, Lamin-B1 domains show a minor decrease in intra-domain contact intensities that might suggest less compacted domains, and significantly increased cis inter-domain contact, maybe due to lack of trans-chromosomal contacts. Topology of Lamin B1, H3K4me3 and trans-contacts on five-model bundles of low-resolution X chromosome models. Regions of low mapability have been excluded. Scale bar, 1 μm.

Extended Data Figure 6. Interchromosomal contacts.

a, Comparison of observed coverage of the trans-chromosomal 1 Mb square bins of each cell (red lines), versus predicted coverage assuming a binomial model (random uniform distribution of contacts to bins; black dashed line). Observed coverage is consistently higher than the uniform model, indicating the highly non-random distribution of trans-chromosomal contacts to genomic bins. b, Trans-chromosomal contact enrichment around observed trans contacts as a function of the contacts total distance on both chromosomes (Manhattan distance in the contact map). Observed and expected (by random uniform contact distribution) number of contacts are counted around each trans contact, and their ratio is shown for the 9 real cells (blue; where RE1 is Bgl II) and reshuffled cells (red), at two different scales. c, Left panel, trans contacts were classified according to H3K4me3 density of the domains they associate: High and low for top and bottom 25th percentiles, respectively, Mid for 25th-75th percentiles. Shown is the log ratio of the contingency table counts with the expected counts generated by multiplying the corresponding marginal probabilities for each group (chi-square test; p = 5.8e-18). To make sure this phenomena is not caused by the trans enrichment of active domains and depletion of non-active ones, only the top 15th percentile trans enriched domains from each cell were used. Middle panel, similar to left panel but contacts are classified by their associated domain gene density (chi-square test; p = 2.3e-12). Right panel, similar to left panel but using domains in the top 40th percentile of gene density, classifying by their H3K4me3 density, to test H3K4me3 enrichment beyond gene density (chi-square test; p = 3.6e-06). In all cases active/gene-rich domains preferentially interact with each other, although active domains (high H3K4me3 density) interact beyond that expected by their gene density.

Extended Data Figure 7. Chromosomal interfaces.

a, The number of interacting chromosomes per chromosome is depicted in circles sized according to the number of single cells the value was observed in, while ordering chromosomes by the number of transcription start sites (TSSs) in each chromosome which is shown by blue bars. Only autosomes are displayed. Spearman correlation between the number of TSSs and the mean value of the number of interacting chromosomes per chromosome is 0.18. Two chromosomes were defined as interacting when they had at least one domain-domain interaction (see main text) supported by two or more contacts. The number of interacting chromosomes per chromosome rises together with the number of TSSs. However, the change is small, and the number of interacting autosomal chromosomes per chromosome (the plotted value divided by two) remains between 4 and 6. b, Same as a except that chromosomes ordered by the number of active H3K4me3 domains (the top 25th percentile H3K4me3 peak density domains). c, Same as a except that chromosomes are ordered by the number of non-LAD basepairs in the chromosome. The fraction of a chromosome covered by LADs ranges from 31% to 53% and is correlated with chromosome size (0.52 Spearman). Thus, chromosome lengths span a range of 3.2 fold change, while their non-LAD fraction spans a smaller range of 2.8 fold change. d, Examining the number of contacts between two chromosomes and the chromosomes sizes. The mean number of contacts of each chromosome with others it interacts with is shown for the ten single cells, ordering chromosomes by their size. Chromosome size is correlated with the number of contacts it has, but the dynamic range of this number is small. e, The number of interacting chromosomes per chromosome is depicted in circles sized as the number of single cells the value was observed in, while ordering the ten single cell datasets by the number of trans contacts in each dataset, shown by blue bars. Only autosomes are displayed. Spearman correlations between the number of trans contacts in each dataset and the mean value of the number of interacting chromosomes per chromosome is 0.73. The number of interacting chromosomes per chromosome rises together with the coverage. However, the change is small, and the number of interacting autosomal chromosomes per chromosome (the plotted value divided by two) remains between 4 and 6. f, Example of multi-way chromosomal interfaces. Contact map of chromosomes 3 and 15 in cell-5. Shown is the number of contacts in 1 Mb size bins. Top and bottom 30th percentiles of H3K4me3 peak density domains are marked in light pink and light grey, respectively. Note the grid-like trans contacts arrangement, and the correspondence between the two large trans contact clusters and the organisation of cis contacts in both chromosomes to large “mega domains”.