Space–time correlations in urban sprawl

Abstract

Understanding demographic and migrational patterns constitutes a great challenge. Millions of individual decisions, motivated by economic, political, demographic, rational and/or emotional reasons underlie the high complexity of demographic dynamics. Significant advances in quantitatively understanding such complexity have been registered in recent years, as those involving the growth of cities but many fundamental issues still defy comprehension. We present here compelling empirical evidence of a high level of regularity regarding time and spatial correlations in urban sprawl, unravelling patterns about the inertia in the growth of cities and their interaction with each other. By using one of the world's most exhaustive extant demographic data basis—that of the Spanish Government's Institute INE, with records covering 111 years and (in 2011) 45 million people, distributed among more than 8000 population nuclei—we show that the inertia of city growth has a characteristic time of 15 years, and its interaction with the growth of other cities has a characteristic distance of 80 km. Distance is shown to be the main factor that entangles two cities (60% of total correlations). The power of our current social theories is thereby enhanced.

1. Introduction

The quantitative description of social human patterns is one of the great challenges of this century. Significant advances have been achieved in understanding the complexity of city growth, urban sprawl, electoral processes and many other social systems [1–17]. One finds that the concomitant patterns can be successfully modelled, involving subjacent universal scaling properties [10,14,18,19], fundamental principles—such as the maximum entropy principle [20–24] or the minimum Fisher information [25,26]—or diffusive and aggregative mechanisms for urban sprawl [27–30]. Also, the interaction between cities (as measured by, for instance, the number of crossed phone calls [31] or human mobility [12]) displays predictable characteristics. Thus, it is plausible to conjecture that some kind of universality underlies collective human behaviour [17,23].

However, many fundamental issues still defy comprehension. Our aim in this work is to answer two question regarding city growth and human migrations: (i) is the growth of cities inertial, i.e. does the population growth in the present year depend on the growth of past years? and (ii) does the growth of a city depend on the growth of neighbouring cities, i.e. does the migration of people from one city to another exhibit spatial patterns? Millions of individual decisions, motivated by economic, political, demographic, rational and/or emotional reasons, underlie the growth rate of a city. Accordingly, one may expect some level of randomness and unpredictability. In this vein, one might think that

• (i) if some inertia is present, the growth rate of the present year could be deduced from that in past years, and

• (ii) if some correlation with other cities exists, the growth rate might be predicted from the rates of other cities.

Thus, the observation and detection of regular space–time patterns in urban population evolution could be viewed as constituting an important step towards understanding collective human dynamics at the macro-scale. Indeed, the parametrization of such regularities could lead to a potential improvement of the present population-projection tools and analysis [32–34].

1.1. Urban growth

The evolution of city population has been described with great success in the past by recourse to Gibrat's law, i.e. geometrical Brownian walkers obeying a dynamical equation that exhibits scale-invariance [6,7,13,19,21,23,24,35]

1.1

where X_i(t) is the population at time t of the ith city (of an ensemble of n cities), stands for its temporal change and v_i(t) for the growth rate. One finds in the literature that this rate usually displays stochastic behaviour in the form of a Wiener process that complies with , so that we deal with uncorrelated noise. In spite of its simplicity, this reductionist model is able to describe many of the observations reported for city-rank distributions. Indeed, this equation can be linearized by defining u_i(t) = log[X_i(t)] thus obtaining , which allows one to recover all well-known properties of regular Brownian motion [21]. Indeed, a ‘thermodynamics of urban population flows’—with the pertinent observables—can be derived following the analogy with physics presented in [23]. However, uncorrelated evolution is assumed in [23] for the sake of simplicity, which entails operating with the equivalent of a scale-free ideal gas. Such an assumption was sufficient for explaining the main properties of the macroscopic state of an ensemble of cities, but a higher level theory that would provide deeper understanding is desirable. Indeed, some sort of interaction between cities is of course to be expected, as well as some kind of inertia. The ensuing correlations are of great importance to understand the complex patters of migration and to improve our predictive power with regards to the subjacent dynamics.

We present in this work empirical evidence of such correlations in the population dynamics of Spain. In §2.1, we first analyse the statistical properties of cities’ growth rates, reconfirming both proportional growth and other previous observations presented in the literature. We pass next to analyse, in §2.2, the time correlation of the growth rates, using demographic data from a time window of 111 years. We encounter a remarkably regular behaviour. We continue, in §2.3, with the analysis of inter-city correlations: instead of comparing each individual growth rate with the average in its surroundings—as found in the literature—we study here correlations of the growth rate for each particular pair of cities. This is akin to describing the raw two-body interaction between cities and is expected to be of a more fundamental nature than the just mentioned literature studies, that involve mean-field, or coarse-grained, descriptions of the interactions we are interested in. Inspired by physics, we compare the city–city correlation with the distance between them, which leads us to define a characteristic correlation distance. Finally, some discussion and conclusions are given in §3.

2. Results

An exhaustive census dataset is indeed needed, something not easy to come by. Fortunately, the Spanish Government's Institute INE [36] provides information about the population of 8100 municipalities—the smallest administrative unit—over a period of 111 years, from 1900 to 2011. They are distributed over a surface of approximately 500 000 km² inhabited by more than 45 million people (2011). Figure 1a displays the spatial distribution of the Spanish municipalities, and figure 1b their time evolution. A typical diffusion pattern is visible. The population's arithmetic and geometric means are also plotted. The former grows with time but the later diminishes, indicating that the population has descended in a majority of towns, reflecting on the migration from countryside to large cities, a common pattern in most of the world. This diffusion process is readily discernible: one appreciates that the width of the distribution indeed grows.

Figure 1.

Characteristics of the dataset. (a) Spatial distribution of Spanish municipalities. Circle's sizes are proportional to the population's logarithm. (b) Evolution of all municipalities. We also give the population per town (solid line, arithmetic mean; dashed line, geometric mean). (c) Variance of the population-change versus population for each municipality (dots). The median value (dotted line) clearly follows equation (2.2) (solid line). (Online version in colour.)

2.1. Statistical properties of growth rates

In order to analyse in more detail the underlying dynamics, we base our considerations on the developments of earlier studies [21,23,24]. It is shown there that the dynamical growth equation for city populations exhibits the general appearance

2.1

where w_i(t) is a Wiener coefficient independent of v_i(t). We face stochastic proportional growth in the first term to which a finite-size contribution (FSC) is added in the second one. The later becomes small for large sizes but is important for small ones. The second term can be regarded as ‘noise’ and is thus expected to be independent of the proportional growth. Accordingly, the variance of the growth over the population —a quantity defined only for convenience in representing the data—can be written as

2.2

where σ_vi and σ_wi are the associated deviations of v_i and w_i, respectively. (Note that we have followed the approximation made in [23], where it is shown that the variation of the population X_i is much smaller than the variation of the growth rates.)

Comparison with the data entails appealing to numerical time derivatives for each . We use yearly data from 1996 till 2011 (whenever the appropriate datasets are available for each intermediate year) to generate the graph of figure 1c, which displays the —pairs for all the Spanish municipalities. One computes

2.3

2.4

where T = 14 is the total number of datasets used for this calculation. The median nicely fits equation (2.2), with σ_v = 0.0119 and σ_w = 0.47, respectively. Note that FSC fluctuations are larger than multiplicative ones, the later dominating, of course, for large sizes. The transition between both regimes occurs at inhabitants.

2.2. Empirical observation of inertial growth

To find whether there exists a systematic dependence between successive yearly growths (or inertia), we consider first the n-cities average and variance such that

2.5

and

2.6

where x_i(t) = X_i(t)/N(t) with N(t) the total population at time t, excluding in this fashion the effects of the total population growth. Time correlations have been obtained via the Pearson product-moment correlation coefficient (Corr) between datasets pertaining to different years t and t + Δt as

2.7

The mean correlation as a function of the time-interval Δt is obtained as the average

2.8

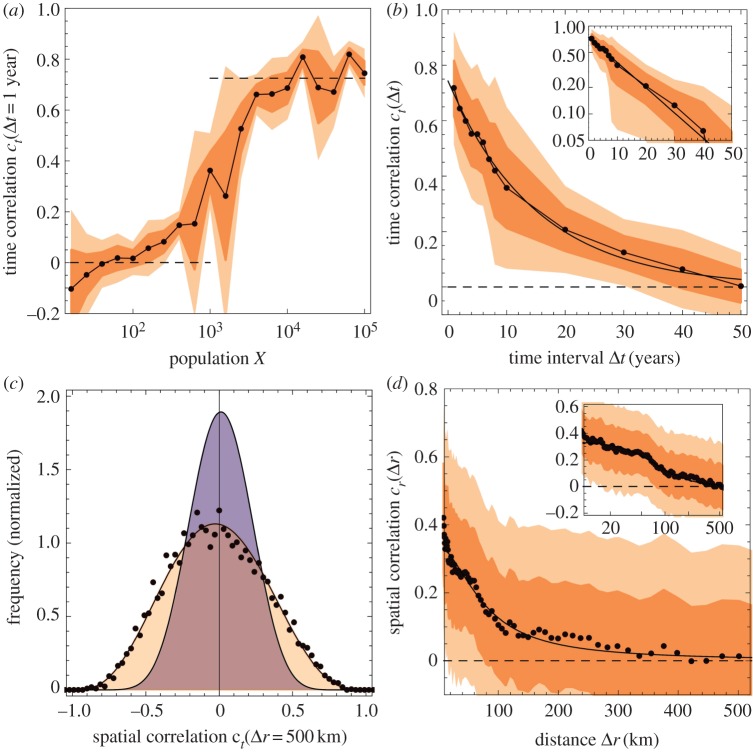
where T is now the total number of available datasets for each case. We study first such correlations as a function of the population window, where two different situations are encountered. Within a standard deviation, no correlations exist for low populations, but they are significative for large ones, as indicated in figure 2a. The transition between the two ensuing regimes takes place at populations of approximately 1000 inhabitants. Thus, for the finite-size term in (2.3) no time correlations are detected. They do appear, though, in the proportional growth regime. Accordingly, we evaluate time correlations for municipalities with populations of more than 10 000 inhabitants during a period of up to 50 years. We find that correlations decay as the time-interval Δt between observations increases (figure 2b). In a logarithmic representation of the mean value of the correlations, we find a linear relationship with time (inset of figure 2b), leading to a nice fit via an exponential function of the form

2.9

with a_t = 0.74 ± 0.02 and τ = 15 ± 1 years. The coefficient of determination R² is equal to 0.997. Accordingly, the correlation's mean time in the demographic flux is around 15 years.

Figure 2.

Empirical space–time correlations of population growth. (a) Time correlations versus town sizes for yearly relative growths (dotted line). The shaded area represents the width determined by one standard deviation (darker shadow) and by two of them (lighter shadow). Horizontal dashed lines are just visual aids for the limits at low and high population. (b) Time correlation for the relative growth of towns populated by more that 10 000 inhabitants. Shaded areas represent widths determined by one (darker shadow) and two (lighter shadow) standard deviations, respectively. Inset: same representation, but in a log scale. The exponential fit of equation (2.9) acquires thus more visibility. (c) Comparison of widths: bivariate normal versus empirical correlations distribution. (d) Spatial correlation of Spain's municipalities’ relative growth for populations larger than 10 000 inhabitants. In black, the Lorentz shape of equation (2.12) (for α = 2) compared with the empirical mean (dots). Inset: same representation, with a log scale for the distance. (Online version in colour.)

2.3. Empirical observation of spatial correlations

We pass now to a study of the demographical entanglement between two given cities, as represented by spatial correlations. The correlation coefficient between the ith and jth city reads

2.10

where the covariances, variances and means are time averages as in equation (2.3). Among a host of possible entanglement factors, we choose here to study the simplest one: distance between cities Δr. Accordingly, we evaluate correlations between cities versus their pertinent distance dist(i,j) via the histogram

2.11

We find that for towns with more than 10 000 inhabitants—within the proportional growth regime—the mean value of the spatial correlation is positive and decays with distance. In a logarithmic representation for the distance, we find that this decay is slower than exponential (inset of figure 2d), following a power law for large distances but saturating at short distances. The simplest analytical form that describes this behaviour is an expression of the form

2.12

Indeed, the correlation is finite at Δr = 0 and decays as ∼Δr^–α for large distances. Fitting this function to the data, we obtain a_r = 0.33 ± 0.02, r₀ = 76 ± 10 km, and α = 1.8 ± 0.3, with a coefficient R² of 0.9159. Instead, fixing for convenience α = 2 (that yields a Lorentz function), we get a_r = 0.33 ± 0.01 and r₀ = 79 ± 8 km, with R² = 0.9156. As the concomitant two ways of fitting are indistinguishable according to the R² coefficient, we adopt α = 2 for simplicity. As a consequence, the typical ‘demographic distance’ turns out to be (on average) of approximately 80 km, decaying with r^–2 at large distances. Thus, we face long-range correlations. The influences of other factors, though, make these correlations vanish at about 500 km. We use our data to compare (i) the width of c(Δr) with (ii) that expected for a bivariate normal distribution [37] (see appendix A). The empiric width is larger than the bivariate one: 0.327 versus 0.204 (figure 2c), indicative of the presence of additional, distance-independent, correlations. We deduce that the separation between towns, that is, their mutual distance, is the origin of about a 60% of the total correlation between them.

3. Discussion and conclusion

Summing up, we have demonstrated that the relative growth of a city's population exhibits both (i) inertia and (ii) correlation with the relative growth of neighbouring cities, with distance as the main variable that underlies the town–town interaction. Indeed, these patterns can be used to improve the predictive power of present techniques for demographic projection. However, further improvements are needed in order to identify the undefined correlations within the actual data whose existence we have discovered. We expect that these correlations will depend on local circumstances and also on the particular socio-economic status of each city. Indeed, economic factors such as the market area, market potential or basin of attraction, will contribute to that undefined 40% of the total correlation. One important contribution to these undefined correlations can be attributed to the fact that we use distances between cities regardless of the transportation network. It is expected that the correlation between two well-connected cities (in terms of roads, trains and/or air bridges) will be larger than that of two other cities, separated by the same distance, but without these facilities (or with natural barriers between them as seas, rivers or mountains). Even if all these effects are compensated at the macroscopic level and distance becomes a good observable as we have shown here, a more accurate microscopic determination of the fundamental behaviour of interactions should include these particular local variations, using, for example, the mean time required for travelling from one city to the other. In addition, we have implicitly treated the cities as point-like particles in the sense of idealized bodies of zero dimension—i.e. with no internal structure nor extension in space. This reductionistic ideal scenario helps us to isolate effects or mechanisms and works well at the scale of the distances studied here, but the internal structure of cities should become important at those distances where the correlation saturates (less than 10 km, as shown in the inset of figure 2d). We think that it will be interesting to understand the influence of the correlations here displayed on the morphology of the cities, and we hope that both the interplay between them and the associated mechanisms of road and diffusion dynamics studied in, e.g. [27–30], will be unravelled in the near future. In view of our results, a quantitative model for the evolution of city populations should be able to include these correlations, as well as all the other well-known features of city growth’ statistics, such as the power-law or lognormal distribution of city populations. Work on this subject is in progress.

Appendix A. Distribution of correlation coefficients

For a bivariate normal distribution, the distribution of correlation coefficients is given by

A1

where c stands for the correlation value that one might numerically obtain using equation (2.10), C is the actual correlation value and T the number of data-point used to evaluate c.

Funding statement

This work was partially supported by Social Thermodynamics Applied Research (SThAR) (to A.H. and R.H.), and the project PIP1177 of CONICET (Argentina), and the projects FIS2008-00781/FIS (MICINN)-FEDER, EU, Spain (to A.R.).