High-order fractional partial differential equation transform for molecular surface construction

Abstract

Fractional derivative or fractional calculus plays a significant role in theoretical modeling of scientific and engineering problems. However, only relatively low order fractional derivatives are used at present. In general, it is not obvious what role a high fractional derivative can play and how to make use of arbitrarily high-order fractional derivatives. This work introduces arbitrarily high-order fractional partial differential equations (PDEs) to describe fractional hyperdiffusions. The fractional PDEs are constructed via fractional variational principle. A fast fractional Fourier transform (FFFT) is proposed to numerically integrate the high-order fractional PDEs so as to avoid stringent stability constraints in solving high-order evolution PDEs. The proposed high-order fractional PDEs are applied to the surface generation of proteins. We first validate the proposed method with a variety of test examples in two and three-dimensional settings. The impact of high-order fractional derivatives to surface analysis is examined. We also construct fractional PDE transform based on arbitrarily high-order fractional PDEs. We demonstrate that the use of arbitrarily high-order derivatives gives rise to time-frequency localization, the control of the spectral distribution, and the regulation of the spatial resolution in the fractional PDE transform. Consequently, the fractional PDE transform enables the mode decomposition of images, signals, and surfaces. The effect of the propagation time on the quality of resulting molecular surfaces is also studied. Computational efficiency of the present surface generation method is compared with the MSMS approach in Cartesian representation. We further validate the present method by examining some benchmark indicators of macromolecular surfaces, i.e., surface area, surface enclosed volume, surface electrostatic potential and solvation free energy. Extensive numerical experiments and comparison with an established surface model indicate that the proposed high-order fractional PDEs are robust, stable and efficient for biomolecular surface generation.

1. Introduction

Recently, great interests have been witnessed in fractional calculus modeling in many fields of science and engineering, from geophysics to biology. Fractional derivatives extend the concept of ordinary derivatives and serve as a good tool for taking into account memory mechanism in the random walk and anomalous diffusion in physical problems [17, 36]. In fact, a fractional derivative occurs as common as an exponent. For example, it is well known that the Kolmogorov scaling exponent that predicts turbulent energy spectrum follows a power law E(w)∝ w^−p, where w is the wavenumber, p is a real number, and 0 < p < 3. Such a power law in the wavenumber corresponds to the fractional derivative of order α in the coordinate space, since the inverse Fourier transform of an exponent gives rise to a derivative of the same order. Fractional derivative has found its success in physical and biological modeling [2, 10, 70], financial analysis [26, 44, 46], and image processing [3]. Currently, most attention in the field is paid to the fractional derivatives of order less than 2. High-order fractional derivatives are hardly used, partly due to the limited understanding of their physical meanings. Geometric flows have become an established approach to image analysis, data processing and surface generation in the past two decades. Particularly, the application of mean curvature flows has been a popular subject in applied mathematics for image analysis, material design [40, 49, 50] and surface processing [71]. The first use of partial differential equations (PDEs) for image analysis dates back to 1983 [64]. Witkin noticed that the evolution of an image under a diffusion operator is mathematicaly equivalent to the standard Gaussian low-pass filtering for image denoising [64]. A major advance in this topic was due to Perona and Malik, who introduced an anisotropic diffusion equation [43] to protect image edges during the diffusion process. The Perona-Malik equation is nonlinear and stimulated many interests in applied mathematics [14, 43, 51, 59, 61]. Over the past two decades, many related mathematical techniques, such as the level set formalism devised by Osher and Sethian [42, 49], Mumford-Shah variational functional [38], and total variation methods [45], have been widely used for image analysis [9, 12, 41, 45, 48].

Another aspect in geometric flow development is the use of high-order geometric PDEs for image processing or surface analysis. The Willmore flow, proposed in 1920s, is a fourth-order geometric PDE. Motivated by the hyperdiffusion in the pattern formation in alloys, glasses, polymer, combustion, and biological systems, Wei introduced one of the first families of arbitrarily high-order geometric PDEs for edge-preserving image restoration in 1999 using the Fick’s law [59]

$$\frac{\partial u(\mathbf{r},t)}{\partial t}=-\sum _q\nabla ·{\mathbf{j}}_q+e(u(\mathbf{r},t),|\nabla u(\mathbf{r},t)|,t),\mathbf{r}\in {ℝ}^n,q=0,1,2,\cdots$$ (1)

where u(r, t) is the processed image function, $\nabla =\frac{\partial }{\partial \mathbf{r}}$, and e(u(r, t), |∇u(r, t)|, t) is a nonlinear operator. The nonlinear hyperflux j_q is given by

$${\mathbf{j}}_q=-d_q(u(\mathbf{r},t),|\nabla u(\mathbf{r},t)|,t)\nabla {\nabla }^{2q}u(\mathbf{r},t),$$ (2)

where d_q(u(r, t), |∇u(r, t)|, t) are edge sensitive diffusion coefficients.

Equation (1) is subject to the initial image data u(r, 0) = X(r) and appropriate boundary conditions. The essential idea of Equation (1) is to accelerate the noise removal in the Perona-Malik equation [43] by higher order derivatives, which is more efficient in noise dissipation.

As a generalization of the Perona-Malik equation, the hyperdiffusion coefficients d_q(u, |∇u|, t) in Eq. (1) can also be chosen as the Gaussian form

$$d_q(u(\mathbf{r},t),|\nabla u(\mathbf{r},t)|,t)=d_{q0}\text{exp}[-\frac{|{\nabla }^{q}u{|}^2}{2{\sigma }_q^2}],q=0,1,$$ (3)

where the constant d_q0 depends on the noise level, and σ₀, σ₁ are chosen as the local statistical variances of u and ∇u, respectively, i.e.,

$${\sigma }_q^2(\mathbf{r})=\overline{|{\nabla }^{q}u-\overline{{\nabla }^{q}u}{|}^2}.$$ (4)

The notation $\overline{Y(\mathbf{r})}$ above denotes the local average of Y (r) centered at position r. The measure based on the local statistical variance is important for discriminating image features from noise. As a result, one can bypass the image preprocessing, i.e., the convolution of the noise image with a smooth mask in the application of the PDE operator to noisy images, which is a very tricky process in the application of geometric flows to noisy iamges. High order geometric PDEs have been widely applied to image and surface analysis [4, 13, 14, 28, 29, 34, 53, 59, 66]. Recently, arbitrarily high-order geometric PDEs have been modified for molecular surface formation and evolution [4]

$$\frac{\partial S}{\partial t}={(-1)}^q\sqrt{g(|\nabla {\nabla }^{2q}S|)}\nabla ·\left(\frac{\nabla ({\nabla }^{2q}S)}{\sqrt{g(|\nabla {\nabla }^{2q}S|)}}\right)+P(S,|\nabla S|),$$ (5)

where S is the hypersurface function, g(|∇∇^2qS|) = 1 + |∇∇^2qS|² is the generalized Gram determinant and P is a generalized potential term, including microscopic interactions in biomolecular surface construction. When q = 0 and P = 0, Eq. (5) recovers the mean curvature flow used in our earlier construction of minimal molecular surfaces [6]. It reproduces the surface diffusion flow [4] when q = 1 and P = 0. It has been shown that the surface generated with the fourth order geometric PDE demonstrates a morphology distinguished from that obtained with the mean curvature flow. Over the past decade, the mathematical analysis of high-order geometric PDEs has attracted much attention. For example, Bertozzi and Greer have analyzed fourth order nonlinear PDEs in the Sobolev space and proved the existence and uniqueness of the solution to a case with H¹ initial data and a regularized operator [7, 28, 29]. Xu and Zhou [65] showed the well-posedness of the solution of fourth order nonlinear PDEs. Recently, Jin and Yang have found that the mathematical structure of Wei’s fourth order equation differs from that of other fourth order PDEs derived from variational formulation [33]. These authors proved the existence of the strong solution of Wei’s fourth order equation. Most recently, Guidotti and Longo have shown the existence of the solution to a class of fourth order diffusion operators [31] and proposed two enhanced fourth order diffusion models for image denoising [30]. Due to the stiffness of high-order nonlinear PDEs, computational techniques for solving higher order geometric PDEs are important issues. Alternating direction implicit (ADI) schemes are developed in the literature for integrating high-order nonlinear PDEs [4, 63]. However, in the treatment of digital images, signals and data, the mesh sizes can be set to unit. As such, the numerical stability problem of high-order PDEs is gone.

For a long time, the study of geometric flows for image analysis had been essentially limited to the construction of nonlinear PDE based low-pass filters. From the point of view of image and signal processing, low-pass filters are just one specific type of filters, while other filters, such as high-pass filters and band-pass filters are equally important. This problem was first addressed by Wei and Jia [61], who introduced the nonlinear PDE based high-pass filters for image edge detection in 2002,

$$u_t(\mathbf{r},t)=F_1(u,\nabla u,{\nabla }^{2}u,\dots )+{\epsilon }_u(v-u)$$ (6)

$$v_t(\mathbf{r},t)=F_2(v,\nabla v,{\nabla }^{2}v,\dots )+{\epsilon }_v(u-v)$$ (7)

where u(r, t) and v(r, t) are scalar fields, ε_u and ε_v are coupling strengths. Here F₁ and F₂ are general nonlinear diffusion operators, and can be chosen as the Perona-Malik operator F₁ = ∇·d₁(|∇u|)∇ and F₂ = ∇·d₂(|∇v|)∇. The initial values for both nonlinear evolution equations are chosen to be the same image, i.e., u(r, 0) = v(r, 0) = X(r). As a nonlinear dynamic system, the time evolution of Eqs. (6) and (7) will eventually lead to a synchronization in the solution for positive nonzero coupling coefficients. In image processing, Eqs. (6) and (7) are designed to evolve at dramatically different time scales, for example, d₂₀ ≫ d₁₀ ≥ 0. The image edges are obtained as the difference [61]

$$w(\mathbf{r},t)=u(\mathbf{r},t)-v(\mathbf{r},t).$$ (8)

It was shown that Eq. (8) behaves like a band-pass filter when d₂₀ ≫ d₁₀ ~ 0. The essential idea of this approach is that when two coupled evolution PDEs are evolving at dramatically different speeds, the difference of the two low-pass PDE operators gives rise to a band-pass or high-pass filter, depending on the selection of diffusion parameters. The coupling terms (ε_u(v−u)) play the role of relative fidelity, and balance the disparity of two images. The nonlinear PDE based high-pass filters have been extensively validated. In particular, they work extremely well for images with large amount of textures, i.e., the Barbara image, and outperform classical Sobel, Prewitt, and Canny operators [52, 61].

A major extension of our earlier nonlinear PDE based high-pass filters is the introduction of the PDE transform [55, 56, 58], which is a systematic method for decomposing images, signals, and data into various functional modes. Functional modes are mode components which share the same band of frequency as well as same category, i.e., trend, edge, texture, noise etc. A major motivation in this development is the empirical mode decomposition (EMD), which enables the processing of non-uniform and non-stationary signals [32, 57]. However, the PDE transform is typically more robust than the Hilbert-Huang transform [32] and can be easly applied to multi-dimensional data. Like the wavelet transform, PDE transform iteratively decomposes data into physically meaningful functional modes and allows perfect reconstruction. Unlike the wavelet transform, which typically offers fixed time-frequency localization, the PDE transform gives controlled time-frequency localization by adjusting the order of the PDE and/or the evolution time. The result of the wavelet transform is normally in the frequency representation or wavelet subspaces, while the outcome of the PDE transform is still in the physical representation, which is convenient for subsequent processing. Once the intrinsic functional modes are obtained by the PDE transform, subsequent processing or secondary processing of the individual functional modes enables us to achieve our goals of signal, image, surface and data analysis. Typical tasks include edge detection, feature extraction, trend estimation, enhancement, denoising, texture analysis, segmentation, pattern recognition, etc [55, 56, 58]. In addition to these tasks, the PDE transform has also been applied to the surface construction of proteins and viruses [76]. Although all of the important apparatuses for the PDE transform were developed in our earlier work, namely, arbitrarily high-order nonlinear PDE filters [59] and nonlinear PDE based band-pass or high-pass filters [61], the PDE tranform offers a renewed understanding about geometric PDE based methods and a new tool for signal, image and data analysis.

The objective of the present work is to introduce arbitrarily high-order fractional PDEs and the fractional PDE transform for the analysis of molecular surfaces in molecular biosciences. Since arbitrarily high integer order nonlinear PDEs was originally introduced to account for hyperdiffusion in physical and biological systems [59], it is natural to consider arbitrarily high-order fractional PDEs and the fractional PDE transform, which utilizes arbitrarily high-order fractional derivatives. It is well known that fractional derivatives can be defined in a few different ways. We discuss the finite difference, the Fourier representation and the integral forms of fractional derivatives. A variational derivation of fraction PDEs is presented. To avoid the strict stability constraints of solving high-order fractional PDEs and to achieve the desirable efficiency in the surface generation, we make use of the fast fractional Fourier transform (FFFT) algorithm to realize the fractional PDE transform. The present algorithm is of order O(N lnN). Extensive numerical test and application validate the proposed fractional PDE transform.

This paper is organized as follows. Section 2 is devoted to the theory and formulation of arbitrarily high order fractional PDEs and fractional PDE transform. We first briefly discuss three different fractional approaches to review the concepts and establish notations. Then a variational derivation of fractional PDE transform is presented and an arbitrarily highorder fractional PDE are derived by using the fractional hyperdiffisuon. Numerical methods for solving the high-order fractional PDEs are given in section 3. The performance of the proposed high-order fractional PDEs for molecular surface generation is also examined. In this section, we investigate three sets of initial data for their performance in the molecular surface generation with different orders and propagation time periods of the proposed high-order fractional PDEs. In addition, the computational efficiency, as well as surface areas and surface enclosed volumes of the present method is studied for a large set of proteins, including some very large proteins. In section 4, we present the application of the proposed approach to the electrostatic analysis via the Poisson-Boltzmann model. Finally, we consider the solvation analysis of 17 molecules and compare our model prediction with experimental data, which leads to an excellent agreement. This paper ends with conclusion remarks.

2. Theory and algorithm

This section provides theory and algorithm for arbitrarily high-order fractional PDEs and fractional PDE transform. To establish notations, we first briefly discuss a few approaches for fractional derivatives. The fractional PDE transform is constructed via a variational analysis.

2.1. Fractional derivatives

There are many different approaches for the definition and understanding of fractional derivatives. Among them, fractional finite difference schemes, fractional Fourier representations and the integral forms of fractional derivatives are the most popular ones.

2.1.1. Fractional finite difference schemes

Finite differences provide a natural representation of fractional derivatives. There are three types of standard finite difference schemes, namely, forward, backward and central finite differences. As a consequence, three fractional finite difference schemes can be defined accordingly. For any integer α > 0, the α-th order backward finite difference operator is given by [36]

$${\mathrm{\Delta }}_{h,b}^{\alpha }u(x)=\sum _{m=0}^{\alpha }{(-1)}^m\left(\begin{array}{c}\hfill \alpha \hfill \\ \hfill m\hfill \end{array}\right)u(x-mh),h>0,$$ (9)

where the Binomial coefficients

$$\left(\begin{array}{c}\hfill \alpha \hfill \\ \hfill m\hfill \end{array}\right)=\frac{\alpha !}{m!(\alpha -m)!}.$$ (10)

For example, when α = 1 and 2, the first and second order backward finite difference schemes are

$$\frac{{\mathrm{\Delta }}_{h,b}u(x)}{h}=\frac{u(x)-u(x-h)}{h}$$ (11)

and

$$\frac{{\mathrm{\Delta }}_{h,b}^{2}u(x)}{h^2}=\frac{u(x)-2u(x-h)+u(x-2h)}{h^2},$$ (12)

respectively.

Equation (9) can be generalized to the case for any real number α > 0, in which the Binomial coefficients are expressed in terms of Gamma function Γ, i.e.,

$$\left(\begin{array}{c}\hfill \alpha \hfill \\ \hfill m\hfill \end{array}\right)=\frac{\mathrm{\Gamma }(\alpha +1)}{\mathrm{\Gamma }(m+1)\mathrm{\Gamma }(\alpha -m+1)},$$

and hence

$${\mathrm{\Delta }}_{h,b}^{\alpha }u(x)=\sum _{m=0}^{\frac{a_2-a_1}{h}}{(-1)}^m\frac{\mathrm{\Gamma }(\alpha +1)}{\mathrm{\Gamma }(m+1)\mathrm{\Gamma }(\alpha -m+1)}u(x-mh),$$

where a₁ and a₂ are the lower and upper bound of differentiation, respectively. Thus, the factional derivative of order α can be defined as

$$u^{(\alpha )}=\underset{h\to 0}{\text{lim}}\frac{{\mathrm{\Delta }}_{h,b}^{\alpha }u}{h^{\alpha }}.$$ (13)

One special property of the fractional finite difference operator in Eq. (9) is that it utilizes all the node points to the left. Similarly, one can define the fractional derivatives of α-th order by forward and central finite difference operators. Finite difference based fractional derivatives find their applications in anomalous diffusion [37].

2.1.2. Fractional Fourier schemes

It is well known that Fourier transform provides a practical approach for computing integer derivatives and solving differential equations. It can be similarly used for fractional derivatives [36]. Consider the Fourier transform

$$\widehat{u}(w)={\int }_{-\infty }^{\infty }{e}^{-iwx}u(x)dx.$$ (14)

The Fourier transform of the backward finite difference operator in Eq. (9) is given by

$$\widehat{{\mathrm{\Delta }}_{h,b}^{\alpha }u}(w)=\sum _{m=0}^{\infty }{(-1)}^m\left(\begin{array}{c}\hfill \alpha \hfill \\ \hfill m\hfill \end{array}\right)e^{-imhw}\widehat{u}(w)={(1-e^{-ihw})}^{\alpha }\widehat{u}(w),$$ (15)

where Binomial coefficients vanish when m > α. Consequently, the corresponding Fourier transform for (13) is

$$\widehat{u^{(\alpha )}}(w)=\underset{h\to 0}{\text{lim}}\frac{\widehat{{\mathrm{\Delta }}_{h,b}^{\alpha }u}}{h^{\alpha }}=\underset{h\to 0}{\text{lim}}{\left(\frac{1-e^{-ihw}}{h}\right)}^{\alpha }\widehat{u}(w)={(iw)}^{\alpha }\widehat{u}(w),$$ (16)

where the last step makes use of the Taylor expansion e^−ihw = 1 − ihw + O(h²) as h → 0.

There are many other ways to derive Eq. (16). Consider the central finite difference in the Fourier domain defined as [3]

$$\widehat{D^{n}u}=(e^{ihw/2}-e^{-ihw/2})\widehat{D^{n-1}u}=\cdots ={(e^{ihw/2}-e^{-ihw/2})}^n\widehat{u},$$ (17)

where the n th-order finite difference Dⁿu is defined by

$$D^{n}u(x)=D(D^{n-1}u)=\cdots =D^{n-1}(Du)=D^{n-1}\left(u\right(x+\frac{h}{2})-u(x-\frac{h}{2}\left)\right).$$ (18)

As an extension of the Fourier transform of the nth-order finite difference, one has

$$\widehat{D^{\alpha }u}={(e^{ihw/2}-e^{-ihw/2})}^{\alpha }\widehat{u}.$$ (19)

Consequently, generalized fractional-order derivative is given by

$$\widehat{u^{(\alpha )}}=\underset{h\to 0}{\text{lim}}\frac{\widehat{D^{\alpha }u}}{h}=\underset{h\to 0}{\text{lim}}{\left(\frac{e^{ihw/2}-e^{-ihw/2}}{h}\right)}^{\alpha }\widehat{u}={(iw)}^{\alpha }\widehat{u},$$ (20)

where the last step uses Taylor expansion e^ihw/2 = 1 + ihw/2 + O(h²) and e^−ihw/2 = 1 − ihw/2 + O(h²) when h → 0. As a result, Eq. (16) is also concluded.

When α is an integer, i.e., α = n, Eq. (16) becomes

$$\widehat{u^{(n)}}={(iw)}^n\widehat{u},$$ (21)

which is consistent with the classical derivative in the Fourier representation. Moreover, when α = 2m is an even number, we have

$$\widehat{u^{(2m)}}={(-1)}^m{(w)}^{2m}\widehat{u}.$$ (22)

Furthermore, using the Euler’s formula i = exp(iπ/2), Eq. (16) can be reformulated as

$$\widehat{u^{(\alpha )}}=e^{i\alpha \pi /2}{w}^{\alpha }\widehat{u}.$$ (23)

The expression in Eq. (16) can be numerically computed via Eq. (23).

2.1.3. Integral forms

For any real number α > 0, the Caputo fractional derivative of order α is defined as [11]

$$D^{\alpha }u=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_0^x\frac{u^{(n)}(t)}{{(x-t)}^{\alpha +1-n}}dt,n-1<\alpha <n,$$ (24)

where it requires the absolute integrability of u up to the n-th integer derivatives. Meerschaert has developed a discrete approximation to integral form of fractional derivative in Eq. (24) based on the shifted Gr�unwald approximation [37].

Somewhat less restrictive integral definitions have also been given in the literature by making use of Mittag-Leffler-type functions [35]. For any real number β > 0, denote by I^βf(x) the Riemann-Liouville integral

$$I_{t_1,t_2}^{\beta }u(x)=\frac{1}{\mathrm{\Gamma }(\beta )}{\int }_{t_1}^{t_2}u(t){(x-t)}^{\beta -1}dt.$$ (25)

Then the left and right Riemann-Liouville fractional derivatives of order α for a function u(x) are given by [1]

$$D_l^{\alpha }u=\frac{d^n}{d{x}^n}{I}_{\alpha ,x}^{n-\alpha }u(x)$$ (26)

and

$$D_r^{\alpha }u={(-1)}^n\frac{d^n}{d{x}^n}{I}_{x,b}^{n-\alpha }u(x),$$ (27)

respectively. In the integral, a and b are the lower and upper bounds, which are typically taken as −∞ and ∞, respectively. The right Riemann-Liouville fractional derivative operates on the right (or future) state of the function u(x) and thus is less popular in the literature. However, it is useful in variational formulations.

If α is an integer, these derivatives are defined in the usual sense, namely

$$D_l^{\alpha }u=\frac{d^{\alpha }}{d{x}^{\alpha }}u(x),\alpha =1,2,\cdots ,$$ (28)

and

$$D_r^{\alpha }u={(-1)}^{\alpha }\frac{d^{\alpha }}{d{x}^{\alpha }}u(x),\alpha =1,2,\cdots .$$ (29)

The left Riemann-Liouville fractional derivative is one of the most popular definitions. Some interesting properties and history of Riemann-Liouville fractional derivatives have been discussed in Ref [35].

2.2. High-order fractional PDEs and fractional PDE transform

2.2.1. Review of integer-order PDE transform

The PDE transform of arbitrarily high integer order PDEs has been introduced in our earlier work [55, 58]. Since variational approaches have found their success in a variety of scientific and engineering fields [6, 16, 18–20, 45, 60, 62], a variational derivation of the PDE transform has also been presented [55, 76]. Here we briefly review the variational derivation of the PDE transform. Let r = (x, y, z) ∈ ℝ³ and denote by $\nabla =\frac{\partial }{\partial r}$ a gradient operator in ℝ³. For any integer q > 0, we consider the energy functional

$$E(u,{\nabla }^{q}u)=\int [\mathrm{\Lambda }(|{\nabla }^{q}u{|}^2)+\epsilon {(X-u)}^2]d\mathbf{r},$$ (30)

where ε is a constant, ε(X − u)² is the fidelity term, X is the original data, and Λ(·) is an appropriate penalty function.

Some of the most commonly used penalty functions include the Tikhonov form [20, 34]

$$\mathrm{\Lambda }(x^2)=x^2,$$ (31)

the mean curvature form

$$\mathrm{\Lambda }(x^2)={({\sigma }^2+x^2)}^{\frac{1}{2}},$$ (32)

and the Gaussian form

$$\mathrm{\Lambda }(x^2)=e^{x^2/2{\sigma }^2}.$$ (33)

Minimizing the energy functional (30) by using the Euler-Lagrange equation, we have

$${\nabla }^q{\mathrm{\odot }}^q{\mathrm{\Lambda }}_{uq}(|{\nabla }^{q}u{|}^2){\nabla }^{q}u+\epsilon (X-u)=0,$$ (34)

where ⊙^q represents an appropriate inner product and

$${\mathrm{\Lambda }}_{uq}={(-1)}^{q+1}\partial \mathrm{\Lambda }/\partial |{\nabla }^{q}u{|}^2.$$ (35)

To efficiently solve Eq. (34), we introduce an artificial time t and convert it into a time-dependent PDE

$$\frac{\partial u}{\partial t}={\nabla }^q{\mathrm{\odot }}^q{\mathrm{\Lambda }}_{uq}(|{\nabla }^{q}u{|}^2){\nabla }^{q}u+\epsilon (X-u).$$ (36)

Equation (36) is essentially equivalent to our earlier variational derivation of the PDE transform [55], however, in our Ref. [55], there is a typo, specifically, in page 2003, Λ_uj (·) and Λ_vj (·) should be defined as Λ_uj (·) = (−1)^j+1∂Λ_u/∂|D^ju|² and Λ_vj (·) = (−1)^j+1∂Λ_v/∂|D^jv|²respectively.

Given the initial data X, the PDE transform is realized by an iterative process of Eq. (36). Denote the solution of Eq. (36) by X̌ (t) such that

$${\mathrm{X̌}}^k(\mathbf{r},t)=ℒX^k(\mathbf{r}),$$ (37)

where ℒ is the solution operator associated with Eq. (36), i.e., ℒu(r, 0) = u(r, t). Here X̌^k (r, t) are intrinsic functional modes and X^k (r) is the kth residue function defined by

$$X^1=X(\mathbf{r})$$ (38)

and

$$X^k=X^1-\sum _{j=1}^{k-1}{\mathrm{X̌}}^j,k=2,3,\cdots .$$ (39)

Obviously, there is a perfect reconstruction of the original data X in terms of all the functional modes and the last residue

$$X=\sum _{j=1}^{k-1}{\mathrm{X̌}}^j+X^k.$$ (40)

Note that the PDE transform given in Eq. (37) recursively extracts functional modes based on the input residue function. Due to change of initial data during the iterative procedure, the PDE transform is a nonlinear process even if a linear PDE operator is employed.

The first functional mode produced by the present PDE transform is the trend of the data, i.e., a low frequency mode. The residue of the trend is an edge function, i.e., a high frequency mode, including possible noisy. By systematically repeating the low-pass PDE transform (37), one can extract all the desirable higher order mode functions step by step [58].

2.2.2. Variational derivation of high-order fractional PDEs

Motivated by the PDE transform and fractional derivatives, we propose a fractional PDE transform. A key component of the fractional PDE transform is an arbitrarily high-order fractional PDE, which is defined via the fractional variational principle. Many authors have discussed the fractional variational principle [1, 3]. For any α ∈ ℝ and 0 < α < ∞, denote by ${\nabla }^{\alpha }=(\frac{{\partial }_l^{\alpha }}{\partial x^{\alpha }},\frac{{\partial }_l^{\alpha }}{\partial y^{\alpha }},\frac{{\partial }_l^{\alpha }}{\partial z^{\alpha }})$ a gradient vector in ℝ³, where $\frac{{\partial }_l^{\alpha }}{\partial x^{\alpha }}$ is the left Riemann-Liouville fractional derivative of order α in x, according to Eq. (26), similar notations are adopted for the fractional derivatives in y and z. The adjoint of ∇^α is defined as ${\nabla }_{*}^{\alpha }=(\frac{{\partial }_r^{\alpha }}{\partial x^{\alpha }},\frac{{\partial }_r^{\alpha }}{\partial y^{\alpha }},\frac{{\partial }_r^{\alpha }}{\partial z^{\alpha }})$, with the right Riemann-Liouville fractional derivative in (27).

We now consider the general energy functional

$$E(u,{\nabla }^{\alpha }u,{\nabla }_{*}^{\alpha }u)=\int F(u,{\nabla }^{\alpha }u,{\nabla }_{*}^{\alpha }u)d\mathbf{r}=\int [\mathrm{\Lambda }(|{\nabla }^{\alpha }u{|}^2,|{\nabla }_{*}^{\alpha }u{|}^2)+\epsilon {(X-u)}^2]d\mathbf{r},$$ (41)

where Λ and ε(X − u)² are similar to the corresponding terms in Eq. (30). The Euler-Lagrange equation of (41) is [1]:

$$\frac{\partial F}{\partial u}+{\nabla }_{*}^{\alpha }·\frac{\partial F}{\partial {\nabla }^{\alpha }u}+{\nabla }^{\alpha }·\frac{\partial F}{\partial {\nabla }_{*}^{\alpha }u}=0.$$ (42)

Applying (42) to (41), we obtain

$$\frac{1}{2}{\nabla }_{*}^{\alpha }·{\mathrm{\Lambda }}_{u\alpha }^l+\frac{1}{2}{\nabla }^{\alpha }·{\mathrm{\Lambda }}_{u\alpha }^r+\epsilon (X-u)=0,$$ (43)

where

$${\mathrm{\Lambda }}_{u\alpha }^l=-\partial \mathrm{\Lambda }/\partial {\nabla }^{\alpha }u\text{and}{\mathrm{\Lambda }}_{u\alpha }^r=-\partial \mathrm{\Lambda }/\partial {\nabla }_{*}^{\alpha }u.$$ (44)

Note that Eq. (43) is in the similar fashion as Eq. (34).

Remarks

1. We can introduce an artificial time t and convert Eq. (43) into a time-dependent fractional PDE

   $$\frac{\partial u}{\partial t}=\frac{1}{2}{\nabla }_{*}^{\alpha }·{\mathrm{\Lambda }}_{u\alpha }^l+\frac{1}{2}{\nabla }^{\alpha }·{\mathrm{\Lambda }}_{u\alpha }^r+\epsilon (X-u),$$ (45)

   then the fractional PDE transform is constructed by Eq. (37) with the solution operator ℒ defined via Eq. (45).
2. Furthermore, setting Λ = Λ (μ, v) with $\mu =|{\nabla }^{\alpha }u{|}^2,v=|{\nabla }_{*}^{\alpha }u{|}^2$, we can apply the chain rule to (44), i.e.,

   $${\mathrm{\Lambda }}_{u\alpha }^l=-\frac{\partial \mathrm{\Lambda }}{\partial \mu }\frac{\partial \mu }{\partial {\nabla }^{\alpha }u}=-2\frac{\partial \mathrm{\Lambda }}{\partial \mu }{\nabla }^{\alpha }u\doteq -2{\mathrm{\Lambda }}_{\mu }{\nabla }^{\alpha }u$$ (46)

   and

   $${\mathrm{\Lambda }}_{u\alpha }^r=-\frac{\partial \mathrm{\Lambda }}{\partial v}\frac{\partial v}{\partial {\nabla }_{*}^{\alpha }u}=-2\frac{\partial \mathrm{\Lambda }}{\partial v}{\nabla }_{*}^{\alpha }u\doteq -2{\mathrm{\Lambda }}_v{\nabla }_{*}^{\alpha }u.$$ (47)

   Substituting (46)-(47) into (45), we obtain

   $$\frac{\partial u}{\partial t}=-{\nabla }_{*}^{\alpha }·({\mathrm{\Lambda }}_{\mu }{\nabla }^{\alpha }u)-{\nabla }^{\alpha }·({\mathrm{\Lambda }}_v{\nabla }_{*}^{\alpha }u)+\epsilon (X-u),$$ (48)

   where ${\mathrm{\Lambda }}_{\mu }(|{\nabla }^{\alpha }u{|}^2,|{\nabla }_{*}^{\alpha }u{|}^2),{\mathrm{\Lambda }}_v(|{\nabla }^{\alpha }u{|}^2,|{\nabla }_{*}^{\alpha }u{|}^2)$ can be viewed as anisotropic diffusion coefficients.
3. A special case is that when only ${\nabla }^{\alpha }u(\text{or}{\nabla }_{*}^{\alpha }u)$ appears in (41) and Λ takes the simple linear function Λ(μ) = μ, Eq. (48) turns into

   $$\frac{\partial u}{\partial t}=-{\nabla }_{*}^{\alpha }·{\nabla }^{\alpha }u+\epsilon (X-u).$$

   By (28) and (29), we can recover the simple heat equation $\frac{\partial u}{\partial t}={\nabla }^{2}u+\epsilon (X-u)\text{for}\alpha =1$.

2.2.3. Fractional hyperdiffusions derivation of high-order fraction PDEs

In this section, we derive from Eq. (48) an arbitrarily high-order fractional hyperdiffusion equation which has the similar structure of the hyperdiffusion equation (1). Actually, letting

$$\mathrm{\Lambda }=\mathrm{\Lambda }(\mu ),\mu =\sum _{q=1}^m|{\nabla }^{{\alpha }_q}u{|}^2,$$

where m ∈ 𝒩, α_q ∈ℝ, and 0 < α₁ < α₂ < … < α_m < ∞, we have, according to Eq. (48),

$$\{\begin{array}{c}\frac{\partial u}{\partial t}=-\sum _{q=1}^m{\nabla }_{*}^{{\alpha }_q}·{\mathbf{j}}^{{\alpha }_q}+e(u,\sum _{q=1}^m|{\nabla }^{{\alpha }_q}u|,t),\hfill \\ {\mathbf{j}}^{{\alpha }_q}=d_{{\alpha }_q}(u,|{\nabla }^{{\alpha }_q}u|,t){\nabla }^{{\alpha }_q}u,\hfill \end{array}$$ (49)

where $e(u,\sum _{q=1}^m|{\nabla }^{{\alpha }_q}u|,t)=\epsilon (X-u)\text{and}{d}_{{\alpha }_q}(u,\sum _{q=1}^m|{\nabla }^{{\alpha }_q}u|,t)={\Lambda }_{\mu }(\sum _{q=1}^m|{\nabla }^{{\alpha }_q}u{|}^2)$ .

Setting m = 1, α_m = 1, e(u(r, t), |∇u(r, t)|, t) = 0, and recalling (28)-(29), one can reproduce the well-known Perona-Malik equation for anisotropic diffusion [43]:

$$\frac{\partial u}{\partial t}=\nabla ·[d_{\alpha }(|\nabla u|,t)\nabla u].$$

In the current work we study the high-order fractional hyperdiffusion equation with the linear form of Λ, i.e, Λ(μ) = μ, and neglect the term e(u, |∇^αqu|, t).

2.3. Numerical algorithms

In our previous work, high-order nonlinear evolution PDEs have made vital contributions to mode decomposition [58], image analysis [55], and molecular surface generation [76]. However, solving high-order PDE in Eq. (45) directly in physical domain can be numerically difficult for some practical applications. A major problem in solving high-order nonlinear evolution PDEs is their stability constraints: in general, in explicit numerical methods, the time increment Δt needs to be proportional to the n-th power of the spatial discretization h, i.e., Δt ~ hⁿ, for an n-th order PDE. Although the constraint has little impact to most image analysis, in which the spacing h is unit, it does lead to some difficulties in other applications. Typically, alternating direction implicit (ADI) methods are implemented to by-pass the stability constraint in solving high-order PDEs [4]. Another approach used in previous PDE transform is the Fourier pseudospectral method via the fast Fourier transform (FFT). These techniques can be analogically applied to the fractional high-order PDE transform. In such an approach, one has to linearize Eq. (49) and then solves original nonlinear equation by an iterative procedure as shown in Section 2.2.1.

We consider a linearized fractional PDE of (49), i.e. Λ(μ) = μ, μ = |∇^αu|², and m = 1, then

$$\frac{\partial u}{\partial t}=-d_q{\nabla }_{*}^{\alpha }u,\alpha \in {ℝ}^{+},$$ (50)

where d_q is a coefficient independent of u. Denote by ℱ[u](iw) the discrete Fourier transform of u(r, t), t ≥ 0.

When Eq. (50) is subject to initial value u(r, 0) = X^k and periodic boundary conditions, it can be easily solved in the Fourier representation. The Fourier transform of Eq. (50) is given by

$$\frac{\partial ℱ[u](\mathbf{w})}{\partial t}=-d_qℱ[{\nabla }_{*}^{\alpha }·{\nabla }^{\alpha }u](\mathbf{w}),$$ (51)

Because of relations

$$ℱ[D_l^{\alpha }u]={(i\mathbf{w})}^{\alpha }ℱ[u](\mathbf{w}),ℱ[D_r^{\alpha }u]={(i\mathbf{w})}^{\alpha }ℱ[u](\mathbf{w}),$$ (52)

Eq. (51) turns into

$$\frac{\partial ℱ[u](\mathbf{w})}{\partial t}={(-1)}^{\alpha +1}{i}^{2\alpha }{(\mathbf{w})}^{2\alpha }{d}_qℱ[u](\mathbf{w})t\ge 0,$$ (53)

where i^2α is evaulated as i^2α = e^iαπ. Therefore, we iteratively solve the linearized high-order fractional PDE until a predesigned accuracy is reached. We can express the solution of the original nonlinear high-order PDE as [55]

$${\widehat{\mathrm{X̌}}}^k(\mathbf{w})=\widehat{ℒ}{\widehat{X}}^k(\mathbf{w})$$ (54)

where $\widehat{\mathrm{X̌}}$ and X̌^k are the Fourier transforms of X̌^k and X^k respectively. Here Fourier transform of the evolution operator is ℒ̌ = exp((−1)^α+1i^2a(w)^2αd_qt. The solution algorithm developed in the above Fourier domain is called a fast PDE transform.

Given initial value u(r, 0) = X^k the evolution PDE (50) is solved by the fast Fourier transform (FFT) as shown in Eq. (54). Specifically, after computing ǔ = FFT(u) by the FFT, we apply the fraction PDE transform in the Fourier space given by Eq. (54) so as to obtain $\widehat{ǔ}=\widehat{ℒ}\widehat{u}$ with corresponding propagation time t. Finally, the inverse FFT (IFFT) is implemented for $\widehat{ǔ}$ to produce ũ = IFFT $(\widehat{ǔ})$. As a result, the new value of u after propagation time t, i.e., u(r, t), will be given by ũ. In our experiments, the FFT is implemented by the ‘fftw’ software package (www.fftw.org).

It is noted that since the fractional PDE transform is implemented in Fourier space, the term (iw)^α will involve the complex number when α is not an even integer. Moreover, the complex $\widehat{ǔ}$ will result in complex ũ. However, the information of the biomolecular surface is preferably represented by the real number as the isosurface is from the value of u(r, t), which should be real. In the practical implementation, one can either take the real component of Eq. (53) (see Ref. [3] for a similar treatment) or the amplitude of the term (iw)^α. In this work, we explore the performance of both approaches.

3. Numerical test and validation

In this section, the proposed fractional PDE transform is tested and validated by molecular surface generation. The initial condition of Eq. (50) is set as initial biomolecular surface data and the isosurface obtained from the solution u(r, t) at time t will be a desired molecular surface after the PDE transform.

3.1. Initial data for evolution PDEs

The initial value of Eq. (50) is set to be a molecular hypersurface function, which contains atomic coordinates and radius of a molecule. In our computation, three types of initial data are used.

3.1.1. Type I: Piecewise-constant initial values

Piecewise-constant initial values are commonly used in our earlier work for molecular surface generation [5, 6, 18]. In this work, we set the piecewise-constant initial value as

$$u(\mathbf{r},0)=\{\begin{array}{cc}0,\hfill & \mathbf{r}\in {\cup }_{i}O({\mathbf{r}}_i,r_i);\hfill \\ 1,\hfill & \text{otherwise},\hfill \end{array}$$ (55)

where r_i and r_i are the atomic coordinate and radius of atom i, respectively. The union of all atomic spheres O(r_i, r_i) is denoted by ∪_iO(r_i,r_i). This type of piecewise-constant initial value is different from the initial value in our geometry flow based solvation model [18], where the two constants 0 and 1 are switched.

3.1.2. Type II: Maximum Gaussian initial values

The second type of initial values is defined by the maximum of Gaussian functions [25, 76] as follows

$$u(\mathbf{r},0)={\text{max}}_i\left(s\text{exp}\right(-\frac{|\mathbf{r}-r_i{|}^2-r_i^2}{r_e^2}\left)\right).$$ (56)

In this work, we set s = 1 and r_e = 3 as recommended in the literature [25].

3.1.3. Type III: Summation Gaussian initial values

The third type of initial values is taken from the summation of Gaussian functions [8, 22, 27],

$$u(\mathbf{r},0)=\sum _i\text{exp}(-\kappa (|r-r_i{|}^2-r_i^2)).$$ (57)

In our simulation, we set the decay rate κ = 1 [72].

The initial molecular surface can be obtained as the isosurface by setting u(r, 0) = S, where S is a pre-designated isovalue of u, for example, u(r, 0) = 1 [72, 76]. Although the two types of Gaussian initial data are able to offer smoother isosurfaces, they may still result in isosurfaces with singularities as demonstrated in the following sections.

3.2. Effects of fractional order and propagation time

It is noted from the evolution PDE in Eq. (50) that, the performance of the proposed fractional PDE transform depends on the fractional order α, propagation time t, and diffusion coefficient d_q. In the present work, we mainly focus on the role of fractional order and propagation time while set d_q = 1. Also note that the order α is currently serving as a continuous parameter and its values have been extended from positive integers to general positive real numbers. The optimal choices of α in various applications are worthwhile to be studied in the future.

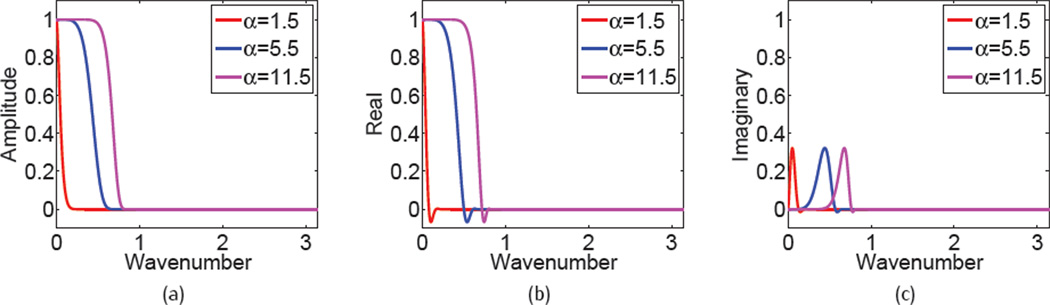
Figure 1 shows the Fourier response of the fractional PDE transform, which is equivalent to the operator ℒ̌ in Eq. (54) at different orders. The overall amplitudes of the Fourier responses of fractional PDE transforms with different orders are given in Figure 1(a), and 1(b)-(c) show the corresponding real and imaginary components, respectively. It can be concluded that the amplitude of Fourier response behaves like classic filters. However, the real component has unfavorable negative values, and the magnitude of the imaginary component is relatively small. These results provide an understanding of the behavior of high-order fractional PDEs.

Fig. 1.

Frequency response of Eq. (53) with t = 10² and different orders. (a) Over all amplitude, (b) Real component, (c) Imaginary component. Red: α = 1.5, blue: α = 5, 5, and purple: α = 11.5.

Figure 1(a) also depicts the effects of fractional PDE transform with different orders (α = 1.5, 5.5, 11.5). With a fixed propagation time t = 10², the fractional PDE transform of order α = 1.5 offers a low-pass filter for very low frequency components. Whereas, the fractional PDE transform of order α = 11.5 is able to pass a much larger range of frequency components. Based on this feature we choose different fractional orders in mode decompositions and other applications of high-order PDEs.

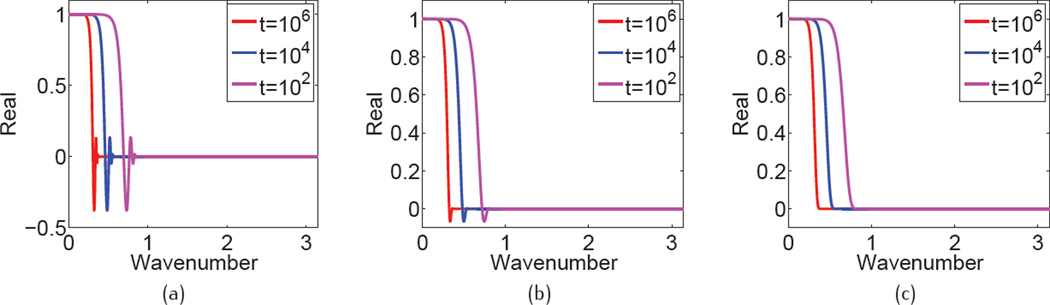
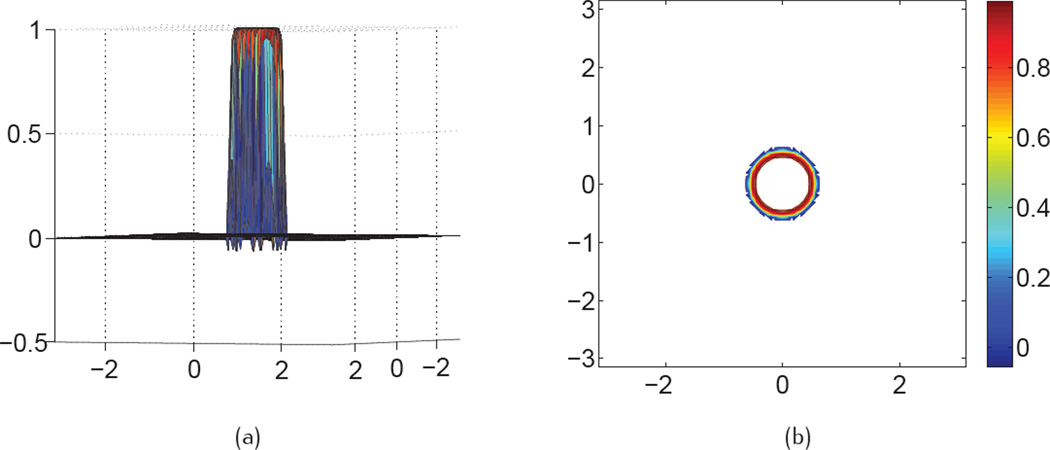
The effect of propagation time, which is equivalent to the impact of the nonlinear coefficient in the PDE transform, is shown in Figure 2, with fixed fractional orders α ∈ (11, 12) and different propagation time. From Figure 2 (a) to Figure 2 (c), there display the real components of the Fourier response of the fractional PDE transform with order α = 11.2, α = 11.5 and α = 12.0, respectively. It is concluded that the longer the propagation time is, the faster is the damping of real component. Thus we can conjecture that in order to obtain a smoother molecular surface, a longer propagation time is preferred. We also need to keep in mind that the molecular surface can not be over-smoothed or over-smeared, otherwise it will become unphysical. It is observed that when the fractional order is closer to an odd number, the real components become more and more oscillatory with all propagation time. Furthermore, Figure 3(a) shows the visualization of real component of Fourier response in 2D for α = 11.5 and t = 10², Figure 3(b) depicts its contours. Since there are negative oscillations in the Fourier response, there are corresponding oscillations in contours as shown in Figure 3(b).

Fig. 2.

Real component of frequency response of Eq. (53) in 1D, with different values of α and t: (a) α = 11.2, (b) α = 11.5, (b) α = 12.0. Red: t = 10⁶, blue: t = 10⁴, and purple: t = 10².

Fig. 3.

Real component of Fourier response of Eq. (53) in 2D for α = 11.5 and t = 10². (a) function value view, (b) contour view.

3.2.1. Test on a three-atom system

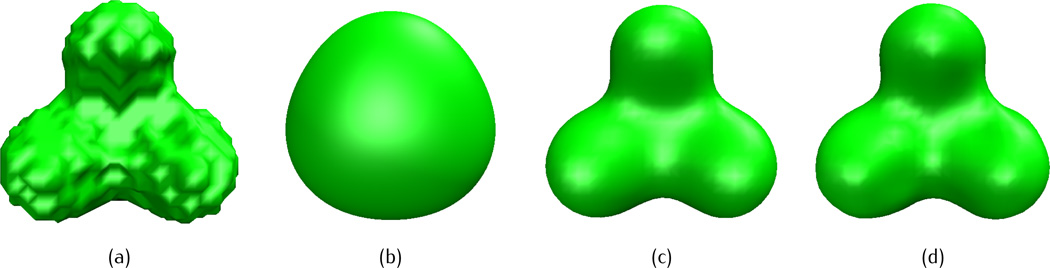
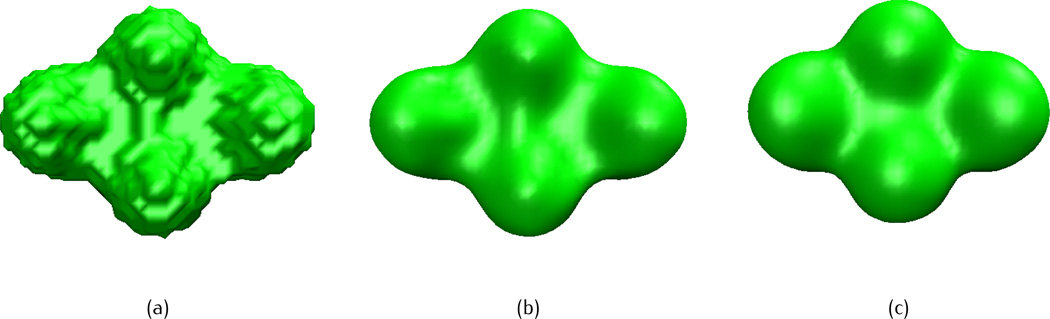
We start the test cases with a simple three-atom system, in which the initial atomic coordinates are given as (0, 0, 1.8), (0, 0,−1.8), (0, 3.12, 0) with a uniform radius of 1.8. Figure 4 shows the isosurface of three-atom system from piecewise constant initial value (Figure 4 (a)) and after fractional PDE transform by different fractional orders α = 1.5 (Figure 4 (b)), 5.5 (Figure 4(c)) and 11.5 (Figure 4(d)), the propagation time is t = 10² and the isovalue is taken as u(r, t) = 1. We conclude that the piecewise constant initial value does not give an acceptable molecular surface and the low order transform (α = 1.5) over-smears the molecular surface. Similar problem of a low order PDE transform at α = 2 was also found by Zheng et al [76]. However, both high-orders transforms (α = 5.5 and α = 11.5) render satisfying molecular surfaces. In the work of integer PDE transform based biomolecular surface generation [76], although α = 6.0 works well for small molecular systems, it was found that α = 6.0 over-smears large biomolecules such as proteins. In the following test cases, we use the fractional order α = 11.5.

Fig. 4.

Isosurfaces of a three-atom system after the fractional PDE transform of different fractional orders with the piecewise constant initial value. The isovalue is taken as u(r, t) = 1 and propagation time is t = 10². (a) Initial value, (b) α = 1.5, (c) α = 5.5, (d) α = 11.5.

3.2.2. Test on a four-atom system

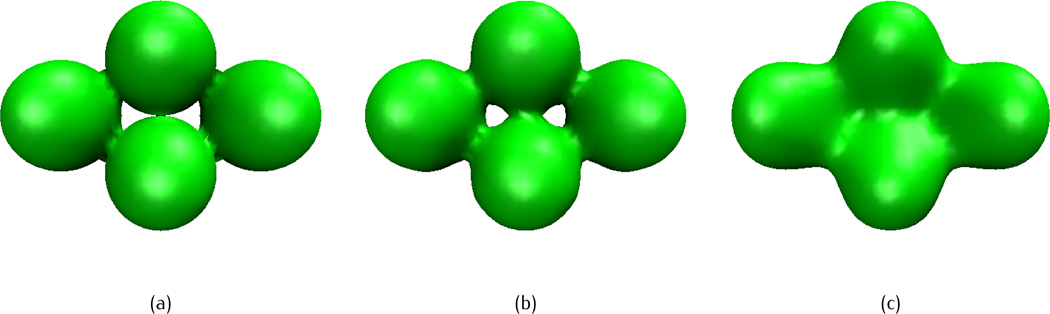
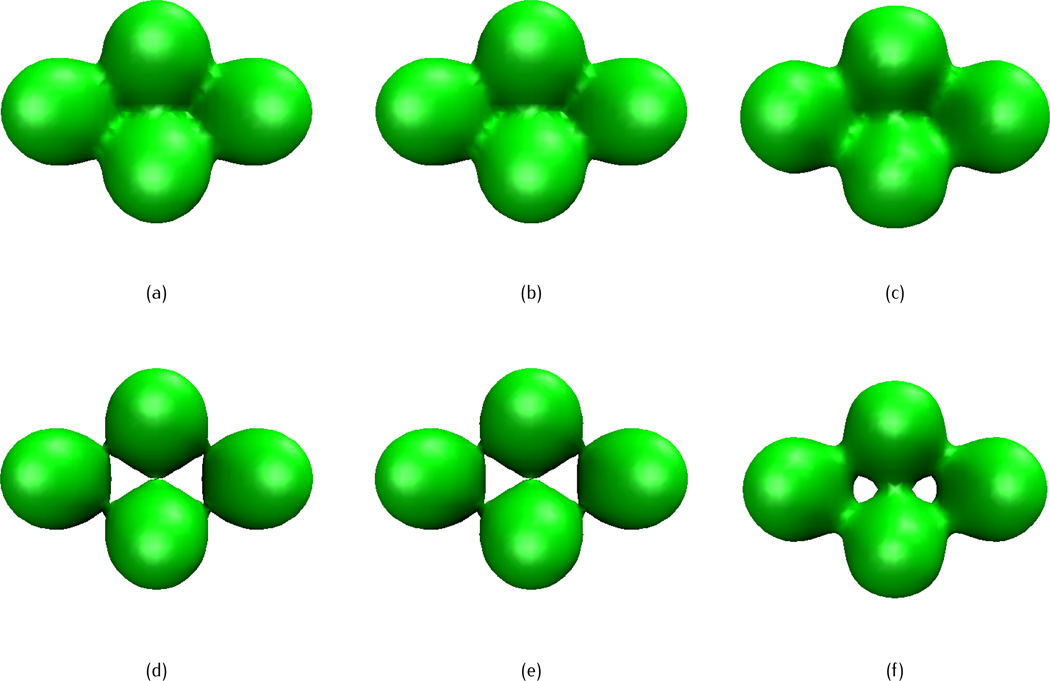
We next test the effects of different propagation time and choices of initial data through a four-atom system, in which the initial atomic coordinates are given as (0, 0, 1.8), (0, 0,−1.8), (0, 3.12, 0) and (0,−3.12, 0), with a uniform radius of 1.8. The fractional PDE transforms of different propagation time with three types of initial data discussed in section 3.1, are illustrated in Figures 5, 6 and 7, respectively, with the isovalue u(r, 0) = 1 and order α = 11.5. For the initial molecular surfaces, the one from Type I is non-smooth (Figure 5(a)), isosurface of Type II has singularities (Figure 6(a)), and Type III is smooth (Figure 7(a)). However, it should be noted that the three types of initial values have different ranges: initial data of Type I is restricted within the range [0, 1], while the values of Types II and III can be greater than one. Although the isosurface of Type III is smooth at u(r, 0) = 1, the surface from other isovalues may not be. For example, the surface obtained by setting u(r, 0) = 2, as showed in Figure 7(d), has obvious singularities.

Fig. 5.

Isosurface of a four-atom system after fractional PDE transform of order α = 11.5 and different propagation time, with the piecewise constant initial value. The isovalue is taken as u(r, t) = 1 (a) initial value, (b) t = 1, (c) t = 10⁴.

Fig. 6.

Isosurfaces of a four-atom system after fractional PDE transform of order α = 11.5 and different propagation time, with maximum Gaussian initial value. The isovalue is taken as u(r, t) = 1. (a) Initial value, (b) t = 1, (c) t = 10⁴.

Fig. 7.

Isosurfaces of a four-atom system after fractional PDE transform of oder α = 11.5 and different propagation time, with the summation Gaussian initial value. The isovalue is taken as u(r, t) = 1 for (a)-(c) and u(r, t) = 2 for (d)-(f). (a) Initiale value, (b) t = 1, (c) t = 10⁴, (d) initial value, (e) t = 1, (f) t = 10⁴.

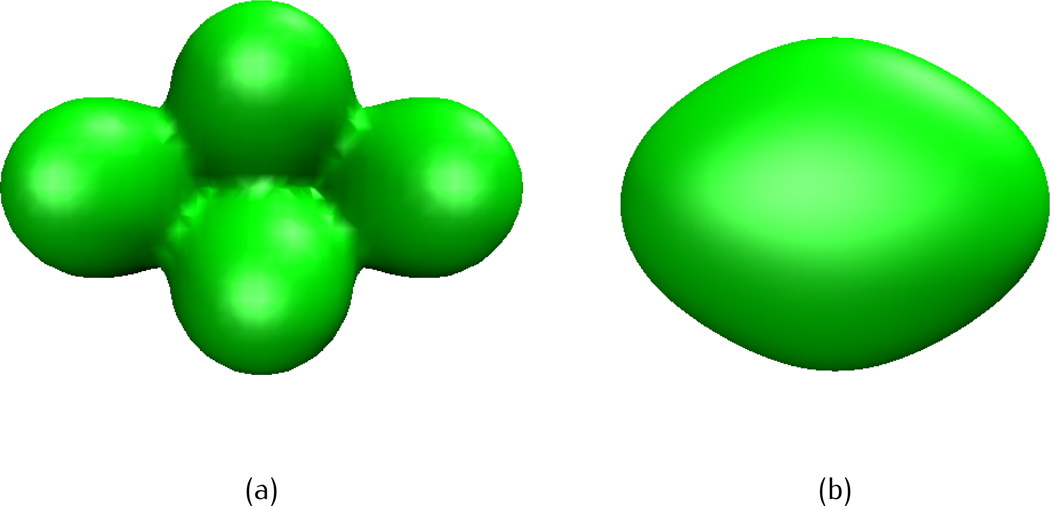
It is noted that Type II initial value depends on the parameter r_e and Type III data relies on the decay rate κ. Figure 8 shows the isosurfaces from Type III initial data at two different decay rates, κ = 1 and κ = 1/9. It is observed that κ = 1 gives a much better resolution of the molecular surface than κ = 1/9 does, this fact is consistent with the previous results [72].

Fig. 8.

Isosurface of a four-atom system with initial value of Type III (Summation Gaussian initial values) at different κ. The isovalue is taken as u(r, 0) = 1. (a) κ = 1, (b) κ = 1/9.

The results after fractional PDE transform with order α = 11.5 after different propagation time are illustrated in the rest subfigures of Figures 5, 6 and 7. Although the piecewise constant (Type I) initial data is non-smooth, it can offer smooth surfaces by the fractional PDE transform after certain proper propagation time, as noted in Figures 6(b) and (c). On the other hand, the singularities resulting from Type II initial data can also be removed at a long propagation time t = 10⁴ but not after a short time t = 1. Moreover, it is difficult to filter the singularities in the isosurface u(r, t) = 2 with Type III initial value. One may also pay attention to the time cost for generating three types of initial surfaces. Since Types II and III involving searching the maximum or taking the summation, they require more CPU time than Type I does. Indeed, for the four-atom system at h = 1, the computational results show that the CPU cost for surface generation using Type I initial data is about 0.001 seconds, while about 0.2 seconds for using Types II and III initial data.

3.2.3. Test on two proteins

The fractional PDE transform method is further validated on realistic proteins. In our numerical experiments, the protein data, i.e., atomic coordinates and radii, are obtained from the PDB bank (www.pdb.org) and prepared with the PDB2PQR package [21]. Two proteins, PBD IDs 1R69 and 1FCA, are used in our test. The results are depicted in Figures 9 and 10, respectively. Initial values of Type I are used for both proteins (Figure 9(a) and 10(a)). Different orders (α = 1.5, 11.5) and the same propagation time (t = 10⁴) are applied to the protein 1R69, see Figure 9(b)-(c), while different propagation time (t = 1, 10⁴) and the same order (α = 11.5) are for the protein 1FCA, see Figure 10(b)-(c). It can be concluded that the transform with relatively longer propagation time and higher order produces better molecular surfaces.

Fig. 9.

Surface of a protein (PDB code: 1R69) after fractional PDE transform of propagation time t = 10⁴ and different orders. The isovalue is taken as u(r, t) = 1. (a) Initial value (Type I), (b) α = 1.5, (c) α = 11.5;

Fig. 10.

Surface of a protein (PDB code: 1FCA) after fractional PDE transform of order α = 11.5 at different propagation time. The isovalue is taken as u(r, t) = 1. (a) initial value (Type I), (b) t = 10⁰, (c) t = 10⁴;

Based on the tests on the model three/four-atom systems and the realistic proteins, we summarize that even with the simplest Type I initial surface, satisfactory molecular surfaces can be obtained if the parameters are chosen properly. Specifically, we use order α = 11.5, propagation time t = 10⁴ and isosurface u(r, t) = 1 for later applications unless other values are indicated. The initial values are all of Type one for connivence.

3.3. Computational efficiency

Computational efficiency is a crucial issue in molecular surface generation. Surface generation time is a bottleneck for many practical applications such as the Poisson-Boltzmann based molecular dynamics [23] and the solution of coupled nonlinear Poisson-Nernst-Planck equations [74, 75]. Here we examine the computational efficiency of the fractional PDE transform based biomolecular surface generation. Table 1 compares the CPU costs (in seconds) for surface generation in Cartesian meshes between the fractional PDE transform (FPDE) with α = 11.5, t = 10⁴ and the MSMS approach [47] at a typical triangle density 10. In the table, N_a is the total number of atoms in the protein after the PDB2PQR conversion. The total time T_tot of the MSMS approach includes the CPU cost from generating surface in the 2D Lagrangian representation T_s and the time cost of converting it to the 3D Eulerian representation T_c, which is required in many applications [76]. Essentially, the CPU time used to create a triangular representation of a protein surface, i.e., T_s, is similar to the total CPU time for the the present fractional PDE transform to generate a 3D Eulerian representation of the protein surface. However, the additional CPU used in the Eulerian conversion is quite large, which causes problems in our earlier molecular dynamics simulations [23]. Moreover, the MSMS method encounters problem in generating the triangular surface meshes for three relatively large proteins, 2NCD, 1IWO and 2E2J at the designed density 10. The present fractional PDE transform is very stable and robust for large proteins.

Table 1.

Comparison of CPU costs (in seconds) for surface generation in Cartesian meshes by the fractional PDE transform (FPDE) with α = 11.5, t = 10⁴ and the MSMS approach. N_a: total number of atoms; T_s: CPU time for MSMS to generate surface in 2D Lagrangian representation; T_c: CPU time for converting the Lagrangian representation to 3D Eulerian representation. T_tot: Total CPU cost for FPDE and MSMS; h: grid resolution.

PDB-ID	Na	Ts by MSMS	h = 1			h = 0.5
			MSMS		FPDE	MSMS		FPDE
			Tc	Ttot	Ttot	Tc	Ttot	Ttot
1R69	596	0.49	2.84	3.33	0.05	2.93	3.42	0.32
1A2S	667	0.43	3.00	3.43	0.06	3.25	3.68	0.53
1SH1	702	0.56	3.13	3.69	0.09	3.27	3.83	0.43
2PDE	729	0.46	2.91	3.37	0.11	3.31	3.77	1.28
1VII	828	0.54	3.03	3.57	0.06	3.82	4.36	0.60
1A7M	858	0.64	3.73	4.37	0.05	3.90	4.54	0.57
1VJW	903	0.65	3.59	4.24	0.08	3.56	4.21	0.67
1FCA	997	0.62	3.52	4.14	0.08	3.72	4.34	0.55
1HPT	1272	0.92	5.11	6.03	0.07	5.21	6.13	1.08
1MBG	1435	0.96	5.15	6.11	0.11	5.34	6.30	1.21
1A63	2065	1.38	7.92	9.30	0.19	8.09	9.47	1.20
1SVR	2809	1.58	8.73	10.31	0.19	9.29	10.87	1.82
2NCD	5665	N/A	N/A	N/A	0.94	N/A	N/A	9.35
1IWO	30870	N/A	N/A	N/A	3.20	N/A	N/A	23.97
2E2J	58046	N/A	N/A	N/A	3.48	N/A	N/A	31.36

It is interesting to note that the computational cost scales essentially linearly with respected to the number of atoms in proteins for the present fractional PDE transform approach.

3.4. Surface areas and surface enclosed volumes

To quantitatively characterize the surface generated by the fraction PDE transform, we examine the surface areas and their enclosed volumes for a number of proteins. These quantities are frequently used in biophysical modeling, such as the solvation free energy estimation.

The results of fractional PDE transform are in the Eulerian representation, i.e., a 2D surface of a biomolecule embedded in a 3D Cartesian grid. One has to extract the surface area and the enclosed volume by appropriate computational algorithms. A second-order surface integration scheme has been developed in our earlier work [23]

$${\int }_{\mathrm{\Gamma }}f(x,y,z)dS\approx \sum _{(i,j,k)\in l}(f(x_o,y_j,z_k)\frac{|n_x|}{h}+f(x_i,y_o,z_k)\frac{|n_y|}{h}+f(x_i,y_j,z_o)\frac{|n_z|}{h})h^3$$ (58)

where h is the grid resolution, (x_o, y_j, z_k) is the intersecting point of the surface Γ and the meshline that passes through the point (x_i, y_j, z_k), and n_x is the x component of the unit normal vector at (x_o, y_j, z_k). Similar notations are used for y and z directions. The summation involves irregular grid points which are the points with at least one neighbor from the other side of the surface Γ in the second-order finite difference discretization. Here I is the set of irregular grid points inside or on the interface [23]. Formula (58) is used for surface area calculation by setting f = 1.

The volume integral of a function f is approximated by

$${\int }_{\Omega m}f(x,y,z)d\mathbf{r}\approx \frac{1}{2}(\sum _{(i,j,k)\in J_1}f(x_i,y_j,z_k)h^3+\sum _{(i,j,k)\in J_2}f(x_i,y_j,z_k)h^3)$$ (59)

where J₁ is the set of the points inside Ω_m and J₂ = J₁ ∪J_Irr where J_Irr indicates the set of irregular points. The volume is obtained by setting f = 1 in Eq. (59).

Table 2 lists surface areas and surface enclosed volumes of protein surfaces generated by both the fractional PDE transform and the MSMS approach. In this test, the fractional PDE transform is of order 11.5, propagation time t = 10⁴, and the grid resolution is 0.5 Å. It can be concluded that the present results are quite consistent with those obtained from the MSMS package, thus the proposed PDE transform is useful in practical applications.

Table 2.

Comparison of surface areas (unit: Ų), surface enclosed volumes (unit: ų) and electrostatic free energies of solvation ΔG_p (unit: kcal/mol) with surfaces generated by the fractional PDE transform (FPDE) and the MSMS approach. The grid resolution is 0.5 Å.

PDB-ID	FPDE			MSMS
	Area	Volume	ΔGp	Area	Volume	ΔGp
1VJW	2847.6	7626.1	−1236.0	2785.8	7693.2	−1237.9
1FCA	2723.2	6857.1	−1206.0	2546.9	7028.1	−1200.1
1SH1	2680.7	6418.2	−746.9	2743.8	6400.7	−753.3
1R69	2978.9	8817.1	−1081.9	3054.5	8777.2	−1089.5
1MBG	2980.2	7896.8	−1337.9	3070.7	7843.3	−1346.1
1A2S	4316.1	11629.6	−1902.1	4436.8	11569.7	−1913.5
1SVR	4582.6	11990.2	−1699.0	4644.0	11961.9	−1711.2
1VII	2402.0	5091.7	−888.3	2476.2	5050.7	−901.5
2PDE	2659.2	6080.3	−805.3	2715.9	5994.6	−820.9
1A7M	7514.9	24125.5	−2129.9	7733.6	24025.1	−2155.5
1A63	6884.9	18168.8	−2347.0	6973.7	18121.1	−2373.5
1HPT	3182.9	7706.9	−807.5	3262.9	7660.9	−811.6

4. Applications

Solvent-solute interface plays a critical role in implicit solvent models for applications to electrostatic calculation, solvation analysis and molecular dynamics simulations. It is also important in variational multiscale models for biomolecular systems [60, 62]. In this section, we first apply the fractional PDE transform based biomolecular surfaces to electrostatic calculation of a group of proteins and then analyze the solvation free energies of a set of small compounds, for which have the experimental data are available.

4.1. Electrostatic analysis of 15 proteins

4.1.1. Electrostatic potential

Once the surface has been generated, the electrostatic potential can be evaluated according to the Poisson equation [15, 24, 67]

$$-\nabla ·(\epsilon \nabla \phi )=\sum _j{q}_j\delta (\mathbf{r}-{\mathbf{r}}_j),$$ (60)

where q_j are the (fractional) charges of atoms at position r_j (j = 1, 2, …, N_a). The dielectric function ε is defined as a piecewise constant function

$$\epsilon (\mathbf{r})=\{\begin{array}{cc}{\epsilon }_m,\hfill & \mathbf{r}\in {\Omega }_m,\hfill \\ {\epsilon }_s,\hfill & \mathbf{r}\in {\Omega }_s,\hfill \end{array}$$ (61)

where ε_m = 1 and ε_s = 80 are the dielectric constants in the molecular and solvent regions, respectively, these two regions are separated by the molecular surface. Equation (60) is a typical elliptic interface problem with discontinuous coefficients and singular sources. It is very difficult to construct second-order convergent methods for this equation in the biomolecular context due to the geometric complexity, complex interface, singular charge sources and geometric singularities [15, 24, 67]. In this work, we make use of the second-order convergent matched interface and boundary (MIB) method [15, 68, 69, 73, 77, 78] to solve Eq. (60).

Figure 11 displays the electrostatic surface potential of three proteins obtained from solving the Poisson equation (60). These potential values are projected on the protein surfaces generated by using the proposed fractional PDE transform. In the figures, red and blue colors represent negative and positive surface electrostatic potentials, respectively. Surface electrostatic potential is highly correlated with ligand binding domains, which are important to drug design.

Fig. 11.

Surface electrostatic potentials of three proteins based on the molecular surface after fractional PDE transform with α = 11.5 and t = 10⁴. (a) PDB code: 1VII, (b) PDB code: 1FCA, (3) PDB code:1R69. Red: negative potential, blue: positive potential.

4.1.2. Electrostatic solvation free energy

With the solution of the Poisson equation, one can calculate electrostatic solvation free energies of proteins by

$$\mathrm{\Delta }{G}_p=\frac{1}{2}\sum _j{q}_j(\phi ({\mathbf{r}}_j)-{\phi }_{\mathrm{h}\mathrm{o}\mathrm{m}\mathrm{o}}({\mathbf{r}}_j)),$$ (62)

where φ and φ_homo correspond to the electrostatic potentials in the inhomogeneous and homogeneous environments, respectively.

Electrostatic solvation free energies of twelve proteins are listed in Table 2. Results are computed by using two types of surface definitions, namely, solvent excluded surface generated by using the MSMS and the fractional PDE transform based surface. A good consistence is obtained between these two methods.

4.2. Solvation analysis of 17 small compounds

Total solvation free energies, which include both polar (i.e., electrostatic solvation free energies ΔG_p) and nonpolar solvation free energies G_np, are measured in many experiments. The latter component of solvation free energy can be modeled in many ways. One of the most commonly used model can be expressed as [18, 54]

$$G_{\mathrm{n}\mathrm{p}}=\gamma \text{Area}+p\text{Vol}+{\int }_{{\Omega }_s}{\rho }_s{U}^{\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{a}}d\mathbf{r},$$ (63)

where γ is the surface tension, p is the hydrodynamic pressure, ρ_s is the solvent bulk density, Ω_s denotes the solvent accessible region, and U_att(r) is the solute-solvent van der Waals interaction potential at point r. The first term γArea is the surface energy, which describes the disruption of intermolecular and/or intramolecular bonds that occurs when the surface of a molecule is created in the solvent. The second term pVol measures the mechanical work of creating the vacuum of a biomolecular size in the solvent. The hydrophobic effect in the first two terms are partially compensated by the third term ∫_Ωsρ_sU^attdr, which describes the attractive dispersion effects near the solvent-solute interface. The reader is referred to Ref. [18] for detailed description of the van der Waals interaction.

One of the important applications of FPDE transform-based solute-solvent interface is the calculation of total solvation energies. As stated in Section 3.4, all the terms in Eq. (63) can be calculated from the molecular surfaces generated from FPDE transform of various types of initial data, and according to Section 4.1.2, the analysis of electrostatic free energies also requires the definition of solute-solvent interface.

In Table 3, there list calculated total solvation free energies of a set of 17 small compounds, compared with corresponding experimental data. The nonpolar free energy G_np and electrostatic energy ΔG_p are calculated by Eqs. (62) and (63), respectively, based on the molecular surface based on the FPDE transform with order α = 11.5 and propagation time t = 10⁴. The reader is referred to Ref. [19] for a detailed description of atomic coordinate and charge parameters. The total solvation free energy ΔG = G_np+ ΔG_p. For comparison, the corresponding experimental measurements (Exptl) of these compounds are also listed. We can conclude that the application of FPDE transform-based molecular surface in calculations of free solvation energy is validated, because the agreement between the simulations and experimental data is fairly good. The root mean square error (RMSE) of the computation results is 1.77 kcal/mol and the average error is 1.42 kcal/mol. In comparison, Nicholls et al [39] reported a RMSE of 1.87 kcal/mol for the same set of molecules by the linear Poisson model and further, the RMSE was reduced to 1.71 ± 0.05 kcal/mol [39] by their explicit solvent approach, which is much more expensive. Additionally, the RMSE in the current work is only slightly greater than the one (RSME=1.76 kcal/mol) reported in [18], where the biomolecular surface is defined and generated from a nonlinear mean curvature flow equation so extra computational efforts are necessary. Therefore, FPDE transform-based molecular surface provides a relatively good foundation to predict the solvation energies for this set of molecules.

Table 3.

Computation of solvation free energies ΔG (kcal/mol) for the 17 small compounds based on the molecular surface generated by fractional PDE transform with order α = 11.5 and propagation time t = 10⁴. G_np: nonpolar component; ΔG_p: polar component; Exptl: experimental data; Error: ΔG_p - Exptl.

Compound	Gnp	ΔGp	ΔG	Exptl	Error
glycerol triacetate	3.38	−13.54	−10.16	−8.84	−1.32
benzyl bromide	2.00	−5.68	−3.67	−2.38	−1.29
benzyl chloride	1.97	−5.70	−3.73	−1.93	−1.8
m-bis(trifluoromethyl)benzene	4.38	−3.35	1.03	1.07	−0.04
N,N-dimethyl-p-methoxybenzamide	2.85	−10.43	−7.57	−11.01	3.44
N,N-4-trimethylbenzamide	2.71	−8.56	−5.85	−9.76	3.91
bis-2-chloroethyl ether	2.09	−4.57	−2.48	−4.23	1.75
1,1-diacetoxyethane	2.39	−8.77	−6.39	−4.97	−1.42
1,1-diethoxyethane	2.13	−4.52	−2.39	−3.28	0.89
1,4-dioxane	1.38	−6.85	−5.47	−5.05	−0.42
diethyl propanedioate	2.67	−9.04	−6.37	−6.00	−0.37
dimethoxymethane	1.34	−5.23	−3.89	−2.93	−0.96
ethylene glycol diacetate	2.31	−9.88	−7.57	−6.34	−1.23
1,2-diethoxyethane	2.14	−5.30	−3.15	−3.54	0.39
diethyl sulfide	1.74	−2.93	−1.2	−1.43	0.23
phenyl formate	1.98	−8.22	−6.25	−4.08	−2.17
imidazole	1.11	−13.45	−12.34	−9.81	−2.53

Figure 12 depicts the surface morphologies and surface electrostatic potentials of 9 compounds. It is seen that fraction PDE transform offers useful information of molecular morphology, which is crucial to the understanding of molecular physical, chemical and biological properties.

Fig. 12.

Illustration of surface electrostatic potentials of nine small compounds at their corresponding isosurfaces u(r, 10⁴) = 0.5. (a) benzyl bromide, (b) bis-2-chloroethyl ether, (c) 1,1-diacetoxyethane, (d) diethyl propanedioate, (e) diethyl sulfide, (f) dimethoxymethane, (g) m-bis benzene, (h) N,N-4-trimethylbenzamide, (i) phenyl formate.

5. Concluding remarks

The emergence of complexity in self-organizing biological systems poses exciting challenges to their quantitative descriptions and predictions. Images, surfaces and visualization of complex biomolecules, such as proteins, DNAs, RNAs, molecular motors and viruses, are crucial to the understanding and conceptualization of biomolecular systems, which in turn can have significant impacts in biomedicine, rational drug design, drug discovery and gene therapy. Partial differential equations (PDE) transform is a new approach for mode decomposition of images, surfaces and data [55, 58]. It makes use of arbitrarily high-order nonlinear PDEs for the control of time-frequency localization and the regulation of spatial resolution. The PDE transform has found its success in the analysis of non-stationary signals and noisy images [55, 56, 58]. Recently, it has also been applied to the molecular generation of biomolecules [76]. However, our previous PDE transform depends on the use of integer order PDEs of arbitrarily high-orders. In this work, we extend the PDE transform to fractional PDE transform by using fractional derivatives of arbitrarily high orders.

Fractional derivative or fractional calculus has received much attention in the past decade. Its concept naturally arises in science and engineering, and includes integer derivatives as special cases. However, most work in the field involves only relatively low order fractional derivatives. Fractional derivatives of orders higher than 2 are seldom used. It is not clear that how to use arbitrarily high-order fractional derivatives in theoretical modeling and practical computation.

To demonstrate the utility of fractional derivatives of arbitrarily high-orders, we propose high-order fractional PDEs and the corresponding fractional PDE transform. Using the fractional variational principle, we construct nonlinear fractional PDEs based fractional hyperdiffusion. Introducing an artificial time, the resulting high-order fractional PDEs are converted to time-evolution fractional PDEs. Numerical techniques based on fast fractional Fourier transform (FFFT) are developed to compute the high-order fractional PDEs in three-dimensional 3D setting.

The proposed high-order fractional PDEs are applied to the surface construction of macromolecular surfaces, which are crucial components in the implicit solvent models [24], charge transport models [74] and variational multiscale models [60, 62]. We consider three types of initial values to study the proposed high-order fractional PDEs. Additionally, we examine the effect of the orders of fractional PDEs on the surface morphology. It is found that high-order fractional PDEs are crucial to the quality of molecular surfaces. We also test the impact of the PDE integration time on surface generation. Moreover, we examine the computational efficiency of the present method. Efficiency is one of major motivations for developing new surface generation methods. It is found that the proposed high-order fractional PDEs are of linear scaling with respect to number of atoms in a molecule. We further validate the present method by quantitative analysis of surface areas and surface enclosed volumes of proteins. Finally, the surfaces constructed by the present approach is applied to a couple of biophysical problems, namely, the electrostatic analysis via the Poisson equation and the solvation analysis via a full solvation model. The results from these biophysical problems indicate that the proposed high-order fractional PDE transform is a robust and efficient method for macromolecular surface generation.