Abstract
The accumulation of sub-rupture tendon fatigue damage in the extracellular matrix, particularly of type I collagen fibrils, is thought to contribute to the development oftendinopathy, a chronic and degenerative pathology of tendons. Quantitative assessment of collagen fibril alignment is paramount to understanding the importance of matrix injury to cellular function and remodeling capabilities. This study presents a novel application of edge detection analysis to calculate local collagen fibril orientation in tendon. This technique incorporates damage segmentation and stratification by severity which will allow future analysis of the direct effect of matrix damage severity on the cellular and molecular response.
Introduction
Accumulation of fiber microtrauma with repetitive sub-threshold loading is a contributory factor to the pathogenesis of tendinopathy (Renstrom and Johnson, 1985). In addition to impairing mechanical function (Fung et al., 2009; Andarawis-Puri et al., 2011), tendon matrix damage also likely affects tenocyte homeostasis (Andarawis-Puri et al., 2012). Technical methods for quantifying the extent of local structural damage in biological injury models are critical for understanding the disease process.
Collagen fibril alignment, and thus matrix damage, has been measured using various techniques including FFT (Fung et al., 2010; Chaudhuri et al., 1987) and polarized light (Dickey et al., 1998; Thomopoulos et al., 2006). Fung et al. utilized second harmonic generation (SHG) microscopy to image type I collagen to study damage accumulation in a rat patellar tendon overuse model and found damage patterns progressed with fatigue injury from initial small fiber kink deformations, to fiber dissociations, to higher level fiber discontinuities and tendon rupture (Fung et al., 2010). We have previously developed a Fast Fourier Transform (FFT) method to quantify fiber alignment without bias and inter-rater variability and showed increasing levels of fiber deformation with progressive fatigue levels (Fung et al., 2010). Here we present a novel image processing technique based on edge detection, which has not been reported in the tendon or ligament literature that enables quantification of local fibril orientation and damage region segmentation. Edge detection has been previously applied in biological studies studying cellular and cytoskeletal alignment (Kemeny and Clyne, 2011; Karlon et al., 1999; Yoshigi et al., 2003; Vartanian et al., 2008), but has not been utilized to study tendon damage. In addition to identifying damage areas, the presented algorithm expands on our previous methods by classifying damage regions by area and severity. The method is computationally efficient and enables calculation of angular orientation at the fibril level.
Edge Detection Theory
Edge detection finds edges by calculating intensity changes and determining the orientation of the maximum intensity gradient (Karlon et al., 1999; Yoshigi et al., 2003; Kaunas et al., 2005). The Laplacian is found in two directions, x and y, and an intensity gradient vector is found for each pixel. The local orientation is normal to the direction of the intensity gradient vector. Sobel operators, which approximate the gradient of intensity in both horizontal (Equation 1) and vertical (Equation 2) directions have been used to reduce gradient computation times (Sobel and Feldman, 1968; Duda and Hart, 1973; Yoshigi et al., 2003). The matrix operators, Kx and Ky, are applied separately to intensity values at each pixel, Iij, and surrounding neighbors to produce measurements of the gradient component, Gx (Equation 3) and Gy (Equation 4), in which * denotes a 2-D convolution operation (Duda and Hart, 1973; Yoshigi et al., 2003). Magnitude (G) and direction (Θ) of the pixel intensity gradient is determined by Equation 5 and Equation 6 (Duda and Hart, 1973; Yoshigi et al., 2003), respectively. MATLAB's® element-by-element calculation and fast filtering techniques can implement edge detection algorithms that are robust to noise and computationally efficient (Kemeny and Clyne, 2011).
Methods
Specimen Preparation
Rat tail tendons (RTTs) from 9 month old, female Sprague-Dawley rats (n=5) were harvested and placed in phosphate-buffered saline (PBS). RTTs were gripped between custom sand-paper grips for a 50mm length and mounted in a materials testing system (Instron 8872, MA) with a 2.5-lb load cell (Transducer Techniques, CA) and 37°C PBS bath. Tendons were divided into groups, one group of non-loaded controls and remaining groups fatigue loaded to 2.5% strain at 0.5Hz, sinusoidal waveform for 50, 100, 200, or 500 cycles (n=10/group; 2 RTTs assigned randomly from each individual tail per group).
SHG Image Acquisition
RTTs were mounted and imaged in PBS using a multiphoton microscope (Olympus FluoView FV1000MPE, Japan) equipped with a pulsed-IR laser (Coherent Chameleon Vision II, CA). Collagen fibrils were imaged at three locations with SHG imaging (60× magnification, LUMPFL W/IR, NA 0.90) using a 760nm excitation wavelength. The image used to develop the algorithm is shown in Figure 1a.
Figure 1. (a) Representative Image for Code Development and Visualization of Normalized Pixel Intensity Gradient in (b) the Horizontal Direction (Gx) and (c) the Vertical Direction (Gy).

Matlab® Image Processing
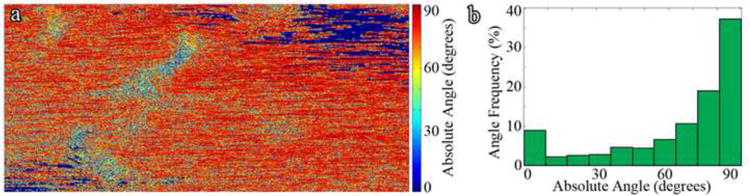
Images were processed with Matlab® (Version 2010a) without enhancement or thresholding. Grayscale images were converted from 8-bit to double precision floating point values and Sobel filters (Equation 1 and Equation 2) applied separately to detect edges. The normalized pixel intensity gradient in the x- (Figure 1b) and y-directions (Figure 1c) are then visualized. Pixel angular orientations, Θ, were calculated by Equation 6 and converted to degrees. Orientations ranged from −90° to 90° with ±90° corresponding to non-damaged regions. Angle magnitudes were obtained and displayed as an image to visualize calculated collagen orientations (Figure 2a) and as a histogram to assess angular distributions (Figure 2b). Zero degree regions (Figure 2a – dark blue) coincide with regions in the SHG image that are over- or under-saturated and are excluded from analysis. Data averaging and noise filtering was necessary to remove false positive damage regions in SHG images, likely due to imaging artifact, and was accomplished by averaging angle magnitudes in 10 by 20 pixel sub-sections, which was designed to favor fibrils oriented longitudinally over the normal direction of fibril alignments.
Figure 2. (a) Angle Magnitude Plot Prior to Data Filtering and (b) Histogram of Angle Magnitudes Prior to Data Filtering.
Tendon segmentation from background and removal of regions that are over- or under-saturated due to artifact is necessary for damage area quantification (Supplemental Information). Imaging artifacts are filtered by thresholding and regional intensity filtering (Supplemental Information).
Damage Segmentation
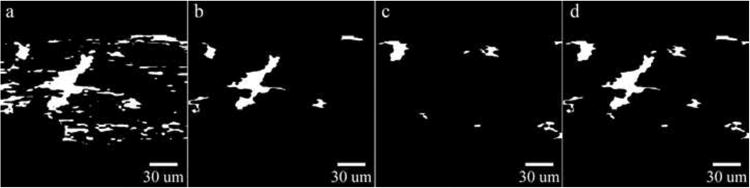
Damage segmentation is performed on the final filtered average angle magnitude plot after tendon segmentation from background and artifact filtering. The image is thresholded by defining all angles greater than 64 degrees (qualitatively set by visual inspection) as non-damaged and equal to zero and all other angles equal to one (Figure 3a). Noise is removed by morphological opening and serial erosions performed to remove regions connected by only branch-points. Damage regions are labeled and properties assessed using MATLAB®. Artifactual regions and tissue voids were filtered using set region criteria (Supplemental Table 1) and a final segmented image is obtained (Figure 3b). Enhanced detection of low and moderate damage regions is achieved by passing the horizontally filtered image, Gy, through the vertical filter, Kx, and computing Θ from Gy and Gyx. The image is thresholded by setting all artificial angles greater than 48 degrees (qualitatively set by visual inspection) as non-damaged and equal to zero and all other values equal to one. This artificial angle was qualitatively set and not equivalent to collagen fiber angles. Damage regions are sorted to distinguish between non-damaged regions and artifacts. Criteria are set to identify regions of low to moderate severity and the binary output of filtered damage segments is shown in Figure 3c. Damage regions from the original segmentation (Figure 3b) and sensitized segmentation (Figure 3c) are combined to obtain the final binary segmented image (Figure 3d).
Figure 3. a) Binary Output of Segmented Damage, b) Original Filtered Binary Damage, c) Sensitized Filtered Binary Damage, and d) Final Merged and Filtered Binary Damage.
Damage Severity Sorting
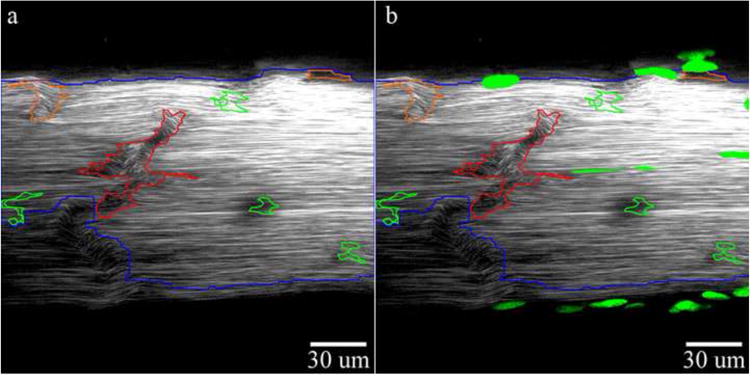
Segment properties were obtained by built-in MATLAB® region property functions. Properties of pixel area, mean and standard deviation of angles, mean and standard deviation of the top 10%, and mean intensity value were obtained. Damage severity stratification criteria to group segments into low, moderate, or high levels were defined based on the distribution of segment properties across 50 selected images across injury levels. The distribution of region properties (Figure S3) was used to subjectively define initial damage criteria (Supplemental Table 2) and criteria were then further refined qualitatively to match manual damage assessment. Criteria were included to re-classify damage segments into lower severity groupings if specific criteria were un-met. Criteria in this study were based on angles derived from sensitized angle calculations and not true angle calculations since artificial angles provided greater differentiation between groups due to a larger property distribution range. Classified regions are visualized by overlaying color outlines signifying damage severity (red-high, orange-moderate, or green-low) on the original image (Figure 4a). Total damage area in each group is calculated by dividing the sum pixel total in a group per image and normalizing to the total tendon area in pixels. Damage value per group is expressed as a percentage or area fraction. Fluorescent markers, such as cell nuclei, imaged with SHG data, can be merged with the segmented image (Figure 4b).
Figure 4. (a) Final Damage Segmentation With Damage Severity Sorting (Red Outlines-High Damage, Orange Outlines-Moderate Damage, Green Outlines-Low Damage) and (b) Final Damage Segmentation With Cell Overlay.
Processing Time
Analysis of one image using a Core i7 1.73GHz, 64-bit processor with 4GB of RAM was approximately 18 seconds.
Comparison to Manual Damage Segmentation
Damage criteria were validated by binary comparison between automated and manual damage segmentations. A non-biased analyst was trained to identify and judge matrix damage regions by severity and analyzed each image 3 times. Binary coincidence of regions in both manual and automated segmentation methods was used to assess accuracy.
Results
Assessment of Angular Orientations in Damage Severity Groups
Since artificial angles were used to bin segmentations by severity, estimations of true angular deviations within these regions were investigated. High damage regions had true mean angular deviations of 30 degrees from normal and top 10% of angles greater than 38 degrees from normal. Moderate damage regions had true mean angular deviations between 25 to 30 degrees from normal and top 10% of angles greater than 32 degrees from normal. Low damage regions had true mean angular deviations less than 25 degrees from normal and top 10% of angles greater than 24 degrees from normal.
Comparison Between Manual and Automated Segmentation
The trained analyst had no intra-observer variability. The edge detection and segmentation method identified 100% of high, 90% of moderate, and 70% of low damage regions found by the analyst. The edge detection algorithm had a false positive rate of 0% in high, 23% in moderate, and 75% in low damage regions. False positives in moderate and low regions were 0.26% and 0.5% of total area, respectively.
Discussion
The presented method provides the unique ability to identify, quantify, and stratify damage by severity and represents progress in our ability to accurately quantify and assess fatigue damage in overuse models. Qualitative inspection of damage regions identified by the algorithm found that the routine correctly identified damage and closely outlined damage for the full range of expected damage. Damage criteria developed for automated image analysis corresponded to qualitative manual assessments, providing method validation and enabling its use for analyzing SHG images. Although the number of false positives in the automated method was high in moderate and low damage groups, regions accounted for an insignificant image area, suggesting the program is susceptible to noise in moderate and low damage regions.
Although the segmentation program analyzes damage in two dimensions, batch processing of image stacks enables three-dimensional damage reconstruction and visualization. Future improvements may incorporate three-dimensional volumetric damage calculations. Addition of high axial-resolution stacks and three-dimensional Sobel filters may enable calculation of fibril orientation in three axes and improved damage assessment. In addition to SHG imaging, multiphoton microscopy allows for simultaneous acquisition of fluorescent molecular data. By image overlay onto segmented tendons, it is possible to interrogate the importance of matrix damage to cell behavior.
The presented method is dependent on image quality and is adversely affected by artifact. The method requires consistent image acquisition for accurate comparisons between groups. In this study, SHG images showed inconsistencies in illumination across the image likely due to tissue alignment with the microscope. RTT thickness and curvature likely introduce image artifacts through the depth and along the width of the tendon, which may account for illumination inconsistencies and edge hyperintensities. Improved imaging with better depth penetration, resolution, and reduced artifact may be achieved with plastic embedding and imaging with oil immersion lenses. Due to the presence of artifact, the program is unlikely to find differences in low damage groups; however the method is appropriate for probing differences between low and severe damage severities. The method is inappropriate for evaluation of cross-width tendon ruptures without definition of additional criteria. Currently, the program is optimized for damage patterns observed in RTTs and translation to other tendons requires minor modifications.
Conclusions
The presented technique is the first implementation of edge detection to analyze collagen orientation in fatigued tendon and the first program developed to segment and quantify matrix damage by area and severity. Correlation between automated and manual damage segmentations showed the automated technique is acceptable, enabling non-biased and reproducible analysis of tendon images that significantly reduces analysis time. The algorithm represents an important advancement in tendon damage assessment allowing for correlation of damage with cellular and molecular responses and studies of the importance of damage in the progression of tendinopathy.
Supplementary Material
Figure S1: (a) Original Image, (b) Binary Tendon Segmentation and (c) Segment Overlay (blue)
Figure S2: (a) Non-filtered, Thresholded Angle Magnitude Plot and (b) Filtered Average Angle Magnitude Plot with Regional Maxima (◊) and Minima (Ο) Removed
Figure S3: (a) Mean Angle and (b) Mean Angle of Top Ten Percent of Angles in Damaged Regions in Images Selected Across Samples
Supplemental Table 1: Region Filtering Criteria
Supplemental Table 2: Damage Severity Criteria
Acknowledgments
The authors would like to acknowledge the following for their contributions to this study: Victor Friedrich, Ph.D., Rumana Huq, and Nisha George.
| Equation 1 |
| Equation 2 |
| Equation 3 |
| Equation 4 |
| Equation 5 |
| Equation 6 |
Footnotes
Appointments: Stephen J. Ros, Ph.D. – MSTP Candidate Year VIII, Icahn School of Medicine at Mount Sinai, New York, NY, Nelly Andarawis-Puri, Ph.D. &ndash, Assistant Professor, Leni and Peter W. May Department of Orthopaedics, Icahn School of Medicine at Mount Sinai, New York, NY, Evan L. Flatow, M.D. - Lasker Professor of Orthopaedic Surgery, Leni & Peter W. May Department of Orthopaedics, Icahn School of Medicine at Mount Sinai, New York, NY
Name of Department Work is Attributed To: Leni & Peter W. May Department of Orthopaedics, Icahn School of Medicine at Mount Sinai, New York, NY
Conflict of Interest Statement: All authors on this manuscript (Stephen J. Ros, Ph.D., Nelly Andarawis-Puri, Ph.D., and Evan L. Flatow, M.D.) have no financial or personal relationships with other people or organizations that could inappropriately influence or bias this work.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Andarawis-Puri N, Sereysky JB, Jepsen KJ, Flatow EL. The relationships between cyclic fatigue loading, changes in initial mechanical properties, and the in vivo temporal mechanical response of the rat patellar tendon. Journal of Biomechanics. 2011;45(1):59–65. doi: 10.1016/j.jbiomech.2011.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andarawis-Puri N, Sereysky JB, Sun HB, Jepsen KJ, Flatow EL. Molecular response of the patellar tendon to fatigue loading explained in the context of the initial induced damage and number of fatigue loading cycles. Journal of Orthopaedic Research. 2012;30(8):1327–1334. doi: 10.1002/jor.22059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhuri S, Nguyen H, Rangayyan RM, Walsh S, Frank CB. A Fourier domain directional filtering method for analysis of collagen alignment in ligaments. IEEE Transactions on Biomedical Engineering. 1987;34(7):509–518. doi: 10.1109/tbme.1987.325980. [DOI] [PubMed] [Google Scholar]
- Dickey JP, Hewlett BR, Dumas GA, Bednar DA. Measuring collagen fiber orientation: a two-dimensional quantitative macroscopic technique. Journal of Biomechanical Engineering. 1998;120(4):537–540. doi: 10.1115/1.2798026. [DOI] [PubMed] [Google Scholar]
- Duda RO, Hart PE. Pattern Classification and Scene Analysis. John Wiley & Sons, Inc.; New York, NY: 1973. [Google Scholar]
- Fung DT, Sereysky JB, Basta-Pljakic J, Laudier DM, Huq R, Jepsen KJ, Schaffler MB, Flatow EL. Second harmonic generation imaging and Fourier transform spectral analysis reveal damage in fatigue-loaded tendons. Annals of Biomedical Engineering. 2010;38(5):1741–1751. doi: 10.1007/s10439-010-9976-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung DT, Wang VM, Laudier DM, Shine JH, Basta-Pljakic J, Jepsen KJ, Schaffler MB, Flatow EL. Subrupture tendon fatigue damage. Journal of Orthopaedic Research. 2009;27(2):264–273. doi: 10.1002/jor.20722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlon WJ, Hsu PP, Li S, Chien S, McCulloch AD, Omens JH. Measurement of orientation and distribution of cellular alignment and cytoskeletal organization. Annals of Biomedical Engineering. 1999;27(6):712–720. doi: 10.1114/1.226. [DOI] [PubMed] [Google Scholar]
- Kaunas R, Nguyen P, Usami S, Chien S. Cooperative effects of Rho and mechanical stretch on stress fiber organization. Proceedings of the National Academy of Sciences USA. 2005;102(44):15895–15900. doi: 10.1073/pnas.0506041102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kemeny SF, Clyne AM. A simplified implementation of edge detection in MATLAB is faster and more sensitive than fast fourier transform for actin fiber alignment quantification. Microscopy and Microanalysis. 2011;17(2):156–166. doi: 10.1017/S143192761100002X. [DOI] [PubMed] [Google Scholar]
- Renstrom P, Johnson RJ. Overuse injuries in sports. A review. Sports Medicine. 1985;2(5):316–333. doi: 10.2165/00007256-198502050-00002. [DOI] [PubMed] [Google Scholar]
- Sobel I, Feldman JA. A 3×3 isotropic gradient operator for image processing. Stanford University; Stanford, CA: 1968. [Google Scholar]
- Thomopoulos S, Marquez JP, Weinberger B, Birman V, Genin GM. Collagen fiber orientation at the tendon to bone insertion and its influence on stress concentrations. Journal of Biomechanics. 2006;39(10):1842–1851. doi: 10.1016/j.jbiomech.2005.05.021. [DOI] [PubMed] [Google Scholar]
- Vartanian KB, Kirkpatrick SJ, Hanson SR, Hinds MT. Endothelial cell cytoskeletal alignment independent of fluid shear stress on micropatterned surfaces. Biochemical and Biophysical Research Communications. 2008;371(4):787–792. doi: 10.1016/j.bbrc.2008.04.167. [DOI] [PubMed] [Google Scholar]
- Yoshigi M, Clark EB, Yost HJ. Quantification of stretch-induced cytoskeletal remodeling in vascular endothelial cells by image processing. Cytometry Part A. 2003;55(2):109–118. doi: 10.1002/cyto.a.10076. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1: (a) Original Image, (b) Binary Tendon Segmentation and (c) Segment Overlay (blue)
Figure S2: (a) Non-filtered, Thresholded Angle Magnitude Plot and (b) Filtered Average Angle Magnitude Plot with Regional Maxima (◊) and Minima (Ο) Removed
Figure S3: (a) Mean Angle and (b) Mean Angle of Top Ten Percent of Angles in Damaged Regions in Images Selected Across Samples
Supplemental Table 1: Region Filtering Criteria
Supplemental Table 2: Damage Severity Criteria


