Quantifying the reliability of image replication studies: the image intra-class correlation coefficient (I2C2)

Abstract

This manuscript proposes the image intra-class correlation (I2C2) coefficient as a global measure of reliability for imaging studies. The I2C2 generalizes the classic intra-class correlation (ICC) coefficient to the case when the data of interest are images, thereby providing a measure that is both intuitive and convenient. Drawing a connection with classical measurement error models for replication experiments, the I2C2 can be computed quickly, even in high-dimensional imaging studies. A nonparametric bootstrap procedure is introduced to quantify the variability of the I2C2 estimator. Furthermore, a Monte Carlo permutation is utilized to test reproducibility versus a zero I2C2, representing complete lack of reproducibility. Methodologies are applied to three replication studies arising from different brain imaging modalities and settings: Regional Analysis of VolumEs in Normalized Space (RAVENS) imaging for characterizing brain morphology, seed-voxel brain activation maps based on resting state functional MRI (fMRI), and fractional anisotropy (FA) in an area surrounding the corpus callosum via diffusion tensor imaging (DTI). Software and data are provided to ensure rapid dissemination of methods. Resting state functional MRI (fMRI) brain activation maps are found to have low reliability ranging between 0.2 to 0.4.

1 Introduction

Replication is the cornerstone of science. Its absence reduces any scientific endeavor to a set of unverified beliefs. Brain imaging studies are no exception, though they have several specific characteristics that conspire to make quantification of reliability especially difficult. First, measurements are complex and idiosyncratic for each modality. Second, the definition of the actual target to be measured is often imperfect. Third, the data sets are large and not amenable to standard investigations of replication. Fourth, there is relatively little crosspollination of research between different imaging modalities. Finally, setting up replication experiments can be difficult under many scenarios.

A variety of methods have been proposed for measuring the reliability of images, particularly in the context of functional neuroimaging studies (see [4] for an overview). One approach, the intra-class correlation (ICC) ([33]), can be used to measure the similarity between region of interest (ROI) summaries of activation, intensity or shape metrics in multiple subjects under two or more experimental replications. Another approach, the Dice coefficient ([28]) measures what proportion of voxels exceed a threshold, such as one indicating activation, in both of two separate imaging sessions. A third approach, predictive modeling, measures the ability of a training data set to predict the structure of test data. One of the best established predictive modeling techniques within functional neuroimaging is the nonparametric prediction, activation, influence, and reproducibility sampling approach (NPAIRS [34]), which has been used to illustrate how small changes in an fMRI processing pipeline can have dramatic effects on final results.

In this work, we propose a general model for brain imaging replication studies and introduce the image intra-class correlation (I2C2) as a measure of data reliability. This measure generalizes the classic (scalar) ICC to the case when the measurement target is an image. Resampling approaches are then developed to quantify I2C2 variability under the replication design and to test whether it is different from the I2C2 obtained under a random permutations of subject matching. Notably, the proposed framework is applied to three replication studies utilizing data from different brain imaging modalities. These include: Regional Analysis of Volumes in NormalizEd Space (RAVENS) imaging (a technique used to investigate localized changes in brain morphology) [13], seed-voxel brain connectivity maps based on resting state functional magnetic resonance imaging (rs-fMRI), and fractional anisotropy (FA) measured using diffusion tensor imaging (DTI) in an area surrounding the corpus callosum.

2 The image intra-class correlation coefficient

To better understand the underlying issue, consider the most basic replication study where J = 2, scalar replicate measurements are collected for each of I subjects. An example would be measuring total white matter brain volume from two imaging sessions. Yet even in such a straightforward setting, the study of and expectations for the extent of replication can vary quite dramatically. For example, consider the difference between study designs: in one study, replicate images are collected on the same day, using the same brand of scanner, processed by the same technicians versus a second study, where replicate images are collected weeks apart, in different laboratories, with different technicians and different scanners. Using our example for context, let X_i denote the true (unknown) white matter volume and W_ij the white matter volume measurements from two replications. Succinctly, the observed W_ij are the measured proxies of the measurement of interest, X_i. The classical measurement error model [6, 17] in replication studies is

$$W_{ij}=X_i+U_{ij},$$ (1)

with assumptions that the measurements, X_i, are independent across subjects and the measurement errors, U_ij, are independent across both subjects and replicates and are mutually independent of X_i, for i = 1, …, I, and j = 1, J = 2. Conceptually, U_ij is the error that occurs during each individual measurement of the true target, X_i. The classical measurement error model further assumes that the measurement error variates, U_ij have the same variance, ${\sigma }_U^2$. Likewise, we denote the variance of X_i by ${\sigma }_X^2$. This model is then equivalent to an one-way ANOVA model with random effects. Notice that the observed measurements, W_ij, for the same subject, i, are correlated, as they share the same X_i. Specifically, the correlation is equal to

$$\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}(W_{i1},W_{i2})=\frac{{\sigma }_X^2}{{\sigma }_X^2+{\sigma }_U^2}=\frac{{\sigma }_W^2-{\sigma }_U^2}{{\sigma }_W^2}=1-\frac{{\sigma }_U^2}{{\sigma }_W^2}.$$

This is the well known intra-class correlation (ICC) coefficient. Here the “class” is the replication experiment and the correlation is between replicated measurements for the same subject. In the measurement error literature ICC is referred to as the reliability ratio. The ICC is a scale-free quantity between 0 and 1, where 0 corresponds to exact independence of measurements W_i1 and W_i2; that is, they are unrelated, despite attempting to measure the same underlying quantity. Correspondingly, 1 indicates perfect reliability for every subject, W_i1 = W_i2 = X_i. Estimation is simple; ${\sigma }_W^2$ can be estimated as the variance of the W_ij and ${\sigma }_U^2$ can be estimated by the variance of (W_i2 − W_i1)/2.

Generalizations of the ICC to high-dimensional multivariate settings, such as images, are not obvious. However, a need for reliability metrics from these settings arises frequently. For example, the target of measurement might be a measure of brain morphology in a template (see Section 4.1), an rs-fMRI connectivity map (see Section 4.2), an FA map in a region of interest such as the area surrounding the corpus callosum (see Section 4.3), etcetera. In specific terms, let X_i(υ) be the (unknown) true image and W_ij(υ) be the proxy measurements of X_i(υ) at voxel υ. The classical image measurement error can then be written as

$$W_{ij}(\upsilon )=X_i(\upsilon )+U_{ij}(\upsilon ),$$ (2)

where all images are represented as V × 1 dimensional vectors; W_ij = {W_ij(υ) : υ = 1, …, V} are the observed proxy images; X_i = {X_i(υ) : υ = 1, …, V} are the true images, assumed to be independent across subjects, and U_ij = {U_ij(υ) : υ = 1, …, V} are the measurement error images, assumed to be independent across subjects, replicates and (mutually) of X_i. Here, i = 1, …, I, and j = 1, …, J_i. Thus, we consider a general case involving different numbers of replicates per subject, J_i of any value greater than or equal to 2.

The model further assumes that the measurement error vector, U_ij, has covariance K_U and X_i has covariance, K_X; that is, cov(U_ij, U_ij) = K_U and cov(X_i, X_i) = K_X. These cannot be directly estimated, as the U_ij and X_i are unobserved. Note that the covariance operator of the observed data K_W = cov(W_ij, W_ij), a quantity directly estimable from the data, can be written as K_W = K_X + K_U via the straightforward application of the multivariate variance operator to (2). Exactly, paralleling the univariate setting, K_X is interpreted as the within-subject covariance and K_U as the covariance of the measurement error.

Based on the aforementioned connection with the classical measurement error model (1), we propose the following image intra-class correlation (I2C2) coefficient

$$\rho =\frac{\text{trace}(K_X)}{\text{trace}(K_W)}=\frac{\text{trace}(K_W)-\text{trace}(K_U)}{\text{trace}(K_W)}=1-\frac{\text{trace}(K_U)}{\text{trace}(K_W)}.$$ (3)

One possible way of calculating I2C2 is to estimate the smoothed covariance matrices using Multilevel Functional Principal Component Analysis (MFPCA) [14] or its extension to high-dimensional data [37]. Alternatively, we obtain the following method of moments estimators based on formulas from [6] to reduce the computational cost,

$$\widehat{\text{trace}}(K_W)=\frac{1}{{\sum }_{i=1}^I{J}_i-1}\sum _{i=1}^I\sum _{j=1}^{J_i}\sum _{\upsilon =1}^V{\{W_{ij}(\upsilon )-\mathrm{W̅}‥(\upsilon )\}}^2,$$

and

$$\widehat{\text{trace}}(K_U)=\frac{1}{{\sum }_{i=1}^I(J_i-1)}\sum _{i=1}^I\sum _{j=1}^{J_i}\sum _{\upsilon =1}^V{\{W_{ij}(\upsilon )-{\mathrm{W̅}}_i․(\upsilon )\}}^2.$$

Here W̅‥(υ) = ∑_i,j,υ W_ij(υ)/IJ is the average of all images over all subjects and visits and ${\mathrm{W̅}}_{i․}(\upsilon )={\sum }_{j=1}^{J_i}{W}_{ij}(\upsilon )/J_i$ is the average image for subject i over all visits j. Thus, an estimate of I2C2 can be reached by entering these estimates into equation (3).

Calculating the I2C2 is both quick and scalable, because it does not require dealing with the V × V dimensional matrices. Indeed, the computational burden for calculating trace(K_W) and trace(K_U) is linear in V. Moreover, the formulas separate by subject, making the calculations simple and easy to implement even on very modest computational resources. Both MATLAB [23] and R [27] code are provided for calculating I2C2 at http://www.biostat.jhsph.edu/~ccrainic/software.html. In practice one may also be interested in the reliability of imaging in a particular region of interest (ROI). The formulae for an ROI are almost identical to the ones for the whole-image, except that the summation over υ is done only within the ROI mask. This is especially useful when one suspects that the reliability of image measurements varies across functional or anatomical area brain regions.

To assess the variability of the I2C2 parameter, a method is proposed to calculate a confidence interval by nonparametrically bootstrapping subjects and applying the same estimation procedure for every bootstrap sample. There are multiple sources of variability for the I2C2 estimator, but the major source will be the limited number of subjects, I, and the imbalance in the number of replicates, where applicable.

Lastly, the distribution of the I2C2 under complete random sampling, i.e. no reliability, is investigated. In this case, the model is W_ij = U_ij, and recall that the U_ij are independent. Draws from such a null distribution can be realized using using permutation sampling. More precisely, all indexes, (i, j), are collected and relabeled as k_i,j for $k_{i,j}=1,\dots ,({\sum }_{i=1}^I{J}_i)$. Let σ(k_i,j) be a random permutation obtained by sampling the k-vector without replacement. Denote the image corresponding to σ(k_i,j) by W̃_ij and estimate the I2C2 coefficient for the model W̃_ij = X̃_i + Ũ_ij. Under permutation, the (i, j) pairing does not have the same sense as before, because the images W̃_ij are not necessarily from the same subject. By breaking the subject associations via random permutation, a null distribution that is otherwise close to the variation in the data is obtained. Because the number of resamples must be large to minimize Monte Carlo error, for both bootstrapping and permutation testing, the speed of the proposed methods is crucial. Below, we first investigate the “reliability” of this proposed metric in the next section, and show how these quantities can be calculated and used in three different imaging applications in section 4.

3 Simulations

The I2C2 metric is developed based on the assumptions that the signal and noise are independent and normally distributed across repeated measurements. Using extensive simulations we investigate the effects of various model violations on estimating I2C2. In particular, we examine the performance of our algorithm when the model is correctly- and incorrectly specified. When the model is miss-specified we study scenarios where: 1) replication errors are non-Gaussian; 2) replication errors are correlated over repetitions; and 3) the signal is correlated with the replication errors.

3.1 Correctly-specified model

Consider the data generating mechanism W_ij(υ) = X_i(υ) + U_ij(υ), i = 1, 2, ⋯, I; j = 1, J_i; υ ∈ 𝒱, where each subject i has J_i images repeatedly measured on a group of voxels 𝒱. Let U_ij(υ) = V_ij(υ) + ε_ij(υ), where X_i(υ) and V_ij(υ) are mutually uncorrelated with smooth covariance operators, and ε_ij(υ) are the i.i.d. for each voxel, repetition and subject. Generate $X_i(\upsilon )=\mu (\upsilon )+{\sum }_{k=1}^{K_1}{\xi }_{ik}{\varphi }_k(\upsilon )$ and $V_{ij}(\upsilon )={\sum }_{k=1}^{K_2}{\zeta }_{ijk}{\psi }_k(\upsilon )$, where ${\xi }_{ik}~N(0,{\lambda }_k^X)$ and ${\zeta }_{ijk}~N(0,{\lambda }_k^V)$. To approximate the DTI-MRI example in Section 4, we set μ(υ) to be the vector obtained by concatenating the population average of corpus callosum images. Let 𝒱 = {υ₁, υ₂, ⋯, υ_V}, then V = 38 × 72 × 11. We set K₁ = K₂ = 4, ${\lambda }_k^X=1400\times {0.5}^{k-1}$ and ${\lambda }_k^V=840\times {0.5}^{k-1}$, k = 1, 2, 3, 4. The eigenfunctions ϕ_k(υ) and ψ_k(υ) are chosen to be orthonormal blocks as in [37]. Data was simulated for I = 200 subjects, each with J_i = 2 replications. By definition, the theoretical I2C2 is ${\sum }_k^{K_1}{\lambda }_k^X/({\sum }_k^{K_1}{\lambda }_k^X+{\sum }_k^{K_2}{\lambda }_k^V+V{\sigma }^2)$. We show the results for the following distributions of ε_ij(υ): Gaussian, heavy-tail t and mixture normal with two components. For each scenario, we conduct 100 iterations.

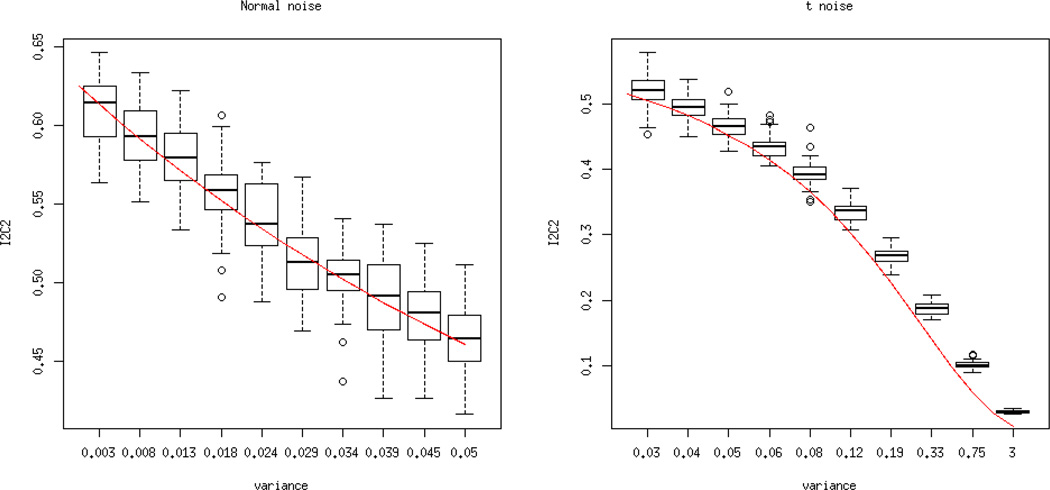
• ε_ij(υ) ~ N (0, σ²). The model is correctly specified and results are highly reliable; see the left panel in Figure 1. The boxplots show the distribution of estimated I2C2 over 100 iterations with respect to a range of signal-to-noise ratios. The red line indicates the theoretical I2C2 values as a function of σ².

• ε_ij(υ) ~ t₃/s, s = 0.5 × (1 : 20). Here the t distribution generates measurement errors with a heavy tail distribution and a variance controlled by s. Results are displayed in the right panel of Figure 1. Performance is very good, though a slight overestimation can be noted in the very low signal-to-noise scenarios.

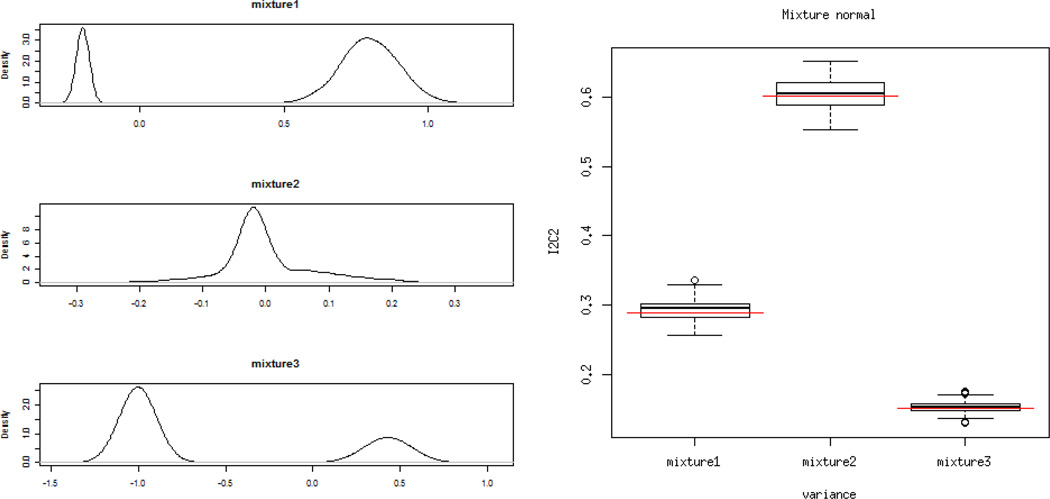
• ${\epsilon }_{ij}(\upsilon )~pN({\mu }_1,s_1^2)+(1-p)N({\mu }_2,s_2^2)$. This scenario corresponds to the case when measurement error has two possible sources. We simulate the case when the noise distribution is a mixture of two normal components. We consider the following three settings corresponding to three different reliability ratios: 1) p = 0.8, μ₁ = −0.2, μ₂ = 0.8, s₁ = 0.005 and s₂ = 0.1; 2) p = 0.5, μ₁ = −0.02, μ₂ = 0.02, s₁ = 0.02 and s₂ = 0.1; 3) p = 0.3, μ₁ = −1, μ₂ = 0.43, s₁ = 0.05 and s₂ = 0.1. The parameters are chosen so that the distribution of the noise has mean 0. The density of selected distributions and the estimated I2C2 under each setting are shown on Figure 2 indicating excellent performance of the I2C2 estimators.

We conclude that the I2C2 is properly recovered when the model is correctly specified. This is due to the fact that we use a method of moments estimator that is insensitive to the distribution of measurement error.

Figure 1.

Left panel: true I2C2 (red line) and estimated I2C2 (boxplots over 100 simulations) for ε_ij(υ) ~ N (0, σ²) and a range of σ². Right panel: true I2C2 (red line) and estimated I2C2 (boxplots over 100 simulations) for ε_ij(υ) ~ t₃/s and a range of t distribution variances.

Figure 2.

Left panel: density plots of the mixture normal distributions used for measurement noise. Right panel: true I2C2 (red lines) and estimated I2C2 (boxplots) for the different mixtures of normal distributions.

3.2 Misspecified model

When the model assumptions are violated, we show that the estimated I2C2 still reflects the magnitude of reliability. Note that the theoretical I2C2 can be equivalently defined as I2C2 = ∑_υ∈𝒱 Cov{W_ij(υ), W_ij′ (υ)}/∑_υ∈𝒱 Var{W_ij(υ)}. Thus, I2C2 is a measure of the fraction of variability that is shared among repeated measurements, without distinguishing whether the correlation is from the signal or the noise. We consider the following scenarios where correlation among images is not only due to signal, but also to the correlation of replication errors. This violates a basic assumption of measurement, though, in the absence of gold standard measurements it is hard to check whether the true errors are correlated.

• Correlated noise across replications. Consider the case when ε_ij(υ) ~ N (0, σ²), and corr{ε_ij(υ), ε_ij′ (υ) = ρ} for every j ≠ j′. The theoretical I2C2 is $({\sum }_k^{K_1}{\lambda }_k^X+V\rho {\sigma }^2/({\sum }_k^{K_1}{\lambda }_k^X+{\sum }_k^{K_2}{\lambda }_k^V+V{\sigma }^2)$, which is larger than the one in the uncorrelated case. Similarly to the previous analysis, we examine the estimated I2C2 with respect to σ² and ρ. The mean square errors (MSEs) of the estimated I2C2 under a range of correlations ρ are shown in the left panel of Table 1.

  The case when noise variables are not exchangeable is more difficult because defining the true I2C2 becomes tricky. For example, consider the case of AR(1) dependence, that is ε_ij+1(υ) = αε_ij(υ) + z_ij+1(υ), ε_i1(υ) ~ N (0, σ²), and z_ij(υ) ~ N (0, (1 − α²)σ²) to ensure that ε_ij(υ)′s have the same marginal distributions. A possible way to define I2C2 is to start with the pairwise correlations

  $$\mathrm{I}2\mathrm{C}{2}_{jj\prime }=\sum _{\upsilon \in 𝒱}\text{Cov}\{W_{ij}(\upsilon ),W_{ij\prime }(\upsilon )\}/\sum _{\upsilon \in 𝒱}\text{Var}{\{W_{ij}(\upsilon )\}}^{1/2}\text{Var}{\{W_{ij\prime }(\upsilon )\}}^{1/2}.$$

  The true I2C2 could then be defined as the average of all possible pairs $\mathrm{I}2\mathrm{C}2=\frac{1}{\left(\begin{array}{c}\hfill J\hfill \\ \hfill 2\hfill \end{array}\right)}{\sum }_{j<j\prime }\mathrm{I}2\mathrm{C}{2}_{jj\prime }$. This is a rather contrived example, though our simulations indicate good estimation of this I2C2 (results not shown).
• Consider now the case when the true underlying image intensity is correlated with the magnitude of noise at each voxel. Consider W_ij(υ) = X̃_i(υ) + Ũ_ij(υ), where X̃_i(υ) = X_i(υ) + z_i and Ũ_ij(υ) = V_ij(υ) + υ_ij and X_i(υ), V_ij(υ) are generated as the previous sections. Correlation between signal and noise is using the trivariate normal distribution N (0, Σ) for {z_i, υ_i1, υ_i2}, where

  $$\mathrm{\Sigma }=\left(\begin{array}{ccc}\hfill {\sigma }_x^2\hfill & \hfill \rho {\sigma }_{xu}^2\hfill & \hfill \rho {\sigma }_{xu}^2\hfill \\ \hfill \rho {\sigma }_{xu}^2\hfill & \hfill {\sigma }_u^2\hfill & \hfill 0\hfill \\ \hfill \rho {\sigma }_{xu}^2\hfill & \hfill 0\hfill & \hfill {\sigma }_u^2\hfill \end{array}\right).$$

  We assume that ${\sigma }_{xu}^2={\sigma }_x^2$ and ${\sigma }_u^2=5{\sigma }_x^2$. In this case the theoretical I2C2 is $\{{\sum }_k^{K_1}{\lambda }_k^X+V(1+2\rho ){\sigma }^2\}/\{{\sum }_k^{K_1}{\lambda }_k^X+{\sum }_k^{K_2}{\lambda }_k^V+V(6+2\rho ){\sigma }^2\}$. By varying the correlation ρ, we examine the estimated I2C2 in right panel of Table 1.

Simulation results demonstrate the robustness of the I2C2 estimation approach when there is correlation among noise variables or between the signal and the noise. However, it is important to note that I2C2 is not designed to distinguish between these cases and is unbiased with respect to the true correlation; this true correlation may be different from the proportion of variability explained when model assumptions are violated. We now proceed to show how I2C2 can be calculated and used in three different imaging applications.

Table 1.

MSE of the estimated I2C2 under a range of correlations, both for correlated noise case and for correlated signal and noise.

	Correlated noise				Correlated signal and noise
ρ	0.11	0.42	0.74	0.89	0.11	0.42	0.74	0.89
true I2C2	0.41	0.54	0.67	0.74	0.27	0.33	0.37	0.40
estimated I2C2	0.41	0.54	0.67	0.74	0.29	0.33	0.38	0.41
MSE	2.95e-4	2.08e-4	2.21e-4	1.66e-4	2.91e-3	3.35e-3	3.55e-3	2.82e-3

4 Methods

4.1 RAVENS acquisition

This work employs the “Multimodal MRI Reproducibility Resource” [22], colloquially known as the Kirby21 dataset, which is publicly available through the Neuroimaging Informatics Tools and Resources Clearinghouse (www.nitrc.org). The Kirby21 dataset consists of test-retest structural MRI and resting state fMRI scans from 21 healthy adult volunteers with no history of neurological conditions (11 male and 10 female, aged 31.76 ± 9.47 years) who were each scanned twice on the same day. Further details of the study can be found in [22].

The structural MRI data were acquired on a 3.0T scanner (Achieva, Philips Medical Systems) using a high resolution 3D magnetization-prepared rapid acquisition of gradient echoes (MPRAGE) sequence with resolution: 1.0 × 1.0 × 1.2 mm; TR:~6.7ms; TE:3.1ms; TI=842ms; flip angle: 8°; SENSE factor:2). All images were spatially normalized via registration of T1 maps into the mean template generated using ANTS [2, 1]. Details of how the average template are generated can be found in [7]. All T1 images were segmented into ventricles (VN), gray matter (GM), and white matter (WM) using Lesion-TOADS [32]. After segmentation, the final tissue maps of VN, WM and GM were spatially normalized using the HAMMER-SUITE [31] to generate RAVENS images. Finally, the RAVENS maps were smoothed individually with a 4-mm FWHM Gaussian kernel using SPM8.

4.2 fMRI acquisition

The Kirby21 data set was also used to investigate the reproducibility of seed-based functional connectivity analysis using the Kirby21 dataset follows. In short, two 7-min resting state scans were acquired from each participant using a single-shot, partially parallel (SENSE) gradient-recalled echo planar sequence with an ascending slice order (TR/TE = 2000/30 ms, FA = 75, 3-mm axial slices with a 1-mm slice gap) and an 8-channel head coil. Participants were instructed to relax and fixate on a cross-hair while remaining as still as possible. The two resting state scans were separated by a short break during which the participant exited the scanner; the T1-weighted anatomical image described in section 4.1 was also acquired to be used as a template for spatial registration of the functional images.

Image processing was performed using SPM8 and custom MATLAB scripts. Anatomical images were registered to the first functional volume and normalized to MNI space using unified segmentation/normalization (SPM8). Functional data were adjusted for slice time acquisition as well as participant motion and were transformed to MNI space. Nuisance covariates from white matter and CSF were estimated using CompCor [3] and regressed from the data along with the motion realignment estimates, their derivatives, global mean signal, and linear trends. Data were then spatially smoothed (6-mm kernel) and temporally filtered using a 0.01–0.10 pass-band filter. Data from one participant was excluded from analysis due to a misalignment of the first and second resting state scans.

Seed voxel analysis is commonly used in fMRI studies to analyze the functional connectivity of the brain via a seed voxel from a region of interest. Here, we investigated the reproducibility of this approach for our dataset considering 4 different seeds, each with a 6-mm radius: the posterior cingulate cortex (labeled PCC) [16], the premotor area (labeled M3) [9] and 2 seeds from the dorsal-ventral extremes of the motor strip, the dorsal seed representing lower limb control (labeled M1) [24] and the ventral one corresponding to oromotor function (labeled M5). MR time series were averaged across voxels within each seed, and a correlation map for each of the resulting 4 time courses was then obtained with each voxel in the brain.

4.3 DTI-MRI acquisition

The data were collected as part of an ongoing observational study being conducted at the National Institutes of Health and at Johns Hopkins University. Study participants with MS were recruited from the outpatient neurology clinic and healthy volunteers from the community. Prior to MRI scanning, all participants gave signed, informed consent, and all procedures were approved by the institutional review board. Cohort characteristics are summarized in [15, 18]. Longitudinal analyses of the DTI-MRI sub-study can be found in [19, 38].

Scans were performed on a 3T scanner (Intera; Philips, Best, The Netherlands) over a 4.6 year period, using the body coil for transmission and either a 6-channel head coil or the 8 head elements of a 16-channel neurovascular coil for reception (both coils are made by Philips). Each session included two sequential DTI scans using a conventional spin-echo sequence and a single-shot EPI readout. Whole-brain data was acquired in nominal 2.2mm isotropic voxels with the following parameters: TE, 69ms; TR, automatically calculated (shortest); slices, 60 or 70; parallel imaging factor, 2.5; non-collinear diffusion directions, 32 (Philips overplus high scheme); high b-value, 700 s/mm²; low b-value (b0), approximately 33 s/mm²; repetitions, 2; reconstructed in-plane resolution, 0.82 × 0.82 mm. A 3D gradient-echo magnetization-transfer sequence was also performed with segmented EPI readout (nominal acquired resolution, 1.5 × 1.5 × 2.2 mm; TE, 15ms; TR, 64 ms; parallel imaging factor, 2; EPI factor, 7; magnetization-transfer pulse, sinc-shaped, 1.5kHz off-resonance; repetitions, 3), the data from which were rigidly registered to the DTI scan before calculation of MTR maps (defined as 1 minus the voxel-wise ratio of data from this sequence to those obtained using the same sequence without the magnetization-transfer pulse). Prior to analysis, data were adjusted to account for changes in average tract-specific MRI indices that resulted from the scanner upgrades that inevitably occur over the course of a study such as this. The procedure by which this adjustment was made has been previously described [20].

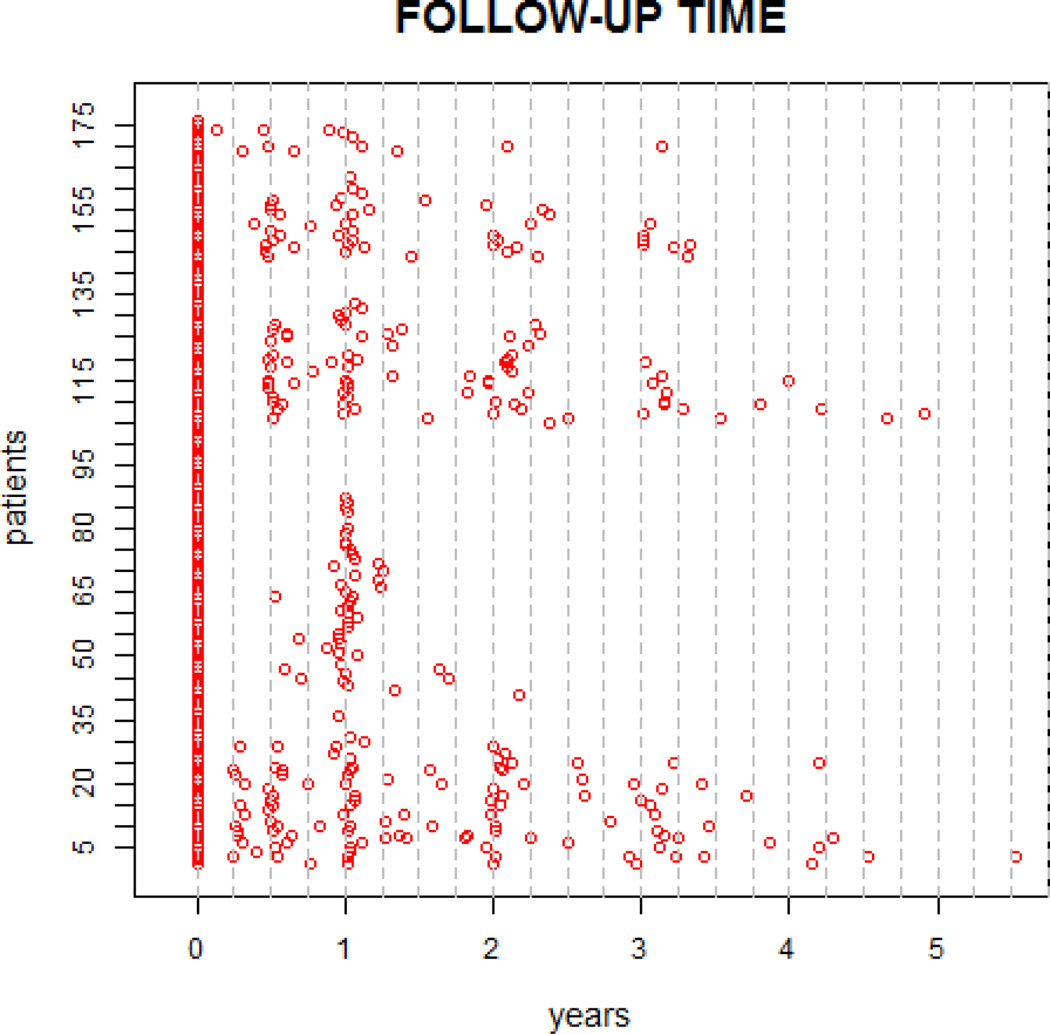
The diffusion-weighted scans were processed using CATNAP (Landman et al., 2007) to create maps of fractional anisotropy (FA), mean diffusivity (MD), axial diffusivity (AD) and radial diffusivity (RD). These four quantities, together with MTR, are hereafter termed MRI indices. Whole-brain MRI indices were calculated by slice-wise averaging of all diffusion-weighted images, removal of the low-intensity voxels that are characteristic of extracerebral tissues on these images, and final removal of voxels with MD > 1.7µm²/ms to exclude cerebrospinal fluid [26]. The resulting brain mask was applied to all DTI maps and also to the coregistered MTR maps. The images were obtained from a natural history study, where 176 MS patients were followed up to 5.5 years, which generated a total of 446 MRI scans. The number of scans per subject varied from 1 to 6. The scanning time is shown in Figure 5 where time zero indicates the first scan. For illustration purposes, we focus on the measurements in a region of 30096 voxels that contains the corpus callosum. At each voxel, data are FA weighted by the probability of being in the corpus callosum. Images are registered using affine transformations.

Figure 5.

Image scanning time for 176 patients. Every person has a baseline scan at time 0. The x axis is time in years. The y axis are patient IDs. We match visit number from different patients by rounding their scan time to quarter month, as indicated by gray dashed lines.

5 Results

5.1 RAVENS replication results

RAVENS maps produce an image of the deformation of the brain necessary to fit in a given template and are proxies of brain morphology. Here the focus is on ventricular, white matter, and gray matter regions considered separately, segmented via Lesion-TOADS [32]. The measurement error is an uncontrollable combination of sources including image acquisition, biological error (natural within-day brain variation), movement, magnetic field inhomogeneities, pre-processing, spatial normalization, and segmentation. Apportioning error variability is beyond the scope of this paper. Instead, interest lies in first establishing that estimating the effect of total measurement error variability (regardless of its source) is possible and then in investigating its impact on image reliability.

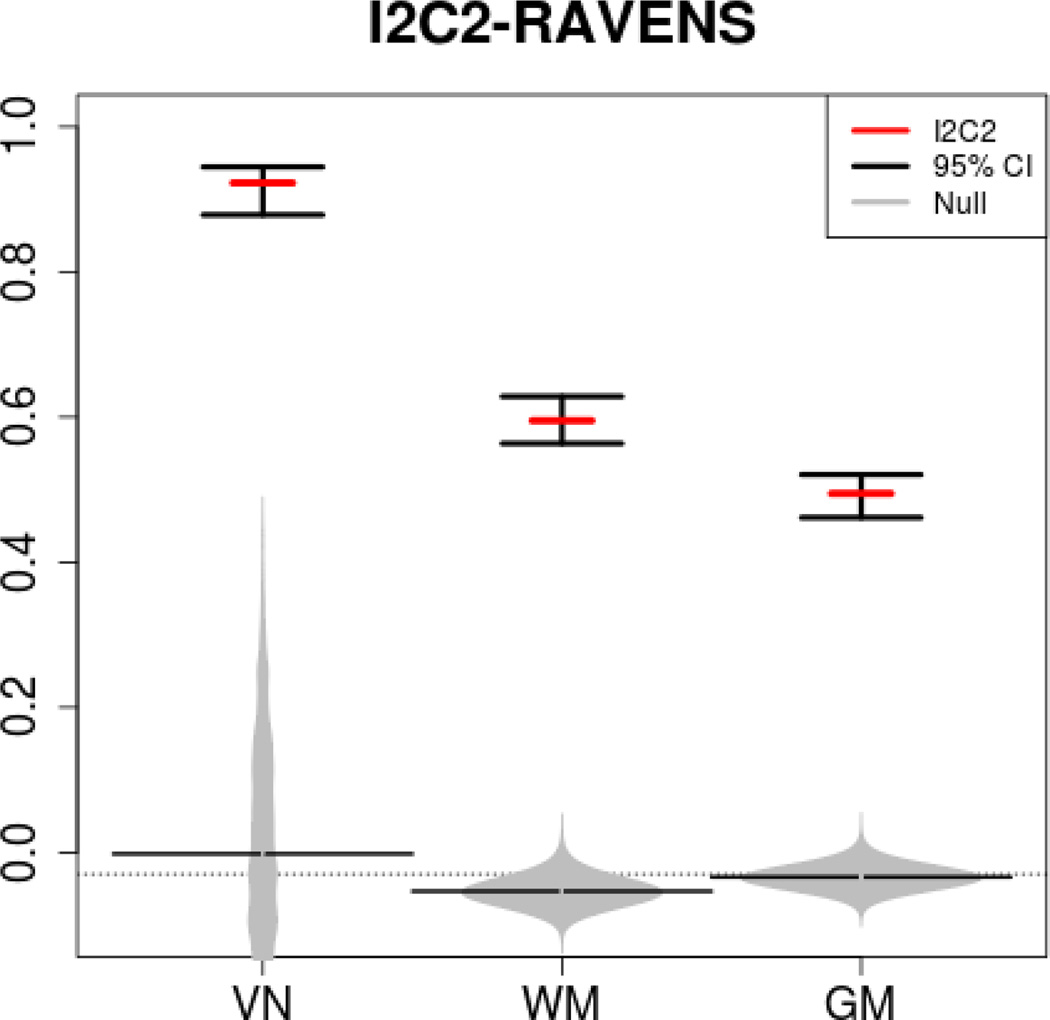
Figure 3 displays the I2C2 estimators (ρ̂) as a red line with 95% equal tail probability confidence intervals obtained using the nonparametric bootstrap of subjects. The reliability in the ventricles is by far the largest roughly (0.9) followed by reliability in white matter (0.55) and gray matter (0.45). Determining the source and type of error could be done, for example, by investigating various ROI’s or by inspecting the principal components of measurement error variability based on HD-MFPCA [37]. The distributions of I2C2 estimators under zero reliability ρ̂₀ is shown in gray with the median displayed as a black horizontal line. These results indicate strong evidence that the observed reliability values are inconsistent with zero reliability. Interestingly, the null distribution (gray histogram plot) for ventricles has a long right tail with non-trivial probability above 0.3. This is somewhat unexpected, and may indicate stronger between subject correlations of measurement error processes in the ventricles. Further investigating this postulate is left for future study.

Figure 3.

Estimated I2C2 (red horizontal lines) and 95% equal tail probability confidence intervals for ventricles, white matter and gray matter RAVENS images. Gray distributions correspond to the I2C2 estimator under the zero reliability assumption (random permutations of labels).

5.2 fMRI replication results

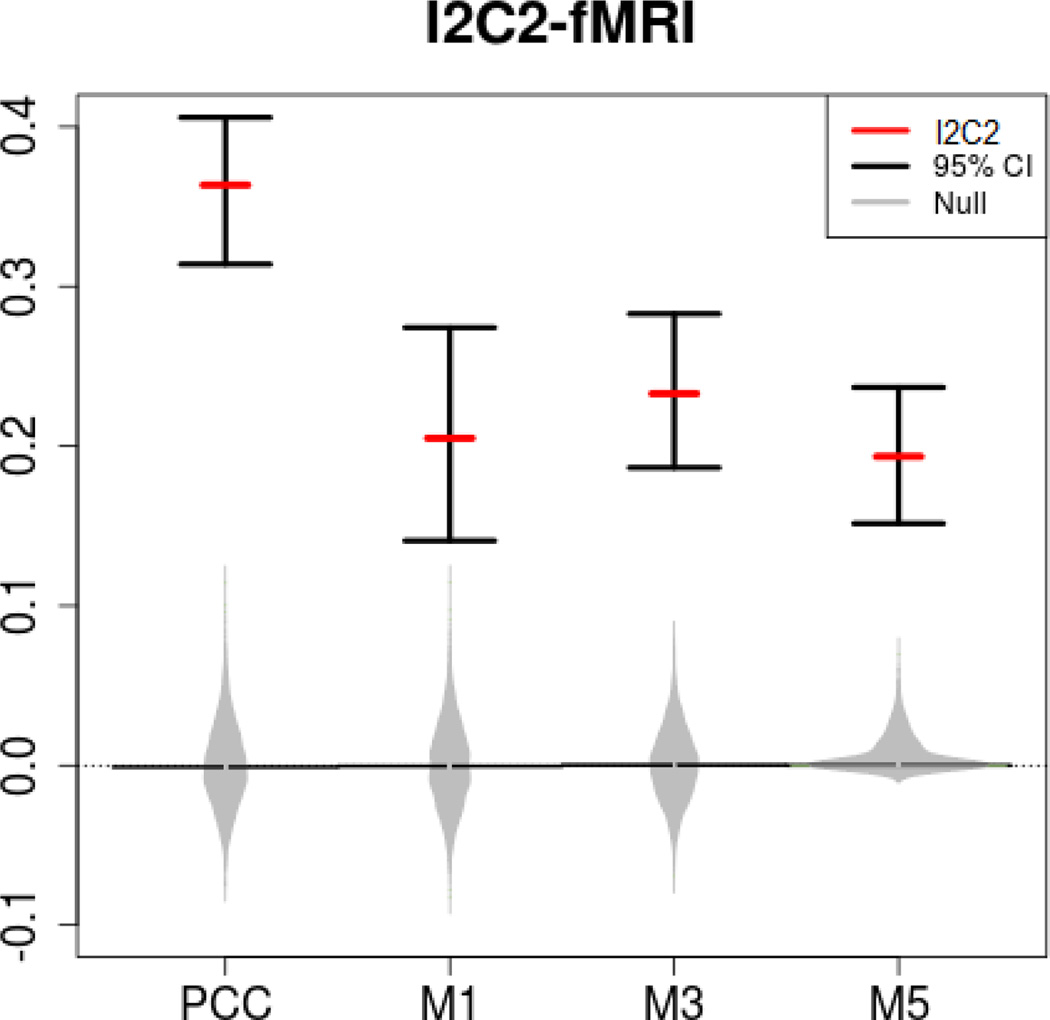
The I2C2 metric was used to quantify the reproducibility of the resulting connectivity map (correlation matrix) for each of the four seed regions. Results are shown in Figure 4 using the same notation and symbols as in Figure 3. The overall message is that the seed-voxel based correlation maps are not reliable, with the reliability estimates varying between approximately 0.20 (for M1, M3, and M5) and 0.37 (for PCC). These low values suggest that state-of-the-art seed-voxel-based correlation maps based on resting state fMRI data are unreliable, though the PCC seems to indicate higher (nearly double) reliability than other regions. Thus, caution is warranted in the interpretation of these maps and in the analysis of connectivity maps obtained from thresholding unreliable fMRI resting state correlation operators. These results are inconsistent with the large and increasing literature [5, 8, 12, 21, 25, 29, 30, 35, 36, 39, 40] on resting state fMRI that reports high reliability of measurements. Much deeper investigation is needed to address these divergent findings, establish identical estimands, estimators and evaluation procedures. Our procedure provides a clear, simple, and easy to use step in this direction.

Figure 4.

Estimated I2C2 (red horizontal lines) and 95% equal tail probability confidence intervals for fMRI seed-voxel correlation maps for the posterior cingulate cortex (PCC), the dorsal region of the motor cortex corresponding to control of the lower limbs (M1), the premotor cortex (M3) and the ventral-most region of the motor cortex corresponding to oro-motor function (M5). Gray distributions correspond to the I2C2 estimator under the zero reliability assumption (random permutations of labels).

5.3 DTI-MRI replication results

To highlight methods, a subset of the complete data collection consisting of subjects who have more than 6 visits was selected. This reduced the data set to 117 scans from 18 subjects: 14 subjects with 6 scans, 1 with 7, 2 with 8, and 1 with 10. Henceforth, the subset is viewed as the complete data set with no further reference of the omitted subjects. We also consider four further subsets labeled as “T≤4”, “T≤3”, “T≤2”, and “T≤1”. The notation refers to the number of years since the baseline scan, as, for example, the T≤4 dataset considers only images obtained within the first 4 years from the baseline scan, resulting in 110 scans from the 18 subjects (4 ~ 5, 11 ~ 6, 3 ~ 8 where 4 ~ 5 refers to 4 subjects with 5 scans). The T≤3 dataset contains 88 scans broken down as 6 ~ 4, 9 ~ 5, 2 ~ 6, and 1 ~ 7. The T≤2 data set contains 70 scans broken down as 7 ~ 3, 7 ~ 4, 3 ~ 5, 1 ~ 6, and 1 ~ 7. Finally, the T≤1 data set contains 45 scans, 1 ~ 1, 1 ~ 4, 8 ~ 2, and 8 ~ 3.

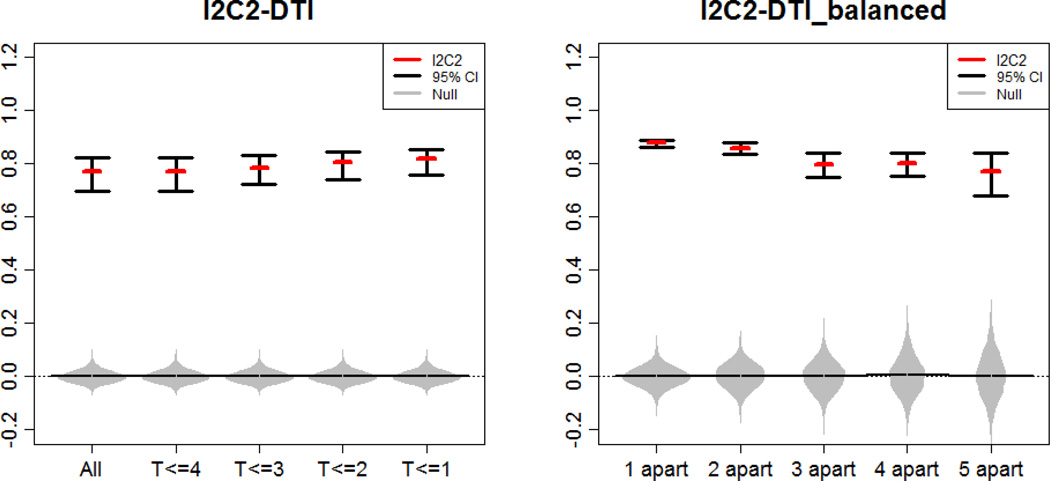
In [38] the existence of a longitudinal change over time in these data was studied with the finding that less 1% of the variability was explained by longitudinal within-subject changes. Thus, modeling these data as exchangeable image measurement error processes is likely a valid approximation of the underlying processes. All five data sets are unbalanced, having a different number of replicates per subject. The left panel in Figure 6 displays the reliability estimators (red horizontal line) and the associated equal tail probability 95% confidence intervals. These results indicate that the reliability of these measurements hovers slightly below 0.8, which is consistent with the findings in [38].

Figure 6.

Estimated I2C2 (red horizontal lines) and 95% equal tail probability confidence intervals for FA in an area containing the corpus callosum. Gray distributions correspond to the I2C2 estimator under the zero reliability assumption (random permutations of labels). Left panel results are based on 18 subjects who have at least 6 visits (“All”) and subsets of the “All” data set containing all scans within the first 4, 3, 2, and 1 year from baseline, respectively. Right panel results are based on pairs of imaging obtained at most 1, 2, 3, 4, and 5 years apart. The number of subjects in each data set (from left to right) was: 119, 64, 49, 31, 18, respectively.

Our work investigated the reliability of the imaging studies as a function of time by selecting subjects who have at least two replications and constructing five additional replication sub-studies labeled “1 apart”, “2 apart”, “3 apart”, “4 apart” and “5 apart”, respectively. To be specific, each such sub-study contains exactly two replicates per subject: the baseline observation and the replicate that is closest to being 1, 2, 3, 4, or 5, years apart, respectively. The number of subjects in each data set was 119, 64, 49, 31, 18, respectively, with more subjects in data sets with shorter between-observations intervals.

The right panel in Figure 6 displays the reliability estimators for these replication studies as a function of how many years apart images were taken. The estimated reliability of observations taken within one year of each other is quite high, roughly 0.9, which indicates that there are very few changes in the FA measurements along the corpus callosum of MS subjects within one year. This may be good news for individuals with MS if the lack of measured neuronal fiber integrity via FA represents actual fiber integrity. However, this finding may be disheartening to investigators searching for biomarkers of neuronal fiber degradation, if degradation is actually there. As expected, the reliability of image replication decreases with the increased time between visits, with median reliability roughly around 0.8 for images collected 5 years apart. However, this decline in reliability is relatively small and likely to be indicative of small observable longitudinal changes. The variability around the estimated I2C2 also increases from the replication study “1 apart” to “5 apart”, though this is most likely due to the decrease in sample size from 119 to 18 subjects with repeat samples.

6 Discussion

This manuscript proposes an extension of the classical intra-class correlation coefficient to image replication studies. The resulting parameter, denoted I2C2, provides a global measurement of reliability that is intuitive and easy to calculate. Moreover, I2C2 can readily be calculated for given ROIs by simply restricting the summations in Section 1 to those voxels within the ROI mask. In practice, one may actually report the I2C2 on a partition of the image in mutually disjoint ROIs, say R₁, …, R_P. Then I2C2 can be calculated for each R_p, p = 1, …, P and compared to the overall I2C2. Areas of unexpectedly small estimated I2C2 may further indicate the source and type of measurement error. Another practical approach would be to calculate the I2C2 hierarchically, i.e. at the voxel level, then at overlapping neighborhoods of increasing size and, ultimately, at the image level. This could provide an interesting multi-resolution approach to visualizing the structure of the measurement error.

An equally simple measure of reproducibility could be the average of ICC at the voxel levels. An unbiased estimator of the average ICC would then be

$$1-\frac{1}{V}\frac{{\sum }_i{J}_i-1}{{\sum }_i(J_i-1)}\sum _{\upsilon =1}^V\frac{{\{W_{ij}(\upsilon )-{\mathrm{W̅}}_i․(\upsilon )\}}^2}{{\sum }_{i=1}^I{\sum }_{j=1}^{J_i}{\{W_{ij}(\upsilon )-W_{‥}(\upsilon )\}}^2}.$$

Irrespective of the replication estimand and estimation procedure the subject-level bootstrap and permutation tests introduced in this paper can be applied. However, there are reasonable arguments for considering I2C2. Indeed, the variability attributable to variation among subjects is equal to trace(K_X) whereas the variability attributable to visits is trace(K_U). Thus, I2C2 is the proportion of variability explained by subject-level variability out of the total variability of the data in the multivariate image measurement error model. In contrast, the average ICC is the average of the proportion of variability explained by subject-level variability out of the total variability of the data in the sequence of univariate (marginal) measurement error models. This distinction has practical implications. Consider, for example, the case of an experiment where there are 1000 voxels in every image. At 500 voxels the absolute variability of the data and reliability is very low. However, at the other 500 voxels the variability and reliability are large. In this context the average ICC would place too much emphasis on the low variability voxels because it ignores the relative variability of the data at different voxels. A second problem occurs at locations with small visit-to-visit variability, as this variance is used in the denominator of the ICC estimator and may lead to serious computational instabilities.

While data rarely satisfy the measurement error model (2) exactly, the model is a reasonable starting point for defining the data structure under explicit assumptions. Model assumptions notwithstanding, we prefer this explicit statistical approach to an algorithmic one that obscures assumptions. Moreover, the model can easily be extended to include some obvious data supported complications. For example, if each visit has a different mean, one can easily expand the model to include (so-called) batch or visit effects

$${\mathit{W}}_{ij}={\mathit{B}}_j+{\mathit{X}}_i+{\mathit{U}}_{ij},$$

as proposed in [14]. Here the images B_j are visit-specific fixed effect images. Such deterministic changes across all subjects from one visit to another could be due to the use of different scanners, imaging parameters, scanner drift, etc. In quality control, agriculture and lab sciences such effects arise from a batch being run for measurement or assay (hence the term “batch effect”). For subjects returning to a scanner, batches are visits. Note that the visit-specific effects can be easily estimated as ${\mathit{B̂}}_j={\sum }_{i=1}^I{\mathit{W}}_{ij}/I$ and one can define the I2C2 for the residuals W_ij − B̂_j.

In more complex models, one may also be interested in, or worried about, the longitudinal effects of collecting the data. For example, in the DTI study, some images are taken within a few months of each other, whereas other images are collected years apart. In such situations, it is reasonable to add a term that accounts for longitudinal changes. A reasonable model for such an approach could be

$${\mathit{W}}_{ij}=\mathit{B}(T_{ij})+{\mathit{X}}_{i,0}+{\mathit{X}}_{i,0}{T}_{ij}+{\mathit{U}}_{ij},$$

where B(T_ij) is an effect that depends on time of the visit, T_ij, as in most longitudinal studies, visits are not equally spaced. In this model B (T_ij) + X_i,0 is the true unobserved image at baseline (T_ij = 0), B(T_ij) + X_i,0 + X_i,0T_ij is the true unobserved image at time T_ij > 0, and U_ij is the image measurement error process. Estimation of these type of models is thoroughly discussed in [19, 38], but it is worth noting that reasonable assumptions about the data can easily be incorporated into statistical models.

Regardless of the model under investigation, the image error process, U_ij, deserves particular attention. Indeed, from all models discussed in this paper one can estimate the covariance operator, K_U, and the first eigenvectors can be visually inspected. This provides clues into the structure of measurement error. For further reading on measurement error modeling we recommend [6, 17]. For the effect of image measurement error on estimating associations with outcomes we recommend [10] while for inference in the means of two imaging processes we recommend [11].