Abstract
The Adjective Rating Scale of Withdrawal (ARSW) is commonly used to assess opiate withdrawal in clinical practice and research. The aims of this study were to examine the factor structure of the ARSW, test measurement invariance across gender and treatment groups, and assess longitudinal measurement invariance across the clinical trial. Secondary data analysis of the National Drug Abuse Treatment Clinical Trials Network 000-3, a randomized clinical trial comparing two tapering strategies, was performed. The ARSW was analyzed at baseline, end of taper and 1-month follow-up (N =515 opioid-dependent individuals). A 1-factor model of the ARSW fit the data and demonstrated acceptable reliability. Measurement invariance was supported across gender and taper groups. Longitudinal measurement invariance was not found across the course of the trial, with baseline assessment contributing to the lack of invariance. If change over time is of interest, change from post-treatment through follow-up may offer the most valid comparison.
Keywords: Opiate withdrawal, opiate dependence, measurement invariance, psychometrics
1. Introduction
Assessment of opioid withdrawal is important to clinically manage opioid dependent individuals (Tompkins, Bigelow, Harrison, Johnson, Fudala & Strain, 2009). Opioid withdrawal is a function of the severity of physical dependence on opioids and the occupancy of the μ receptor at a specific time (Wesson & Ling, 2003). Withdrawal is assessed in treatment and recovery from opioid addiction in both research and clinical settings. One common scale used to examine withdrawal is the Adjective Rating Scale for Withdrawal (ARSW) (Bickel, Stitzer, Bigelow, Liebson, Jasinski, & Johnson, 1988a; Bickel, Stitzer, Bigelow, Liebson, Jasinski, & Johnson, 1988b; Amass, Kamien, & Mikulich, 2000). As it was developed, the ARSW was one of two 20-item adjective scales that were given to assess opiate withdrawal and opiate effects (Bickel at el, 1988a; Bickel at el, 1988b), and was later trimmed to 16 items (Amass et al., 2000) that assessed symptoms such as painful joints, poor appetite, trouble getting to sleep, etc. The ARSW is typically summed to create a total score, and the scores have been used to assess subjective ratings of withdrawal across treatment groups (Amass et al., 2000; Bickel at el, 1988a; Ling et al, 2005; Ling et al, 2009; Ziedonis et al., 2009) and over time (Amass et al., 2000; Bickel at el, 1988a; Bickel at el, 1988b; Ling et al, 2005; Ziedonis et al., 2009), typically in combined samples of men and women (Amass et al., 2000; Bickel at el, 1988a; Ling et al, 2005, Ling et al, 2009; Ziedonis et al., 2009).
Although the ARSW is a widely used measure of withdrawal in clinical trials, there is surprisingly little psychometric evaluation of this measure. To our knowledge, there is no published work on the factor structure or reliability of this scale. Additionally, measurement invariance of the ARSW across groups or over time has not yet been tested. The demonstration of measurement invariance is critical in order to effectively compare different groups on a latent construct (Cheung & Rensvold, 2002; Vandenberg & Lance, 2000; Brown, 2006; Steenkamp & Baumgartner, 1998; Chen et al., 2005). In clinical trials, if measures are not invariant, there is the potential for bias in clinicians’ interpretation of patient outcomes, complicating the interpretation of treatment effects (McHorney & Fleishman, 2006). For example, although treatment or taper groups may both have the potential to experience withdrawal similarly, one treatment group may endorse more withdrawal symptoms compared to the other treatment group, even though both groups are experiencing the same amount of withdrawal. This same issue of measurement inequality may occur across gender.
Longitudinal measurement invariance is used to evaluate the temporal change in a construct and, similar to testing measurement invariance across groups, is needed prior to comparing means over time (Vandenberg & Lance, 2000; Brown, 2006). For example, endorsement of withdrawal symptoms may change over time even though actual levels of withdrawal are consistent over time. This concern is highlighted in the clinical management of opioid withdrawal as assessing change in withdrawal over the course of treatment is crucial. Without testing the assumptions related to multiple-group and longitudinal measurement invariance, one cannot know whether 1) detected differences in withdrawal are true differences across groups or due to differences in assessment or structure of withdrawal across the groups, and 2) detected changes in withdrawal over time reflect true changes or are due to changes in assessment or structure of withdrawal.
The aims of this study are to build on previous work that utilized the ARSW by 1) examining the assumed unidimensionality of withdrawal by testing a 1-factor model of the ARSW, 2) provide a measure of ARSW reliability, 3) examine measurement invariance across gender and taper groups, and 4) assess longitudinal measurement invariance at pre-treatment, post-treatment, and at 1-month follow-up in a sample of opioid-dependent individuals enrolled in a clinical trial. If measurement invariance is demonstrated across groups and/or over time, differences in latent means will be examined.
2. Materials and Methods
2.1 Clinical Trials Network 000-3
Participants were from the National Drug Abuse Treatment Clinical Trials Network Number 0003 (Ling et al., 2009). This was a randomized, parallel-group, open-label study design consisting of two buprenorphine/naloxone taper periods for opioid-dependent individuals. The participants first completed baseline assessments and were then stabilized on buprenorphine/naloxone. After the stabilization phase, the patients were stratified across the maintenance dose (8, 16 or 24mg) of buprenorphine/naloxone and then randomized to the 7-day or 28-day taper groups. Follow-up measures were collected at 1-month and 3-month post-taper.
2.2 Measures
The ARSW is a 16-item self-report scale of opiate withdrawal symptoms (e.g., Muscle cramps, Hot or cold flashes, Runny nose, Tense/jittery) in which individuals rate the withdrawal adjectives on a 9-point scale from none to severe, with a maximum score of 144 (Bickel et al, 1988a; Bickel at el, 1988b; Amass et al., 2000).
2.3 Study Sample
The final intention-to-treat sample was 516 participants who were potentially available for data collection at the end of the taper. Data were not available for one participant at baseline and was therefore excluded from the current analyses at that phase of the study. The effective sample size for the current investigation was n = 515. Self-report gender, age and ethnicity were assed at screening. This sample consisted of 346 males (67%) and 169 females (33%) (7-day taper group: male = 171, female = 83; 28-day taper group: male = 175, female = 86), with a mean age of 35.91 (SD = 10.45). Seventy-one percent identified as Caucasian, 11% as African American, 7% as Hispanic, 9% as multiple races and 2% as “other.” Participants were from 11 out-patient treatment programs from 10 cities in the United States.
2.3 Statistical Analyses
As noted in the applied measurement invariance literature (Barbosa-Leiker, Wright, Burns, Parks, & Strand, 2011; Barbosa-Leiker, in press), a series of analyses to examine measurement invariance were conducted after separate confirmatory factor analyses were fit for each group. Configural invariance (Horn & McArdle, 1992) examined if there was an equal factor structure across the groups (Vandenberg & Lance, 2000). This tested the final single-occasion model and examined if the theoretical framework of the ARWS was the same across taper groups and gender. Metric invariance (Horn & McArdle, 1992) tested if the relationships of ARSW items were equivalent for like items across taper groups and gender (i.e., constrained factor loadings). Lastly, scalar invariance (Meredith, 1993) constrained the intercepts of like item to be equal across groups to test whether differences in means of the items were due to differences in the construct (Steenkamp & Baumgartner, 1998). This step evaluated whether observed values of the ARSW items were equivalent across taper groups and gender when there was a constant level of withdrawal. After the demonstration of scalar invariance across taper groups and gender is shown, mean differences across taper groups and gender can be attributed to true differences in the construct (Vandenberg & Lance, 2000; Brown, 2006).
If withdrawal was invariant across groups, longitudinal measurement invariance was conducted following the above steps across baseline, end of taper, and at 1-month post-taper follow-up. Once measurement invariance was demonstrated across taper groups, gender, and over the course of the clinical trial and follow-up, differences across taper group, gender (regardless of taper group), and across the phases of the clinical trial in the withdrawal latent factor means were tested via Z-tests. Latent factor means were examined in this way so as to map directly onto the tests of invariance.
Overall model fit was evaluated using the robust comparative fit index (CFI; study criterion ≥ 0.900), the robust root mean square error of approximation (RMSEA; study criterion ≤ 0.080), and the robust standardized root mean square residual (SRMR; study criterion ≤ 0.080). For tests of measurement invariance, a change in CFI between comparison and nested models of ≥ −0.010 in addition to a change in RMSEA of ≥ 0.015 or a change in SRMR of ≥ 0.030 (for loading invariance) and ≥ 0.010 (for intercept invariance) will be used (Chen, 2007). For latent means analyses, differences are considered significant at p ≤ .05.
All primary statistical testing was conducted in Mplus, Version 6 (Muthén, 1998–2010), using the robust maximum likelihood (MLR) estimator. There was 43% missing data in both taper groups from baseline to 1-month follow-up. Missing data was handled with full information maximum likelihood using all available data (Enders, 2010).
3. Results
3.1 1-factor model
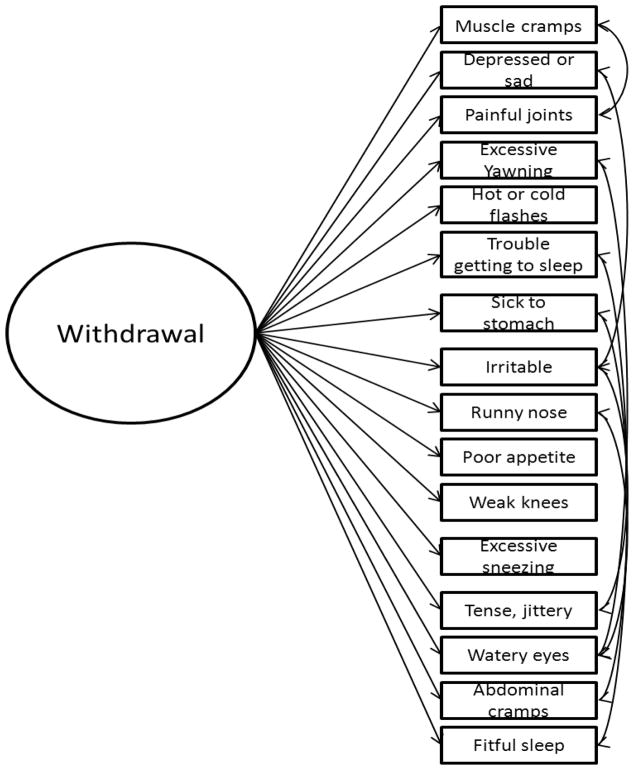
Mean scale scores, standard deviations, and reliability coefficients over time within each group are presented in Table 1. The 1-factor model, with 7 correlated residuals, is presented in Figure 1. The correlated residuals (Muscle cramps with Painful joints, Depressed or sad with Irritable, Excessive yawning with Watery eyes, Trouble getting to sleep with Fitful sleep, Sick to stomach with Abdominal cramps, Irritable with Tense, jittery, and Runny nose with Watery eyes) were added one at a time based on the similarity of symptoms and modification indices across the groups. Fit indices, presented in Table 2 indicated that this model fit the data well for each group and at each time point (CFIs ≥ .900, RMSEAs ≤ .081, SRMRs ≤ .068).
Table 1.
Mean scores (standard deviation) and reliability coefficients for the Adjective Rating Scale for Withdrawal
| Total score | Cronbach’s alpha | |
|---|---|---|
| Males | ||
| Baseline (n = 346) | 60.61 (32.05) | .93 |
| End of taper (n = 244) | 19.51 (24.10) | .95 |
| 1-month follow-up (n =192) | 12.49 (18.76) | .94 |
| Females | ||
| Baseline (n = 169) | 65.23 (32.26) | .93 |
| End of taper (n = 128) | 21.28 (28.10) | .95 |
| 1-month follow-up (n = 103) | 16.59 (24.46) | .95 |
| 7-day taper | ||
| Baseline (n = 254) | 62.82 (31.65) | .93 |
| End of taper (n = 201) | 22.03 (25.98) | .95 |
| 1-month follow-up (n = 146) | 14.30 (22.47) | .95 |
| 28-day taper | ||
| Baseline (n = 261) | 61.45 (32.70) | .93 |
| End of taper (n= 171) | 17.88 (24.81) | .95 |
| 1-month follow-up (n = 149) | 13.56 (19.50) | .95 |
Figure 1.
The 1-factor model of the Adjective Rating Scale for Withdrawal. For presentation purposes, individual item residuals are not displayed. Correlated residuals include: Muscle cramps with Painful joints, Depressed or sad with Irritable, Excessive yawning with Watery eyes, Trouble getting to sleep with Fitful sleep, Sick to stomach with Abdominal cramps, Irritable with Tense, jittery, and Runny nose with Watery eyes.
Table 2.
1-factor model of Adjective Rating Scale for Withdrawal for each group at each time point
| df | χ2 | CFI | RMSEA | SRMR | |
|---|---|---|---|---|---|
| Males | |||||
| Baseline | 97 | 202 | 0.954 | 0.056 | 0.041 |
| End of taper | 97 | 180 | 0.934 | 0.059 | 0.049 |
| 1-month follow-up | 97 | 180 | 0.918 | 0.067 | 0.058 |
|
| |||||
| Females | |||||
| Baseline | 97 | 201 | 0.916 | 0.079 | 0.059 |
| End of taper | 97 | 164 | 0.916 | 0.073 | 0.054 |
| 1-month follow-up | 97 | 162 | 0.900 | 0.081 | 0.058 |
|
| |||||
| 7-day taper | |||||
| Baseline | 97 | 195 | 0.941 | 0.063 | 0.045 |
| End of taper | 97 | 205 | 0.904 | 0.074 | 0.060 |
| 1-month follow-up | 97 | 171 | 0.915 | 0.072 | 0.068 |
|
| |||||
| 28-day taper | |||||
| Baseline | 97 | 206 | 0.942 | 0.066 | 0.049 |
| End of taper | 97 | 153 | 0.937 | 0.058 | 0.051 |
| 1-month follow-up | 97 | 123 | 0.964 | 0.042 | 0.045 |
Note. CFI = robust comparative fit index; RMSEA = robust root mean square error of approximation; SRMR = robust standardized root mean square residual. χ2 tests were significant at p < .001.
3.2 Measurement Invariance across Groups
The fit for tests of measurement invariance across gender at baseline, end of taper, and 1-month follow-up are presented in Table 3. Results indicated that the configural, metric, and scalar invariance models showed adequate fit at pre-treatment, post-treatment, and follow-up. There was not a decrement in fit when going from the configural invariance models to metric invariance models at baseline, end of taper, and follow-up. Further, there was not a decrement in fit when going from the metric invariance models to scalar invariance models at baseline, end of taper, and follow-up.
Table 3.
Measurement Invariance of the Adjective Rating Scale for Withdrawal across Gender at 3 time points
| df | χ2 | CFI | RMSEA | SRMR | Δdf | ΔCFI | ΔRMSEA | ΔSRMR | |
|---|---|---|---|---|---|---|---|---|---|
| Time 1: Baseline | |||||||||
| Configural | 194 | 403 | 0.941 | 0.065 | 0.048 | ||||
| Metric | 209 | 428 | 0.939 | 0.064 | 0.053 | 15 | −0.002 | −0.001 | +.005 |
| Scalar | 224 | 466 | 0.932 | 0.065 | 0.055 | 15 | −0.007 | +0.001 | +.002 |
| Time 2: End of taper | |||||||||
| Configural | 194 | 344 | 0.927 | 0.065 | 0.051 | ||||
| Metric | 209 | 355 | 0.930 | 0.061 | 0.059 | 15 | +0.003 | −0.004 | +0.008 |
| Scalar | 224 | 387 | 0.921 | 0.063 | 0.061 | 15 | −0.009 | +0.002 | +0.002 |
| Time 3: 1-month follow-up | |||||||||
| Configural | 194 | 343 | 0.912 | 0.072 | 0.058 | ||||
| Metric | 209 | 375 | 0.902 | 0.073 | 0.084 | 15 | −0.010 | +0.001 | −0.026 |
| Scalar | 224 | 404 | 0.891 | 0.074 | 0.085 | 15 | −0.011 | +0.001 | +0.001 |
Note. CFI = robust comparative fit index; RMSEA = robust root mean square error of approximation; SRMR = robust standardized root mean square residual. χ2 tests were significant at p < .001.
The fit for the tests of measurement invariance across treatment groups (7-day taper group vs. 28-day taper group) at baseline, end of taper, and 1-month follow-up are shown in Table 4. Results indicated that the configural, metric, and scalar invariance models showed adequate fit at baseline, end of taper, and follow-up. There was not a decrement in fit when going from the configural invariance models to metric invariance models at baseline, end of taper, and follow-up. Lastly, there was not a decrement in fit when going from the metric invariance models to scalar invariance models at baseline, end of taper, and follow-up.
Table 4.
Measurement Invariance of the Adjective Rating Scale for Withdrawal across Treatment Groups at 3 time points
| df | χ2 | CFI | RMSEA | SRMR | Δdf | ΔCFI | ΔRMSEA | ΔSRMR | |
|---|---|---|---|---|---|---|---|---|---|
| Time 1: Baseline | |||||||||
| Configural | 194 | 400 | 0.941 | 0.064 | 0.047 | ||||
| Metric | 209 | 423 | 0.939 | 0.063 | 0.051 | 15 | −0.002 | −0.001 | +.004 |
| Scalar | 224 | 440 | 0.938 | 0.061 | 0.051 | 15 | −0.001 | −0.002 | 0 |
| Time 2: End of taper | |||||||||
| Configural | 194 | 357 | 0.919 | 0.067 | 0.056 | ||||
| Metric | 209 | 371 | 0.919 | 0.065 | 0.068 | 15 | 0.000 | −0.002 | +0.012 |
| Scalar | 224 | 392 | 0.916 | 0.063 | 0.069 | 15 | −0.003 | −0.002 | +0.001 |
| Time 3: 1-month follow-up | |||||||||
| Configural | 194 | 295 | 0.937 | 0.060 | 0.057 | ||||
| Metric | 209 | 316 | 0.933 | 0.059 | 0.074 | 15 | −0.004 | −0.001 | +0.017 |
| Scalar | 224 | 336 | 0.930 | 0.058 | 0.075 | −0.003 | −0.001 | +0.001 | |
Note. CFI = robust comparative fit index; RMSEA = robust root mean square error of approximation; SRMR = robust standardized root mean square residual. χ2 tests were significant at p < .001.
With measurement invariance of the 1-factor model of the ARSW demonstrated across gender and treatment groups, latent means analysis was conducted to determine differences in withdrawal scores across groups. Results indicated that ARSW scores did not differ across men and women at baseline (Z = 1.64, p = .10), end of taper (Z = .36, p = .72), or at follow-up (Z = .92, p = .36). Additionally, ARSW scores did not differ across the 7-day and 28-day taper groups at baseline (Z = −.62, p = .54), end of taper (Z = −1.58, p = .12), or at follow-up (Z = −.38, p = .70).
3. 3 Longitudinal Measurement Invariance
With measurement invariance demonstrated across gender and treatment groups, longitudinal measurement invariance was performed on the total sample. The fit of the 1-factor model of the ARSW at baseline, end of taper, and 1-month follow-up is shown in Table 5. This model fit the data well at each phase of the trial (CFIs ≥ .943, RMSEAs ≤ .061, SRMRs ≤ .049).
Table 5.
1-factor model of the Adjective Rating Scale for Withdrawal at each time point
| df | χ2 | CFI | RMSEA | SRMR | |
|---|---|---|---|---|---|
| Baseline | 97 | 281 | 0.946 | 0.061 | 0.042 |
| End of taper | 97 | 200 | 0.943 | 0.053 | 0.043 |
| 1-month follow-up | 97 | 143 | 0.966 | 0.040 | 0.049 |
Note. CFI = robust comparative fit index; RMSEA = robust root mean square error of approximation; SRMR = robust standardized root mean square residual. χ2 tests were significant at p < .001.
Table 6 provides the fit for the longitudinal tests of invariance of the ARSW over baseline, end of taper, and 1-month follow-up. The configural invariance model indicated good fit. The metric invariance model also indicated good fit, and did not result in a decrement of fit when compared to the configural invariance model. The scalar invariance model indicated adequate fit, but resulted in a decrement of fit when compared to the metric invariance model. Therefore, the metric model is put forth as the final model of longitudinal invariance for the ARSW.
Table 6.
Longitudinal Measurement Invariance of the Adjective Rating Scale for Withdrawal
| df | χ2 | CFI | RMSEA | SRMR | Δdf | ΔCFI | ΔRMSEA | ΔSRMR | |
|---|---|---|---|---|---|---|---|---|---|
| Randomization vs. Baseline vs. 1-month follow-up
| |||||||||
| Configural | 1008 | 1870 | 0.910 | 0.041 | 0.059 | ||||
| Metric | 1038 | 1958 | 0.904 | 0.041 | 0.065 | 30 | −0.006 | 0 | +0.006 |
| Scalar | 1068 | 2133 | 0.889 | 0.044 | 0.075 | 32 | −0.015 | +0.003 | +0.010 |
|
| |||||||||
| Baseline vs. End of taper
| |||||||||
| Configural | 433 | 837 | 0.937 | 0.043 | 0.049 | ||||
| Metric | 448 | 916 | 0.927 | 0.045 | 0.060 | 79 | −0.010 | +0.002 | +0.011 |
| Scalar | 463 | 1028 | 0.912 | 0.049 | 0.073 | 16 | −0.015 | +0.004 | +0.013 |
|
| |||||||||
| Baseline vs. 1-month follow-up
| |||||||||
| Configural | 433 | 771 | 0.940 | 0.039 | 0.057 | ||||
| Metric | 448 | 826 | 0.933 | 0.040 | 0.064 | 79 | −0.007 | +0.001 | +0.007 |
| Scalar | 463 | 906 | 0.922 | 0.043 | 0.075 | 16 | −0.011 | +0.003 | +0.011 |
|
| |||||||||
| End of taper vs. 1-month follow-up
| |||||||||
| Configural | 433 | 827 | 0.911 | 0.047 | 0.061 | ||||
| Metric | 448 | 838 | 0.911 | 0.046 | 0.064 | 79 | 0 | −0.001 | +0.003 |
| Scalar | 463 | 873 | 0.907 | 0.046 | 0.064 | 16 | −0.004 | 0 | 0 |
Note. CFI = robust comparative fit index; RMSEA = robust root mean square error of approximation; SRMR = robust standardized root mean square residual. Bolded values indicate a decrement of fit in change statistics. χ2 tests were significant at p < .001.
In order to determine if there was a specific time in the clinical trial that was contributing to the lack of longitudinal invariance, invariance was assessed for baseline vs. end of taper, baseline vs. follow-up, and end of taper vs. follow-up. From baseline to end of taper, fit indices indicate that the metric invariance model resulted in a decrement of fit compared to the configural invariance model, as well as a decrement in fit from the metric invariance model to the scalar invariance model. From baseline to follow-up, the metric invariance model did not result in a decrement of fit compared to the configural invariance model, but it did result in a decrement in fit from the metric invariance model to the scalar invariance model. When examining longitudinal measurement invariance across end of taper and follow-up, results indicate that the metric invariance model did not result in a decrement of fit compared to the configural invariance model, and there was not a decrement in fit from the metric invariance model to the scalar invariance model.
As longitudinal invariance was not demonstrated at the scalar level across baseline, end of taper, and 1-month follow-up, it is not recommended to assess change in latent means over time; observed changes in the ARSW may be due to changes in assessment or structure of the ARSW. However, latent means can be analyzed across end of taper to follow-up as longitudinal measurement invariance was supported at those two post-treatment phases. Results showed that ARSW scores decreased from end of taper to follow-up (Z = −3.97, p = .001).
4. Discussion
In a series of psychometric analyses, results indicated that the ARSW was a reliable, 1-factor model of withdrawal that was invariant across gender and treatment groups, however longitudinal measurement invariance was not supported. This research first sought to examine the unidimensionality of withdrawal by testing a 1-factor model of the ARSW and to provide measures of reliability at baseline, end of taper (7-day taper vs. 28-day taper), and at 1-month follow-up of a clinical trial of opioid-dependent individuals. A 1-factor model with 7 correlated residuals indicated good fit for men and women and across the phases of the clinical trial, thereby supporting the use of a single total score of withdrawal for the ARSW. Although the RMSEA at follow-up for the females was slightly elevated at .081, the model was deemed adequate since the discrepancy in the fit criterion and the actual fit was low (.001). Additionally, the ARSW appeared to be a reliable scale in men and women and for both taper groups.
Next, measurement invariance across gender at each of the phases of the clinical trial was examined. Although the fit at follow-up had a slightly lowered CFI value for the scalar invariance model (.89) and elevated SRMR values for the metric (.084) and scalar invariance models (.085), we proceeded to examine the changes in fit indices across the measurement invariance model for this time point since the discrepancy in the fit criterion and the actual fit was low (≤ .009). Tests of measurement invariance across gender indicated that the ARSW measured withdrawal equivalently in men and women at each phase of the clinical trial. This finding is especially important for trials that have opiate-dependent men and women combined in one sample (Amass et al., 2000; Bickel at el, 1988a; Ling et al, 2005, Ling et al, 2009; Ziedonis et al., 2009) and for clinicians assessing withdrawal in both men and women. Additionally, the latent means of withdrawal were similar for men and women at each phase of the clinical trial indicating that men and women report equivalent levels of withdrawal during the course of the trial. This finding is line with Ling et al. (2009) who reported no gender differences across ARSW raw means at baseline or during the randomization phase of the this clinical trial.
Tests of measurement invariance across taper group indicated that the ARSW is measuring withdrawal equivalently in the 7- and 28-day taper groups at each phase of the clinical trial. This finding therefore supports the use the ARSW to assess withdrawal across 7- vs. 28-day buprenorphine/naloxone taper groups. As was found when testing differences in withdrawal across taper groups in the raw means (Ling et al., 2009), the latent means analysis indicated that withdrawal was similar across taper groups at each phase of the clinical trial.
As change in withdrawal is often examined in clinical trials (e.g., Amass et al., 2000; Bickel at el, 1988a; Bickel at el, 1988b; Ling et al. 2005; Ziedonis et al., 2009) as well as in the clinical management of opioid withdrawal, longitudinal measurement invariance is important in determining if the change is true change in withdrawal or due to changes in measurement properties of the ARSW. Results indicated that over three phases of the clinical trial (baseline, end of taper, and 1-month follow-up), the differences in means of the indicators may not be due to differences in the actual construct (i.e., withdrawal) or that observed values of the ARSW items at any factor value are not equivalent over time. Thus, interpretation of change in ARSW values may be misleading as observed change may be in part due to unstable measurement properties of the scale. Clinically, this suggests that predicted values of the ARSW items may change over time even if there is a constant level of withdrawal. Therefore, although withdrawal may remain unchanged, the ARSW item values may fluctuate. An individual may have an unchanged true level of withdrawal over the course of treatment or opioid withdrawal management, yet ARSW item values may lead clinicians to believe withdrawal has increased or decreased over time.
Additional analyses examined the three phases of the clinical trial with results indicating the phase of the study that was non-invariant was at baseline. However, longitudinal measurement invariance was demonstrated across end of taper and 1-month follow-up, indicating that the measurement of the ARSW across these two phases is equivalent. As such, latent means were analyzed across the randomization phase and 1-month follow-up, and results indicated that withdrawal decreased over time as expected.
Clinically, the lack of longitudinal measurement invariance from baseline to end of taper may be due to the heterogeneity of the sample on a number of factors that may affect how withdrawal is measured (e.g., greater variation of opioid use or dependence among the sample prior to treatment) or other unmeasured variables. After participants completed treatment, where the buprenorphine/naloxone dosages were tailored to each individual during the stabilization phase, the sample was more homogeneous, or more standardized, and may remain so through follow-up. It is for these reasons that the measurement of withdrawal during pre-treatment may not be the same as in post-treatment. It may be that repeated measures of the withdrawal during treatment are longitudinally invariant, just as this research found that repeated measures of the withdrawal post treatment are longitudinally invariant. Note that while participants were not in clinical withdrawal states at baseline, the demonstration of measurement invariance of withdrawal is still recommended in order for means to be compared over those time points.
There are several limitations to this study. First, the 1-factor model of the ARSW contains seven correlated residuals. As the items in each correlated residual appear highly related in wording (e.g., Trouble getting to sleep and Fitful sleep), yet separate from the other pairs (e.g., Watery eyes with Runny nose), there appears to be several other reasons for the items to relate to one another above and beyond the construct of withdrawal. For example, participants may endorse ARSW items that are related to other psychological or physical health issues (e.g., psychological stress causing problems with sleep, or allergy problems causing watery eyes and a runny nose) that are not due to opiate withdrawal. Therefore, additional research may investigate revising the scale, perhaps eliminating pairs of items assessing similar symptoms, or reduce it to items that most readily compare to ancillary medications for withdrawal symptoms (see Amass et al., 2004). Next, only three phases of CTN-0003 were analyzed. We sought to investigate pre-treatment, post-treatment, and follow-up phases in order to examine the full range of the ARSW measurement properties. As withdrawal is typically assessed at numerous times throughout clinical trials, longitudinal analyses including more than three time points are justified. Lastly, the analyses presented here are limited to the CTN-0003 data, and therefore measurement invariance of the ARSW across other treatments, tapering schedules, dosages, etc., is needed.
The ARSW appears to be measuring withdrawal equivalently across gender and buprenorphine/naloxone taper periods in opioid-dependent individuals. We recommend that researchers and clinicians using this tool analyze ARSW total scores across groups at each time point separately (see Ling et al., 2009 for an example). If change over time is of interest, then change from post-treatment through follow-up may offer the most valid comparison; pre-treatment ARSW values may not be assessing withdrawal in the same way as post-treatment and follow-up values. Clinicians may wish to examine change from any point after the initial assessment of opioid withdrawal (e.g., after buprenorphine is first given to the patient) to any subsequent clinical assessment of withdrawal. Future research is needed to replicate these findings in other trials, in various clinical settings, and across other demographic groups in order to fully assess the measurement properties of the ARSW.
Acknowledgments
The project described was supported by a Pilot Study Support Program as part of the Center for Advancing Longitudinal Drug Abuse Research (CALDAR, award number P30DA016383) from the National Institute on Drug Abuse (NIDA). The content is solely the responsibility of the authors and does not necessarily represent the official views of NIDA or the National Institute of Health. This project was also supported by a grant to the Clinical Trials network Pacific Northwest Node (award number 5 U10 DA013714-10) from the National Institute on Drug Abuse (NIDA; Donovan and Roll, Co-PIs) and the Department of Justice, the Life Science Discovery Fund (Roll, PI).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Celestina Barbosa-Leiker, Washington State University, College of Nursing, PO Box 1495, Spokane, WA, 99210-1495, USA. Washington State University, Department of Psychology, PO Box 4820, Pullman, WA, 99164-4820, USA.
Sterling McPherson, Washington State University, College of Nursing, PO Box 1495, Spokane, WA, 99210-1495, USA. Washington State University, Department of Psychology, PO Box 4820, Pullman, WA, 99164-4820, USA.
Mary Rose Mamey, Washington State University, Department of Psychology, PO Box 4820, Pullman, WA, 99164-4820, USA.
G. Leonard Burns, Washington State University, Department of Psychology, PO Box 4820, Pullman, WA, 99164-4820, USA.
John Roll, Washington State University, College of Nursing, PO Box 1495, Spokane, WA, 99210-1495, USA. Washington State University, Department of Psychology, PO Box 4820, Pullman, WA, 99164-4820, USA.
References
- Amass L, Kamien JB, Mikulich SK. Efficacy of daily and alternate-day dosing regimens with the combination buprenorphine-naloxone tablet. Drug and Alcohol Dependence. 2000;58:143–152. doi: 10.1016/s0376-8716(99)00074-5. [DOI] [PubMed] [Google Scholar]
- Amass L, Ling W, Freese TE, Reiber C, Annon JJ, Cohen AJ, et al. Bringing buprenorphine-naloxone detoxification to community treatment providers: The NIDA Clinical Trials Network field experience. The American Journal on Addiction. 2004;13:S42–S66. doi: 10.1080/10550490490440807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbosa-Leiker C. Factor analysis applied to the metabolic syndrome: A review. In: Berhardt LV, editor. Advances in Medicine and Biology. Vol. 59. Hauppauge, NY: Nova Science Publishers, Inc; (in press) [Google Scholar]
- Barbosa-Leiker C, Wright BR, Burns GL, Parks CD, Strand P. Is the assessment of the metabolic syndrome stable over time? Testing longitudinal measurement invariance of the metabolic syndrome. Annals of Epidemiology. 2011;21:111–117. doi: 10.1016/j.annepidem.2010.10.001. [DOI] [PubMed] [Google Scholar]
- Bickel WK, Stitzer ML, Bigelow GE, Liebson IA, Jasinski DR, Johnson RE. A clinical trial of buprenorphine: Comparison with methadone in the detoxification of heroin addicts. Clinical Pharmacology & Therapeutics. 1988a;43:72–78. doi: 10.1038/clpt.1988.13. [DOI] [PubMed] [Google Scholar]
- Bickel WK, Stitzer ML, Bigelow GE, Liebson IA, Jasinski DR, Johnson RE. Buprenorphine: Dose-related blockade of opioid challenge effects in opioid dependent humans. The Journal of Pharmacology and Experimental Therapeutics. 1988b;247:47–53. [PubMed] [Google Scholar]
- Brown TA. Confirmatory factor analysis for applied research. New York: Guilford Press; 2006. [Google Scholar]
- Chen FF, Sousa KH, West SG. Testing Measurement Invariance of Second-Order Factor Models. Structural Equation Modeling. 2005;12:471–492. [Google Scholar]
- Chen FF. Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling. 2007;14:464–504. [Google Scholar]
- Cheung GW, Rensvold RB. Evaluating goodness-of-fit indexes for testing measurement invariance. Structural Equation Modeling. 2009;9:233–255. [Google Scholar]
- Enders CK. Applied Missing Data Analysis. New York, NY: Guilford Press; 2010. [Google Scholar]
- Horn JL, McArdle JJ. A practical and theoretical guide to measurement invariance in aging. Experimental Aging Research. 1992;18:117–144. doi: 10.1080/03610739208253916. [DOI] [PubMed] [Google Scholar]
- Ling W, Amass L, Shoptaw S, Annon JJ, Hillhouse M, Babcock D, et al. A mulit-center randomized trial of buprenorphine-naloxone versus clonidine for opioid detoxification: findings from the National Institute on Drug Abuse Clinical Trials Network. Addition. 2005;100:1090–1100. doi: 10.1111/j.1360-0443.2005.01154.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ling W, Hillhouse M, Domier C, Doraimani G, Hunter J, Thomas C, et al. Buprenorphine tapering schedule and illicit opioid use. Addiction. 2009;104:256–265. doi: 10.1111/j.1360-0443.2008.02455.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McHorney CA, Fleishman JA. Assessing and understanding measurement equivalence in health outcomes measures. Medical Care. 2006;44:S205–S210. doi: 10.1097/01.mlr.0000245451.67862.57. [DOI] [PubMed] [Google Scholar]
- Meredith W. Measurement invariance, factor analysis and factorial invariance. Psychometrika. 1993;58:525–543. [Google Scholar]
- Steenkamp J-BEM, Baumgartner H. Assessing measurement invariance in cross-national consumer research. Journal of Consumer Research. 1998;25:78–90. [Google Scholar]
- Tompkins DA, Bigelow GE, Harrison JA, Johnson RE, Fudala PJ, Strain EC. Concurrent validation of the Clinical Opiate Withdrawal Scale (COWS) and single-item indices against the Clinical Institute Narcotic Assessment (CINA) Opioid Withdrawal Instrument. Drug and Alcohol Dependence. 2009;105:154–159. doi: 10.1016/j.drugalcdep.2009.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandenberg RJ, Lance CE. A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research. Organizational Research Methods. 2000;3:4–69. [Google Scholar]
- Wesson DR, Ling W. The Clinical Opiate Withdrawal Scale (COWS) Journal of Psychoactive Drugs. 2003;35:253–259. doi: 10.1080/02791072.2003.10400007. [DOI] [PubMed] [Google Scholar]
- Ziedonis DM, Amass L, Steiberg M, Woody G, Krejci J, Annon JJ, et al. Predictors of outcome for short-term medically supervised opioid withdrawal during a randomized, multicenter trial of buprenorphine-naloxone and clonidine in the NIDA clinical trials network drug and alcohol dependence. Drug and Alcohol Dependence. 2009;99:28–36. doi: 10.1016/j.drugalcdep.2008.06.016. [DOI] [PMC free article] [PubMed] [Google Scholar]