Reaction pathways and free energy profiles for spontaneous hydrolysis of urea and tetramethylurea: Unexpected substituent effects

Abstract

It has been difficult to directly measure the spontaneous hydrolysis rate of urea and, thus, 1,1,3,3-tetramethylurea (Me₄U) was used as a model to determine the “experimental” rate constant for urea hydrolysis. The use of Me₄U was based on an assumption that the rate of urea hydrolysis should be 2.8 times that of Me₄U hydrolysis because the rate of acetamide hydrolysis is 2.8 times that of N,N-dimethyl-acetamide hydrolysis. The present first-principles electronic-structure calculations on the competing non-enzymatic hydrolysis pathways have demonstrated that the dominant pathway is the neutral hydrolysis via the CN addition for both urea (when pH<~11.6) and Me₄U (regardless of pH), unlike the non-enzymatic hydrolysis of amides where alkaline hydrolysis is dominant. Based on the computational data, the substituent shift of free energy barrier calculated for the neutral hydrolysis is remarkably different from that for the alkaline hydrolysis, and the rate constant for the urea hydrolysis should be ~1.3×10⁹-fold lower than that (4.2×10⁻¹² s⁻¹) measured for the Me₄U hydrolysis. As a result, the rate enhancement and catalytic proficiency of urease should be 1.2×10²⁵ and 3×10²⁷ M⁻¹, respectively, suggesting that urease surpasses proteases and all other enzymes in its power to enhance the rate of reaction. All of the computational results are consistent with available experimental data for Me₄U, suggesting that the computational prediction for urea is reliable.

Introduction

Urea is a biologically interesting molecule. It is a nonvolatile and environmentally benign material used primarily as fertilizer, ^1–2 and is essentially no danger to environment, plants, animals. and human.³ At room temperature, pure urea is stable due to its resonance stabilization (estimated to be 30–40 kcal/mol).⁴ However, in aqueous solution, urea will gradually degrade into ammonia and carbon dioxide. The degradation mechanism of urea has been extensively studied over the past century.^5–7 Werner,⁷ Fawsitt,⁸ and Robert⁹ found that the decomposition of urea takes place in a stepwise manner with the production of intermediate cyanate. Theoretical studies have been carried out to explore the molecular mechanisms for the non-enzymatic urea degradation,^10–12 prosing various mechanisms, such as unimolecular elimination, intermolecular elimination/hydrolysis processes.

It is commonly accepted that in aqueous solution urea is decomposed mostly by elimination reaction. In fact, the non-enzymatic hydrolysis of urea is so slow that it has never been observed experimentally. However, in the body, urea is decomposed mostly by urease through hydrolysis.^12–16 Hence, the hydrolysis of urea has attracted considerable research interest to estimate the proficiency of urease-catalyzed urea hydrolysis.

Extensive theoretical studies have been performed on the non-enzymatic hydrolysis of urea.^{11–12, 17–18} According to these studies, the non-enzymatic hydrolysis of urea may proceed in three possible ways, i.e. acid-catalyzed, base-catalyzed, and neutral hydrolysis reactions (Scheme 1).^{11–12, 17–18} In addition, the neutral hydrolysis of urea may take place through two competing pathways, namely, CO addition (APOE mechanism) and CN addition pathway (APNE mechanism). Estiu et al.^{12, 18} computationally studied these reaction pathways at the MP2/6-311++G** level, and predicted that at 298 K the activation free energies for the acid-catalyzed, base-catalyzed, APOE, and APNE pathways were 36.0, 24.9, 43.2, and 53.7 kcal/mol, respectively. Their computational data suggested that at the physiological condition the base-catalyzed hydrolysis reaction is the most favorable pathway for the hydrolysis of urea. Kallies et al.¹³ studied the APOE and APNE pathways for the urea hydrolysis at the B3LYP/6-31G* level. Contrary to the results obtained by Estiu et al.,¹⁸ the calculations by Kallies et al. supported that the APNE pathway is more favorable than the APOE pathway.

Scheme 1.

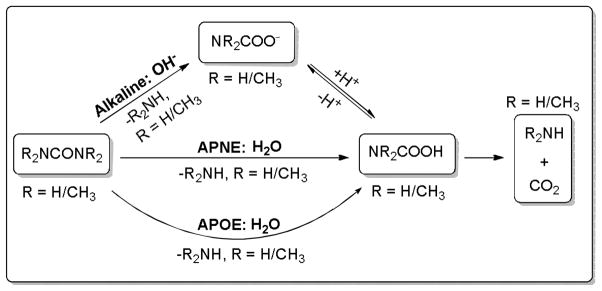
Hydrolysis reaction pathways of urea (R = H) and Me₄U (R = CH₃) examined in this study. Alkaline pathway: attack of a hydrated hydroxide ion at the carbonyl carbon of urea/Me₄U; APOE pathway: attack of a solvent water molecule at the carbonyl carbon accompanied by the oxygen of urea/Me₄U extracting a proton from a water molecule; APNE pathway: attack of a solvent water molecule at the carbonyl carbon accompanied by a nitrogen atom of urea/Me₄U accepting a proton from a water molecule. The acid-catalyzed reaction pathway of urea/Me₄U hydrolysis is not included here.

As mentioned above, the non-enzymatic hydrolysis of urea has never been observed experimentally. To determine the hydrolysis rate of urea, 1,1,3,3-tetramethylurea (Me₄U) was used by Callahan et al.¹⁹ and the rate constant for the hydrolysis of Me₄U was determined to be 4.2×10⁻¹² s⁻¹. According to earlier studies on amide hydrolysis reactions, the rate constant of spontaneous hydrolysis of acetamide is 2.8 times the rate of N,N-dimethyl-acetamide hydrolysis.¹⁹ Assuming that this ratio of the rate constants could be applied to urea and Me₄U, the rate constant of urea spontaneous hydrolysis was estimated to be 1.17×10⁻¹¹ s⁻¹ (at 298.15 K).¹⁹ However, it has been known that the hydrolysis of acetamide follows an alkaline hydrolysis mechanism, whereas the experiments carried out by Callahan et al.¹⁹ clearly indicated that the hydrolysis of Me₄U followed a neutral hydrolysis mechanism because the rate of Me₄U hydrolysis did not change when the pH of the solution changed from 4 to 10. Therefore, it is unclear or questionable whether the ratio of the rates for the spontaneous hydrolysis of acetamide and N,N-dimethyl-acetamide can really be applied to that for the spontaneous hydrolysis of urea and Me₄U. The answer to this question will determine whether the estimated rate constant (1.17×10⁻¹¹ s⁻¹) for the spontaneous hydrolysis of urea is reliable or not.

The above analysis prompted us to more carefully examine the hydrolysis mechanisms of urea and Me₄U at the same levels of theory. In this computational study, the possible pathways of urea and Me₄U hydrolysis mentioned above were examined at high levels of first-principles electronic structure theory accounting for the solvent effects, and the dominant pathway and the corresponding energetics were determined. Based on the first-principles electronic structure calculations, the substituent effect of N-substituted urea derivative was discussed and the key factor affecting the hydrolysis of these compounds was identified. The computational results provide novel insights into the fundamental reaction mechanism for the hydrolysis of urea and its derivatives. In particular, this study clearly demonstrates that the substituent effect on the rate constants for the hydrolysis of urea and Me₄U is remarkably different from that observed for the hydrolysis of amides, and that the rate constant for the urea hydrolysis should be ~1.2×10⁹-fold lower than that (4.2×10⁻¹² s⁻¹) measured for the Me₄U hydrolysis.

Methods

Density functional theory (DFT) with Becke’s three-parameter hybrid exchange functional and the Lee-Yang-Parr correlation functional (B3LYP)^20–22 in combination with the 6-31+G* basis set was used to fully optimize the geometries of reactants and products, and also were used to search for all possible geometries of transition states and intermediates. Vibrational frequency calculations were carried out to ensure that the geometries are indeed local minimal or saddle points on the potential energy surfaces and to determine the zero-point vibrational and thermal corrections to the Gibbs free energies. Intrinsic reaction coordinate (IRC) calculations were performed to confirm the correct connections between reactants, transition states, intermediates, and products on the potential energy surfaces.

The geometries optimized at the B3LYP/6-31+G* level were used to perform single-point energy calculations by using the B3LYP method with four different basis sets: 6-31++G**, 6-311++G**, aug-cc-pVDZ, and aug-cc-pVTZ. Previous studies indicated that electron correlation effects are not important in the geometry optimizations and solvent shift calculations, but are important in calculating the relative energies of the geometries.²³ Thus, these geometries were also used to perform the second-order Møller-Plesset (MP2) single-point energy calculations with seven different basis sets, 6-31+G*, 6-31++G**, 6-311++G**, 6-311++G (2d,2p), and aug-cc-pVXZ (X = D, T, and Q). Then the energies calculated with aug-cc-pVXZ basis sets were extrapolated to the frozen-core complete basis set (CBS) limit.²⁴ Additional calculations at the coupled-cluster with single and double substitutions with a non-iterative triples correction (CCSD(T)) level were also carried out with the 6-31++G** and aug-cc-pVDZ basis sets. The best estimate of the electronic energy in the gas phase is the extrapolated MP2/CBS energy value plus the energy shift from the MP2/aug-cc-pVDZ value to the CCSD(T)/aug-cc-pVDZ value.

The geometries optimized at the B3LYP/6-31+G* level in the gas phase were also used to perform self-consistent reaction field (SCRF) single-point energy calculations at the HF/6-31+G* level. Previous computational studies demonstrated that solvent effects have little influence on the geometries of chemical reaction systems and the corresponding energy barriers.²⁵ Geometrical parameters optimized in the gas phase are quite similar to the ones optimized in the aqueous solution, and the free energy barriers calculated by using the geometries optimized in the gas phase are very close to the corresponding ones calculated by using the geometries optimized in aqueous solution. Hence, all of our energy calculations in the present study were based on the geometries optimized in the gas phase.

The SCRF procedure employed in this work is known as the surface and volume polarization for electrostatics (SVPE)^26–28 accounting for solute-solvent electrostatic interactions. The SVPE method is also known as the fully polarizable continuum model (FPCM),^{23–24, 29–35} as it fully accounts for both surface and volume polarization effects in solute-solvent electrostatic interactions.^36–37 In the SVPE procedure,^{27–28, 38} the solute cavity surface is defined as a solute electron-charge isodensity contour determined self-consistently during the SVPE interaction process, and the SVPE results converge to the exact solution of the Poisson’s equation with a given numerical tolerance. The converged SVPE results merely rely on the contour value at a given dielectric constant and a certain quantum mechanical calculation level.²⁷ Our previous calculations on hydroxide ion-catalyzed hydrolysis of a series of carboxylic acid esters and phosphate esters showed that the energy barriers determined by the SVPE calculations using both the default 0.001 au and 0.002 au contours were all qualitatively consistent with the corresponding experimental activation energies.^{23, 38–39} As the SVPE procedure using 0.001 au contour was shown to be reliable for evaluating the bulk solvent effects,^{29–31, 33–35, 39–43} the 0.001 au²⁷ contour was also used in this study for all of the SVPE calculations. The dielectric constant (ε) used in the SVPE calculations for solvent water is dependent on the temperature (T),⁴⁴ with ε = 78.5 at T = 298.15 K. The free energies in solution were obtained by adding the gas phase free energies to solvent shifts obtained from the SVPE calculations.

All calculations were performed by using a local version⁴⁵ of the Gaussian 03 program⁴⁶ in which the SVPE solvation model was implemented. All of the computations in this study were carried out on a Dell supercomputer cluster with 384 nodes or 4,768 processors at the Computer Center of the University of Kentucky.

Results and discussion

Reaction Pathways and Free Energy Barriers for Hydrolysis of Urea

Previous studies indicated that urea will first be hydrolyzed to intermediate NH₂COOH and then NH₂COOH will be hydrolyzed to ammonia and carbon dioxide.⁴⁷ The latter reaction was proved to be rather fast and, thus, the overall hydrolysis rate of urea is controlled by the first stage (i.e. the reaction from urea to NH₂COOH).⁴⁷ Hence, our study was focused on the first stage of urea hydrolysis. Data from our reaction-coordinate calculations demonstrate that, in aqueous solution, urea can be hydrolyzed to NH₂COOH by a) attacking of a hydrated hydroxide ion at the carbonyl carbon, b) attacking of a solvent water molecule at the carbonyl carbon accompanied by the oxygen of urea extracting a proton from a water molecule, and c) attacking of a solvent water molecule at the carbonyl carbon accompanied by a nitrogen atom of urea extracting a proton from a water molecule. Below we discuss the pathways one by one, along with a detailed discussion of the free energy barriers and the dominant reaction pathway.

Attack of a hydrated hydroxide ion at the carbonyl carbon (alkaline pathway)

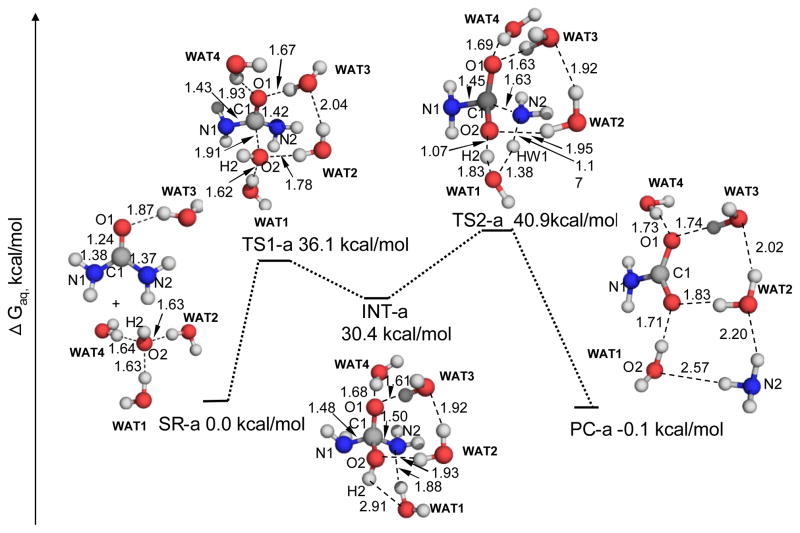
In this process, the oxygen atom of the hydroxide ion will attack the carbonyl carbon of urea to form a tetrahedral intermediate (INT-a in Figure 1) via transition state 1 (TS1-a in Figure 1). Four water molecules (denoted as WAT1, WAT2, WAT3, and WAT4) were involved in the reaction-coordinate calculations. In TS1-a, WAT1 gradually moves from the hydroxide ion to the N2 atom of an NH₂ group. Meanwhile, WAT3 and WAT4 form two hydrogen bonds with the carbonyl oxygen (O1) with O-H distances of 1.93 and 1.67 Å, respectively. The hydrogen-bonding interaction will help to stabilize the negative charge accumulated on the carbonyl oxygen during the nucleophilic attack. In the INT-a structure, WAT1 connects the leaving –NH₂ group and the hydroxyl group (formed in the first step) with two hydrogen bonds. The N2-C1 distance is elongated to 1.50 Å, as compared with the corresponding value of 1.37 Å in the reactant complex SR-a. In TS2-a, this –NH₂ group extracts a proton from WAT1. In turn, WAT1 extracts a proton (atom H2) from the hydroxyl group. This double proton transfer process leads to the cleavage of the C1-N2 bond and the release of an NH₃ molecule.

Figure 1.

Geometric parameters and free energy profile for the alkaline hydrolysis of urea. These geometries were optimized at the B3LYP/6-31+G* level. The relative free energies shown for these geometries include the zero-point and thermal corrections and solvent shifts, in addition to the single-point electronic structure energies calculated from the best estimate of the gas-phase results. The best estimate of the gas-phase electronic structure energy is the extrapolated MP2/CBS energy value plus the energy shift from the MP2/aug-cc-pVDZ value to the CCSD(T)/aug-cc-pVDZ value.

Attack of a solvent water molecule at the carbonyl carbon accompanied by the oxygen of urea extracting a proton from a water molecule (APOE mechanism)

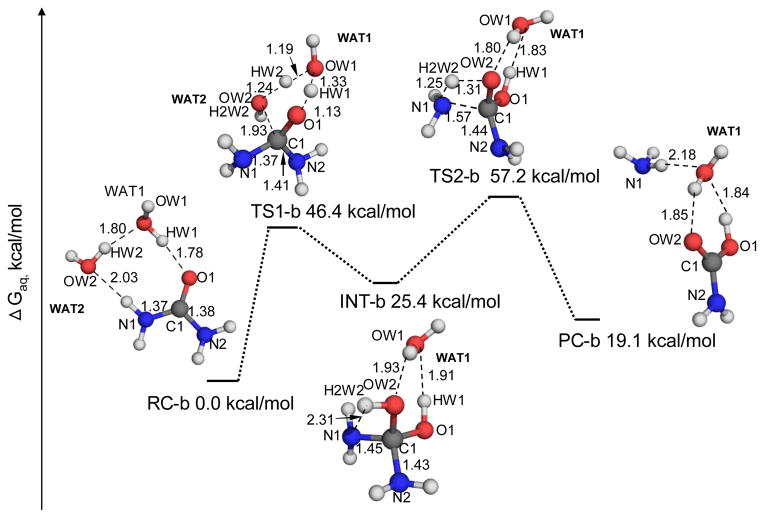
A water molecule can also serve as a nucleophile to attack the carbonyl carbon of urea. As one can see in Figure 2, two water molecules (WAT1 and WAT2) are involved in this two-step reaction. In the first reaction step, WAT1 acts as a proton shuttle to transfer a proton from WAT2 to the carbonyl carbon of urea. Meanwhile, the oxygen atom of WAT2 attacks the carbonyl carbon of urea to form a tetrahedral intermediate INT-b. In the geometry of INT-b, a hydrogen atom (H2W2) from WAT2 forms a hydrogen bond with a nitrogen atom (N1) of an –NH₂ group with an inter-atomic distance of 2.31 Å, indicating that this proton has a tendency to transfer to the N1 atom. In the subsequent reaction step, N1 accepts this proton, which leads to the cleavage of the N1-C1 bond. The obtained geometric parameters for the reactant complex (RC-b in Figure 2), the first transition state TS1-b, and the intermediate INT-b are similar to the corresponding parameters described by Estiu et al..¹⁸ However, in the work described by Estiu et al., the tetrahedral intermediate INT-b directly collapsed to the products ammonia and carbamic acid without any transition state (i.e. they did not find a transition state between the intermediate and products), which is remarkably different to our finding in the present study. Further, our energetic data reveal that the free energy of the second transition state (TS2-b) which Estiu et al.¹⁹ did not find is even higher than that for the first transition state TS1-b. Hence, the rate-determining reaction step is associated with transition state TS2-b, and the overall free energy barrier for this reaction pathway should be the free energy change from RC-b to the TS2-b.

Figure 2.

Geometric parameters and free energy profile for the APOE pathway of the urea hydrolysis. These geometries were optimized at the B3LYP/6-31+G* level, and their free energies were calculated in the same way as that noted in the Figure 1 caption.

Attack of a solvent water molecule at the carbonyl carbon accompanied by a nitrogen atom of urea attracting a proton from a water molecule (APNE mechanism)

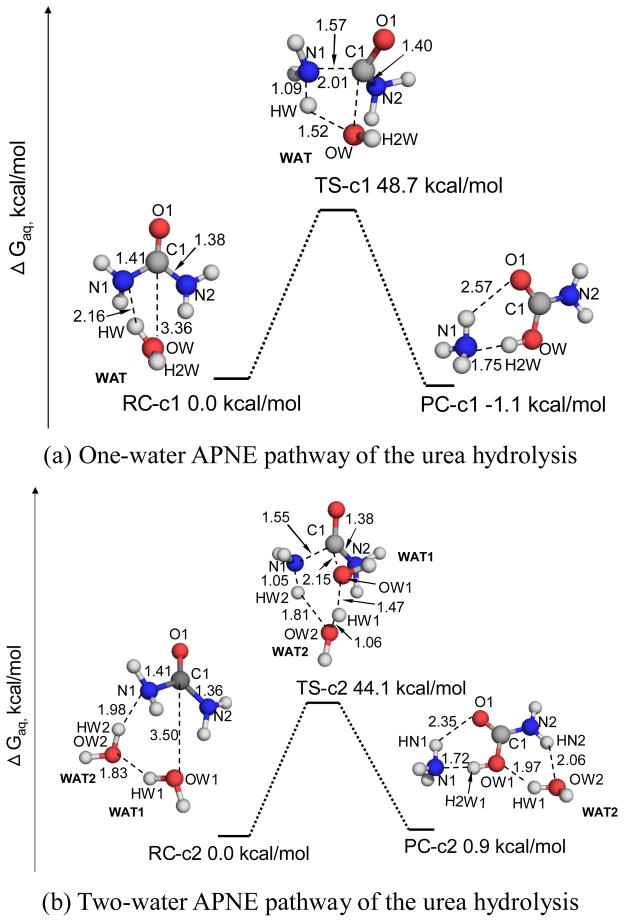
Besides the APOE mechanism described above, the attacking water molecule can directly transfer a proton to the leaving –NH₂ group without the relay of the carbonyl oxygen of urea. However, the pathway (denoted as one-water APNE mechanism) of urea hydrolysis remains largely unexplored.^{13, 20} As shown in Figure 3a, in the reactant complex RC-c1 a water molecule forms a hydrogen bond with an –NH₂ group of urea with an N1-HW distance of 2.16 Å. The inter-atomic distance between the water oxygen OW and the carbonyl carbon is 3.36 Å, indicating that the water is well positioned to attack the carbonyl carbon. In the transition state TS-c1, a four-membered ring is formed among atoms OW, C1, N1, and HW. The attacking water WAT has almost transferred the proton (HW) to the N1 atom with an HW-N1 distance of 1.09 Å. Meanwhile, the inter-atomic distance C1-N1 elongates to 1.57 Å, indicating that the –NH₂ group will leave the carbonyl carbon after accepting the proton from the attacking water.

Figure 3.

Geometric parameters and free energy profiles for (a) one-water APNE pathway, and (b) two-water ANPE pathway of the urea hydrolysis. These geometries were optimized at the B3LYP/6-31+G* level, and their free energies were calculated in the same way as that noted in the Figure 1 caption.

The nucleophilic attack process mentioned above can also be facilitated by involving a second water molecule to the reaction system (denoted as two-water APNE mechanism). As one can see from Figure 3-b, the additional water molecule (WAT2) connects the attacking water molecule (WAT1) and the leaving –NH₂ group with two hydrogen bonds. In the transition state (TS-c2), a six-membered ring forms among atoms OW1, HW1, OW2, HW2, N1, and C1, and WAT1 attacks the carbonyl carbon and WAT2 acts as a proton shuttle to pass a proton from WAT1 to the leaving amino group.

It should be noted that transition state TS-c2 with a six-membered ring should be more stable than transition state TS-c1 with a four-membered ring, because the six-membered ring is less strained than the four-membered ring. Thus, the two-water APNE pathway is expected to be more favorable than the one-water APNE pathway.

Calculated free energy barriers

Using the optimized geometries for the reactants, transition states, and intermediates in the gas phase, Gibbs free energies were calculated in aqueous solution. The free energies calculated for these geometries are the single-point electronic structure energies calculated at various levels, plus the zero-point vibration and thermal corrections and the solvent shifts. The calculated free energies were used to evaluate the free energy barriers for the hydrolysis of urea and Me₄U in aqueous solution associated with various reaction pathways. As seen in Table 1, the relative magnitudes of the free energy barriers calculated at various levels are generally consistent with each other. To avoid possible confusion, unless stated clearly otherwise, the discussion below will always refer to the values obtained from the best estimate at 298.15 K indicated in Table 1.

Table 1.

Calculated Gibbs free energy barriers (in kcal/mol) for various reaction pathways of the hydrolysis of urea and Me₄U in aqueous solution at 298.15 K.^a

Theoretical level	Urea hydrolysis				Me4U hydrolysis
	Alkaline	APOE	One-water APNE	Two-water APNE	Alkaline	Two-water APNE
B3LYP/6-31+G*	46.4	59.1	45.4	41.3	46.2	31.5
B3LYP/6-31++G**	48.7	60.4	46.3	42.7	47.7	32.2
B3LYP/6-311++G**	50.8	63.0	47.1	43.3	49.4	32.6
B3LYP/aug-cc-pVDZ	49.9	60.7	46.4	43.2	48.0	32.3
B3LYP/aug-cc-pVTZ	52.4	63.8	48.5	45.0	52.6	33.4
MP2/6-31+G*	37.8	57.1	46.3	40.6	35.3	27.8
MP2/6-31++G**	39.8	58.3	47.5	42.3	36.5	28.9
MP2/6-311++G**	41.3	57.0	48.8	43.9	37.5	30.5
MP2/6-311++G(2d,2p)	41.5	57.8	48.0	42.9	38.6	30.2
MP2/aug-cc-pVDZ	38.7	56.6	45.7	41.0	35.6	27.2
MP2/aug-cc-pVTZ	39.5	56.7	46.8	41.9	38.2	29.1
MP2/aug-cc-pVQZ	40.7	57.0	47.2	42.4	39.6	29.9
MP2/CBS	41.5	57.3	47.4	42.7	40.4	30.4
CCSD(T)/6-31++G**	39.2	58.2	48.9	43.8	34.6	30.3
CCSD(T)/aug-cc-pVDZ	38.1	56.5	47.0	42.4	33.9	28.5
Best estimateb	40.9	57.2	48.7	44.1	38.7	31.7
Experimental valuec	Uncertain				32.9

^aAll energy calculations were performed by using the geometries optimized in the gas phase at the B3LYP/6-31+G* level. The obtained free energy barriers were based on the single-point energy calculations at various levels, plus the zero-point vibration and thermal corrections calculated at the B3LYP/6-31+G* level and the solvent shifts calculated at the HF/6-31+G* level (using the default 0.001 a.u. contour). Gibbs free energies calculated in the gas phase are provided as Supplementary Information (Table S1).

^bThe best estimate was the extrapolated MP2/CBS value plus the shift from the MP2/aug-cc-pVDZ value to the corresponding CCSD(T)/aug-cc-pVDZ value.

^cExperimental value from ref.19.

The alkaline hydrolysis of urea is a hydrolysis reaction with hydroxide ion. It has been known that the aqueous solvation of the hydroxide ion is extremely strong and its first solvation shell (three water molecules)⁴⁰ must be included explicitly in the QM reaction-coordinate calculations.^{23, 48} Without explicitly including the first solvation shell, the QM calculations always considerably underestimated the free energy barriers. Explicitly including the first solvation shell in the QM reaction-coordinate calculations and employing the computational protocol similar to what we used in the present study, the calculated free energy barriers are all in good agreement with the available experimental data.^{23, 48} In fact, Estiu et al.¹⁸ carried out the QM calculations on alkaline hydrolysis of urea without explicitly including the first solvation shell of hydroxide ion in the QM calculations, and their calculations led to a rather low free energy barrier of 24.9 kcal/mol. Including the first solvation shell of hydroxide ion, our QM calculations predict the overall free energy barrier for alkaline hydrolysis of urea to be 40.9 kcal/mol, as seen from the calculated free energy profile depicted in Figure 1.

For the neutral urea hydrolysis, there are three reaction pathways, including the APOE, one-water APNE, and two-water APNE pathways. As seen in Figure 2, the rate-determining transition state for the APOE pathway should be the one (TS2-b) for the second reaction step (in which the N-O bond gradually breaks), with the overall free energy barrier being 57.2 kcal/mol. The free energy barriers for the one-water and two-water APNE pathways were calculated to be 48.7 and 44.1 kcal/mol, respectively, as seen in Figure 3. Within these three neutral urea hydrolysis pathways, the free energy barrier (44.1 kcal/mol) calculated for the two-water APNE pathway is 13.1 kcal/mol lower than that (57.2 kcal/mol) for the APOE pathway or 4.6 kcal/mol lower than that (48.7 kcal/mol) for the one-water APNE pathway. So, within the neutral urea hydrolysis, the two-water APNE pathway should be dominant.

In comparison between the dominant neutral hydrolysis pathway (the two-water APNE) and the alkaline hydrolysis pathway, which pathway is more favorable? In terms of the calculated free energy barriers, the overall free energy barrier (40.9 kcal/mol) calculated for the alkaline hydrolysis pathway is 3.2 kcal/mol lower than that (44.1 kcal/mol) calculated for the two-water APNE pathway, indicating that the reaction rate constant for the second-order alkaline hydrolysis of urea should be larger than that for the neutral hydrolysis of urea. To further discuss the relative importance of different reaction pathways, we estimated the rate constants by using the calculated free energy barriers and imaginary vibrational frequencies of the transition states. The rate constants were estimated according to the transition state theory (TST) without dealing with the solvent relaxations and accounting for the tunneling corrections using the Wigner expression (in which the transmission coefficient g(T) = 1 − (ihν^≠/RT)²/24, where ν^≠ is the frequency of the imaginary vibration mode of the transition state).^49–56 Thus, the reaction rate constants for the alkaline hydrolysis and the neutral hydrolysis were predicted to be 6.00×10⁻¹⁸ s⁻¹ and 2.32×10⁻²⁰ s⁻¹ (see Table S2 in Supplementary Information for the detailed computational data), respectively, at the room temperature (298.15 K). Hence, the (second-order) rate constant (k_a = 6.00×10⁻¹⁸ s⁻¹) calculated for the alkaline hydrolysis of urea is ~260-fold larger than that (k_c2 = 2.32×10⁻²⁰ s⁻¹) calculated for the neutral urea hydrolysis.

On the other hand, the two reaction pathways involve different reactants. The alkaline hydrolysis involves both urea and hydroxide ion (HO⁻), whereas the neutral hydrolysis involves only urea with solvent water. Urea is a common reactant for the two pathways. However, for the other reactant of the alkaline hydrolysis, the concentration of HO⁻ is dependent on the pH of the reaction solution. The relative contributions of different reaction pathways to the total hydrolysis rate are determined by not only the relative rate constants, but also the relative concentrations of the involved reactants. Neglecting the insignificant contributions from the APOE and one-water APNE reaction pathways, the total hydrolysis rate v of urea is given by

$$\mathrm{v}=k_{\mathrm{a}}[\text{urea}][{\text{HO}}^{-}]+k_{\mathrm{c}2}[\text{urea}]$$ (1)

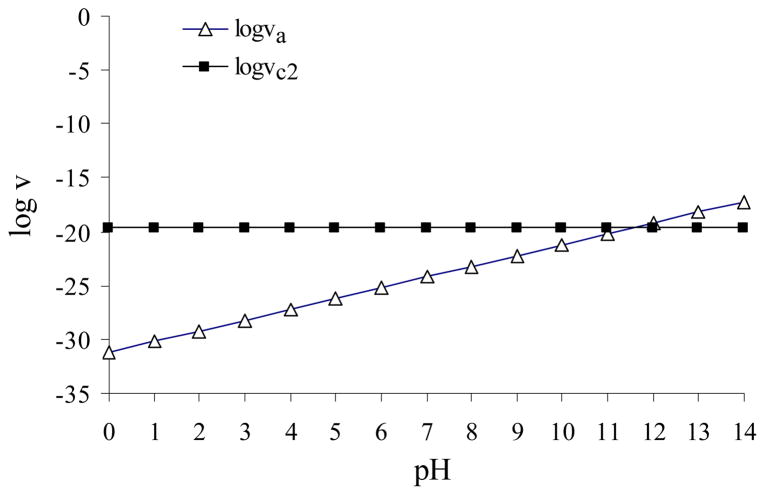
in which k_a and k_c2 refer to the rate constants of the alkaline hydrolysis and two-water APNE pathways, respectively. Depicted in Figure 4 is the pH dependence of the log{k_a[urea][HO⁻]} and log{k_c2[urea]} values, where the concentration of urea is assumed to be 1 M (the standard state). As seen in Figure 4, when pH < ~11.6, the calculated log{k_c2[urea]} value is always significantly larger than the calculated log{k_a[urea][HO⁻]} value, indicating that the two-water APNE is the dominant reaction pathway for urea hydrolysis when pH < ~11.6. Only when pH > ~11.6, the alkaline hydrolysis can be the primary reaction pathway for urea.

Figure 4.

Plots for the calculated log(v_a) and log(v_c2) values versus the pH of the reaction solution at T = 298.15 K. Here, v_a = k_a[urea][HO⁻] and v_c2 = k_c2[urea] corresponding to the alkaline hydrolysis and two-water APNE pathways, respectively.

Our computational results are remarkably different from those reported by Estiu et al.¹⁸ in terms of the dominant reaction pathway. Their computational results suggested that the dominant urea hydrolysis pathway is the alkaline hydrolysis (whose first-order hydrolysis rate would be pH-dependent), mainly due to the reason that their reaction-coordinate calculations (without explicitly including first solvation shell of the hydroxide ion) significantly underestimated the free energy barrier for the alkaline hydrolysis as mentioned above.

Reaction Pathways and Free Energy Barriers for Hydrolysis of Me₄U

As mentioned above, Me₄U is a model compound used to study the non-enzymatic hydrolysis rate of urea. In the present study, we also investigated the hydrolysis pathways of Me₄U. Not surprisingly, our calculated results reveal that, in aqueous solution, Me₄U will be hydrolyzed to (CH₃)₂NCOOH via reaction pathways similar to those of the urea hydrolysis. The competing reaction pathways of the Me₄U hydrolysis are similar to those of the urea hydrolysis. For example, the alkaline hydrolysis of Me₄U consists of two reaction steps, and the two-water APNE pathway is a single-step process. Below we discuss the results calculated for the dominant reaction pathway (i.e. the two-water APNE) and the alkaline hydrolysis reaction pathway for the Me₄U hydrolysis.

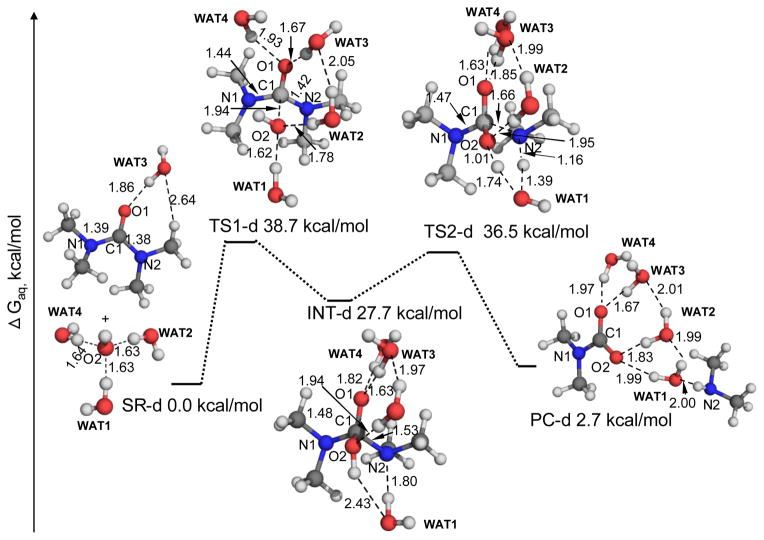
As seen in Figures 5 and 6, key geometric parameters for the reactant complexes, transition states, and intermediate along the reaction path of the Me₄U hydrolysis are similar to the ones of the urea hydrolysis (shown in Figures 1 to 3). However, in these geometries the C-N distances between the carbonyl carbon and the nitrogen atom of the leaving -NH₂ group are slightly longer than the corresponding ones for the urea hydrolysis, implying that the C-N bond in Me₄U is more apt to be broken than the one in the urea during the reaction process. Indeed, for the reaction steps involving the C-N bond breaking (i.e. the second step of the alkaline hydrolysis pathway and the two-water APNE pathway), the free energy barriers calculated for the Me₄U hydrolysis are generally lower than the corresponding free energy barriers calculated for the urea hydrolysis. As a result, the rate-determining step for alkaline hydrolysis of Me₄U becomes the first step, as seen in Figure 5. The free energy profile calculated for the alkaline hydrolysis of Me₄U is remarkably different from that (Figure 1) for alkaline hydrolysis of urea in which the second reaction step is rate-determining.

Figure 5.

Geometric parameters and free energy profile for the alkaline hydrolysis pathway of Me₄U. These geometries were optimized at the B3LYP/6-31+G* level, and their free energies were calculated in the same way as that noted in the Figure 1 caption.

Figure 6.

Geometric parameters and free energy profile for the two-water APNE pathway of the Me₄U hydrolysis. These geometries were optimized at the B3LYP/6-31+G* level, and their free energies were calculated in the same way as that noted in the Figure 1 caption.

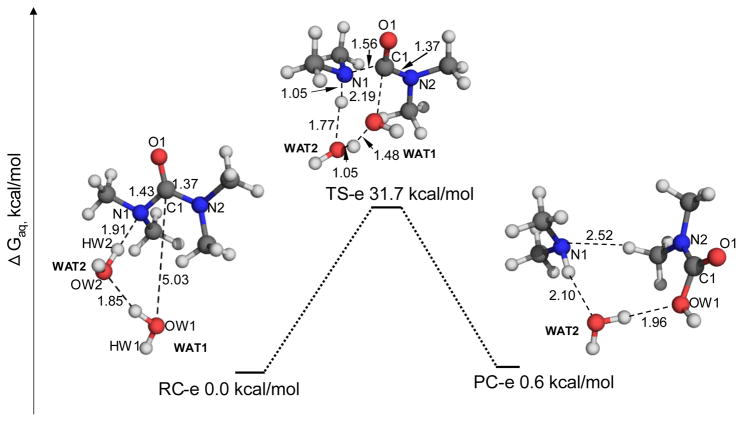
As seen in Figures 5 and 6, the overall free energy barriers calculated for the alkaline hydrolysis and two-water APNE pathways are 38.7 and 31.7 kcal/mol, respectively. According to these energetic data, the dominant reaction pathway for the Me₄U hydrolysis is the two-water APNE, similar to the case of urea hydrolysis. Within the dominant reaction pathway (i.e. the two-water APNE) for both urea and Me₄U, it is remarkable to note that the free energy barrier calculated for the Me₄U hydrolysis is ~12.4 kcal/mol lower than that calculated for the urea hydrolysis.

Comparison with Available Experimental Data and the Best Estimate of the Reaction Rate Constant for the Urea Hydrolysis

Below we first discuss the results obtained at 298.15 K. It is important to compare the calculated energetic results with available experimental kinetic data. According to our computational results discussed above, the dominant urea hydrolysis pathway should be the two-water APNE (with a free energy barrier of 44.1 kcal/mol) when pH < ~11.6, and the dominant Me₄U hydrolysis pathway should also be the two-water APNE (with a free energy barrier of 31.7 kcal/mol) regardless of pH.

What are the actual experimental data available for comparison? As mentioned above, the non-enzymatic hydrolysis of urea has never been observed experimentally. On the other hand, it has been widely accepted within the chemistry community that the hydrolysis of urea should be similar to that of Me₄U, because the hydrolysis of acetamide is similar to that of N,N-dimethyl-acetamide.¹⁹ According to the earlier studies on amide hydrolysis reactions, the rate constant for acetamide hydrolysis is 2.8 times the rate constant for N,N-dimethyl-acetamide hydrolysis.¹⁹ Assuming that this ratio of the rate constants could be applied to the hydrolysis of urea and Me₄U, in order to determine the hydrolysis rate of urea, Me₄U was used by Callahan et al.¹⁹ for the kinetic analysis at various pH values between 4 and 10, and the rate constant for the hydrolysis of Me₄U was determined to be 4.2×10⁻¹² s⁻¹, corresponding to the activation free energy of 32.9 kcal/mol. Their kinetic analysis also revealed that the first-order rate constant was invariant between pH 4 and 10, which is consistent with our computational results that the dominant pathway of Me₄U hydrolysis is the two-water APNE (a neutral hydrolysis pathway whose rate constant is independent of the pH). The experimental activation free energy of 32.9 kcal/mol is close to our calculated free energy barrier of 31.7 kcal/mol.

Further, it should be noted that the above-mentioned experimental value of 32.9 kcal/mol at 298.15 K was actually extrapolated from the kinetic data measured at high temperatures (402–523 K). One may argue that the relative magnitudes of activation free energies associated with various reaction pathways at the high temperatures may be different from those at room temperature (298.15 K), as both the dielectric constant⁴⁴ and pH value of water⁵⁷ at high temperatures (402–523 K) are different from those at room temperature. Thus, the dominant reaction pathway at high temperatures may or may not be the same as that at room temperature. To examine this issue, we also evaluated the activation free energies and hydrolysis rates for the two different pathways of Me₄U hydrolysis at high temperatures (402–523 K), enabling us to compare the computational results with the corresponding experimental kinetic data measured at the same temperatures ranging from 402 K to 523 K (see Table 2 for the details).¹⁹ As seen in Table 2, the calculated ratio of the neutral hydrolysis rate to the alkaline hydrolysis rate is 1.4×10¹² at 298.15 K and 2.1×10⁹–4.0×10⁹ at 402–523 K. These data indicate that the neutral hydrolysis is also the dominant reaction pathway for Me₄U hydrolysis at 402–523 K, and that the temperature did not change the dominant hydrolysis pathway. The computationally predicted values of the Me₄U hydrolysis rate (k_e in Table 2) for the dominant reaction pathway (neutral hydrolysis) are all reasonably close to the corresponding experimental values, suggesting that the results obtained from this computational study are reliable. It is reasonable to predict the kinetic properties of urea hydrolysis in light of the results from the current computational study. Thus, below we revisit the previously estimated “experimental” rate constant (1.17×10⁻¹¹ s⁻¹)¹⁹ for the urea hydrolysis and re-estimate this essential kinetic parameter based on our computational data.

Table 2.

Calculated Gibbs free energy barriers (in kcal/mol) and rate constants for the alkaline and two-water APNE pathways of the Me₄U hydrolysis in aqueous solution at various temperatures (298.15 K and 402–523 K).

T (K)	Solution parametersa			Computational datab							Expt.c
	ε	pKW	pOH	gd	ge	ΔGd	ΔGe	kd (s−1)	ke (s−1)	ve/vd	kexp
298	78.5	14.0	7.00	1.05	1.03	38.7	31.7	2.2×10−16	3.0×10−11	1.4×1012	4.0×10−12
402	47.8	11.9	5.95	1.03	1.02	43.2	36.7	2.3×10−11	8.0×10−8	3.1×109	8.4×10−8
408	46.7	11.8	5.90	1.03	1.02	43.4	36.8	4.0×10−11	1.4×10−7	2.8×109	1.2×10−7
425	42.7	11.6	5.80	1.02	1.02	44.2	37.2	1.4×10−10	5.6×10−7	2.6×109	4.3×10−7
433	41.6	11.6	5.80	1.02	1.02	44.6	37.4	2.3×10−10	1.0×10−6	2.8×109	1.0×10−6
437	40.7	11.5	5.75	1.02	1.02	44.7	37.5	3.4×10−10	1.4×10−6	2.3×109	1.3×10−6
456	37.2	11.4	5.70	1.02	1.01	45.6	37.8	1.1×10−9	6.3×10−6	2.8×109	2.4×10−6
467	35.5	11.3	5.65	1.02	1.01	46.1	38.1	2.2×10−9	1.2×10−5	2.6×109	4.3×10−6
473	34.7	11.2	5.60	1.02	1.01	46.3	38.2	3.4×10−9	1.9×10−5	2.3×109	7.1×10−6
482	33.1	11.2	5.60	1.02	1.01	47.2	38.4	3.4×10−9	3.4×10−5	4.0×109	1.1×10−5
493	30.9	11.1	5.55	1.02	1.01	47.5	38.6	7.6×10−9	6.9×10−5	3.2×109	1.7×10−5
503	29.5	11.1	5.55	1.02	1.01	47.7	38.8	1.7×10−8	1.3×10−4	2.7×109	2.9×10−5
512	28.2	11.1	5.55	1.02	1.01	47.8	39.0	3.6×10−8	2.1×10−4	2.1×109	4.1×10−5
523	26.9	11.0	5.50	1.02	1.01	48.5	39.3	5.1×10−8	3.6×10−4	2.3×109	6.1×10−5

^aThe experimental dielectric constant (ε) and pK_W values of water at various temperatures came from ref.⁴⁴ and ref.⁵⁷, respectively. The pOH (=−log[OH⁻]) values were determined from the corresponding pK_W values.

^bThe subscripts d and e refer to the alkaline and two-water APNE pathways of Me₄U hydrolysis, respectively. ΔG_x (x = d or e) represents the calculated Gibbs free energy barrier in aqueous solution. The obtained free energy barriers were based on the best-estimate single-point energy (MP2/CBS), plus the zero-point vibration and thermal corrections calculated at the B3LYP/6-31+G* level and the solvent shifts calculated at the HF/6-31+G* level (using the default 0.001 a.u. contour). g_x (x = d or e) is the calculated transmission coefficient (tunneling factor), and k_x (x = d or e) is the rate constant calculated accounting for the tunneling factor. The ratio of the neutral hydrolysis rate to the alkaline hydrolysis rate was defined as v_e/v_d = k_e[Me₄U][H₂O]/k_d[Me₄U][HO⁻] in which [H₂O] = 55.6 M.

^cThe experimental rate constant (k_exp) values at 402–523 K were based on the Figure 1 reported in ref.19. The figure in ref.19 was digitized to obtain the values of 1000/T (which gives T in K) and logk_exp (which gives k_exp in s⁻¹) at all of the available data points. When one temperature was associated with two different logk_exp values in the figure, the average of the two logk_exp values was taken. The kinetic data from the digitized figure show an empirical equation: $\text{log}{k}_{exp}=-5.0261\times (1000/T)+5.4511$. This empirical equation was used for extrapolation to 298.15 K, giving k_exp(298.15K) = 4.0×10⁻¹² s⁻¹. The extrapolated k_exp(298.15K) value of 4.0×10⁻¹² s⁻¹ is close to the k_exp(298.15K) value of 4.2×10⁻¹² s⁻¹ extrapolated by the original authors of ref.19, suggesting that the digitization of the figure was reasonable and the possible errors of the digitization may be close to ~5%.

The rate constant of urea hydrolysis was estimated to be 1.17×10⁻¹¹ s⁻¹ (at 298.15 K) by Callahan et al.¹⁹ because they assumed that the rate constant for urea hydrolysis should be 2.8 times the rate constant for Me₄U hydrolysis and because the rate constant for Me₄U hydrolysis was 4.2×10⁻¹² s⁻¹. However, it has been known^{47, 58} that the dominant pathway of amide hydrolysis is the alkaline hydrolysis (whose first-order rate constant is dependent on pH) and the first reaction step is rate-determining, whereas the dominant hydrolysis pathway for urea and Me₄U is the neutral hydrolysis (whose first-order rate constant is independent of pH) as revealed by both the experimental observation¹⁹ and our current computational data. The observed substituent shift of the rate constant for the alkaline hydrolysis of acetamide and N,N-dimethyl-acetamide is not necessarily applicable to that for the neutral hydrolysis of urea and Me₄U. So, the previously estimated “experimental” rate constant (1.17×10⁻¹¹ s⁻¹)¹⁹ for the urea hydrolysis is questionable.

In fact, the reaction pathways and free energy barriers for alkaline hydrolysis of a series of amides, including formamide, N-methylacetamide, N,N-dimethylformamide, and N,N-dimethylacetamide, were examined in our previously reported computational study⁴⁸ using a computational protocol (including the same computational protocol evaluating the solvent shifts) which is essentially the same as that used in the present study. The calculated free energy barriers for the dominant reaction pathway (alkaline hydrolysis) are in good agreement with the corresponding experimental data for all amides examined. Both the computational and experimental data revealed that the methyl groups increase the free energy barrier for the first reaction step (the rate-determining step) of alkaline hydrolysis of the amides.⁴⁸ Similar to the substituent shifts for the first reaction step of the alkaline hydrolysis of amides, the methyl groups also increase the free energy barrier for the first step of alkaline hydrolysis of Me₄U from 36.1 kcal/mol for urea to 38.7 kcal/mol for Me₄U. The remarkable differences are: (1) the rate-determining transition state for alkaline hydrolysis of urea is TS2, instead of TS1; (2) the neutral hydrolysis (via the two-water APNE pathway) is faster than the alkaline hydrolysis for urea when pH < ~11.6 and for Me₄U regardless of pH. So, the experimentally observable substituent shift should be associated with the neutral hydrolysis for urea and Me₄U.

Regarding the neutral hydrolysis via the two-water APNE pathway, the free energy barrier calculated for Me₄U is 12.4 kcal/mol lower than that calculated for urea, because the methyl groups make the C-N bond in Me₄U longer and easier to be broken during the reaction (as noted in the aforementioned discussion). The substituent shift of the free energy barrier calculated for the neutral hydrolysis is remarkably different from that for the first step of the alkaline hydrolysis. Based on the calculated free energy barrier difference of 12.4 kcal/mol between urea and Me₄U for the dominant hydrolysis pathway, we may reasonably estimate that the rate constant for the urea hydrolysis should be ~1.3×10⁹-fold lower than that (4.2×10⁻¹² s⁻¹) measured for the Me₄U hydrolysis. So, the best estimate of the rate constant (k_non ≈ k_c2) for the spontaneous urea hydrolysis should be 3.2×10⁻²¹ s⁻¹ (corresponding to a half-life of 6.3×10¹² years), much smaller than the previously estimated “experimental” rate constant (1.17×10⁻¹¹ s⁻¹).¹⁹ This implies that the rate enhancement/catalytic proficiency of urease (an enzyme which catalyzes urea hydrolysis in the body) was underestimated by ~3.7×10⁹ fold, and that the spontaneous hydrolysis of urea occurs at a rate that is far below our present limits of detection.

It has been known that k_cat (catalytic rate constant) = 3.6×10⁴ s⁻¹ and K_M (Michaelis-Menten constant) = 4×10⁻³ M for urease-catalyzed hydrolysis of urea.¹⁹ According to the previously estimated “experimental” rate constant (1.17×10⁻¹¹ s⁻¹),¹⁹ k_cat/k_non (rate enhancement) ≈ 3×10¹⁵ and (k_cat/K_M)/k_non (catalytic proficiency) ≈ 8×10¹⁷ M⁻¹. In light of the best estimate (k_non = 3.2×10⁻²¹ s⁻¹) in the present study, we should have k_cat/k_non ≈ 1.2×10²⁵ and (k_cat/K_M)/k_non ≈ 3×10²⁷ M⁻¹, suggesting that urease surpasses proteases and all other enzymes^19,59 in its power to enhance the rate of reaction.

Conclusion

The reaction-coordinate calculations on the competing non-enzymatic hydrolysis pathways have demonstrated that the dominant reaction pathway is the neutral hydrolysis via the two-water APNE for both urea (with a free energy barrier of 44.1 kcal/mol) when pH < ~11.6 and Me₄U (with a free energy barrier of 31.7 kcal/mol) regardless of pH. The computationally determined dominant reaction pathway is qualitatively consistent with the reported experimental observation that the first-order rate constant for the hydrolysis of Me₄U was not dependent on pH of the reaction solution. Quantitatively, the free energy barrier of 31.7 kcal/mol calculated for the Me₄U hydrolysis is reasonably close to the experimental activation free energy of 32.9 kcal/mol (associated with the rate constant of 4.2×10⁻¹² s⁻¹). The agreement between our computational results and the available experimental kinetic data suggests that the results obtained from this computational study are reliable, and that it is reasonable to revisit the substituent effects and predict the kinetic properties of urea hydrolysis in light of the results from the current computational study.

It has been demonstrated that the substituent effects on the hydrolysis rate for urea and Me₄U are remarkably different from previously observed substituent effects on the hydrolysis rate for amides, due to the difference in the dominant reaction pathway, i.e. the alkaline hydrolysis for amides (with the first reaction step being rate-determining) versus the neutral hydrolysis via the two-water APNE for urea and Me₄U. For both the amides and urea/Me₄U, the methyl groups on the N atom(s) slightly increase the free energy barrier for the first step of the alkaline hydrolysis, but considerably decrease the free energy barrier for the two-water APNE pathway. The substituent shift of the free energy barrier calculated for the neutral hydrolysis is remarkably different from that for the first step of the alkaline hydrolysis. Hence, computational data reveal that the observed substituent shift of the rate constant for the alkaline hydrolysis from acetamide to N,N-dimethyl-acetamide is not applicable to that for the neutral hydrolysis from urea to Me₄U.

Based on the calculated free energy barrier difference of 12.4 kcal/mol between urea and Me₄U for the dominant hydrolysis pathway, we may reasonably estimate that the rate constant for the urea hydrolysis should be ~1.3×10⁹-fold lower than that (4.2×10⁻¹² s⁻¹) measured for the Me₄U hydrolysis. So, the best estimate of the rate constant for the spontaneous urea hydrolysis should be 3.2×10⁻²¹ s⁻¹ (corresponding to a half life of 6.3×10¹² years), much smaller than the previously estimated “experimental” rate constant (1.17×10⁻¹¹ s⁻¹). This implies that the rate enhancement/catalytic proficiency of urease was underestimated by ~3.7×10⁹ fold, and that the spontaneous hydrolysis of urea occurs at a rate that is far below our present limits of detection. According to our best estimate of the spontaneous hydrolysis rate constant of urea, the rate enhancement and catalytic proficiency of urease should be 1.2×10²⁵ and 3×10²⁷ M⁻¹, respectively, suggesting that urease surpasses proteases and all other enzymes in its power to enhance the rate of reaction.

In addition, this study has clearly demonstrated that the substituent effects on the reactions of one type of compounds could be remarkably different from those on the reactions of another type of compounds, even if the compounds and reactions are all similar. One must be cautious to apply the experimentally observed substituent effects for the reactions of another type of compounds to the reactions of the compounds in question.