Dynamic Contrast Enhanced MRI Parameters and Tumor Cellularity in a Rat Model of Cerebral Glioma at 7T

Abstract

Purpose

To test the hypothesis that a non-invasive dynamic contrast enhanced MRI (DCE-MRI) derived interstitial volume fraction (v_e) and/or distribution volume (V_D) were correlated with tumor cellularity in cerebral tumor.

Methods

T₁-weighted DCE-MRI studies were performed in 18 athymic rats implanted with U251 xenografts. After DCE-MRI, sectioned brain tissues were stained with Hematoxylin and Eosin for cell counting. Using a Standard Model (SM) analysis and Logan graphical plot, DCE-MRI image sets during and after the injection of a gadolinium contrast agent were used to estimate the parameters plasma volume (v_p), forward transfer constant (K^trans), v_e, and V_D.

Results

Mean parameter values in regions where the SM was selected as the best model were: (mean ± S.D.): v_p = (0.81±0.40)%, K^trans = (2.09±0.65) ×10⁻² min⁻¹, v_e = (6.65±1.86)%, and V_D = (7.21±1.98)%. The Logan-estimated V_D was strongly correlated with the SM’s v_p+v_e (r = 0.91, p < 0.001). The parameters, v_e and/or V_D, were significantly correlated with tumor cellularity (r ≥ −0.75, p < 0.001 for both).

Conclusion

These data suggest that tumor cellularity can be estimated non-invasively by DCE-MRI, thus supporting its utility in assessing tumor pathophysiology.

Introduction

Dynamic contrast enhanced MRI (DCE-MRI), since it is minimally invasive and free of radiation exposure, is becoming the technique of choice for assessing cerebral vascular permeability (1). A series of T₁-weighted images are acquired before, during, and after the injection of a contrast agent (CA), and a pharmacokinetic model is employed to estimate blood-to-brain transfer parameters.

The microvascular leakage of a CA can be parameterized by its plasma volume (v_p), forward transvascular transfer constant (the rate of vessel-to-tissue leakage of the CA) K^trans, and, if the leakage occurs swiftly enough, by the CA’s reverse transfer constant (the rate of tissue-to-vessel CA return), k_ep (2-6). If there are no active transport mechanisms, and no trapping of CA in either vascular or extravascular compartments, and when all three parameters (v_p, K^trans, and k_ep) can be stably estimated, the derivation of the interstitial volume fraction, v_e, then follows the relationship: ${\mathrm{V}}_{\mathrm{e}}=\frac{{\mathrm{K}}^{\mathrm{trans}}}{{\mathrm{k}}_{\mathrm{ep}}}$.

While the use of graphical methods for estimating model parameters has decreased in proportion to the availability of modern computers, graphical methods’ utility for examining model plausibility remains. Two commonly applied graphical methods in concentration-time studies are the Patlak plot (2), and Logan plot (7,8). The Patlak plot was introduced in MRI (9) to estimate K^trans in a rat model of transient cerebral ischemia, and the extended Patlak method (3) has been used in a rat model of cerebral tumor (9). This latter method, or the equivalent extended Tofts model (4), also known as the standard model (SM), is now frequently used for the estimation of the vascular parameters v_p, K^trans, and v_e in DCE-MRI_. However, DCE-MRI-derived v_e has not yet been evaluated as a true measure of interstitial space in brain tumor, nor has its relationship to tumor cellularity been examined. As for the Logan plot, we know of no instance of its use in DCE-MRI for the estimation of distribution volume (i.e., plasma volume, v_p, plus interstitial volume, v_e, expressed as a fraction), and no examination of its relationship to tumor cellularity. In this study, we introduce the Logan plot in DCE-MRI for the estimation of distribution volume (V_D) in an experimental cerebral tumor and assess its relationship to tumor cellularity.

Several studies have reported the correspondence of DCE-MRI-derived vascular parameters with histological findings, including tumor extracellular space, micro-vascular density, vascular endothelial growth factor, and tumor grade (10-12). In a study that is particularly relevant to the considerations of this study, Aref et al. demonstrated a strong correlation between a DCE-MRI-derived estimate of extracellular space volume fraction, and extracellular space in a rat model of chemically induced mammary tumors (10).

Since tumor cellularity, i.e., the number of cells in a given volume of tumor tissue, is an important factor for proliferative activity (13), a comparison between noninvasive MRI measures and histology is a significant test for validation of the clinical utility of DCE-MRI-derived parameters. Thus, the objective of this study was to test the hypothesis that tumor cellularity and a DCE-MRI-derived estimate of v_e and/or V_D were correlated in experimental cerebral tumor. In the course of examining the evidence, a number of other measures were examined, but the relation between tumor cellularity and the DCE-MRI estimated v_e and/or V_D was the main consideration of this analysis.

Theory

The Patlak Graphical Analysis and Its Relationship to the SM

A simplified matrix-based model mathematically equivalent to the Crone-Renkin single-capillary model with no extra- to intra-vascular efflux was introduced by Patlak et al (2). Subsequently the original Patlak model was extended to allow for efflux from interstitial space to the vasculature (3). The extended Patlak model is identical to the extended Tofts, or consensus model (4), and is herein referred to as the standard model (SM). The SM describes the concentration of contrast agent in tissue after intravenous administration:

$$C_t\left(t\right)=K^{trans}{\int }_0^t{C}_p\left(\tau \right)e^{-k_{ep}(t-\tau )}d\tau +V_p{C}_p\left(t\right),$$ (1)

where t is time, C_p(t) and C_t(t) are the time-varying plasma and tissue concentrations of CA, respectively, K^trans is the forward transfer constant of CA between blood plasma and interstitial space, k_ep is the reverse transfer rate constant from the interstitial space to the vascular compartment, and v_p is the vascular plasma volume fraction.

If it is assumed that the change in longitudinal relaxation rate (R₁ = 1/T₁) is proportional to tissue concentration of the contrast agent (14), the observation equation equivalent to the SM equation is;

$$(1-Hct)\Delta R_{1t}\left(t\right)=K^{trans}{\int }_0^t\Delta R_{1a}\left(\tau \right)e^{-k_{ep}(t-\tau )}d\tau +V_p\Delta R_{1a}\left(t\right),$$ (2)

where ΔR_1a and ΔR_1t refer to the subtraction of the pre-contrast relaxation rate from its post-contrast value at artery and tissue respectively and Hct is the hematocrit at the level of the microvasculature. In what follows, Hct was assumed to be 0.45 (15), which may uniformly bias the results presented below, but will not affect the correlations presented.

Plotting the ratio $\frac{(1-Hct)\Delta R_{1t}\left(t\right)}{\Delta R_{1a}\left(t\right)}$ versus $\frac{{\int }_0^t\Delta R_{1a}\left(\tau \right)e^{-k_{ep}(t-\tau )}d\tau }{\Delta R_{1a}\left(t\right)}$, with k_ep optimized to provide the best fit (in the least-squares sense) of the model to the data yields the extended Patlak plot, with a slope of K^trans and an ordinate intercept of v_p. In the tumor, since, within the duration of the DCE experiment, the CA leaks from the microvasculature at a high enough rate to begin to equilibrate between the intra- and extra-vascular space, k_ep can also be estimated. Because this model fits three parameters; v_p, K^trans, and k_ep, it is called Model 3. We emphasize that Model 3 results are identical to the results produced by the SM, but with the proviso that the SM has been tested against a reduced model, and thus more reliably represents the data. Note that, since an estimate of v_e requires the ratio K^trans/k_ep, DCE-MRI estimates of interstitial volume can be reliably performed only in Model 3 regions. The same goes for Logan analysis estimates of V_D (see below).

In some regions with CA leakage, but no measurable back-flux to the vasculature (i.e. k_ep = 0), only two parameters, K^trans and v_p, can be estimated. The model in this case has 2 parameters and is named Model 2. In normal brain, there is usually little or no measurable leakage of CA from the microvasculature. In that case, K^trans = k_ep = 0; the one parameter to be estimated is v_p and is accordingly identified as Model 1. Model selection proceeded as previously described (6): for each voxel the preferred model was selected by the application of an F-test criterion.

Logan Plot

The tissue and plasma concentration of the contrast agent as a function of time is (7,8);

$$\frac{{\int }_0^t{C}_t\left(\tau \right)d\tau }{C_t\left(t\right)}=V_D\frac{{\int }_0^t{C}_p\left(\tau \right)d\tau }{C_t\left(t\right)}+Const$$ (3)

where C_p(t) and C_t(t) are the plasma and tissue concentrations of CA, respectively, V_D is the distribution volume, and, if an equilibrium has been established between the vascular compartment and the tissue compartment, Const is a constant. We note that the Logan plot fits a different portion of the data in DCE-MRI studies than the SM: the SM depends on changes in the response function (relative to the input function) to estimate the rate parameters K^trans and k_ep, while the Logan analysis demands that the response function does not change relative to the input function. Thus, the two analyses fit much different portions of the input-response data, albeit they both require a measure of the data from time t=0. Note that, even if k_ep is not explicitly estimated (Equation 2), but expressed as $\frac{K^{trans}}{V_e}$ in the exponent of the kernel, it is only through dynamic changes that the term can be estimated.

Since the change in longitudinal relaxation rate is assumed to be approximately proportional to tissue concentration of the contrast agent, the observation equation for the Logan plot becomes:

$$(1-Hct)\frac{{\int }_0^t\Delta R_{1t}\left(\tau \right)d\tau }{\Delta R_{1t}\left(t\right)}=V_D\frac{{\int }_0^t\Delta R_{1a}\left(\tau \right)d\tau }{\Delta R_{1t}\left(t\right)}+Const$$ (4)

where ΔR_1a(t) and ΔR_1t(t) refers to the subtraction of the pre-contrast relaxation rate from its post-contrast value at artery and tumor region respectively as a function of time, and Hct is the hematocrit.

If there is a time after which the plot of $(1-Hct)\frac{{\int }_0^t\Delta R_{1t}\left(\tau \right)d\tau }{\Delta R_{1t}\left(t\right)}$ versus $\frac{{\int }_0^t\Delta R_{1a}\left(\tau \right)d\tau }{\Delta R_{1t}\left(t\right)}$ yields a straight line, the slope of the fitted straight line gives the distribution volume. Once again, the graphical nature of this statement is central to the choice of model. Generally in this paper, data were examined visually for conformance to the model before selection of the point for starting the fit of the Logan plot. This procedure can be automated if it is to be performed on a voxel-by-voxel basis, but a preliminary visual examination of grouped data should be performed before moving on to a voxel-by-voxel procedure.

ΔR₁ Calculation Theory

Under the conditions of the experiment, i.e. using a dual-echo gradient echo sequence (the mgems sequence in the Agilent VNMRj library), and assuming that the flip angle is a known constant across the brain of the rodent, an estimate of the time trace of ΔR₁ can be calculated from the following:

$$S\left(t\right)=\frac{\epsilon M_{0}sin\left(\theta \right)(1-e^{-TR{R}_1\left(t\right)})e^{-TR{R}_2^{\ast }\left(t\right)}}{1-cos\left(\theta \right)e^{-TR{R}_1\left(t\right)}},$$ (5)

where S(t) the signal intensity at time t, ε is the detection efficiency, εM₀ is the magnetization of the protons, θ is the tip-angle, TR is the repetition time between pulses, TE is the echo time (the time between the center of the excitation pulse and the readout gradient) and R*₂(t) is the transverse relaxation rate. Equation 5 can be solved for R1(t):

$$R_1\left(t\right)=\frac{1}{TR}ln\left\{\frac{1-\left(\frac{S\left(t\right)cos\left(\theta \right)}{\epsilon M_0{e}^{-TE{R}_2^{\ast }}sin\left(\theta \right)}\right)}{1-\left(\frac{S\left(t\right)}{\epsilon M_0{e}^{-TE{R}_2^{\ast }}sin\left(\theta \right)}\right)}\right\}$$ [6]

Methods

These studies were conducted with the approval of the Henry Ford Hospital Institutional Animal Care and Use Committee (IACUC).

Animal Preparation

U251 tumor induction: Athymic rats were inoculated intracerebrally as follows: animals were anesthetized with 80 mg/kg ketamine and 15 mg/kg xylazine i.m. The surgical zone was swabbed with Betadine solution, the eyes coated with Lacri-lube and the head immobilized in a small animal stereotactic device (Kopf, Cayunga, CA). After draping, a 1 cm incision was made 2mm right of the midline and the skull was exposed. A burr hole was drilled 3.5 mm to the right of bregma, taking care not to penetrate the dura. A #2701 10μL Hamilton syringe with a 26s gauge needle containing U251MG tumor cells freshly harvested from log phase growth (5 × 10⁵ in 10 μl of PBS) was lowered to a depth of 3.0 mm and then raised back to a depth of 2.5mm. Cells were then injected at a rate of 0.5 μL/10 s until the entire volume was injected. Tumors in animals implanted following this technique grow to about 5 mm diameter by 21 days post-implantation. On or a few days after day 18, each animal was anesthetized (isofluorane 4% for knockdown, 0.75 to 1.5% for maintenance, balance N₂O:O₂ = 2:1 and allowed to spontaneously respire. A tail vein was cannulated for the administration of CA. Body temperature was maintained constant (37°C) with a warm air supply monitored via an intrarectal type T thermocouple.

MRI Study

DCE-MRI studies were performed using a 7T magnet in 18 athymic rats at 18 ± 3 days after tumor implantation. The image sets were acquired on a DirectDrive Varian (now Agilent, Santa Clara, California) 20 cm bore system with a 32×32 mm FOV. Coils were a Bruker-supplied volume resonator and a Bruker 2 cm surface coil for rat brain imaging. High-resolution T1-weighted spin-echo images were acquired pre- and post-CA (FA = 90°, 180°, matrix 256×192, 27 slices, 0.5 mm thickness, NE = 1, NA = 4, TE/TR = 16/800 ms). Prior to the DCE-MRI sequence, and immediately after, two Look-Locker sequences (LL) sequences were run so that a voxel-by-voxel estimate of T₁ in the tissue could be made pre- and post-CA administration. LL sequence parameters were as follows: FA = 15°, matrix 128×64, five 2.0 mm slices, no gap. NE=24 inversion-recovery echoes on 50 ms intervals, TE/TR=4.0/2000 ms.

The DCE-MRI sequence was a dual-echo gradient-echo (2GE) sequence, the “mgems” sequence in the Agilent VnmrJ library. It acquired 150 image sets at 4.0 s intervals: (FA = 27°, matrix = 128×64, three 2.0 mm slices, NE= 2, NA=1, TE1/TE2/TR = 2.0/4.0/60 ms). At image 15 of the 2GE sequence Bolus injection of the CA (Magnevist, Bayer Healthcare Pharmaceuticals, Wayne, New Jersey), 0.25 mmol/kg at undiluted concentration, no flush, was performed by hand push, followed by a slight draw-back. Following the post-contrast LL sequence, a Pulsed Gradient Spin-Echo DWI sequence (matrix 128×64, thirteen 1mm slices, TR = 1500 ms, TE= 40 ms, NE=1, b-values = 0, 1217 s/mm², gradient amplitude = 1.07 mT/cm, gradient duration = 10 ms) was run to generate a parametric map of apparent diffusion coefficient (ADC). These studies carried over from a previous study that employed two CAs of different weights (Magnevist, then Gd-labeled albumin), with the ADC studies conducted after the first study in order to save time and allow for partial clearance of the first CA. Thus, there may be some small bias in the results (16). However, since all the studies were conducted in the same manner, and the results examined through correlation, we judged that inferences drawn from this study might still be useful.

Histology

At sacrifice, animals were deeply anesthetized with ketamine/xylazine and transcardiacally perfused with saline followed by 4% paraformaldehyde. After carefully removing the brains from the skull, they were post-fixed in same fixative overnight. Coronal sections grossly containing and adjacent to the tumor were obtained using a rat-brain matrix (Activational Systems, Inc., Warren, MI). The brain tissue was processed using a VIP Tissue Tek Processing center, prior to embedding. Seven micrometer sections were cut and placed on Superfrost Plus (Fisher Scientific) slides and stained with hemaoxylin and eosin (H&E) for evaluation of tumor ROIs. Additional sections were obtained for immunohistochemistry (IHC) staining. Images were collected using a Nikon Eclipse E800 Microscope equipped with ACT1C software.

H&E stained slides were used for cell density measurements. Regions of interest (ROIs) were chosen in the tumor interior and in the tumor periphery. The area of the field of view in each ROI was 4000μm by 3000μm. A comparative ROI was chosen within the contralateral hemisphere, usually within the caudate putamen. Both 1× low magnification of the entire coronal section and 10× higher magnification images were collected. Images were imported into ImageJ (NIH, version1.43u), and converted to 8 bits for analysis. A thresholding range of 133 to 193 was used, depending on the contrast of the H&E staining. The numbers of nuclei were manually counted in a sampling of regions and compared with the automated count to ensure accuracy. The particle analysis function used was set to collect particles in the range of 15 to 70 μm². This was used to count cell nuclei and therefore used as the basis for the cell numbers measures.

Arterial Input Function

Because of the difficulty of directly estimating the arterial input function (AIF) from MRI data, a radiotracer assay-based input function obtained from a previous investigation (17) was used in the dynamic MRI studies. Nagaraja et al (17) have shown that, starting at about two minutes after injection of CA, the radiological and MRI measures of blood concentrations of CA track each other very well. In a number of studies, we examined the tissue response in a brain area where minimal leakage was known to occur. It was clear from an examination of the time trace of ΔR₁ that the early portion of the tissue response curve did not resemble that of an input function, presumably because of the dispersion in time of the CA arriving at, and passing through, the vascular system of the tissue, and also possibly because of limited water exchange across the blood-brain barrier. However, during the latter two-thirds of the study, the tissue response and the radiological standard curve we used appeared to agree, in line with Nagaraja’s observations. Accordingly, the latter two-thirds of the time trace of the radiological curve and the tissue trace of ΔR₁(t) in the caudate putamen were integrated and used to scale the radiological curve. It was assumed that: 1) no vascular leakage of CA occurred in the caudate putamen region contralateral to the tumor, and 2) the plasma volume of the caudate putamen was 1% (18). The integrated area of the radiotracer AIF was scaled so that its area was 100 times that of the integrated area of the average value of ΔR₁(t) in the caudate putamen of the opposite hemisphere. The 1% figure adopted was larger than Bereczki’s estimates (0.8% - 0.9%, table 5 of the Bereczki paper (18)) because that work, as the authors noted, estimated only plasma volumes in vessels below 50 μm. All the volumes estimated in this paper are relative to the estimate of v_p in the caudate putamen; we took the value of 1% so that relative volumes measured elsewhere could be easily understood in relation to caudate putamen plasma volumes. This method is a combination of the reference region approach of Yankeelov et al (19) and the original Tofts approach that used a group-averaged input function (20).

Parameter Estimation - Computational and Statistical Methods

The analysis of the Look-Locker data followed that of Gelman et al (21). Briefly, since it was determined that, for a typical study, the flip angle, θ, did not vary by more than a few percent across a rat brain, a whole-brain estimate of θ was first performed by using a boxcar-smoothed set of inversion-recovery images and employing a Simplex least-squares minimum finder in 3 parameters to freely fit εM₀, T₁, and θ voxel-by-voxel in the smoothed images (this ε was not the same as that of the DCE-MRI sequence). The flip angle was then fixed at the mean of its global estimate for the brain and a Simplex minimum finder in 2 parameters was employed in the unsmoothed data to produce a voxel-by-voxel estimate of T₁ and εM₀.

We note that the 2000 ms repetition time of the LL sequence was too short to allow the inverted magnetization to fully relax to its equilibrium value. An iterative procedure to estimate the equilibrium value of the magnetization (M_ss in equation 1 of Gelman et al (21)) in the computational estimate of T₁ was employed to adjust for the short TR’s, allowing an unbiased estimator of T₁ to be produced.

Consider Equations 5 and 6. Besides R₁(t) and R₂*(t) which vary across the experiment, the parameters εM₀ and θ, which do not vary across the experiment, must be estimated. Our practice was to estimate R₂* using the log ratio of the first and second echo, to fix the value of θ at 27°, and to use maps of R₁ constructed from Look-Locker maps, in combination with the amplitude of the DCE data at the beginning and end of the study, to estimate εM₀, as described in the following paragraph.

The three unknowns in the DCE-MRI sequence (Equation 5) were R₁(t), θ, and εM₀. The measured quantity was S(t). It was assumed that the tip angle θ was known. In the period before the administration of contrast agent, using the voxel-by-voxel estimate of R₁(t < t_inj), produced by the prior LL measurements, where t_inj was the time of contrast agent injection, the quantity εM₀ was estimated using equation 5. Using the post-study estimates of R₁ and the last few points of the DCE-MRI data where the data was changing slowly, the quantity εM₀ was similarly estimated, and the average of the two estimates was taken. Assuming that the efficiency for detection did not change after the injection of contrast agent, this allowed R₁(t) to be estimated across time by means of Equation 6.

The practice of calculating R₁ via Look-Locker sequences prior to and after the DCE-MRI study allowed εM₀ to be estimated under conditions of no contrast agent, and approximately constant tissue contrast agent concentration. This considerably stabilized the estimate of εM₀, and thus of R₁(t) because it fixed the beginning and end points of the R₁(t) curve. The quantity ΔR₁(t) in equation 4 was generated by subtracting the pre-contrast estimate of R₁(t) from the subsequent estimates of R₁(t).

All results are reported as the mean ± standard deviation. The standard error of the means in this sample of 18 studies is the standard deviation divided by 4.24.

The adjusted input function and tissue time trace of ΔR₁ were used to estimate pharmacokinetic parameters using the SM, as in Bagher-Ebadian et al. (6). For each voxel, data points were fitted to model 1, 2, and 3, an F-statistic was generated to select the preferred model, and the parameters available under that model were mapped. However, for the Logan plot, the adjusted input function and time trace of ΔR₁ in tumor tissue was used to generate the Logan graphical plot. The trend of the plot was then visually inspected for each animal individually to choose the starting time point for the straight line fitting of the plot, after which the slope of the fitted straight line was measured as an estimate of the distribution volume.

In order to estimate the DCE parameters for examining their correlation to tumor cellularity, a 5×4 pixel ROI was visually selected on parametric maps to correspond to the areas from the cell counting on histology. Since only one slice on MRI data set was used to make the comparison, anatomical markers such as lateral ventricles, coronal shape and tumor area comparison (on high resolution T₁ weighted image) were used to select the MRI maps and further pinpoint the histological (Histo) ROI onto the matching parametric maps. Hereafter, this 5×4 pixel ROI is named as the Histo sub-region.

Other Statistical Methods

The correlation of the Logan estimate of V_D, compared to the SM V_D, was examined by linear regression; their absolute estimates were assessed for differences via a paired t-test. Other relationships reported herein (e.g., the association between ADC and cell count) were assessed similarly.

Results

Eighteen DCE-MRI animal studies and corresponding histological findings were available. All studies were the second study of a test-retest paradigm, with 24 h between studies. Test-retest findings are reported elsewhere (22). Mean tumor age was 18 ± 3 days. All tumors were seen clearly on post-contrast T₁-weighted images, ADC maps, and H&E-stained tissue slides.

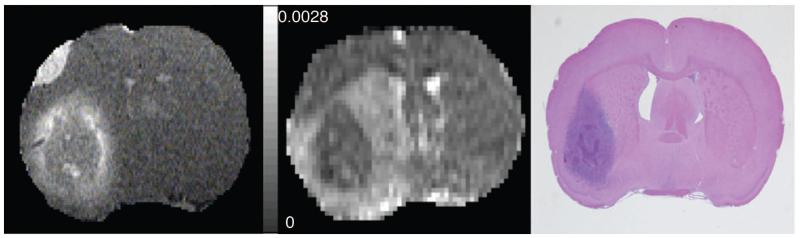
To introduce the findings, the data from an animal (#18) studied 21 days post-implantation will be presented. For the example animal, the mean ADC value (averaged from x, y, and z direction of the center image) was (9.3±2.5)×10⁻⁴ mm²/s. A post-contrast T₁-weighted image, the corresponding ADC map (averaged from x, y, and z direction) from the center slice and an H&E-stained tissue slide approximating the position of the MR image of the example animal are shown in Figure 1.

Figure 1.

Left: High-resolution post-contrast T₁-weighted image. Middle; Corresponding centrally located ADC maps. Right; H&E staining of a centrally located tissue slice approximating the position of the MRI image.

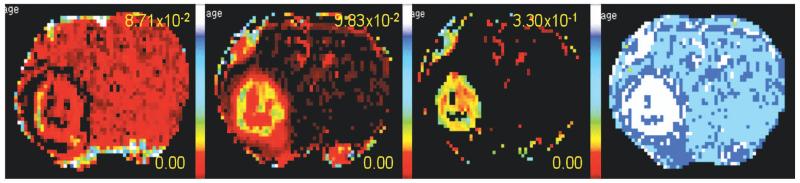
Under the conditions of the experiment, the first pass of the contrast agent produced a signal decrease due to T₂* dephasing in many tissues, particularly in highly vascular regions of the tumor and in blood. Using the T₂*-corrected time trace of 2GE data, the pre-contrast R₁ values, flip angle and repetition time, the time trace of ΔR₁ was calculated pixel-by-pixel across the entire image set. The time trace of ΔR₁ in turn was used to produce the parametric maps. The parametric maps for v_p, K^trans, v_e, and an F-test based model selection are shown in Figure 2. From the model selection map, we see that Model 1 predominated in normal non-leaky brain tissue, showing little or no leakage of contrast agent. Model 3 predominated in regions associated with a high density of tumor cells, as determined by examination of post-mortem tissue slides. Model 2 bordered Model 3 regions, showing leakage at reduced rates.

Figure 2.

Parametric maps left to right: v_p, K^trans, v_e and Model selection. For the Model selection map, white is Model 3 acceptance, dark blue is Model 2 acceptance, light blue is Model 1 acceptance.

As noted earlier, v_e and V_D, estimates of interstitial space can only be measured when CA leaks from the capillary into the interstitial space in an amount sufficient to measure its back flux to the vasculature. Since the primary goal for the present study was to study the relationship between tumor cellularity and DCE-MRI-derived estimates of interstitial space, only the data from Model 3 regions were analyzed. The parameter values in Model 3 regions varied considerably from animal to animal, with the mean values v_p = (0.81±0.40)%, K^trans = (2.08±0.65) ×10⁻² min⁻¹, and v_e = (6.65±1.86)%.

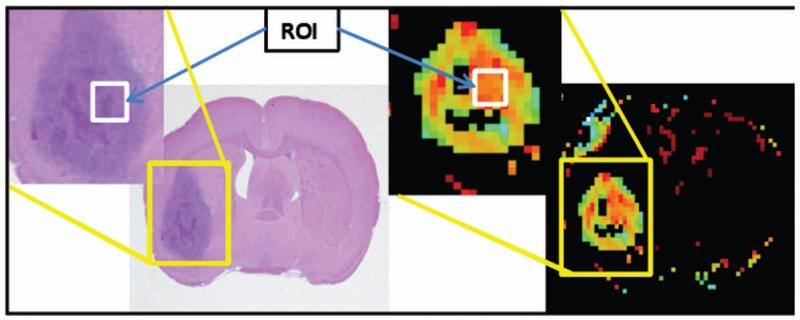
Figure 3 shows the H&E-stained tissue slide with corresponding parametric map of v_e. The white box on the magnified image shows the Histo sub-region chosen for cell counts and parameter values respectively. The mean parameter values estimated in the Histo sub-region were v_p = (0.81±0.44)%, K^trans = (2.08±1.45) ×10⁻² min⁻¹, and v_e = (6.99±1.45)%.

Figure 3.

Left: H&E-stained tissue slide corresponding to parametric map. Right: Parametric map of v_e (only in the model 3 region can v_e be calculated). The white box drawn on the detail images shows the ROIs selected for cell count and v_e values.

For each time point, the average ΔR₁ across the points of the Model 3 region and Histo sub-region was determined and used as a measure of the CA concentration for the purpose of producing a Logan plot. Figure 4 (top) plots the data as an extended Patlak plot in the Model 3 region; the slope of the fitted straight line gives K^trans. In this example, although the overall fit is excellent (R² = 0.992), there is a clear deviation from linearity in the early time points. The sources of this deviation are briefly considered in the Discussion.

Figure 4.

Top: Patlak graphical analysis of the data in the Histo sub-region. The solid line shows the linear fit of the data points; the slope of the line yields the forward transfer constant, K^trans. Bottom: Logan graphical analysis of the data in the same sub-region. The solid line shows the linear fit of the data in the range 90:150, the slope of the line yields an estimate of distribution volume of about 9%.

Figure 4 (bottom) plots the data as a Logan plot in the same region, with fitting for a straight line between abscissa values of 90:150 min. In that region, the graph was linear by inspection. The slope of the fitted line was 0.0897, equivalent to a distribution volume, V_D, of 8.97%.

For the sample of 18 animals in the study, the mean V_D measured in Model 3 region was (7.21±1.98)%, roughly half that of normal brain parenchyma (23). V_D estimated by two independent methods, SM and Logan analysis, was highly correlated (r = 0.91, p < 0.001), where, for the SM method, V_D was calculated as the sum of v_e and v_p. The mean SM V_D (7.46%) did not differ significantly from that of the Logan V_D (7.21%) (t=0.38, N= 18, p = 0.70). This was a confirmatory result, since the two methods used primarily early data in the SM pharmacokinetic approach, and primarily late data in the Logan pharmacokinetic approach.

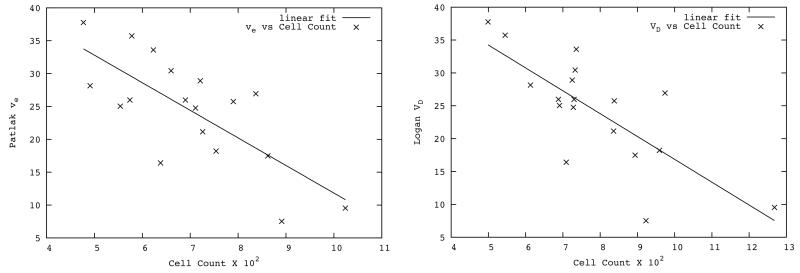
Cell counts from the Histo sub-region adjacent to the tumor core region varied from 751 to 3776 with mean(±standard deviation) 2442±840. Figure 5 (left) shows a scatter plot of the SM estimated v_e versus tumor cellularity. Figure 5 (right) shows the scatter plot of the Logan plot estimated V_D versus tumor cellularity. A linear regression of tumor cellularity with both v_e estimated via SM and V_D via Logan plot showed an inverse relationship, with a strong correlation (r = −0.75 for v_e and r = −0.76 for V_D, p-value < 0.001 for both). The mean SM estimated distribution volume (plasma volume plus interstitial volume) was also highly correlated with tumor cellularity (r = −0.76, p-value < 0.001). Thus, a measure of interstitial volume fraction (v_e) estimated from the SM, and distribution volume from both SM and Logan analyses were highly (negatively) correlated with the tumor cellularity.

Figure 5.

Left: Scatter plot of Patlak plot estimates of interstitial volume versus tumor cellularity in the Histo sub-region. The solid line shows the linear fitting of the plot (r = 0.75, p < 0.001). Right: Scatter plot of Logan plot estimates of distribution volume (V_D) versus tumor cellularity measured in the Histo sub-region. Solid line shows the linear fitting of the plot (r = 0.76, p < 0.001).

The relationship of tumor cellularity and the apparent diffusion coefficient (ADC) was also examined. A significant correlation with ADC (r = 0.54, p-value < 0.05) was observed. Notably, this relationship was not as strong as those of the DCE-MRI measures, although, since the ADC estimate occured post-contrast, the result might be weakened.

Discussion

In this study we measured DCE-MRI parameters using a dual-echo gradient-echo sequence in a rat model of cerebral glioma at 7T in order to establish their relationship to tumor cellularity. The mean DCE parameter values measured in Model 3 regions and/or the Histo sub-regions were in agreement to those of similar measures in human glioblastoma using DCE-MRI (6), or CT perfusion (24), and in a rat model of 9L glioma using DCE-MRI (25). In this latter reference, however, estimates of v_e were much higher than our estimates. Whether the 9L glioma differs so radically from the U251 model used herein, or the differing analyses employed produce much different estimates of k_ep, remains to be determined. One possibility is that, since all the volume estimates were indexed to the plasma volume of the caudate putamen, the 1% value we used for plasma volume fraction in that tissue was too small.

The mean values in the entire Model 3 region and the Histo sub-region did not differ for v_p and K^trans. However for interstitial volume_, the mean values in the Histo sub-region were slightly elevated compared to Model 3 region; the difference in mean values between two regions was not significantly different from zero (p = 0.57). As noted, the Histo sub-region was typically selected nearer the tumor core region, and so that might be a reason for the higher estimates of v_e in the Histo sub-region compared to the Model 3 region as a whole. In a study in a rat model of 9L glioma, v_e was also found to be elevated in the tumor core region (25). This result supports our higher estimates of mean v_e and/or V_D values in the Histo sub-region comparison to the Model 3 region.

Although a number of DCE-MRI studies in glioma have evaluated blood volume and permeability, only a few have estimated interstitial volume and its relation to histological findings. In a study in human glioma, estimation of interstitial volume was helpful in differentiating gliomas from other brain tumors; increasing interstitial volume tended to correlate with increasing tumor grades (12). In a study of a rat model of chemically induced mammary tumors, Aref et al. demonstrated that interstitial volume fraction measured by DCE-MRI was correlated with histologically measured extracellular space fraction (10).

In another study in a rat model of 9L tumor, Chenevert et al. reported an increased volume of water in the interstitial compartment with decrease in cellularity following the chemotherapeutic (Carmustine) intervention (26). A strong correlation of mean ADC values with tumor cellularity (r=0.78) was also demonstrated, and also that those values were highly sensitive to changes in cellularity. This increase in interstitial volume could be due to vasogenic edema or shifts of intracellular water to the extracellular space associated with tumor cell necrosis. This result demonstrates the relationship of tumor cellularity with interstitial volume and ADC values; a decrease in cellularity causes the increase in the interstitial volume and ADC values.

The present study has demonstrated the first use of a Logan plot in DCE-MRI, showing a strong correlation between tumor cell count and DCE-MRI derived interstitial volume and/or distribution volume estimated from two independent methods, SM and Logan analyses. The findings imply that the DCE-MRI estimated interstitial volume fraction and/or distribution volume can be used as a biomarker for tumor cellularity. They support not only the utility of DCE-MRI in assessing vascular permeability but also suggest that a measure of tumor cellularity is available for assessing and potentially classifying gliomas. Thus, DCE-MRI with appropriate model selection may be a useful tool for both the diagnosis and evaluation of therapeutic response in patients with gliomas.

Given that an estimate of V_D is available from the SM’s estimate of v_p+v_e, one might reasonably ask “why generate a Logan plot of V_D?” There are two arguments for the use of the Logan analysis. The first is that, in the event that a binding potential for a Gd-tagged agent that does bind to elements of the parenchyma (e.g. gadofosveset (27)) is needed, the operating characteristics of a compound that does not bind will be useful.

A second, and perhaps more relevant, support for Logan analysis when a nonbinding CA is an indicator is that the Logan estimate of V_D is likely to be more stable and less dependent on technique than that of the SM. In the SM, v_e is estimated from the ratio K^trans/k_ep, and is thus a derived parameter. Both of the parameters from which it is derived are rates: these cannot be estimated from equilibrium data, but must utilize those portions of the data that are dynamically changing with respect to the input function. Thus, when tissue in a DCE-MRI study is viewed as an input-response system, the response measures in the SM and the Logan graphical analysis fit much different portions of the response curves for their estimates of distribution volume, albeit they both require an integral of the input and response from time zero. In this presentation, it is gratifying that the two estimates are in good agreement, but we note the likelihood that SM estimates of distribution volume will be more dependent on high temporal resolution estimates of the input and tissue response function than will the Logan analysis. In support of this hypothesis, we note that, if the data of the example animal, with intrinsic 4 s time resolution, is binned into 12 s bins, the Logan estimate of V_D changes from 0.89 to 0.92, while the SM estimate changes from 0.11 to 0.17. However, since the operating characteristics of the Logan plot in DCE-MRI have not been explored, some caution should be exercised in assuming that it is less sensitive than the SM to temporal sampling rates.

We note also the evident deviation of the data from the straight-line extended Patlak fit in the early time points of Figure 4a (the extended Patlak approach is equivalent, as we have noted, to the SM). This is despite an excellent overall fit of the model to the data (R² = 0.992). Excellent fits of this nature are standard in this approach; in the 18 studies, the lowest R² in Model 3 grouped data was 0.972, and the group mean was 0.993. Nevertheless, for the summed data the fit is typically not perfect. As Figure 4a implies, there may be some additional systematic behavior in the first few minutes of tissue response that is not accounted for in the model.

The candidates for this systematic behavior are numerous. On the luminal side of the microvasculature, it may be that, in this particular animal, the radiological input function is not correct; it may be that the heterogeneity of the tumor in the Model 3 region changes the arrival time and shape of the input function across the regions of the tumor, and thus, while the radiological input function is approximately correct, the input function at the various tumor regions is not; in a related hypothesis, it may be that the dispersion of the arterial input function due to flow changes the input at the tissue level; it may be that restricted water exchange in the microvasculature of the tumor changes the apparent longitudinal relaxivity of the tissue in a concentration-dependent manner(28-30). In the tissue, it may be that transport of the CA takes place at a relatively high rate, thus draining the tissue of CA and violating the model, which requires that CA, once it extravasates, is reabsorbed in the vasculature of the same voxel. All of these possibilities are plausible, and in fact may all contribute to the behavior of the signal in varying amounts.

The two effects that most probably account for the early deviation of the data from the linearity of the extended Patlak plot are transvascular water exchange effects and/or dispersion of the AIF due to flow. Unfortunately, it may not be possible to distinguish between the two.

As to whether water exchange affects the Logan analysis results, Li et al (31) undertook a DCE-MRI study at 11.7T in a rat model of cerebral glioma, with sequence parameters similar to this study, and included water exchange in their modeling. The dose of CA used in their study (0.5 mmol/kg) was twice that of ours, but they concluded that, while transvascular water exchange was observable, producing a negative bias in the estimate of plasma volume, transcytolemmal water exchange was not observable. That is to say, extravasated contrast agent produced an approximately linear response in tissue ΔR₁. Recent modeling that incorporates a full three-compartment water exchange model (32) supports this conclusion; for the relatively low values of K^trans observed in cerebral glioma, transcytolemmal water exchange has little effect. Thus, in the portion of the curve to which the Logan plot applies, when the arterial concentration has decreased, and equilibrated with the extravascular concentration of contrast agent, water exchange effects are probably minimal. This tends to support the use of the Logan analysis in MRI, since it can eliminate one potential source of bias.