Examining the causes of memory strength variability: Recollection, attention failure, or encoding variability?

Abstract

A prominent finding in recognition memory is that studied items are associated with more variability in memory strength than new items. Here, we test three competing theories for why this occurs - the encoding variability, attention failure, and recollection accounts. Distinguishing amongst these theories is critical because each provides a fundamentally different account of the processes underlying recognition memory. The encoding variability and attention failure accounts propose that old item variance will be unaffected by retrieval manipulations because the processes producing this effect are ascribed to encoding. The recollection account predicts that both encoding and retrieval manipulations that preferentially affect recollection will affect memory variability. These contrasting predictions were tested by examining the effect of response speeding (Experiment 1), dividing attention at retrieval (Experiment 2), context reinstatement (Experiment 3), and increased test delay (Experiment 4) on recognition performance. The results of all four experiments confirmed the predictions of the recollection account, and were inconsistent with the encoding variability account. The evidence supporting the attention failure account was mixed, with two of the four experiments confirming the account and two disconfirming the account. These results indicate that encoding variability and attention failure are insufficient accounts of memory variance, and provide support for the recollection account. Several alternative theoretical accounts of the results are also considered.

A major focus of memory research is to identify the theory that provides the most comprehensive and parsimonious account of recognition memory. To this end, numerous single-and dual-process models have been developed to measure the processes believed to support recognition performance (e.g., Clark & Gronlund, 1996; DeCarlo, 2002; 2003; Malmberg, 2008; Ratcliff & Starns, 2009; Wixted 2007; Yonelinas, 1994, 2002) and many of these models have been developed within the framework provided by signal detection theory (Green & Swets, 1988; Macmillan & Creelman, 2005; for review, see Yonelinas & Parks, 2007). Signal detection approaches to recognition memory propose that each item on a memory test is associated with some amount of memory strength or evidence. The memory strengths for studied and new items are represented by two overlapping Gaussian distributions, with studied items on average having higher memory strengths than new items. Test items with a memory strength exceeding a criterion are endorsed as items that were studied (i.e., “old”) whereas items that fall below the criterion are identified as items that were not studied (i.e., “new”).

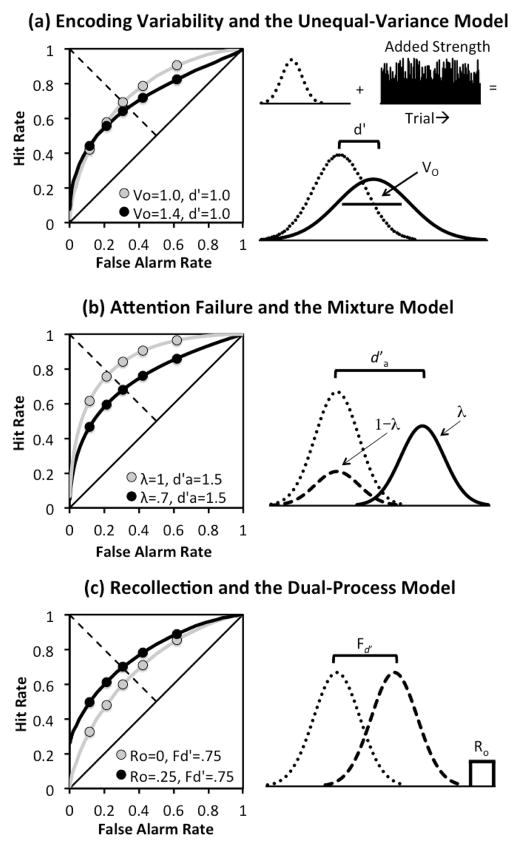
A ubiquitous finding arising from the recognition memory literature is that studied items are associated with not just greater memory strength compared to new items, but also with more variability in memory strengths (Ratcliff, Sheu, & Gronlund, 1992; Wixted, 2007; Yonelinas & Parks, 2007). We refer to this latter finding as the old item variance effect (Koen & Yonelinas, 2010). This effect is readily apparent in the asymmetry observed in receiver operating characteristic (ROC) curves – a plot of the hit rate against the false alarm rate across different levels of response bias (MacMillan & Creelman, 2005). Although several signal detection models have been developed to mathematically produce an increase in old item variance (for review, see Yonelinas & Parks, 2007), the psychological constructs that underlie this finding are not well understood. Our present goal is to critically test the predictions of three theoretical accounts (i.e., interpretations) of the old item variance effect (see Figure 1): (1) the encoding variability interpretation of the unequal-variance model (Wixted, 2007), (2) the attention failure interpretation of the mixture model (DeCarlo, 2002; 2003), and (3) the recollection interpretation of the dual-process model (Yonelinas, 1994, 1999). Below, we describe each theoretical account along with the mathematical models used to test its predictions.

Figure 1.

Receiver operating characteristic (ROC) curves and memory strength distributions related to the different accounts of memory variability. All models assume that new items are associated with some low level of memory strength which is normally distributed. (a) According to the encoding variability account old items are more variable than new items because of trial-to-trial variability in the amount of strength added to each item during encoding, which adds both strength (d′) and variability (V_o) to the old item distribution (right panel). (b) The attention failure account proposes that old items are more variable because the strength distribution reflects a mixture of two classes of items – items that were attended to at the time of encoding (λ) and have strength added (d′_a), and items that are not attended to (1 - λ) have no strength added (d′_na = 0). (c) The recollection account proposes that old items are more variable because the strength distribution reflects a mixture of items that are familiar (F_d′) and those that were recollected (R_o).

The Encoding Variability Account

Probably the most familiar signal detection model is the equal-variance model that underlies the common d′ index of discriminability (e.g., Macmillan & Creelman, 2005). The model assumes that old and new items are associated with Gaussian strength distributions of equal variability. This model is incompatible with the old item variance effects seen in recognition memory, but an extension of the equal-variance model, the unequal-variance signal detection model (Egan, 1958; Green & Swets, 1988; MacMillan & Creelman, 2005; Wixted, 2007), can produce the old item variance effect simply by including an additional parameter that measures the variance (i.e., standard deviation) of old items (V_o) relative to new items (Figure 1a).

Although the inclusion of the V_o parameter is useful in describing recognition data, little effort has been put forth to provide a theoretically meaningful interpretation of the V_o parameter. One possible interpretation is that V_o indexes the amount of trial-to-trial variability added to memory strength during encoding (Wixted, 2007); we refer to this as the encoding variability account (Figure 1a; Koen & Yonelinas, 2010; 2013). The addition of varying amounts of strength to items in a study list increases both the strength and variability of the old item distribution (cf., DeCarlo, 2010; Jang, Mickes, & Wixted, 2012).

Whether the encoding variability account provides a sufficient explanation of the old item variance effect is not yet clear because only one study has attempted to directly test it (Koen & Yonelinas, 2010). In that study, the amount of encoding variability during the study phase was experimentally manipulated by having participants complete two study and test phases. In the low encoding variability condition, participants studied each word at a constant presentation rate (2.5 s/item). However, in the high encoding variability condition, participants studied half the items for a long duration (4 s/item) and the other half for a short duration (1 s/item). Increasing encoding variability did not lead to the expected increase in old item variance, and in fact led to a slight decrease. Moreover, as described below, the results were found to confirm the predictions of an alternative account (i.e., the recollection account). These findings, however, were met with criticism (Jang et al., 2012; Starns, Rotello, & Ratcliff, 2012; for rebuttal, see Koen & Yonelinas, 2013), therefore additional evidence is warranted before it can be firmly concluded that the encoding variability account is insufficient.

Here, we further test the adequacy of the encoding variability account by examining how the V_o parameter behaves across different retrieval conditions. To the extent that trial-to-trial variability in the amount of strength added during the study phase is the only factor underlying increased old item variance, manipulating variables at retrieval should not affect estimates of V_o (derived from the unequal-variance model). However, finding that retrieval manipulations influence estimates of V_o will provide evidence that the encoding variability account is an insufficient explanation of the old item variance effect.

It is important to highlight that finding the encoding variability account to be an insufficient explanation of the old item variance effect would not imply that encoding variability has no influence on recognition performance. This result would indicate that encoding variability is not in itself a full explanation of the old item variance effect, but it does not rule out the possibility that it plays some role (see Koen & Yonelinas, 2013). Moreover, such a result has no bearing on other possible accounts of the old item variance effect that could be proposed within the framework of an unequal-variance model. That is, one could still maintain an unequal-variance signal detection model in which old item variance is explained by an additional process or alternative mechanism to encoding variability.

The Attention Failure Account

The mixture signal detection model proposes that old items are associated with more variability than new items because the old item distribution reflects a mixture of two latent types or classes of items (see Figure 1b; DeCarlo, 2002). When two equal-variance Gaussian distributions that differ in strength are mixed together, the resultant old item distribution will have increased variability in memory strengths (DeCarlo, 2002; 2003; 2010). The mixture model itself does not specify the source or mechanism behind the mixing that occurs in the old item distribution, but one theoretical account of this model proposes that fluctuations of attention during encoding lead to mixing (DeCarlo, 2002; 2003). That is, individuals may pay attention to some items but fail to attend to others, a proposal we refer to as the attention failure account. According to this hypothesis, the mixing parameter (λ) of the mixture model reflects the probability that an item is attended to during encoding. Items that are attended to have memory strength added to them (d′_a) whereas unattended items do not (d′_na = 0) (i.e., the distribution for unattended items is identical to the new item distribution). There are a number of studies that provide support for the attention failure account. For example, estimates of λ are increased by manipulations that are expected to increase the likelihood of attending to an item during encoding, such as increases in presentation frequency (DeCarlo, 2003; 2010), presentation duration, (DeCarlo, 2002; 2008), the length of the study list (DeCarlo, 2008), and the availability of attentional resources during encoding (e.g., full vs. divided attention; DeCarlo, 2010).

Nevertheless, very few attempts have been made to examine how the attention failure interpretation of the mixture model fairs across different retrieval conditions (but see Harlow & Donaldson, 2013). The experiments reported below critically test the attention failure account because this account predicts that estimates of λ will remain invariant across retrieval manipulations. Similar to the encoding variability hypothesis, this prediction rests on the assumption that increased old item variance is a result of factors at encoding (i.e. fluctuations of attention). Thus, finding differences in the λ parameter of the mixture model across different retrieval manipulations would indicate that an attention failure account is not sufficient to explain the old item variance effect.

Finding that the attention failure account is an insufficient explanation of the old item variance effect would not imply that attention failure does not sometimes occur during encoding, nor would it indicate that one could not develop another theoretical explanation of the old item variance effect using a mixture model. Rather, such a finding would only indicate that the attention failure account is not in itself a full explanation, and that the mixture model would need to incorporate either a different explanation of old item variance or add additional processes to accommodate the results.

The Recollection Account

The dual-process signal detection model proposes that recognition memory can be based on recollection of qualitative details about a studied event, or on assessments of familiarity (Yonelinas, 1994, 1999; for review, see Yonelinas, 2001a; 2002; Yonelinas et al., 2010). According to the dual-process model, recollection (R_o) occurs for some items but fails for others (i.e., the items fall below the recollective threshold; Yonelinas et al., 2010). When recollection occurs, it is associated with retrieval of specific contextual details about an event’s prior occurrence (Mandler, 1980; Tulving, 1985; Yonelinas, 2002). In contrast, familiarity (F_d′) is represented as an equal-variance signal detection process; studied items are more familiar than unstudied items, but are associated with the same amount of variability in memory strength (see Figure 1c; Yonelinas, 1994; 2002; Yonelinas & Parks, 2007). In tests of item recognition, the contribution of recollection is believed to cause old items to be more variable than new items because both recollection and familiarity contribute to recognition of studied items, whereas in most cases only familiarity contributes to memory judgments of new items. Thus, old items will have more variable memory strengths when the contribution of recollection is greater than zero. While there is considerable evidence that recollection and familiarity are functionally dissociable processes (Diana, Reder, Arndt, & Park, 2006; Kelley & Jacoby, 2000; Mandler, 1980; Rugg & Curran, 2007; Yonelinas, 2001a; 2002; Yonelinas et al., 2010), there is still debate surrounding the idea that a threshold recollection process is responsible for increases in memory variability (Jang et al., 2012; Koen & Yonelinas, 2010; 2013; Starns, Ratcliff, & McKoon, 2012; Starns, Rotello, & Ratcliff, 2012; Wixted, 2007; Yonelinas, 2001a; Yonelinas & Parks, 2007).

Evidence in support of the recollection account comes from a number of studies (for reviews, see Yonelinas, 2002; Yonelinas et al., 2010). For example, the Koen & Yonelinas (2010) study discussed above provided support for the recollection account by showing that the amount of old item variance measured from recognition memory ROCs was reliably predicted by estimates of recollection and familiarity derived from remember-know reports. Importantly, the unequal-variance model was unable to account for this observed relationship between confidence judgments and remember-know reports (Koen & Yonelinas, 2010; also see Yonelinas, 1994, 2001b). However, the veracity of these results have been questioned (Jang et al., 2012; Starns, Rotello, & Ratcliff, 2012; but see Koen & Yonelinas, 2013), and to our knowledge the predictions of the recollection account have not been pitted against the predictions of the attention failure account. Thus, direct tests of the adequacy of the recollection, attention failure, and encoding variability accounts are warranted.

One feature that differentiates the recollection account from the encoding variability and attention failure accounts is that it predicts that the old item variance effect should be influenced by both encoding and retrieval manipulations. That is, if greater old item variance is due to recollection, then any manipulation that selectively or disproportionality increases recollection should also increase old item variance. For this reason, we focused on examining the effects of several retrieval manipulations on recognition memory ROCs. Specifically, we targeted retrieval manipulations that are known to either selectively or preferentially influence recollection. If the recollection account is correct, we should find that these retrieval manipulations do impact the old item variance effect and more specifically they should affect the R_o parameter rather than the F_d′ parameter. Finding that the dual-process model’s parameters behave in a manner inconsistent with the predictions of the recollection account would suggest that the R_o and F_d′ parameters are not indexing recollection and familiarity, respectively. Such a finding would not necessarily indicate that recollection and familiarity do not contribute to recognition performance, nor would it rule out alternative interpretations of the dual-process model’s parameters, but it would indicate that recollection alone is not a sufficient account of old item variance.

Overview of the Present Experiments

Our present focus is to determine the viability of the encoding variability, attention failure, and recollection accounts when variables at retrieval that are thought to selectively or disproportionally affect recollection-based recognition are manipulated. To this end, we examined how speeding recognition responses (Experiment 1), dividing attention (Experiment 2), context reinstatement (Experiment 3), and test delay (Experiment 4) affect the parameter estimates of the unequal-variance, mixture, and dual-process models. Many studies have indicated that recollection is preferentially affected by speeded responding at test (e.g., Koen & Yonelinas, 2011; McElree, Dolan, & Jacoby, 1999; Yonelinas & Jacoby, 1994; 1996; but see Starns, Ratcliff, & McKoon, 2012), dividing attention during retrieval (e.g., Dodson & Johnson, 1996; Gruppuso, Lindsay, & Kelley, 1997; Skinner & Fernandes, 2008), and context reinstatement (e.g., Gruppuso, Lindsay, & Masson, 2007; Macken, 2002; Markopoulos, Rutherford, Cairns, & Green, 2010; but see Hockley, 2008). Similarly, although increasing study-test delay leads to decreases in both recollection and familiarity, it typically has a larger impact on recollection compared to familiarity (e.g., Brainerd, Wright, Reyna, & Mojardin, 2001; Brainerd, Reyna, & Estrada, 2006; Mandler, 1980; Yonelinas, 2002; but see Yonelinas & Levy, 2002, for effects of very brief delays on familiarity).

The encoding variability account predicts that these retrieval manipulations should influence the unequal-variance model estimates of d′, but not V_o. Similarly, the attention failure account predicts that the above retrieval manipulations will affect mixture model estimates of d′_a, but not λ. The predictions derived from the above accounts come about because they both ascribe the process hypothesized to cause the old item variance effect to encoding. In contrast, the recollection account predicts that these manipulations will impact the R_o parameter and leave F_d′ relatively unaffected (Experiments 1–3) or affect estimates of F_d′ less compared to estimates of R_o (Experiment 4).

To our knowledge, the effects of the above variables on recognition memory ROCs and on the parameter estimates of the unequal-variance, mixture, and dual-process models are unknown, so the current studies will provide novel empirical results. The one exception is with respect to the response speeding manipulation in Experiment 1. One previous study that examined ROCs in rodents (Sauvage, Beer, & Eichenbaum, 2010), and another that examined recognition ROCs in humans (Koen & Yonelinas, 2011) found that response speeding selectively reduced estimates of R_o. However, another study with humans found that response speeding led to a selective reduction in F_d′ (Starns, Ratcliff, & McKoon, 2012). These mixed findings indicate that additional empirical work examining the effect of speeded recognition on recognition ROCs is warranted.

Experiment 1: Self-Paced vs. Speeded Recognition Tests

In Experiment 1, we examined how speeding recognition memory responses affected recognition memory ROCs. After studying a long list of words, participants completed five old/new recognition memory tests under speeded or self-paced instructions. Response bias (i.e., the amount of points awarded for correct old and new responses) was varied across the five recognition tests (Koen & Yonelinas, 2011; see also Snodgrass & Corwin, 1988). Recognition memory ROCs were constructed by plotting the hit rate (i.e., correct ‘old’ judgments) on the y-axis and false alarm rate (i.e., incorrect ‘old’ judgments) on the x-axis for each recognition test.

Method

Participants and Design

Fifty-four participants completed this experiment for partial fulfillment of a course requirement at the University of California, Davis. The first 27 participants were given self-paced tests, and the remaining 27 were given speeded recognition tests¹.

Materials

Six-hundred words from the English Lexicon Project Database (Balota, Yap, Cortese, Hutchinson, Kessler, Loftis, et al., 2007) were used as stimuli. For each participant, 300 words were randomly selected to serve as study materials and the remaining 300 served as lures during the five test phases (60 old and 60 new words per test). An additional 48 words were selected to serve as primacy buffers (12 words), recency buffers (12 words), and lures on the six practice tests (24 words). The primacy and recency buffers served as the old items on the practice test phases. Each of the six practice tests contained four old words (two primacy and two recency items) and four new words. The stimuli in this and all other experiments were presented using E-Prime v1.2 software (www.pstnet.com).

Procedure

After informed consent, participants were presented with a list of 300 words presented for 1500 ms followed by a 500 ms inter-trial-interval (ITI), and were required to make an abstract/concrete judgment about each word while it was on the screen. A brief 1 min math filler task of basic addition, subtraction, and multiplication was completed following the study phase.

Next, participants completed five recognition memory tests in which they were presented with a mixture of 60 studied words and 60 new words and instructed to identify previously studied words as ‘old’ and words that were not studied as ‘new’. The five tests, whose presentation order was randomized for each participant, differed with respect to response bias manipulations (for a full description of each response bias test, see Koen & Yonelinas, 2011). Response bias was manipulated using a payoff matrix such that the amount of points awarded for a correct response and the amount of points lost for an incorrect response varied for old and new items across the five test phases. For example, on the most conservative test, 1 and 10 points were awarded for correct old and new responses, respectively, whereas 10 and 1 points were deducted for incorrect old and new responses, respectively. In contrast, the most liberal response bias test reversed the point structure of the most conservative test (e.g., 10 and 1 points awarded for correct old and new responses, respectively). Two of the remaining tests manipulated bias in a similar manner but awarded or deducted 5 points instead of 10. The remaining test was a neutral bias test such that 1 point was awarded for correct responses whereas 1 point was deducted for incorrect responses. Each test was preceded by a practice phase where participants received trial-by-trial feedback to ensure that they understood the point structure for correct and incorrect old and new responses. Trial-by-trial feedback was not included in the critical test phases, but participants were informed of the amount of points they earned following at the end of each test phase. After completing the experiment, participants were debriefed and thanked for their participation.

Participants in the self-paced condition were given an unlimited amount of time to respond whereas participants in the speeded condition were only given 1500 ms to enter their response before a buzzer sounded. If the buzzer sounded, participants were instructed to enter their response quickly to move on to the next trial. After a response was entered, the current trial disappeared and was replaced with a 500 ms ITI before the next trial.

Results and Discussion

In all of the experiments, the parameters of the unequal-variance, mixture, and dual-process signal detection models were estimated using maximum likelihood estimation. All results were considered significant at p < .05. Cohen’s d (Cohen, 1988) estimates are provided for each statistical test.

Overall Recognition Accuracy

The hit rate and false alarm rates were determined by the proportion of ‘old’ responses to studied and new items, respectively, across all five tests (see Table 1). As expected, overall recognition accuracy (measured as d′) was significantly lower for participants in the speeded recognition test compared to participants in the self-paced test, t(52) = 3.03, p < .01, d = .83.

Table 1.

Average hit rates, false alarm rates, and d′ estimates for Experiments 1–4.

	Hit Rate	False Alarm rate	d′
Experiment 1
Self-Paced	.78 (.02)	.33 (.02)	1.27 (.07)
Speeded	.72 (.02)	.38 (.02)	.94 (.08)
Experiment 2
Full Attention	.76 (.01)	.25 (.01)	1.47 (.06)
Divided Attention	.75 (.02)	.32 (.02)	1.24 (.05)
Experiment 3
Same Context	.71 (.02)	.25 (.02)	1.29 (.09)
Different Context	.60 (.03)	-	1.00 (.09)
Experiment 4
Immediate	.77 (.02)	.37 (.02)	1.18 (.06)
24-hr Delayed	.63 (.02)	.42 (.02)	.57 (.04)

Note. Standard errors of the mean are provided in parentheses. The false alarm rates for same and different context items in Experiment 3 are identical because there was only one group of new items. The self-paced data in Experiment 1 were previously published in Koen & Yonelinas (2011).

Recognition ROCs

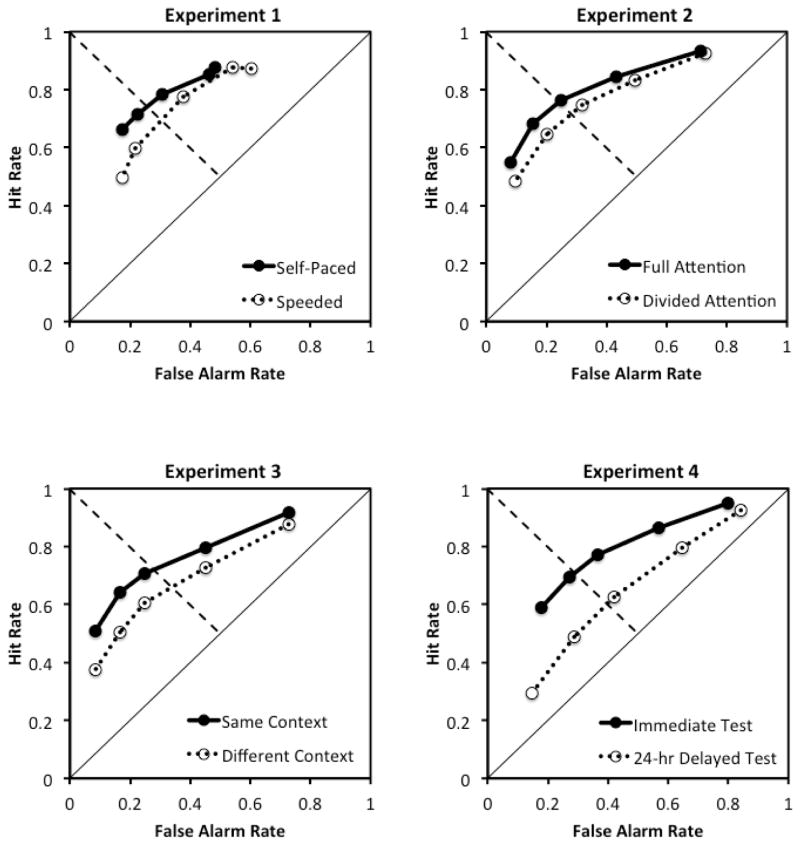
The aggregate ROCs are plotted in Figure 2a, and mean parameter estimates for the unequal-variance, mixture, and dual-process models are shown in Figure 3. The results were inconsistent with the predictions of the encoding variability account. Specifically, speeding recognition responses at retrieval significantly reduced estimates of d′[t(52) = 3.30, p < .01, d = .90], and, most importantly, estimates of V_o [t(52) = 2.22, p < .05, d = .61]. The effect of speeded responses on V_o is problematic because this parameter is assumed to reflect an encoding process rather than a retrieval process. In contrast, the results were consistent with the predictions of the attention failure account. Speeding recognition responses significantly reduced estimates of d′_a [t(52) = 2.80, p < .01, d = .76], but had no effect on estimates of λ [t(52) = .21, p = .83, d = .06] which is consistent with the assumption that attention failure at encoding was not impacted by the manipulation of response speeding at retrieval. Additionally, the results were consistent with the predictions of the recollection account, as speeding recognition responses significantly reduced estimates of R_o [t(52) = 3.64, p < .001, d = .99], which was expected because recollection is a relatively slow retrieval process, but had no effect on estimates of F_d′ [t(52) = .74, p = .46, d = .20].

Figure 2.

The aggregate ROCs for the self-paced and speeded conditions (Experiment 1, top left), the full and divided attention conditions at retrieval (Experiment 2, top right), same and different context items (Experiment 3, bottom left), and the immediate and 24-hr delayed tests (Experiment 4, bottom right). Note that the ROCs for the self-paced condition in Experiment 1 were initially reported in Koen & Yonelinas (2011).

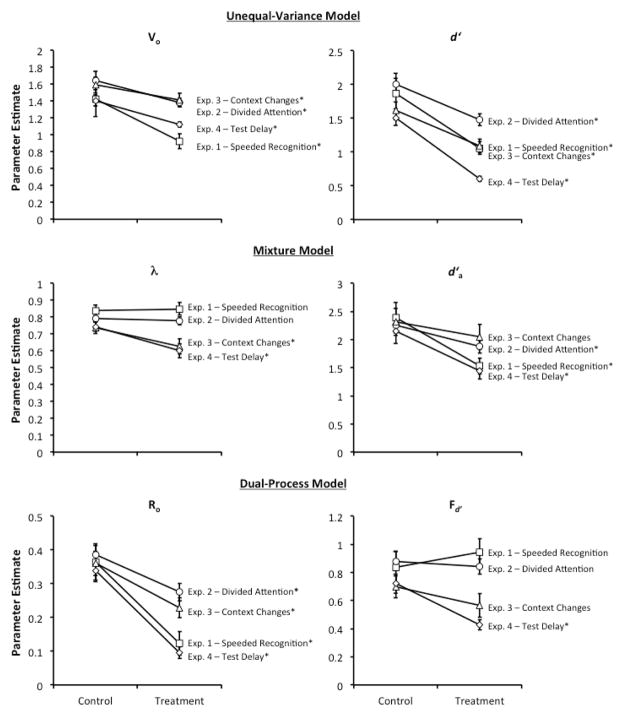
Figure 3.

Average parameter estimates for the unequal-variance, mixture, and dual-process model in Experiments 1–4. The control condition refers to the parameter estimates for the self-paced group (Experiment 1, squares), the full attention condition (Experiment 2, circles), the same context items (Experiment 3, triangles), and the immediate test (Experiment 4, diamonds). The treatment condition refers to the parameter estimates for the speeded group, the divided attention condition, the different context items, and the 24-hr delayed test for Experiments 1–4, respectively. An * next to the experiment label indicates that the difference between the control and treatment conditions were significantly different at p < .05. Note that the R_o and F_d′ estimates for the self-paced data were initially reported in Koen & Yonelinas (2011).

In addition, the current finding that response speeding disrupts estimates of R_o more than F_d′ converges with the results of two prior studies using ROCs to examine speeded recognition (Koen & Yonelinas, 2011; Sauvage et al., 2010). However, these results are inconsistent with results from a study by Starns, Ratcliff, and McKoon (2012; see also Ratcliff & Starns, 2009) which suggested that response speeding reduced estimates of F_d′, not R_o. It is not clear why the Starns, Ratcliff, and McKoon (2012) study demonstrated divergent results, but the differences could be due the limited number of subjects examined in that study (i.e., N=4), differences in how response bias was manipulated (i.e., they used a proportion old manipulation to manipulate response bias), or because they more heavily emphasized response speed in their speeded recognition condition. Future work directly comparing these methodological differences may clarify the differences across studies.

In summary, the results provide support for the predictions of both the attention failure account (i.e., speeding responses did not reduce the λ parameter, as expected if it reflected an attention process at encoding), and the recollection account (i.e., speeding responses reduced the R_o but not the F_d′ parameter, as expected if R_o indexes recollection-based recognition). In contrast, the results were not consistent with the encoding variability account because speeding responses during the time of retrieval decreased the V_o parameter. This indicates that V_o cannot be explained solely as arising from trial-to-trial variability in the amount of strength added to trials during encoding.

Experiment 2: Full vs. Divided Attention Recognition Tests

Experiment 2 investigated how divided attention during retrieval affected recognition memory ROCs. Participants completed a study phase followed by four test phases. Two recognition tests were completed under full attention whereas the remaining two tests were completed during a concurrent tone-monitoring task (i.e., divided attention). Participants entered their old and new responses using a 6-point confidence scale (6 = sure old, 1 = sure new), and recognition ROCs were constructed based on the confidence responses (for review, see Yonelinas & Parks, 2007). The first (i.e., left-most) point of the ROC is the proportion of old (y-axis) and new (x-axis) items receiving a “6” response, the next point is the proportion of old and new items receiving a “6” or a “5” response, and so on.

Method

Participants

Fifty-one participants from the University of California, Davis participated in this experiment either individually or in groups of two or three for partial fulfillment of a course requirement. Data from three participants were excluded from the analysis for failure to follow instructions. The results reported below are based on data from the remaining 48 participants.

Materials

The materials comprised 400 words from the MRC Psycholinguistic Database (Coltheart, 1981). Two hundred words were randomly selected as the study items for each participant with the remaining 200 words serving as the new items on the recognition test. These materials were used to make four test lists (two full attention tests and two divided attention tests) each containing 50 studied and 50 new words. The words were randomly assigned to these lists. An additional 16 words were selected to serve as primacy buffers (4 words), recency buffers (4 words), and lures on the four practice tests (8 words). The primacy and recency buffers served as the old items on the practice test phases. Each of the practice tests contained two old words (a primacy and recency buffer) and two new words.

Two tones (100 Hz and 145 Hz) were selected and simultaneously presented with the words on both the full and divided attention tests. The 100 Hz tone was presented with half of the old and new trials on each recognition test, and the 145 Hz tone was presented on the remaining test trials.

Procedure

In the study phase, participants were instructed that they would be presented with a list of words to study for subsequent memory tests. Each word was presented for 1.5 s, and there was a 500 ms fixation cross between words. To encourage effective encoding, participants made an abstract/concrete judgment for each study word. Next, participants completed a series of math problems, which served as a filler task. For the filler task, participants were instructed that they would have five minutes to reduce as many polynomial equations as possible. If a participant finished early, they were instructed to sit and wait quietly for remaining time.

After the filler task, participants were told that their memory for the words in the study phase would be tested across four different test phases, and that each test phase would be preceded by a practice. Two of the tests were full attention tests and two were divided attention tests, and these were counterbalanced using an ABBA scheme. On each test, participants were instructed to identify previously studied words as ‘old’ and words they did not study (i.e., lure words) as ‘new’ using a 6-point confidence scale (1-sure new, 2-maybe new, 3-guess new, 4 guess old, 5-maybe old, 6-sure old). Participants were informed of the importance of using the full range of responses so that they accurately reported how confident they were that each test word was old or new.

On the divided attention test, participants were required to make memory judgments while listening for a target tone. The target tone was determined before each test phase and counterbalanced across the two divided attention tests (e.g., the 100 Hz tone was the target tone on the first and second divided attention tests an equal number of times across participants). Both tones served as the target tone on one divided attention test for each participant. Participants were instructed that they needed to listen for this tone throughout the course of the test phase because they would be asked to indicate whenever it occurred.

During each divided attention test trial, an old or new word was presented in conjunction with a 100 Hz or 145 Hz tone for 500ms. Participants were then given 1.5 s to enter their memory response using the 6-point confidence scale, followed by a 1 s window to enter their target tone detection response. If the tone presented with the word was the target tone, participants made a ‘yes’ response by pressing ‘a’ on the keyboard. If it was not the target tone, they made a ‘no’ response by pressing ‘s’ on the keyboard. There was a 500 ms ITI before the next trial began.

The procedure for the full attention test phases was nearly identical to the divided attention test phase, with two exceptions: (1) participants were instructed that the tone presented with a test word was not relevant (i.e., a target tone was not specified), and (2) there was no prompt to enter a response regarding the tone (i.e., after the memory response judgment, the test phase moved directly to the next trial with only a 500 ms fixation cross).

Results and Discussion

Target Tone Detection Performance

Responses for the target tone detection task that were not entered within the allotted time were not logged and thus unavailable for analysis. The proportion of missed tone responses occurred on approximately a tenth of the trials [M = .12, SE = .03]. Accuracy [M = .72, SE = .02] on the target tone detection task – defined as the proportion of correct responses conditional on a response being given – was significantly above chance [t(47) = 9.68, p < .001].

Missed Recognition Responses

As with the tone judgments described above, responses to the memory probes that were not made in the allotted time were not logged and thus not included in the analysis. A 2 (test condition: divided or full attention) by 2 (item type: old or new) repeated measures ANOVA revealed no difference in the rate of missed responses between old and new items and no interaction between test condition and item type, Fs < 1. Not surprisingly, there were significantly more missed recognition responses on the divided attention test [M = .03, SE = .005] compared to the full attention test [M = .01, SE = .005; F(1,47) = 8.72, MS_e = .002, p < .005, η_p² = .16]. We did not expect the difference in the number of missed recognition responses to significantly alter the results because they occurred rather infrequently [M = .02, SE = .003].

Overall Recognition Accuracy

The hit rate and false alarm rates were determined by the proportion of 6, 5, and 4 responses given to old and new items, respectively (see Table 1). Overall recognition accuracy (measured with d′) was significantly lower on the divided attention test compared to the full attention test [t(47) = 4.79, p < .001, d = .57].

Recognition ROCs

The aggregate ROCs are plotted in Figure 2b and the mean parameter estimates are presented in Figure 3. The parameters of the unequal-variance model behaved in a manner inconsistent with the predictions of the encoding variability account as dividing attention during retrieval significantly reduced estimates of both V_o [t(47) = 2.55, p < .05, d = .45], and d′ [t(47) = 4.04, p < .001, d = .60]. Consistent with the attention failure account, dividing attention had no effect on mixture model estimates of λ [t(47) = .48, p = .64, d = .07], but significantly reduced estimates of d′_a [t(47) = 3.26, p < .01, d = .51]. Likewise, dividing attention at retrieval significantly reduced dual-process model estimates of R_o [t(47) = 3.62, p < .001, d = .57], but not F_d′ [t(47) = .60, p = .55, d = .09].

These results replicate the pattern of data observed in Experiment 1, and further suggest that the attention failure and recollection accounts are viable interpretations of the old item variance effect (i.e., dividing attention at time of test did not affect the parameter of the mixture model believed to reflect attention during encoding, and did reduce the recollection parameter of the dual-process model), whereas the encoding variability account is not a sufficient theoretical account (i.e., dividing attention at time of test influenced the V_o parameter indicating that it is not determined entirely by encoding variability).

Experiment 3: Same vs. Different Contexts

In this experiment we investigated how context shifts during retrieval affected recognition memory ROCs. After studying a list of object-scene pairs, participants were tested on their recognition memory for the objects. At test, half of the studied objects were paired with the same scene (same context trials) whereas the other half were paired with a scene presented with a different object during the study phase (different context trials). ROCs were constructed in a similar fashion to Experiment 2.

Method

Participants

Twenty-five undergraduates from the University of California, Davis participated in this study either individually or in groups of two or three for partial fulfillment of a course requirement. One participant’s data was discarded for failure to follow instructions. The results reported below are based on the data from the remaining 24 participants.

Materials

The materials consisted of 240 line drawings of nameable objects on a white background and 240 scenes. The objects were randomly paired with a scene, and the resultant pairs were divided into four groups of 60 pairs for counterbalancing. For the purpose of describing the counterbalancing scheme, the four groups are referred to with the letters A–D.

The study list consisted of 180 pairs from three groups (e.g., groups A, B, and C) and the presentation order of the trials was randomized for each participant. The test list also contained 180 pairs. Of the 180 object-scene pairs on the test list, 60 objects were paired with the same scenes they were presented with during the study phase (same context trials), 60 objects paired with different studied scenes (different context trials), and 60 objects were new and paired with scenes presented in the study phase (new trials). Same context trials consisted of re-presenting the object-scene pair from the study phase during the test phase (e.g., group A pairs). Different context trials were created by randomly pairing the objects from the group B pairs with scenes from the group C pairs. Lastly, new trials were created by combining objects from group D, which were not presented during the study phase, with the scenes from group B. Thus, the objects from group C, which were studied, did not appear in the test phase, and the scenes from group D were not presented at all during the course of the experiment. The four groups of object-scene pairs were rotated through four counterbalancing conditions such that each object and scene appeared in all conditions an equal number of times across participants. An additional eight object-scene pairs served as primacy and recency buffers in the study phase.

Design and Procedure

After informed consent, participants were told that there would be three phases in the experiment. In the study phase, participants encoded a series of object-scene pairs for a subsequent test with the object superimposed over the center of each scene. Each trial was presented for 800 ms, followed by a 200 ms ITI. While studying the pairs, participants were instructed to judge if the object was likely to be found in the scene by making a “yes” or “no” response. This was done to ensure the participants integrated the object and scene (e.g., Gruppuso et al., 2007). After the study phase, participants were allotted ten minutes to complete the same filler task that was used in Experiment 2.

Finally, the participants completed the recognition test phase. Participants were informed that their memory for the objects would be tested, and not their memory for the scenes. Furthermore, they were told that all of the background scenes presented in the test phase would be scenes that were presented during the study phase, whereas some of the objects would be old and others would be new. Participants were instructed to provide their old and new memory responses using a 6-point confidence scale with the same instructions used in Experiment 2.

Results and Discussion

Overall Recognition Performance

As expected, overall recognition accuracy, measured with d′, was significantly higher for same compared to different context items [t(23) = 5.84, p < .001, d = 0.67; see Table 1].

Recognition ROCs

Figure 2c plots the aggregate ROCs, and Figure 3 presents the mean parameter estimates. Note that in fitting each model to the observed ROCs, an equality constraint was placed on the criterion parameters for the same and different context items because there was only one class of new items.

Similar to Experiments 1 and 2, the parameters of the unequal-variance model did not behave in accordance with the predictions of the encoding variability account. Specifically, estimates of V_o were significantly lower for different context trials compared to same context trials [t(23) = 2.09, p < .05, d = .42]. The same pattern was also observed for estimates of d′ [t(23) = 7.79, p < .001, d = .90]. In contrast to the previous experiments, context shifts caused the mixture model’s parameters to behave in a manner inconsistent with the attention failure account. Specifically, estimates of λ were significantly higher for same, compared to different, context trials [t(23) = 3.16, p < .01, d = .56]. Estimates of d′_a were not significantly different between same and different context trials [t(23) = .91, p = .37, d = .23]. The results were once again consistent with the recollection account’s interpretation of the dual-process model’s parameters. Estimates of F_d′ were not significantly different for the same and different context items [t(23) = 1.54, p = .14, d = .33], whereas estimates of R_o were significantly higher for same compared to different context items [t(23) = 4.66, p < .001, d = .82].

In sum, these current results are consistent with the previous two experiments in providing evidence consistent with the recollection account’s interpretation of the dual-process signal detection model. Likewise, the data reported up to this point have indicated that the encoding variability account does not provide an adequate explanation of the unequal-variance model’s parameters. Unlike the previous two experiments, the parameters of the mixture model in the current study behaved in a manner inconsistent with the predictions of the attention failure account.

Experiment 4: Immediate vs. Delayed Tests

This final experiment examined how recognition memory is affected by a 24-hr test delay. During the first session, participants studied a list of words and completed an immediate recognition test for half of the studied items. Participants returned 24-hrs later to complete a second, delayed recognition test for the other half of the studied items. Recognition ROCs were constructed in a manner similar to Experiments 2 and 3.

Method

Participants

Fifty-three undergraduates from the University of California, Davis participated in this experiment either individually, or in groups of two or three for partial fulfillment of a course requirement. Data from five participants were excluded because of a failure to show up for the second session (n = 3), a computer malfunction (n = 1), or a failure to follow instructions (n = 1). Data from the remaining 48 participants were included in the results reported below.

Materials

The materials in this experiment consisted of 600 words from the MRC Psycholinguistic Database (Coltheart, 1981). The words were divided into four groups of 150 for counterbalancing purposes. The study list comprised two groups of words, as well as an additional eight primacy and eight recency buffers, which were not tested. The items on the immediate test consisted of one group of 150 studied words and one group of 150 lure words. The remaining studied and new word groups served as test probes on the delayed test. Thus, there was no overlap in the items appearing on the immediate and delayed recognition tests. The word groups were counterbalanced such that each word served as an old and new word on the immediate and delayed tests an equal number of times across participants.

Design and Procedure

There were four phases in the experiment: (1) study phase, (2) filler task, (3) immediate test, and (4) 24-hour delayed test. The experiment was completed across two sessions, with the study phase, filler task, and immediate test occurring in the first session and the delayed test occurring in the second session. In the study phase, participants were presented with a list of words to study for later memory tests. Each word was presented for 1.5 s, followed by a 250 ms ITI, and participants made an abstract/concrete judgment on each word. Next, participants were allotted 10 minutes to complete the same filler task used in Experiments 2 and 3.

Participants then completed the immediate test and, upon returning for the second session, completed the delayed test. The order of old and new words was randomized on both tests. Participants made their old and new decisions using a 6-point confidence scale, and were given the same instructions used in the preceding experiments. After a response was entered, there was a 250 ms ITI before the next word appeared. Before the delayed test phase, participants were informed that none of the words on the prior test would appear on the delayed test.

Results and Discussion

Overall Recognition Performance

Overall recognition accuracy, measured with d′, was significantly lower on the delayed recognition test compared to the immediate test [t(47) = 12.52, p < .001, d = 1.67; see Table 1].

Recognition ROCs

The aggregate ROCs and the average parameter estimates are plotted in Figure 2d and 3, respectively. Consistent with the previous three experiments, these results were inconsistent with the encoding variability account. Estimates of both V_o [t(47) = 4.09, p < .001, d = .81], and d′ [t(47) = 9.89, p < .001, d = 1.62] were significantly lower on the delayed test compared to the immediate test. In addition, similar to Experiment 3, the parameters of the mixture model behaved in a manner inconsistent with the attention failure account. Delaying the recognition test significantly reduced estimates of λ [t(47) = 3.59, p < .001, d = .59], and d′_a [t(47) = 3.97, p < .001, d = .55]. Finally, the recognition results were consistent with the recollection account. First, estimates of both R_o [t(47) = 8.25, p < .001, d = 1.50], and F_d′ [t(47) = 5.02, p < .001, d = .77] were significantly lower on the 24-hr delayed recognition test. An examination of the effect sizes revealed that the effect of a 24-hr test delay was approximately twice as large on estimates of R_o compared to estimates of F_d′.

The data presented in the current study are similar to those of the prior experiment in showing that the encoding variability and attention failure accounts are insufficient explanations of the unequal-variance and mixture model’s parameters, respectively. However, the results from this experiment converge with those of Experiments 1–3 in that they provide additional support for the recollection account’s interpretation of the dual-process model’s parameters.

Assessment of Model Fit

Before discussing the implications of the results from Experiments 1–4, it is useful to examine how well the unequal-variance, mixture, and dual-process models fit the data. Measures of model fit for each experiment are shown in Table 2, and the aggregate response frequencies are included in the Appendix. The model fits in our experiments were in line with previous recognition memory studies of this type (for review, see Yonelinas & Parks, 2007). Each of the three models provided a statistically acceptable account of the data for the majority of participants. That is, the unequal-variance, mixture, and dual-process signal detection models provided an acceptable fit (i.e., not statistically rejected at p < .05 based on the G statistic) for 89%, 86%, and 83% of the participants, respectively. Note that the summed G values for each model were statistically significant for almost every experiment, which indicates that the models did deviate significantly from the data. This, however, is expected given a substantial amount of statistical power (e.g., Jang, Wixted, & Huber, 2011). In addition, as shown previously, there was considerable variability in which model provided the best fit across participants (e.g., Jang et al., 2011; Kapucu, Macmillan, & Rotello, 2010). Specifically, 40% of the 174 participants across all experiments were best fit (i.e., lowest G value) by the unequal-variance model, 29% by the mixture model, and 31% by the dual-process model.

Table 2.

Goodness of fit measures for the unequal-variance, dual-process, and mixture signal detection models in Experiments 1–4.

	Exp. 1	Exp. 2	Exp. 3	Exp. 4
Unequal-Variance
G	229.63 (p < .001)	362.36 (p < .01)	171.72 (p = .06)	331.56 (p < .05)
% Best Fit	46%	40%	25%	39%
% Rejected	13%	15%	4%	8%
Mixture
G	320.70 (p < .001)	359.09 (p < .01)	162.25 (p = .14)	353.04 (p < .01)
% Best Fit	28%	35%	42%	19%
% Rejected	19%	15%	4%	13%
Dual-Process
G	327.80 (p < .001)	435.97 (p < .001)	180.53 (p < .05)	355.31 (p < .01)
% Best Fit	26%	25%	33%	42%
% Rejected	17%	23%	8%	17%

Note. The degrees of freedom for Experiments 1–4 are 162, 288, 244, and 288, respectively. The G values are based on sum of G across all participants within an experiment, with the p value in parentheses. Note that a significant G value indicates that the null hypothesis that the model produced the observed data is rejected. The % best fit represents the number of participants that were best fit by a model based on the lowest G value of the three models. The % rejected reflects the number of times a model was rejected across all participants in the experiment, and was based on a G value greater than a critical G with 6 degrees of freedom at p < .05.

One must be cautious in using the goodness of fit measures provided in Table 2 to determine which model provides the best account of the data because these models typically all provide very good fits to the observed ROC data (Yonelinas & Parks, 2007), and because these measures do not take into account differences in the complexity of a model’s functional form (i.e., how the parameters are combined in the equation; Pitt & Myung, 2002). Models with the same number of parameters can still differ in complexity, which can result in the model over-fitting the data (Pitt & Myung, 2002). Recent evidence has shown that the unequal-variance model has a more complex functional form than the mixture and dual-process models (Kellen & Klauer, 2011; Klauer & Kellen, 2011; for related findings, see Jang et al., 2011). Thus, it is possible that the “best fitting model” based on the fit statistics reported in Table 2 are influenced by model complexity. For example, the largest difference in model fit was observed in Experiment 1, where the unequal-variance model performed considerably better than the other two models. A substantial portion of this difference was due to the unequal-variance model’s ability to fit a somewhat unusual participant ROC more adequately than the other two models. This participant’s ROC had one point that was far below chance (i.e., the hit rate was lower than the false alarm rate), whereas the other ROC points were well above chance. The unequal-variance model was able to account for this ROC very well compared to the mixture and dual-process models. Specifically, G was 6.18, 62.94, and 62.94 for the unequal-variance, mixture, and dual-process models, respectively.

General Discussion

The goal of the present investigation was to test the validity of the encoding variability, attention failure, and recollection accounts of the old item variance effect, based on the unequal-variance, mixture, and dual-process models, respectively. Although each theoretical account can explain changes in variance produced by encoding manipulations, only the recollection account predicts that retrieval manipulations should also play a critical role in determining old item variance. To test these conflicting predictions, we examined old item variance across four retrieval manipulations: response speeding (Experiment 1), dividing attention (Experiment 2), context reinstatement (Experiment 3), and delaying the recognition test (Experiment 4).

The results from all four experiments provided evidence against the encoding variability account. That is, in every experiment the retrieval manipulation led to significant changes in estimates of old item variance (i.e., the V_o parameter of the unequal-variance model). If old item variance reflects encoding variability alone, then V_o should not have been sensitive to retrieval manipulations. In contrast, the attention failure account was consistent with the results from Experiments 1 and 2. Speeding recognition responses and dividing attention during recognition selectively affected mixture model estimates of d′_a, not estimates of λ. This makes good sense given that attention during encoding should not be affected by manipulations that occur during retrieval. The results from Experiments 3 and 4, however, were inconsistent with the attention failure account. Specifically, changing contextual details during retrieval (Experiment 3) and delaying the test phase (Experiment 4) significantly decreased estimates of λ (also see Harlow & Donaldson, 2013). This finding should not occur if this parameter reflects the probability of attending to an item during encoding.

In contrast to the encoding variability and attention failure accounts, the results from all four experiments were consistent with the predictions of the recollection account. Speeding recognition responses, dividing attention, and changing the contextual details all led to decreases in dual-process model estimates of R_o with little or no change in F_d′. In addition, delaying the test phase for approximately 24-hrs was expected to have a larger impact on recollection than familiarity; this prediction was also supported by the current results. These predictions about ROC estimates of R_o and F_d were based on existing dual-process theories of recognition memory, and empirical results from studies using remember/know and process dissociation methods (for review, see Yonelinas, 2002).

The results provide clear evidence in support of the recollection account and show that the encoding variability and attention accounts are insufficient. Nonetheless, it is important to reiterate that these results do not demonstrate that encoding variability or attention failure do not influence recognition memory. We assume that these phenomena must occur to some extent. What the current results do show, however, is that these two psychological processes in themselves are inadequate explanations of the old item variance effect that is observed in studies of recognition memory. Therefore, there must be something more than encoding variability or attention failure that is needed to account for the existing results. Our view is that this ‘something else’ is recollection. That is, many retrieval manipulations have been shown to disproportionately influence recollection. Thus, from the viewpoint of the recollection account, it should be no surprise that retrieval manipulations will impact the old item variance effect. In fact, as we have shown here, the literature on recollection and familiarity provides a very useful guide in predicting how experimental manipulations will affect the ROC parameter estimates derived from the dual-process signal detection model, and in turn, old item variance.

Alternative accounts of old item variance

Although the old item variance effect cannot be sufficiently explained by either the encoding variability or the attention failure accounts, this does not indicate that the unequal-variance and mixture models are incorrect characterizations of recognition memory. Thus, it is useful to ask how one might try to explain the old item variance effect using these two models, given that we now know that encoding variability and attention failure notions are insufficient.

Within the unequal-variance signal detection model, what process other than encoding variability could be influencing old item variance? One possibility is that an additional process that occurs during the retention interval might counteract the increase in old item variance that is caused by encoding variability. For example, strong items from the old item distribution might be forgotten more quickly over a retention interval compared to weak items. The differential forgetting rates of strong and weak items could thus result in reduced measures of old item variance after a delay than in an immediate test. This approach might account for the delay effects seen in Experiment 4, but it is not readily evident how it could account for the results from the other three experiments. It may be the case, however, that another post-encoding process, such as how well the test probe is encoded or attended to, could account for the observed results. This is discussed more thoroughly in the context of the mixture model.

A second alternative is that there may be two different signal detection processes that are summed together to produce a single old item memory strength value (Ingram, Mickes, & Wixted, 2012; Wixted & Mickes, 2010). If the two old item signals are summed together, their variance should be greater than that of the new items. Moreover, if the two signals were functionally dissociable, like recollection and familiarity, then it is possible that memory strength and old item variance may be experimentally separable, in line with the empirical ROC literature (see Yonelinas & Parks, 2007).

Whether these theoretical alternatives would be able to account for recognition ROCs is unknown. In either case, a challenge for any theory based on a pure signal-detection model is that results from ROC (e.g., Yonelinas, 1999), second-choice (Parks & Yonelinas, 2009), and memory precision (Harlow & Donaldon, 2013) studies of associative and source memory converge in showing the need to incorporate some type of memory threshold or mixture to account for recognition data.

Within the mixture model, what process other than attention failure could be determining old item variance? One possibility is that it may be necessary to relax the assumption that attention at encoding can fail entirely. That is, perhaps in the two experiments that were problematic for the attention failure account (i.e., the context reinstatement and test delay experiments), the unattended items were not completely unattended (i.e., d′_na = 0), but rather were only very poorly attended (i.e., d′_a > d′_na > 0). In order to test this, we refit the mixture model to the data while allowing the strength of unattended items to be estimated (i.e., d′_na). Critically, the results with respect to estimates of λ were unchanged by this modification. Thus, allowing variation in the memory strength of unattended or poorly attended items does not overcome the shortcomings of the attention failure account.

Another extension of the attention failure account is to propose that fluctuations of attention occur during both encoding and retrieval. This could manifest itself in such a way that the diagnostic features initially encoded are not attended to during retrieval, and such an event would likely result in a failure to reinstate an encoded memory (e.g., Nairne, 2002). While this modification to the attention failure account may prove useful in future studies, there are some concerns that will need to be addressed. First, it is unclear if this modification can simultaneously account for our findings that λ can be reduced by some retrieval manipulations (e.g., context shifts and delayed testing, Experiments 3 and 4, respectively), but not by others (e.g., speeded recognition and divided attention during retrieval, Experiments 1 and 2, respectively). Second, whether such a model would allow one to separate the two attentional processes from ROC data is unclear. It will be important to investigate this possibility in future studies.

One final possibility is to apply the recollection account to the mixture model, as proposed by Onyper, Zhang, and Howard (2010). Indeed, the dual-process signal-detection model is a simplified version of a more complex mixture model (cf., DeCarlo, 2007). According to Onyper et al. (2010), the λ parameter reflects the probability that an item is recollected. Recollected items are associated with a Gaussian distribution of memory strengths, as are items that are not recollected (i.e., items whose recognition is based on familiarity). Although this account is a very plausible alternative explanation of the mixture model’s parameters, it is unclear if recollection needs to be modeled as a Gaussian distribution under all conditions, or under very specific circumstances. This issue is discussed in more detail below.

Future developments of the dual-process model

The results from all four experiments join a growing body of literature supporting the recollection account’s proposal that the R_o and F_d′ parameters of the dual-process model index the contribution of recollection- and familiarity-based recognition, respectively (Koen & Yonelinas, 2010; Yonelinas, 1997; 1999; 2001b; for review, see Yonelinas 2001a; Yonelinas et al., 2010). In addition, the results converge with another recent study that tested the predictions of the recollection account (Experiment 5B in Aly & Yonelinas, 2012). That is, if the increased old item variability that is seen in item recognition arises because recollection contributes to the strength distribution of old items, then it should be possible to reverse the variance effect in situations where recollection contributes to recognizing new, but not old, items. To test this prediction, participants were presented with a list of scenes and were given an item recognition confidence test for old and new scenes. However, unlike most prior studies, the new items were highly similar to old items, such that small objects were added or removed from studied scenes (e.g., an office scene may have a keyboard in one version and not the other). Under these conditions, recollection is not useful in determining that an old item is old because there are numerous features in every scene (old and new) that can be recollected, and recollection of many ‘old’ details is not diagnostic that the scene is completely unchanged. In contrast, if participants detect that a feature has changed (e.g., they notice the keyboard is missing), recollection of that detail will be very useful in identifying a new scene as ‘new’. The ROCs in this experiment showed that the old items had significantly less variability than did the new items – exactly the opposite of what is typically seen in recognition memory – and therefore provided strong evidence that it is recollection that underlies the memory variability effects.

An important challenge for the dual-process model is to determine how well the recollection account performs when examining manipulations that are predicted to influence familiarity, rather than recollection. The recollection account predicts that such variables would affect estimates of F_d′, but not estimates of R_o. Two such manipulations have already been explored and provide results that are consistent with the recollection account. For example, Diana, Yonelinas, & Ranganath (2008) predicted that familiarity would make a larger contribution to source recognition when the item and source information were treated as a single holistic item rather than an arbitrary relation. Indeed, unitized encoding compared to non-unitized encoding led to increased ROC estimates of F_d′ with little or no change in estimates of R_o (see also Diana, Yonelinas, & Ranganath, 2010; Haskins et al., 2008; Quamme et al., 2007; but see Mickes, Johnson, & Wixted, 2010).

As another example, several neuroanatomical models of recognition memory propose that the perirhinal cortex is involved in familiarity-based item recognition rather than recollection (e.g. Aggleton & Brown, 1999; Eichenbaum, Yonelinas, & Ranganath, 2007; Yonelinas et al., 2010; see also Eichenbaum, Otto, & Cohen, 1994). Thus, selective perirhinal cortex damage could in principle affect the F_d′ parameter of the dual-process model, but not R_o. This prediction has been confirmed in a patient with a selective lesion to the perirhinal cortex (Bowles, Crupi, Mirsattari, Pigott, Parrent, Pruessner, et al., 2007). An analysis of this patient’s ROCs showed significant declines in estimates of familiarity (F_d′), but not in recollection (R_o; see also Aly, Yonelinas, Kishiyama, & Knight, 2011, for a similar pattern of data in patients lesions to the lateral prefrontal cortex). Future work should examine how variables predicted to influence familiarity affect the F_d′ parameter of the dual-process model, and attempt to doubly dissociate recollection and familiarity within the same set of participants.

There are, however, aspects of the ROC literature that appear problematic for the dual-process model. For instance, there have been a few reports of ROCs that exhibit an S-shape when plotted in z-space (e.g., DeCarlo, 2007, 2008; Onyper et al., 2010; Sherman, Atri, Hasselmo, Stern, & Howard, 2003). The dual-process model can produce linear and U-shaped z-ROCs, but not S-shaped zROCs. In contrast, a full mixture model can accommodate all of these types of functions. If these effects can be verified and nuisance accounts like aggregation and truncation artifacts can be ruled out (see Yonelinas & Parks, 2007), then this would represent an important challenge for the dual-process model.

A related challenge for the recollection account of the dual-process model are results suggesting that recollection can contribute to ROCs in a more continuous manner at least under some conditions (Harlow & Donaldson, 2013; Elfman, Parks, & Yonelinas, 2008; Mickes, Wais, & Wixted, 2009; Onyper et al., 2010; Parks, Murray, Elfman, & Yonelinas, 2011). These findings are not necessarily inconsistent with a threshold view of recollection because recollection can still be continuous above a threshold (for further discussion, see Yonelinas et al., 2010). This evidence does suggest, however, that it may be necessary to estimate the shape of both the recollection and familiarity distributions in some cases. For example, recollection begins to exhibit a more continuous strength distribution under conditions of high feature overlap (Elfman et al., 2008) and increased stimulus complexity (Harlow & Donaldson, 2013; Parks et al., 2011). In order to account for these effects it has proven useful to estimate not only the probability that recollection occurs but also to make additional assumptions about the shape and strength of the recollective distributions (cf., Sherman et al., 2003; Onyper et al., 2010). Future work is required to determine if such approaches are necessary under all conditions or just in some special circumstances.

Conclusions

The present experiments examined the encoding variability (Wixted, 2007), attention failure (DeCarlo, 2002; 2003), and recollection (Yonelinas, 1994; 1999) explanations of the old item variance effect. The results proved problematic for the encoding variability and the attention failure accounts. In contrast, the data confirmed the predictions of the recollection account, providing evidence that the parameters of the dual-process model do index recollection- and familiarity-based recognition memory. Although future work will be necessary to test alternative accounts for the old item variance effect, the results suggest that the encoding variability and attention failure accounts in themselves are not sufficient to explain the variance effects seen in recognition memory.

Appendix

Aggregate response frequencies for Experiments 1–4.

	Response Bias Test/Rating Bin
	6	5	4	3	2	1
Experiment 1
Self-Paced
Hits	-	1075	1155	1271	1380	1421
Misses	-	545	465	349	240	199
False Alarms	-	281	367	497	748	781
Correct Rejections	-	1339	1253	1123	872	839
Speeded
Hits	-	806	969	1259	1419	1416
Misses	-	814	651	361	201	204
False Alarms	-	282	354	613	880	976
Correct Rejections	-	1338	1266	1007	740	644
Experiment 2
Full Attention
Old	2604	634	384	389	422	309
New	379	356	454	871	1335	1365
Divided Attention
Old	2241	763	469	385	439	349
New	456	484	538	827	1078	1269
Experiment 3
Old - Same Context	732	191	95	130	170	122
Old - Different Context	540	187	143	179	215	176
New	120	122	114	292	399	393
Experiment 4
Immediate Test
Old	4238	774	547	678	600	363
New	1295	667	684	1437	1678	1439
24-hr Delayed Test
Old	2110	1405	1002	1220	921	542
New	1053	1030	953	1611	1427	1126

Note. From left to right, the columns in Experiment 1 represent the data for the most conservative response bias test to the most liberal response bias test. The columns for Experiments 2–4 refer to the frequency of confidence responses in each rating bin (6 – ‘sure old’ to 1 – ‘sure new’).