A Biophysically-based Mathematical Model for the Catalytic Mechanism of Glutathione Reductase

Abstract

Glutathione reductase (GR) catalyzes the reduction of oxidized glutathione (GSSG) to reduced glutathione (GSH) using NADPH as the reducing cofactor, and thereby maintains a constant GSH level in the system. GSH scavenges superoxide (O₂^·−) and hydroxyl radicals (OH^·) non-enzymatically or by serving as an electron donor to several enzymes involved in reactive oxygen species (ROS) detoxification. In either case, GSH oxidizes to GSSG and is subsequently regenerated with the catalytic action of GR. Though GR kinetic mechanism has been extensively studied under different experimental conditions with variable substrates and products, the catalytic mechanism has not been studied in terms of a mechanistic model that accounts for the effects of the substrates and products on the reaction kinetics. The aim of the current study is therefore to develop a comprehensive mathematical model for the catalytic mechanism of GR. We use available experimental data on GR kinetics from various species/sources to develop the mathematical model and estimate the associated model parameters. The model simulations are consistent with the experimental observations that GR operates via both ping-pong and sequential branching mechanisms based on relevant concentrations of its reaction substrate GSSG. Furthermore, we show the observed pH-dependent substrate-inhibition of GR activity by GSSG and bi-modal behavior of GR activity with pH. The model presents a unique opportunity to understand the effects of products on the kinetics of GR. The model simulations show that under physiological conditions, where both substrates and products are present, the flux distribution depends on the concentrations of both GSSG and NADP⁺ with ping-pong flux operating at low levels and sequential flux dominating at higher levels. The kinetic model of GR may serve as a key module for the development of integrated models for ROS scavenging system to understand protection of cells under normal and oxidative stress conditions.

Introduction

The maintenance of physiological levels of reactive oxygen species (ROS) within the cell is crucial for both signaling and mitigating oxidative stress [1-6]. Though there are multiple sources of ROS in the excitable cell, superoxide (O₂^·−) produced by the mitochondrial electron transport chain (ETC) is the dominant source [2, 5, 7, 8]. Subsequently, O₂^·− can react with nitric oxide (NO^·) to form peroxynitrite (ONOO^-), a deleterious oxidant capable of initiating lipid peroxidation and oxidation of thiols, thus damaging mitochondrial proteins [4, 9-12]. Usually, O₂^·− upon its production is rapidly converted into hydrogen peroxide (H₂O₂) through the enzymes superoxide dismutases (SOD). The excess production of H₂O₂ can then lead to the formation of the highly reactive hydroxyl radical (OH^·) in the presence of reduced transition metals (e.g., Fe²⁺) via the Fenton reaction [4]. Owing to the high toxicity of ROS, mammalian cells have developed a network of scavenging enzymes which converts H₂O₂ to H₂O [4, 13]. Catalase is one such enzyme and it converts H₂O₂ to O₂ and H₂O, and it is highly expressed in peroxisomes [14]. Glutathione (GSH) and thioredoxin (Trx) systems are the two main H₂O₂ scavenging systems that have been characterized in different cell types from different organs [13]. H₂O₂ is mainly decomposed by the enzyme glutathione peroxidase (GPx) which uses reduced glutathione (GSH) as a substrate [15]. Trx coupled with thioredoxin reductase (TrxR) works in concert with peroxiredoxins (Prx) and glutaredoxin (Grx) which also uses GSH as a substrate [13, 16, 17]. Thus, the capacity of the systems that use GSH to remove H₂O₂ depends on both activities of these enzymes and GSH concentration. Because GSH and GSSG act as a conserved moiety in the ROS scavenging system, the GSH/GSSG couple provides an estimate of cellular redox buffering capacity and plays a central role in maintaining redox balance [18, 19].

GSH is a tripeptide and one of the most abundant low molecular weight free radical scavengers in the cell [20, 21]. Since GSH is required for scavenging H₂O₂, recycling GSSG back into GSH is critical for the cell. Glutathione reductase (GR) is a ubiquitous enzyme which converts GSSG into GSH with the help of electrons from NADPH [22]. GR belongs to the family of NADPH-dependent oxidoreductases and is present in both prokaryotes and eukaryotes [23]. The enzyme is a homodimeric protein containing FAD and a disulfide at its active site. The dimeric form of the enzyme is critical for its function as both subunits contribute essential residues to the constitution of the active site [24]. Distinct binding sites on the enzyme for NADPH and GSSG have been observed in crystal structures [25]; however, the exact sequence of binding events is not clearly understood as both substrates simultaneously bind or GSSG binds after the release of the product NADP⁺.

The catalytic mechanism of GR is complex and has been studied by several groups using spectroscopic, kinetic and genetic approaches from a variety of sources: from bacteria to mammalian cells [26-34]. However, it was Mannervik [29] who first hypothesized that a simple ping-pong mechanism was not sufficient in describing the observed product (NADP⁺) inhibition on the initial-velocity data. Instead, Mannervik suggested that GR operates according to a branched mechanism involving both ping-pong and sequential branches. Initial-velocity studies performed by Calberg and Mannervik [27] from rat liver in the absence of products and the non-linear inhibition pattern observed with product NADP⁺ in their study contradicts a simple ping-pong mechanism. Lopez-Barea and Lee [28] obtained GR from mouse liver and their initial-velocity studies in the absence of products suggested a similar behavior with GSSG-dependent substrate-inhibition by NADPH. However, the effects of products were not reported. The initial-velocity data of Montero et al. [30] from P. blakesleeanus was the first study that extensively characterized the kinetic mechanism by performing experiments on forward reaction and effects of both products and pH on the initial-velocities. The observed data both in the presence and absence of products were consistent with a branched mechanism with GSSG-dependent substrate-inhibition by NADPH. The study also hypothesized that, at low concentrations of GSSG, the ping-pong mechanism prevails, whereas at high concentrations of GSSG, the sequential ordered mechanism appeared to dominate [30]. In this work, Montero et al. also concluded that the enzyme activity is inhibited at acidic pH as the GSSG concentration is increased. In contrast, the initial-velocity data in the absence of products of Ulusu and Tandogan [33] from bovine liver and Worthington and Rosemeyer [34] from human erythrocytes suggested a simple ping-pong mechanism. However, the competitive inhibition of NADP⁺ observed with respect to NADPH rules out a simple ping-pong and a combination of ping-pong and sequential random ordered mechanisms. Although the GR kinetic mechanism has been extensively studied under different experimental conditions with variable substrates and products [27-30, 33, 34], the catalytic mechanism has not been studied in terms of a mechanistic mathematical model that accounts for the effects of the substrates and products on the reaction kinetics.

Current integrated models of ROS scavenging [35-38] use the flux expressions for GR that are not based on mechanistic details and cannot describe the available kinetic data [27-30, 33, 34]. Although Mannervik [29] and Montero et al. [30] proposed similar kinetic schemes, initial-velocity only for the forward reaction in the absence of products was considered to formulate simplified mathematical models. Thus, their models are not able to characterize product-inhibition data. Furthermore, of these models, only Montero et al. developed a detailed branched formulation with the formation of a dead-end product with NADPH to explain the observed GSSG-dependent substrate-inhibition. However, they did not include any mechanistic details for the observed pH-dependent substrate-inhibition data by GSSG. Furthermore, the kinetic parameters estimated from their analyses were based on the assumption of low GSSG concentrations in the absence of products. However, under oxidative stress conditions, it is argued that GSSG concentrations are much higher [39-41], but recent studies on compartment-specific real-time measurements suggest that the cytosolic GSSG is tightly controlled even during severe oxidative stress [42]. Thus, simulation of GR kinetics over whole range of [GSSG] would have physiological and pathophysiological significance. Considering the importance of GR in maintaining cellular GSH levels in the presence of products, a complete mechanistic model which characterizes both the initial-velocity and product-inhibition data would help in understanding how the ROS scavenging system maintains the physiological ROS levels in the cell.

In this study, we developed a mathematical model to characterize the kinetic mechanism of GR from different species/sources under different experimental conditions by considering the kinetic scheme proposed by Mannervik [29] and Montero et al. [30] in the presence of products (NADP⁺ and GSH). We also extended the scheme by incorporating random protonation of the NADPH-bound intermediate complex to form the activated complexes and formation of related proton-bound dead-end complexes in the sequential branch to explain the bi-modal behavior of GR activity with pH [34] and pH-dependent substrate-inhibition of GR activity by GSSG [30]. Thus, to the best of our knowledge, the current model is the first instance where with a single generalized kinetic scheme, we are able to reproduce the diverse experimental data on the initial-velocity of GR from different species/sources [27, 28, 30, 33, 34]. The model of this sort may assist with the mechanistic understanding of the role of GR in ROS scavenging systems in normal cells and in various pathologies such as cardiac ischemia/reperfusion injury and other oxidative stress conditions [43-45].

Methods

Five sets of available experimental data [27, 28, 30, 33, 34] on the initial-velocities that include product-inhibition and pH-dependent kinetics have been used to identify the catalytic mechanism and the relevant mathematical model for GR kinetics.

Proposed unified kinetic mechanism for GR

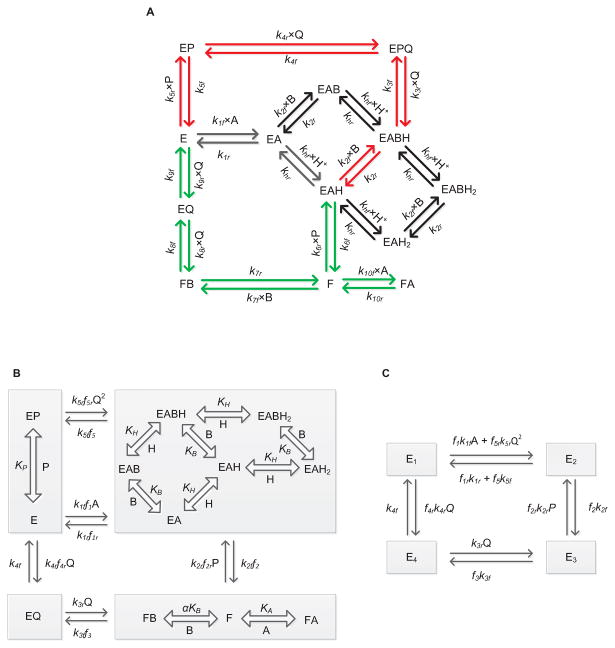
Figure 1A shows the schematics of the proposed unified catalytic mechanism that is used to derive the mathematical model of GR in this study. Here, the free enzyme E binds first with the substrate NADPH (A), thereby forming the E-NADPH complex (EA). Random protonation and GSSG (B) binding takes place at this complex to form activated single proton-bound intermediate complexes (EAH and EABH). Dead-end complexes (EAH₂ and EABH₂) are formed when these enzyme states are diprotonated.

Figure 1.

(A) Basic scheme for the catalytic mechanism of glutathione reductase (GR). Free enzyme (E) interacts with the substrate NADPH first and random protonation and GSSG binding takes place at this complex to form activated single proton bound intermediate complex (E-NADPH-H) and dead-end complexes. Branching takes place at this complex (E-NADPH-H) to form sequential (red) and ping-pong branches (green). E and F indicate oxidized and reduced forms of the free enzyme, respectively. EX and EXH (X = NADPH (A), GSSG (B), NADP⁺ (P) and GSH (Q)) represents enzyme substrate/product complexes. k_if and k_ir (i = 1-10) are forward and backward rate constants for the respective interaction. k_hf and k_hr are forward and backward rate constants for the proton binding to the intermediate complex and formation of dead-end complexes. (B, C) Reduced scheme of GR under rapid-equilibrium assumption. A, B, P, Q and H represent concentrations of NADPH, GSSG, NADP⁺, GSH and protons, respectively. K_B, K_P K_H and K_IA are dissociation constants for the respective rapid equilibrium interactions and α is the cooperative binding for GSSG. k_if and k_ir (i = 1-5) are forward and backward rate constants for the respective interactions. E1, E2, E3 and E4 are intermediate enzyme states and f_i indicates the associated binding polynomial for each enzyme-complex transition.

Branching takes place from the activated EAH complex based on the concentration of GSSG leading to the ping-pong (green arrows) and sequential branches (red arrows). In the ping-pong branch, once the first product is released, the reduced form of the enzyme F further interacts with either GSSG or NADPH in the next step. Based on the concentrations of the substrates, the interaction of F with NADPH leads to the formation of a dead-end FA complex [30]; the interaction of F with GSSG leads to the formation of final product GSH in subsequent steps regenerating the oxidized free enzyme E. On the other hand, a high initial concentration of GSSG in the reaction medium leads to an ordered sequential pathway resulting in the formation of the activated EABH complex. This proton-bound ternary complex subsequently leads to the formation of reaction products while releasing the free enzyme E. The random protonation of NADPH-bound intermediate complex and proton-bound dead-end complexes in the sequential branch were motivated by the experimentally observed bi-modal behavior of GR activity with pH [34] and GSSG concentration dependent accumulation of reaction products at acidic pH [30, 46].

Figures 1B and 1C show the reduced forms of the GR kinetic mechanism (Figure 1A) that are based on the assumptions of rapid equilibrium of selected binding/unbinding steps to derive the mathematical model for GR kinetics. For example, we assumed that the binding/unbinding of the reaction components are much faster than the intermediate enzyme complex reaction rates where the enzyme state changes from free enzyme E to the reduced form of the enzyme F. In addition, the protonation steps are assumed to be rapid. Specifically, in Figure 1A, there are three slow binding/unbinding steps of state change, namely EAH to F, FB to EQ and EABH (or) FPBH to EPQ, while the rest of the steps are assumed to be in rapid equilibrium. These assumptions greatly simplify the derivation of the kinetic flux expression for GR and reduce the number of unknown parameters to be estimated for the model.

Kinetic flux expression for GR

The KAPattern package [47] was used to derive the net reaction velocity equation for GR based on steady-state assumption for the reduced kinetic schemes shown in Figures 1B and 1C. Defining A, B, P, Q and H as the concentrations of NADPH, GSSG, NADP⁺, GSH and protons, respectively, the net reaction velocity equation is given by:

$$v=\frac{E_0\left(\begin{array}{l}(A{f}_1{f}_5{k}_{1f}{k}_{5f}-Q^2{f}_{1r}{f}_{5r}{k}_{1r}{k}_{5r})(f_3{k}_{3f}{k}_{4f}+P{f}_{2r}{k}_{2r}{k}_{4f}+PQ{f}_{2r}{k}_{2r}{k}_{3r})\\ +(A{f}_1{f}_2{f}_3{k}_{1f}{k}_{2f}{k}_{3f}{k}_{4f}-P{Q}^2{f}_{1r}{f}_{2r}{f}_{4r}{k}_{1r}{k}_{2r}{k}_{3r}{k}_{4r})\end{array}\right)}{\left(\begin{array}{l}(f_2{k}_{2f}{k}_{4f}+f_3{k}_{3f}{k}_{4f}+P{f}_{2r}{k}_{4f}{k}_{2r}+Q{f}_3{k}_{2f}{k}_{3r}+f_2{f}_3{k}_{2f}{k}_{3f}+PQ{f}_{2r}{k}_{2r}{k}_{3r})(f_{5r}{k}_{5r}{Q}^2+A{f}_1{k}_f)\\ +(f_3{k}_{3f}{k}_{4f}+Q^2{k}_{3r}{f}_{4r}{k}_{4r}+P{f}_{2r}{k}_{2r}{k}_{4f}+Q{f}_3{f}_{4r}{k}_{3f}{k}_r+PQ{f}_{2r}{k}_{2r}{k}_{3r}+PQ{f}_{2r}{f}_{4r}{k}_{2r}{k}_{2r}{k}_{4r})\\ (f_5{k}_{5f}+f_{1r}{k}_{1r})+f_2{f}_3{k}_{2f}{k}_{3f}{k}_{4f}+Q^2{f}_2{f}_{4r}{k}_{2f}{k}_{3r}{k}_{4r}+Q{f}_2{f}_3{f}_{4r}{k}_{2f}{k}_{3f}{k}_{4r}+P{Q}^2{f}_{2r}{f}_{4r}{k}_{2r}{k}_{3r}{k}_{4r}\end{array}\right)}$$ (1)

where k_if and k_ir (i = 1-5) represent forward and reverse rate constants for the interactions shown in Figure 1B; fi indicates the corresponding fractional occupancy factors, defined by:

$$\begin{array}{l}{f}_1=f_{4r}=\frac{1}{1+\frac{P}{K_P}};f_{1r}=\frac{\frac{K_H}{H}}{\left(1+\frac{B}{K_B}\right)\left(\frac{K_H}{H}+1+\frac{H}{K_H}\right)};f_2=\frac{1}{\left(1+\frac{B}{K_B}\right)\left(\frac{K_H}{H}+1+\frac{H}{K_H}\right)};\\ f_{2r}=\frac{1}{1+\frac{B}{\alpha K_B}+\frac{A}{K_{IA}}};f_3=\frac{\frac{B}{\alpha K_B}}{1+\frac{B}{\alpha K_B}+\frac{A}{K_{IA}}};f_5=\frac{\frac{B}{K_B}}{\left(1+\frac{B}{K_B}\right)\left(\frac{K_H}{H}+1+\frac{H}{K_H}\right)};f_{5r}=\frac{\frac{P}{K_P}}{1+\frac{P}{K_P}}\end{array}$$ (2)

where K_IA and K_H represent substrate-inhibition constant with respect to NADPH and pH, respectively; K_P and K_B represent dissociation constant for NADP and GSSG, respectively, while α is the cooperative binding constant for GSSG. It is clear from Equation (1) that the flux expression contains two velocity terms in the numerator indicating flux through sequential and ping-pong branches.

Equilibrium constant K_eq for GR

The enzyme GR reduces GSSG to GSH using the following reference reaction [48]:

$${\mathit{\text{GSSG}}}^{2-}+{\mathit{\text{NADPH}}}^{4-}+H^{+}\iff 2{\mathit{\text{GSH}}}^{-}+{\mathit{\text{NADP}}}^{3-}$$ (3)

The reference reaction is unambiguously balanced in terms of mass and charge and we calculated the equilibrium constant based on the reference reaction. The standard Gibb's free energy of reference reaction is then computed as:

$${\mathrm{\Delta }}_r{G}_{\mathit{\text{GR}}}^0=2{\mathrm{\Delta }}_f{G}_{\mathit{\text{GSH}}}^0+{\mathrm{\Delta }}_f{G}_{{\mathit{\text{NADP}}}^{+}}^0-{\mathrm{\Delta }}_f{G}_{\mathit{\text{GSSG}}}^0-{\mathrm{\Delta }}_f{G}_{\mathit{\text{NADPH}}}^0-{\mathrm{\Delta }}_f{G}_{H^{+}}^0$$ (4)

where the Gibb's free energy of formation of each species was obtained from Alberty's thermodynamic data [49], and corrections for pH, ionic strength and temperature were made where appropriate. The apparent equilibrium constant for the reference reaction is calculated as:

$$K_{\mathit{\text{eq}},\mathit{\text{GR}}}={\left(\frac{{[{\mathit{\text{GSH}}}^{-}]}^2[{\mathit{\text{NADP}}}_{\mathit{\text{ox}}}^{3-}]}{[{\mathit{\text{GSSG}}}^{2-}][{\mathit{\text{NADPH}}}_{\mathit{\text{red}}}^{4-}][H^{+}]}\right)}_{\mathit{\text{eq}}}=exp\left[\frac{{\mathrm{\Delta }}_r{G}_{\mathit{\text{GR}}}^0}{\mathit{\text{RT}}}\right]$$ (5)

Thermodynamic constraints

All the model parameters cannot vary independently. At equilibrium, the net reaction rate is zero, and correspondingly, the ratio of the product of forward rate constants and reverse rate constants is equal to the equilibrium constant, resulting in two thermodynamic constraints for the kinetic parameters:

$$\frac{k_{1f}{k}_{5f}}{K_B}=\frac{k_{1r}{k}_{5r}{K}_H}{K_P}{K}_{\mathit{\text{eq}},\mathit{\text{GR}}};\frac{k_{1f}{k}_{2f}{k}_{3f}{k}_{4f}}{\alpha K_B}=k_{1r}{k}_{2r}{k}_{3r}{k}_{4r}{K}_H{K}_{\mathit{\text{eq}},\mathit{\text{GR}}}$$ (6)

where K_eq,GR represents the apparent equilibrium constant for the reference reaction of Equation (3).

Parameter estimation and sensitivity analysis

Equation (1) contains 15 unknown and two known parameters of enzyme concentration (E₀) and thermodynamic equilibrium constant (K_eq,GR). Two unknown parameters can be obtained from the thermodynamic constraints of Equation (6). We constrained parameters k_3r and k_5r using these thermodynamic constraints, and remaining 13 unknown parameters, including parameters for the inhibitory effects of pH (K_H), were estimated using the available diverse experimental data from the literature [27, 28, 30, 33, 34], as discussed above. A combined least-square estimation technique was used to fit the model simulated outputs to the available experimental data:

$$\underset{\varphi }{minE}(\varphi ),E(\varphi )=\sum _k^{N_{exp}}\frac{1}{N_{\mathit{\text{data}}}}\left(\sum _j^{N_{\mathit{\text{data}}}}{\left(\frac{J_j^{\mathit{\text{data}}}-J_j^{mod\mathit{\text{el}}}(\varphi )}{max(J_j^{\mathit{\text{data}}})}\right)}^2\right)$$ (7)

where N_exp is the number of experiments and N_data is the number of data points in a particular experiment, $J_j^{\mathit{\text{data}}}$ are the experimental data and $J_j^{\text{model}}(\varphi )$ are the corresponding model simulation outputs. The accuracy and robustness of the model fitting to the data are assessed based on the value of mean residual error E( ) and sensitivities of J( ) to perturbations in the optimal parameter estimates.

The normalized local sensitivity coefficients of the model parameters are computed as:

$$S_{{\varphi }_i}=\frac{1}{M_i}\sum _{{\forall }_i:S_{{\mathrm{\Phi }}_{i,j}}\ne 0}{S}_{{\mathrm{\Phi }}_{i,j}};S_{{\varphi }_{i,j}}=\left(\left|\frac{\partial ln{J}_j}{\partial ln{\varphi }_i}\right|\right)\approx \left|\frac{J_j({\varphi }_i+0.001{\varphi }_i)-J_i({\varphi }_i-0.001{\varphi }_i)}{0.002J_j({\varphi }_i)}\right|,$$ (8)

where □_i is the i^th parameter, J_j is the model simulation for j^th data point, M is the number of non-zero velocities for the parameter □_i and $S_{{\varphi }_i}$ denotes the normalized sensitivity coefficient for the parameter □_i. A higher sensitivity value indicates that a small change in a given parameter value will result in a significant change in the model output. On the other hand, a small sensitivity value for a given parameter indicates that the parameter should be fixed and removed from the parameter estimation procedure.

Results

In this section, we provide the detailed model parameterization and characterization of the experimental data on GR kinetics in different species using the unified kinetic mechanism of Figures 1B and 1C. We independently estimated all the unknown kinetic parameters of the model using both forward and product- inhibition data for each experimental data set for each species/sources [27, 28, 30, 33, 34]. Since some of the experimental data did not include product-inhibition studies and the parameters in the model were correlated, we used sensitivity analysis for the parameters by fixing the least sensitive parameter for some data set and the remaining parameters were estimated. The resulting parameter values are tabulated in Table 1, along with the local sensitivity coefficients for each parameter.

Table 1.

Estimated model parameter values for GR kinetics obtained from different species/sources.

	Rat liver [27]		Mouse liver [28]		Erythrocytes [34]		Bovine liver [33]		P. blakesleeanus[30]
Parameter	Value	Sensitivity	Value	Sensitivity	Value	Sensitivity	Value	Sensitivity	Value	Sensitivity
klf (μM-1 min-1)	3.4×103	0.34	2.8×103	0.15	3.3×103	0.25	9.9×102	0.41	2.3×103	0.26
klr (min-1)	1.5×102	4.3×10-3	1.5×102	1×10-6	2.5×105	0.04	6.5×104	0.05	6.4×104	0.07
k2f (min-1)	1.1×106	0.03	1.9×107	0.03	6.7×107	0.024	6.7×107	0.041	6.7×107	0.1
k2r (μM-1 min-1)	1.3×104	0.035	-	-	9.1×104	0.058	3.4×104	0.06	4.6×106	0.22
k3f (min-1)	7.8×104	0.31	3.4×104	0.54	2.7×104	0.54	1.3×105	0.24	1.0×105	0.32
k4f (min-1)	5.6×104	0.07	3.2×104	0.28	1.7×105	0.054	8.1×104	0.20	8.0×104	0.22
k4r (μM-1 min-1)	-	-	-	-	-	-	10.2	0.06	1.32	0.24
k5f (min-1)	9.5×104	0.24	2.1×105	0.03	5.8×104	0.2	2.2×105	0.11	1.2×105	0.1
Kp (μM)	93	0.24	-	-	237	0.22	50	0.42	152	0.31
KB (μM)	56	0.39	88	0.3	54	0.25	22	0.16	25.7	0.22
KIA (μM)	1.0×107	4×10-7	436	0.06	8.0×106	8×10-7	8×106	1×10-6	82	0.08
α	2.83	0.26	1.78	0.27	1.2	0.20	9.8	0.13	2.7	0.2
KH (μM)	0.1a		0.1a		0.1a		0.1a		0.03	0.029
Keq,GRb	1.6×108		9.2×107		1.6×108		1.2×108		2.1×108

^aParameter fixed based on the pK information from [34].

^bNot an adjustable parameter and calculated based on thermodynamic data. ‘^-’These parameters do not play a role in fitting the experimental data for the respective data set and can be fixed based on the other data sets.

The model fittings to the initial-velocity data of GR obtained from different species/sources [27, 28, 30, 33, 34], in the absence or presence of products, are illustrated in Figures 2-5. The effects of pH on the GR activity are described in Figure 6. Based on the estimated parameter values, we further analyzed the fractional contributions of ping-pong and sequential branch fluxes towards the total GR flux, as well as the effects of products and pH on each flux in Figure 7. Furthermore, to mimic in vivo conditions, we assumed constant pools of GSH and NADPH and simulated the fractional contributions of individual fluxes towards the total GR flux for different pH in Figure 8. Although the reported data in the literature were presented as double reciprocal plots, we converted them to normal initial-velocity versus substrate data for the convenience of model simulations and parameter estimation. All the reported data were rigorously checked for inconsistencies in the measurements/units by comparing each individual plot with other similar plots in each study, and discrepancies such as amounts of enzyme used were taken care of by incorporating suitable scaling factors for the enzyme activity in the model.

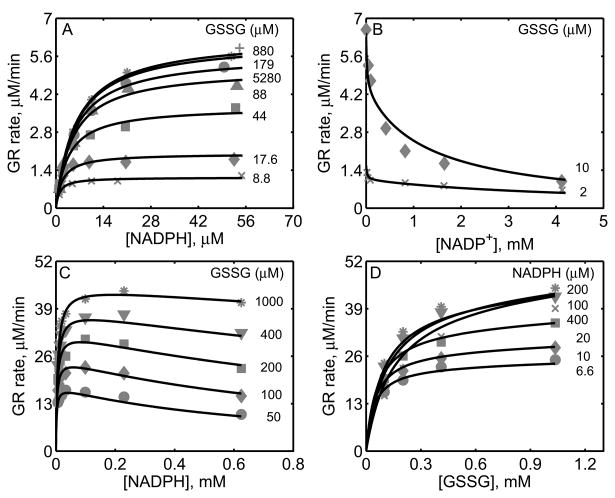
Figure 2.

Characterization of the initial-velocity data of GR from rat liver [27] and mouse liver [28]. For GR obtained from rat liver studies, the enzyme assays were carried out with 0.3 nM of enzyme at pH 7.6 and 30°C. (A) Model fits to the initial-velocity data with varying [NADPH] and different [GSSG]. (B) Model fits to the effect of product NADP⁺ on the activity of GR for two different [GSSG] at a fixed [NADPH] (10.7 μM). For GR obtained from mouse liver studies, the enzyme assays were carried out with 2.6 nM of enzyme at pH 7.0 and 25°C. (C) Model fits to the initial-velocity data with varying [NADPH] and different [GSSG]. (D) Model fits to the initial-velocity data with varying [GSSG] and different [NADPH].

Figure 5.

Characterization of the initial-velocity data of GR purified from P. blakesleeanus [30]. Here the enzyme assays were carried out at pH 7.5 and 30°C. (A) Model fits to the initial-velocity data with varying [NADPH] and different [GSSG]. (B) Model fits to the initial- velocity data with varying [GSSG] and different [NADPH]. (C) Model fits to the effect of product NADP⁺ on the activity of GR with varying [NADPH] at a fixed 1 mM [GSSG]. (D) Model fits to the effect of product NADP⁺ on the activity of GR with varying [GSSG] at a fixed 40 μM [NADPH]. (E) Model fits to the effect of product GSH on the activity of GR with varying [NADPH] at a fixed 1 mM [GSSG]. (F) Model fits to the effect of product GSH on the activity of GR with varying [GSSG] at a fixed 40 μM [NADPH]. The estimated enzyme concentrations used in all above experiments were 0.7 nM.

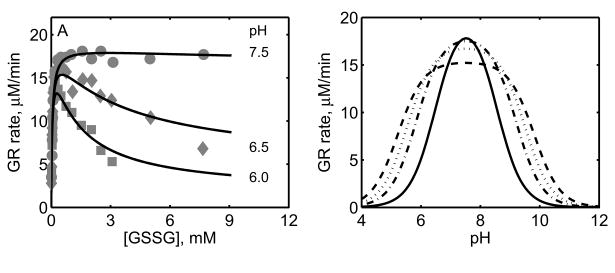
Figure 6.

Effect of pH on GR activity. (A) Initial-velocity of GR with variable [GSSG] at a fixed 100 μM [NADPH] for three different pH values. Here the experimental conditions are similar to Figure 5. (B) Model simulations for GR activity with varying pH for four different [GSSG] and at fixed [NADPH] (0.1 mM). Here, dashed, dotted, dash-dotted and solid line represent 0.25, 0.5, 1 and 5 mM of [GSSG], respectively.

Figure 7.

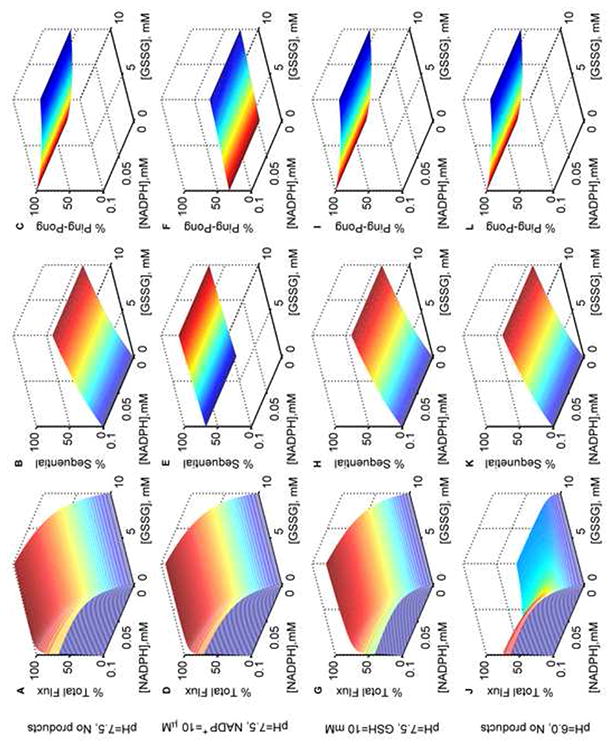
Model simulations for the % total, % sequential and % ping-pong fluxes of GR. Normalized fluxes of GR with both varying NADPH and GSSG in the absence of products at optimal pH 7.5: (A) total flux, (B) sequential flux, and (C) ping-pong flux; with NADP⁺ (10 μM) as the only product inhibitor: (D) total flux, (E) sequential flux, and (F) ping-pong flux; with GSH (10 mM) as the only product inhibitor: (G) total flux, (H) sequential flux, and (I) ping-pong flux. Normalized fluxes of GR with both varying NADPH and GSSG in the absence of products and at acidic pH 6.0: (J) total flux, (K) sequential flux, and (L) ping-pong flux. Model was simulated using estimated parameters from Montero et al. [30]. All the total flux values were obtained by dividing with the maximum flux value in the absence of products. Ping-pong and sequential fluxes were calculated as the fraction of the total flux for the respective substrate concentrations.

Figure 8.

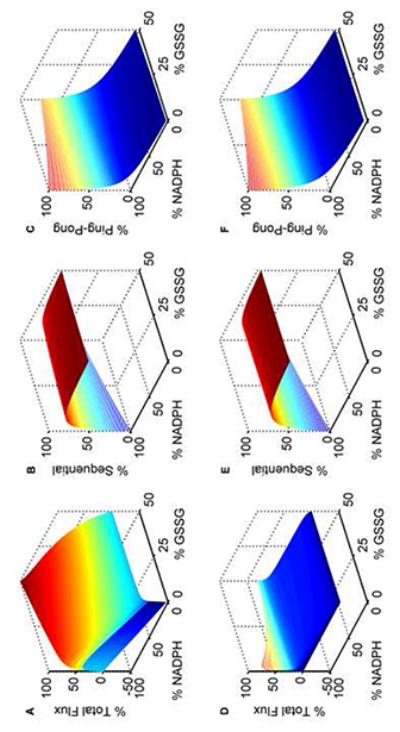
Model simulations of GR kinetics for in vivo-like conditions. The GSH and NADPH pools are set to 10 mM and 0.1 mM, respectively. The % GSSG is calculated as the ratio of its concentration to the total GSH pool concentration (G_tot), which is defined as G_tot = GSH + 2×GSSG. Percentage fluxes of GR with both varying NADPH and GSSG at optimal pH 7.5: (A) total flux, (B) sequential flux, and (C) ping-pong flux. At acidic pH 6.0: (D) total flux, (E) sequential flux, and (F) ping-pong flux. The model was simulated using estimated parameters from Montero et al. [30]. All the total flux values were obtained by dividing with the maximum flux value in the absence of products. Ping-pong and sequential fluxes were calculated as the fraction of the total flux for the respective substrate concentrations.

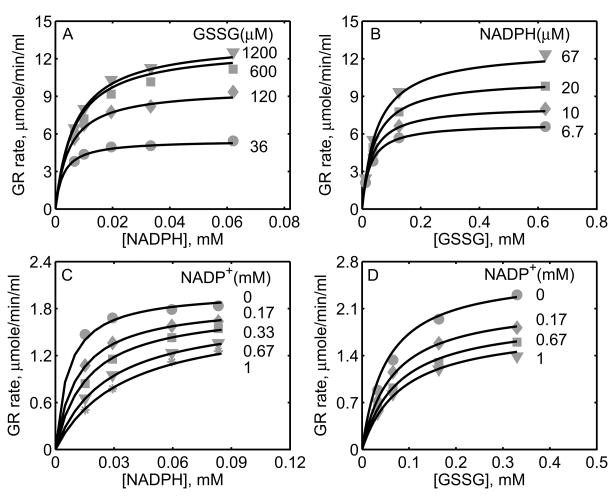
Figure 2A shows the model simulations of the experimental data obtained from Calberg and Mannervik [27] on the initial-velocity of GR obtained from rat liver with NADPH as the variable substrate at different [GSSG] in the absence of products. The enzyme concentration used in the study was 0.3 nM at pH 7.6, and based on the components of the reaction medium, the ionic strength is estimated to be 0.23 M at 30°C. The initial-velocity of GR was increased with increasing [GSSG] and reached saturation depending on the concentration of NADPH. However, for [GSSG] above 1 mM, the initial-velocity was inhibited as indicated in Figure 2A for [GSSG] of 5.28 mM (circles). The corresponding solid lines in Figure 2A are the model description of the experimental data and the model was able to characterize the data both at low and high [GSSG] accurately. Figure 2B shows the effect of the product NADP⁺ on the initial-velocity of GR for two different [GSSG] (2 and 10 μM) at a fixed [NADPH] (10.7 μM). Here, a non-linear inhibition pattern was observed with respect to NADP⁺ and the developed kinetic model was able to show such behavior for the two concentrations of GSSG.

Similarly, we used the experimental data on forward velocities of GR obtained from mouse liver of Lopez-Barea and Lee [28] to identify the kinetic parameters of the proposed GR model for the mouse liver. The experiments in this study were conducted using 2.6 nM of enzyme at pH 7.0 and ionic strength of 0.2 M at 25°C. Figures 2C and 2D show the model fittings to initial-velocity data of GR obtained from mouse liver with NADPH and GSSG, respectively, as the variable substrates at different concentrations of the other substrate. As shown in the figure, the model was able to accurately describe the observed data under both conditions. Since the products NADP⁺ and GSH were not present in the reaction medium, we were not able to estimate the parameters related to product-inhibition (k_2r, k_4r and K_P). As such, these parameters are not sensitive to the forward velocities and fixed based on the other studies, as shown in Table 1.

The experimental data set of Worthington and Rosemeyer [34], which reported forward initial-velocity and the effect of the product NADP⁺ on GR activity purified from human erythrocytes, was also used to parameterize and validate the proposed kinetic scheme. These data were used to estimate 11 of the 13 unknown parameters. The parameter related to pH (K_H) was fixed based on the pK information from this study and the parameter related to the effect of product GSH (k_4r) on GR activity was fixed based on other studies. The experiments were carried out using 0.6 μM of the enzyme at pH 7.0 and ionic strength of 0.1 M at 25°C. Figures 3A and 3B show the model fittings to the initial-velocity data with NADPH and GSSG as the variable substrates for four different concentrations of the other substrate, respectively. The model was able to accurately describe the observed initial-velocity data under both cases. In other experiments on GR kinetics with NADP⁺ as the product inhibitor, the initial-velocity was decreased with both NADPH (Fig. 3C) and GSSG (Fig. 3D) as the variable substrates at a fixed concentration of the other substrate. The corresponding model simulations show that the proposed branching mechanism reproduces the product-inhibition data.

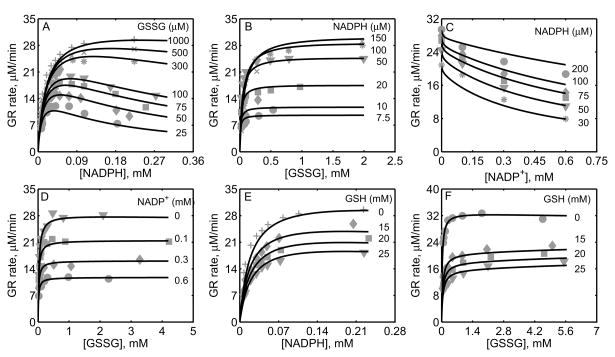
Figure 3.

Characterization of the initial-velocity data of GR purified from human erythrocytes [34]. Here enzyme assays were carried out with 0.6 μM of enzyme for forward studies at pH 7.0 and 25°C. (A) Model fits to the initial-velocity data with varying [NADPH] and different [GSSG]. (B) Model fits to the initial-velocity data with varying [GSSG] and different [NADPH]. (C) Model fits to the effect of product NADP⁺ on the activity of GR with varying [NADPH] at a fixed 1 mM [GSSG]; the enzyme concentration used here was 0.08 μM. (D) Model fits to the effect of product NADP⁺ on the activity of GR with varying [GSSG] at a fixed 100 μM [NADPH]; the enzyme concentration used here was 0.1 μM.

In a recent study, Ulusu and Tandogan [33] performed kinetic experiments on GR, purified from bovine liver, at pH 7.4 and ionic strength estimated to be 0.2 M at 37°C. The data from this study were used to characterize the kinetic mechanism of GR using the proposed hybrid branching scheme. The 12 unknown kinetic parameters were estimated by fitting the model to all the experimental data and the parameter related pH (K_H) was fixed based on the pK information from Worthington and Rosemeyer study [34]. Since the exact amount of the enzyme used in their study was not reported, we estimated the value to be approximately 0.7 nM based on the initial-velocity measurements. Figure 4A shows the model fittings to the initial-velocity data with GSSG as the variable substrate for four different [NADPH]. Initial-velocity increased with increasing [NADPH] and both model simulations and experimental data were in agreement with each other for the range of substrate concentrations used. Furthermore, in the presence of products, the activity of GR decreased with increasing product [NADP⁺] as shown in Figures 4B and 4C with NADPH and GSSG as the variable substrates, respectively. The respective experimental data and model simulations with GSH as the product inhibitor are shown in Figures 4D and 4E. Here [GSH] used were much higher compared to [NADP⁺]. In all of the above four cases, the model simulations are in agreement with the experimental data.

Figure 4.

Characterization of the initial-velocity data of GR purified from bovine liver [33]. For GR obtained from bovine liver the initial-velocity experiments were carried out at pH 7.4 and 37°C. (A) Model fits to the initial-velocity data with varying [GSSG] at different [NADPH]. (B) Model fits to the effect of product NADP⁺ on the activity of GR with varying [NADPH] at fixed 0.7 mM of [GSSG]. (C) Model fits to the effect of product NADP⁺ on the activity of GR with varying [GSSG] at fixed 100 μM of [NADPH]. (D) Model fits to the effect of product GSH on the activity of GR with varying [NADPH] at a fixed 0.7 mM [GSSG]. (E) Model fits to the effect of product GSH on the activity of GR with varying [GSSG] at a fixed 100 μM [NADPH]. The estimated enzyme concentrations used in all above experiments were 0.7 nM.

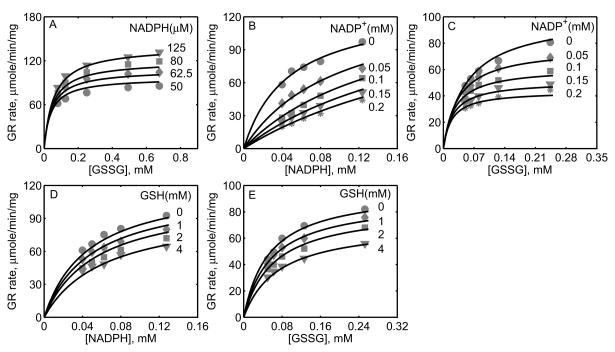
Figure 5 shows the model fittings to the initial-velocity data of GR obtained from P. blakesleeanus from Montero et al. [30], both in the absence and presence of products NADP⁺ and GSH. The experiments in their study were performed at pH 7.5 and ionic strength of 0.12 M at 30°C. Figure 5A shows the rate of GR with [NADPH] as the variable substrate for different [GSSG]. Here, the initial-velocity increases with increasing [GSSG] and attains saturation at high [NADPH]. However, for GSSG at lower concentrations (e.g. [GSSG] <= 100 μM), NADPH inhibits the GR activity. Model simulations were able to explain the data for both the lower and higher [GSSG]. Figure 5B shows the model fittings to the initial-velocity data with GSSG as the variable substrate for different [NADPH]. Here, the initial-velocity increases with increasing [NADPH] and attains saturation at high [GSSG]. The model simulations were consistent with the experimental observations.

Figures 5C-5F show the model fittings to the product-inhibition data of GR obtained from P. blakesleeanus [30]. Figure 5C illustrates the inhibition of GR activity by NADP⁺ as the product for different [NADPH] at a fixed [GSSG] of 1 mM. As shown in the figure, NADP⁺ competitively inhibits the GR activity with decreasing [NADPH]. The model was able to accurately capture the inhibition data for the range of [NADPH] used in the study. Furthermore, Figure 5D shows the model fittings to the product-inhibition data with GSSG as the variable substrate for four different [NADP⁺] at a fixed [NADPH] of 30 μM. The GR activity decreases with increasing [NADP⁺] and the model simulations are in agreement with the experimental data. Similarly, the proposed model characterizes well the product-inhibition data in the presence of the product GSH with NADPH (Fig. 5E) and GSSG (Fig. 5F) as the variable substrates. Here, the GR activity decreases with increasing [GSH], however the concentrations required are higher (> 25 mM) compared to that of NADP⁺.

We further characterized the effects of pH on the activity of GR as shown in Figure 6. Here, the initial-velocity data in the absence of products have been used to estimate the relevant parameters of the model involving pH (K_H). The experimental data shown in Figure 6 in Montero et al. [30] were used to identify the parameter K_H. Figure 6A shows the effect of pH on the GR activity with GSSG as the variable substrate. At the optimal pH value (7.5), the activity of GR remains at the saturated levels irrespective of the GSSG concentration. However, at the acidic pH values, the rate decreased as the concentration of GSSG increased. The model simulations are in agreement with the experimental data indicating that the proposed mechanism of random protonation and GSSG binding of NADPH-bound enzyme complex to form single protonated intermediate active states and formation of diprotonated dead-end complexes in the sequential branch could be the possible mechanism for the observed pH-dependent substrate-inhibition phenomenon. Similarly, Figure 6B shows the effect of pH on GR activity that was simulated for four different [GSSG] (0.25, 0.5, 1 and 5 mM) with varying pH at a fixed [NADPH] (0.1 mM). The model observed initial-velocity of GR was inhibited at both acidic and alkaline pH values and inhibitory pattern depends on [GSSG] as observed experimentally [30, 34, 46].

Thus, the proposed branching mechanism with one proton-bound active intermediate states and formation of diprotonated dead-end complexes in the sequential branch, describes well the diverse initial-velocity data of GR obtained from different species. In order to ascertain the contributions of individual fluxes towards the total GR flux, the estimated model parameter values from the experimental data of Montero et al. [30] were further used to simulate the model and quantify the fractional fluxes of ping-pong and sequential branches in the absence and presence of the product NADP⁺ or GSH at the optimal (pH 7.5) and acidic pH (6.0), which are shown in Figure 7.

Figure 7A shows the surface plot of the total flux of GR with both varying [NADPH] and [GSSG] in the absence of products at the optimal pH of 7.5. The corresponding individual contributions of sequential and ping-pong fluxes were calculated based on the fraction of the total flux for each pair of substrate concentration, which are shown in Figures 7B and 7C, respectively. These model simulations clearly show that as the concentrations of GSSG increase, the percentage of ping-pong flux decreases irrespective of the concentration of NADPH, and the percentage of sequential flux peaks at 50% for high [GSSG] (Fig. 7B). In the presence of 10 μM [NADP⁺] as the product inhibitor, the total GR flux decreases only by a small amount (Fig. 7D). Interestingly, under these conditions, this small amount of NADP⁺ switched the flux towards the sequential branch regardless of the [GSSG] as shown in Figures 7E and 7F. In contrast, in the presence of 10 mM GSH as the product inhibitor, flux through both sequential and ping-pong branches were inhibited simultaneously with sequential path contributing very little at low [GSSG] (Figs. 7H and 7I). The corresponding total flux was only slightly inhibited as shown in Figure 7G. Since acidic pH was experimentally shown to inhibit the initial-velocity of GR, based on the concentrations of GSSG, we simulated the distribution of flux in the absence of products for acidic conditions at a pH of 6.0. In this case, the fluxes through both sequential (Fig. 7K) and ping-pong (Fig. 7L) branches were not affected relative to the optimal pH conditions. However, the total flux was reduced considerably at low [GSSG] and inhibition was more pronounced at high [GSSG] as shown in Figure 7J.

To mimic physiological conditions, we set the GSH and NADPH pools of 10 mM [50] and 0.1 mM [51], respectively, and simulated the fractions of total GR flux contributed by ping-pong and sequential branch fluxes with both the substrates and products present [2, 52]. Figure 8 shows the surface plot of the variations of the percentage total and individual fluxes for percentage variations in both GSSG and NADPH levels at optimal (7.5; Figs. 8A-8C) and acidic pH (6.0; Figs. 8D-8F) conditions. As seen in Figure 8A, the maximum forward flux was observed in the absence of products. However, the maximum reverse flux at both high GSH and NADP⁺ concentrations was only 30% of the corresponding maximum flux in the forward direction. Figures 8B and 8C show the corresponding fractional contribution of sequential and ping-pong branch fluxes towards the total flux. Initially, at very low [GSSG] and at high [NADPH], the majority of the GR flux is through the ping-pong branch which decreased marginally as percentage GSSG is increased. In contrast, the ping-pong flux is decreased independent of [GSSG] for the decreased [NADPH]/[NADP⁺] ratios (Fig. 8C). An opposite behavior is observed for the sequential branch where the percentage sequential flux increased independent of [GSSG] for the decreased [NADPH]/[NADP⁺] ratios (Fig. 8B). A similar phenomenon was observed under acidic conditions of pH 6.0 (Figs. 8E and 8F). Here, the total flux was reduced and the inhibition pattern was more pronounced at higher GSSG concentrations (Fig. 8D).

Discussion

GSH is a crucial component of ROS scavenging system and decreased GSH pool sizes have been linked to widespread mitochondrial damage [52-55]. GSH is oxidized to GSSG in H₂O₂ detoxification. Since transportation of GSSG to and from the cytosol is slow, therefore, it has to be reduced back to GSH [39]. This reduction is catalyzed by the enzyme GR, using NADPH as the reducing cofactor. A number of kinetic studies are available in the literature that explain the catalytic mechanism of GR in different species/sources [27, 28, 30, 33, 34]. However, there is no single mechanism and a relevant kinetic model that explains all the data observed from these studies. Although a number of mitochondrial and cellular ROS handling models have used the kinetics of GR in their integrated models [35-38], the mechanism of GR was not consistent with the observed experimental studies. Even though GR obtained from human erythrocytes in the absence of products indicated a sequential ordered mechanism [56], there is no conclusive experimental evidence that shows the mechanism is an ordered sequential mechanism in the presence of products. Rather, it was observed through forward rate data in some studies that the mechanism of GR follows a simple ping-pong mechanism rather than a sequential ordered mechanism [33, 34, 57]. Additional studies on GR from different species are consistent with a branched mechanism [27-30, 33, 34]. The GR flux expression used in the integrated models [35-38] thus far is based on the assumption of a sequential mechanism and cannot describe the kinetic data both in the presence and absence of reaction products (GSH and NADP⁺) from various studies. Also none of the modeling studies performed previously include the available experimental data [27, 28, 30, 33, 34] and cannot describe the product-inhibition on GR kinetics. In the current study, we proposed a unified kinetic scheme and developed a comprehensive mathematical model to address the effects of products and pH on the catalytic activity of GR.

For the development of the GR kinetic model, we started with the assumption that the mechanistic scheme contains either the ping-pong or the sequential branch. The resultant flux expressions were then used to fit the available experimental data [27, 28, 30, 33, 34]. Although, both schemes were able to describe some aspects of the experimental data on forward reaction (results not shown), they failed to explain the substrate and product-inhibition data from different studies. Subsequently, we used a combination of ping-pong and sequential scheme proposed by Mannervik [29] and Montero et al. [30] and included the random protonation and GSSG binding of NADPH-bound intermediate complex to form single protonated intermediate complexes to be the activated form and formation of related diprotonated dead-end complexes in the sequential branch (Fig. 1). For derivation of the flux expression, we assumed rapid equilibrium for reactions of substrates/products with the free enzyme, and subsequent enzyme modification reactions were assumed to be rate limiting. However, the resultant flux expression was not able to describe the complete initial-velocity and product-inhibition data (results not shown), indicating more steps in the reaction scheme could be rate-limiting. Thus, we used KAPattern method [47] to obtain the general rate expression for the kinetic scheme shown in Figure 1A, based on the steady-state assumption for GR reaction. The steady-state rate expression derived from the KAPattern package had 24 parameters (individual rate constants) to estimate. We reduced this complexity by performing multiple iterations of rapid equilibrium assumptions for some steps in the mechanistic scheme shown in Figure 1A, and performed optimization to fit the experimental data for each rate expression obtained. The reduced scheme shown in Figures 1B and 1C which includes partial rapid equilibrium assumption for binding of GSSG and NADP⁺ to form the enzyme substrate complexes and formation of dead-end products with respect to NADPH and protons best describes all the experimental data under consideration with only 15 unknown parameters. The analysis also shows that binding of NADPH and GSH to the free enzyme are rate limiting steps in addition to the steps where enzymes state changes from oxidized form E to reduced form F.

We estimated the unknown kinetic parameters of the model independently for each GR data set purified from different species [27, 28, 30, 33, 34]. We simultaneously used both forward and product-inhibition data to fit the unknown parameters whenever such data was available. In the case of only forward data, the parameters related to products were fixed based on the values from complete data sets. Furthermore, all the parameters of the model are not independent. They were constrained by thermodynamic constraints, using the apparent equilibrium constant. Thus, two of the total 15 unknown parameters were calculated from apparent equilibrium relation and the remaining 13 unknown parameters were estimated. The estimated final parameters were not unique for all data sets (see Table 1) and the observed differences may be partly due to the bias in the parameter estimation with insufficient data (e.g. unavailability of the product inhibition data) and/or due to the differences in GR extracted from different source/species. We performed residual and sensitivity analyses as described in the Method section to ascertain the goodness-of-fit of the model and the corresponding sensitivity coefficients are tabulated in Table 1 for each parameter. The residual analysis suggests that the model parameters were robust to small changes in parameter values (results not shown). The observed differences in the parameter values between different studies can be attributed to the variations in the experimental conditions (e.g. ionic strength and temperature) and/or the enzyme source/species. Thus, rather than a unique set of parameters, a range of values for each parameter best explains the mechanism of GR from different species/sources.

The kinetic studies performed on GR from P. blakesleeanus [30] in the absence of products revealed that the catalytic mechanism of GR showed substrate-inhibition by NADPH for concentrations above 40 μM. The inhibition pattern was dependent on [GSSG] with inhibition occurring only below 25 μM. In contrast, for high [GSSG], though inhibition by NADPH was abolished, the double reciprocal lines were merging on to the y-axis against the parallel lines observed at lower GSSG concentrations. The model describes well these observed initial-velocity data (Figs. 5A and 5B) and the estimated dissociation constant for GSSG (K_B) (25.7 μM) is close to the K_m value of GSSG (38 μM) reported in the experimental study by Montero et al. [30]. The kinetic data from mouse liver [28] also showed strong substrate-inhibition by NADPH at lower [GSSG] similar to the study by Montero et al. but the straight lines in the double reciprocal plots were parallel even at high [GSSG]. However, the kinetic data with respect to GSSG as the variable substrate at fixed [NADPH], the straight lines of the double reciprocal plots were parallel only at low fixed [NADPH] (< 50 μM) and converging on to the y-axis for high [NADPH] for both studies indicating the involvement of two branches (ping-pong and sequential). The proposed scheme in our study is consistent with the kinetic data for forward reaction in both P. blakesleeanus and mouse liver, and the values of the kinetic parameters indicate that two alternative branches exists for the mechanism of GR with a dead end-product formation with the substrate NADPH.

In the absence of products, the model simulations shown in Figures 7B and 7C indicate that for low [GSSG], the mechanism can be approximated by a ping-pong mechanism, whereas at high [GSSG], the sequential branch mostly dominates. In the absence of products, the ratio of sequential (ν_s) to ping-pong (ν_p) flux is given by ν_s/ν_p =(k_5f/k_2f)×GSSG indicating that the contributions of individual fluxes towards the total GR flux was regulated mainly by the rate constants k_2f and k_5f (see Fig. 1B) and the concentration of GSSG. Thus, the proposed branching scheme of GR elucidated by the model simulation results strengthens the existence of a critical [GSSG] above which the mechanism of GR was dominated by sequential pathway.

The initial-velocity studies performed on GR from rat liver [27], bovine liver [33], and human erythrocytes [34] did not show substrate-inhibition by NADPH. The estimated parameter value for substrate-inhibition by NADPH (K_IA) shown in the Table 1 for these studies were very high leading to no measurable accumulation of the F-NADPH complex. A very low sensitivity coefficient for this parameter also showed that the parameter is not relevant in fitting these experimental data and can be fixed at a large value, indicating no substrate-inhibition by NADPH for these species. As discussed above, in the absence of products, the mechanism can also be explained by a simple ping-pong mechanism for the case of GR from human erythrocytes [34] and bovine liver [33]. However, in the case of GR from rat liver [27], a simple ping-pong mechanism was not sufficient to explain the forward reaction data indicating the need for product-inhibition studies in the determination of the true catalytic mechanism.

Since the initial-velocity data on GR form different species for the forward reaction [28, 30, 33, 34] and also the model fittings to these data were not consistent in predicting a single mechanism for GR, the kinetic studies on the effect of products on the enzyme activity were essential in understanding the mechanism. Product-inhibition studies performed with NADP⁺ as the only product, revealed that NADP⁺ was a competitive inhibitor with respect to NADPH [27, 30, 33, 34]. This inhibition pattern is to be expected in an ordered sequential mechanism but not in the classic ping-pong mechanism. The proposed unified scheme in our study efficiently describes the kinetic data of NADP⁺ product-inhibition in various species as shown by Figures 2B, 3C, 3D, 4B, 4C, 5C and 5D. Furthermore, the model simulation studies performed in the case of NADP⁺ as the only product inhibitor (Fig. 7F), revealed that the presence of 10 μM of product NADP⁺ significantly changes the flux distribution with majority of flux diverting to the sequential branch (Fig. 7E). The study indicates that, in the presence of the product NADP⁺, the reaction flux through ping-pong branch was diverted due to the high value of a second order rate constant (k_2r) leading to the formation of EAH complex. In contrast, the model simulations performed with parameters estimated from Ulusu and Tandogan [33] data suggested that the presence of NADP⁺ only marginally altered the flux distribution (see Fig. S1 in the Supplementary figures) owing to the observation of only parallel lines in the initial-velocity measurements and no substrate-inhibition by NADPH. Correspondingly, the estimated value of a second order rate constant (k_2r) leading to the formation of EAH complex was reduced 100-fold compared to the Montero et al. [30] (see Table 1) indicating decreased flux through the sequential branch.

The product-inhibition studies with GSH were markedly inconsistent for different species. On the one hand, GR obtained from P. blakesleeanus [30] displays a mixed type inhibition by GSH with respect to NADPH and a complex non-linear inhibition pattern with respect to GSSG. On the other hand, studies from the bovine liver [33] and human erythrocytes [34] show a non-competitive inhibition with respect to both substrates. We were able to independently describe these diverse kinetic data using the proposed unified mechanistic scheme (Fig. 1) for each study. The model simulations for the effect of GSH on the flux distribution show that GSH equally inhibits both branches linearly resulting in a behavior similar to the forward case (Figs. 7H and 7I). The inhibition by GSH shows that only a small reduction in total flux was observed at 10 mM concentration (Fig. 7G). In contrast, the model simulation studies performed with the parameters estimated from Ulusu and Tandogan [33] where substrate-inhibition by NADPH was not observed and only parallel lines in the double-reciprocal plots of initial-velocity vs. substrates were observed suggested a similar behavior, however the percentage total flux was 20% more decreased than that observed with the Montero et al. [30] (see Fig. S1G in the Supplementary figures). This indicates that the inhibition of GSH on the activity of GR is not consistent and depends on the source of GR. Model simulations with constant GSH and NADPH pools for Montero et al. [30] have further shown that, under physiological conditions, the rate of GR is sensitive to the redox state of the GSH and NADPH pools. The flux is mainly ping-pong at very low concentrations and then switches to sequential as the [GSSG] and [NADP⁺] increased. A similar behavior observed with Ulusu and Tandogan [33] however the percentage distribution of flux via the sequential branch was not strong (see Fig. S2 in the Supplementary figures) as it was observed with Montero et al. [30] reflecting the observed differences in the data. The maximum initial-velocity observed in the presence of NADP⁺ at high GSSG shows that the flux through the sequential branch is higher compared to the ping-pong branch. The simulation results suggest that under severe oxidative stress conditions due to altered GSH and NADPH redox states, the mechanism of GR operates more by the sequential pathway where the GR flux is higher yielding quicker regeneration of GSH.

Although the mechanism of GR was consistent with a branched mechanism, the initial-velocities with varying [GSSG] and pH suggested acidic pH-dependent inhibition by GSSG. The reaction scheme proposed by Montero et al. [30] was not able to predict such a behavior, and they suggested a different mechanism might be involved. Using the proposed unified mechanistic scheme in our study, where random protonation and GSSG binding of intermediate complexes E-NADPH to form single protonated active intermediate enzyme complexes and formation of the diprotonated dead-end complexes in the sequential branch was included, the model is able to describe such pH-dependent data. It appears that at [GSSG] above 0.1 mM, the flux through the sequential branch increases and the high concentration of protons leads to the accumulation of the dead-end proton complexes [46]. Although De Arriaga et al. [46] suggested the involvement of cooperativity in proton binding depending on the GSSG and pH value, we assumed a unity cooperativity coefficient for proton binding for simplification. The model simulation studies strengthen the notion that, under acidic conditions (e.g. pH = 6.0), flux through both ping-pong and sequential branch is considerably inhibited due to the dead-end complex formation. It appears that, under acidic conditions, the activity of GR is normally inhibited as the concentrations of GSSG increases. Furthermore, the model was also able to mimic the bi-modal behavior observed with varying pH in some of the experimental studies [27, 34]. Thus, the unified branching scheme proposed in Figure 1 efficiently describes all the initial-velocity and product-inhibition data for GR obtained from different species/sources [27, 28, 30, 33, 34].

In conclusion, we developed a thermodynamically balanced mathematical model of GR kinetics based on a unified catalytic mechanism, which includes formation of dead-end products in both ping-pong and sequential branches with respect to NAPDH and pH, respectively. In the proposed mechanism, free enzyme binds to the substrate NADPH and branching takes place based on the concentration of GSSG and NADP⁺. Thus, the model simulations of the proposed branching scheme are consistent with the experimental data and strengthen the GSSG concentration dependent switching mechanism. The kinetic model describes the diverse initial-velocity and product-inhibition data in different species/sources [27, 28, 30, 33, 34]. Thus, it presents a unique opportunity to understand the effect of products on the activity of GR which is crucial for understanding its role under pathophysiological conditions. We obtained a range of parameters for the catalytic mechanism which explains all the kinetic data in the absence and presence of both products. We hypothesize that under physiological conditions, the mechanism of GR likely involves an alternative ping-pong and sequential pathway depending on the concentrations of GSSG and NADP⁺; although a branching scheme was necessary to attain the maximum velocities. Thus, the current model should be thought of as a quantitative representation of the kinetics of this enzyme that is consistent with the available data and therefore useful as a component for integrated modeling of biochemical systems and a template model for investigating other two substrate enzymes with similar regulatory mechanisms. We believe that the developed unified mechanism may serve as a mean to further explore the role of GR in cellular and mitochondrial ROS scavenging systems.

Highlights.

• We develop a comprehensive mathematical model for the catalytic mechanism of GR.

• It is capable of explaining diverse experimental data sets on GR kinetics.

• It provides unique understanding of the effects of products and pH on GR kinetics.

• GR reaction operates via a combined ping-pong and sequential pathway.

• GR mechanism switches to sequential pathway at higher [NADP⁺] and [GSSG].