Abstract
Weak and ultra-weak protein-protein association play a role in molecular recognition, and can drive spontaneous self-assembly and aggregation. Such interactions are difficult to detect experimentally, and are a challenge to the force field and sampling technique. A method is proposed to identify low-population protein-protein binding modes in aqueous solution. The method is designed to identify preferential first-encounter complexes from which the final complex(es) at equilibrium evolves. A continuum model is used to represent the effects of the solvent, which accounts for short- and long-range effects of water exclusion and for liquid-structure forces at protein/liquid interfaces. These effects control the behavior of proteins in close proximity and are optimized based on binding enthalpy data and simulations. An algorithm is described to construct a biasing function for self-adaptive configurational-bias Monte Carlo of a set of interacting proteins. The function allows mixing large and local changes in the spatial distribution of proteins, thereby enhancing sampling of relevant microstates. The method is applied to three binary systems. Generalization to multiprotein complexes is discussed.
Keywords: protein-protein association, weak and ultra-weak interactions, macromolecular interfaces, aqueous interfaces, long-range solvent effects
I. Introduction
Cellular signal transduction involves networks of protein-protein interactions that transmit information.1,2 Many of these proteins interact with more than one partner and can form stable multiprotein hetero-complexes.2,3 A number of pathologies have been linked to disruptions of the delicate balance of forces between proteins, most commonly as a result of mutations4 or partial misfolding.5 Understanding the physicochemical basis of macromolecular association in solution is then a requisite to understand many biological processes in the cell, from subcellular organization3 to physiological function and disease.6,7 To elucidate the origin of specificity and affinity structural information is often combined with microcalorimetric and kinetic data,8 but microscopic insight is often limited. Moreover, recent advances in paramagnetic relaxation enhancement techniques have revealed the existence of transient, ultra-weak protein self-associations that are difficult to detect with conventional biophysical methods.9,10 Data suggest that proteins can interact at multiple sites, forming an ensemble of binding modes with very low populations.11 These transient complexes can play a role in protein recognition, and may drive spontaneous self-assembly of higher-order architectures.11 These studies have shown that ultra-weak association is controlled mainly by electrostatics, although hydrophobic interactions also play a role.11 Crowded environments12 could strengthen weak electrostatic interactions, which may explain the relatively high aggregation state of soluble proteins in living cells.13
The study of macromolecular complexation requires not only prediction of highly-specific binding modes, a common goal in computational biology,14,15 but also calculation of association/dissociation rates, binding enthalpies and entropies, and detection and characterization of weak and ultra-weak association. These are major challenges for the force field, as it must describe the physics of a variety of aqueous environments and thermodynamic conditions, and the unique properties of aqueous interfaces. The protein environment is determined by several factors, including the amount of water excluded by neighboring proteins, complexes, and assemblies. The incomplete and anisotropic hydration created by these structures affect the magnitude and direction of forces induced by water.16 The protein environment is also characterized by the properties of water close to the protein surface.17–22 Aqueous interfaces are involved in many effects elicited by ions and cosolutes, including protein denaturation, stabilization, aggregation, and dissociation.23–25 Aqueous interfaces display non-bulk behavior that can propagate a few hydration layers into the bulk. For example, neutron scattering and X-ray diffraction data suggest that simple ions can affect the water structure beyond their first hydration shells,26 whereas osmotic stress experiments show that membranes and nucleic acid arrays affect the water behavior up to a few nanometers from their surfaces.27,28 Deeper interfaces have been reported in colloidal systems.29–31 Transferring these findings to the cytosol is problematic because experiments are difficult to design and interpret, often leading to conflicting conclusions.13,32 For example, NMR data suggest that the dynamics of cell water do not differ much from the dynamics of bulk water,33 implying that only the first hydration shells are affected. However, neutron scattering and X-ray data indicate a larger proportion of non-bulk water,34,35 suggesting deeper interfacial regions.
A continuum solvent model that incorporates some of these effects has been described,16 and is reviewed in Section II. The model accounts for the effects of liquid-structure forces at aqueous interfaces, and for short- and long-range electrostatic effects of water exclusion. The latter partially determine binding free energies,16 and is optimized here based on binding enthalpy data.
Thermodynamic calculations and prediction of binding modes also require an efficient method for sampling the configuration space. Configurational bias Monte Carlo (MC) has long been used in the condensed state,36 including polymers37,38 and crystals,39 and is used here to enhance sampling of physically relevant microstates of a set of interacting proteins in solution. The configuration space generally includes both the spatial distribution of proteins and their internal conformations. The focus here is on the spatial distribution. Biased MC of internal degrees of freedom have been reported previously40–42 and used in ab initio prediction of polypeptides conformations in solution.16,40,43,44 Both methods can be combined to address the problem posed by the presence of multiple conformers and by induced fit during protein recognition and association, as discussed in Section V. A critical step in a biased scheme is the selection of the biasing function, which could hinder rather than improve sampling if not properly chosen. A function that approximates the canonical distribution (unknown a priori) can greatly improve statistics and convergence, especially when large structural changes are needed to visit many configurations with statistical significance. An efficient method to construct such a function is presented in Section III. The method is applied in Section IV to three binary systems. Extension to multiprotein complexes is discussed in Section V.
II. Solvent effects: Electrostatic and liquid-structure forces
Biomolecules interact through non-covalent forces, which are strongly modulated (e.g., electrostatics) or directly elicited (e.g., hydrophobicity) by the aqueous medium. In molecular mechanics the electrostatic force Fi on an atom i of a system composed of N atoms is given by Fi = −∇iEe, where Ee is the total electrostatic energy of the system in solution. The magnitude and direction of hydration forces determine the binding process. These forces are sensitive to the configuration of the system, which is determined by the N atomic coordinates r ≡ {r1, r2, …, rN}. In the screened Coulomb potentials-based (SCP) model45–47 Ee is given by16
| (1) |
where qi is the charge of atom i. In this phenomenological partition the first sum is the interaction energy term, and the second sum is the self-energy term. The total energy in the SCP model also contains a cavity-formation term and a correction to account for the effects of liquid-structure forces (SIF) at aqueous interface (not discussed; see16,47). The mean-field effects of SIF are recast in R and optimized to reproduce the hydrogen-bond energies of all amino-acid pairs, as estimated from a systematic calculation of potentials of mean force in explicit water.16 Both the screening functions D and the effective radii R depend on the system configuration. Modeling this dependence in a computationally efficient manner is a challenge, but essential to correctly represent both the magnitude and direction of hydration forces. A summary of the model follows.
II.1. Electrostatic effects of water exclusion
The screening functions in Eq. (1) are given by16 Di(x;r) = (1 + ε0)/{1 + k exp[−αi (r)x]} −1 and Dij(x;r) = (1 + ε0)/{1 + k exp[−αij (r)x]} −1, where ε0 is the static permittivity of the solvent, and k is a constant. The dependence of Di on the system configuration is through the screening coefficients αi, given by16
| (2) |
where J runs over the M residues of the proteins, and rIJ is the distance between the Cα atoms of residues I and J; A > 0 and α0,i determine the screening assigned to the atom i in the fully-hydrated residue I. The screening coefficients αij depend on the configuration through
| (3) |
where . The characteristic lengths σ and σ’ control the long-range decay of electrostatic water-exclusion effects.16 Both α0,i and ε0 depend on the temperature, and α0,i depends on the charge distribution as well.47 The effective radii Ri depend on the local structure through46
| (4) |
where Rw,i is a charge-dependent radius of the fully-hydrated atom i, and j runs over Nc(i) atoms such that rij < rc, and ai > 0; rc is a convenient threshold beyond which electrostatic interactions is said to be long ranged (according to previous theoretical estimates,47 rc ~ 10 Å; in the SCP model it is chosen as rc = 5.6 Å, i.e., two hydration shells). Unlike σ and σ’ in Eqs. (2) and (3), the characteristic length τi determines the short-range decay of the electrostatic effects of water exclusion.16
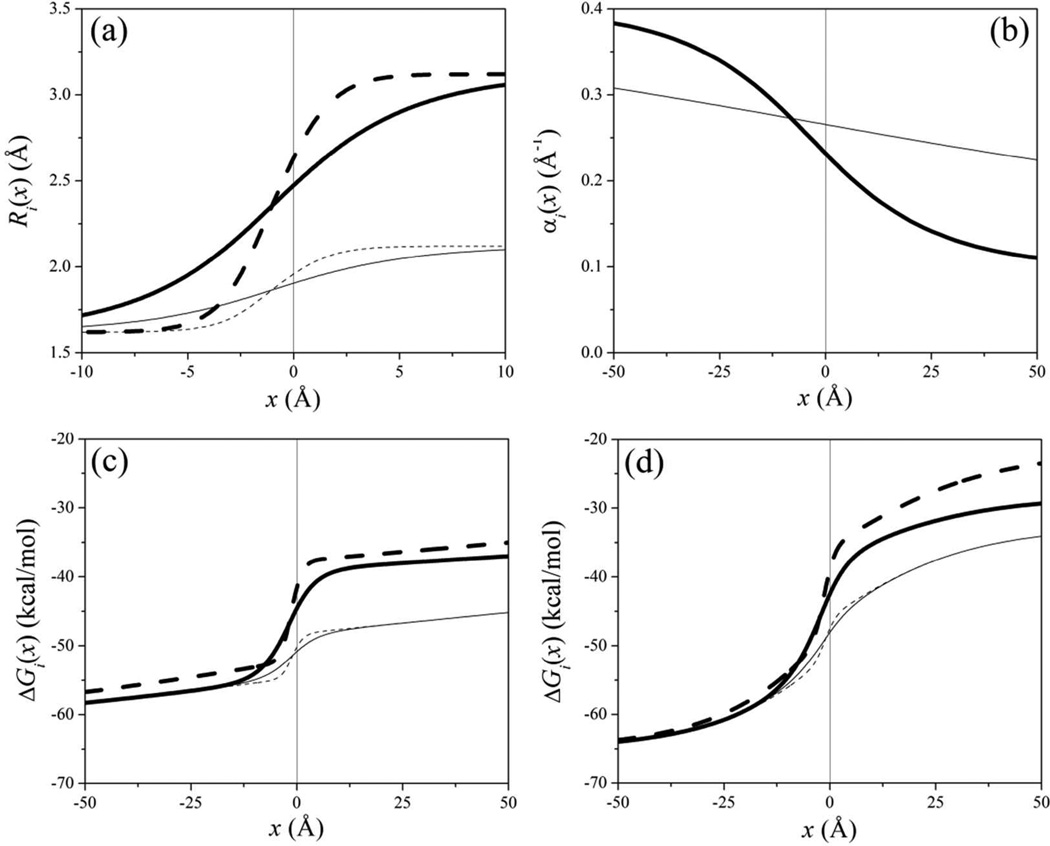
The summations in Eqs. (2)−(4) are suitable simplifications of general sums over the N atoms of the system,16,45,46 and make the model highly efficient.48,49 Figure 1 shows α, R, and the self-energy of a charge q crossing a planar interface. All the variables change smoothly with the distance, from their values in bulk water (x → −∞) to those in the interior of an infinitely large water-excluding cavity (x → +∞). The rates of changes with the distance from the surface depend on the values of σ in Eq. (2); and of τ and a in Eq. (4). For a molecule, the magnitude and direction of hydration forces depend on the values of a, τ, σ, and σ’ assigned to each atom. Careful optimization is thus necessary to model the effects of water on a protein close to another protein, a membrane, or a solid surface.50–52 The exponential functions in Eqs. (2)–(4) have been chosen for computational convenience and may need revision to better represent the decay of the electrostatic free energy with the distance from a real surface.
Figure 1.
Behavior of (a) the effective radius R, (b) the screening parameter α, and (c, d) the self-energy ΔG of a point charge q = +1 close to a planar aqueous interface, as described by the SCP continuum solvent model [Eqs. (1–4)]. The interface is located at x = 0, with water filling the space x < 0 and an idealized protein occupying the region x > 0. (a) From Eq. (4), using a = Rw + 1.5 Å (thick lines) and a = Rw + 0.5 Å (thin), for τ = 3.125 Å (solid) and τ = 1.0 Å (dashed). The parameter a determines the total change in effective radius between bulk water (x → −∞) and bulk protein (complete dehydration, x → ∞); τ determines the rate of change as the particle crosses the interface. (b) From Eq. (2), using σ = 15 Å (thick); σ = 75 Å (thin). (c) From Eq. (1) with σ = 75 Å and effective radii plotted in panel (a). (d) Same as in (c), using σ = 15 Å. The protein, which determines the planar aqueous interface, was modeled as two superimposed three-dimensional cubic lattices, one representing the positions of Cα atoms in Eq. (2), with a side length of 7 Å; and the other one representing the position of all atoms in Eq. (4), with a side length of 2 Å (assuming an average volume of ~180 Å3 per amino acid,16 and ~20 atoms per amino acid).
II.2 Model refinement
Electrostatic effects in the SCP model have been optimized previously using experimental hydration data45 and results from dynamics simulations in explicit water.16,53 Molecules used in the parameterization were small (amino acid and side-chain analogs), so the model better represents short-and medium-range water effects rather than long-range effects. Applications have thus been limited to peptides and small proteins at infinite dilution.16,46,49,54 For larger systems and for processes where large amount of water are excluded from the environment (e.g., protein-protein association) consideration must be given to long-range effects. Barnase and barstar associate mainly by electrostatic forces,55 so this complex (PDB code 1brs) is used here to optimize σ and σ’ in Eqs. (2) and (3). To estimate the dissociation energy canonical MC simulations are carried out at T = 25 °C and fixed (standard) protonation states, using the united-atom representation (param19) of the CHARMM force field.48 The dissociation energy ΔEd is calculated as the energy difference between the bound and unbound states, i.e., ΔEd = Eb − E∞, where Eb = Z−1Σi Ei exp(−Ei/kT) ≈ Σi Ei/Nb, and Ei and Nb in the last sum are the electrostatic energy [cf. Eq. (1)] of an accepted conformation i and the total number of accepted conformations in the bound state, respectively; E∞ is the energy of the system with the proteins widely separated from each other. Trial moves consist of rigid-body rotations, translations, and roto-translations chosen with equal probabilities. Side-chain conformations have negligible effects on long-range electrostatics, so dihedral angle movements are not included. If long-range electrostatic effects are ignored (in practice, σ → ∞ and σ’ → ∞) the dissociation energy is estimated at ΔEd ~ 22.8 kcal/mol (estimated sampling errors within ~kT). This value changes with σ and σ’ since these parameters affect the interaction and the self-energy terms in Eq. (1) independently.16 These parameters can be adjusted to more closely reproduce the experimental binding enthalpy of the complex at the same pH and temperature, measured56 at ΔHb ~ 19.3 kcal/mol. The optimized parameters follow a continuous line in the σ-σ’ plane (not shown), and σ = 59 Å and σ’ = 37 Å are chosen here, which reproduce the experimental value within thermal energy. Two assumptions have been made. First, ΔHb = ΔUb + pΔV ≈ ΔUb ≈ ΔEe, i.e., changes in volume upon dissociation are neglected, and the internal energy U of the system is calculated with the continuum solvent model, and thus contains the free energy of the solvent; the SCP model also includes a standard term for the energy of cavity formation16 (not discussed). Second, the van der Waals (vdW) contribution to the dissociation energy has been omitted. This is a common assumption57 based on the notion that the degree of packing of atoms is similar in a protein and in water occupying the same space. However, recent ITC experiments in a number of protein-ligand complexes have shown that dispersion forces are actually quite strong and contribute significantly to the binding enthalpy when the binding pocket is sub-optimally hydrated.58 The importance of dispersion forces in binding has long been recognized59 and simple models have been proposed to include them in a continuum representation.60,61 In small non-polar molecules these corrections play a measurable but modest role, especially when compared to other interfacial effects operating in heterogeneous polar molecules, such as SIF.47,62–64 Dispersion however can no longer be ignored in larger systems and/or extended interfaces, or in cases where the interface is highly structured, and proper representation is ultimately needed to study protein association quantitatively. A simple thermodynamic cycle shows that the net vdW contribution to the binding energy between two proteins (1 and 2) can be approximated by ΔVvdW ≈ −V12 + V1B + V2A − VA’B’. Here, Vij is the vdW interaction energy between i and j, where A’ and B’ represent regions of bulk water with the same shape and volumes as proteins 1 and 2, respectively; A and B are the same regions of water but in contact with protein 2 and 1, respectively. Molecular dynamics simulations have been carried out here to estimate the relative magnitude of these terms, using the all-atom (param22) CHARMM force field and the TIP3P water model in a cubic cell of ~93 Å side lengths, with periodic boundary conditions and particle-mesh Ewald summation. For barnase (1) and barstar (2), V1B ≈ 71 kcal/mol, V2A ≈ 28 kcal/mol, and VA’B’ ≈ 11 kcal/mol. The direct protein-protein vdW energy is V12 ≈ 118 kcal/mol, so ΔVvdW ≈ 30 kcal/mol. Therefore, replacing a protein by water only partially offsets the direct interaction V12. Although the values obtained here contain artifacts of the force field (e.g., the water model and the LJ function/parameters), the magnitude of ΔVvdW should indicate that the assumption does require a closer inspection. These effects may have implications in the study of weak and ultra-weak association.
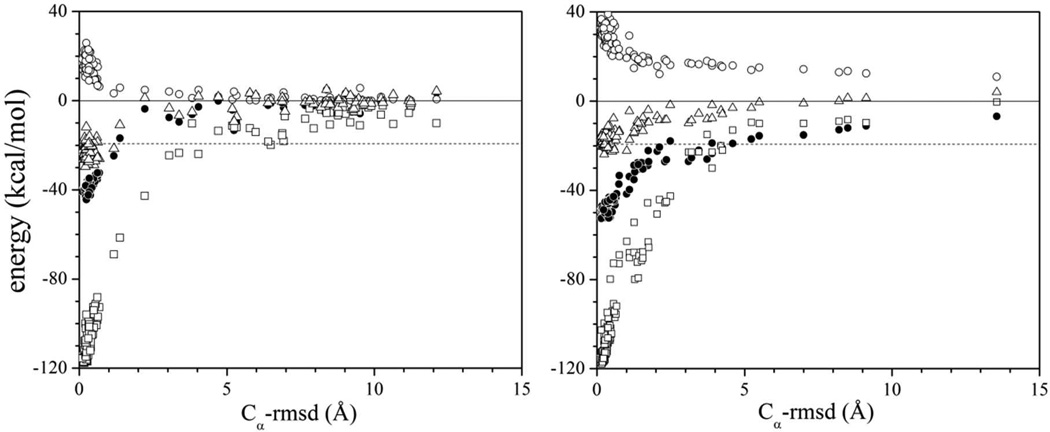
The energy of barnase and barstar along a path connecting the bound and unbound states can be calculated by gradually heating the native complex.16 A set of relaxed structures (decoys) that includes near native and fully dissociated conformations can be generated by a MC simulation. Figure 2 shows the components of the non-bonded energy as a function of a reaction coordinate. The electrostatic interaction energy and the self-energy are shown with and without long-range water-exclusion effects included. The self-energy favors dissociation, whereas the interaction energy favors association.16 The correct interaction results from the critical balance between these strong opposite effects. The direct vdW energy (V12; above) is also shown for comparison. Inclusion of dispersion effects of water exclusion in the SCP model will be reported in a future study.
Figure 2.
Non-bonded energy decomposition of the barnase-barstar complex during dissociation by heating, calculated with the SCP continuum solvent model as implemented in the CHARMM program (version c35b4), with (a) and without (b) long-range water-exclusion effects: protein-protein van der Waals energy (squares), electrostatic interaction energy [black circles; first term in Eq. (1)], and self-energy [open circles; second term in Eq. (1)]. The total electrostatic energy Ee [Eq. (1)] of the system is also shown (triangles) and determines the dissociation enthalpy. The reaction coordinate is the Cα-rmsd with respect to the crystal structure of the complex (PDB 1brs). The limits σ → ∞ and σ’ → ∞ in Eqs. (2) and (3) lead to over-stabilization of the complex by ~3.5 kcal/mol. Optimized values σ = 59 Å and σ’ = 37 Å lead to a dissociation energy equal to the measured ΔHb = 19.3 kcal/mol of the complex.
III. Prescreening of binary binding modes
Forces between macromolecules in solution operate at different length-scales and play different roles in the binding process. The method described in this section relies on the assumption that preferential first encounters are driven mainly by electrostatic interactions and by hydrophobic forces. Electrostatic forces operate at short and long range, while hydrophobicity acts only at short range (when the protein surfaces are a few hydration shells apart). Hydrogen bonds operate at even shorter distances and may determine specificity but not first-contact modes. Surface potential complementarity can then be used to identify tentative modes of association that are most likely involved in first encounters. The final mode or modes of binding develop from these contacts and are determined by the complete force field. Surface-topography complementarity is not enforced because proteins can change conformation upon binding, a process not addressed here (see Section V).
III.1. Complementarity of surface electrostatic potential
Each protein of the complex is treated separately and at infinite dilution in pure water. For a given NMR or X-ray structure the Poisson equation is solved numerically (the problem posed by the presence of multiple conformers is discussed in Section V). The electrostatic potential ϕ is then mapped onto a grid of points Rn on the molecular surface, defined by the Lee-Richard method with a probe radius rp = 1.4 Å, yielding ϕn ≡ ϕ(Rn).
Electrostatic (polar) interactions
Local maxima ϕM,i ≡ ϕ(RM,i) (i = 1,…, NM) and minima ϕm,i ≡ ϕ(Rm,i) (i = 1,…, Nm) of the surface potential are calculated numerically: a local maximum exists at point Ri if ϕi > ϕj (or ϕi < ϕj for a minimum) for all surface points Rj such that |Rj − Ri| < γ, where γ is a characteristic length scale of the potential variations on the surface. This value is protein-dependent and somewhat arbitrary, but enough resolution can generally be achieved with γ = Raa + 2Rw ~ 6.3 Å (Raa ~ 3.5 Å is the average radius of an amino acid in a protein, and Rw ~ 1.4 Å is the radius of a water molecule). This value is also computationally convenient as it leads to relatively small NM and Nm for most proteins (see Section IV). Because of the discrete nature of the grid, ϕn shows large variations between neighboring points. Moreover, a local extremum carries no information on the spread of the potential on the local surface patch. To correct for these limitations RM,i and ϕM,i are reweighted, as
| (5) |
| (6) |
(likewise for a minimum) where 𝒩i is the number of surface grid points such that |Rn − RM,i| < γ and ϕn > 0 (or ϕn < 0 for a minimum). Because RM,i given by Eq. (5) do not generally lie on the molecular surface, they are projected onto the closest surface grid point.
With this procedure each protein p in a complex is represented by a reduced set of N(p) points, consisting of maxima and minima of the surface potential. Modes of electrostatic complementarity between proteins 1 and 2 are obtained upon minimization of the two-way norm,
| (7) |
where the distances are given in Å and the potentials in kcal mol−1 C−1; a is set to 1 C Å mol/kcal, so e is dimensionless. Index j in the first and second term determines the point on protein 2 closest to point in protein 1, i.e., ; a similar definition holds for j in the third and fourth terms, after switching indices 1 and 2. The potentials and are, respectively, a maximum and a minimum on protein p, while is either a minimum or a maximum on protein p. The form of Eq. (7) is suggested by the electrostatic energy of two interacting charges of radii d/2 separated by a distance R12 = r12 + d; here d ~3 Å, about twice the average van der Waals radius that defines the molecular surface. The term S12 in Eq. (7) prevents structural overlaps. This is usually accounted for by the r−12 term of a LJ potential, but is represented here by an atom-centered hard-sphere model.
Hydrophobic (non-polar) interactions
Analogous procedure can be used to determine non-polar complementarity. A subset of surface grid points {Rn’} ⊂ {Rn} with potentials {ϕn} is first selected, such that | ϕn | < ϕ0, where ϕ0 is an appropriate threshold. Calculation on the active form of Calmodulin (PDB 1cll) and a number of small alkanes suggests that using ϕ0 ~ 0.1 V may be sufficient to identify all the functionally-important non-polar regions in a protein. Local minima of the absolute value of the potential, ψm, i ≡ | ϕm, i |, are then calculated numerically in the new domain {Rn’}, where ϕm, i ≡ ϕ(Rm’,i) and i = 1,…, Nm’. The Nm’ positions and the absolute values of the potentials are adjusted according to Eq. (5) and Eq. (6), but using ψ instead of ϕ. Low surface potential is a necessary but insufficient condition to predict a hydrophobic region. Many points of low ϕ result simply from being at the boundary between regions of positive and negative fields. However, the average of | ϕ | over a patch [Eq. (4)] allows discrimination of bona fide hydrophobic patches that could be involved in first encounters. With this procedure each protein p in a complex is represented by a reduced set of points consisting of all the non-polar centers Rm’,i on the proteins surfaces, each characterized by a degree of polarity defined by ψm, i. Local surface area accessibility65,66 is used to define an appropriate norm. This is a simple but physically reasonable approximation commonly used in implicit solvation. Modes of non-polar complementarity between proteins 1 and 2 are obtained through a minimization of the two-way norm,
| (8) |
where θ is the Heaviside step function and Rw is the radius of a water molecule; the dimensionless parameters b(p) < 0 are discussed below. Unlike the summations in Eq.(7), which covers all the points (maxima and minima) throughout the proteins surfaces, the summations in Eq. (8) are restricted to L(p) points r(p) (a subset of the grid point Rn’ such that |r(p) − Rm’| < γ and | ϕ(r(p)) | < ϕ0) on the local surface patch surrounding each hydrophobic center Rm’; in practice γ = 2Rw = 2.8 Å. Indexes i and j are defined as in Eq. (7). The first term in Eq. (8) quantifies the degree of burial of a hydrophobic patch in protein 1 by a hydrophobic patch in protein 2; the second term yields the degree of burial of patch 2 by patch 1.
III.2. Norm optimization
Optimization of e
In this section a “point” refers to either a maximum or a minimum of the surface electrostatic potential. Optimization of e is carried out by first selecting a point i with coordinate Ri in protein 1 and a point j with coordinate Rj in protein 2 are first selected such that their potentials ϕi and ϕj have opposite signs. There are a total of such (i, j) pairs. The two points are then superimposed and the proteins oriented, as follows: a vector νi is defined on protein 1 as νi = Σn (Rn − Ri), where n runs over all the grid points on the surface such that | Rn − Ri | < s, where s defines the size of a local patch of surface centered at i; statistics of protein/protein interfaces in the PDB suggests s = 10 Å. A vector νj is defined similarly on protein 2. If νi,o = νi/|νi| and νj,o = νj/|νj| are unit vectors pointing outwardly from the surfaces, the initial orientation is such that νi,o = −νj,o. Although this is not strictly necessary since the optimization protocol can rapidly find conformations with no structural overlaps regardless of the initial orientation, it prevents unnecessary clashes at the outset of the simulation.
The setup described above leaves only one degree of freedom, namely, rotation by an angle ω around the axis νi,o. This way Nω initial conformations with random ω are selected for each pair (i, j). Any of these initial conformations should converge to the same optimized structure, but this is not always the case in practice, especially for rugged interfaces, due to imperfect sampling. Equation (7) is optimized by simulated annealing MC using a Boltzmann-like distribution f = exp(−e/T), where T is a dimensionless cooling parameter. Protein 1 (chosen as the larger protein of the pair) is fixed during the optimization, while protein 2 is translated, rotated, or roto-translated randomly with equal probabilities. Rotations are defined by an angle γ about a randomly-selected axis Ω that passes through point j. Trial moves are selected randomly from Gaussian distributions with standard deviations σt (translations) and σr (rotations) using the Box-Muller method. These are set initially at σt = 2.8 Å, i.e., one hydration layer allowed at the interface, and σr = 180°. Both distributions are adjusted on the fly during the simulation to keep the acceptance rate above 0.4 (see below). A constraint is imposed on translations such that | Ri − Rj | < Rc, which forces i to remain close to j throughout the optimization process; Rc is initially set at Rc = 2.8 Å, and trial moves that violate this distance criterion are rejected. The simulation starts at a (system-dependent) temperature TM = 10Ntot maxij(|ϕiϕj|)/d, which is decreased logarithmically in NT steps up to the lowest temperature, here Tm ~ 10−3 (in practice NT = 20). A total of 104 trial moves are performed at each temperature; this limited sampling justifies the choice of Nω initial structures. If the acceptance rate at a given temperature is less than 0.4, both σt and σr are rescaled by a factor 2/3 at the next temperature. There is no need to impose detailed balance at this stage.
Evaluation of S12 in Eq. (7) requires the calculation of distances dkl between a surface atom k in protein 1 and a surface atom l in protein 2. A trial move is rejected if dkl < Rvdw,k + Rvdw,l + c for any pair of atoms; here Rvdw,k and Rvdw,l are the van der Waals radii of the atoms; c ≥ 0 is a soft-core parameter that can be used to improve sampling of structures that are locally trapped due to the constrain | Ri − Rj | < Rc imposed in the initial alignment. This problem can arise in the presence of very irregular interfaces, whereby either i or j are buried in crevices. This is the case of residues that tend to confer binding-specificity, which are often “locked” into a cavity in the host protein (see Section IV). In the protocol proposed here c = 0, and the problem posed by locally-trapped structures is circumvented by rescaling Rc by a factor 1.2 every 104 moves, up to a maximum of 2Rc (i.e., two hydration layers allowed at the interface, at most). This relaxation criterion is physically more appealing, and is applied only at the highest temperature TM. Once a structure is accepted, the simulation at TM continues for another 104 moves, and the acceptance rate is calculated over this latter period. If the rate at TM is still zero after 105 moves and once the constraint reached 2Rc, the initial alignment is discarded (this situation has been observed in few of the several tests performed).
Optimization of Eq. (7) requires finding closest neighbors to either points or atoms in each trial move. These queries are of two kinds: (1) find point i on the surface of one protein that is closest to a point j on the surface of the other protein to evaluate the electrostatic terms; (2) find atom k in one protein that is closest to an atom l in the other protein to evaluate S12. In both cases a search based on Delaunay triangulation is used, which speeds computation one order of magnitude when compared to a direct search over pairs.
For each pair (i, j), the Nω optimized structures can be grouped into conformational families. The Cα-root mean square deviations (RMSD) between all the structures are first calculated after superimposing protein 1. These values are stored in a Nω × Nω symmetrical arrangement and clustered using a hierarchical technique67 according to the maximum intra-cluster RMSD variance (δ) desired (in practice, δ = 5 Å). The process yields Nδ d Nω clusters (conformational families). For each of the clusters, the structure with the lowest RMSD with respect to all other members of the same cluster is selected as a representative member of the family. The optimization thus generates structures {s1, s2, …, sΓ} as potentially relevant electrostatic-driven binding modes that warrant further scrutiny with the complete force field. The index m in {sm} represents a convenient array unrelated to the values of the optimized norm.
Optimization of h
The same algorithm is used. A “point” refers now to one of the non-polar centers. In analogy with the setup described above, point i and j are selected on the protein 1 and 2, respectively, yielding a total of (i, j)-pairs. For each pair, the proteins are aligned as described above. The parameters b(p) in Eq. (8) is chosen as to reflect the degree of polarity of the patch, and is given by b(p) (ϕ) = A + B |ϕ|, where A = −b(0) and B = b(0) / |ϕ0|. Thus, the more polar the patch is, the weaker the hydrophobic effect expected; and vice versa. Any positive value can be chosen for b(0); here b(0) = 4.2 (if the summations in h had dimensions of Å2, solubility data of alkanes suggest45 ~4.2 kcal/mol/Å2). The simulated annealing MC optimization is carried out with a distribution f = exp(−h / T) and a maximum temperature TM = 10b(0)maxij (2L), where L depends on i and j according to the surface area of the patch. For each (i, j)-pair clustering of the Nω initial alignments generates N'δ conformational families. Optimization of h yields a total of structures {s'1, s'2, …, s'Γ'} as potentially-relevant hydrophobicity-driven first-encounter modes.
III.3. Probability maps and biased sampling
The Λ = Γ + Γ’ conformations {sm} = {s1, s2,…,sΓ} ∪ {s'1, s'2, …, s'Γ'} identified from optimization of e and h are treated on equal basis. Each mode is a potentially-relevant first encounter mode, and its relative importance is determined by a screening protocol described below. A probability distribution can be constructed from {sm} and used as the biasing function in the full MC simulation. In each trial move a structure sm is first selected randomly out of the Λ potential modes. Moves consist of translations, rotations, and roto-translations of protein 2 selected with equal probabilities, while protein 1 remains fixed over the course of the simulation. Random rotations of side-chain dihedral angles are a fourth type of movement and can be applied to both proteins with equal probability.16 At the beginning of the simulation the center of mass of protein 1 is positioned at the origin of the laboratory coordinate system, and rotated such that its primary axis of inertia is oriented in the z direction (I(1) = k̂). The secondary and tertiary axes of inertia are oriented in the x and y directions, respectively (I(2) = î and I(3) = ĵ). All movements of protein 2 are thus relative to the molecular frame of protein 1, so simple coordinates transformations can be applied to the equations derived below if protein 1 is moved, e.g., when more than two proteins are involved.
The six degrees of freedom necessary to position protein 2 relative to protein 1 are determined by six random variables ui (i =1, …, 6) distributed uniformly in the interval [0, 1]. A translation is defined by the transformation r = rm + Δr, where rm are the coordinates of protein 2 in the selected mode sm and Δr = (x, Δy, Δz) is a random displacement obtained from normal distributions with zero mean and non-unit variance, according to the transformations , where σx, σy and σz are the standard deviations in each direction.
A rotation is defined by the transformation r = R̅rm where the matrix R̅ represents a random rotation of protein 2 by an angle Δγ around a random axis determined by the unit vector Ω = (ωx, ωy, ωz) that passes through the center of mass of protein 2. In quaternion notation this matrix is given by
| (9) |
where q = (q0, q1, q2, q3) = (cos α, ωx sin α, ωy sin α, ωz sin α) and α = (π/360) Δγ, with γ in degrees. To keep track of coordinate changes the vector Ω is obtained from a random rotation of the primary axis of inertia of protein 2 in the mode sm, as determined by the ortho-normal components , where (m, θm) are the angles in spherical coordinates. The rotation matrix is then defined by the transformations φ = φm + Δφ and θ = θm + Δθ, and by a rotation Δγ around this new axis, where are the corresponding Box-Muller transformations, and σφ, σθ and σγ the standard deviations. Normal distributions of ϕ and θ are not necessary since the main restriction is on Δγ, but imposed here for completeness.
In thermodynamic equilibrium strict detailed balance implies that the old (o) and the new (n) states are related through68 Poπo→n = Pnπn→0, where P is the corresponding Boltzmann occupancy probability, and π is the transition probability between the states, given by πo→n = αo→n po→n and πn→o = αn→o pn→o. Here α is the underlying matrix of the Markov process and p is the acceptance probability given by
| (10) |
where ΔE = En − Eo, and E is the energy of each state, now calculated with the complete force field. The ratio of a priori probabilities in Eq. (10) can be estimated from a sum of Gaussian distributions over the Λ binding modes. Defining the linear array η = (η1, η2, η3, η4, η5, η6) = (x, y, z, φ θ γ), the probability of generating a trial move within an element δη centered at η given that a mode m has been selected, is
| (11) |
where gi are the normal distributions
| (12) |
and ηi,m and σi,m are the value of ηi and its standard deviation in mode m. The total probability is
| (13) |
where hm is the probability of selecting mode m. Introducing Eq. (12) into Eq. (13) yields
| (14) |
where and , with
| (15) |
so the ratio of probabilities in Eq. (10) is given by
| (16) |
where κm can be adjusted on-the-fly through σi,m to control the acceptance rate per mode, if needed; the same approach applies to hm and Jm, although the latter also accommodate changes in the coordinates ηi,m of the mode as new structures are accepted. If σi,m and ηi,m are kept fixed over the course of a simulation (i.e., fixed a priori probabilities), the biasing function is non-adaptive; if σi,m and/or ηi,m change, the function is adaptive.
Screening of binding modes
The probability hm in Eq. (16) is defined over the discrete set {sm}, and is chosen here as a Boltzmann-like distribution
| (17) |
where and λ is a scaling factor discussed below. Energies are measured with respect to the fully dissociated state, ΔEm = Em − E∞, where Em is the energy of the complex in mode m now calculated with the complete force field. These energies are calculated as canonical averages over short MC simulations of the complex in mode m, , where and Nm are the energies and the number of accepted structures. The simulation is biased and non-adaptive, determined by hm = 1 and hk ≠ m = 0, thus Eq. (16) is simplified to
| (18) |
with J given by
| (19) |
where x is either o or n. The parameter λ ≥ 1 in Eq. (17) is used to smooth the distribution {hm} over the set {sm}. This is a safeguard measure against limitations of the prescreening protocol (including the definition of the norm) and the force field to properly identify physically relevant first-encounter modes of association. Small errors in the estimation of energies in Eq. (17) may eliminate modes (in practice, hm << 1) that are worth sampling, or over emphasize sampling of less important modes, thus compromising the efficiency of the method. This problem is alleviated by using λ > 1 (see Section IV), in a process akin to high-temperature annealing.
Self-adaptive biased Monte Carlo
strict detailed balance is imposed by using Eq. (16) in the acceptance criterion established by Eq. (10). In the self-adaptive biased sampling used here both σi,m and ηi,m in Eq. (16) and Eq. (19) are allowed to change over the course of the simulation. The probability distribution {hm} could also change to improve efficiency by increasing/decreasing sampling of certain modes as the simulation progresses, but this adaptation is not used here. An acceptance rate bm is calculated for each mode every 103 times the mode is selected, and σi,m is then scaled up or down to keep the acceptance rate of that mode within a predetermined value. The same scaling factor applies to all the degrees of freedom, except σφ,m and σθ,m. Each time a mode m is selected the coordinates ηi,m are updated to the last accepted structure for that mode. This is accomplished in practice by translating the center of mass and rotating the primary axis of inertia of protein 2 to the corresponding values of the accepted structure; translations and rotations Δηi are then measured with respect to the new mode coordinates ηi,m. If Δηi in an accepted move is larger than 2σi for a given mode m, then σi,m is reset to its original value since it is possible that a new local minimum has been identified.
IV. Results
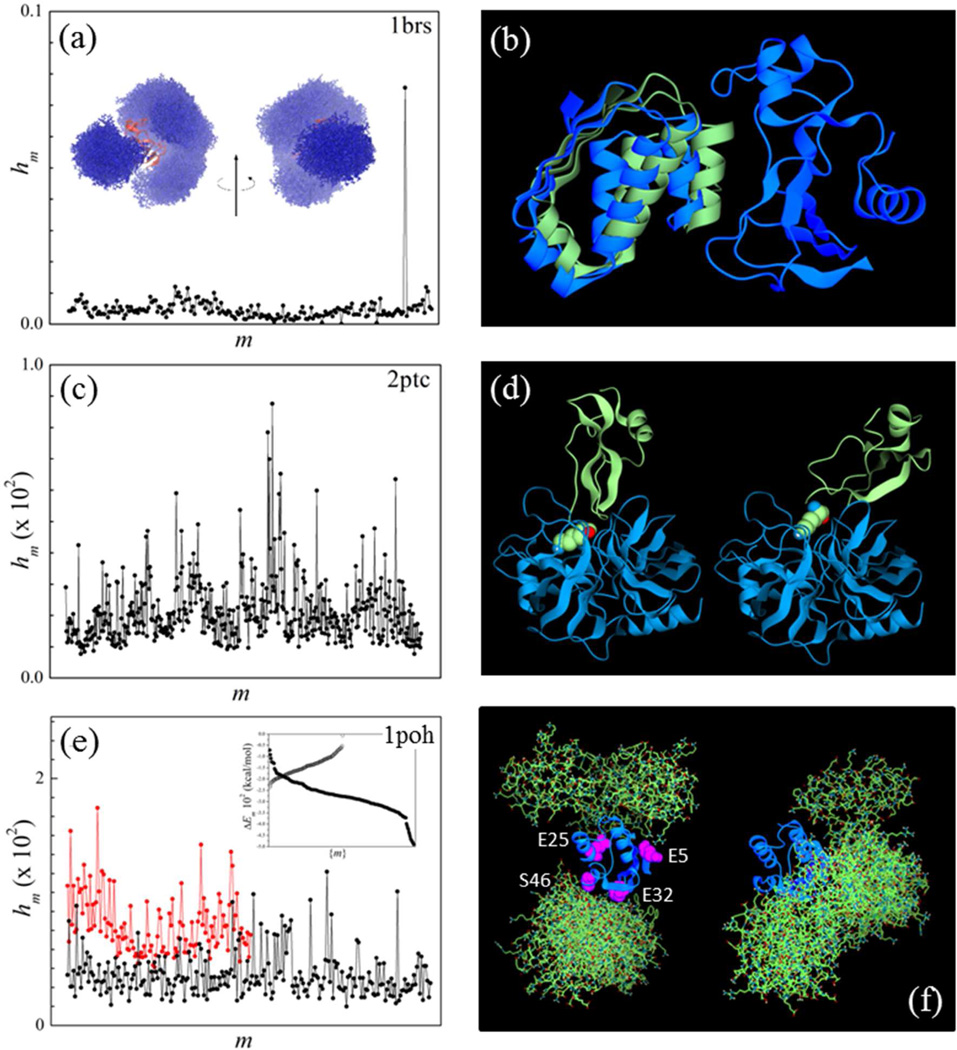
Three binary complexes are chosen to illustrate the application of the method: Barnase/barstar (1brs) has long been used in experimental and computational studies of protein binding.55,69,70 The complex has been used here as a guide for model refinement. The other complexes considered are: trypsin bound to a protein inhibitor (2ptc) and histidine-containing phosphocarrier protein HPr (1poh). These complexes were chosen here because they challenge different aspects of the method: in the bound state, a specificity-conferring Lys residue (K15) in the ligand of 2ptc is buried into a narrow cavity of the protein, so the complex provides a stringent test for the sampling method; 1poh has been shown to form ultra-weak self-association, with negligible dimerization in solution, so the complex provides a stringent test for the continuum model.
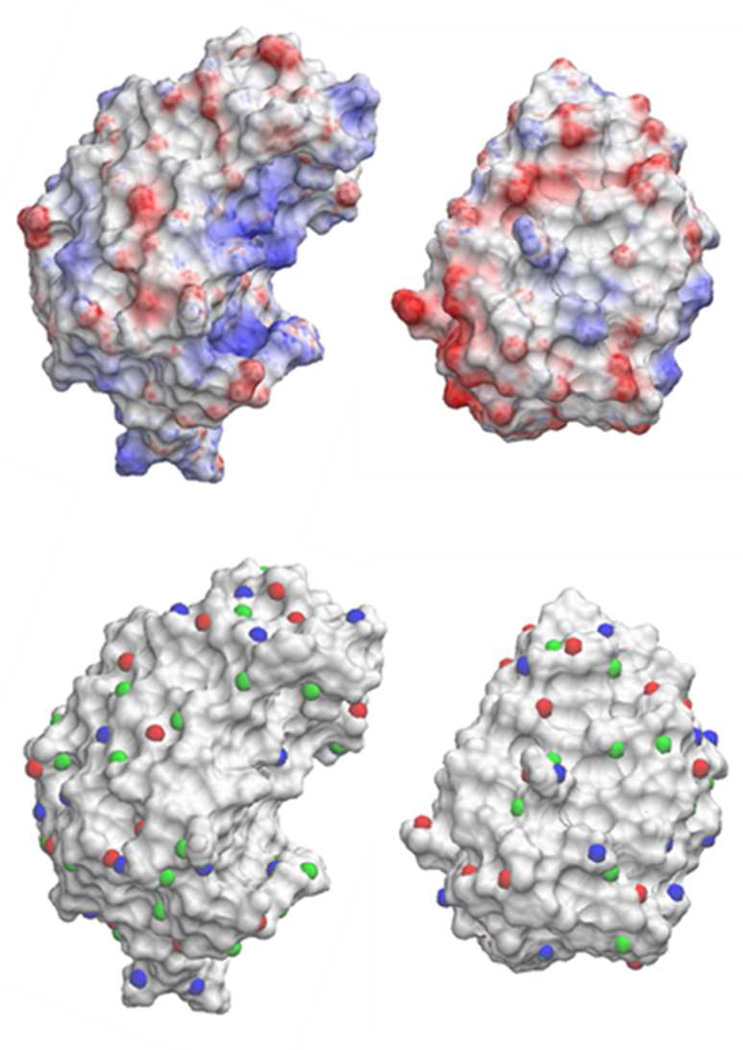
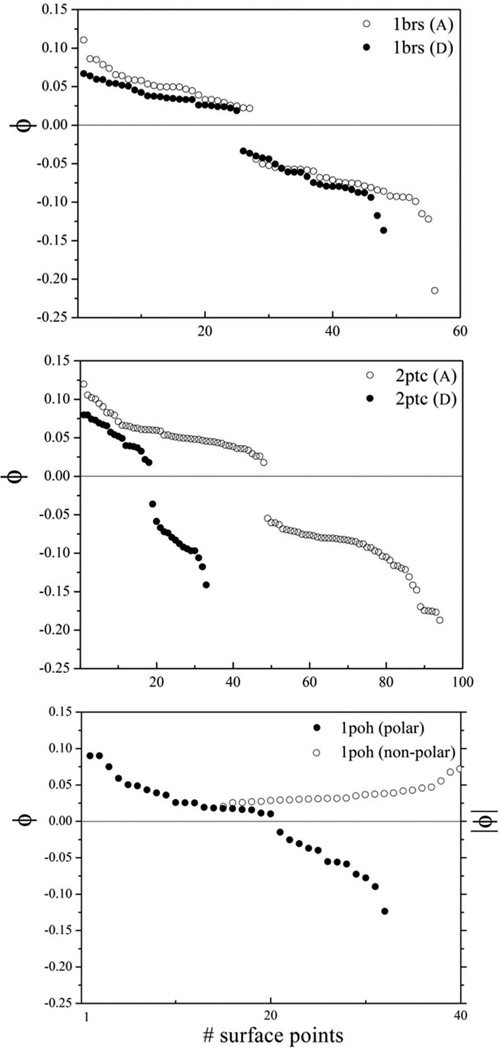
Figure 3 shows the electrostatic potential on the molecular surface of barnase and barstar, calculated as standard solutions of the Poisson equation. Barnase (protein 1) has 27 local maxima and 29 minima, and 36 non-polar centers, whereas barstar (protein 2) has 25 maxima and 23 minima, and 29 non-polar centers, yielding Ntot = 1346 initial (i, j) pairs to be considered for optimization of e and N’tot = 1044 for h. For the other two complexes, Ntot = 1548 (2ptc) and 480 (1poh), and N’tot = 988 (2ptc) and 676 (1poh). Figure 4 shows the values of the potential (in Volts) at the maxima and minima; the values of | ϕ | in 1poh is also shown for comparison. It is not possible to decide from these values alone which (i, j) pairs are more likely to be involved in first encounters, so all the pairs should in principle be considered in the optimization of the norms. To reduce the computational cost only the ten highest maxima and the ten lowest minima in each protein are used in the optimization of e. This simplification yields 200 (i, j) pairs; and for each of these pairs Nω = 24 initial alignments are generated. Experiments have shown that electrostatics is the main force that controls binding in the three complexes; hydrophobicity plays a role only in HPr. This knowledge a priori allows a convenient simplification by omitting the optimization of h in 1brs and 2ptc. This simplification applies only to the prescreening stage. The SCP model does contain45 a simplified “hydrophobic term” (not discussed here; see Section V) which is used in both the screening stage and in the full MC simulation. Thus, bypassing the optimization of h in a particular system (here brbs and 2ptc) does not mean that hydrophobic interactions are ignored; it only means that hydrophobicity does not determine the first encounters. In contrast, for 1poh only non-polar patches with | ϕ |< 0.03 V (suggested by the surface potentials of calcium-loaded calmodulin) are considered [cf. Fig. 4].
Figure 3.
Electrostatic potential (upper panel) on the molecular surface of barnase (left) and barstar (right) calculated from conventional numerical solutions of the Poisson equation (εp = 2; εw = 78). Positions of maxima (blue) and minima (red) and non-polar centers (green) are calculated from Eq. (5) and (6) (lower panel).
Figure 4.
Values (in Volt) of the maxima and minima of the surface potentials ϕ in the three systems studied (chain A in 1brs is barnase and trypsin in 2ptc). The absolute values ψ = | ϕ | of the surface potential at the non-polar centers in 1poh are also shown.
After norm optimization and clustering, a total of 218 binding modes are obtained for 1brs, 474 for 2ptc, and 243 (polar) and 123 (non-polar) for 1poh. The inset of Fig. 5a shows the superposition of all the modes in 1brs, with barnase at the center. Two major first-contact regions are apparent, each containing multiple orientations of barstar; the most populated region is located in the vicinity of the native binding site of barnase. For the other two complexes there are multiple binding regions surrounding the central protein 1, with the most scattered distribution observed in 1poh (see below). Optimization of e took ~30–50 min per mode, depending on the complex; 90% of the CPU time was used to compute the electrostatic component of the norm [first four terms of Eq. (7)] and the remainder 10% for the calculation of S12. Optimization of h took ~30 min per node, but this can be reduced substantially by decreasing the number of points L used to define the area of the patch in Eq. (8) (here L ~ 80–100). The optimization was performed in Matlab using standard functions from the statistic toolbox, and on a single 2.8 GHz Intel X5660 processor with 24 GB memory. The code was not parallelized.
Figure 5.
(a) Probability distribution of prescreened modes of the barnase/barstar complex calculated from Eq. (17) with λ = 25. The mode m’ with the highest weight hm’ is near-native. Inset: prescreened modes of barstar (atom representation; blue) and barnase (ribbon; red) obtained upon optimization of the electrostatic norm e [Eq. (7)]. These putative electrostatic-driven first-contact modes determine the biasing function for the self-adaptive conformational bias MC sampling. (b): Mode m’ (blue) and crystal structure (green) of barnase bound to barstar. (c) Same as in (a) for 2ptc. (d) Trypsin/inhibitor complex (2ptc): crystal structure (left) and prescreened mode m’ with the smallest Cα-rmsd with respect to the crystal structure (right); m’ has the fifth highest weight in (c); K15 of the inhibitor protein is shown (purple). (e): Same as in (a) 1poh (black); probability distribution obtained upon optimization of the hydrophobic norm h [Eq. (8)] is also shown (red). Inset: energy of pre-screened modes (polar: solid circles; non-polar: open circles); (f) Histidine-containing phosphocarrier protein HPr (1poh): conformations of the ten highest hm modes obtained upon optimization of e (electrostatic modes; left) and h (hydrophobic modes; right) superimposed to a central HPr protein; amino acids used as labels in a recent NMR study of ultra-weak self-association are shown.
Screening of the prescreened modes was performed with biased non-adaptive MC (103 steps) at 25 °C (for 1brs and 2ptc) and 35 °C (1poh), using σx = σy = σz = 0.5 Å; σφ = σθ = 90°, and σγ = 2.5°. The united-atom (param19) representation of the CHARMM force field48 was used, with the SCP model16 implemented in the version c35 of the CHARMM program. No cutoffs were applied to the non-bonded interactions in order to account for long-range effects. Figure 5 (left panels) shows the probability distributions hm of prescreened modes {m} using a smoothing parameter λ = 25; only one mode stands out in 1brs, with a weight hm’ ≈ 0.08. This mode is very close to the native complex and has a Cα-rmsd of ~1.9 Å with respect to the crystal structure (Fig. 5b; blue). This shows that electrostatic pre-screening followed by screening with the complete force field is sufficient to identify a near-native conformation in the barnase/barstar complex. This is probably the case for other systems driven to association by strong electrostatic interactions. The hm distributions in the other complexes are qualitatively different (Figs. 5c and 5e): for 2ptc the closest prescreened mode to the native complex has a Cα-rmsd of ~5 Å (Fig. 5d), and corresponds to the fifth highest weight hm. As in 1brs, this mode is a good candidate for first contact since K15 in the ligand is near the pocket in trypsin and oriented towards it (Fig. 5d, right). For 1poh several electrostatic modes also have similar weights (Fig. 5e; black), and the highest ten modes are shown in Fig. 5f (left). These modes are clustered close to residues E5, E25, E32 and S46, which were used as labels in a recent NMR study11 of ultra-weak self-association of HPr. The weights of the hydrophobic modes are also shown for comparison (Fig. 5e; red); the ten modes with the highest weights are displayed in Fig. 5f (right). Electrostatic and hydrophobic modes plotted in Fig. 5e are normalized independently for clarity. The scattered distribution of both types of modes (Fig. 5f) and the similarity of weights (Fig. 5e) are consistent with multiple first-encounters between the proteins and may reflect the non-specific nature of the association. The inset to Fig. 5e shows the energies ΔEm of the modes [in Eq. (17)]. Despite the substantial energy overlap between electrostatic and hydrophobic modes it is apparent that first encounters in HPr are driven mainly by electrostatics.
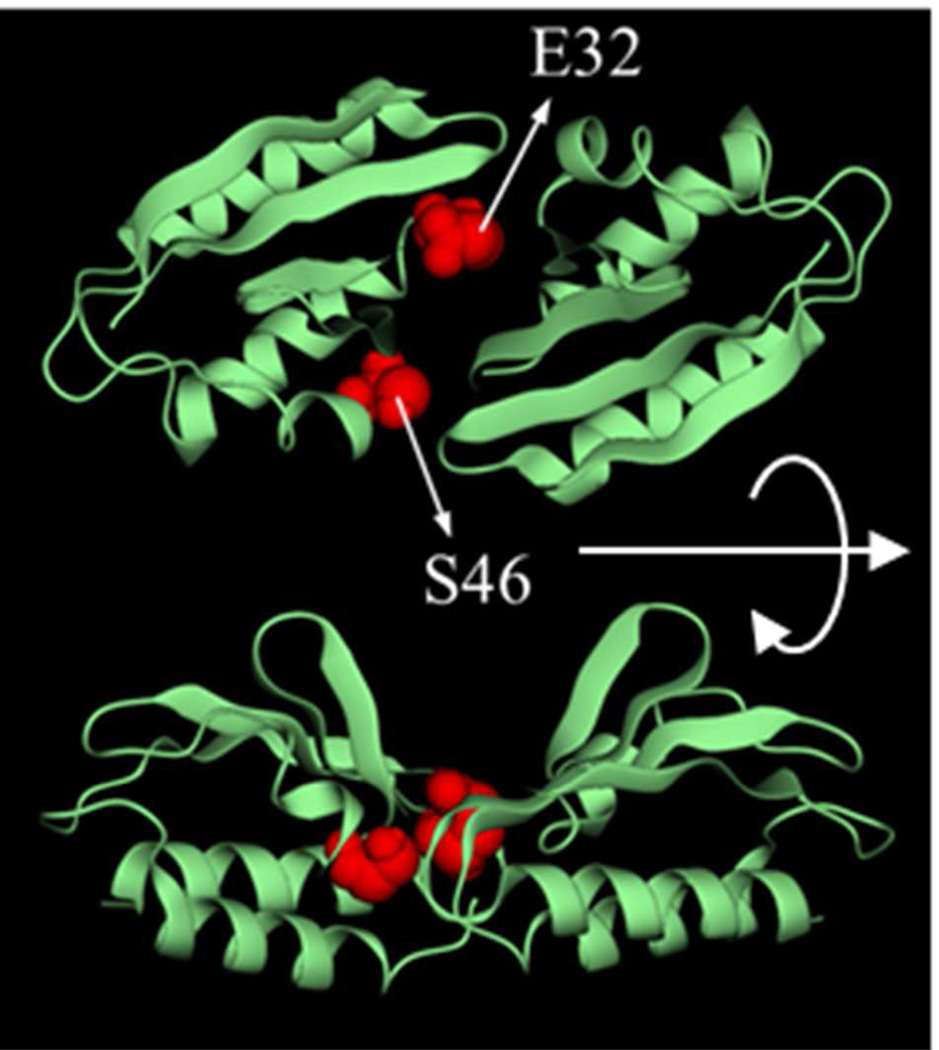
The complete sets {hm} in Fig. 5 were used to create the initial spatial distributions for the self-adaptive MC sampling. Simulations were performed at the same temperature used for screening, and consisted of 106 steps with σx = σy = σz = 2.5 Å; σφ = σθ = 90° and σγ = 20°. These values were chosen based on a number of combinations tested. Changing these values has no major effect in the results discussed below, but important variations in efficiency were observed due to convergence problems. In these simulations only ηi,m are adapted, while σi,m remains fixed regardless of the acceptance rate per mode. Simulations were performed in a single processor with a non-parallelized version of the SCP model, and took ~24−48 CPU hours, depending on the complex. The parallel version of the SCP model scales well up to 24 processors, and can reduce the simulation time one order of magnitude. For 1brs the native complex (Fig. 5b; green) was identified within a few thousands steps. Because there are 234 prescreened modes, the overall acceptance rate is small since all the modes are selected for trial moves, albeit with probabilities determined by hm. The conformational distribution obtained upon convergence is very narrowly centered in a single mode identified as native. For 2ptc convergence takes much longer but the native complex was also identified correctly. The dissociation energy of the native complex is estimated at ~5.5 kcal/mol; and the association is thus strong and specific. For 1poh a single mode is also obtained (Fig. 6), but the distribution of accepted structures is much broader than in the other two complexes, which is consistent with a shallower energy surface. The predicted native complex is quite symmetrical, with residues E32 and S46 at the protein/protein interface. Dissociation from this structure requires a very small energy, only ~1.3 kcal/mol, but this is still too large and the presence of stable homodimers cannot be ruled out at 35 °C. Experiments carried out at this temperature indicate that HPr form multiple transient associations, but no specific homo-dimerization.11 There are several possible explanations for this discrepancy that warrant further scrutiny: i) backbone flexibility may need to be included to obtain a more accurate canonical distribution. Given the transient nature of the association it is unlikely that induced fit is involved, so conformational selection may be a more important mechanism in this case (Section V); ii) current force fields are not yet accurate enough to discriminate ultra-weak modes, although progress being made, especially in the treatment of non-bonded terms (e.g., inclusion of polarizability), as these are most relevant in protein-protein interactions. Improvements and careful optimization of the solvent model, especially the treatment of the aqueous interface is an essential component and must be pursued simultaneously; iii) specific water-mediated interactions at the protein interfaces may also be important, and a continuum model cannot represent them properly unless some degree of granularity is introduced. In addition, liquid-structure forces (SIF) are non-pairwise additive and costly to compute. An algorithm has been reported to include SIF in a continuum model for use in Langevin dynamics47; iv) changes in protonation states upon pKa shifts have been ignored and could change the interaction energy landscape; a primitive version of the SCP model has been used to predict pH-dependent properties in proteins71 and is well suited for on-the-fly assignment of protonation states, at the expense of CPU time. These limitations apply to all protein-protein interactions but are more problematic when dealing with weak and ultra-weak associations. These interactions thus provide a stringent benchmark for further development.
Figure 6.
Symmetrical homodimer (representative member of the ensemble) obtained upon convergence of the self-adaptive biased MC simulation. The binding energy of this state is estimated at ~1.3 kcal/mol.
Overlooking potentially relevant modes during prescreening and/or screening (possibly due to limitations in the norm optimization protocol, the norm itself, or the force field) is of concern since success of the method hinges on having identified a mode with sufficiently large probability to be selected during sampling. To test the robustness of the method to changes in the hm distribution, the main mode m’ in 1rbs was removed from the set (in practice, hm’ = 0). In this case the simulation takes much longer to converge, but the native complex is also identified within a few hundred thousand steps. In this case a secondary mode with a small weight slowly moves towards the native conformation during the self-adaptive process and takes over the local distribution left unpopulated when m’ was removed. This drift of a distant mode towards the native mode is possible because several prescreened modes m ≠ m’ have Cα-rmsd in the ~2 4 Å range with respect to the crystal structure. Therefore, given the chance to be selected they make important contributions to the acceptance rate once m’ is removed. This also highlights the importance of smoothing hm through λ.
V. Discussion
Weak and ultra-weak interactions can play a role in protein recognition and drive spontaneous self-assembly and aggregation of larger multimeric complexes, such as crystals, amyloid fibrils, and virus capsids. These interactions are difficult to detect experimentally. They also present a major challenge to the Hamiltonian because effects that can be ignored or treated in simplified ways in small systems at infinite dilution now require adequate treatment and optimization. These include the effects of interfaces, and long-range electrostatic and non-electrostatic effects of water exclusion. The problem posed by interfaces is complex and multifaceted, involving the dielectric19,20,47,72 and the structural47,73 response of the liquid, and its dynamic19,20 and entropic17 contributions. In particular, the entropy of an aqueous interface is difficult to capture in a mean field approximation. The entropy can be divided into an orientational and a translational contribution. The orientational component is related to the static dielectric response of the interface, and an algorithm has been proposed to estimate it self-consistently in a continuum approximation.72 The translational behavior is more complicated and is related to the mobility of water in the hydration shells. Recent simulations have shown that water in the second shell of a DNA molecule is more mobile than water in either the first shell or the bulk phase.17 Because of the substantial changes in surface hydration upon protein association or dissociation, different hydration shells may contribute differently to the free energy of binding. These effects need additional studies, especially in large complexes, and may eventually require proper implementation in a continuum model. The SCP model partially contains both components of the entropy, which is reflected in the sigmoidal shape of the screening functions D and in the mean field effects of SIF through R. In contrast to the entropy of water, the entropy of the molecular system under consideration can be calculated directly from the statistical distributions obtained from the biased sampling; backbone flexibility may introduce practical but not conceptual complications. Methods also exist to estimate the vibrational entropy contributions.
Although short-range electrostatic effects of water-exclusion [represented in the self-energy term of Eq. (1) through the conformation-dependence of R given by Eq. (4)] make important contributions to the binding energy, long-range corrections [represented in by both the interaction and the self-energy terms through the conformation-dependence of D’s given by Eqs. (2) and (3)] cannot be ignored. The problem posed by long-range bulk-water electrostatics in modeling hydration forces has been discussed.74 These effects become increasingly important as the size of the system increases, e.g., during aggregation or self-assembly, or in crowded environments. Ignoring these corrections introduces an error of ~3.5 kcal/mol (~20%) in the binding enthalpy of the barnase/barstar complex as estimated with the SCP model. Errors of this magnitude can be ignored when predicting specific (usually strong) binding modes, but are clearly unacceptable in thermodynamic calculations and for prediction of weak association for which chemical accuracy is ultimately needed. It has been shown here that long-range electrostatics can be fine-tuned to provide a better estimate of binding enthalpies. The balance between interaction and self-energy terms in Eq. (1) is critical to reproduce the correct binding energy because they oppose each other. Long-range electrostatic contributions in real systems may decay more rapidly or more slowly than the exponential decays modeled by Eqs. (2) and (3), and systematic calculations in systems of different sizes should be performed to refine the model.
There is experimental evidence that dispersion forces make important contributions to protein-ligand binding enthalpy.58 This has long been recognized59 and attempts have been made to include a dispersion term in implicit solvent models. Except in the case of purely non-polar solutes such corrections can be neglected since even in small polar or charged molecules other effects at the aqueous interface (e.g., the dielectric response of the liquid and liquid-structure forces) play a more important role.75 In larger systems/interfaces, however, their contribution can be substantial and no longer be ignored. Thus, both long-range electrostatics and dispersion contribute to the cohesive energy of a macromolecular complex. The simulations discussed in Section II.2 support these findings. Non-electrostatic effects of water exclusion may actually play an important role in weak and ultra-weak association.
Developments of the SCP model have hitherto focused on electrostatics and liquid-structure forces at protein/water interfaces. These are the most important effects in a large class of biological systems, including proteins and nucleic acids, ions, osmolytes and cryoprotectants (see review in32,75). In other bioactive macromolecules (e.g., Ca2+-loaded Calmodulin used in Section III) hydrophobic interactions are known to be a key feature of their function. A more advanced treatment of hydrophobicity in the SCP model may thus be desirable. However, modeling hydrophobic forces in molecules of arbitrary shapes and morphologies is difficult76–80 and has not yet been addressed in a practical manner. In small non-polar molecules improvements have been reported with rather minor changes to the commonly used solvent-accessible surface-area model.81–84 It is unclear whether more sophisticated treatments are needed in real proteins (generally characterized by sparse distributions of relatively small hydrophobic patches punctuated by regions of high polarity and local charge).32 Recent dynamics simulations of small amphiphilic molecules have provided insight into the role of the micro-complexity of water on the hydrophobic effect in systems that more closely resemble the heterogeneity of real protein surfaces.85 Simulations have also shown that such surfaces display a behavior in between that of an idealized hydrophobic surface (a common theoretical construct) and one that is strongly hydrophilic.86 Unlike protein electrostatics there is a paucity of useful experimental information that can be used to validate hydrophobic models, so carefully-designed simulations may ultimately be needed to advance the field.
A method has been described to construct a biasing function for efficient configurational bias simulations that allows detection of weak and ultra-weak binding modes and populations. The method has been tested in three binary complexes, but can be extended to multiprotein systems provided that complexation occurs through a succession of binary reactions. This extension is required to simulate crowded environments or subcellular processes where multimeric complexes (averaging four or more units per complex2,3) are common. In a recent assessment87 of experimental methods aimed at predicting protein-protein binding in a three-component systems only nine out of twelve participant groups were able to conclude that barnase and BiNase2 compete for binding to barstar, so that the formation of a ternary complex is not possible. Multi-component systems present a greater challenge, especially if some of the proteins interact weakly or no-specifically. Therefore, having the capability to explore efficiently (that is, rapidly and with statistical significance) the spatial distribution of many proteins simultaneously is desirable. The biasing function proposed here allows mixing large and local changes in the protein spatial distributions, which enhances sampling of microstates that may be overlooked with non-biased sampling. The method can also be used to identify regions at a protein surface that are most likely to bind ions and cosolutes since they may be attracted to multiple sites. These molecules affect almost all macromolecular properties (including protein denaturation, stabilization, aggregation, and dissociation), and can interact specifically and non-specifically with the proteins.
It has been assumed that preferential encounters in solution are driven by electrostatic and hydrophobic forces, and the norms e and h defined in Eqs. (7) and (8) reflect this assumption. The functional forms of the norms are adequate simplification of the physical effects that each intends to describe, and designed specifically for computational efficiency. Electrostatic complementarity has long been used as a strategy to predict specific binding modes,55 but this approach alone is insufficient to predict weaker association,88 a problem compounded in the case of non-specific and multiple binding modes. The approach has been extended and used here only to identify first-encounter modes. The binding modes obtained from norm optimization determine the spatial distribution from which the complexes evolve. The final mode (or modes) of association are obtained from the canonical distribution upon convergence of the self-adaptive biased sampling.
Proteins in aqueous solution display varying degrees of backbone flexibility. Statistics from the PDB have revealed that many proteins undergo only small changes in their overall fold upon binding (typically ~1 Å in Cα-rmsd) as their interfaces are largely pre-formed.88 The rigid-backbone approximation is thus reasonable in many cases and has been used successfully to predict the structure of unknown complexes.89 This approximation is usually the first stage in almost all docking algorithms,90–92 and good estimates of binding modes in this initial stage is critical. The rigid-backbone approximation might actually suffice in the case of weak or ultra-weak binding because these interactions are short-lived, possibly lasting less than the time-scale necessary to induce backbone conformational changes (although this is a conjecture that needs experimental corroboration). Important exceptions however exist since flexibility is at the core of protein function. For example, trypsin-TPI undergoes rigid-backbone association, but the closely-related trypsinogen-TPI does not. In general, oligomeric proteins and antigen-antibody complexes tend to challenge this assumption. Moreover, some DNA- and RNA-protein complexes are known to undergo co-folding during recognition and binding.93 Even proteins typically thought of as rigid in solution undergo localized conformational changes, usually in unstructured regions such as loops. A recent study of the dynamics of ubiquitin94 suggests that the forty-plus crystal structures of this rather rigid protein in the PDB are likely conformers pre-selected by the ligand. Upon association of a given conformer there appear to be only small rearrangements of the backbone and the side chains. This example illustrates a general feature of macromolecular association, namely, the coexistence of induced fit and conformational selection. The method presented in this paper can be adapted to incorporate both. Because of the transient nature of weak and ultra-weak binding conformational selection is probably more important than induced fit. Induced fit is most robustly addressed molecular dynamic simulations using explicit water or by Langevin dynamics with the SCP model for consistency.95 In this brute-force approach each binding mode identified by the method is used as a starting structure in the dynamics. An alternative is to allow backbone conformational changes over the course of the MC simulation. This is most efficiently carried out in the context of scaled collective variables,96,97 which allows concerted movements of the backbone dihedral angles to improve the acceptance rate. This method has been used previously to study unstructured segments in globular proteins98 and transmembrane receptors.42 A priori knowledge of flexible segments, e.g., from crystallographic temperature factors or principal component analysis of a dynamic trajectory,94,99 can reduce the computational cost by restricting collective movements to those regions only.98 On the other hand, conformational selection can be incorporated in a straightforward manner with no additional modifications of the method presented in this paper. However, this requires identifying structural families of each molecule in solution prior to binding. Each conformation can then be treated independently. Induced fit can in turn be introduced in each sub-system as described. Identifying structural families in solution is not straightforward, and different methods should probably be used depending on the system size. Configurational bias MC simulations (e.g., conformational memories41) can efficiently identify multiple conformers in peptides41,44 and is probably the preferred method for small systems.
Acknowledgment
This study utilized the high-performance computer capabilities of the Biowulf PC/Linux cluster at the NIH. This work was supported by the NIH Intramural Research Program through the CIT and NINDS, and by the Internal NIST Research Fund.
References
- 1.Stelzl U, Worm U, Lalowski M, Haenig C, Brembeck FH, Goehler H, Stroedicke M, Zenkner M, Schoenherr A, Koeppen S, et al. A Human Protein-Protein Interaction Network: A Resource for Annotating the Proteome. Cell. 2005;122:957–968. doi: 10.1016/j.cell.2005.08.029. [DOI] [PubMed] [Google Scholar]
- 2.Krogan NJ, Cagney G, Yu H, Zhong G, Guo X, Ignatchenko A, Li J, Pu S, Datta N, Tikuisis AP, et al. Global Landscape of Protein Complexes in the Yeast Saccharomyces Cerevisiae. Nature. 2006;440:637–643. doi: 10.1038/nature04670. [DOI] [PubMed] [Google Scholar]
- 3.Alber F, Dokudovskaya S, Veenhoff LM, Zhang W, Kipper J, Devos D, Suprapto A, Karni-Schmidt O, Williams R, Chait BT, et al. The Molecular Architecture of the Nuclear Pore Complex. Nature. 2007;450:695–701. doi: 10.1038/nature06405. [DOI] [PubMed] [Google Scholar]
- 4.Herman ML, Farasat S, Steinbach PJ, Wei MH, Toure O, Fleckman P, Blake P, Bale SJ, Toro JR. Transglutaminase-1 (TGM1) Gene Mutations in Autosomal Recessive Congenital Ichthyosis: Summary of Mutations (Including 23 Novel) and Modeling of TGase-1. Human Mutation. 2009;30:537–547. doi: 10.1002/humu.20952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Prusiner SB. Prions. Proc. Nat. Acad. Sci. (USA) 1998;95:13363–13383. doi: 10.1073/pnas.95.23.13363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Colland F, Jacq X, Trouplin V, Mougin C, Groizeleau C, Hamburger A, Meil A, Wojcik J, Legrain P, Cauthier JM. Functional Proteomics Mapping of a Human Signaling Pathway. Genome Res. 2004;14:1324–1332. doi: 10.1101/gr.2334104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Goehler H, Lalowski M, Stelzl U, Waelter S, Stroedicke M, Worm U, Droege A, Lindenberg KS, Knoblich M, Haenig C, et al. A Protein Interaction Network Links GIT1, an Enhancer of Huntingtin Aggregation, to Huntington's Disease. Mol. Cell. 2004;15:853–865. doi: 10.1016/j.molcel.2004.09.016. [DOI] [PubMed] [Google Scholar]
- 8.Nienhaus GU, editor. Protein-Ligand Interactions: Methods and Applications. Humana Press; 2005. [Google Scholar]
- 9.Clore GM, Tang C, Iwahara J. Elucidating Transient Macromolecular Interactions using Paramagnetic Relaxation Enhancement. Curr. Op. Struc. Biol. 2007;17:603–616. doi: 10.1016/j.sbi.2007.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tang C, Iwahara J, Clore GM. Visualization of Transient Encounter Complexes in Protein-Protein Association. Nature. 2006;444:383–386. doi: 10.1038/nature05201. [DOI] [PubMed] [Google Scholar]
- 11.Tang C, Ghirlando R, Clore G. Visualization of Transient Ultra-Weak Protein Self-Association in Solution using Paramagnetic Relaxation Enhancement. J. Amer. Chem. Soc. 2008;130:4048–4056. doi: 10.1021/ja710493m. [DOI] [PubMed] [Google Scholar]
- 12.Ellis RJ. Macromolecular Crowding: Obvious but Underappreciated. TIBS. 2001;26:597–604. doi: 10.1016/s0968-0004(01)01938-7. [DOI] [PubMed] [Google Scholar]
- 13.Luby-Phelps K. Cytoarchitecture and Physical Properties of Cytoplasm: Volume, Viscosity, Diffusion, Intracellular Surface Area. Int. Rev. Cytol. 2000;192:189–221. doi: 10.1016/s0074-7696(08)60527-6. [DOI] [PubMed] [Google Scholar]
- 14.Tuffery P, Derremaux P. Flexibility and Binding Affinity in Protein-Ligand, Protein-Protein and Multi-Component Protein Interactions: Limitations of Current Computational Approaches. J. R. Soc. Interface. 2012;9:20–33. doi: 10.1098/rsif.2011.0584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Meiler J, Baker D. Rosetaligand: Protein-Small Molecule Docking with Full Side-Chain Flexibility. Proteins. 2006;65:538–548. doi: 10.1002/prot.21086. [DOI] [PubMed] [Google Scholar]
- 16.Hassan SA, Steinbach PJ. Water-Exclusion and Liquid-Structure Forces in Implicit Solvation. J. Phys. Chem. B. 2011;115:14608–14682. doi: 10.1021/jp208184e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pascal TA, Goddard WA, III, Maiti PK, Vaidehi N. Role of Specific Cations and Water Entropy on the Stability of Branched DNA Motif Structures. J. Phys. Chem. B. 2012;116:12159–12167. doi: 10.1021/jp306473u. [DOI] [PubMed] [Google Scholar]
- 18.Oleinikova A, Sasisanker P, Weingartner H. What can really be Learned from Dielectric Spectroscopy of Protein Solutions? A Case Study of Ribonuclease A. J. Phys. Chem. 2004;108:8467–8474. [Google Scholar]
- 19.Schroder C, Rudas T, Boresch S, Steinhauser O. Simulation Studies of the Protein-Water Interface: I. Properties at the Molecular Resolution. J. Chem. Phys. 2006;124:234907. doi: 10.1063/1.2198802. [DOI] [PubMed] [Google Scholar]
- 20.Rudas T, Schroder C, Boresch S, Steinhauser O. Simulation Studies of the Protein-Water Interface. II. Properties at the Mesoscopic Resolution. J. Chem. Phys. 2006;124:234908. doi: 10.1063/1.2198804. [DOI] [PubMed] [Google Scholar]
- 21.Merzel F, Smith JC. Is the First Hydration Shell of Lysozyme of Higher Density than Bulk Water? Proc. Nat. Acad. Sci. (USA) 2002;99:5378–5383. doi: 10.1073/pnas.082335099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Loffler G, Schreiber H, Steinhauser O. Calculation of the Dielectric Properties of a Protein and its Solvent: Theory and a Case Study. J. Mol. Biol. 1997;270:520–534. doi: 10.1006/jmbi.1997.1130. [DOI] [PubMed] [Google Scholar]
- 23.Schellman JA. Fifty Years of Solvent Denaturation. Biophys. Chem. 2002;96:91–101. doi: 10.1016/s0301-4622(02)00009-1. [DOI] [PubMed] [Google Scholar]
- 24.Timasheff SM. The Control of Protein Stability and Association by Weak Interactions with Water: How Do Solvents Affect These Processes? Annu. Rev. Biophys. Biomol. Struct. 1993;22:67–97. doi: 10.1146/annurev.bb.22.060193.000435. [DOI] [PubMed] [Google Scholar]
- 25.Arakawa K, Timasheff SM. The Stability of Proteins by Osmolytes. Biophys. J. 1985;47:411–414. doi: 10.1016/S0006-3495(85)83932-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mancinelli R, Botti A, Bruni F, Ricci MA, Soper AK. Perturbation of Water Structure due to Monovalent Ions in Solution. Phys. Chem. Chem. Phys. 2007;9:2959–2967. doi: 10.1039/b701855j. [DOI] [PubMed] [Google Scholar]
- 27.Parsegian VA. Protein-Water Interactions. Int. Rev. Cytol. 2002;215:1–31. doi: 10.1016/s0074-7696(02)15003-0. [DOI] [PubMed] [Google Scholar]
- 28.Parsegian VA, Rau DC. Water near Intracellular Surfaces. J. Cell Biol. 1984;99:196–200. doi: 10.1083/jcb.99.1.196s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zheng J-M, Pollack GH. Long-range Forces Extending from Polymer-Gel Surfaces. Phys. Rev. E. 2003;68:031408. doi: 10.1103/PhysRevE.68.031408. [DOI] [PubMed] [Google Scholar]
- 30.Larsen AE, Grier DG. Like-Charge Attractions in Metastable Colloidal Crystallites. Nature. 1997;385:230–233. [Google Scholar]
- 31.Crocker JC, Grier DG. When Like Charges Attract: The Effect of Geometrical Confinement on Long-Range Colloidal Interactions. Phys. Rev. Lett. 1996;77:1897–1900. doi: 10.1103/PhysRevLett.77.1897. [DOI] [PubMed] [Google Scholar]
- 32.Hassan SA, Mehler EL. In Silico Approaches to Structure and Function of Cell Components and their Assemblies: Molecular Electrostatics and Solvent Effects. In: Egelman E, editor. Comprehensive Biophysics. Vol. 9. Oxford: Academic Press; 2012. pp. 190–228. [Google Scholar]
- 33.Halle B. Protein Hydration Dynamics in Solution: a Critical Survey. Phil. Trans. R. Soc. Lond. B. 2004;359:1207–1223. doi: 10.1098/rstb.2004.1499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Frolich A, Gabel F, Jasnin M, Lehnert U, Oesterhelt D, Stadler M, Tehei M, Weik M, Wood K, Zaccai G. From Shell to Cell: Neutron Scattering Studies of Biological Water Dynamics and Coupling to Activity. Faraday Disc. 2009;141:117–130. doi: 10.1039/b805506h. [DOI] [PubMed] [Google Scholar]
- 35.Tehei M, Franzetti B, Wood K, Gabel F, Fabiani E, Jasnin M, Zamponi D, Oesterhelt D, Zaccai G. Neutron Scattering Reveals Extremely Slow Cell Water in Dead Sea Organism. Proc. Nat. Acad. Sci. (USA) 2007;104:766–771. doi: 10.1073/pnas.0601639104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Siepmann JI. Configurational-bias Monte Carlo: Background and Selected Applications. In: van Gunsteren WF, Weiner PK, Wilkinson AJ, editors. Computer Simulations of Biomolecular Systems: Theoretical and Experimental Applications. Vol. 2. Leiden: ESCOM; 1993. pp. 249–264. [Google Scholar]
- 37.Siepmann JI, Frenkel D. Configurational Bias Monte Carlo: A New Sampling Scheme for Flexible Chains. Molecular Physics. 1992;75:59–70. [Google Scholar]
- 38.de Pablo JJ, Jain TS. A biased Monte Carlo Technique for Calculation of the Density of States of Polymer Films. J. Chem. Phys. 2002;116:7238–7244. [Google Scholar]
- 39.Falcioni M, Deem MW. A biased Monte Carlo Scheme for Zeolite Structure Solution. J. Chem. Phys. 1999;110:1754–1767. [Google Scholar]
- 40.Steinbach PJ. Exploring Peptide Energy Landscapes: A Test of Force Fields and Implicit Solvent Models. Proteins. 2004;57:665–677. doi: 10.1002/prot.20247. [DOI] [PubMed] [Google Scholar]
- 41.Guarnieri F, Weinstein H. Conformational Memories and the Exploration of Biologically Relevant Peptide Conformations: An Illustration for the Gonadotropin-releasing Hormone. J Amer. Chem. Soc. 1996;118:5580–5589. [Google Scholar]
- 42.Mehler EL, Hassan SA, Kortagere S, Weinstein H. Ab initio Computer Modeling of Loops in G-Protein Coupled Receptors: Lessons from the Crystal Structure of Rhodopsin. Proteins. 2006;64:673–690. doi: 10.1002/prot.21022. [DOI] [PubMed] [Google Scholar]
- 43.Hassan SA, Mehler EL. A General Screened Coulomb Potential Based Implicit Solvent Model: Calculation of Secondary Structure of Small Peptides. Int. J. Quant. Chem. 2001;83:193–202. [Google Scholar]
- 44.Hassan SA, Guarnieri F, Mehler EL. Characterization of Hydrogen Bonding in a Continuum Solvent Model. J. Phys. Chem. B. 2000;104:6490–6498. [Google Scholar]
- 45.Hassan SA, Guarnieri F, Mehler EL. A General Treatment of Solvent Effects Based on Screened Coulomb Potentials. J. Phys. Chem. B. 2000;104:6478–6489. [Google Scholar]
- 46.Hassan SA, Mehler EL, Zhang D, Weinstein H. Molecular Dynamics Simulations of Peptides and Proteins with a Continuum Electrostatic Model Based on Screened Coulomb Potentials. Proteins. 2003;51:109–125. doi: 10.1002/prot.10330. [DOI] [PubMed] [Google Scholar]
- 47.Hassan SA. Liquid-structure Forces and Electrostatic Modulation of Biomolecular Interactions in Solution. J. Phys. Chem. B. 2007;111:227–241. doi: 10.1021/jp0647479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Brooks BR, Brooks CL, III, MacKerrel ADM, Jr, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, et al. CHARMM: The Biomolecular Simulation Program. Comp. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Juneja A, Ito M, Nilsson L. Implicit Solvent Models and Stabilizing Effects of Mutations and Ligand on the Unfolding of the Amyloid β-Peptide Central Helix. J. Chem. Theory Comput. 2013;9:834–846. doi: 10.1021/ct300941v. [DOI] [PubMed] [Google Scholar]
- 50.Schreiber G, Fersht AR. Rapid Electrostatically Assisted Association of Proteins. Nature. 1996;3:427–431. doi: 10.1038/nsb0596-427. [DOI] [PubMed] [Google Scholar]
- 51.Xu X-HN, Yeung ES. Long-range Electrostatic Trapping of Single-Protein Molecules at a Liquid-Solid Interface. Science. 1998;281:1650–1653. doi: 10.1126/science.281.5383.1650. [DOI] [PubMed] [Google Scholar]
- 52.Gray JJ. The Interaction of Proteins with Solid Surfaces. Curr. Op. Struc. Biol. 2004;14:110–115. doi: 10.1016/j.sbi.2003.12.001. [DOI] [PubMed] [Google Scholar]
- 53.Hassan SA. Intermolecular Potentials of Mean Force of Amino Acid Side Chain Interactions in Aqueous Medium. J. Phys. Chem. B. 2004;108:19501–19509. [Google Scholar]
- 54.Okur A, Miller BT, Joo K, Lee JA, Brooks BR. Generating Reservoir Conformations for Replica Exchange through the Use of the Conformational Space Annealing Method. J. Chem. Theory Comput. 2013;9:1115–1124. doi: 10.1021/ct300996m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lee LP, Tidor B. Barstar is Electrostatically Optimized for Tight Binding to Barnase. Nature. 2001;8:73–76. doi: 10.1038/83082. [DOI] [PubMed] [Google Scholar]
- 56.Frisch C, Schreiber G, Johnson CM, Fersht AR. Thermodynamics of the Interaction of Barnase and Barstar: Changes in Free Energy versus Changes in Enthalpy on Mutation. J. Mol. Bio. 1997;267:696–706. doi: 10.1006/jmbi.1997.0892. [DOI] [PubMed] [Google Scholar]
- 57.Vajda S, Weng ZP, Rosenfeld R, DeLisi C. Effect of Conformational Flexibility and Solvation on Receptor-Ligand Binding Free Energies. Biochemistry. 1994;33:13977–13988. doi: 10.1021/bi00251a004. [DOI] [PubMed] [Google Scholar]
- 58.Malham R, Johnstone S, Bingham RJ, Barratt E, Phillips SEV, Laughton CA, Homans SW. Strong Solute-Solute Dispersive Interactions in a Protein-Ligand Complex. J. Amer. Chem. Soc. 2005;127:17061–17067. doi: 10.1021/ja055454g. [DOI] [PubMed] [Google Scholar]
- 59.Floris F, Tomasi J. Evaluation of the Dispersion Contribution to the Solvation Energy: A Simple Computational Model in the Continuum Approximation. J. Comput. Chem. 1989;10:616–627. [Google Scholar]
- 60.Zacharias M. Continuum Solvent Modeling of Nonpolar Solvation: Improvement by Separating Surface Area dependent Cavity and Dispersion Contributions. J. Phys. Chem. A. 2003;107:3000–3004. [Google Scholar]
- 61.Wagoner JA, Baker NA. Assessing Implicit Models for Nonpolar Mean Solvation Forces: The Importance of Dispersion and Volume Terms. Proc. Nat. Acad. Sci. (USA) 2006;103:8331–8336. doi: 10.1073/pnas.0600118103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Durell SR, Brooks BR, Ben-Naim A. Solvent-Induced Forces Between Two Hydrophilic Groups. J. Phys. Chem. 1994;98:2198–2202. [Google Scholar]
- 63.Ben-Naim A. Solvent-Induced Forces in Protein Folding. J. Phys. Chem. 1990;94:6893–6895. [Google Scholar]
- 64.Bruge F, Fornilli SL, Malenkov GG, Palma-Vittorelli MB, Palma MU. Solvent-Induced Forces on a Molecular Scale: Non-Additivity, Modulation and Causal Relation to Hydration. Chem. Phys. Lett. 1996;254:283–291. [Google Scholar]
- 65.Tanford C. Interfacial Free Energy and the Hydrophobic Effect. Proc. Nat. Acad. Sci. (USA) 1979;76:4175–4176. doi: 10.1073/pnas.76.9.4175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Hermann RB. Theory of Hydrophobic Bonding. II. Correlation of Hydrocarbon Solubility in Water with Solvent Cavity Surface-Area. J. Phys. Chem. 1972;76:2754–2759. [Google Scholar]
- 67.Szekely GJ, Rizzo ML. Hierarchical Clustering via Joint Between-Within Distances: Extending Ward's Minimum Variance Method. J. Classif. 2005;22:151–183. [Google Scholar]
- 68.Allen MP, Tildesley DJ. Computer Simulation of Liquids. Oxford: Clarendon Press; 1987. [Google Scholar]
- 69.Gabdoulline RR, Wade RC. Protein-Protein Association: Investigation of Factors Influencing Association Rates by Brownian Dynamics Simulations. J Mol Biol. 2001;306:1139–1155. doi: 10.1006/jmbi.2000.4404. [DOI] [PubMed] [Google Scholar]
- 70.Hoefling M, Gottschalk KE. Barnase-Barstar: From First Encounter to Final Complex. J. Struct. Biol. 2010;171:52–63. doi: 10.1016/j.jsb.2010.03.001. [DOI] [PubMed] [Google Scholar]
- 71.Shan J, Mehler EL. Calculation of pKa in Proteins with the Microenvironment Modulated-Screened Coulomb Potential (MM-SCP) Proteins. 2011;79:3346–3355. doi: 10.1002/prot.23098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Hassan SA. Self-Consistent Treatment of the Local Dielectric Permittivity and Electrostatic Potential in Solution for Polarizable Macromolecular Force Fields. J. Chem. Phys. 2012;137:074102. doi: 10.1063/1.4742910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Hassan SA. Amino Acid Side Chain Interactions in the Presence of Salts. J. Phys. Chem. B. 2005;109:21989–21996. doi: 10.1021/jp054042r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Masella M, Borgis D, Cuniasse P. A Multiscale Coarse-Grained Polarizable Solvent Model for Handling Long Tail Bulk Electrostatics. J. Comput. Chem. 2013;34:1112–1124. doi: 10.1002/jcc.23237. [DOI] [PubMed] [Google Scholar]
- 75.Hassan SA, Mehler EL. Modeling Aqueous Solvent Effects through Local Properties of Water. In: Feig M, editor. Modeling Solvent Environments: Applications to Simulation of Biomolecules. Weinheim: Wiley-VCH; 2010. [Google Scholar]
- 76.Chandler D. Interfaces and the Driving Force of Hydrophobic Assembly. Nature. 2005;437:640–647. doi: 10.1038/nature04162. [DOI] [PubMed] [Google Scholar]
- 77.Jensen TR, Ostergaard M, Reitzel N, Balashev K, Peters GH, Kjaer K, Bjornholm T. Water in Contact with Extended Hydrophobic Surfaces: Direct Evidence of Weak Dewetting. Phys. Rev. Lett. 2003;90:086101. doi: 10.1103/PhysRevLett.90.086101. [DOI] [PubMed] [Google Scholar]
- 78.Pratt LR. Molecular theory of Hydrophobic Effects: She is too Mean to have her Name Repeated. Annu. Rev. Phys. Chem. 2002;53:409–436. doi: 10.1146/annurev.physchem.53.090401.093500. [DOI] [PubMed] [Google Scholar]
- 79.Hummer G, Garde S, Garcia AE, Pratt EA. New Perspectives on Hydrophobic Effects. Chem. Phys. 2000;258:349–370. [Google Scholar]
- 80.Lum K, Chandler D, Weeks JD. Hydrophobicity at Small and Large Length Scales. J. Phys. Chem. B. 1999;103:4570–4577. [Google Scholar]
- 81.Ashbaugh HS, Kaler EW, Paulaitis ME. A "Universal" Surface Area Correlation for Molecular Hydrophobic Phenomena. J. Am. Chem. Soc. 1999;121:9243–9244. [Google Scholar]
- 82.Wallqvist A, Gallicchio E, Levy RM. A Model for Studying Drying at Hydrophobic Interfaces: Structural and Thermodynamic Properties. J. Phys. Chem. B. 2001;105:6745–6753. [Google Scholar]
- 83.Cramer CJ, Truhlar DG. An SCF Solvation Model for the Hydrophobic Effect and Absolute Free Energies of Aqueous Solvation. Science. 1992;256:213–217. doi: 10.1126/science.256.5054.213. [DOI] [PubMed] [Google Scholar]
- 84.Wagner F, Simonson T. Implicit Solvent Models: Combining an Analytical Formulation of Continuum Electrostatics with Simple Models of the Hydrophobic Effect. J. Comp. Chem. 1999;20:322–335. [Google Scholar]
- 85.Tan ML, Cendagorta JR, Ichiye T. Effects of Microcomplexity on Hydrophobic hydration in Amphiphiles. J. Amer. Chem Soc. 2013;135:4918–4921. doi: 10.1021/ja312504q. [DOI] [PubMed] [Google Scholar]
- 86.Giovambattista N, Lopez CF, Rossky PJ, Debenedetti PG. Hydrophobicity of Protein Surfaces: Separating Geometry from Chemistry. Proc. Nat. Acad. Sci. (USA) 2008;105:2274–2279. doi: 10.1073/pnas.0708088105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Yamniuk AP, Edavettal SC, Bergqvist S, Yadav SP, Doyle ML, Calabrese K, Parsons JF, Eisenstein E. ABRF-MIRG Benchmark Study: Molecular Interactions in a Three-Component System. J. Biomol. Tech. 2012;23:101–114. doi: 10.7171/jbt.12-2303-003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Kleanthous C, editor. Protein-Protein Recognition. New York: Oxford University Press; 2000. [Google Scholar]
- 89.Strynadka NCJ, Eisenstein M, Katchalski-Katzir E, Shoichet BK, Kunts I, Abagyan R, Totrov R, Janin J, Cherfils J, Zimmermann F, et al. Molecular Docking Programs Successfully determine the Binding of a β-lactamase Inhibitory Protein to term-1 β-Lactamase. Nature Struct. Biol. 1996;3:233–239. doi: 10.1038/nsb0396-233. [DOI] [PubMed] [Google Scholar]
- 90.Lensink MF, Mendez R, Wodak SJ. Docking and scoring protein complexes: Capri 3rd Edition. Proteins. 2007;69:704–718. doi: 10.1002/prot.21804. [DOI] [PubMed] [Google Scholar]
- 91.Ritchie DW. Recent Progress and Future Directions in Protein-Protein Docking. Curr. Protein Pept. Sci. 2008;9:1–15. doi: 10.2174/138920308783565741. [DOI] [PubMed] [Google Scholar]
- 92.Vakser JA, Kundrotas P. Predicting 3D Structures of Protein-Protein Complexes. Curr. Pharm. Biotechnol. 2008;9:57–66. doi: 10.2174/138920108783955209. [DOI] [PubMed] [Google Scholar]
- 93.Chen Y, Varani G. Protein Families and RNA Recognition. FEBS J. 2005;272:2088–2097. doi: 10.1111/j.1742-4658.2005.04650.x. [DOI] [PubMed] [Google Scholar]
- 94.Lange OF, Lakomek N-A, Faris C, Schroder GF, Walter KFA, Becker S, Meiler J, Grubmuller H, Griesinger C, de Groot BL. Recognition Dynamics up to Microseconds Revealed from an RDC-Derived Ubiquitin Ensemble in Solution. Science. 2008;320:1471–1475. doi: 10.1126/science.1157092. [DOI] [PubMed] [Google Scholar]
- 95.Li X, Hassan SA, Mehler EL. Long Dynamics Simulations of Proteins using Atomistic Force Fields and a Continuum Representation of Solvent Effects: Calculation of Structural and Dynamic Properties. Proteins. 2005;60:464–484. doi: 10.1002/prot.20470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Go N, Noguti T, Nishikawa T. Dynamics of a Small Globular Protein in terms of Low-Frequency Vibrational Modes. Proc. Nat. Acad. Sci. (USA) 1983;80:3696–3700. doi: 10.1073/pnas.80.12.3696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Noguti T, Go N. Efficient Monte Carlo Method for Simulation of Fluctuating Conformations of Native Proteins. Biopolymers. 1985;24:527–546. doi: 10.1002/bip.360240308. [DOI] [PubMed] [Google Scholar]
- 98.Hassan SA, Mehler EL, Weinstein H. Structure Calculations of Protein Segments Connecting Domains with Defined Secondary Structure: A Simulated Annealing Monte Carlo Combined with Biased Scaled Collective Variables Technique. In: Hark K, Schlick T, editors. Lecture Notes in Computational Science and Engineering. Vol. 24. New York: Springer; 2002. pp. 197–231. [Google Scholar]
- 99.Cardone A, Hassan SA, Albers RW, Sriram RD, Pant HC. Structural and Dynamic Determinants of Ligand Binding and Regulation of Cyclin-Dependent Kinase 5 by Pathological Activator p25 and Inhibitory Peptide CIP. J. Mol. Bio. 2010;401:478–492. doi: 10.1016/j.jmb.2010.06.040. [DOI] [PMC free article] [PubMed] [Google Scholar]