Abstract
We have developed a mathematical model of the rat’s renal hemodynamics in the nephron level, and used that model to study flow control and signal transduction in the rat kidney. The model represents an afferent arteriole, glomerular filtration, and a segment of a short-loop nephron. The model afferent arteriole is myogenically active and represents smooth muscle membrane potential and electrical coupling. The myogenic mechanism is based on the assumption that the activity of non-selective cation channels is shifted by changes in transmural pressure, such that elevation in pressure induces vasoconstriction which increases resistance to blood flow. From the afferent arteriole’s fluid delivery output, glomerular filtration rate is computed, based on conservation of plasma and plasma protein. Chloride concentration is then computed along the renal tubule based on solute conservation that represents water reabsorption along the proximal tubule and the water-permeable segment of the descending limb, and chloride fluxes driven by passive diffusion and active transport. The model’s autoregulatory response is predicted to maintain stable renal blood flow within a physiologic range of blood pressure values. Power spectra associated with time series predicted by the model reveal a prominent fundamental peak at ~165 mHz arising from the afferent arteriole’s spontaneous vasomotion. Periodic external forcings interact with vasomotion to introduce heterodynes into the power spectra, significantly increasing their complexity.
Keywords: autoregulation, myogenic response, renal hemodynamic
1 Introduction
For an animal’s kidney to function normally, glomerular filtration rate must stay within a narrow window despite changes in arterial pressure. That goal is accomplished by autoregulatory mechanisms. One such mechanism is the myogenic response, in which the afferent arteriole dilates or constricts in response to several signals, including blood pressure and tubuloglomerular signal from macula densa [4, 10, 12].
The afferent arteriole arises from the renal artery and branches into glomerular capillaries. A portion of the blood plasma delivered by the afferent arteriole is filtered through the glomerulus into the nephron. Via the myogenic response, vascular smooth muscles of the afferent arteriole respond to increased intraluminal pressure or stretch with active force development, thereby enabling the vessel to constrict. In the arteriolar system, the myogenic response is thought to be important for local autoregulation of blood flow and regulation of capillary pressure [21, 22].
Like many other small arteries and arterioles, the renal afferent arteriole exhibits spontaneous rhythmic activity, a.k.a. vasomotion [30]. Vasomotion is spontaneous in the sense that vascular tone oscillates independently of heart beat, innervation, or respiration. The driving stimulus of vasomotion is believed to be the oscillations intrinsically appearing in the electrical activity of the cells that form the arteriolar walls [26, 10]. Vasomotion is blocked by the same blockers (such as calcium and potassium membrane channels blockers) that eliminate the myogenic response; thus, the two are believed to be functionally related [6, 26].
Another renal autoregulatory mechanism is the tubuloglomerular feedback (TGF) system, which is a negative feedback loop in which the chloride ion concentration is sensed downstream in the nephron by the macula densa cells. Experiments in rats have demonstrated that TGF may induce regular oscillations in nephron flow and related variables (e.g., intratubular fluid pressure and solute concentrations) [11, 18]. In the case of spontaneously hypertensive rats, TGF-mediated oscillations can be irregular and appear to have characteristics of chaos [9, 32]. We have previously studied the signal transduction process along the loop of Henle [16, 17]. That transduction process involves the transformation of variations in tubular fluid flow rate into chloride ion concentration variations in tubular fluid alongside the macula densa. Owing to the nonlinearity of that transformation, harmonic frequencies are generated and contribute to the complexity of TGF-mediated oscillations. However, those models do not represent the afferent arteriole, which is the effector of both the myogenic response and TGF.
In this study, we have developed a mathematical model of renal hemodynamics in the rat kidney. This is the first mathematical model that combines (i) detailed representation of ionic transport, membrane potential, and contraction of the afferent arteriole smooth muscle cells; (ii) myogenic responses induced by steady pressure steps and oscillatory pressure variations; (iii) glomerular filtration; and (iv) detailed representation of tubular fluid flow and Cl− transport. Using this model, we investigated the extent to which autoregulation is attained by the myogenic response, and we studied the signal transduction properties of the vascular and nephron segments, and the extent to which they generate or suppress harmonic frequencies. A better understanding of those properties should clarify the roles of those segments in the regulation of single nephron glomerular filtration rate (SNGFR) and of water and electrolyte delivery to the distal nephron. Model results suggest that heterodyning may contribute to a low frequency oscillation that have been seen in vivo and in vitro [13, 14, 31], and that is slower than the responses of the constituent components represented in this model.
2 Mathematical Model
To model hemodynamics control in the rat kidney, we developed a model that combines: (i) an afferent arteriole model previously developed by us [29]; (ii) a glomerular filtration model developed by Deen et al. [5]; (iii) a renal tubule model previously developed by us [17]. A schematic diagram for the combined model is given in Fig. 1.
Figure 1.
Schematic diagram of the model nephron. Afferent arteriole is shown with a reduced number of vascular smooth muscles (VSM). Arrows indicate myogenic response (red), and key fluid flow variables (black).
We represent an afferent arteriole segment of length LAA. The submodel consists of a series of NAA vascular smooth muscle cells that form the vascular wall and an endothelial layer. Smooth muscle cells communicate through electrical currents passing between them and also through the endothelium. Each smooth muscle cell represents membrane potential, cytosolic Ca2+ dynamics, cross-bridges cycling, and muscle mechanics. The model smooth muscles also incorporate the myogenic response, which enables the vessel to constrict when luminal pressure increases, and vice versa. Luminal blood flow is assumed to be pressure driven. A detailed description of the submodel and a complete set of model equations can be found in Refs. [1, 29]. Below we summarize key model equations. Model smooth muscle cells are linearly indexed with i, where i ranges from 1 (cell proximal to the renal artery) to NAA (cell proximal to the glomerulus).
The rates of change of the membrane potentials of the smooth muscle cell and the associated endothelial compartment are given by
| (1) |
| (2) |
where Cm and Ce denote the smooth muscle and endothelial cell capacitances, respectively. Equation (1) incorporates the leak current IL, ionic fluxes mediated by voltage-gated and voltage-calcium-gated Ca2+ and K+ channels, denoted ICa and IK, gap-junction communication between adjacent smooth muscle cells Im–m, current between smooth muscles and the endothelial compartment Im–e, and a current induced by the myogenic response [29]. Equation (2) describes endothelial cell membrane potential in terms of intercellular current between smooth muscle and endothlial cells, and between adjacent endothelial cell compartments. These currents (except for Imyo, see below) are given by
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Boundary conditions are required to complete Eqs. (6) and (7). Consider Eq. (6). At i = 1, we assume that smooth muscle cells further than a distance of LAA (length of the model afferent arteriole) upstream are synchronized so Im–m = 0, and we assume that Im–m decreases linearly to zero along that segment (−LAA ≤ z < 0), which implies that . Analogous boundary conditions are imposed at i = N and on Eq (7).
The gating of K+ channels ni(t) is described by
| (9) |
where ci denotes free cytosolic Ca2+ concentration. The potential v3, which determines the voltage at which half of the K+ channels are open, depends on free cytosolic Ca2+: v3(c) = v6 + 0.5v5 tanh((c − c3)/c4). The equilibrium distribution of open K+ channels is given by
| (10) |
The gating of the Ca2+ channels is assumed to be at equilibrium
| (11) |
The Ca2+ current ICa induces changes in free cytosolic Ca2+ concentration ci(t), which is given by
| (12) |
The above equation represents Ca2+ influx through the membrane channels, and models the extrusion as a first-order decay. The nonlinear rate constant is obtained by assuming that free cytosolic Ca2+ is in equilibrium with various buffers; for more details see Refs. [1, 8].
An important characteristic of the afferent arteriole’s myogenic response is the asymmetry in its response times for vasoconstriction and vasodilation [20, 21]: the initial delay in the activation of a pressure-dependent vasoconstriction was observed to be ~0.3 s, with the time-profile of the response approximated by an exponential having a time constant of 4 s. In contrast, vasodilation exhibits a longer initial delay of ~1 s, with a response that can be approximated by two exponentials having time constants of 1 and 14 s, respectively. That response time asymmetry may be attributable to the independently regulated pathways for constriction and dilation; however, the details involved are not well understood and are beyond the scope of this work. To represent the response time asymmetry, we adopt an empirical approach and model the dynamics of by
| (13) |
where denotes luminal pressure, denotes target current, given by
| (14) |
where Cm is the cell capacitance. The reference pressure is the pressure that the i-th smooth muscle segment is normally exposed to, which decreases linearly from 100 mmHg to 50 mmHg along the vessel. For −20 ≤ p ≤ 90 mmHg, Fmyo(p) is the piecewise cubic polynomial, with its values Fmyo(pk) and slopes at points pk displayed in Table I for k = 1, …, 12. For p < −20 mmHg, Fmyo(p) is set to Fmyo(p1), and for p > 90 mmHg to Fmyo(p) = Fmyo(p12). The different rate constants kinc and kdec in Eq. (13), corresponding to pressure increase and decrease, yield a faster vasoconstrictive response compared to vasodilation. The response delay τm in Eq. (13) is set to 0.3 s for increasing pressure, and to 1 s for decreasing pressure [20, 21].
Table I.
Parameters that define the piecewise cubic spline Fmyo(p) for −20 ≤ p ≤ 90 mmHg.
| k | pk | Fmyo(pk) |
|
|
|---|---|---|---|---|
| - | mmHg | mV·s −1 | mV·s−1·mmHg−1 | |
| 1 | −20.0 | −2.84 | 0.00 | |
| 2 | −10.0 | −2.26 | 0.05 | |
| 3 | 0.00 | −0.46 | 0.24 | |
| 4 | 10.0 | 2.40 | 0.34 | |
| 5 | 20.0 | 6.01 | 0.38 | |
| 6 | 30.0 | 9.85 | 0.39 | |
| 7 | 40.0 | 13.75 | 0.39 | |
| 8 | 50.0 | 17.60 | 0.38 | |
| 9 | 60.0 | 21.38 | 0.39 | |
| 10 | 70.0 | 25.36 | 0.41 | |
| 11 | 80.0 | 29.50 | 0.46 | |
| 12 | 90.0 | 33.75 | 0.00 |
Free cytosolic Ca2+ facilitates phosphorylation and cross-bridges formation that results in the development of tension in the vascular wall. Let ωi(t) denote the fraction of cross-bridges formed. The rate of change of ωi(t) is given by
| (15) |
where is the phosphorylation level; for details see [1, 8].
Muscle mechanics for each smooth muscle segment are represented by a modified Maxwell model, where a viscous component, an elastic component of length , and a contractile component are connected in parallel. Further, the contractile component consists of a contractile element of length and an elastic element of length , which are connected in series. The rate of contraction of the contractile element is
| (16) |
and the rate of change of the overall muscle circumferential length is
| (17) |
That is, muscle tone is determined by the forces exerted by the hoop stress developed by the elastic and contractile components, which can be found in Ref. [8, 29]. The force developed by transmural pressure is given by fP (xc, PAA) = PAARAA(xc), with the pressure exterior to the vascular wall assumed to be zero. If muscles are assumed to be incompressible, then luminal radius is related to circumferential length by , where A is muscle cross-sectional area.
Luminal fluid flow is described as quasi-steady Poiseuille flow
| (18) |
Inflow pressure at z = 0, denoted P0(t), is assumed known a priori. The model arteriole segment is assumed to be connected in-series to a fixed downstream resistor (ΩAA), with outflow pressure PAA–end assumed constant. Volumetric blood flow rate QAA(t) is given by
| (19) |
where μAA is luminal fluid viscosity. Equation (19) assumes that volumetric blood flow rate is uniform throughout the arteriole and the downstream resistor.
To model glomerular filtration, we adopt a model developed by Deen et al. [5]. The glomerulus is modeled as a single capillary extending from y = 0 to y = LGL, which corresponds to the connections with the afferent and efferent arterioles, respectively. Let QGL(y, t) and CGL(y, t) denote the volumetric plasma flow rate and plasma protein concentration, respectively. Conservation of plasma mass implies that
| (20) |
where Kf is the filtration coefficient, PGL(y, t) is the hydrostatic pressure,
| (21) |
is the colloidal osmotic pressure inside the glomerular capillaries, and PT (0, t) is the proximal tubule inflow pressure (predicted by the tubule submodel, below). We assume a linear pressure decrease along the glomerular capillary
| (22) |
where ΔPGL is a constant, and PAA(LAA, t) is the pressure at the end of the afferent arteriole. Conservation of protein mass yields CGL(y, t)QGL(y, t) = CGL(0, t)QGL(0, t), which together with Eq. (20) results in
| (23) |
The inflow plasma protein concentration is fixed at CGL(0, t) = 5.5 g/dl. The inflow rate is
| (24) |
where QAA(t) is the volumetric flow rate delivered by the afferent arteriole, given in Eq. (19), and Ht is the hematocrit. By integrating Eq. (23), one obtains CGL(LGL, t), which is used to compute QGL(LGL, t) from the conservation of plasma mass. Single nephron glomerular filtration rate is then given by
| (25) |
The tubule submodel represents a proximal tubule and a short loop of Henle, which consists of a descending limb and an ascending limb. The model tubule spans from x = 0 to x = LT, where LT = 1.58 cm, with the proximal tubule spanning the initial 1 cm and the thick ascending limb the terminal 0.5 cm. Along the tubule, the model predicts fluid pressure PT (x, t), fluid flow rate QT (x, t), and fluid Cl− concentration CT (x, t), which is believed to be a key signal for the tubuloglomerular feedback mechanism (not represented in this study). The tubular walls are assumed to be compliant, with a radius that depends passively on transmural pressure gradient
| (26) |
where PT,ext is the extratubular pressure, αT (x) characterizes tubular compliance, and βT (x) is the unpressurized radius.
Tubular fluid is assumed to be pressure-driven. At the entrance of the model tubule (i.e., x = 0), flow rate equals the glomerular filtration rate QF (t) (predicted by the glomerular filtration submodel, Eq. (25)). The end of the model tubule (i.e., x = LT) is connected in series to a downstream resistor (ΩT) with the end-pressure fixed at PT–end.
The proximal tubule and the initial segment of the descending limb are water permeable. Taking into account transmural water flux, denoted by ΦT (x, t), pressure and flow rate along the model tubule are given by
| (27) |
| (28) |
It has been observed experimentally that along the proximal tubule increases in filtration rate incur a concomitant increase in proximal reabsorption [28]; such proportional changes are called glomerular-tubular balance [7]. Micropuncture experiments have shown that ~2/3 of the water and Cl− are reabsorbed along the proximal convoluted tubules. Thus, with a base-case glomerular filtration rate of 30 nl/min (denoted QT0), water flow rate into the proximal straight tubule is 10 nl/min. Given these considerations, the transmural water flux term ΦT (x, t) is given as a step-like function, constructed so that the model predicts a steady-state water flow rate that is consistent with the above measurements and that is ~ 7.0 nl/min at the loop bend [17]:
| (29) |
To compute model solutions, Eqs. (27) and (28) were combined to eliminate QT, yielding the PDE
| (30) |
Equation (30) was solved simultaneously with Eq. (27) for PT and QT. Boundary conditions for the system are QT (0, t) = QF (t), and QT (LT, t) = (PT (LT, t) − PT–end)/ΩT, where PT–end and ΩT denote the end pressure and downstream resistance, respectively. Micropuncture studies in rat [3] suggests a passive dependence of distal tubule resistance on tubular pressure. Thus, the model assumes a sigmoidal dependence of ΩT on distal pressure, given by
| (31) |
where P̄T is the average of PT (LT, t) and PT–end, and P̄T;ref is a constant reference pressure.
Chloride ion (Cl−) concentration is given by conservation of mass
| (32) |
where RT,ss(x, t) is the steady-state tubular radius, and CT,ext(x) is the extratubular (interstitial) Cl− concentration, which is set to 115 mM along the cortex and increases linearly along the corticomedullary axis to 275 mM at the outer-inner medullary boundary. The first term inside the large pair of parentheses corresponds to active solute transport characterized by Michaelis-Menten-like kinetics of maximum active transport rate Vmax(x) and Michaelis constant KM; the other term represents transepithelial diffusion, characterized by transmural Cl− permeability κ(x). Fluid entering the proximal tubule is assumed to have constant Cl− concentration 115 mM.
Parameters and numerical method
Parameter values for the afferent arteriole and tubule submodels can be found in Refs. [29, 17]. Parameters that have not been previously reported or differ from values in Refs. [29, 17], as well as parameters for the glomerular filtration submodel, are summarized in Table II.
Table II.
| Afferent arteriole | * | ac | 2.81 | dimensionless |
| * | we | 0.17 | dimensionless | |
| μAA | 16.0 | cP | ||
|
| ||||
| Glomerular filtration | * | Kf | 2.07 | nl·min−1·mmHg−1 |
| ΔPGL | 3.02 | mmHg | ||
| Ht | 0.45 | dimensionless | ||
| αGL1 | 1.63 | mmHg·dl·g−1 | ||
| αGL2 | 0.29 | mmHg·dl2·g−2 | ||
| LGL | 1 | dimensionless | ||
|
| ||||
| Tubule | * | LT | 1.58 | cm |
| * | μT | 0.67 | cP | |
| PT–end | 2.00 | mmHg | ||
| ΩT,ref | 0.71 | mmHg·min·nl−1 | ||
| sΩ,T | 0.86 | mmHg−1 | ||
| P̄T,ref | 4.5 | mmHg | ||
| ΦT,base,PCT | 0.02 | nl·min−1·cm−1 | ||
| ΦT,base,PST | 0.05 | nl·min−1·cm−1 | ||
| * | κPST,PCT | 0.60 | μm·s−1 | |
| * | κDL,TAL | 0.40 | μm·s−1 | |
| * | Vmax,PCT | 8.40 | nmol·cm−2s−1 | |
| * | Vmax,PST,DL | 0.0 | nmol·cm−2s−1 | |
| * | Vmax,TAL | 18.15 | nmol·cm−2s−1 | |
indicates values modified from the listed references.
To compute numerical solutions for the model equations, we first discretized the model equations in space. For the model afferent arteriole, we computed model solution at locations , for i = 1, ···, NAA and hAA = LAA/NAA. Each grid point zi represents a smooth muscle cell model. For the model tubule, we computed model solution at xi = (i − 1)hT, for i = 1, ···, NT and hT = LT/(NT − 1). A uniform spatial grid was not used for the glomerular filtration model, as explained below. Only the tubule submodel includes PDEs, namely (30) and (32); the afferent arteriole and glomerular filtration submodels includes ODEs, in time or space only. The PDEs of the tubule submodel were first discretized in space using the centered difference method adopted in Ref. [15]. The resulting system of coupled ODEs was integrated in time using an adaptive time-stepping method based on numerical differential formulae (matlab ode15s). During each time step, the afferent arteriole flow Eq. (18), and glomerular protein conservation Eq. (20) must be integrated in space. An adaptive Runga-Kutta method (RK45) was used to integrate Eq. (23), whereas Eq. (18) was numerically integrated using the Trapezoidal rule. An adaptive method was not used for the latter so that the fluid pressure is known at the locations of the smooth muscle cells. Note that the myogenic response, Eq. (13), involves delay. Because a variable time-stepping method was used, model solution may not have been computed at time tn − τm, and thus the delayed values and may not be known. In that case, their values were approximated by interpolation.
In the numerical discretization, we set NAA and NT to 101 and 543, respectively, and we constrained the time-step not to exceed 0.3 s, which is the shorter delay τm associated with the vasoconstrictive response.
As in Ref. [17], the profiles αT (x), βT (x), ΦT,base(x), RT,ss(x), Vmax(x), κ(x), and CT,ext(x) are given as piecewise functions. To avoid numerical errors that may arise from using a centered finite-difference method to compute the derivatives of discontinuous functions, we replaced them by appropriate smooth approximations.
3 Results
Using base-case parameters and a fixed afferent arteriole inflow pressure of P0(t) = 100 mmHg, we computed fluid pressure, fluid flow rate, and luminal radius along the model vessel and nephron, and we also computed Cl− concentration along the proximal tubule and loop of Henle. Model variables associated with the afferent arteriole exhibit spontaneous limit-cycle oscillations (vasomotion): the interactions of Ca2+ and K+ fluxes, which are mediated by voltage-gated and voltage-calcium-gated channels, respectively, give rise to periodicity in the transport of those two ions. This results in time-periodic variations in cytoplasmic Ca2+ concentration, phosphorylation, and cross-bridges formation with the attending muscle stress, similar to results obtained in previous modeling studies [8, 1, 29]. Periodic variations in vascular luminal radius translate into variations in vascular resistance, fluid pressure, fluid flow, glomerular filtration rate, and eventually, tubular flow and solute transport. Figure 2 depicts the time courses of fluid pressure, and fluid flow at the entrance, middle, and exit of the afferent arteriole, as well as fluid pressure, fluid flow, and tubular fluid Cl− concentration at the entrance of the proximal tubule, loop bend, and macula densa. Time averaged values of model’s predictions are summarized in Table III.
Figure 2.
Base-case predictions. A1, A2: pressure and flow rate in the afferent arteriole (AA); B1, B2: pressure and flow rate along the proximal tubule and loop of Henle; C1, C2: tubular fluid Cl− concentration at loop bend and macula densa, respectively.
Table III.
Time-averaged base-case predictions at steady afferent arteriole inflow pressure of 100 mmHg. P0 and PD denote afferent arteriole entrance and exit pressure, respectively. Subscripts T, LB, and MD denote tubular entrance, loop bend, and macula densa, respectively.
| P0 | 100.00 | mmHg |
| PD | 49.87 | mmHg |
| QAA | 319.27 | nl·min−1 |
|
| ||
| PT | 13.02 | mmHg |
| PLB | 8.87 | mmHg |
| PMD | 7.03 | mmHg |
|
| ||
| QT | 30.07 | nl·min−1 |
| QLB | 7.16 | nl·min−1 |
| QMD | 7.16 | nl·min−1 |
|
| ||
| CT | 115.00 | mM |
| CLB | 250.41 | mM |
| CMD | 32.15 | nM |
Snapshots in time of pressure, flow rate, and Cl− concentration are shown in Fig. 3. Flow rate along the afferent arteriole is constant, which results in an approximately linear decrease in fluid pressure, whereas flow rate decreases along the proximal tubule and loop of Henle as determined by the outward-directed water flux term ΦT (x, t). Chloride concentration along the proximal tubule remains almost flat, increases along the descending limb and then progressively decreases along the thick ascending limb.
Figure 3.
Spatial profiles of fluid pressure (solid lines) and flow rate (dashed lines) along the afferent arteriole (A) and along the proximal tubule and loop of Henle (B). C: tubular fluid Cl− concentration profile. Afferent arteriole and tubular lengths are normalized by LAA and LT, respectively. Dotted line indicate the position of the loop bend. Profiles change dynamically due to spontaneous vasomotion. Profiles shown are snapshots at time t = 25 s (see Fig. 2).
Autoregulatory response to steady pressure perturbations
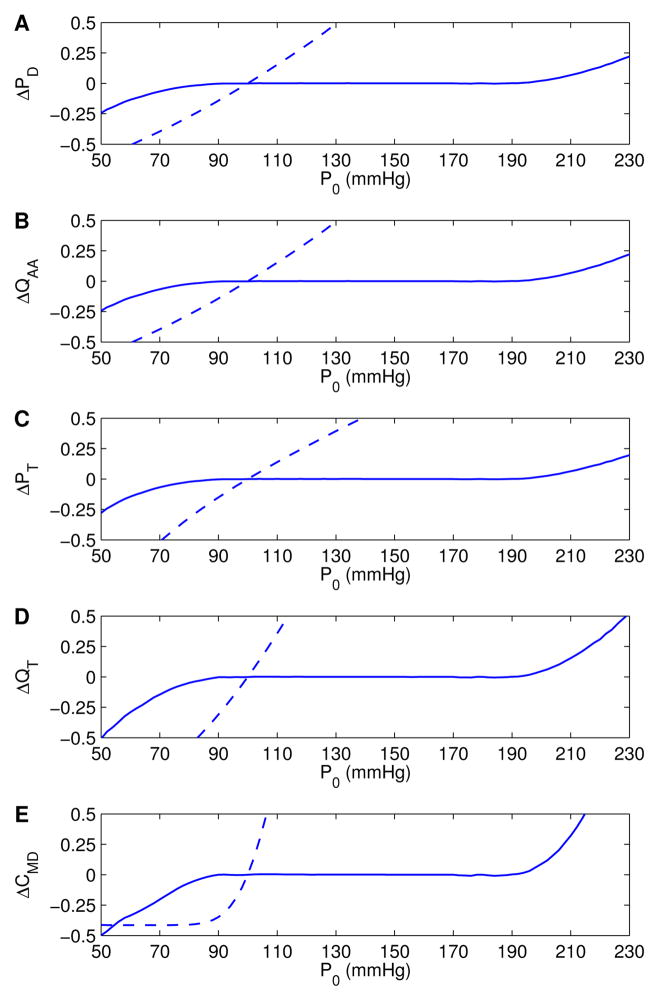
We studied the model’s response to sustained P0(t) perturbations. Figure 4 displays the normalized deviations of time-averaged pressure and flow at various locations within the model nephron, and Cl− concentration at the macula densa, as functions of a range of time-independent P0 values. These deviations were normalized by the corresponding base-case values of Table III. Two sets of simulations were carried out: one with the full model (solid lines), and one with the myogenic response disabled (dashed lines). The latter case was implemented by setting the myogenic current to zero.
Figure 4.
Autoregulatory responses to sustained steady P0 perturbations, obtained with (solid lines) and without (dashed lines) the myogenic response. Results are shown as deviations from base-case values, normalized by respective reference values (listed in Table III). A, B: afferent arteriole outflow pressure and flow rate, respectively; C, D: proximal tubule inflow pressure and flow rate, respectively; E: tubular fluid Cl− concentration at macula densa.
At low inflow pressure (P0 < 100 mmHg), the full model predicts vasodilation, which reduces vascular resistance and raises downstream pressure; at high pressure (P0 > 100 mmHg), the afferent arteriole smooth muscle cells constrict, with opposite effects. With these myogenic responses, the model attains a hemodynamic “plateau” for P0 that falls within the range 90–190 mmHg, where time-averaged downstream fluid pressure and flow values remain close to base-case values.
The sigmoidal dependence of on pressure deviations (see Table I) implies lower and upper limits beyond which the induced fails to provide further alteration in smooth muscle membrane potential. Due to this restriction, vascular diameter at low (P0 < 80 mmHg) or high (P0 > 200 mmHg) pressures does not adjust sufficiently. As a result, some of the pressure perturbation is transmitted downstream. Because the model afferent arteriole fails to adequately compensate, outflow delivery deviates noticeably from base case.
When the myogenic response was disabled, the model predicted a steady increase in vascular and tubular fluid pressure and flow, as P0 was increased. It is noteworthy that macula densa Cl− concentration is highly sensitive to increases in tubular inflow conditions (Fig. 4E). However, at low inflow pressure and tubular flow, Cl− concentration at thick ascending limb becomes low enough that the active reabsorption of Cl− is sufficiently slow to be balanced by the passive diffusion into the lumen. At this point, a “static head” is reached, in which the axial gradient of the luminal Cl− concentration profile near the macula densa approaches zero, and Cl− concentration at macula densa no longer decreases as inflow pressure is further lowered.
Response to step-pressure changes
We simulated the responses of flow and Cl− transport to a rapid step-like increase and decrease in P0(t). Specifically, the afferent arteriole inflow pressure had the form
| (33) |
where P̄0 = 100 mmHg, Pp = 15 mmHg, and sp = 0.10 s. With these parameters, the pressure step approximately completes within ~0.5 s. Results are shown in Fig. 5.
Figure 5.
Model responses to step-pressure changes in afferent arteriole inflow pressure. Solid lines: step-increase; dashed lines: step-decrease. A, B: afferent arteriole inflow and outflow pressures, respectively; C, D: proximal tubule inflow pressure and flow rate, respectively; E: tubular fluid Cl− concentration at macula densa.
With both pressure up- and down-steps, the responses of pressure and flow rate at the afferent arteriole and the proximal tubule were almost instant. In contrast, the response of the macula densa Cl− concentration had a delay of ~5 s. Following the step perturbations, all variables underwent a transient overshoot that lasted considerably longer for the pressure down-step than the pressure up-step. Characteristically, the Cl− concentration response induced by the pressure down-step was fully developed within ~40 s, while for the pressure up-step the response was fully developed within ~25 s. It is also noteworthy that the deviation in macula densa Cl− concentration, relative to its base-case value, is much larger than the corresponding relative change in pressures and flow rates.
Spectral response to sinusoidal pressure perturbations
To study the characteristics of the transduction of oscillations in P0(t) into oscillations in fluid flow and tubular Cl− transport, we superimposed a sinusoidal perturbation onto P0(t), i.e., for t ≥ 0 we applied an inflow pressure of
| (34) |
where P̄0 = 100 mmHg and Pp = 2.5 mmHg. The frequency fext was varied between 0 and 250 mHz.
Figure 6 shows the power spectral density of proximal tubule inflow pressure for three fext values: 0, 30, 60 mHz. To compute power spectra, we sampled the proximal tubule inflow pressure at 80 Hz, over the time window 100 ≤ t ≤ 1738 s. At t = 100 s, practically all transient responses had dissipated. The sampled pressure values were normalized by 13 mmHg and the resulting time series was used to compute power spectra.
Figure 6.
Proximal tubule inflow pressure responses to pressure perturbations at fext = 60 mHz (A1), 30 mHz (B1), and 0 mHz (C1, unperturbed pressure, i.e., Fig. 2B1). Corresponding power spectra are shown in A2, B2, C2, respectively. Dotted lines denote fext and vasomotion frequency fmyo.
The case with fext = 0 corresponds to the base case where no external forcing was applied; thus, Fig. 6C1 is the same as the top time course in Fig. 2B1. In this case, model variables oscillated with frequency fmyo = 165 mHz, driven by the spontaneous vasomotion exhibited by the afferent arteriole. The spectrum shown in Fig. 6C2 contains a single peak at fmyo. The harmonics 2fmyo, 3fmyo, etc. are also present (harmonics not shown).
Sinusoidal forcing introduces complexities into the power spectra of the system. When an external forcing of 30 mHz was applied, the resulting power spectrum (Fig. 6B2) shows not only the frequencies of the forcing and vasomotion (at 30 and 165 mHz, respectively), harmonics of the forcing (60, 90, 120, 150 mHz), but also linear combinations of these frequencies (105, 135, 195 mHz), which arise from a phenomenon known as heterodyning (see Discussion). A similar analysis can be applied to the power spectrum obtained when a 60 mHz forcing was imposed (Fig. 6A2).
The model’s response to P0 oscillations at frequencies 0–250 mHz is summarized in Fig. 7, which shows the power spectral density (color coded) of the frequency components (horizontal axis) corresponding to the forcing frequencies. The magenta lines identify spectral peaks, which arise from vasomotion, external forcing, heterodyning, and harmonics. The line labelled fmyo, which corresponds to vasomotion, runs parallel to the fext-axis, which suggests that the vasomotion frequency is insensitive to the forcing frequency of the applied perturbations. The line labelled fext, which corresponds to the frequency of the external forcing, extends from the origin and runs diagonally across the f–fext plane. One can also discern additional lines that extend from the origin. These lines, which can be approximated by f = kfext, where k = 2, 3, …, correspond to the harmonics of the forcing frequency. Heterodyning, which generates frequencies from mixing the forcing and myogenic frequencies, gives rise to lines αfmyo ± βfext = 0, where α and β are integers.
Figure 7.
Contour of power spectral density of proximal tubule inflow pressure obtained for forcing frequencies fext 0–250 mHz. Peaks arising from forcing (fext) and vasomotion (fmyo) are identified, as well as harmonics and major heterodynes.
Interestingly, the model also revealed a small range of fext for which only one dominant frequency can be identified. That region corresponds to the narrow sparse band of 160 ≤ fext ≤ 170 mHz in Fig. 4. In this region, fext is sufficiently close to fmyo that the two oscillations synchronize, resulting in the disappearance of all frequencies that would otherwise be generated from heterodyning.
Next we considered the signal transduction properties of different segments of the nephron. To that end, we applied sinusoidal inflow pressure perturbations at 30 mHz, and computed oscillations in tubular fluid pressure, fluid flow, and chloride concentration at the proximal tubule entrance, loop bend, and macula densa. Those time courses, normalized by the respective reference values (listed in Table III), are shown in Fig. 9. Due to the tortuosity of the proximal tubule which results in a model tubule of considerable length, and to the nonlinear dependence of ΩT on distal tubular pressure, significant damping is observed in the pressure oscillations. A comparison of proximal tubule inflow and thick ascending limb outflow pressure time courses reveals an amplitude reduction of ~75% in agreement with measurements [?]. If ΩT were fixed, the amplitude damping is lowered to ~50% (results not shown).
Figure 9.
Pressure, flow, and [Cl−] oscillations, driven by sinusoidal pressure forcing at 30 mHz, obtained at proximal tubule entrance (top row), loop bend (middle row), and macula densa (bottom row). Time courses have been normalized by respective reference values (listed in Table III).
The more significant damping on flow oscillations along the proximal tubule and descending limb is attributable to the assumption of fractional reabsorption, such that water reabsorption is proportional to glomerular filtration rate (Eq. (29)). Recall that boundary chloride concentration at the proximal tubule was assumed constant. Thus, the oscillations in [Cl−] at the loop bend arose from oscillations in fluid flow rate and the resulting oscillations in Cl− transport along the proximal tubule and descending limb. It is noteworthy that Cl− oscillations of significant amplitude were generated both at low and high frequencies. A comparison between the [Cl−] profiles at loop bend and macula densa suggests that the thick ascending limb imposes significant damping on [Cl−] oscillations, especially at high frequencies. In other words, the thick ascending limb serves as a low-pass filter for the [Cl−] signal.
Besides mediating spontaneous vasomotion, the myogenic response determines arteriolar flow and pressure, and thus also tubular transport. To study the impacts of the myogenic response on the spectral complexity of the tubular fluid oscillations, we repeated the above simulations for fext = 30 and 60 mHz, with the myogenic response disabled. That is, we set for all smooth muscles. The resulting proximal tubule inflow pressure time courses and the corresponding power spectral densities are shown in Fig. 8. A comparison of Fig. 8, panels A2 and B2, with Fig. 6, panels A2 and B2, suggests that the absence of the myogenic response significantly reduces the spectral complexity of the tubular flow oscillations. In Figs. 8A2 and 8B2, the only clearly identifiable peaks are found at fmyo = 165 mHz, and fext = 30 or 60 mHz, and at the major heterodynes at fmyo ± fext. Unlike in Fig. 6, harmonics and other heterodynes are substantially weaker.
Figure 8.
Proximal tubule inflow pressure responses to pressure perturbations at fext = 60 mHz (A1) and 30 mHz (B1), obtained with the myogenic response disabled. Corresponding power spectra are shown in A2, B2, respectively. Dotted lines denote fext and vasomotion frequency fmyo.
Spectral response to sinusoidal electrical perturbations
Besides the myogenic response considered thus far, the afferent arteriole is the effector also of a number of other regulatory mechanisms. One such mechanism is the TGF mechanism, by which an electrical signal is sent to distal afferent arteriole cells to induce vasoconstriction or vasodilation in response to variations in luminal fluid Cl− concentration near the macula densa. It is known that TGF can lead to oscillations in tubular fluid flow and Cl− transport. To simulate that oscillatory signal, and to study the spectral complexity of the tubular flow oscillations that the signal generates, we kept P0 constant at 100 mmHg and applied a sinusoidal current
| (35) |
to the membrane potential dynamics, Eq. (1), of the 20 smooth muscles proximal to the glomerulus. To facilitate a comparison between these simulations with the ones carried with sinusoidal pressure perturbations, the amplitude Ip was set to 4 mV·s−1, so that at fext = 30 mHz the amplitudes of the induced proximal tubule pressure oscillations were similar in the two sets of simulations.
The electrical perturbation induced periodic polarization and depolarization in the 20 afferent arteriole cells to which the current was applied, as well as in all upstream arteriole cells, albeit to a lesser extent, owing to the intercellular coupling via gap junctions and via the endothelium.
The interactions among spontaneous vasomotion (at fmyo) and electrically-induced vasomotion (at fext) resulted in composite periodic oscillations in vascular resistance, afferent arteriole flow, glomerular filtration rate, tubular flow, and Cl− transport. Proximal tubule inflow pressure oscillations are shown in Fig. 10(A1 and B1), for fext = 60 and 30 mHz. The power spectra, obtained as described above, exhibit complexity similar to those obtained for sinusoidal pressure perturbations (compare with Fig. 6). Harmonics and heterodynes can be identified in the power spectra (Fig. 10, A2 and B2). Further, a contour plot of power spectral density as a function of f and fext is qualitatively similar to Fig. 7 (not shown).
Figure 10.
Proximal tubule inflow pressure responses to electrical perturbations at fext = 60 mHz (row A) and 30 mHz (row B), and corresponding power spectra. Dotted lines denote fext and vasomotion frequency fmyo.
4 Discussion
We have developed a mathematical model that simulates fluid flow along the afferent arteriole, glomerulus, and short-loop nephron in a rat kidney. The model predicts dynamical fluid pressure, flow rate, and Cl− concentration profiles (Fig. 3). Also, within the afferent arteriole smooth muscles, the model predicts that interactions among Ca2+ and K+ membrane transports spontaneously generate cytosolic Ca2+ oscillations resulting in vasomotion with frequency ~165 mHz [1, 29].
The model afferent arteriole’s myogenic response is based on the assumption that changes in luminal pressure induce changes in the activity of nonselective cation channels, which in turn changes the smooth muscle cell membrane potential that sets the vascular tone and thus resistance to blood flow. Through its myogenic response, the model afferent arteriole is effective in maintaining almost stable afferent arteriole’s outflow for steady inflow pressure in the range 90–190 mmHg. As a result, flow and Cl− transport in the renal tubule are also stabilized in that range of inflow pressures (Fig. 4). A stable glomerular filtration rate is essential for maintaining normal kidney functions. Abnormally high arteriolar pressure that is not effectively regulated by the afferent arteriole may lead to damages in the glomerulus, whereas exceedingly low glomerular filtration may impair the elimination of waste products such as urea and creatinine. Indeed, failure to adjust doses of drugs that are normally excreted by the kidneys, e.g., aminoglycoside antibiotics and heparin, may lead to accumulation of those drugs at toxic levels.
In addition to studying the model’s response to steady pressure perturbations, we obtained model results for periodic pressure or electrical forcing. A prediction of the model nephron is that heterodyning increases the complexity of the power spectra associated with the oscillations of fluid flow and Cl− transport variables. Heterodyning is the phenomenon in which when two input frequencies (which, in our case, correspond to spontaneous vasomotion and the pressure or electrical forcing) are combined in a nonlinear signal processor, new frequencies are generated that are linear combinations of the original frequencies. As can be observed in Figs. 6, 7, 8, and 10, the heterodynes are associated with frequencies at approximately αfmyo + βfext, where α and β are integers. The strongest of such peaks are predicted at the frequencies fmyo ± fext. These peaks have been previously identified experimentally using spectral analysis in Sprague-Dawley and spontaneously hypertensive rats [27, 2].
With appropriate forcing frequencies, the model predicts spectral peaks in the low frequency band around or below 10–20 mHz (see Figs. 6, 7, and 10). These peaks are heterodynes that arise from the interaction between the external forcing and the spontaneous vasomotion, or between their harmonics. (Note that TGF may be seen as an instance of (almost) periodic external electrical forcing.) It has been previously proposed that spectral peaks in this frequency range, which have been identified in vivo and in vitro using spectral analysis [13, 14, 31], indicate the existence of a third autoregulatory mechanism. Our model results suggest that heterodyning may explain, or at least contribute to, the generation of these slow oscillations.
Previous efforts in modeling renal autoregulation include a model of the myogenic control of the afferent arteriole by Lush and Fray [23], who used that model to study the steady-state autoregulation of renal blood flow in the dog kidney. Further, Moore et al. [25] presented a steady-state model of the renal vascular and tubular systems to simulate TGF and myogenic mechanisms. Because these models focused on steady-state autoregulation, details of the kinetics of the ionic transport and arteriolar muscle mechanisms were not represented.
In this study, the representation of the smooth muscle cells in the afferent arteriole submodel is based on our previous work [1, 29], which was in turn based on a model for the cat cerebral arterioles developed by Gonzalez-Fernandez and Ermentrout [8], with appropriate adjustments in parameters and the addition of the myogenic response. The model in Ref. [8] was also adopted by Marsh et al. [24] to study the interactions between myogenic response and TGF. In that model, myogenic responses were generated only by oscillatory transmural pressure, although experimental observations have indicated that changes in mean pressure also induce myogenic responses [20]. In contrast, our model exhibits myogenic responses as a function of both pressure and its rate of change, with the current associated with the myogenic response chosen such that the autoregulatory plateau agrees with experimental findings (Fig. 4). Another difference is that the myogenic model in Ref. [24] represents only two myogenically active afferent arteriolar segments. Thus, each submodel represents a rather long segment along the afferent arteriole, whereas in the present study, each afferent arteriolar cell submodel roughly corresponds to an afferent arteriole cell [19], with parameters adjusted for each cell based on the observation that the arteriolar cells are exposed to different external environments (e.g., intravascular fluid pressure).
The present model can be used as an essential component in models of integrated renal hemodynamic regulation. An important renal autoregulatory mechanism that is not represented in the current model is the tubuloglomerular feedback (TGF) system, which is a negative feedback loop in which glomerular filtration rate is adjusted according to Cl− concentration that is sensed downstream in the nephron tubule by the macula densa cells. Our decision not to include TGF in this study was driven by the goal to paint a clear picture of the roles of myogenic response and vasomotion, and their interactions, in renal blood flow, and our belief that the inclusion of a feedback mechanism should be done only after a thorough understanding of the individual components.
By incorporating the TGF response in future studies, one may study the interactions between the myogenic and TGF responses, which share the afferent arteriole as a common effector. Further down the road, by coupling a number of these nephrovascular hemodynamics models, one can investigate the propagation of vasomotor and TGF response along the renal vasculature.
Acknowledgments
This research was supported, in part, by the National Institutes of Health, National Institute of Diabetes and Digestive and Kidney Diseases, via grant DK089066.
Footnotes
Portions of this work were presented at Experimental Biology 2012 (FASEB J 26:690.2, 2012)
References
- 1.Chen J, Sgouralis I, Moore LC, Layton HE, Layton AT. A mathematical model of the myogenic response to systolic pressure in the afferent arteriole. Am J Physiol Renal Physiol. 2011;300:F669–F681. doi: 10.1152/ajprenal.00382.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chon KH, Raghavan R, Chen Y-M, Marsh DJ, Yip K-P. Interactions of TGF-dependent and myogenic oscillations in tubular pressure. Am J Physiol|Renal Physiol. 2005;288:F298–F307. doi: 10.1152/ajprenal.00164.2004. [DOI] [PubMed] [Google Scholar]
- 3.Cortell S, Gennari FJ, Davidman M, Bossert WH, Schwartz WB. A definition of proximal and distal tubular compliance. practical and theoretical implications. J Clin Invest. 1973 Sep;52(9):2330–9. doi: 10.1172/JCI107422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cupples WA, Braam B. Assessment of renal autoregulation. American Journal of Physiology-Renal Physiology. 2007;292(4):F1105–F1123. doi: 10.1152/ajprenal.00194.2006. [DOI] [PubMed] [Google Scholar]
- 5.Deen WM, Robertson CR, Brenner BM. A model of glomerular ultrafiltration in the rat. Am J Physiol. 1972;223(5):1178–1183. doi: 10.1152/ajplegacy.1972.223.5.1178. [DOI] [PubMed] [Google Scholar]
- 6.Fujii KENICHIRO, Heistad DONALDD, Faraci FRANKM. Ionic mechanisms in spontaneous vasomotion of the rat basilar artery in vivo. The Journal of physiology. 1990;430(1):389–398. doi: 10.1113/jphysiol.1990.sp018297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gertz KH, Mangos JA, Braun G, Paget HD. On the glomerular tubular balance in the rat kidney. Pflügers Archiv Eur J Physiol. 1965;285:360–372. doi: 10.1007/BF00363236. [DOI] [PubMed] [Google Scholar]
- 8.Gonzalez-Fernandez JM, Ermentrout B. On the origin and dynamics of the vasomotion of small arteries. Math Biosci. 1994;119:127–167. doi: 10.1016/0025-5564(94)90074-4. [DOI] [PubMed] [Google Scholar]
- 9.Holstein-Rathlou N-H, Leyssac PP. TGF-mediated oscillations in the proximal intratubular pressure: Differences between spontaneously hypertensive rats and Wistar-Kyoto rats. Acta Physiol Scand. 1986;126:333–339. doi: 10.1111/j.1748-1716.1986.tb07824.x. [DOI] [PubMed] [Google Scholar]
- 10.Holstein-Rathlou N-H, Marsh DJ. Renal blood flow regulation and arterial pressure fluctuations: a case study in nonlinear dynamics. Physiol Rev. 1994;74:637–681. doi: 10.1152/physrev.1994.74.3.637. [DOI] [PubMed] [Google Scholar]
- 11.Holstein-Rathlou NH, Marsh DJ. Oscillations of tubular pressure, flow, and distal chloride concentration in rats. American Journal of Physiology-Renal Physiology. 1989;256(6):F1007–F1014. doi: 10.1152/ajprenal.1989.256.6.F1007. [DOI] [PubMed] [Google Scholar]
- 12.Just A. Mechanisms of renal blood flow autoregulation: dynamics and contributions. Am J Physiol Regul Integr Comp Physiol. 2007;292:R1–17. doi: 10.1152/ajpregu.00332.2006. [DOI] [PubMed] [Google Scholar]
- 13.Just A, Arendshorst WJ. Dynamics and contribution of mechanisms mediating renal blood flow autoregulation. Am J Physiol Regul Integr Comp Physiol. 2002;285:R619–R631. doi: 10.1152/ajpregu.00766.2002. [DOI] [PubMed] [Google Scholar]
- 14.Just A, Ehmke H, Toktomambetova L, Kirchheim HR. Dynamic characteristics and underlying mechanisms of renal blood flow autoregulation in the conscious dog. Am J Physiol Renal Physiol. 2001;280:F1062–F1071. doi: 10.1152/ajprenal.2001.280.6.F1062. [DOI] [PubMed] [Google Scholar]
- 15.Layton AT. Feedback-mediated dynamics in a model of a compliant thick ascending limb. Math Biosci. 2010;228:185–194. doi: 10.1016/j.mbs.2010.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Layton AT, Moore LC, Layton HE. Tubuloglomerular feedback signal transduction in a compliant thick ascending limb. Am J Physiol Renal Physiol. 2009 doi: 10.1152/ajprenal.00732.2010. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Layton AT, Pham P, Ryu H. Signal transduction in a compliant short loop of Henle. Int J Numer Methods Biomed Eng. 2012;28(3):369–380. doi: 10.1002/cnm.1475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Leyssac PP, Holstein-Rathlou NH. Effects of various transport inhibitors on oscillating tgf pressure responses in the rat. Pflügers Archiv European Journal of Physiology. 1986;407(3):285–291. doi: 10.1007/BF00585304. [DOI] [PubMed] [Google Scholar]
- 19.Loutzenhiser Kathy, Loutzenhiser Rodger. Angiotensin ii–induced ca2+ influx in renal afferent and efferent arterioles differing roles of voltage-gated and store-operated ca2+ entry. Circulation research. 2000;87(7):551–557. doi: 10.1161/01.res.87.7.551. [DOI] [PubMed] [Google Scholar]
- 20.Loutzenhiser R, Bidani A, Chilton L. Renal myogenic response: kinetic attributes and physiologic role. Circ Res. 2002;90:1316–1324. doi: 10.1161/01.res.0000024262.11534.18. [DOI] [PubMed] [Google Scholar]
- 21.Loutzenhiser R, Bidani A, Wang X. Systolic pressure and the myogenic response of the renal afferent arteriole. Acta Physiol Scand. 2004;181:404–413. doi: 10.1111/j.1365-201X.2004.01312.x. [DOI] [PubMed] [Google Scholar]
- 22.Loutzenhiser Rodger, Griffin Karen, Williamson Geoffrey, Bidani Anil. Renal autoregulation: new perspectives regarding the protective and regulatory roles of the underlying mechanisms. American Journal of Physiology-Regulatory, Integrative and Comparative Physiology. 2006;290(5):R1153–R1167. doi: 10.1152/ajpregu.00402.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lush DJ, Fray JCS. Steady-state autoregulation of renal blood flow: a myogenic model. Am J Physiol Reg Int Comp Physiol. 1984;247:R89–R99. doi: 10.1152/ajpregu.1984.247.1.R89. [DOI] [PubMed] [Google Scholar]
- 24.Marsh DJ, Sosnovtseva OV, Chon KH, Holstein-Rathlou N-H. Nonlinear interactions in renal blood flow regulation. Am J Physiol Regul Integr Comp Physiol. 2005;288:R1143–R1159. doi: 10.1152/ajpregu.00539.2004. [DOI] [PubMed] [Google Scholar]
- 25.Moore Leon C, Rich Adam, Casellas Daniel. Ascending myogenic autoregulation: interactions between tubuloglomerular feedback and myogenic mechanisms. Bulletin of mathematical biology. 1994;56(3):391–410. doi: 10.1007/BF02460464. [DOI] [PubMed] [Google Scholar]
- 26.Osol GEORGE, Halpern WILLIAM. Spontaneous vasomotion in pressurized cerebral arteries from genetically hypertensive rats. American Journal of Physiology-Heart and Circulatory Physiology. 1988;254(1):H28–H33. doi: 10.1152/ajpheart.1988.254.1.H28. [DOI] [PubMed] [Google Scholar]
- 27.Raghavan R, Chen X, Yip K-P, Marsh DJ, Chon KH. Interactions between TGF-dependent and myogenic oscillations in tubular pressure and whole kidney blood flow in both SDR and SHR. Am J Physiol Renal Physiol. 2006;290:F720–F732. doi: 10.1152/ajprenal.00205.2005. [DOI] [PubMed] [Google Scholar]
- 28.Schnermann J, Briggs JP. Function of the juxtaglomerular apparatus: Control of glomerular hemodynamics and renin secretion. In: Alpern RJ, Hebert SC, editors. Seldin and Giebisch’s The Kidney. Physiology and Pathophysiology. 4. Elsevier Academic Press; Amsterdam; Boston: 2008. pp. 589–626. [Google Scholar]
- 29.Sgouralis I, Layton AT. Autoregulation and conduction of vasomotor responses in a mathematical model of the rat afferent arteriole. Am J Physiol Renal Physiol. 2012 doi: 10.1152/ajprenal.00589.2011. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Siegel G, Ebeling BJ, Hofer HW, Nolte J, Roedel H, Klubendorf D. Vascular smooth muscle rhythmicity. Mechanisms of blood pressure waves. 1984:319–338. [Google Scholar]
- 31.Siu KL, Sung B, Cupples WA, Moore LC, Chon KH. Detection of low-frequency oscillations in renal blood flow. Am J Physiol Renal Physiol. 2009;297:F155–F162. doi: 10.1152/ajprenal.00114.2009. [DOI] [PubMed] [Google Scholar]
- 32.Yip K-P, Holstein-Rathlou N-H, Marsh DJ. Chaos in blood flow control in genetic and renovascular hypertensive rats. Am J Physiol (Renal Fluid Electrolyte Physiol 30) 1991;261:F400–F408. doi: 10.1152/ajprenal.1991.261.3.F400. [DOI] [PubMed] [Google Scholar]