Abstract
We review inference under models with nonparametric Bayesian (BNP) priors. The discussion follows a set of examples for some common inference problems. The examples are chosen to highlight problems that are challenging for standard parametric inference. We discuss inference for density estimation, clustering, regression and for mixed effects models with random effects distributions. While we focus on arguing for the need for the flexibility of BNP models, we also review some of the more commonly used BNP models, thus hopefully answering a bit of both questions, why and how to use BNP.
Keywords: Nonparametric models, Dirichlet process, Polya tree, dependent Dirichlet process
1 Introduction
All models are wrong, but some are useful (Box 1979). Most statisticians and scientists would agree with this statement. In particular, it is convenient to restrict inference to a family of models that can be indexed with a finite dimensional set of parameters. Under the Bayesian paradigm inference builds on the posterior distribution of these parameters given the observed data. In anticipation of the upcoming generalization we refer to such inference as parametric Bayes. However, it can be dangerous to forget the simplification implied by this process. There are problems where inference under the simplified model can lead to misleading decisions and inference. We discuss a class of statistical inference approaches that relaxes this framework by allowing for a richer and larger class of models. This is achieved by considering infinite dimensional families of probability models. Priors on such families are known as nonparametric Bayesian (BNP) priors.
For example, consider a density estimation problem, with observed data yi ~ G, i = 1, . . . , n. Inference under the Bayesian paradigm requires a completion of the model with a prior for the unknown distribution G. Unless G is restricted to some finite dimensional parametric family this leads to a BNP model with a prior p(G), that is a probability model for the infinite dimensional G. A related application of BNP priors on random probability measures is for random effects distributions in mixed effects models. Such generalizations of parametric models are important when the default choice of multivariate normal random effects distribution might understate uncertainties and miss some important structure. Another important class of BNP priors is priors on unknown functions, for example a prior p(f) for the unknown mean function f(x) in a regression model yi = f(xi) + εi.
In this article we review some common BNP priors. Our argument for BNP inference rests on a set of examples that highlight typical situations where parametric inference might run into limitations, and BNP can offer a way out. Examples include a false sense of posterior precision in extrapolating beyond the range of the data, the restriction of a density estimate to a unimodal family of distributions and more. One common theme is the honest representation of uncertainties. Restriction to a parametric family can mislead investigators into an inappropriate illusion of posterior certainty. Honest quantification of uncertainty is less important when the goal is to report posterior means E(G | y), but could be critical if either the primary inference goal is to characterize this uncertainty or the goal is prediction, if the probability model is part of a decision problem, or if the nonparametric model is part of a larger encompassing model. Some of these issues are highlighted in the upcoming examples. For each example we briefly review appropriate methods, but without any attempt at an exhaustive review of BNP methods and models. For a more exhaustive discussion of BNP models see, for example, recent discussions in Hjort et al. (2010), Hjort (2003), Müller and Rodríguez (2013), Müller and Quintana (2004), Walker et al. (1999), and Walker (2013).
2 Density Estimation
2.1 Dirichlet Process (Mixture) Models
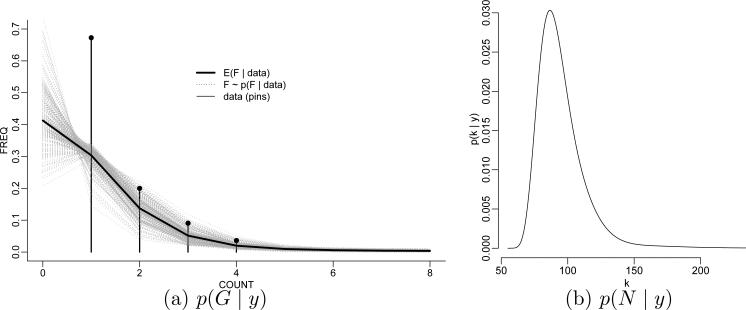
Example 1 (T-cell diversity). Guindani et al. (2012) estimate an unknown distribution F for count data yi. Assuming yi ~ F, i = 1, . . . , n, i.i.d., the problem can be characterized as inference for the unknown F. The data are shown in Table 1. The application is to inference for T-cell diversity. Different types of T-cells are observed with counts yi. T-cells are white blood cells and are a critical part of the immune system. In particular, investigators are interested in estimating F(0), for the following reason. The experiment generates a random sample of T-cells from the population of all T-cells that are present in a probe. The sample is recorded by tabulating the counts yi for all observed T-cell types, i = 1, . . . , n. However, some rare but present T-cell types, i = n+1, . . . , N, might not be recorded, simply by sampling variation, that is when yi = 0 for a rare T-cell type. Naturally, zero counts are censored by the nature of the experiment. Inference for F(0) would allow us to impute the number of not observed zero counts and thus infer the total number of T-cell types. The latter is an important characteristic of the strength of the immune system.
Table 1.
Clonal size distribution for one of the experiments reported in Guindani et al. (2012, Table 2). For example, there are f1 = 37 T-cell receptor types that were observed once (yi = 1) in the data, f2 = 11 that were observed twice (yi = 2), etc. The number f0 of T-cell receptors that were not observed in the sample (yi = 0) is censored. (We thank the discussant Peter Hoff for correcting an error in the original manuscript.)
| yi = j | 0 | 1 | 2 | 3 | 4 | other |
| frequency fj | – | 37 | 11 | 5 | 2 | 0 |
Table 1 shows the observed data yi for one of the experiments reported in Guindani et al. (2012, Table 2). There are n = 55 distinct T-cell receptor sequences. The total number of recorded T-cell receptor sequences is .
Table 2.
Number of patients ni and number of responses yi for sarcoma subtypes i = 1,..., n.
| Intermediate Prognosis |
Intermediate (ctd.) |
Good Prognosis |
||||||
|---|---|---|---|---|---|---|---|---|
| subtype | ni | yi | subtype | ni | yi | subtype | ni | yi |
| Leiomyosarcoma | 28 | 6 | Synovial | 20 | 3 | Ewing's | 13 | 0 |
| Liposarcoma | 29 | 7 | Angiosarcoma | 15 | 2 | Rhabdo | 2 | 0 |
| MFH | 29 | 3 | MPNST | 5 | 1 | |||
| Osteosarcoma | 26 | 5 | Fibrosarcoma | 12 | 1 | |||
Figure 1 shows the empirical distribution together with a BNP estimate E(F | y). Inference on F (·) allows imputation of N – n, the number of zero-censored T-cells. A parametric model Fθ (y), like a simple Poisson model or a finite mixture of Poissons models would report misleadingly precise inference for θ – and thus Fθ (0) – based on the likelihood . Guindani et al. (2012) use instead a Dirichlet process (DP) mixture of Poisson model for F. We discuss details below. Figure 1b shows the posterior distribution p(N | y) under the same model that was used for the posterior inference in Figure 1a.
Figure 1.
T-cell diversity. Panel (a) shows the data (as pin plot) and a posterior sample F ~ p(F | y) under a DP mixture prior (grey curves) and the posterior estimate F̄ = E(F | y) (black curve). The plotted curves connect the point masses F(i) and F̄(i) for better display (the connection itself is meaningless). Panel (b) shows the implied posterior p(N | y) on the total number of T-cell types.
The DP prior (Ferguson 1973) is arguably the most commonly used BNP prior. We write G ~ DP(α, G★) for a DP prior on a random probability measure G. The model uses two parameters, the total mass parameter α and the base measure G★. The base measure specifies the mean, E(G) = G★. The total mass parameter determines, among other implications, the uncertainty of G. Consider any (measureable) set A. Then the probability G(A) under G is a beta distributed random variable with G(A) ~ Be [αG★(A), α(1 – G★(A))]. Similarly, for any partition {A1, A2, . . . , AK} of the sample space S, i.e., for i ≠ j and , the vector of random probabilities (G(A1), . . . , G(AK)) follows a Dirichlet distribution, p(G(A1), . . . , G(AK)) ~ Dir(αG★(A1), . . . , αG★(AK)). This property is a defining characteristic. Alternatively the DP prior can be defined as follows. Let δx(·) denote a point mass at x. Then G is a discrete probability measure
| (1) |
with , i.i.d., and for vh ~ Be(1, α), i.i.d. The constructive definition (1) is known as the stick-breaking representation of the DP prior (Sethurman 1994). For a recent discussion of the DP prior and basic properties see for example Ghosal (2010). An excellent review of several alternative constructions of the DP prior is included in Lijoi and Prünster (2010).
Implicit in this constructive definition is the fact that a DP random measure is a.s. discrete and can be written as a sum of point masses . In many applications the a.s. discreteness of the DP is awkward. For example, in a density estimation problem, yi ~ G(·), i = 1, . . . , n, it would be inappropriate to assume G ~ DP if the distribution were actually known to be absolutely continuous. A simple model extension fixes the awkward discreteness by assuming yi ~ F and
| (2) |
In words, the unknown distribution is written as a mixture with respect to a mixing measure with DP prior. Here p(y | θ) is some model indexed by θ. The model is known as the DP mixture (DPM) model. If desired, a continuous distribution p(y | θ) creates a continuous probability measure F. Often the mixture is written as an equivalent hierarchical model, by introducing latent variables θi:
| (3) |
Marginalizing with respect to θi, model (3) reduces again to , i.i.d., as desired.
Example 1 (ctd.). Let Poi(y; θ) denote a Poisson model with parameter θ. In Guindani et al. (2012) we use a DPM model with p(y | θ) = Poi(y; θ). Here the motivation for the DPM is the flexibility compared to a simpler parametric family. Also, the latent variables θi that appear in the hierarchical model (3) are attractive for this application to inference for T-cell diversity. The latent θi become interpretable as mean abundance of T-cell type i. The use of the BNP model for F(·) addressed several key problems in this inference problem. The BNP model allowed the critical extrapolation to F(0) without relying on a particular parametric form of the extrapolation. And equally important, the extrapolation is based on a coherent probability model. The latter is important for the derived inference about N. In Figure 1a, the grey curves illustrate the posterior distribution p(F | y). The implied histogram of F(y) at y = 0 estimates p(F(0) | y) and it implies in turn the posterior distribution p(N | y) for the primary inference target that is shown in Figure 1b. Implementing the same inference in a parametric model would be challenging.
In the context of inference for SAGE (serial analysis of gene expression) data, Morris et al. (2003) use parametric inference for similar data. However, in their problem estimation of N is not the primary inference target. Their main aim is to estimate the unknown prevalance of the different species, equivalent to estimating F(i), i ≥ 1 in the earlier description.
One of the attractions of DP (mixture) models is easy computation, including the availability of R packages. For example, posterior inference for DP mixture models and many extensions is implemented in the R package DPpackage (Jara et al. 2011).
2.2 Polya Tree Priors
Many alternatives to the DP(M) prior for a random probability measure G have been proposed in the BNP literature. Especially for univariate and low-dimensional distributions the Polya tree (PT) prior (Lavine 1992, 1994; Mauldin et al. 1992) is attractive. It requires no additional mixture to create absolutely continous probability measures.
The construction is straightforward. Without loss of generality assume that we wish to construct a random probability measure G(y) on the unit interval, 0 ≤ y ≤ 1. Essentially we construct a random histogram. We start with the simplest histogram, with only two bins by splitting the sample space into two subintervals B0 and B1 and assigning random probability
and Y1 = G(B1) = 1 – Y0 to the two intervals, using a beta prior to generate the random probability Y0. Next we refine the histogram by splitting B0 in turn into two subintervals and similarly for . We use the random splitting probabilities Y00 ≡ G(B00 | B0) ~ Be(a00, a01) and Y10 ≡ G(B10 | B1) ~ Be(a10, a11). Again let Y01 = 1 – Y00 etc. Let ε = ε1 · · · εm denote a length m binary sequence. After m refinements we have a partition {Bε1 ··· εm; εj ∈ {0, 1}} of sample space with
In summary, the PT prior is indexed by the nested sequence of partitions π = {Bε} and the beta parameters . We write . One of the attractions of the PT prior is the easy prior centering at a desired prior mean G★. Let qa denote the quantile with G★{[0, qa]} = a. Fix B0 = [0, q1/2), B1 = [q1/2, 1], B00 = [0, q1/4), B01 = [q1/4, q1/2), . . . , B11 = [q3/4, 1], B000 = [0, q1/8), etc. In other words, we fix π as the dyadic quantiles of the desired G★. If additionally αε = cm is constant across all level m subsets, then E(G) = G★, as desired. Alternatively, for arbitrary π, fixing aεx = cmG★(Bεx)/G★(Bε), x = 0, 1 also implies E(G) = G★. With a slight abuse of notation we write and G ~ PT(π, G★) to indicate that the partition sequence or the beta parameters are fixed to achieve a prior mean G★. A popular choice for cm is cm = cm2, which guarantees an absolutely continous random probability measure G (Lavine 1992). On the other hand, with aε = αG★(Bε), and thus aε = aε0 + aε1, the PT reduces to a DP(α, G★) prior with an a.s. discrete random probability measure G.
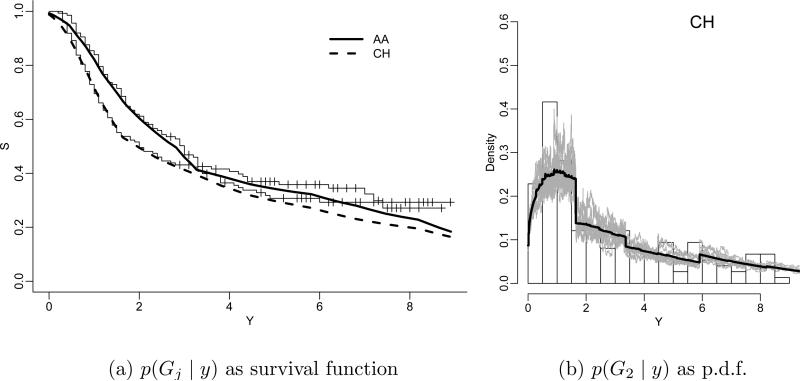
Example 2 (Prostate cancer study). Zhang et al. (2010) use a PT prior to model the distribution of time to progression (TTP) for prostate cancer patients. The data are available in the on-line supplementary materials for this paper (TTP, treatment indicator and censoring status). The application also includes a regression on a longitudinal covariate and a possible cure rate. For the moment we only focus on the PT prior for the survival time. The study includes two treatment arms, androgen ablation (AA) and androgen ablation plus three 8-week cycles of chemotherapy (CH). Zhang et al. (2010) used a PT prior to model time to progression yi for n1 = 137 patients under CH and for n2 = 149 under AA treatment. Let G1 and G2 denote the distribution of time to progression under AA and CH treatment, respectively. We assume with aε = cm2 and centering measure , a Weibull distribution with τ = 4.52 and β = 1.23.
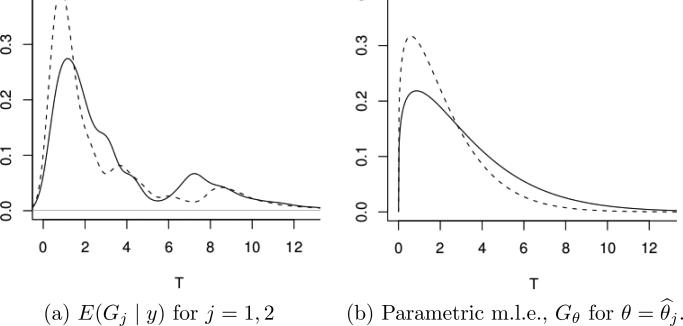
Figure 2a shows the data as a Kaplan-Meier plot together with the posterior estimated survival functions. Inference for G1 and G2 is under , independently across G1 and G2, for fixed . Inference in Zhang et al. (2010) is based on a larger model that includes the PT prior as a submodel for the TTP event times. Additionally, the model adds the possibility of patients being cured of the disease, i.e., the model replaces i.i.d. sampling of TTP's Tji ~ Gj by a hierarchical model with p(wji = 1) = pj and p(Tji | wji = 0) = Gj where wji is an indicator for a patient under treatment j being cured, and pj is the cured fraction under treatment j. Also, the model includes an additional regression on a longitudinal covariate yji = (yjik, k = 1, . . . , nji) (prostate specific antigen, PSA). For the implementation of inference on these two additional model features it is important that posterior inference on Gj remain flexible and be fully model-based. In particular, inference on the tails of Gj immediately impacts inference on the cured fractions, as it speaks to the possibility of possible (latent) later TTP beyond the censoring time. The full description of uncertainties is equally important for the regression on longitudinal PSA measurements. The imputed Gj is used to impute latent TTP values for susceptible patients. Imputed large TTP's could easily become influential outliers in the regression problem. Figure 3 shows inference on Gj, now also including the cured fraction and the regression on PSA. See Zhang et al. (2010) for details on the implementation of the regression model. The secondary mode around T = 8 is interesting from a clinical perspective, but would be almost impossible to find with parametric inference. It was not revealed by the initial Kaplan-Meier plot. A parametric model can only accommodate such features if the possibility of a second mode were anticipated in the model construction. But this is not the case here.
Figure 2.
The horizontal axis indicates years after treatment. In panel (a), the step function shows the Kaplan-Meier (KM) estimates (with censoring times marked as +). The solid line and the dashed line are estimates based on the BNP model. Panel (b) shows the posterior p(G2 | y) and the posterior mean E(G2 | y) (thick line).
Figure 3.
Prostate cancer study. Inference from Zhang et al. (2010) on Gj. The model included a cured fraction and a regression on a longitudinal covariate (prostate specific antigen) in addition to yji ~ Gj.
A minor concern with inference under the PT prior in some applications is the dependence on the chosen partition sequence. Figure 2b shows inference for G1, represented by its probability density function. The partition boundaries are clearly visible in the inference. This is due to the fact that the PT prior assumes independent conditional splitting probabilities Yε, independent across m and across the level m partitioning subsets. The same independence persists a posteriori. There is no notion of smoothing inference on the splitting probabilities across partitioning subsets. This awkward dependence on the boundaries of the partitioning subsets can easily be mitigated by defining a mixture of PTs (MPT), mixing with respect to the parameters of the centering measure . Let η denote the parameters of the centering measure . In the example, η = (τ, β). We augment the model by adding a hierarchical prior p(β), leaving τ fixed. This leads to an MPT model, . Here indicates a PT prior for the random probability measure G, with the nested partition sequence defined by dyadic quantiles of G★ and beta parameters . Such MPT constructions were introduced in Hanson (2006) and in a variation in Paddock et al. (2003). In the prostate cancer data, the estimated survival curve remains practically unchanged from Figure 2a. The p.d.f. is smoothed (not shown).
Branscum et al. (2008) report another interesting use of PT priors. They implement inference for ROC (receiver operating characteristic) curves based on two independent PT priors for the distribution of scores under the true positive (G1) and true negative population (G0), respectively. In this application uncertainty about Gj is critical. A commonly reported summary of the ROC curves is the area under the curve (AUC), which can be expressed as AUC = p(X > Y ) for X ~ G1 and Y ~ G0. Complete description of all uncertainties in the two probability models is critical for the estimate of the ROC curve. A fortiori, it is critical for a fair characterization of uncertainties about the ROC curve. The latter becomes important, for example, in biomarker trials (Pepe et al. 2001). Uncertainty about the ROC curve in an earlier still exploratory trial is used to determine the sample size for a later prospective validation trial. A complete description of uncertainties is critical in such applications.
Finally, a brief note on computation. Posterior updating for a PT prior is straightforward. It is implemented in the R package DPpackage (Jara et al. 2011). The definition of a PT prior for a multivariate random probability measure requires a clever definition of the nested partition sequence and can become cumbersome in higher dimensions. Hanson and Johnson (2002) propose a practicable construction for multivariate PT construction centered at a multivariate normal model.
2.3 More Random Probability Measures
Many alternative priors p(G) for random probability measures have been proposed. Many can be characterized as natural generalizations or simplifications of the DP prior. Ishwaran and James (2001) propose generalizations and variations based on the stick-breaking definition (1). The finite DP is constructed by truncating (1) after K terms, with vK = 1. The truncated DP is particularly attractive for posterior computation. Ishwaran and James (2001) show a bound on the approximation error that arises when using inference under a truncated DP to approximate inference under the corresponding DP prior. The beta priors for vh in (1) can be replaced by any alternative vh ~ Be(ah, bh), without complicating posterior simulations. In particular, vh ~ Be(1 – a, b+ha) defines the Pitman Yor process with parameters a, b (Pitman and Yor 1997).
Alternatively we could focus on other defining properties of the DP to motivate generalizations. For example, the DP can be defined as a normalized gamma process (Ferguson 1973). The gamma process is a particular example of a much wider class of models known as completely random measures (CRM) (Kingman 1993, chapter 8). Consider any non-intersecting measureable subsets A1, . . . , Ak of the desired sample space. The defining property of the CRM μ is that the μ(Aj) be mutually independent. The gamma process is a CRM with μ(Aj) ~ Ga(Mμ0(A), 1), mutually independent, for a probability measure μ0 and M > 0. Normalizing μ by G(A) = μ(A)/μ(S) defines a DP prior with base measure proportional to μ0. Replacing the gamma process by any other CRM defines alternative BNP priors for random probability measures.
Such priors are known as normalized random measures with independent increments (NRMI) and were first described in Regazzini et al. (2003) and include a large number of BNP priors. A recent review of NRMI's appears in Lijoi and Prünster (2010). Besides the DP prior other examples are the normalized inverse Gaussian (NIG) of Lijoi et al. (2005a) and the normalized generalized gamma process (NGGP), discussed in Lijoi et al. (2007). The construction of the NIG in many ways parallels the DP prior. Besides the definition as a CRM, a NIG process G can also be characterized by a normalized inverse Gaussian distribution (Lijoi et al. 2005a) for the joint distribution of random probabilities (G(A1), . . . , G(Ak)), and like for the DP the probabilities for cluster arrangements defined by ties under i.i.d. sampling are available in closed form. For the DP, we will still consider this distribution in more detail in the next section. The NIG, as well as the DP are special cases of the NGGP.
Two recent papers (Barrios et al. 2013; Favaro and Teh 2013) describe practicable implementions of posterior simulation for mixtures with respect to arbitrary NRMIs, based on a characterization of posterior inference in NRMIs discussed in James et al. (2009) who characterize p(G | y) under i.i.d. sampling yi ~ G, i = 1, . . . , n, from a random probability measure G with NRMI prior. Both describe algorithms specifically for the NGGP. Both use conditioning on the same latent variable U that is introduced as part of the description in James et al. (2009). Favaro and Teh (2013) describe what can be characterized as a modified version of the Polya urn. The Polya urn defines the marginal distribution of (y1, . . . , yn) under the DP prior, after marginalizing with respect to G. We shall discuss the marginal model under the DP in more detail in the following section. Barrios et al. (2013) describe an approach that includes sampling of the random probability measure. This is particularly useful when desired inference summaries require imputation of the unknown probability measure. The methods of Barrios et al. (2013) are implemented in the R package BNPdensity, which is available in the CRAN package repository (http://cran.r-project.org/).
3 Clustering
3.1 DP Partitions
The DP mixture prior (3) and variations are arguably the most popular BNP priors for random probability measures. The popularity is mainly due to perhaps two reasons. One is computational simplicity. In model (3) it is possible to analytically marginalize with respect to G, leaving a model in θi only. This greatly simplifies posterior inference. The second, and related, reason is the implied clustering. As samples from a discrete probability measure G, the latent θi include many ties. One can use the ties to define clusters. Let , k = 1, . . . , K denote the K ≤ n unique values among the θi, i = 1, . . . , n. Then , k = 1, . . . , K, defines a random partition of the experimental units {1, . . . , n}. Let ρn = {S1, . . . , SK} denote the random partition. Sometimes it is more convenient to use an alternative description of the partition in terms of cluster membership indicators s = (s1, . . . , sn) with si = k if i ∈ Sk. We add the convention that clusters are labeled in the order of appearance, in particular s1 = 1. One of the attractions of the DP prior is the simple nature of the implied prior p(ρn). Let nk = |Sk| denote the size of the k–th cluster. Then
| (4) |
implying in particular the following complete conditional prior. We write s– for s without si, for the size of Sk without unit i, etc.
| (5) |
Here si = K– + 1 indicates that i forms a new (K– + 1)-st singleton cluster of its own. The probability model (5) is known as the Polya urn.
Many applications of the popular DPM exploit the implied prior p(ρn) in (4). Often the random probability measure G itself is not of interest. The model is only introduced for the side effect of creating a random partition. In such applications the use of the DP prior can be questioned, as the prior p(ρn) includes several often inappropriate features. The cluster sizes are a priori geometrically ordered, with one large cluster and geometrically smaller clusters, including many singleton clusters. However, this is less of a concern when either prediction is the focus or only major clusters are interpreted.
BNP inference on ρn offers some advantages over parametric alternatives. A parametric model might induce clustering of the experimental units, for example, by specifying a mixture model with J terms, . Replacing the mixture model by a hierarchical model, p(yi | si = j, θj) = pj(yi | θj) and p(si = j) = wj with latent indicator variables si implicitly defines a random partition by interpreting the indicators si as cluster membership indicators. Such random partition models are known as model based clustering or mixture of experts models (when the weights are allowed to include a regression on covariates). In contrast to the nonparametric prior, the parametric model requires one to specify the size J of the mixture, either by fixing it or by extending the hierarchical model with a hyperprior on J.
Recall the definition of BNP models as probability models on infinite dimensional random elements. However, there are only finitely many partitions ρn, leaving the question why random partition models should be considered BNP models. Traditionally they are. Besides tradition, perhaps another reason is a one-to-one correspondence between an exchangeable random partition and a discrete probability measure (Pitman 1996, Proposition 13). An exchangeable random partition p(ρn) can always be thought of as arising from the configuration of ties under i.i.d. sampling from a discrete probability measure.
3.2 Hierarchical Extensions
An interesting class of extensions of the basic DP model defines hierarchical models and other extensions to multiple random probability measures. One of the earlier extensions was the hierarchical DP (HDP) of Teh et al. (2006), who define a prior for random probability measures Gj, j = 1, . . . , J, with Gj | G★ ~ DP(M, G★), independently. By completing the model with a prior on the common base measure, G★ ~ DP(B, H), they define a joint probability model for (G1, . . . , GJ). Importantly, the discrete nature of the G★ as a DP random measure itself introduces positive probabilities for ties in the atoms of the random Gj, and thus the possibility of ties among samples θij ~ Gj, i = 1, . . . , nj, and j = 1, . . . , J. We could again use these ties to define a random partition. Let denote the unique values among the θij and define clusters . This defines random clusters of experimental units across j. In summary, the HDP generates random probability measures Gj that share the same atoms across j. However, the random distributions Gj are different. The common atoms have different weights under each Gj. This distinguishes the HDP from the related nested DP (NDP) of Rodríguez et al. (2008). The NDP allows for some of the Gj to be identical. While the HDP uses a common discrete base measure G★ to generate the atoms in the Gj's, the NDP uses a common discrete prior Q(Gj) for the distributions Gj themselves, thus allowing p(Gj = Gj′) > 0 for j ≠ j′. The prior for Q is a DP prior whose base measure has to generate random probability measures which serve as the atoms of Q. Another instance of a DP prior is used for this purpose. In summary, Gj ~ Q and Q ~ DP(M, DP(α, G★)). Another related extension of the DP is the enriched DP of Wade et al. (2011).
3.3 More Random Partitions
Several alternatives to DP priors for random partitions have been discussed in the literature. The special feature of the DP prior is the simplicity of (5). While any discrete random probability measure gives rise to a prior p(ρn), few are as simple as (5). The already mentioned Pitman-Yor process (Pitman and Yor 1997) implies very similar conditionals for si, with
where 0 < β < 1 and α > –β. See also the discussion in Ishwaran and James (2001). Similarly, any NRMI defines a prior p(ρn). For the NGGP Lijoi et al. (2007) give explicit expressions for p(si = k | s–). They discuss the larger family of Gibbs-type priors as a class of priors p(ρn) that include the one implied under the NGGP as a special case. While the simple nature of (5) is computationally attractive, it can be criticized for lack of structure. For example, the conditional probabilities for cluster membership depend only on the sizes of the clusters, not on the number of clusters or the distribution of cluster sizes. For a related discussion see also Quintana (2006) and Lee et al. (2013).
For alternative constructions of p(ρn) we could focus on the form of (4) as a product over functions c(Sk) = α(nk – 1)! that depend on only one cluster at a time. Random partition models of the form for some function c(Sk) are known as product partition models (PPM) (Hartigan 1990). Together with a sampling model that assumes independence across clusters the posterior p(ρn | y) is again of the same form.
Müller et al. (2011) define a variation of the PPM by explicitly including covariates. Let xi denote covariates, let yi denote responses, and let denote covariates arranged by clusters. The goal is to a priori favor partitions with clusters that are more homogeneous in x. Posterior predictive inference then allows one to define regression based on clustering. We define a function such that g(x★) is large for a set of covariates that are judged to be very similar, and small when x★ includes a diverse set of covariate values. The definition of g(·) is problem-specific. For example, for a categorical covariate xi ∈ {1, . . . , Q}, let mk denote the number of unique values xi in cluster k. and we could use . A cluster with all equal xi has the highest similarity. Müller et al. (2011) define the PPMx model
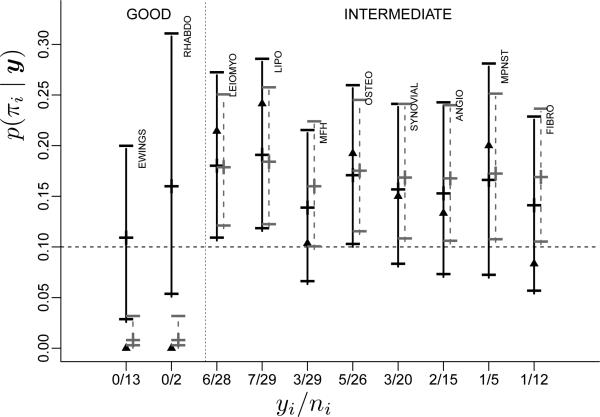
Example 3 (Sarcoma trial). Leon-Novelo et al. (2012) consider clustering of different sarcoma types. Table 2 shows data from a phase II clinical trial with sarcoma patients. Sarcoma is a rare type of cancer affecting connective or supportive tissues and soft tissue (e.g., cartilage and fat). There are many subtypes of sarcomas, reflecting the definition of sarcomas as cancers of a large variety of tissues. Some subtypes are very rare, making it attractive to pool patients across subtypes. Leon-Novelo et al. (2012) propose to pool patients on the basis of a random partition of subtypes. Keeping the clustering of subtypes random acknowledges the uncertainty about the different nature of the subtypes. However, in setting up a prior probability model for the random partition of subtypes, not all subtypes are exchangeable. For example, some are known to have better prognosis than others. Leon-Novelo et al. (2012) exploit this information. Let xi ∈ {–1, 0, 1} denote an indicator of poor, intermediate or good prognosis for subtype i. We define a prior model p(ρn | x1, . . . , xn) with increased probability of including any two subtypes of equal prognosis in the same cluster. Let Q = 3 denote the number of different prognosis types, and let mkq denote the number of xi = q for all i ∈ Sk and the size of the k–th cluster. We use the similarity function The particular choice is motivated mainly by computational convenience.1 It allows a particularly simple posterior MCMC scheme. Müller et al. (2011) argue that with this choice of the posterior distribution on ρn is identical to the posterior in a DPM model under a model augmentation, and thus any MCMC scheme for a DPM models can be used. The important feature, however, is the increased probability for homogeneous clusters. Let Bin(y; n, π) denote a binomial probability distribution for the random variable y with binomial sample size n and success probability π. Let denote cluster specific success rates. Conditional on ρn and π★ we assume a sampling model . The probability model is completed with a conjugate prior for the cluster-specific success rates . Let denote the success probability for sarcoma type i. Figure 4 shows posterior means and 90% credible intervals for πi by sarcoma type, compared with inference under an alternative partially exchangeable model, i.e., a model with separate submodels for xi = –1, 0 and 1. Notice how the BNP model strikes a balance between the separate analysis of a partially exchangeable model and the other extreme which would pool all subtypes. In summary, the use of the BNP model here allowed one to borrow strength across the related subpopulations while acknowledging that it might not be appropriate to pool all.
Figure 4.
Central 90% posterior credible intervals of success probabilities πi for each sarcoma subtype under the BNP model (black lines) and under a comparable parametric model (grey lines). The central marks (“+”) are the posterior means, the triangles are the m.l.e.'s.
A practical problem related to posterior inference for random partitions is the problem of summarizing p(ρn | y). Many authors report posterior probabilities of co-clustering. Let dij denote a binary indicator with dij = 1 when si = sj, and dij = 0 otherwise, and define Dij = p(dij = 1 | y). Dahl (2006) went a step further and introduced a method to obtain a point estimate of the random clusters based on least-square distance from the matrix of posterior pairwise co-clustering probabilities. Quintana and Iglesias (2003) address the problem of summarizing p(ρn | y) as a formal decision problem.
3.4 Feature Allocation Models
In many applications the strict mutually exclusive nature of the cluster sets in a partition is not appropriate. For example, in an application to find sets of proteins that correspond to some common biologic processes, one would want to allow for some proteins to be included in multiple sets, i.e., to be involved in more than one process. Such structure can be modeled by feature allocation models. For example, the Indian buffet process (IBP) (Griffiths and Ghahramani 2006) defines a prior for a binary random matrix whose entries can be interpreted as membeship of proteins (rows) in protein sets (columns). Ghahramani et al. (2007) review some applications of the IBP. An excellent recent discussion of such models and how they generalize random partition models appears in Broderick et al. (2013).
4 Regression
4.1 Nonparametric Residuals
Consider a generic regression problem yi = f(xi) + εi with responses yi, covariates xi and residuals εi ~ p(εi) for experimental units i = 1, . . . , n. In a parametric regression problem we assume that the regression mean function f(·) and the residual distribution p(·) are indexed by a finite dimensional parameter vector, f(x) = fθ(x) and p(ε) = pθ(ε). Sometimes a parametric model is too restrictive and we need nonparametric extensions. The earlier stylized description of a regression problem suggests three directions of such model extensions. We could relax the parametric assumption on f(·), or go nonparametric on the residual distribution pθ(·), or both. We refer to the first as BNP regression with a nonparametric mean function, the second as a nonparametric residual model and the combination as a fully nonparametric BNP regression or density regression.
Hanson and Johnson (2002) discuss an elegant implementation of a nonparametric residual model. Assuming εi ~ G and a nonparametric prior G ~ p(G) reduces the problem to essentially the earlier discussed density estimation problem, the only difference being that now the i.i.d. draws from G are the latent residuals εi. In principle, any model that was used for density estimation could be used. However, there is a minor complication. To maintain the interpretation of εi as residuals and to avoid identifiability concerns, it is desireable to center the random G at zero, for example, with E(G) = 0 or median 0. Hanson and Johnson (2002) cleverly avoid this complication by using a PT prior. The PT prior allows simple centering of G by fixing B0 = (–∞, 0] and , thus fixing the median at 0.
4.2 Nonparametric Mean Function
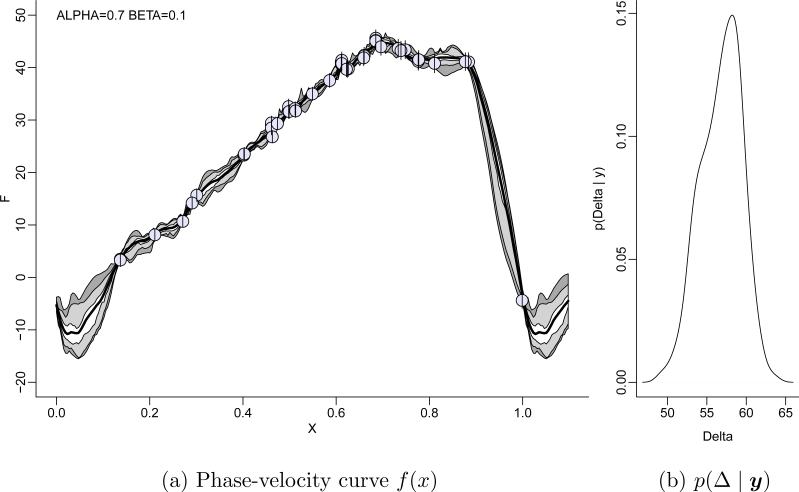
Example 4 (Cepheid data). Barnes et al. (2003) discuss an application of BNP regression to analyze data from Cepheid variable stars. Cepheid variable stars serve as mile stones, or standard candles, to establish distances to galaxies in the universe. This is because the luminosities for these stars are highly correlated with their pulsation periods, allowing indirect measurement of a Cepheid star's luminosity (light output), which in turn can be related to the observed brightness to infer the distance. Calibration of the luminosty-period relation involves a non-linear relationship that includes among others the integral ΔR of radial velocity with respect to phase. Figure 5a plots radial velocity versus phase for the Cepheid variable star T Monocerotis. The circles indicate the observed data points. The short vertical line segments show the (known) measurement error standard deviation. The periodic nature of the data adds a constraint f(0) = f(1) for the phase-velocity curve f(x). The sparse data around x = 0 makes it difficult to determine the regression mean function around x = 0. The many data points in other parts of the curve mislead a parametric model to believe in precisely estimated parameters, including the critical interpolation around x = 0. We therefore consider a nonparametric regression.
Figure 5.
Phase-velocity curve f(x) for T Monocerotis. Panel (a) shows the posterior estimated phase-velocity curve E(f | y) (thick central line), and pointwise central HPD 50% (light grey) and 95% (dark grey) intervals for f(x). The circles shows the data points. Inference is under a BNP model p(f) using a basis expansion of f with wavelets. Panel (b) shows posterior inference on the range Δ = max(f) – min(f).
A convenient way to define a BNP prior for an unknown regression mean function is the use of a basis representation. Let {φj} denote a basis, for example, for square integrable functions. Any function of the desired function space can be represented as
| (6) |
i.e., functions are indexed by the coefficients dh with respect to the chosen basis. Putting a prior probability model on {dh} implicitly defines a prior on f. Wavelets (Vidakovic 1998) provide a computationally very attractive basis. The (super) fast wavelet transform allows quick and computationally efficient mapping between a function f and the coefficients. The basis functions ϕh(·) are shifted and scaled versions of a mother wavelet, ψjk(x) = 2j/2ψ(2jx – k), j ≥ J0, together with shifted versions of the scaling function ϕJ0k(x) = 2J0/2ϕ(2J0x – k), k ∈ Z, i.e.,
| (7) |
The coefficients d = (cJ0k, djk j ≥ J0, k ∈ Z) parametrize the function. The ψjk and ϕJ0k form an orthonormal basis. The choice of J0 is formally arbitrary. Consider J > J0. The mapping between cJk and (cJ0k, djk, j = J0, . . . , J) is carried out by an iterative algorithm known as the pyramid scheme. Let f = (f1, . . . , f2J) denote the function evaluated on a regular grid. In view of the normalization property, ∥ϕJk∥ = 1, scaling coefficients at a high level of detail J are aproximately proportional to the represented function, cJk ≈ 2–J/2fk. Thus for large J the mapping between cJk and (cJ0k, djk, j = J0, . . . , J) effectively becomes a mapping between f and the coefficients and defines the super fast one-to-one map between f and the coefficients that we mentioned before. The nature of the basis functions ψjk as shifted and scaled versions of the mother wavelet allows an interpretation of djk as representing a signal at scale j and shift k. This interpretation suggests a prior probabilty model with increasing probability of zero coefficients, increasing with level of detail j. Barnes et al. (2003) use p(djk = 0) = 1 – αj+1, and a multivariate normal prior for the non-zero djk and cJ0k, conditional on keeping the zero coefficients. And the periodic nature of the function, with f(0) = f(1), adds another constraint. Chipman et al. (1997), Clyde et al. (1998) and Vidakovic (1998) discuss Bayesian inference in similar models assuming equally spaced data, i.e., covariate values xi are on a regular grid. Non-equally spaced data do not add significant computational complications.
Example 4 (ctd.). Figure 5a shows f̄ = E(f | y) under a BNP regresssion model based on (7) with p(djk = 0) = 1 – αj+1 and a multivariate normal dependent prior on cJ. The primary inference target here is the range Δ = max(f) – min(f) whose posterior uncertainty is mostly determined by the uncertainty in f(·) around x = 0 and thus ΔR. Figure 5b shows the implied p(Δ | y).
Morris and Carroll (2006) build functional mixed effects models with hierarchical extensions of (7) across multiple functions. Wavelets are not the only popular basis used for nonparametric regression models. Many alternative basis functions are used. For example, Baladandayuthapani et al. (2005) represent a random function using P-splines.
Gaussian process priors
Besides basis representations like (6), another commonly used BNP prior is the Gaussian process (GP) prior. A random function f(x) with has a GP prior if for any finite set of points , i = 1, . . . , n, the function evaluated at those points is a multivariate normal random vector. Let f★(x), denote a given function and let r(x1, x2) for denote a covariance function, i.e., the (n × n) matrix R with R = r(xi, xj) is positive definite for any set of distinct . We write f ~ GP (f★(x), r(x, y)) if
Assuming normal residuals, the posterior distribution for f = (f(x1), . . . , f(xn)) is multivariate normal again. Similarly, f(x) at new locations xn+i that were not recorded in the data is characterized by multivariate normal distributions again. See O'Hagan (1978) for an early discussion of GP priors, and Kennedy and O'Hagan (2001) for a discussion of Bayesian inference for GP models in the context of modeling output from computer simulations.
4.3 Fully Nonparametric Regression
Regression can be characterized as inference for a family of probability models on y that are indexed by the covariate x, i.e., y | x ~ Gx(y) and a BNP prior on . In BNP regression with a nonparametric mean function the model Gx is implied by a parametric residual distribution and a BNP prior for the mean function f(·). In contrast, in fully nonparametric regression the BNP prior is put on the family .
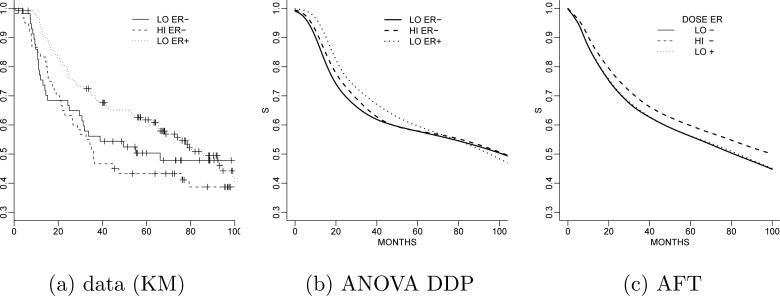
Example 5 (Breast cancer study). We illustrate fully nonparametric regression with surival regression in a cancer clinical trial. The trial is described in Rosner (2005). The data record the event-free survival time ti in months for n = 761 women. A subset of n0 = 400 observations are censored. Researchers are interested in determining whether high doses of the treatment are more effective for treating the cancer compared to lower doses. We consider two categorical and one continuous covariate, and one interaction variable: treatment dose (TRT) (–1 = low, 1 = high), estrogen receptor (ER) status (–1 = negative, 1 = positive), the size of the tumor (standardized to zero mean and unit variance), and a dose/ER interaction (1 if a patient receives high treatment dose and has positive ER status and 0 otherwise). This defines a vector xi of covariates for each patient. The desired inference is to learn about Gx(y) = p(y | x), in particular, the comparison with respect to TRT. Figure 6a shows the data as a Kaplan-Meier plot.
Figure 6.
Cancer clinical trial. Panel (a) shows the data as a Kaplan-Meier (KM) plot arranged by dose and ER status. Posterior survivor functions under the ANOVA DDP model (panel b) and alternatively under the AFT median regression model (panel c). In both plots, the solid line refers to low treatment dose and negative ER status. The dashed line corresponds to high treatment dose and negative ER status, while the long dashed line shows the survival for a patient in the low dose group but with positive ER status.
De Iorio et al. (2009) implement inference using a dependent Dirichlet process model (DDP). The DDP was proposed by MacEachern (1999) as a clever extension of the DP prior for one random probability measure G to the desired prior p(Gx; x ∈ X) for a family of random probability measures. The construction builds on the stick-breaking representation (1) of the DP. Consider a DP prior for Gx,
| (8) |
with independent across h and πh = vh Πl<h(1 – vl) with vh ~ Be(1, M), i.i.d. Definition (8) ensures that , marginally. The key observation is that we can introduce dependence of across x. That is all. By defining a dependent prior on we create dependent random probability measures Gx. As a default choice MacEachern (1999) proposes a Gaussian process prior on on . Depending the nature of the covariate space X other models can be useful too. The DDP model (8) is sometimes referred to as variable location DDP. Alternatively the weights πh(x), or both weights and locations, could be indexed with x, leading to variable weight and variable weight and location DDP.
Example 5 (ctd.). De Iorio et al. (2009) define inference for a set {Gx; x ∈ X} indexed by a covariate vector x that combines two binary covariates and|one continous covariate. In that case, a convenient model for dependent probability distributions on is a simple ANOVA model for the categorical covariates. Adding a continuous covariate (tumor size) defines an ANCOVA model. Figure 6b shows inference under the ANOVA DDP model. For comparison, Figure 6c show inference for the same data under a semiparametric accelerated failure time (AFT) median regression model with a mixture of PT's on the error distribution. The model is described in Hanson and Johnson (2002). The PT is centered at a Weibull model. Panels (b) and (c) report inference for a patient with average tumor size (this explains the discrepancy with the KM plot). The BNP model recovers a hint of crossing survival functions.
A construction similar to the DDP is introduced in Gelfand et al. (2005) who define a spatial DP mixture by considering a DP prior with a base measure G★ which itself is a GP, indexed with a spatial covariate x, say . In other words, a realization of the spatial DP is a random field . Focusing on one location x we see that the spatial DP induces a random probability measure for θ(x), call it Gx. However, the spatial DP defines a stick-breaking mixture of GP realizations, i.e., . For example, one observation (θ(x1), θ(x2)) at a pair of spatial locations is based on one realization of the base measure GP. In contrast, under the DDP a pair of realizations θ(x1), θ(x2), could be based on two realizations of the base measure GP (with the possibility of a tie only because of the discrete nature of the distributions). Under the spatial DP, a sampling model for observed data might still add an additional regression.
Many other variations of the DDP have been proposed, including matrix stick-breaking (Dunson et al. 2008) and the kernel stick-breaking of Dunson and Park (2007). Matrix stick-breaking introduces dependence for a set of random probability measures that are arranged in a matrix, i.e., indexed by two categorical indices, say . In contrast to the common weights πh in the basic DDP model (8) the model uses varying weights and common locations . The construction starts with stick-breaking as in (1), but then assumes vijh= UihWjh with the independent beta priors on Uih and Wjh. Similarly, kernal stick-breaking introduces dependence across random probability measures by replacing vxh in the stick breaking construction by VhK(x, Γh), where Vh is common across all x, K(x, m) is a kernel centered at m and Γh are kernel locations. The intention of the construction is to create πxh that are a continuous function of x. The specific nature of πxh as a function of x is hidden in the kernel.
In the recent literature several alternatives to the DDP have been proposed. Dunson et al. (2007) propose density regression as a locally weighted mixture of a fixed set of independent random probability measures. The weights are written as functions of the covariates. A similar model is the already mentioned kernel stick-breaking process of Dunson and Park (2007). Trippa et al. (2011) define a dependent PT model by replacing the random splitting probabilities Yε by a stochastic process (Yε(x))x∈X, maintaining the marginal beta distribution for any x. Jara and Hanson (2011) propose a similar construction, but with the random splitting probabilties Yε(x) defined by a transformation, for example a logistic transformation, of a GP. The constructed family of dependent random probability measures is known as dependent tail-free processes (DTFP). A special case is the linear dependent tailfree process (LDTFP) that is also discussed in Hanson and Jara (2013).
5 Random effects Distributions
5.1 Mixed effects Models
An important application of nonparametric approaches arises in modeling random effects distributions in hierarchical mixed effects models. Often little is known about the specific form of the random effects distribution. Assuming a specific parametric form is typically motivated by technical convenience rather than by genuine prior beliefs. Although inference about the random effects distribution itself is rarely of interest, it can have implications on the inference of interest, especially when the random effects model is part of a larger model. Thus it is important to allow for population heterogeneity, outliers, skewness, etc.
In this context of a mixed effects model with random effects θi a BNP model can be used to allow for more general random effects distribution G(θi). Let yij = θi + β′xij + εij denote a randomized block ANOVA with residuals εij ~ N(0, σ2), fixed effects β and random effects θi for blocks of experimental units, i = 1, . . . , I. For technically convenient posterior analysis one could assume a normal random effects distribution θi ~ N(0, τ2) and conditionally conjugate priors p(β, σ2, τ2). While the prior for the fixed effects might be based on substantive prior information, the choice of the random effects distribution is rarely based on actual prior knowledge. The relaxation of the convenient, but often arbitrary distributional assumption for the random effects distribution is a typical application of BNP models. A nonparametric Bayesian model can relax the assumption without losing interpretability and without substantial loss of computational efficiency. Many nonparametric Bayes models allow us to center the prior model p(G) around some parametric model pη, indexed by hyperparameters η. For example, we could center a prior p(G) for a random effects distribution G around a N(0, τ2) model with hyperparameter η = τ. The construction allows us to think of the nonparametric model as a natural extension of the fully parametric model.
In the nonparametric extension the random effects distribution itself becomes an unknown quantity. We replace the normal random effects distribution with θi ~ G, G ~ p(G) with a BNP prior p(G) for the unknown G. For later reference we state the full mixed effects model
| (9) |
Here the sampling model p(yij | β, θi) could, for example be an ANOVA model. The nonparametric prior p(G) is a prior for a density estimation with the (latent) random effects θi. We could use any prior that was discussed earlier. The only difference is that now the latent θi replace the observed data in the straightforward density estimation problem. There is one complication. The nature of G(·) as a random effects distribution requires centering at 0 to ensure identifiability. Often, this detail is ignored, or only mitigated by setting up the prior with a prior mean G★ = E(G) such that G★ is centered around 0. However, centering the prior mean does not imply centering of G. A nonzero mean of G could be confounded with corresponding fixed effects. Li et al. (2011) propose a clever postprocessing step of MCMC output to allow the use of DPM models including MCMC without any constraint.
Bush and MacEachern (1996) propose a DP prior for θi ~ G, G ~ DP(G★, M). Kleinman and Ibrahim 1998) propose the same approach in a more general framework for a linear model with random effects. They discuss an application to longitudinal random effects models. Müller and Rosner (1997) use DP mixtures of normals to avoid the awkward discreteness of the implied random effects distribution. Also, the additional convolution with a normal kernel greatly simplifies posterior simulation for sampling distributions beyond the normal linear model. Mukhopadhyay and Gelfand (1997) implement the same approach in generalized linear models with linear predictor and a DP mixture model for the random effect θi. In Wang and Taylor (2001) random effects θi are entire longitudinal paths for each subject in the study. They use integrated Ornstein-Uhlenbeck stochastic process priors for θi.
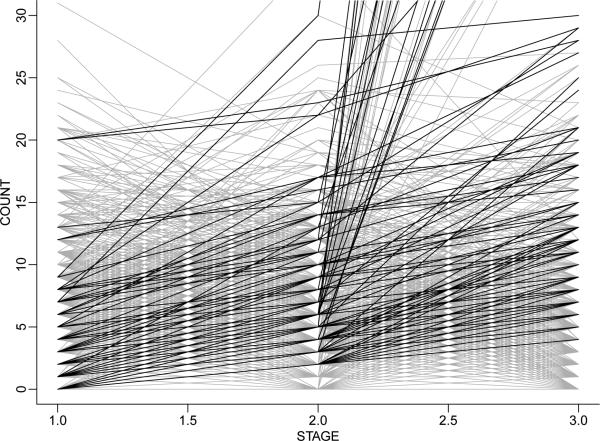
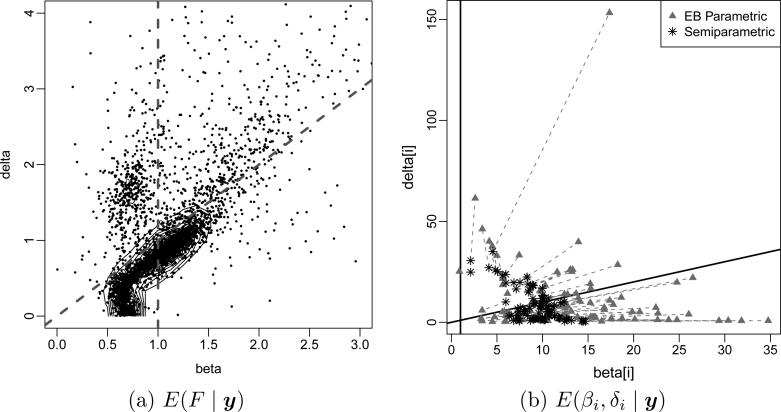
Example 6 (Phage display experiment). Leon-Novelo et al. (2013) discuss an application of BNP priors for random effects distributions that includes a decision problem on top of the inference problem. The BNP prior matters. The decision hinges on a full description of uncertainties in the random effects distribution. Leon-Novelo et al. (2013) analyze count data from a phage display experiment with three stages. The data come from three consecutive human subjects who met the formal criteria for brain-based determination of death. The primary aim of the experiment is to identify peptides that bind with high a nity to particular tissue (bone-marrow, fat, muscle, prostate and skin). Bacteriophages, phages for short, are viruses. They provide a convenient mechanism to study the preferential binding of peptides to tissues, essentially because it is possible to experimentally manipulate the phages to display various peptides on the surface of the viral particle. See Leon-Novelo et al. (2013) for a more detailed description of the experimental setup and the study. The data are tripeptide counts by tissue and stage. The experiment is set up in such a way that peptides that preferentially bind to a particular organ should be recorded with systematically increasing counts over the three stages. The inference goal is to select from a large list of peptide and tissue pairs those with significant increase over stages. Figure 7 shows the data. Let i = 1, . . . , n, index all n = 2763 recorded tripeptide/tissue pairs. Each line connects the three counts yi1, yi2, yi3 for one tripeptide/tissue pair. Of course, even if there were no true preferential binding, and all counts were on average constant across stages, one would expect about 1/4 of the observed counts to be increasing across the 3 stages. The decision problem is to select pairs with significant increase and report them for preferential binding. Let Poi(λ) denote a Poisson distribution. We assume yi1 ~ Poi(μi), yi2 Poi(μiβi) and yi3 ~ Poi(μiδi) for random effects (μi, βi, δi). The event of increasing mean counts becomes Ai = {1 ≤ βi ≤ δi}. We use a random effects distribution (βi, δi) ~ G with BNP prior p(G). Figure 8a shows E(G | y). The event A = {0 < β < δ} is in the right upper quadrant, between the two lines. The main inference summary is the posterior probabilities for increasing mean counts, pi = p(Ai | y). Thresholding pi defines a decision rule δi = I(pi > c) for reporting preferential binding for the tripeptide/tissue pair i. Leon-Novelo et al. (2013) use a bound on the posterior expected false discovery rate to fix the threshold c. Figure 8b highlights the importance of the BNP model here. The figure reports under two alternative models, the described BNP model (marked as “semiparametric” in the figure) and a corresponding parametric model (“EB”). Results in (b) are for a – different – simulated data set. Short line segments connect under the two models for each tripeptide/tissue pair i. The corrections are substantial, impacting the posterior probabilities pi and thus changing the decisions δi for many pairs.
Figure 7.
Observed counts yi1, yi2, yi3 over stages 1 through 3. Each line connects the three counts for one tripeptide-tissue pair. Tripeptide/tissue pairs with increasing counts yi1 + 1 < yi2 and yi2 + 1 < yi3 are plotted in black (adding the increment 1 to avoid a cluttered display). Others are plotted in grey.
Figure 8.
Estimated random effects distribution (panel a) and posterior estimated random effects E(βi, δi | y) (panel b, marked with “*”) versus posterior means under a similar parametric model (“+”). Results in (b) are under a – different – simulated data set.
5.2 Multiple Subpopulations and Classification
The use of BNP priors for random effects distributions becomes particularly useful when the model includes subpopulations, say v = 1, . . . , V with separate, but related random effects distributions Gv. We let and augment (9) to
| (10) |
Here is a BNP prior for a family or random probability measures, for example the DDP model introduced in (8).
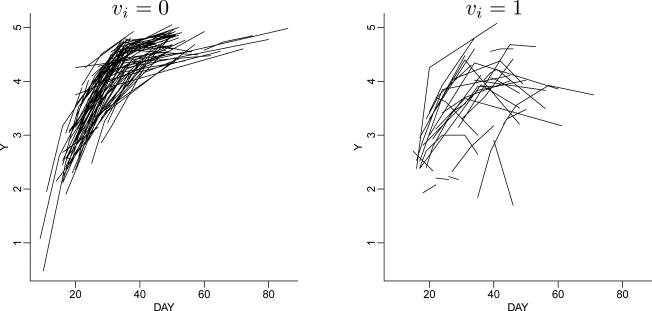
Example 7 (Hormone data). De la Cruz et al. (2007) analyze hormone data for 173 pregnancies. The data report repeat measurements on the pregnancy hormone β-HCG for 173 young women during the first 80 days of gestational age. Figure 9 shows the data. The data include n0 = 124 normal pregnancies and n1 = 49 pregnancies that were classified as abnormal. The goal is to predict normal or abnormal pregnancy for a future woman on the basis of the longitudinal data as it accrues over time. Figure 10c shows the desired inference. The figure plots the posterior probability of a normal pregnancy against the number of hormone measurements for two hypothetical future women, one with a normal pregnancy and one with an abnormal pregnancy. Let yi = (yi1, . . . , yini) denote the β-HCG repeat measurments for the i-th woman, recorded at times tij, j = 1, . . . , nij. Let vi ∈ {0, 1} denote an indicator for abnormal pregnancy. The longitudinal data are modeled as a non-linear mixed-effects model
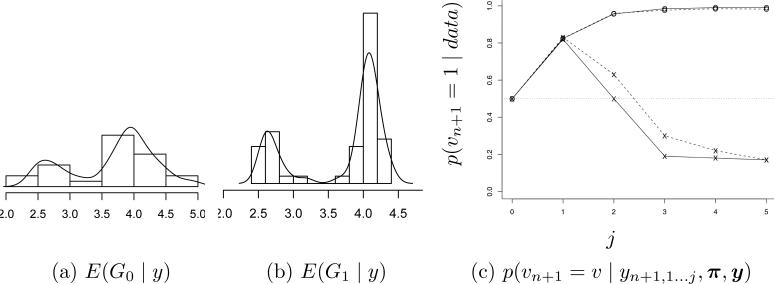
i.e., a logistic regression with coefficients βv and scaled by random effects θi and with normal residuals. Both βv, are specific to each group, v = 0 and v = 1. Let . The model includes a patient-specific random effect θi with θi | vi = x ~ Gv(θi). We assume a BNP prior p(G0, G1). We use an ANOVA DDP prior on . The binary nature of v ∈ {0, 1} makes the model particularly simple, with , where ah0 = 0 and εhv ~ N(0, τ2). The model is completed with a bivariate normal prior G★(mh, ah1) and conditionally conjugate priors for ϕ. Figure 10ab shows the estimated random effects distributions.
Figure 9.
Hormone data. Observed repeat β-HCG measurement for normal (left panel) and abnormal (right) pregnancies.
Figure 10.
Hormone data. Estimated random effects distributions E(Gv | y) for v = 0 (Panel a) and v = 1 (b). Panel (c) shows the classification of a hypothetical (n + 1)-st pregnancy as a function of the number j of observed hormone measurements.
A simple augmentation of model (10) allows to use the same model for classification. First we change indexing of experimental units i to run i = 1, . . . , n across all subgroups, and add vi ∈ {1, . . . , V} as an indicator for unit (patient) i being in group v. Then add a prior p(vi = v) = πv, to get
| (11) |
for v = 1, . . . , V. The expectation in square brackets is with respect to the posterior probability model on , ϕ given the observed data (yi, vi; i = 1, . . . , n).
Example 7 (ctd.). Figure 10c shows the posterior probability p(vn+1 = 1 | yn+1,1...j, y) for two hypothetical future patients i = n + 1, plotted against j = 0, 1, . . . , 6, as repeat observations accrue. The evaluation of the classification rule in (11) makes use of p(G1, G0 | y). The BNP model matters.
6 Asymptotics
With sufficiently large data, the posterior distribution should be concentrated more and more tightly around the true parameter θ0. This property is known as posterior consistency. Posterior consistency statements are results about probabilities under repeat experimentation under some unknown truth θ0, i.e., results about frequentist probabilities. A lot of recent BNP research is concerned with such asymptotic results. In the world of Bayesian nonparametrics, the true parameter is typically an infinite dimensional object. It could be a probability density function, a c.d.f., the spectral density of a time series, etc. We therefore consider distances in function spaces. Some commonly studied metrics in posterior consistency are the Hellinger distance, the Kullback-Leibler metric, and the the L1 metric. Neighborhoods defined by the L1 metric are known as strong neighborhoods. A weak neighborhood V of a function f0 is a set indexed by ε and a finite set of bounded continuous functions ϕ1 . . . ϕk such that . We say that a measure f0 is in the support of a prior p(f) if every weak neighborhood of f0 has positive p measure. For the rest of the discussion we assume that the goal is inference for an unknown distribution F0, and the data are i.i.d. observations, xi ~ F0, i = 1, . . . , n. We say that a model exhibits posterior consistency with respect to a particular topology (strong or weak) if p(U | x1 . . . xn) → 1 a.s.-F0 for all neighborhoods U of F0 corresponding to that topology.
Freedman (1963) proposed tail-free distributions as a class of priors for which posterior consistency holds. Consider a nested sequence of partitions (πm) of the sample space, π1 = {B0, B1}, π2 = {B00, B01, B10, B11}, etc., such that πm+1 is a refinement of πm, i.e., , where ε = e1e2 · · · em is an m-digit binary index. A prior p(G) is called tail-free with respect to a nested sequence of partitions if {G(B0)}, {G(B00 | B0), G(B01 | B0)}, etc. are independent across partitions. Two important priors that exhibit consistency due to a tail-free property are the DP and the PT priors. However the tail-free property is not common and can be destroyed when the process is convoluted with a mixing measure. This concern generated a need to formalize good priors in terms of consistency theorems that impose general sufficient conditions on the true density F0 and the prior p(F). Schwartz's theorem (1965) is the first important step in this direction and forms a strong basis for a lot of subsequent work.
Schwartz (1965) proposed an important condition for consistency. The prior should put positive mass on all Kullback Leibler (KL) neighborhoods of the true density. This is referred to as Schwartz's prior positivity condition or the KL property of the prior. A second condition is the existence of a sequence of uniformly exponentially consistent tests of H0 : F = F0 vs. H1 : F ∈ Uc for every neighborhood U of F0. Together, these conditions ensure consistency. The second condition is readily met for weak topology. Thus, as a corollary, prior positivity becomes a sufficient condition for weak consistency.
We review some results on weak consistency of DPM's of normals models. Let ϕ(x; θ, h) denote a normal p.d.f. with location θ and scale h. We consider DPM models of the form with G ~ DP(G★, M). The model is completed with a prior p(h). We refer to such DPM models as DP location mixture of normals, for short “location mixtures.” Ghosal et al. (1999) prove prior positivity, and hence weak consistency for a location mixture. The sufficient conditions are that the true density itself is a convolution, i.e., where P0 is compactly supported and belongs to the weak support of the DP prior and h0 is in the support of p(h). In the same paper, the result is extended to DPM location-scale mixture of normals , for short “location-scale mixtures.”
To establish strong consistency of DPM of normal models, additional techniques, like constructions of sieves, are required. Using such constructions, Ghosal et al. (1999) prove strong consistency for location mixture priors when the true F0 is in the KL support of the prior, subject to some conditions on p(h) and the tail of the base measure G★ of the DP prior. These conditions are satisfied for a normal base measure for and an inverse gamma prior p(h2). Lijoi et al. (2005b) improved upon these results by replacing the exponential tail condition by . Ghosal and van der Vaart (2001) established a convergence rate of for strong consistency in location-scale mixtures, where k depended on the tail behavior of the base measure. The result assumed that the true densities are DPMs with compactly supported mixing measure and that h is in a bounded interval. Such densities are known as super-smooth. Ghosal and van der Vaart (2007) generalize the result to the larger class of twice differentiable true densities. They assume location mixtures, with the prior pn(h) on the scale changing with sample size. A rate, lower than that in Ghosal and van der Vaart (2001), but equal to an optimal rate of a kernel estimator is obtained in this setting. Tokdar (2006) established both strong and weak consistency for a large class of true densities F0 satisfying for some η > 0. This class includes heavy tailed distributions like the t density. The priors are location-scale mixtures with some regularity conditions on the tail of the base measure G★, which are shown to be satisfied for normal and inverse gamma base measures.
Although most arguments use sieves and Schwartz's framework, there are some alternative approaches too. Walker and Hjort (2002) and Walker (2004, 2003) use the martingale property of marginal densities as a unifying tool. For recent reviews of consistency and convergence rates in DPM models, see Walker et al. (2007) and Ghosal (2010).
Some recent work considers posterior consistency for models beyond DP priors. Jang et al. (2010) showed that in the class of Pitman-Yor process priors, DP priors are the only ones with posterior consistency. Gaussian processes are another important class of priors with well known consistency results. For example, assume a regression setting with binary outcomes yi where the success probabilities p(yi = 1 | xi) are a smooth unknown function f(xi) of a set of covariates xi. Let h(θ) denote an inverse logit link (or any other monotone mapping from ℜ to the unit interval) and define a prior p(f) by assuming f(x) = h[θ(x)] for a Gaussian process θ(x) ~ GP. Ghosal and Roy (2006) discussed posterior consistency for such models. More general results on consistency and rates of convergence for a large class of GP priors (e.g., Brownian motion) are shown in van der Vaart and van Zanten (2008).
7 Conclusion
We tried to motivate BNP inference by a discussion of some important inference problems and examples that highlight the limitations of parametric inference. The statement is meant in reference to a standard, default parametric model. Naturally, in each of these examples one could achieve similar inference with sufficiently complicated parametric models like a finite mixture. However, inference under such models is usually no easier than under the BNP model. For example, inference with a finite mixture model gives rise to all the same complications as a nonparametric mixture, such as the DPM model.
We have not discussed two important aspects of BNP inference. Inference for many models quickly runs into computation intensive posterior inference problems. We did not discuss many such details. Also, a large part of the recent BNP literature is concerned with asymptotic properties of BNP inference, which we only briefly summarized in this review. For an excellent recent review of posterior asymptotics in DP and related models see Ghosal (2010).
Finally, we owe a comment about the term “nonparametric.” We started out by defining BNP as probabilty models for infinite dimensional random quantities like curves or densities. It might be more fittingly called “massively parametric Bayes”. The label nonparametric has been used because inference under BNP models often looks similar to (genuinely) nonparametric classical inference.
Acknowledgments
Both authors were partially funded by grants NIH/CA075981 and R01-CA157458. The data for examples 1 through 4 are available on-line.
This review was sponsored by the Bayesian Nonparametrics Section of ISBA (ISBA/BNP). The authors thank the section officers for the support and encouragement.
Footnotes
Leon-Novelo et al. (2012) use without the (Q – 1)! = 2 factor, which, however, in the light of (4) is equivalent to simply rescaling α by 2.
References
- Baladandayuthapani V, Mallick BK, Carroll RJ. Spatially Adaptive Bayesian Penalized Regression Splines (P-splines). Journal of Computational and Graphical Statistics. 2005;14(2):378–394. 285. [Google Scholar]
- Barnes TG, Jefferys WH, Berger JO, Müller P, Orr K, Rodríguez R. A Bayesian Analysis of the Cepheid Distance Scale. The Astrophysical Journal. 2003;592(1):539, 283, 285. [Google Scholar]
- Barrios EJ, Lijoi A, Nieto-Barajas LE, Prünster I. Modeling with normalized random measure mixture models. Statistical Science. 2013:277. to appear. [Google Scholar]
- Box GEP. Some Problems of Statistics and Everyday Life. Journal of the American Statistical Association. 1979;74:1–4. 269. [Google Scholar]
- Branscum AJ, Johnson WO, Hanson TE, Gardner IA. Bayesian semiparametric ROC curve estimation and disease diagnosis. Statistics in Medicine. 2008;27(13):2474–2496. 275. doi: 10.1002/sim.3250. URL http://dx.doi.org/10.1002/sim.3250. [DOI] [PubMed] [Google Scholar]
- Broderick T, Pitman J, Jordan MI. Feature allocations, probability functions, and paintboxes. 2013;arXiv:1301–6647. 282. [Google Scholar]
- Bush CA, MacEachern SN. A semiparametric Bayesian model for randomised block designs. Biometrika. 1996;83:275–285. 289. [Google Scholar]
- Chipman H, Kolaczyk E, McCulloch R. Adaptive Bayesian Wavelet Shrinkage. Journal of the American Statistical Association. 1997;92:440, 285. [Google Scholar]
- Clyde M, Parmigiani G, Vidakovic B. Multiple Shrinkage and Subset Selection in Wavelets. Biometrika. 1998;85:391–402. 285. [Google Scholar]
- Dahl DB. Model-Based Clustering for Expression Data via a Dirichlet Process Mixture Model. In: Vannucci M, Do K-A, Müller P, editors. Bayesian Inference for Gene Expression and Proteomics. Cambridge University Press; 2006. p. 281. [Google Scholar]
- De Iorio M, Johnson WO, Müller P, Rosner GL. Bayesian Non-parametric Nonproportional Hazards Survival Modeling. Biometrics. 2009;65(3):762–771. 286. doi: 10.1111/j.1541-0420.2008.01166.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De la Cruz R, Quintana FA, Müller P. Semiparametric Bayesian classification with longitudinal markers. Applied Statistics. 2007;56(2):119–137. 291. doi: 10.1111/j.1467-9876.2007.00569.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunson DB, Park J-H. Kernel stick-breaking processes. Biometrika. 2007;95:307–323. 287, 288. doi: 10.1093/biomet/asn012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunson DB, Pillai N, Park J-H. Bayesian Density Regression. Journal of the Royal Statistical Society, Series B: Statistical Methodology. 2007;69(2):163–183. 288. [Google Scholar]
- Dunson DB, Xue Y, Carin L. The Matrix Stick-Breaking Process: Flexible Bayes Meta-Analysis. Journal of the American Statistical Association. 2008;103(481):317–327. 287. [Google Scholar]
- Favaro S, Teh YW. MCMC for Normalized Random Measure Mixture Models. Statistical Science. 2013:277. to appear. [Google Scholar]
- Ferguson TS. A Bayesian analysis of some nonparametric problems. The Annals of Statistics. 1973;1:209–230. 271, 277. [Google Scholar]
- Freedman D. On the asymptotic behavior of Bayes’ estimates in the discrete case. The Annals of Mathematical Statistics. 1963;34(4):1386–1403. 293. [Google Scholar]
- Gelfand AE, Kottas A, MacEachern SN. Bayesian Nonparametric Spatial Modeling With Dirichlet Process Mixing. Journal of the American Statistical Association. 2005;100:1021–1035. 287. [Google Scholar]
- Ghahramani Z, Griffiths T, Sollich P. Bayesian nonparametric latent feature models. In: Bernardo JM, Bayarri M, Berger JO, Dawid AP, Heckerman D, Smith AFM, editors. Bayesian Statistics. Vol. 8. Oxford University Press; 2007. p. 201226.p. 282. [Google Scholar]
- Ghosal S. Hjort, et al., editors. The Dirichlet process, related priors and posterior asymptotics. 2010:22–34. 272, 295. (2010) [Google Scholar]
- Ghosal S, Ghosh J, Ramamoorthi R. Posterior consistency of Dirichlet mixtures in density estimation. Annals of Statistics. 1999;27(1):143–158. 294. [Google Scholar]
- Ghosal S, Roy A. Posterior consistency of Gaussian process prior for nonparametric binary regression. The Annals of Statistics. 2006;34(5):2413–2429. 295. [Google Scholar]
- Ghosal S, van der Vaart A. Entropies and rates of convergence for maximum likelihood and Bayes estimation for mixtures of normal densities. The Annals of Statistics. 2001;29(5):1233–1263. 294. [Google Scholar]
- Ghosal S, van der Vaart A. Posterior convergence rates of Dirichlet mixtures at smooth densities. The Annals of Statistics. 2007;35(2):697–723. 294. [Google Scholar]
- Griffiths T, Ghahramani Z. Infinite latent feature models and the Indian bu et process. In: Weiss Y, Schölkopf B, Platt J, editors. Advances in Neural Information Processing Systems. Vol. 18. MIT Press; 2006. pp. 475–482.pp. 282 [Google Scholar]
- Guindani M, Sepúlveda N, Paulino CD, Müller P. Technical report. Anderson Cancer Center; M.D.: 2012. A Bayesian Semi-parametric Approach for the Differential Analysis of Sequence Counts Data. p. 270.p. 271.p. 272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanson T, Jara A. Surviving fully Bayesian nonparametric regression. In: Damien P, Dellaportas P, Polson NG, Stephens DA, editors. Bayesian Theory and Applications. Oxford University Press; 2013. pp. 593–618.pp. 288 [Google Scholar]
- Hanson T, Johnson W. Modeling Regression Error with a Mixture of Polya Trees. Journal of the American Statistical Association. 2002;97:1020–1033. 276, 283, 286. [Google Scholar]
- Hanson TE. Inference for Mixtures of Finite Polya Tree Models. Journal of the American Statistical Association. 2006;101(476):1548–1565. 275. [Google Scholar]
- Hartigan JA. Partition Models. Communications in Statistics: Theory and Methods. 1990;19:2745–2756. 280. [Google Scholar]
- Hjort NL. Topics in nonparametric Bayesian statistics. In: Green P, Hjort N, Richardson S, editors. Highly Structured Stochastic Systems. Oxford University Press; 2003. pp. 455–487.pp. 270 [Google Scholar]
- Hjort NL, Holmes C, Müller P, Walker SG. Bayesian Nonparametrics. Cambridge University Press; 2010. p. 270.p. 297.p. 299. [Google Scholar]
- Ishwaran H, James LF. Gibbs Sampling Methods for Stick-Breaking Priors. Journal of the American Statistical Association. 2001;96:161–173. 276, 280. [Google Scholar]
- James LF, Lijoi A, Prünster I. Posterior Analysis for Normalized Random Measures with Independent Increments. Scandinavian Journal of Statistics. 2009;36(1):76–97. 277. [Google Scholar]
- Jang GH, Lee J, Lee S. Posterior consistency of species sampling priors. Statistica Sinica. 2010;20(2):581, 295. [Google Scholar]
- Jara A, Hanson T, Quintana F, Müller P, Rosner G. DPpackage: Bayesian Semi- and Nonparametric Modeling in R. Journal of Statistical Software. 2011;40(5):1–30. 273, 276. [PMC free article] [PubMed] [Google Scholar]
- Jara A, Hanson TE. A class of mixtures of dependent tail-free processes. Biometrika. 2011;98(3):553–566. 288. doi: 10.1093/biomet/asq082. URL http://biomet.oxfordjournals.org/content/98/3/553.abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy MC, O'Hagan A. Bayesian Calibration of Computer Models. Journal of the Royal Statistical Society. Series B (Statistical Methodology) 2001;63(3):425–464. 285. URL http://www.jstor.org/stable/2680584. [Google Scholar]
- Kingman JFC. Poisson Processes. Oxford University Press. 277. 1993 [Google Scholar]
- Kleinman K, Ibrahim J. A Semi-parametric Bayesian Approach to the Random Effects Model. Biometrics. 1998;54:921–938. 289. [PubMed] [Google Scholar]
- Lavine M. Some aspects of Polya tree distributions for statistical modelling. The Annals of Statistics. 1992;20:1222–1235. 273, 274. [Google Scholar]
- Lavine M. More aspects of Polya tree distributions for statistical modelling. The Annals of Statistics. 1994;22:1161–1176. 273. [Google Scholar]
- Lee J, Quintana F, Mueller P, Trippa L. Defining Predictive Probability Functions for Species Sampling Models. Statistical Science. 2013:280. doi: 10.1214/12-sts407. to appear. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leon-Novelo L, Bekele B, Müller P, Quintana F, Wathen K. Borrowing Strength with Non-Exchangeable Priors over Subpopulations. Biometrics. 2012;68:550–558. 280, 281. doi: 10.1111/j.1541-0420.2011.01693.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leon-Novelo LG, Müller P, Arap W, Kolonin M, Sun J, Pasqualini R, Do K-A. Semiparametric Bayesian Inference for Phage Display Data. Biometrics. 2013:289, 290. doi: 10.1111/j.1541-0420.2012.01817.x. to appear URL http://dx.doi.org/10.1111/j.1541-0420.2012.01817.x. [DOI] [PMC free article] [PubMed]
- Li Y, Müller P, Lin X. Center-Adjusted Inference for a Nonparametric Bayesian Random E ect Distribution. Statistica Sinica. 2011;21(3):1201–23. 289. doi: 10.5705/ss.2009.180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lijoi A, Mena RH, Prünster I. Hierarchical Mixture Modeling with Normalized Inverse-Gaussian Priors. Journal of the American Statistical Association. 2005a;100(472):1278–1291. 277. [Google Scholar]
- Lijoi A, Mena RH, Prünster I. Controlling the reinforcement in Bayesian non-parametric mixture models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2007;69(4):715–740. 277, 280. [Google Scholar]
- Lijoi A, Prünster I. Hjort, et al., editors. Models Beyond the Dirichlet process. 2010:80–136. 272, 277. (2010) [Google Scholar]
- Lijoi A, Prünster I, Walker SG. On consistency of nonparametric normal mixtures for Bayesian density estimation. Journal of the American Statistical Association. 2005b;100(472):1292–1296. 294. [Google Scholar]
- MacEachern S. ASA Proceedings of the Section on Bayesian Statistical Science. American Statistical Association; Alexandria, VA: 1999. Dependent nonparametric processes. p. 286. [Google Scholar]
- Mauldin RD, Sudderth WD, Williams SC. Polya Trees and Random Distributions. The Annals of Statistics. 1992;20:1203–1221. 273. [Google Scholar]
- Morris J, Baggerly K, Coombes K. Bayesian Shrinkage Estimators of the Relative Abundance of mRNA Transcripts using SAGE. Biometrics. 2003;59:476–486. 273. doi: 10.1111/1541-0420.00057. [DOI] [PubMed] [Google Scholar]
- Morris JS, Carroll RJ. Wavelet-based Functional Mixed Models. Journal of the Royal Statistical Society, Series B: Statistical Methodology. 2006;68(2):179–199. 285. doi: 10.1111/j.1467-9868.2006.00539.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukhopadhyay S, Gelfand A. Dirichlet Process Mixed Generalized Linear Models. Journal of the American Statistical Association. 1997;92:633–639. 289. [Google Scholar]
- Müller P, Quintana F, Rosner G. A product partition model with regression on covariates. Journal of Computational and Graphical Statistics. 2011;20:260–278. 280, 281. doi: 10.1198/jcgs.2011.09066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller P, Quintana FA. Nonparametric Bayesian Data Analysis. Statistical Science. 2004;19:95–110. 270. [Google Scholar]
- Müller P, Rodríguez A. Nonparametric Bayesian Inference. IMS-CBMS Lecture Notes. IMS; 2013. p. 270. [Google Scholar]
- Müller P, Rosner G. A Bayesian population model with hierarchical mixture priors applied to blood count data. Journal of the American Statistical Association. 1997;92:1279–1292. 289. [Google Scholar]
- O'Hagan T. Curve Fitting and Optimal Design for Prediction. Journal of the Royal Statistical Society. Series B (Methodological) 1978;40(1):1–42. 285. URL http://www.jstor.org/stable/2984861. [Google Scholar]
- Paddock SM, Ruggeri F, Lavine M, West M. Randomized Polya Tree Models for Nonparametric Bayesian Inference. Statistica Sinica. 2003;13(2):443–460. 275. [Google Scholar]
- Pepe MS, Etzioni R, Feng Z, Potter JD, Thompson ML, Thornquist M, Winget M, Yasui Y. Phases of Biomarker Development for Early Detection of Cancer. Journal of the National Cancer Institute. 2001;93(14):1054–1061. 276. doi: 10.1093/jnci/93.14.1054. URL http://jnci.oxfordjournals.org/content/93/14/1054.short. [DOI] [PubMed] [Google Scholar]
- Pitman J. Some Developments of the Blackwell-MacQueen Urn Scheme. In: Ferguson TS, Shapeley LS, MacQueen JB, editors. Statistics, Probability and Game Theory. Papers in Honor of David Blackwell. IMS Lecture Notes - Monograph Series; Hayward, California: 1996. pp. 245–268.pp. 279 [Google Scholar]
- Pitman J, Yor M. The Two-Parameter Poisson-Dirichlet Distribution Derived from a Stable Subordinator. The Annals of Probability. 1997;25:855–900. 277, 279. [Google Scholar]
- Quintana FA. A predictive view of Bayesian clustering. Journal of Statistical Planning and Inference. 2006;136:2407–2429. 280. [Google Scholar]
- Quintana FA, Iglesias PL. Bayesian clustering and product partition models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2003;65(2):557–574. 281. URL http://dx.doi.org/10.1111/1467-9868.00402. [Google Scholar]
- Regazzini E, Lijoi A, Prünster I. Distributional Results for Means of Normalized Random Measures with Independent Increments. The Annals of Statistics. 2003;31(2):560–585. 277. [Google Scholar]
- Rodríguez A, Dunson DB, Gelfand AE. The nested Dirichlet process, with Discussion. Journal of the American Statistical Association. 2008;103:1131–1144. 279. [Google Scholar]
- Rosner GL. Bayesian monitoring of clinical trials with failure-time endpoints. Biometrics. 2005;61:239–245. 286. doi: 10.1111/j.0006-341X.2005.031037.x. [DOI] [PubMed] [Google Scholar]
- Schwartz L. On Bayes procedures. Probability Theory and Related Fields. 1965;4(1):10–26. 294. [Google Scholar]
- Sethurman J. A constructive definition of Dirichlet priors. Statistica Sinica. 1994;4:639–650. 272. [Google Scholar]
- Teh YW, Jordan MI, Beal MJ, Blei DM. Sharing Clusters among Related Groups: Hierarchical Dirichlet Processes. Journal of the American Statistical Association. 2006;101:1566–1581. 279. [Google Scholar]
- Tokdar ST. Posterior consistency of Dirichlet location-scale mixture of normals in density estimation and regression. Sankhyā: The Indian Journal of Statistics. 2006;68:90–110. 294. [Google Scholar]
- Trippa L, Müller P, Johnson W. The Multivariate Beta Process and an Extension of the Polya Tree Model. Biometrika. 2011;98(1):17–34. 288. doi: 10.1093/biomet/asq072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Vaart A, van Zanten J. Rates of contraction of posterior distributions based on Gaussian process priors. The Annals of Statistics. 2008;36(3):1435–1463. 295. [Google Scholar]
- Vidakovic B. Nonlinear wavelet shrinkage with Bayes rules and Bayes Factors. Journal of the American Statistical Association. 1998;93:173–179. 283, 285. [Google Scholar]
- Wade S, Mongelluzzo S, Petrone S. An enriched conjugate prior for Bayesian nonparametric inference. Bayesian Analysis. 2011;6(3):359–385. 279. [Google Scholar]
- Walker S. On sufficient conditions for Bayesian consistency. Biometrika. 2003;90(2):482–488. 295. [Google Scholar]
- Walker S. New approaches to Bayesian consistency. The Annals of Statistics. 2004;32(5):2028–2043. 295. [Google Scholar]
- Walker S. Bayeisan nonparametrics. In: Damien P, Dellaportas P, Polson NG, Stephens DA, editors. Bayesian Theory and Applications. Oxford University Press; 2013. pp. 249–270.pp. 270 [Google Scholar]
- Walker S, Damien P, Laud P, Smith A. Bayesian nonparametric inference for distributions and related functions (with discussion). Journal of the Royal Statistical Society, Series B. 1999;61:485–527. 270. [Google Scholar]
- Walker S, Hjort N. On Bayesian consistency. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2002;63(4):811–821. 295. [Google Scholar]
- Walker S, Lijoi A, Prünster I. On rates of convergence for posterior distributions in infinite-dimensional models. The Annals of Statistics. 2007;35(2):738–746. 295. [Google Scholar]
- Wang Y, Taylor JM. Jointly modeling longitudinal and event time data with application to acquired immunodeficiency syndrome. Journal of the American Statistical Association. 2001;96:895–903. 289. [Google Scholar]
- Zhang S, Müller P, Do K-A. A Bayesian Semiparametric Survival Model with Longitudinal Markers. Biometrics. 2010;66(2):435–443. 274. doi: 10.1111/j.1541-0420.2009.01276.x. [DOI] [PMC free article] [PubMed] [Google Scholar]