CENTER-ADJUSTED INFERENCE FOR A NONPARAMETRIC BAYESIAN RANDOM EFFECT DISTRIBUTION

Abstract

Dirichlet process (DP) priors are a popular choice for semiparametric Bayesian random effect models. The fact that the DP prior implies a non-zero mean for the random effect distribution creates an identifiability problem that complicates the interpretation of, and inference for, the fixed effects that are paired with the random effects. Similarly, the interpretation of, and inference for, the variance components of the random effects also becomes a challenge. We propose an adjustment of conventional inference using a post-processing technique based on an analytic evaluation of the moments of the random moments of the DP. The adjustment for the moments of the DP can be conveniently incorporated into Markov chain Monte Carlo simulations at essentially no additional computational cost. We conduct simulation studies to evaluate the performance of the proposed inference procedure in both a linear mixed model and a logistic linear mixed effect model. We illustrate the method by applying it to a prostate specific antigen dataset. We provide an R function that allows one to implement the proposed adjustment in a post-processing step of posterior simulation output, without any change to the posterior simulation itself.

1. Introduction

We propose an adjustment for inference in semiparametric Bayesian mixed effect models with a Dirichlet process (DP) prior on a random effect distribution G. The need for adjustment arises from two challenges. The first is a difficulty in the interpretation of fixed effects that are paired with random effects, due to an identifiability issue. We formally define the notion of paired fixed and random effects later. The second challenge is a similar issue related to the variance components of the random effects. We show that inference based on a conventional interpretation of the fixed effects and variance components is often poor. Using a parametrization with hierarchical centering (Gelfand, Sahu, and Carlin (1995)), we interpret the first two moments of G, denoted by μ_G and Cov_G, as the fixed effects paired with random effects and the variance components of the random effects, respectively. We derive easy-to-evaluate formulas for the posterior moments of μ_G and Cov_G, and propose to use them in a straightforward post-processing step for Markov chain Monte Carlo (MCMC) output. In an application to inference for PSA profiles, we show that the proposed adjustment can significantly change parameter estimates in a typical data analysis: posterior means for some fixed effects change between 11 and 32%; the corresponding posterior standard deviations (SDs) and credible interval (CI) lengths change by more than 200%; the changes in the posterior means, SDs, and lengths of CIs for the variance components are similarly large. We provide an R function for users to implement the proposed procedure.

Linear and generalized linear mixed models (LMMs & GLMMs) are an important and popular tool for analyzing correlated data. The random effects in such models are typically assumed normal, mainly for reasons of technical convenience. However, many applications require a more heterogeneous random effect distribution. For example, potentially relevant subject-specific covariates may not have been measured or are difficult to measure. Missing covariates can lead to a multimodal random effect distribution. In other applications, the distribution of the random effects may be skewed.

Estimation of the random effect distribution is important for predictive inference. Consider, for example, the joint modeling of a primary endpoint and a longitudinal covariate. Valid estimates of the random effects are crucial. Inappropriately assuming normality can lead to excessive shrinkage towards zero and result in poor prediction.

These concerns lead many investigators to use nonparametric alternatives to normal random effect distributions. The DP is a popular choice as a nonparametric prior for the random effect distribution in mixed effect models within the Bayesian framework. For example, Kleinman and Ibrahim (1998b, a) modeled the random effect distribution as

$${\mathit{b}}_i|G\stackrel{i.i.d.}{~}G,G~DP(M,G_0),G_0=N(\mathbf{0},\mathit{D}),$$ (1.1)

where DP(M, G₀) denotes a DP with a total mass parameter M and a base probability measure G₀ (Ferguson (1973)). We refer to a fixed effect as paired with a random effect if the columns in the design matrices of fixed effects and random effects match. See the discussion after equation (2.1) for a formal definition. In short, if the sampling model for the j-th repeated observation for the i-th subject involves a linear predictor ${\eta }_{ij}={\mathbf{x}}_{ij}^T\mathit{\beta }+{\mathbf{z}}_{ij}^T{\mathit{b}}_i$ with fixed effects β, subject-specific random effects b_i and known design vectors x_ij and z_ij, then we refer to a subvector β^R of β as paired with b_i if the corresponding subvector of x_ij matches z_ij, e.g., both contain an intercept. Posterior simulations in a LMM or GLMM based on model (1.1) for the random effects can be carried out using Gibbs sampling. A similar approach has been used by Bush and MacEachern (1996) in randomized block designs and many others. We argue that there is a difficulty in interpreting posterior inference for fixed effects that are paired with random effects in the above models, due to an identifiability issue. With a non-parametric random effect distribution, a difficulty also arises in the interpretation of the variance components of the random effects.

In related work, Newton, Czado, and Chappell (1996) proposed a centrally standardized Dirichlet process prior for the link function in a binary regression, under which each realization of the link function has a median of zero. The approach is restricted to univariate distributions.

We propose a modified DP model and a post-processing procedure to address the aforementioned challenges. The model uses a DP prior for the sum of the random effects and their corresponding fixed effects with a base measure centered at an unknown mean. The post-processing technique is based on an analytic evaluation of the moments of the random moments of a random probability measure with a DP prior. Several recent references have discussed the distribution of these random moments. For example, many authors have discussed the distribution of the mean of a DP random measure, including Hjort and Ongaro (2005) and Lijoi and Regazzini (2004). Epifani, Guglielmi, and Melilli (2006) studied the distribution of the random variance of a DP random measure. Gelfand and Mukhopadhyay (1995) and Gelfand and Kottas (2002) used Monte Carlo integration to evaluate marginal posterior expectation of linear and nonlinear functionals of a nonparametric distribution whose prior is a DP mixture. They approximate the conditional expectation of the functional by a sample of the functional based on the predictive distribution of the parameters of the kernel. In this paper, we instead provide closed-form formulas for the mean and covariance matrix of the (random) moments of a random measure with a DP prior. These expressions can be incorporated into MCMC simulations and used to adjust for inference for both the fixed effects paired with the nonparametric random effects and the second moments of the random effect distribution. We conduct simulation studies to evaluate the performance of the proposed moment-adjustment procedure and illustrate the method by analyzing a prostate specific antigen (PSA) dataset.

The remainder of this article is organized as follows. In Section 2 we discuss a difficulty with the naïve inference in the DP random effect model, propose a modification to the conventional DP prior, and briefly discuss the posterior propriety of the model. In Section 3 we propose adjusted inference for fixed effects paired with random effects, and for the variance components of the random effects. Specifically, in Section 3.1 we derive the posterior mean and variance-covariance matrix for fixed effects that are paired with random effects, using results on the moments of the random first and second moments of a DP random measure. In Section 3.2 we derive new closed-form results concerning the expectation of the random third and fourth moments of a DP. We use these results to report posterior summaries for the (random) covariance matrix of the random effects. In Section 4 we report results from simulation studies to show the performance of the proposed inference procedure in both a LMM and a logistic random effect model. In Section 5 we illustrate the method with inference for the PSA data. We provide concluding remarks in Section 6. Proofs are given in the Appendix.

2. A Hierarchically Centered Dirichlet Process Prior

For convenience, we use a nonparametric GLMM to illustrate our proposed method. However, unless indicated otherwise, all results remain applicable for any nonparametric hierarchical model that contains the DP model (1.1) or (2.3) as a submodel. For example, model (5.1) in our data example contains a nonlinear component.

Suppose y_ij arise independently from an exponential family with mean ${\mu }_{ij}^{\mathbf{b}}$ and variance ${\upsilon }_{ij}^{\mathbf{b}}=\varphi \upsilon ({\mu }_{ij}^{\mathbf{b}})$ with a known dispersion parameter ϕ, conditional on the cluster-specific random effects b_i (q × 1), i = 1, …, m, j = 1, …, n_i. Consider the GLMM

$$g({\mu }_{ij}^{\mathbf{b}})={\eta }_{ij}^{\mathbf{b}},$$ (2.1)

where ${\eta }_{ij}^{\mathbf{b}}={\mathbf{x}}_{ij}^T\mathit{\beta }+{\mathbf{z}}_{ij}^T{\mathit{b}}_i$, g(·) is a monotone differentiable link function with inverse h(·), and the b_i are independent and identically distributed with E(b_i) = 0. Let y_i = (y_i1, …, y_ini)^T and $\mathbf{y}={({\mathbf{y}}_1^T,\dots ,{\mathbf{y}}_m^T)}^T$. Model (2.1) emcompasses the general LMM as a special case. Without loss of generality we assume that the fixed effects are partitioned into (β^F, β^R) and similarly ${\mathbf{x}}_{ij}=({\mathbf{x}}_{ij}^F,{\mathbf{x}}_{ij}^R)$, with ${\mathbf{x}}_{ij}^R={\mathbf{z}}_{ij}$. We refer to β^R as fixed effects paired with the random effects b_i. For example, in equation (4.1), (β₀, β₁) are fixed effects paired with random effects $(b_i^{(1)},b_i^{(2)})$ with ${\mathbf{x}}_{ij}^R={\mathbf{z}}_{ij}={(1,x_{ij})}^T$. If we add an additional term β₂w_ij on the right hand side (RHS) of (4.1), then β₂ is considered a fixed effect that is not paired with either random effect, $b_i^{(1)}$ or $b_i^{(2)}$.

Consider the GLMM (2.1) with the DP prior model (1.1) for the random effects. The model includes the awkward feature that the unknown random effect distribution G has a non-zero mean almost surely. This makes inference on the fixed effects β^R difficult to interpret. Let μ_G = ∫ b_idG(b_i) denote the random mean of G. We argue that, instead of reporting inference on β^R, it is more appropriate to report inference on β_pair ≡ β^R + μ_G.

Following the above arguments, we propose to model the distribution of β^R + b_i as

$${\mathit{\beta }}^R+{\mathit{b}}_i\stackrel{i.i.d.}{~}G,G~DP(M,G_0),G_0=N({\mathit{\beta }}_{\mathbf{b}},\mathit{D}),$$ (2.2)

where β_b is an unknown vector of the mean parameters for the base probability measure. Given a lack of interpretation for inference on β^R and μ_G separately, we propose to remove the paired fixed effects β^R from (2.1). As a result, the random effect vector in the revised model, again denoted by b_i, corresponds to β^R + b_i in the original model. The prior model (2.2) now becomes

$${\mathit{b}}_i\stackrel{i.i.d.}{~}G,G~DP(M,G_0),G_0=N({\mathit{\beta }}_{\mathbf{b}},\mathit{D}).$$ (2.3)

The specification of (2.3) follows the notion of hierarchical centering (Gelfand, Sahu, and Carlin (1995)). We further use β ≡ β^F and ${\mathbf{x}}_{ij}\equiv {\mathbf{x}}_{ij}^F$ to denote the remaining fixed effect vector and corresponding design vector. Instead of inference on β^R in the original model, we report inference on β_pair = μ_G in the revised model. For later reference we state the revised centered GLMM as

$$g({\mu }_{ij}^{\mathbf{b}})={\eta }_{ij}^{\mathbf{b}}\text{with}{\eta }_{ij}^{\mathbf{b}}={\mathbf{x}}_{ij}^T\mathit{\beta }+{\mathbf{z}}_{ij}^T{\mathit{b}}_i.$$ (2.4)

This is the same as model (2.1), except that now x_ij only contains ${\mathbf{x}}_{ij}^F$, and b_i follows (2.3).

We complete the GLMM with commonly used (hyper-)priors on the remaining parameters: we assume a diffuse normal prior for each component of β and β_b, a proper prior to be described below for D, and a diffuse inverse Gamma (IG) prior for the residual variance if the GLMM (2.4) reduces to a LMM. All these priors are assumed independent. For a proper prior for D, we consider both an inverse Wishart (IW) prior (or an IG prior if D reduces to a scalar) and a uniform shrinkage prior (USP) (Natarajan and Kass (2000)). For the latter, we define the USP as if the random effects were normally distributed. See Natarajan and Kass (2000) for corresponding detail.

One can show that under a flat prior for (β, β_b) and a proper prior for both D and M (including the case of M being a constant), the posterior is proper. In the case of a LMM with an improper prior for σ² that is proportional to 1/σ², the posterior is also proper. As a side note, one can also show that an improper prior for M leads to an improper posterior. These results justify the common use of a diffuse normal prior for the fixed effects and a diffuse IG prior for the residual variance, when applicable, provided that the prior for the covariance matrix in the DP base measure is proper. Posterior simulation of the random effects follows the usual posterior MCMC scheme for DP mixture models. The simulation can include the total mass parameter M if the model is augmented with a gamma prior for M. See, for example, Neal (2000) for a review. Posterior simulation of the remaining model parameters can follow Kleinman and Ibrahim (1998a, b).

3. Adjusted Inference for Fixed Effects and Variance Components of the Random Effects

3.1. Adjustment for fixed effects

Let $\mathit{b}={({\mathit{b}}_1^T,\dots ,{\mathit{b}}_m^T)}^T$, b_m+1 be the random effect for a future subject, and $G_{\star }=\{M·N({\mathit{\beta }}_{\mathbf{b}},\mathit{D})+{\sum }_{i=1}^m{\delta }_{{\mathbf{b}}_i}\}/(m+M)$, with δ_bi denoting a point mass at b_i. We further let ${\mathit{\mu }}_{G_{\star }}=M{\mathit{\beta }}_{\mathbf{b}}/(m+M)+({\sum }_{i=1}^m{\mathit{b}}_i)/(m+M)$ and ${\mathbf{\text{Cov}}}_{G_{\star }}=\{M({\mathit{\beta }}_{\mathbf{b}}{\mathit{\beta }}_{\mathbf{b}}^T+\mathit{D})+{\sum }_{i=1}^m{\mathit{b}}_i{{\mathit{b}}_i}^T\}/(m+M)-{\mathit{\mu }}_{G_{\star }}{\mathit{\mu }}_{{{\mathrm{G}}_{\star }}^T}$, the mean and covariance matrix of G_⋆.

Proposition 1. (i) $E({\mathit{\mu }}_G|\mathbf{y})=E({\mathit{\mu }}_{G_{\star }}|\mathbf{y})=E(\frac{M}{m+M}{\mathit{\beta }}_{\mathbf{b}}+\frac{1}{m+M}{\sum }_{i=1}^m{\mathit{b}}_i|\mathbf{y})$; (ii) $\mathit{\text{Cov}}({\mathit{\mu }}_G|\mathbf{y})=E(\frac{{\mathbf{\text{Cov}}}_{G_{\star }}}{m+M+1}|\mathbf{y})+\mathit{\text{Cov}}({\mathit{\mu }}_{G_{\star }}|\mathbf{y})$.

Proof. These are straightforward results of Theorems 3 and 4 of Ferguson (1973).

Proposition 1 suggests that the posterior mean and variance-covariance matrix of μ_G, equivalently β_pair, can be computed based on the posterior samples of (b, β_b, D, M). A CI for the i-th component of μ_G, denoted as μ_G,i, can then be constructed. Specifically, the construction can be based on a normal approximation of the posterior distribution of μ_G,i using the estimated posterior mean E(μ_G,i | y) and the estimated posterior variance, the (i, i)-th element of Cov(μ_G | y).

Corollary 1. Suppose θ is a function of (β, b, β_b, D) and has the same dimension as b_i. Then

1. $E(\mathit{\theta }+{\mathit{\mu }}_G|\mathbf{y})=E(\mathit{\theta }|\mathbf{y})+E(\frac{M}{m+M}{\mathit{\beta }}_{\mathbf{b}}|\mathbf{y})+E(\frac{1}{m+M}{\sum }_{i=1}^m{\mathit{b}}_i|\mathbf{y})$;

2. $\mathit{\text{Cov}}(\mathit{\theta }+{\mathit{\mu }}_G|\mathbf{y})=E(\frac{{\mathbf{\text{Cov}}}_{G_{\star }}}{m+M+1}|\mathbf{y})+\mathit{\text{Cov}}(\mathit{\theta }+{\mathit{\mu }}_{G_{\star }}|\mathbf{y})$.

Proof. E(θ + μ_G | y) and Cov(θ + μ_G | y) can be computed by first conditioning on (β, b, β_b, D, y) and then marginalizing over (β, b, β_b, D).

Corollary 1 is used to make inference for μ_g1 + d_g and μ_g2 + d_η in the analysis of the PSA data in Section 5.

3.2. Adjustment for variance components

In addition to the inference for the fixed effects β_pair, the centered DP GLMM (2.4) and (2.3) also allows us to make inference on the random variance-covariance matrix Cov_G of G. In particular, we have the following proposition.

Proposition 2. (i) $E({\mathbf{\text{Cov}}}_G|\mathbf{y})=E(\frac{m+M}{m+M+1}{\mathbf{\text{Cov}}}_{G_{\star }}|\mathbf{y})$.

Proof. This is another straightforward result of Theorems 3 and 4 of Ferguson (1973).

In order to derive the posterior second moments for Cov_G, we need two lemmas.

Lemma 1. Let P ~ DP(M, α), where M > 0. Suppose Z₁, Z₂ and Z₃ are random variables. If for all i₁, i₂, i₃ ∈ {0, 1}, $\int |Z_1^{i_1}{Z}_2^{i_2}{Z}_3^{i_3}|d\alpha <\infty$, then

$$E\int Z_{1}dP\int Z_{2}dP\int Z_{3}dP={\mu }_1{\mu }_2{\mu }_3+\frac{{\sigma }_{12}{\mu }_3+{\sigma }_{13}{\mu }_2+{\sigma }_{23}{\mu }_1}{M+1}+\frac{2{\sigma }_{123}}{(M+1)(M+2)},$$ (3.1)

where μ_i = ∫ Z_idα, σ_ij = ∫ (Z_i − μ_i)(Z_j − μ_j)dα, i, j = 1, 2, 3, i ≠ j, and σ₁₂₃ = ∫ (Z₁ − μ₁)(Z₂ − μ₂)(Z₃ − μ₃)dα.

See the proof of Lemma 1 in Appendix A.1.

Lemma 2. Let P, α be as in Lemma 1. Let Z₁, Z₂, Z₃ and Z₄ be random variables. If for all i₁, i₂, i₃, i₄ ∈ {0, 1}, $\int |Z_1^{i_1}{Z}_2^{i_2}{Z}_3^{i_3}{Z}_4^{i_4}|d\alpha <\infty$, then

$$E\int Z_{1}dP\int Z_{2}dP\int Z_{3}dP\int Z_{4}dP={\mu }_1{\mu }_2{\mu }_3{\mu }_4+\frac{R_1}{M+1}+\frac{2R_2}{(M+1)(M+2)}+\frac{M{R}_3}{(M+1)(M+2)(M+3)}+\frac{6{\sigma }_{1234}}{(M+1)(M+2)(M+3)},$$ (3.2)

where R₁ = σ₁₂μ₃μ₄ + σ₁₃μ₂μ₄ + σ₁₄μ₂μ₃ + σ₂₃μ₁μ₄ + σ₂₄μ₁μ₃ + σ₃₄μ₁μ₂, R₂ = σ₁₂₃μ₄ + σ₁₂₄μ₃ + σ₁₃₄μ₂ + σ₂₃₄μ₁, R₃ = σ₁₂σ₃₄ + σ₁₃σ₂₄ + σ₁₄σ₂₃, and μ_i, σ_ij, σ_ijk and σ₁₂₃₄ are defined in a similar manner as in Lemma 1.

See the proof of Lemma 2 in Appendix A.2.

Let Cov_G,ij and Cov_G⋆,ij be the (i, j)-th component of Cov_G and Cov_G⋆ for i ≠ j, respectively. Let Var_{G⋆, i} be the (i, i)-th component of Cov_G⋆. For notation in the next result, see Appendix A.3.

Proposition 2. (ii) Recall that [b_m+1 | b, β_b, D, M] = _G⋆. If $b_{m+1}^{(i)}$ is the i-th component of b_m+1, then

$$\mathit{\text{Cov}}({\mathit{\text{Cov}}}_{G,i_1{j}_1},{\mathit{\text{Cov}}}_{G,i_2{j}_2}|\mathbf{y})=E(L_1-L_2-L_3+L_4|\mathbf{y})-E(\frac{m+M}{m+M+1}{\mathit{\text{Cov}}}_{G_{\star },i_1{j}_1}|\mathbf{y}\left)E\right(\frac{m+M}{m+M+1}{\mathit{\text{Cov}}}_{G_{\star },i_2{j}_2}|\mathbf{y}),$$ (3.3)

where

$$L_1=\frac{E[b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}{b}_{m+1}^{(i_2)}{b}_{m+1}^{(j_2)}|G_{\star }]+(m+M)E[b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}|G_{\star }]E[b_{m+1}^{(i_2)}{b}_{m+1}^{(j_2)}|G_{\star }]}{m+M+1},L_2={\mu }_1^{(L_2)}{\mu }_2^{(L_2)}{\mu }_3^{(L_2)}+\frac{{\sigma }_{12}^{(L_2)}{\mu }_3^{(L_2)}+{\sigma }_{13}^{(L_2)}{\mu }_2^{(L_2)}+{\sigma }_{23}^{(L_2)}{\mu }_1^{(L_2)}}{m+M+1}+\frac{2{\sigma }_{123}^{(L_2)}}{(m+M+1)(m+M+2)},L_3={\mu }_1^{(L_3)}{\mu }_2^{(L_3)}{\mu }_3^{(L_3)}+\frac{{\sigma }_{12}^{(L_3)}{\mu }_3^{(L_3)}+{\sigma }_{13}^{(L_3)}{\mu }_2^{(L_3)}+{\sigma }_{23}^{(L_3)}{\mu }_1^{(L_3)}}{m+M+1}+\frac{2{\sigma }_{123}^{(L_3)}}{(m+M+1)(m+M+2)},L_4={\mu }_1^{(L_4)}{\mu }_2^{(L_4)}{\mu }_3^{(L_4)}{\mu }_4^{(L_4)}+\frac{R_1^{(L_4)}}{m+M+1}+\frac{2R_2^{(L_4)}}{(m+M+1)(m+M+2)}+\frac{(m+M)R_3^{(L_4)}}{(m+M+1)(m+M+2)(m+M+3)}+\frac{6{\sigma }_{1234}^{(L_4)}}{(m+M+1)(m+M+2)(m+M+3)}.$$

In particular,

$$\mathit{\text{Var}}({\mathit{\text{Cov}}}_{G,ij}|\mathbf{y})=E(O_1-2O_2+O_3|\mathbf{y})-{\left[E\right(\frac{m+M}{m+M+1}{\mathit{\text{Cov}}}_{G_{\star },ij}|\mathbf{y})]}^2,$$ (3.4)

where

$$O_1=\frac{E({[b_{m+1}^{(i)}{b}_{m+1}^{(j)}]}^2|G_{\star })+(m+M){\left[E\right(b_{m+1}^{(i)}{b}_{m+1}^{(j)}|G_{\star })]}^2}{m+M+1},O_2={\mu }_1^{(O_2)}{\mu }_2^{(O_2)}{\mu }_3^{(O_2)}+\frac{{\sigma }_{12}^{(O_2)}{\mu }_3^{(O_2)}+{\sigma }_{13}^{(O_2)}{\mu }_2^{(O_2)}+{\sigma }_{23}^{(O_2)}{\mu }_1^{(O_2)}}{m+M+1}+\frac{{\sigma }_{123}^{(O_2)}}{(m+M+1)(m+M+2)},O_3={\mu }_1^{(O_3)}{\mu }_2^{(O_3)}{\mu }_3^{(O_3)}{\mu }_4^{(O_3)}+\frac{R_1^{(O_3)}}{m+M+1}+\frac{2R_2^{(O_3)}}{(m+M+1)(m+M+2)}+\frac{(m+M)R_3^{(O_3)}}{(m+M+1)(m+M+2)(m+M+3)}+\frac{6{\sigma }_{1234}^{(O_3)}}{(m+M+1)(m+M+2)(m+M+3)}.$$

See the proof of Proposition 2 (ii) in Appendix A.4.

Remark. Proposition 2 allows us to compute the posterior mean and variance-covariance matrix of Cov_G (it is easiest to write Cov_G as a stacked column vector of its lower-diagonal elements). Noting the typical skewness of the posterior distribution of a variance, we construct a CI for Var_G,i by matching its posterior mean and variance to those of a log-normal distribution. We choose the lognormal distribution because of its positive support. Similar to the approach to constructing a CI for μ_G,i, we use a normal approximation for Cov_G,ij with i ≠ j.

Propositions 1 and 2 hold under model (2.3) for the random effects b_i. Therefore, as long as the posterior samples of (b, β_b, D, M) can be obtained (e.g., through MCMC simulations), one can post-process the samples and report adjusted inference for μ_G and Cov_G, i.e., the “fixed effects” paired with b_i, and the variance components of b_i.

4. Simulation Studies

4.1. A linear mixed model

We conducted a simulation study to examine the performance of the proposed center-adjusted inference in a LMM with nonparametric random intercept and slope. We generated 200 datasets from the LMM

$$Y_{ij}={\beta }_0+b_i^{(1)}+({\beta }_1+b_i^{(2)})x_{ij}+{\epsilon }_{ij},i=1,\dots ,50,j=1,\dots ,10,$$ (4.1)

i.e., with β = (β₀, β₁)′. We used β₀ = 1, β₁ = 1, x_ij = j + 0.025i − 5, ${\epsilon }_{ij}\stackrel{i.i.d.}{~}N(0,{\sigma }^2=1)$, and ${\mathit{b}}_i=(b_i^{(1)},b_i^{(2)})\prime \stackrel{i.i.d.}{~}1/3\times N({\mathit{\mu }}^{(1)},{\mathbf{\Sigma }}^{(1)})+2/3\times N({\mathit{\mu }}^{(2)},{\mathbf{\Sigma }}^{(2)})$, where ${\mathit{\mu }}^{(1)}=({\mu }_1^{(1)},{\mu }_2^{(1)})\prime =(-2,2)\prime ,{\mathbf{\Sigma }}^{(1)}=[{\sigma }_{ij}^{(1)}]$ with ${\sigma }_{11}^{(1)}={\sigma }_{22}^{(1)}=.1$, and ${\sigma }_{12}^{(1)}=-.09;{\mathit{\mu }}^{(2)}=({\mu }_1^{(2)},{\mu }_2^{(2)})\prime =(1,-1)\prime ,{\mathbf{\Sigma }}^{(2)}]=[{\sigma }_{ij}^{(2)}$ with ${\sigma }_{11}^{(2)}={\sigma }_{22}^{(2)}=.5$, and ${\sigma }_{12}^{(2)}=-.45$. Under this bivariate bimodal normal mixture of b_i, we have $E({\mathit{b}}_i)=(b_i^{(1)},b_i^{(2)})\prime \equiv \mathit{\mu }=({\mu }_1,{\mu }_2)\prime =(0,0)\prime$ and $\mathit{\text{Cov}}({\mathit{b}}_i)=\mathit{\text{Cov}}((b_i^{(1)},b_i^{(2)})\prime )\equiv \mathbf{\Sigma }=[{\sigma }_{ij}]$, with σ₁₁ = σ₂₂ = 2.37 and σ₁₂ = −2.33.

We used the semiparametric LMM proposed in Section 2 for analysis. In particular, we used the centered DP prior model (2.3) for b_i. We assumed independent N(0, 10⁴) priors for β_b0, β_b1, and an IG prior IG(10⁻², 10⁻²) for σ². Let I₂ denote the 2 × 2 identity matrix. Recall that D denotes the variance-covariance matrix of the base measure G₀. We assumed an IW prior IW(2, Ω) for D with mean E(D⁻¹) = 2Ω where Ω = 10⁻²I₂. The hyperparameters of the IW prior were chosen such that posterior inference was dominated by the data (c.f., Bernado and Smith (1994)). Posterior propriety follows by Proposition 1. Posterior simulations followed Kleinman and Ibrahim (1998b) with an additional step of sampling β_b. Inference for the fixed effects β ≡ (β₀ β₁)′ and the random effect covariance matrix Σ followed the moment-adjustment procedure proposed in Sections 3.1 and 3.2.

Table A.1 reports relative bias, MSE, CI length (CIL), and coverage probability (CP) for the estimates of the fixed effect intercept and slope using both the traditional DP prior and the proposed centered DP prior approaches using both the IW and USP priors for variance components. Commonly used posterior inference involves larger biases and MSEs, much wider CIs, and either worse coverage probabilities with comparable CI lengths or slightly better coverage probabilities at the cost of doubled or even tripled CI lengths. In contrast, the proposed center-adjusted inference procedure led to estimates of the fixed effects and variance components that had small biases. The 95% coverage probabilities for the fixed effects were close to the nominal values. Note that the corresponding coverage probabilities for the variance components of the random effects using both procedures appeared to be high when the IW prior was used.

Table A.1.

Simulation results using center-adjusted vs conventional (i.e., non-centered and unadjusted) inference using DP prior with M ~ G(2.5, .5) in model (4.1) based on 200 replicates. An IWP or USP was used for D in the DP base measure.

		Center-adjusted				Conventional
Parameter	π(D)	Bias	MSE (SE)	CIL	CP	Bias	MSE (SE)	CIL	CP
β0	IWP	.04	.04 (.004)	.85	.93	.16	.08 (.01)	2.88	.99
	USP	.03	.04 (.004)	.81	.93	.15	.09 (.01)	1.89	.97
β1	IWP	−.04	.04 (.004)	.84	.93	−.15	.08 (.01)	1.88	.80
	USP	−.03	.04 (.004)	.80	.95	−.15	.09 (.01)	1.60	.85
σ2	IWP	.04	.01 (.001)	.29	.94	.04	.01 (.001)	.29	.94
	USP	.04	.01 (.001)	.29	.92	.03	.01 (.001)	.29	.94
σ11	IWP	.01	.10 (.01)	1.62	.99	.15	.33 (.03)	2.44	.99
	USP	−.07	.11 (.01)	1.29	.93	−.20	.31 (.02)	1.46	.45
σ22	IWP	.01	.08 (.01)	1.53	1.00	.16	.30 (.03)	4.31	.96
	USP	−.06	.09 (.01)	1.19	.96	−.20	.31 (.02)	2.49	.98
σ12	IWP	−.01	.09 (.01)	1.54	.99	−.15	.30 (.03)	4.16	1.00
	USP	.06	.09 (.01)	1.20	.94	.20	.31 (.02)	2.44	.99

In light of the documented difficulties with the use of an IG or IW prior for a random effect variance or covariance matrix (Natarajan and McCulloch (1998); Natarajan and Kass (2000); among others), we propose to extend the USP (Natarajan and Kass (2000)) to our semiparametric LMM and GLMM for the covariance matrix D in the DP base measure. While Natarajan and Kass (2000) show posterior propriety under mild conditions in their GLMMs with normal random effects, similar posterior propriety results hold in our semiparametric GLMMs, as implied by Proposition 1. Posterior MCMC simulation can include a Metropolis step for sampling D with an IW density as the proposal. The corresponding simulation results are also reported in Table A.1. The average CI lengths for the variance components now were considerably shorter than their IW counterparts, with the coverage probabilities preserved at a reasonable level (93–96%), being close to the nominal value. Similar results were obtained when varying the prior for M or fixing M to different constants.

4.2. A logistic random effect model

We used the following logistic linear mixed effect model as our simulation truth for the sampling model:

$$\mathit{\text{logit}}(p_{ij})={\beta }_0+b_i^{(1)}+({\beta }_1+b_i^{(2)})x_{ij},i=1,\dots ,100,j=1,\dots ,10,$$ (4.2)

where the x_ij were the same as in Section 4.1. We investigated the performance of the proposed adjustments in inference again using both an IW prior and a USP for the covariance matrix D in the DP base measure. The assumptions on the random effect distribution and the priors for the remaining parameters were similar to those in Section 4.1. We fixed M = 5. When a USP was used, the posterior conditional sampling of D followed the same strategy as for the LMM in Section 4.1. The corresponding results are summarized in Table A.2. Note that when the IW prior was used for D, even after the moment adjustments, the inference for the random effect covariance matrix was still poor and seriously biased. In contrast, the use of the USP resulted in a good performance using the proposed inference on all model parameters, with a minimal bias and a coverage probability that was close to the nominal value.

Table A.2.

Simulation results using center-adjusted vs unadjusted inference using DP prior with M = 5 in model (4.2) based on 200 replicates. An IWP or USP was used for D in the DP base measure.

		Center-adjusted				Conventional
Parameter	π (D)	Bias	MSE (SE)	CIL	CP	Bias	MSE (SE)	CIL	CP
β0	IWP	.03	.06 (.01)	1.01	.97	.04	.13 (.02)	2.68	1.00
	USP	.07	.05 (.01)	.91	.94	.24	.14 (.01)	2.32	1.00
β1	IWP	.03	.07 (.01)	1.16	.97	−.03	.13 (.02)	2.70	1.00
	USP	−.06	.06 (.01)	.96	.93	−.25	.14 (.01)	2.19	1.00
σ11	IWP	.22	1.26 (.19)	4.77	.99	.51	3.83 (.66)	10.11	1.00
	USP	.02	.57 (.09)	3.31	.97	−.19	.58 (.04)	4.54	.99
σ22	IWP	.34	2.04 (.31)	6.26	.99	.50	3.80 (.61)	10.34	1.00
	USP	−.02	.49 (.06)	3.67	.97	−.29	.77 (.04)	4.18	.97
σ12	IWP	−.27	1.32 (.19)	5.26	.99	.50	3.33 (.54)	9.80	1.00
	USP	.03	.39 (.05)	3.13	.92	−.27	.67 (.04)	4.14	.99

5. Application

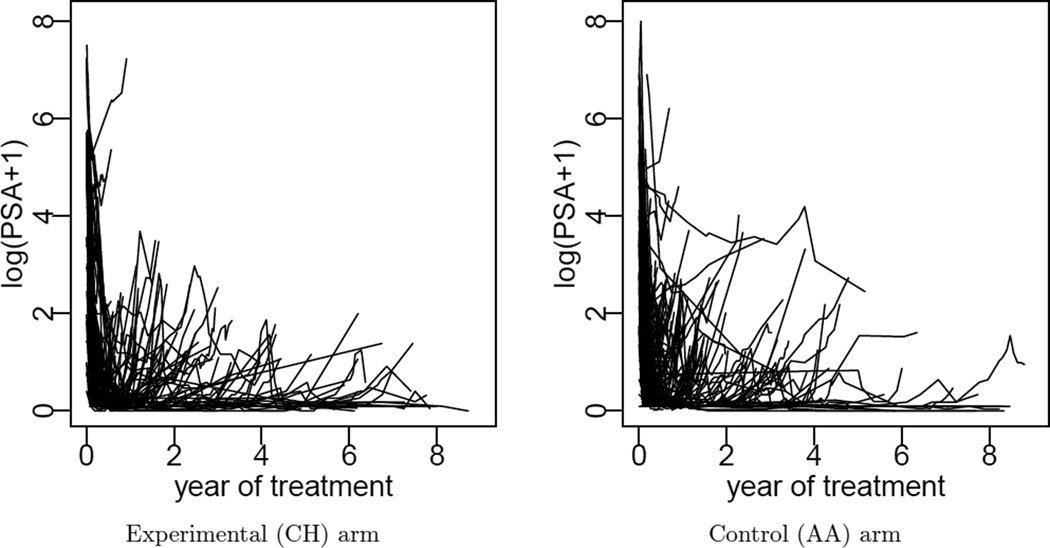
We applied the proposed method to analyze data from a phase III clinical trial with prostate cancer patients. The trial was conducted at M. D. Anderson Cancer Center. The sample size was n = 286 patients. Patients were randomized to two treatment arms: a conventional androgen ablation (AA) therapy (149 patients) and the AA therapy plus three eight-week cycles of chemotherapy (CH) using ketoconazole and doxorubicin (KA) alternating with vinblastine and estramustine (VE) (137 patients). The outcome variable of interest is y = log(PSA+1). PSA level is reported repeatedly over time starting with treatment initiation. The number of repeated measurements varies from 1 to 65 across patients. The investigators were interested in the PSA profiles post initialization of both treatments. Figure A.1 displays the observed PSA trajectories for all patients in each treatment arm. For a more detailed description of the data, see Zhang, Müller and Do (2010).

Figure A.1.

Observed PSA trajectories

We consider a model for the log-transformed PSA level as

$$y_{\upsilon ij}={\mu }_0+{\theta }_{0\upsilon i}+({\theta }_{1\upsilon i}+\upsilon d_g)s_{\upsilon ij}+({\theta }_{2\upsilon i}+\upsilon d_{\eta })(e^{-{\varphi }_{\upsilon }{s}_{\upsilon ij}}-1)+{\epsilon }_{\upsilon ij},$$ (5.1)

where υ = 0 or 1 indicates treatment arm CH or AA, respectively, i (= 1, …, m_υ) denotes the patient ID (in arm υ), and j (= 1, …, n_υi) indicates the measurement number for subject i in arm υ, and s_υij is the time since treatment initiation (measured in years) at the jth repeated observation for patient i in arm υ. The fixed effects d_g and d_η describe the effect of treatment on PSA slope and the size of the initial drop. We assume ${\theta }_{0\upsilon i}\stackrel{i.i.d.}{~}N(0,{\sigma }_0^2),({\theta }_{1\upsilon i},{\theta }_{2\upsilon i})\stackrel{i.i.d.}{~}G\equiv {(G_1,G_2)}^T$ with G ~ DP (M, N (β ≡ (β₁, β₂)′, D ≡ [d_ij])), ${\epsilon }_{\upsilon ij}\stackrel{i.i.d.}{~}N(0,{\sigma }^2)$, and θ_0υi, (θ_1υi, θ_2υi) and ε_υijare mutually independent.

Equation (5.1) models the typical features of PSA profiles for prostate cancer patients post treatment initiation. In particular, PSA levels tend to drop sharply after treatment initiation, and there is an additive increasing trend over time (linear in the log-transformed PSA level). Both, the initial drop and the trend, may differ between treatments.

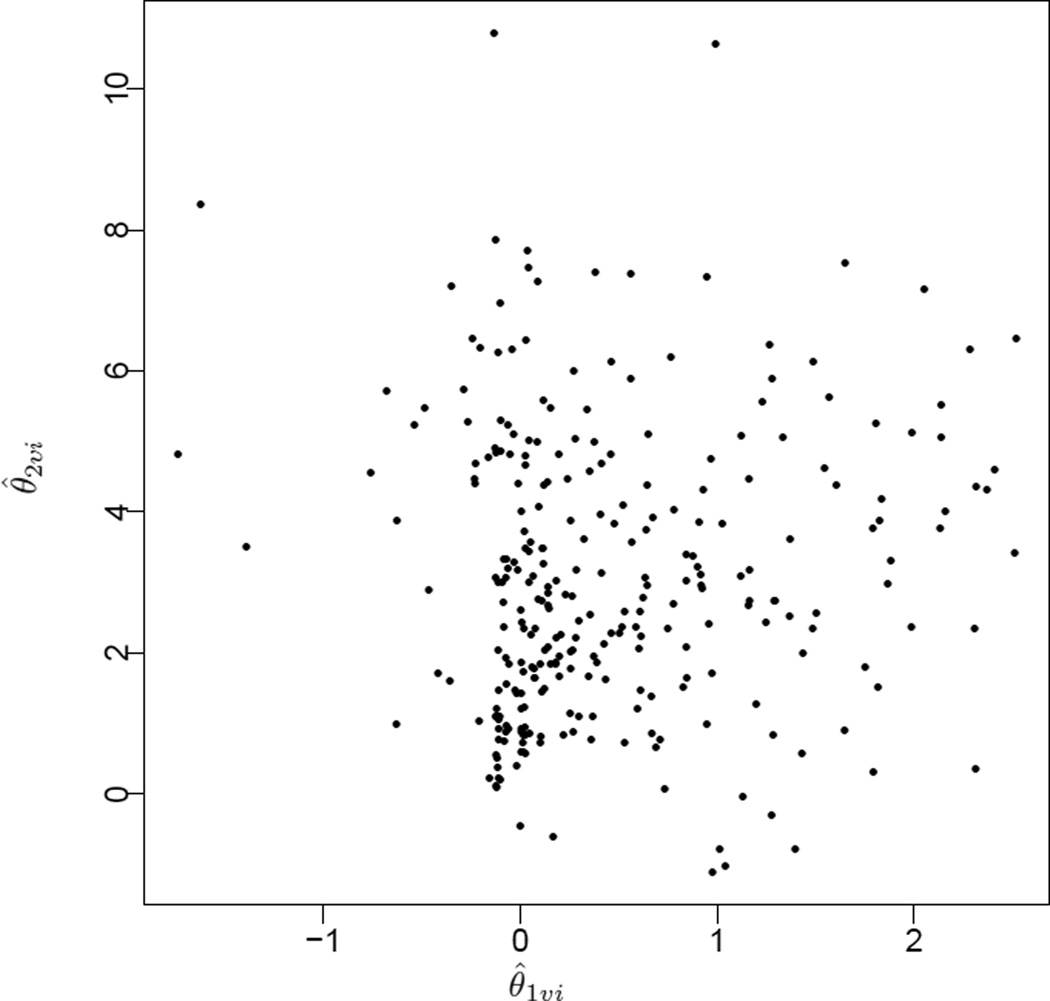
We assume ${\theta }_{0\upsilon i}~N(0,{\sigma }_0^2)$ mainly for simplicity, assuming that neither the distribution of θ_0υinor their estimates are of main scientific interest for the study. A scatterplot of the joint posterior means of (θ_1υi, θ_2υi) (Figure A.2) suggests clear skewness and significant departure from normality (Verbeke and Lesaffre (1996)). This justifies the use of the centered DP prior model for the distribution of (θ_1υi, θ_2υi).

Figure A.2.

A scatterplot of the joint posterior means (θ̂_1υi, θ̂_2υi) assuming normally distributed (θ_1υi, θ_2υi) (with unknown means) in model (5.1)

The prior used for the parameters in model (5.1) was independent across parameters with p(μ₀) = p(β₁) = p(β₂) = p(d_g) = p(d_η) = N(0, 10⁴), p(ϕ₀) = p(ϕ₁) = G(0.01, 0.001), $p({\sigma }_0^2)=p({\sigma }^2)=IG(.01,.01)$, and p(D) = IW(2, 0.01 I₂). Here I₂ denotes a 2 × 2 identity matrix and the IW distribution is parametrized such that E(D⁻¹) = 0.02I₂. We fixed M = 5.

We implemented posterior simulation using a Gibbs sampler. An additional Metropolis step was used to define a transition probability to update ϕ₀ and ϕ₁, respectively. After a burn-in of 5,000 iterations, 20,000 samples were obtained with every 10th saved for posterior inference. Evaluation of Geweke’s statistic (1992) suggested practical convergence of the Markov chains. We applied the adjustments for moments of the DP in posterior inference. Specifically, we report inference on (μ_g1, μ_g2) ≡ (∫ θ_1idG₁(θ_1i), ∫ θ_2idG₂(θ_2i)) as inference on the slope of PSA and the initial drop for arm CH. Similarly, we report inference on (μ_g1 + d_g, μ_g2 + d_η) as inference on the corresponding parameters for arm AA. Denote the 2 × 2 random covariance matrix of (θ_1υi, θ_2υi) by Cov_G = [σ_ij]. We report posterior summaries for σ_ij as inference for the variance components.

The posterior mean of d_η, i.e., the difference in the initial drop in PSA between the conventional AA and CH treatments, was −.15. The corresponding 95% CI was (−.32, .01), suggesting that the new CH treatment likely results in a larger initial drop. The difference in the rate of the drop, i.e., ϕ₁ − ϕ₀, had a posterior mean of −.41 and a 95% CI of (−1.00, .17). The difference in the increase in PSA, or d_g, had a posterior mean of −.01 and a 95% CI of (−.03, −0.0006). This significantly smaller rate of increase in PSA in the conventional AA arm (although the difference is small) might be related to its smaller initial drop.

For comparison, we report posterior inference with and without the proposed adjustment in Table A.3. We report inference on the rate of initial drop in PSA as part of the treatment effect. This is an example of the inference that is not affected by the proposed adjustment. On the other hand, we report inference for all fixed effects that are paired with nonparametric random effects and for the variance components. The posterior mean of the average increase in PSA in each arm changed by approximately 10% between the proposed adjusted and unadjusted inferences. The posterior precision approximately tripled. For the average initial drop in PSA, the posterior mean changed by about 30% with the precision being more than tripled in both treatment arms, as a result of the adjusted inference. Even larger changes were seen in inference for the variance components σ_ij. For example, the posterior mean of the covariance between the two random effects flipped sign under the proposed center-adjusted inference compared to the unadjusted inference. The reported positive covariance estimate was consistent with the scatterplot of the estimated random effects (θ̂_1υi, θ̂_2υi) under a normality assumption (Figure A.2).

Table A.3.

Posterior summaries with and without the proposed adjustment for rate of initial drop in PSA, increase in PSA per year, initial drop in PSA, and variance components based on model (5.1) for the PSA data

Parameter	Adjustment	Posterior Mean	Posterior SD	95% CI
Rate of initial drop in PSA
Arm CH
ϕ0	Cent-Adj/Unadj	8.44	.21	(8.04, 8.87)
Arm AA
ϕ1	Cent-Adj/Unadj	8.03	.20	(7.63, 8.44)
Increase in PSA per year
Arm CH
μ g1	Cent-Adj	.63	.08	(.49, .78)
β1	Unadj	.70	.25	(.24, 1.24)
Arm AA
μg1 + dg	Cent-Adj	.62	.08	(.47, .77)
β1 + dg	Unadj	.69	.25	(.21, 1.22)
Initial drop in PSA
Arm CH
μg2	Cent-Adj	3.32	.14	(3.04, 3.59)
β2	Unadj	4.33	.48	(3.37, 5.28)
Arm AA
μg2 + dη	Cent-Adj	3.17	.14	(2.89, 3.44)
β2 + dη	Unadj	4.18	.48	(3.23, 5.14)
Variance components
σ11	Cent-Adj	1.17	.23	(.78, 1.68)
	Unadj	1.76	.68	(.89, 3.54)
σ22	Cent-Adj	4.76	.51	(3.84, 5.84)
	Unadj	7.82	2.05	(4.65, 12.56)
σ12	Cent-Adj	.35	.17	(.01, .68)
	Unadj	−.22	.60	(−1.70, 1.14)

Finally, we investigated sensitivity of the proposed method with respect to M by considering alternatively a gamma prior for M, e.g., p(M) = G(.8, .4) (with mean = 2 and variance = 5). The results (not shown) followed the same pattern as reported in Table A.3.

6. Discussion

We have proposed a post-processing technique based on moment adjustment for inference on the fixed effects that are paired with random effects and the variance components of the random effects in a Bayesian hierarchical model. A hierarchically centered DP prior is assumed for the random effects distribution. The main results (Propositions 2 and 3) carry fully to any nonparametric Bayesian hierarchical model where a DP prior model (1.1) or (2.3) is assumed. In fact, this also applies to cases where the DP base measure is a parametric distribution other than normal, as long as the following are computable: 1) μ_G* and Cov_G* are needed for the evaluation of the posterior mean and covariance matrix of μ_G and the posterior mean of Cov_G; 2) Up to the fourth moments of G_* is needed for the evaluation of the posterior second moments of Cov_G. The only additional requirements for the proposed method to be applicable are: 1) the posterior samples of the parameters in the DP prior model (1.1) or (2.3) are available; 2) the random mean and/or covariance matrix of the random effects are of scientific interest. In cases where only the predictive inference for the outcome variable is of interest, adjustments for the fixed effects and variance components are not necessary. While the specific expressions for the proposed moment adjustments are lengthy, they are closed-form and easy to evaluate. Most importantly, we provide an R function (freely downloadable from http://odin.mdacc.tmc.edu/~yishengli/DPPP.R) that allows easy implementation by the users.

We have demonstrated through simulations in DP GLMMs that the proposed center-adjusted inference is effective in correcting reported inference for the fixed effects and variance components. We also showed through a data example that the effect of a treatment on patient outcomes (such as the initial drop after treatment initiation and the yearly increase in the PSA level in prostate cancer patients) could be considerably misreported (such as overestimated and poorly inferred) without appropriate adjustments. A practically important feature of the proposed procedure is that the method requires little new model structure and can be implemented at essentially no additional computational cost. The implementation of the method requires essentially only post-processing of the posterior samples of the model parameters.

In applying the proposed inference in DP GLMMs, we also find that the USP leads to in general more robust performance, while the IW prior may result in poor inference for the variance components of the random effects, an issue becoming even more prominent when the data to be analyzed are binary.

Appendix A

A.1. Proof of Lemma 1

Let (𝒳, 𝒜) be the space and σ-field of subsets on which the probability measure α is defined. By Theorem 2 of Ferguson (1973), a Dirichlet process DP(M, α) can be alternatively constructed as $P(A)={\sum }_{j=1}^{\infty }{P}_j{\delta }_{V_j}(A)$, for any A ∈ 𝒜, where P_j are correlated random variables defined in Ferguson (1973) satisfying P_j ≥ 0 and ${\sum }_{j=1}^{\infty }{P}_j=1$, a.s., V_j are i.i.d. random variables with values in 𝒳with probability measure α, and {P_j} and {V_j} are independent. Here δ _x (A) = 1, if x ∈ A; and δ _x (A) = 0 otherwise. Then we have

$$\int Z_{1}dP\int Z_{2}dP\int Z_{3}dP=\sum _i\sum _j\sum _k{Z}_1(V_i)Z_2(V_j)Z_3(V_k)P_i{P}_j{P}_k$$ (A.1)

since all three series are absolutely convergent with probability one (see the proof of Theorem 3, Ferguson (1973)). The infinite summation (A.1) is bounded by

$$\sum _i\sum _j\sum _k|Z_1(V_i)Z_2(V_j)Z_3(V_k)|P_i{P}_j{P}_k.$$ (A.2)

If (A.2) is an integrable random variable, then the expectation of (A.1) can be taken inside the summation sign. Let

• S(1, 1, 3) = ∑_i≠k E[Z₁(V_i)Z₂(V_i)]E[Z₃(V_k)]E(P_iP_iP_k),

• S(1, 2, 3) = ∑_i≠j≠k E[Z₁(V_i)]E[Z₂(V_j)]E[Z₃(V_k)]E(P_iP_jP_k),

• S(1, 1, 1) = ∑_i E[Z₁(V_i)Z₂(V_i)Z₃(V_i)]E(P_iP_iP_i), etc. Then

  $$E\int Z_{1}dP\int Z_{2}dP\int Z_{3}dP=\sum _i\sum _j\sum _{k}E[Z_1(V_i)Z_2(V_j)Z_3(V_k)]E(P_i{P}_j{P}_k)=S(1,2,3)+S(1,1,3)+S(1,2,1)+S(1,2,2)+S(1,1,1)={\mu }_1{\mu }_2{\mu }_3+({\sigma }_{12}{\mu }_3+{\sigma }_{13}{\mu }_2+{\sigma }_{23}{\mu }_1)\{\sum _{i\ne k}E(P_i^2{P}_k)+\sum _{i}E{P}_i^3\}+{\sigma }_{123}\sum _{i}E{P}_i^3.$$

A similar equation shows that (A.2) is integrable. The distribution of the P_i depends on M, but not α, based on its definition (Ferguson (1973)). Hence, analogous to the proof of Theorem 4 of Ferguson (1973), we choose 𝒳 to be the real line, α to give 2/3 probability to −1 and 1/3 probability to 2, and Z₁(x) = Z₂(x) = Z₃(x) ≡ x. Thus μ₁ = μ₂ = μ₃ = 0 and σ₁₂₃ = 2. Hence

$$\sum _{i}E{P}_i^3=\frac{1}{2}E{(\int xdP(x))}^3=\frac{1}{2}E{(3P(2)-1)}^3=\frac{2}{(M+1)(M+2)},$$

since P(2) ~ Beta(M/3, 2M/3). A similar calculation gives us ${\sum }_{i\ne k}E(P_i^2{P}_k)=M/[(M+1)(M+2)]$, by assuming α to give 1/2 probability to each of −1 and 1, and Z₁(x) = Z₂(x) ≡ x and Z₃ ≡ 1. The equality (3.1) is thus proved.

A.2. Proof of Lemma 2

Define S(i, j, k, ℓ) like S(i, j, k) in the proof of Lemma 1. By similar argument to that in the proof of Lemma 1, we have

$$E\int Z_{1}dP\int Z_{2}dP\int Z_{3}dP\int Z_{4}dP=\sum _i\sum _j\sum _k\sum _{l}E[Z_1(V_i)Z_2(V_j)Z_3(V_k)Z_4(V_l)]E(P_i{P}_j{P}_k{P}_l)=S(1,2,3,4)+S(1,1,3,4)+S(1,2,1,4)+S(1,2,3,1)+S(1,2,2,4)+S(1,2,3,2)+S(1,2,3,3)+S(1,1,3,3)+S(1,2,1,2)+S(1,2,2,1)+S(1,1,1,4)+S(1,1,3,1)+S(1,2,1,1)+S(1,2,2,2)+S(1,1,1,1)={\mu }_1{\mu }_2{\mu }_3{\mu }_4+R_1\sum _{i\ne k,k\ne l,l\ne i}E(P_i^2{P}_k{P}_l)+(R_1+R_3)\sum _{i\ne k}E(P_i^2{P}_k^2)+(2R_1+R_2)\sum _{i\ne l}E(P_i^3{P}_l)+({\sigma }_{1234}+R_1+R_2)\sum _{i}E{P}_i^4={\mu }_1{\mu }_2{\mu }_3{\mu }_4+R_1\{\sum _{i\ne k,k\ne l,l\ne i}E(P_i^2{P}_k{P}_l)+\sum _{i\ne k}E(P_i^2{P}_k^2)+2\sum _{i\ne l}E(P_i^3{P}_l)+\sum _{i}E{P}_i^4\}+R_2\{\sum _{i}E{P}_i^4+\sum _{i\ne l}E(P_i^3{P}_l)\}+R_3\sum _{i\ne k}E(P_i^2{P}_k^2)+{\sigma }_{1234}\sum _{i}E{P}_i^4.$$ (A.3)

Assuming α to give 1/2 probability to each of −1 and 1, and Z₁(x) = Z₂(x) = Z₃(x) = Z₄(x) ≡ x, the left hand side (LHS) of (A.3) is

$$E{(\int xdP(x))}^4=E{\{P(1)-P(-1)\}}^4=E{\{2P(1)-1\}}^4=2^{4}EP{(1)}^4-4*2^{3}EP{(1)}^3+6*2^{2}EP{(1)}^2-4*2EP(1)+1.$$

Since P(1) ~ Beta(M/2, M/2), we have

$$EP{(1)}^4=\frac{\frac{M}{2}(\frac{M}{2}+1)(\frac{M}{2}+2)(\frac{M}{2}+3)}{M(M+1)(M+2)(M+3)}=\frac{(M+2)(M+6)}{2^4(M+1)(M+3)},EP{(1)}^3=\frac{\frac{M}{2}(\frac{M}{2}+1)(\frac{M}{2}+2)}{M(M+1)(M+2)}=\frac{(M+4)}{2^3(M+1)},EP{(1)}^2=\frac{M+2}{2^2(M+1)},EP(1)=\frac{1}{2}.$$

The above is based on the moment formula for the beta distribution. Hence, the LHS of (A.3) is 3/[(M + 1)(M + 3)]. On the other hand, the RHS of (A.3) is $3{\sum }_{i\ne k}E(P_i^2{P}_k^2)+{\sum }_{i}E{P}_i^4$. Thus, we have

$$3\sum _{i\ne k}E(P_i^2{P}_k^2)+\sum _{i}E{P}_i^4=\frac{3}{(M+1)(M+3)}.$$ (A.4)

Similarly, if we assume Z₁(x) = Z₂(x) = Z₃(x) = Z₄(x) ≡ x, α to assign 2/3 probability to −1 and 1/3 probability to 2, (A.3) implies

$$2\sum _{i\ne k}E(P_i^2{P}_k^2)+\sum _{i}E{P}_i^4=\frac{2}{(M+1)(M+2)},$$ (A.5)

since P(2) ~ Beta(M/3, 2M/3). Equations (A.4) and (A.5) imply

$$\sum _{i\ne k}E(P_i^2{P}_k^2)=\frac{M}{(M+1)(M+2)(M+3)},$$ (A.6)

$$\sum _{i}E{P}_i^4=\frac{6}{(M+1)(M+2)(M+3)}.$$ (A.7)

Further assuming α to give 2/3 probability to −1 and 1/3 probability to 2, Z₁(x) = Z₂(x) = Z₃(x) ≡ x, and Z₄(x) ≡ 1, an analogous calculation using (A.3) as above yields

$$\sum _{i\ne l}E(P_i^3{P}_l)=\frac{2M}{(M+1)(M+2)(M+3)}.$$ (A.8)

Again, assuming α to give 1/2 probability to each of −1 and 1, Z₁(x) = Z₂(x) ≡ x, and Z₃(x) = Z₄(x) ≡ 1, we obtain

$$\sum _{i\ne k,i\ne l,k\ne l}E(P_i^2{P}_k{P}_l)=\frac{M^2}{(M+1)(M+2)(M+3)}.$$ (A.9)

(3.2) is obtained by plugging (A.6), (A.7), (A.8) and (A.9) into (A.3).

A.3. Notations used for defining L₂ through L₄, O₂ and O₃ in Proposition 2 (ii)

In L₂:

$${\mu }_1^{(L_2)}={\mathit{\text{Cov}}}_{G_{\star },i_1{j}_1}+{\mu }_{G_{\star },i_1}{\mu }_{G_{\star },j_1},{\mu }_2^{(L_2)}={\mu }_{G_{\star },i_2},{\mu }_3^{(L_2)}={\mu }_{G_{\star },j_2},{\sigma }_{23}^{(L_2)}={\mathit{\text{Cov}}}_{G_{\star },i_2{j}_2},{\sigma }_{12}^{(L_2)}=\int b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}{b}_{m+1}^{(i_2)}d{G}_{\star }({\mathit{b}}_{m+1})-({\mathit{\text{Cov}}}_{G_{\star },i_1{j}_1}+{\mu }_{G_{\star },i_1}{\mu }_{G_{\star },j_1})\times {\mu }_{G_{\star },i_2},{\sigma }_{13}^{(L_2)}=\int b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}{b}_{m+1}^{(j_2)}d{G}_{\star }({\mathit{b}}_{m+1})-({\mathit{\text{Cov}}}_{G_{\star },i_1{j}_1}+{\mu }_{G_{\star },i_1}{\mu }_{G_{\star },j_1})\times {\mu }_{G_{\star },j_2},{\sigma }_{123}^{(L_2)}=\int (b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}-{\mu }_1^{(L_2)})(b_{m+1}^{(i_2)}-{\mu }_2^{(L_2)})(b_{m+1}^{(j_2)}-{\mu }_3^{(L_2)})d{G}_{\star }({\mathit{b}}_{m+1});$$

In L₃:

$${\mu }_1^{(L_3)}={\mathit{\text{Cov}}}_{G_{\star },i_2{j}_2}+{\mu }_{G_{\star },i_2}{\mu }_{G_{\star },j_2},{\mu }_2^{(L_3)}={\mu }_{G_{\star },i_1},{\mu }_3^{(L_3)}={\mu }_{G_{\star },j_1},{\sigma }_{23}^{(L_3)}={\mathit{\text{Cov}}}_{G_{\star },i_1{j}_1},{\sigma }_{12}^{(L_3)}=\int b_{m+1}^{(i_2)}{b}_{m+1}^{(j_2)}{b}_{m+1}^{(i_1)}d{G}_{\star }({\mathit{b}}_{m+1})-({\mathit{\text{Cov}}}_{G_{\star },i_2{j}_2}+{\mu }_{G_{\star },i_2}{\mu }_{G_{\star },j_2})\times {\mu }_{G_{\star },i_1},{\sigma }_{13}^{(L_3)}=\int b_{m+1}^{(i_2)}{b}_{m+1}^{(j_2)}{b}_{m+1}^{(j_1)}d{G}_{\star }({\mathit{b}}_{m+1})-({\mathit{\text{Cov}}}_{G_{\star },i_2{j}_2}+{\mu }_{G_{\star },i_2}{\mu }_{G_{\star },j_2})\times {\mu }_{G_{\star },j_1},{\sigma }_{123}^{(L_3)}=\int (b_{m+1}^{(i_2)}{b}_{m+1}^{(j_2)}-{\mu }_1^{(L_3)})(b_{m+1}^{(i_1)}-{\mu }_2^{(L_3)})(b_{m+1}^{(j_1)}-{\mu }_3^{(L_3)})d{G}_{\star }({\mathit{b}}_{m+1});$$

In L₄:

$${\mu }_1^{(L_4)}={\mu }_{G_{\star },i_1},{\mu }_2^{(L_4)}={\mu }_{G_{\star },j_1},{\mu }_3^{(L_4)}={\mu }_{G_{\star },i_2},{\mu }_4^{(L_4)}={\mu }_{G_{\star },j_2},{\sigma }_{12}^{(L_4)}={\mathit{\text{Cov}}}_{G_{\star },i_1{j}_1},{\sigma }_{13}^{(L_4)}={\mathit{\text{Cov}}}_{G_{\star },i_1{i}_2},{\sigma }_{14}^{(L_4)}={\mathit{\text{Cov}}}_{G_{\star },i_1{j}_2},{\sigma }_{23}^{(L_4)}={\mathit{\text{Cov}}}_{G_{\star },j_1{i}_2},{\sigma }_{24}^{(L_4)}={\mathit{\text{Cov}}}_{G_{\star },j_1{j}_2},{\sigma }_{34}^{(L_4)}={\mathit{\text{Cov}}}_{G_{\star },i_2{j}_2},{\sigma }_{123}^{(L_4)}=\int (b_{m+1}^{(i_1)}-{\mu }_1^{(L_4)})(b_{m+1}^{(j_1)}-{\mu }_2^{(L_4)})(b_{m+1}^{(i_2)}-{\mu }_3^{(L_4)})d{G}_{\star }({\mathit{b}}_{m+1}),{\sigma }_{124}^{(L_4)}=\int (b_{m+1}^{(i_1)}-{\mu }_1^{(L_4)})(b_{m+1}^{(j_1)}-{\mu }_2^{(L_4)})(b_{m+1}^{(j_2)}-{\mu }_4^{(L_4)})d{G}_{\star }({\mathit{b}}_{m+1}),{\sigma }_{134}^{(L_4)}=\int (b_{m+1}^{(i_1)}-{\mu }_1^{(L_4)})(b_{m+1}^{(i_2)}-{\mu }_3^{(L_4)})(b_{m+1}^{(j_2)}-{\mu }_4^{(L_4)})d{G}_{\star }({\mathit{b}}_{m+1}),{\sigma }_{234}^{(L_4)}=\int (b_{m+1}^{(j_1)}-{\mu }_2^{(L_4)})(b_{m+1}^{(i_2)}-{\mu }_3^{(L_4)})(b_{m+1}^{(j_2)}-{\mu }_4^{(L_4)})d{G}_{\star }({\mathit{b}}_{m+1}),R_1^{(L_4)}=\sum _{i<j,k<\ell ,i\ne k,i\ne \ell ,j\ne k,j\ne \ell }{\sigma }_{ij}^{(L_4)}{\mu }_k^{(L_4)}{\mu }_{\ell }^{(L_4)},R_2^{(L_4)}={\sigma }_{123}^{(L_4)}{\mu }_4^{(L_4)}+{\sigma }_{124}^{(L_4)}{\mu }_3^{(L_4)}+{\sigma }_{134}^{(L_4)}{\mu }_2^{(L_4)}+{\sigma }_{234}^{(L_4)}{\mu }_1^{(L_4)},R_3^{(L_4)}={\sigma }_{12}^{(L_4)}{\sigma }_{34}^{(L_4)}+{\sigma }_{13}^{(L_4)}{\sigma }_{24}^{(L_4)}+{\sigma }_{14}^{(L_4)}{\sigma }_{23}^{(L_4)},{\sigma }_{1234}^{(L_4)}=\int (b_{m+1}^{(i_1)}-{\mu }_1^{(L_4)})(b_{m+1}^{(j_1)}-{\mu }_2^{(L_4)})(b_{m+1}^{(i_2)}-{\mu }_3^{(L_4)})(b_{m+1}^{(j_2)}-{\mu }_4^{(L_4)})d{G}_{\star }({\mathit{b}}_{m+1}).$$

In O₂:

$${\mu }_1^{(O_2)}={\mathit{\text{Cov}}}_{G_{\star },ij}+{\mu }_{G_{\star },i}{\mu }_{G_{\star },j},{\mu }_2^{(O_2)}={\mu }_{G_{\star },i},{\mu }_3^{(O_2)}={\mu }_{G_{\star },j},{\sigma }_{23}^{(O_2)}={\mathit{\text{Cov}}}_{G_{\star },ij},{\sigma }_{12}^{(O_2)}={\sigma }_{13}^{(O_2)}=\int {\left[b_{m+1}^{(i)}\right]}^2{b}_{m+1}^{(j)}d{G}_{\star }({\mathit{b}}_{m+1})-({\mathit{\text{Cov}}}_{G_{\star },ij}+{\mu }_{G_{\star },i}{\mu }_{G_{\star },j})\times {\mu }_{G_{\star },i},{\sigma }_{13}^{(O_2)}=\int b_{m+1}^{(i)}{\left[b_{m+1}^{(j)}\right]}^{2}d{G}_{\star }({\mathit{b}}_{m+1})-({\mathit{\text{Cov}}}_{G_{\star },ij}+{\mu }_{G_{\star },i}{\mu }_{G_{\star },j})\times {\mu }_{G_{\star },j},{\sigma }_{123}^{(O_2)}=\int (b_{m+1}^{(i)}{b}_{m+1}^{(j)}-{\mu }_1^{(O_2)})(b_{m+1}^{(i)}-{\mu }_2^{(O_2)})(b_{m+1}^{(j)}-{\mu }_3^{(O_2)})d{G}_{\star }({\mathit{b}}_{m+1});$$

In O₃:

$${\mu }_1^{(O_3)}={\mu }_2^{(O_3)}={\mu }_{G_{\star },i},{\mu }_3^{(O_3)}={\mu }_4^{(O_3)}={\mu }_{G_{\star },j},{\sigma }_{12}^{(O_3)}={\mathit{\text{Var}}}_{G_{\star },i},{\sigma }_{34}^{(O_3)}={\mathit{\text{Var}}}_{G_{\star },j},{\sigma }_{13}^{(O_3)}={\sigma }_{14}^{(O_3)}={\sigma }_{23}^{(O_3)}={\sigma }_{24}^{(O_3)}={\mathit{\text{Cov}}}_{G_{\star },ij},{\sigma }_{123}^{(O_3)}={\sigma }_{124}^{(O_3)}=\int {(b_{m+1}^{(i)}-{\mu }_1^{(O_3)})}^2(b_{m+1}^{(j)}-{\mu }_3^{(O_3)})d{G}_{\star }({\mathit{b}}_{m+1}),{\sigma }_{134}^{(O_3)}={\sigma }_{234}^{(O_3)}=\int (b_{m+1}^{(i)}-{\mu }_1^{(O_3)}){(b_{m+1}^{(j)}-{\mu }_3^{(O_3)})}^{2}d{G}_{\star }({\mathit{b}}_{m+1}),R_1^{(O_3)}=\sum _{i<j,k<\ell ,i\ne k,i\ne \ell ,j\ne kj\ne \ell }{\sigma }_{ij}^{(O_3)}{\mu }_k^{(O_3)}{\mu }_{\ell }^{(O_3)},R_2^{(O_3)}={\sigma }_{123}^{(O_3)}{\mu }_4^{(O_3)}+{\sigma }_{124}^{(O_3)}{\mu }_3^{(O_3)}+{\sigma }_{134}^{(O_3)}{\mu }_2^{(O_3)}+{\sigma }_{234}^{(O_3)}{\mu }_1^{(O_3)},R_3^{(O_3)}={\sigma }_{12}^{(O_3)}{\sigma }_{34}^{(O_3)}+{\sigma }_{13}^{(O_3)}{\sigma }_{24}^{(O_3)}+{\sigma }_{14}^{(O_3)}{\sigma }_{23}^{(O_3)},{\sigma }_{1234}^{(O_3)}=\int {(b_{m+1}^{(i)}-{\mu }_1^{(O_3)})}^2{(b_{m+1}^{(j)}-{\mu }_3^{(O_3)})}^{2}d{G}_{\star }({\mathit{b}}_{m+1}).$$

A.4. Proof of Proposition 2 (ii)

Assume [b̃ | G] ~ G and [b_m+1 | b, β_b, D, M] ~ G_*. Let b̃⁽ⁱ⁾ and $b_{m+1}^{(i)}$ be the i-th component of b̃ and b_m+1, respectively. Define I₁ = E(Cov_G,i1j1 · Cov_G,i2j2 | b, β _b, D,M), I₂ = E(Cov_G,i1j1 | b, β _b, D,M), and I₃ = E(Cov_G,i2j2 | b, β _b, D,M). Then Cov(Cov_G,i1j1, Cov_G,i2j2 | y) = E(I₁ | y) − E(I₂ | y)E(I₃ | y). Based on Proposition 3 (i), I₂ = (m + M)Cov_G*,i1j1/(m +M + 1), and I₃ = (m + M)Cov_G*,i2j2/(m +M + 1).

To calculate I₁, we write I₁ = J₁ − J₂ − J₃ + J₄, where

$$J_1=E[\int {\mathit{b̃}}^{(i_1)}{\mathit{b̃}}^{(j_1)}dG(\mathit{b̃})\int {\mathit{b̃}}^{(i_2)}{\mathit{b̃}}^{(j_2)}dG(\mathit{b̃})|\mathit{b},\mathit{\beta },\mathit{D},M],J_2=E[\int {\mathit{b̃}}^{(i_1)}{\mathit{b̃}}^{(j_1)}dG(\mathit{b̃})\int {\mathit{b̃}}^{(i_2)}dG(\mathit{b̃})\int {\mathit{b̃}}^{(j_2)}dG(\mathit{b̃})|\mathit{b},\mathit{\beta },\mathit{D},M],J_3=E[\int {\mathit{b̃}}^{(i_2)}{\mathit{b̃}}^{(j_2)}dG(\mathit{b̃})\int {\mathit{b̃}}^{(i_1)}dG(\mathit{b̃})\int {\mathit{b̃}}^{(j_1)}dG(\mathit{b̃})|\mathit{b},\mathit{\beta },\mathit{D},M],\text{and}{J}_4=E[\int {\mathit{b̃}}^{(i_1)}dG(\mathit{b̃})\int {\mathit{b̃}}^{(j_1)}dG(\mathit{b̃})\int {\mathit{b̃}}^{(i_2)}dG(\mathit{b̃})\int {\mathit{b̃}}^{(j_2)}dG(\mathit{b̃})|\mathit{b},\mathit{\beta },\mathit{D},M].$$

By Theorem 4 of Ferguson (1973),

$$J_1=\frac{\mathit{\text{Cov}}(b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)},b_{m+1}^{(i_2)}{b}_{m+1}^{(j_2)}|G_{\star })}{m+M+1}+\int b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}d{G}_{\star }({\mathit{b}}_{m+1})\int b_{m+1}^{(i_2)}{b}_{m+1}^{(j_2)}d{G}_{\star }({\mathit{b}}_{m+1})=\frac{E[b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}{b}_{m+1}^{(i_2)}{b}_{m+1}^{(j_2)}|G_{\star }]}{m+M+1}+\frac{m+M}{m+M+1}E[b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}|G_{\star }\left]E\right[b_{m+1}^{(i_2)}{b}_{m+1}^{(j_2)}|G_{\star }].$$

To calculate J₂, we apply Lemma 1 for Z₁ = b̃^(i₁)b̃^(j₁), Z₂ = b̃^(i₂), and Z₃ =b̃^(j₂). Following the notations in Lemma 1, we have

$${\mu }_1={\mathit{\text{Cov}}}_{G_{\star },i_1{j}_1}+{\mu }_{G_{\star },i_1}{\mu }_{G_{\star },j_1},{\mu }_2={\mu }_{G_{\star },i_2},{\mu }_3={\mu }_{G_{\star },j_2},{\sigma }_{23}={\mathit{\text{Cov}}}_{G_{\star },i_2{j}_2},{\sigma }_{12}=\int (b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}-{\mu }_1)(b_{m+1}^{(i_2)}-{\mu }_{G_{\star },i_2})d{G}_{\star }({\mathit{b}}_{m+1})=\int b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}{b}_{m+1}^{(i_2)}d{G}_{\star }({\mathit{b}}_{m+1})-({\mathit{\text{Cov}}}_{G_{\star },i_1{j}_1}+{\mu }_{G_{\star },i_1}{\mu }_{G_{\star },j_1})\times {\mu }_{G_{\star },i_2},{\sigma }_{13}=\int b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}{b}_{m+1}^{(j_2)}d{G}_{\star }({\mathit{b}}_{m+1})-({\mathit{\text{Cov}}}_{G_{\star },i_1{j}_1}+{\mu }_{G_{\star },i_1}{\mu }_{G_{\star },j_1})\times {\mu }_{G_{\star },j_2},\text{and}{\sigma }_{123}=\int (b_{m+1}^{(i_1)}{b}_{m+1}^{(j_1)}-{\mu }_1)(b_{m+1}^{(i_2)}-{\mu }_2)(b_{m+1}^{(j_2)}-{\mu }_3)d{G}_{\star }({\mathit{b}}_{m+1}).$$

Plugging the above expressions into (3.1), we obtain J₂. J₃ can be similarly computed.

To calculate J₄, we apply Lemma 2 for Z₁ =b̃^(i₁), Z₂ =b̃^(j₁), Z₃ =b^(i₂), and Z₄ =b^(j₂). Following the notations in Lemma 2, we then have

$${\mu }_1={\mu }_{G_{\star },i_1},{\mu }_2={\mu }_{G_{\star },j_1},{\mu }_3={\mu }_{G_{\star },i_2},{\mu }_4={\mu }_{G_{\star },j_2},{\sigma }_{12}={\mathit{\text{Cov}}}_{G_{\star },i_1{j}_1},{\sigma }_{13}={\mathit{\text{Cov}}}_{G_{\star },i_1{i}_2},{\sigma }_{14}={\mathit{\text{Cov}}}_{G_{\star },i_1{j}_2},{\sigma }_{23}={\mathit{\text{Cov}}}_{G_{\star },j_1{i}_2},{\sigma }_{24}={\mathit{\text{Cov}}}_{G_{\star },j_1{j}_2},{\sigma }_{34}={\mathit{\text{Cov}}}_{G_{\star },i_2{j}_2},{\sigma }_{123}=\int (b_{m+1}^{(i_1)}-{\mu }_1)(b_{m+1}^{(j_1)}-{\mu }_2)(b_{m+1}^{(i_2)}-{\mu }_3)d{G}_{\star }({\mathit{b}}_{m+1}),\text{similarly for}{\sigma }_{124},{\sigma }_{134},\text{and}{\sigma }_{234},\text{and}{\sigma }_{1234}=\int (b_{m+1}^{(i_1)}-{\mu }_1)(b_{m+1}^{(j_1)}-{\mu }_2)(b_{m+1}^{(i_2)}-{\mu }_3)(b_{m+1}^{(j_2)}-{\mu }_4)d{G}_{\star }({\mathit{b}}_{m+1}).$$

Plugging the above expressions into (3.2), we obtain J₄. Thus I₁ is computed, and so is Cov(Cov_G,i1j1, Cov_G,i2j2 | y).

Var(Cov_G,ij | y) can be obtained by replacing i₁ and i₂ by i, and j₁ and j₂ by j in (3.3). The proof is thus completed.