Abstract
The human body can be viewed as a dynamical system, with physiological states such as health and disease broadly representing steady states. From this perspective, and given inter- and intra-individual heterogeneity, an important task is identifying the propensity to transition from one steady state to another, which in practice can occur abruptly. Detecting impending transitions between steady states is of significant importance in many fields, and thus a variety of methods have been developed for this purpose, but lack of data has limited applications in physiology. Here, we propose a model-based approach towards identifying critical transitions in systemic inflammation based on a minimal amount of assumptions about the availability of data and the structure of the system. We derived a warning signal metric to identify forthcoming abrupt transitions occurring in a mathematical model of systemic inflammation with a gradually increasing bacterial load. Intervention to remove the inflammatory stimulus was successful in restoring homeostasis if undertaken when the warning signal was elevated rather than waiting for the state variables of the system themselves to begin moving to a new steady state. The proposed combination of data and model-based analysis for predicting physiological transitions represents a step forward towards the quantitative study of complex biological systems.
Keywords: endotoxemia, systems biology, generalized modeling, bifurcation, stability analysis
1. Introduction
Clinical data can be viewed in the context of the physiological state space, where each physiological parameter represents a dimension and common conditions appear clustered together due to their shared physiological underpinnings (Buchman, 1996). These clusters represent steady states, regions where physiological parameters tend to stay constant in the absence of some perturbation to push the system towards another steady state. From this perspective, there is great value in determining to which steady state a patient belongs and if they are likely to move to another steady state as time progresses and their condition evolves (Buchman, 2010; Cohen, 2012). In terms of a dynamical system, this is equivalent to identifying a forthcoming bifurcation that will lead to a transition from the current steady state to a new steady state. In general, the earlier the diagnosis, the better the outcome, and thus it is important to detect warning signals of deterioration as early as possible. For example, there are approximately 750,000 cases of sepsis leading to 200,000 deaths annually in the US (Angus et al., 2001) and earlier detection of sepsis leads to more effective treatment and improved clinical outcomes, including lower mortality (Ridley, 2005)..
Identifying transitions between steady states of gradually changing dynamical systems is a problem with broad applications in many fields. For this reason, many prior studies have attempted to find markers of a system approaching a critical transition (Dakos et al., 2012; Scheffer et al., 2009). The general concept behind techniques for identifying critical transitions is that, as a dynamical system approaches a bifurcation, characteristic patterns emerge in the output of the system due to the underlying mathematical structures. For instance, the responses of a system to random deviations from its steady state may become slower as the loss of stability is approached, a phenomenon known as “critical slowing down”. Statistically identifying hallmarks of deteriorating stability has yielded impressive results in some instances (Carpenter et al., 2011), but applications in physiology and medicine have been rare (Chen et al., 2012; Mormann et al., 2007; Venegas et al., 2005) likely due to most clinical measurements being relatively low frequency and noisy while the statistical identification of critical transitions traditionally relies on large amounts of data. This has been somewhat assuaged by the advent of modern clinical and experimental techniques, including such technologies as microfluidics and high-throughput transcriptional screening, but the large-scale collection of most physiological data remains invasive and expensive, and thus researchers and clinicians typically remain data-limited. With this in mind, techniques to identify transitions based on limited data are required for physiological applications.
Lade and Gross recently proposed a novel technique for the identifications of critical transitions (Lade and Gross, 2012). Rather than taking a purely statistical approach, they considered the possibility of improving performance by leveraging additional information about the system in question, namely knowledge of its network structure. While detailed models with perfectly identified parameter values are rare, often some very general principles are well established. By using data to numerically estimate the stability of a simple high-level model of a system, Lade and Gross tracked changes in stability over time as new data streamed in. This model-based approach produced intriguing results suggesting that it allows for the robust prediction of forthcoming transitions based on sparser data than prior statistical approaches, making it an ideal candidate for evaluating physiological systems. However, application of Lade and Gross’s approach still requires significant assumptions about the measurability of internal components of the system (such as production and degradation rates), the structure of the system, or both, which may not be feasible in practice.
In this manuscript, we propose an approach for identifying critical transitions and apply it to a model of systemic inflammation that moves between steady states due to a progressing bacterial infection. Based on a combination of data and some high-level knowledge of the system’s network structure, a metric was derived to serve as a warning signal of abrupt transitions between steady states before the state variables begin their trajectories to the new steady state. Intervention to remove the inflammatory instigator proved successful in restoring homeostasis when performed after the warning signal became elevated, but was unsuccessful in this task when initiated later, after the system was already visibly on its trajectory towards a heightened inflammatory state. Critically, this approach requires a minimal amount of assumptions about the availability of data and the structure of the system while still retaining predictive power. Successful translation of the identification of transitions to clinical practice could have a transformational impact on healthcare, and this work represents a step towards that goal.
2. Methods
2.1. Generalized modeling
The study of physiological systems is hindered by both limited data and limited mechanistic knowledge. These practical limitations necessitate the use of analytical methods designed to function in the presence of significant uncertainty. One such approach is generalized modeling (Gross and Feudel, 2006; Kuehn et al., 2012). A generalized model is a system of equations representing interactions between variables based only on placeholder functions, which represent the connectivity between equations without making any assumptions about specific functional forms or parametrizations that all correspond to the same network structures.
Although generalized models cannot simply be simulated forward to study a system because the placeholder functions are not explicitly defined mathematical functions, insights can still be drawn from the analysis of generalized models. For example, stability of a steady state can be quantified by calculating the eigenvalues of the Jacobian matrix, a local linearization of the system (Gross and Feudel, 2006; Kuehn et al., 2012). The Jacobian matrix of a generalized model can be estimated in terms of partial derivatives of placeholder functions. If sufficient data is available, then those partial derivatives can be numerically estimated, and then stability of a system can be assessed without ever assuming any further properties of the system, such as the specific functional forms of the placeholder functions. In a system that is gradually approaching a critical transition, characteristic patterns often arise in the eigenvalues of the Jacobian matrix when a bifurcation occurs. This type of analysis can produce warning signals of an impending critical transition because changes in these eigenvalues often occur before the transition would be otherwise apparent from monitoring the state variables alone (Kuehn, 2011; Lade and Gross, 2012). Thus, if the dynamics of the system are reflected in the generalized model, then stability analysis of the generalized model may produce a quantifiable warning signal of critical transitions (Lade and Gross, 2012).
2.2. Human endotoxemia as a model of systemic inflammation
Human endotoxemia, an experimental model of systemic inflammation, consists of the administration of low doses of endotoxin (lipopolysaccharides, LPS) to healthy human volunteers (Lowry, 2005; Lowry, 2009). This provokes physiological changes that, in part, mimic those occurring in acute and chronic inflammation-linked disorders such as sepsis and trauma (Andreasen et al., 2008; Haimovich et al., 2010; Lowry, 2005; Shanker et al., 2010). Thus, human endotoxemia functions as a practical model of Toll-like receptor 4 agonist-induced systemic inflammation by eliciting neuroendocrine, hemodynamic, and leukocyte transcriptional responses.
The physiological changes occurring in human endotoxemia include transcriptional responses in immune cells through the activation of the inflammation-linked NF-κB, JAK-STAT, and MAPK signaling pathways, which then stimulate the production and release of both pro-inflammatory and anti-inflammatory cytokines, mediators of inflammation and the return to homeostasis, respectively. LPS, and its induced cytokine responses, also propagate through afferent nervous signaling to the central nervous system, which then forms a feedback loop to regulate the progression of inflammation through the release of immunomodulatory hormones and alterations in autonomic activity. We previously modeled these interactions based on data from human endotoxemia experiments (Foteinou et al., 2009a; Foteinou et al., 2009b; Foteinou et al., 2010; Foteinou et al., 2011; Scheff et al., 2010; Scheff et al., 2011). Model equations and parameters are given in the supplementary material.
We studied this system in the presence of a gradually-increasing inflammatory load, mimicking a growing bacterial infection, by assuming linear growth in the production of LPS. Due to a positive feedback loop in the pro-inflammatory response (P), this model is bistable, with one steady state representing healthy homeostasis with low levels of inflammatory mediators, and the other steady state exhibiting heightened levels of inflammatory mediators that persist even when LPS is completely removed. As the bacterial load gradually increases, the system enters a slowly changing intermediate state followed by an abrupt transition to the heightened inflammatory state, as shown in Fig. 1. If it were possible to perfectly model the inflammatory response and identify all model parameters, then that ideal model could be used to reliably predict future transitions. Instead, we use this model as a source of data and evaluate the ability of generalized models of systemic inflammation to predict critical transitions.
Fig. 1. Transition between steady states in chronic inflammation.
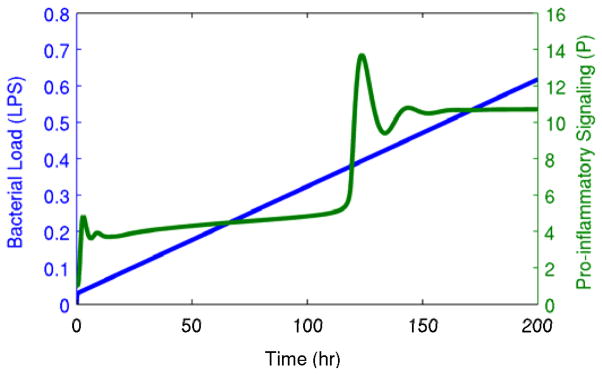
A gradually increasing bacterial load (LPS) produces an abrupt transition from a gradually-changing intermediate state to a heightened persistent inflammatory state. This transition is shown in the pro-inflammatory signaling variable (P), but it is equally apparent in other components of the system.
2.3. Generalized modeling of systemic inflammation
In many respects, a generalized model can be considered to be a mathematical representation of a network diagram, encoding only the components of a system, connections between components, and the directionalities of connections. However, in the context of stability analysis, this network must be relatively simple; otherwise, the number of partial derivative estimates will grow to require an unreasonable volume of data. Therefore, a complex system must be reduced to a limited number of motifs to be represented in a generalized model. In systemic inflammation, key motifs include an injury or pathogen stimulating a pro-inflammatory response; the antagonistic relationship between pro- and anti-inflammatory mediators; and the positive feedback between tissue damage and pro-inflammatory signaling (Vodovotz et al., 2009). These motifs are all represented in the model shown in Fig. 2. Lipopolysaccharides (LPS) stimulate the pro-inflammatory transcriptional response (P), which then activates both central immunomodulatory mechanisms (such as the release of cortisol, F) and peripheral transcriptional responses (A), which both serve to suppress pro-inflammatory activity. Generalized models, listed in Fig. 2B, were constructed as high-level representations of systemic inflammation based on these critical motifs present in the systemic inflammatory response. A variety of models were constructed to more broadly assess performance, as the reduction of a large network to represent a limited number of motifs includes some degree of qualitative analysis. The generalized models evaluated here are those made up of anti- and pro-inflammatory signaling (A-P), cortisol and pro-inflammatory signaling (F-P), either of those models plus LPS (A-LPS-P and F-LPS-P), and all four variables together (A-F-LPS-P). These five models represent every combination of A, F, LPS, and P that include both negative feedback (between P and either A or F) and positive feedback (in the equation for P).
Fig. 2. Network structures of the underlying detailed model and the generalized models.
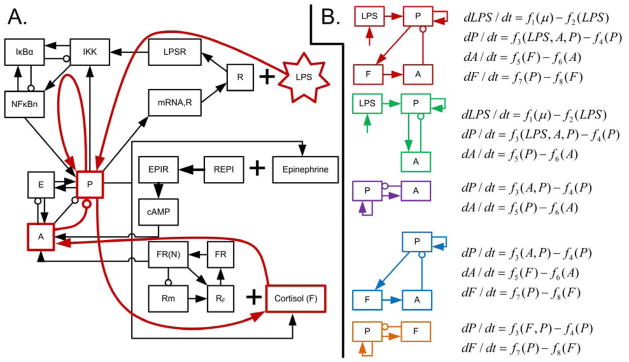
A: network structure of the model of human endotoxemia used to generate data (Foteinou et al., 2010). The red overlaid lines represent a high level simplification of this network structure, which corresponds to the first generalized model in B. B: network structures and equations for all five generalized models considered in this work. The systems are all comprised of, at most, four variables: bacterial load (LPS), pro-inflammatory signaling (P), anti-inflammatory signaling (A), and cortisol (F). The generalized model equations are mathematical formalizations of the network structures.
However, even making broad assumptions to significantly reduce the complexity of a generalized model is not necessarily sufficient to allow for the data-driven estimation of stability. If an equation in a generalized model depends on more than one variable, then its partial derivatives cannot be directly calculated based on measurements of the state variables alone unless some partial derivatives can be measured (e.g. the degradation rate of a variable) and/or some information can be gleaned from other equations (e.g. if the production rate of one variable equals the degradation rate of another) (Lade and Gross, 2012). For a physiological response like systemic inflammation, neither of these options is generally feasible. Instead, we estimated all partial derivatives from measurements of the state variables alone. From the output of the in silico model of systemic inflammation, we sub-sampled only the limited set of state variables used in the generalized models in Fig. 2B to use as input data for the prediction of critical transitions. Using this data to estimate the stability of generalized models requires the estimation of partial derivatives of every generalized model equation. These partial derivatives were estimated by assuming the placeholder functions are linear over a relatively small time window and minimizing the least squared error of the data fit to these equations. Then, these estimated partial derivatives were used to find the eigenvalues of the Jacobian matrix of the generalized model. Repeated application of this process allows for tracking the estimated stability of the generalized model over time. This algorithm is described in more detail in the supplementary material.
A unique feature of this procedure is that the dimensionality of the underlying system (20 equations) is substantially larger than the dimensionality of the generalized models (2–4 equations), whereas previous applications of generalized models for predicting critical transitions used synthetic data from models with the same dimensionality as the generalized models (Lade and Gross, 2012). Therefore, we are testing the hypothesis that only a subset of a system needs to be included in a generalized model to predict critical transitions. A complete formulation of the detailed model as well as the procedures for generating data and evaluating stability are found in the supplementary material.
3. Results
The existence of a critical transition for the detailed model of systemic inflammation in the presence of a gradually increasing bacterial load is shown in Fig. 1. The critical transition that occurs at around 120 hours is abrupt and is preceded only by very gradually changing state variables. Thus, taking a traditional approach and deriving a warning signal based on a cutoff in the state variables would not provide a significant amount of time before the system was already well on its way to its new steady state. Thus, we derived an earlier warning signal of this transition with a minimal amount of assumptions through generalized modeling.
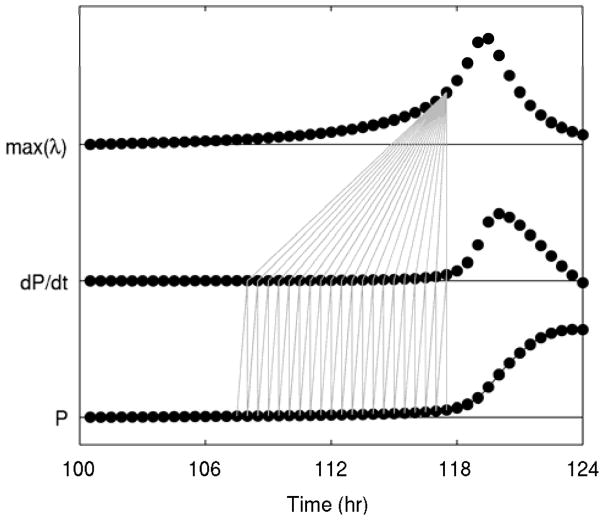
Fig. 3 displays an overview of how the output of the detailed model was translated into a warning signal. First, the state variables of the system were sampled at a constant rate, every 30 minutes in this example. This was done not for every variable in the model, but only for the variables that are included in the generalized model, in this case just pro-inflammatory signaling (P) and anti-inflammatory signaling (A). Then, derivatives of these state variables with respect to time were estimated at every point by using the backwards difference method, so that each estimate contains the most recent information possible. This also provided the opportunity to assess the predictive value of quantifying the time derivatives of state variables. As can be seen in Fig. 3, visible movement in both P and dP/dt occurred at approximately the same time. To evaluate the stability of the generalized model, a time window of 10 hours was used, combining the discretized state variables with the numerical derivatives to estimate partial derivatives of the system and thus estimate the eigenvalues of the two-variable generalized model. This produced two eigenvalues at each time point, of which only the larger eigenvalue is shown, as it dominates the response of the system. Conceivably, the other eigenvalues could provide information about changes in the dynamics of a system, but in all of the scenarios evaluated here, the maximum eigenvalue moved first. Each new estimate at a given time point was calculated based on the data from up to that time point, producing a warning signal updated in real time as data streamed in. The eigenvalue warning signal increased above its homeostatic value substantially earlier than either P or dP/dt, illustrating that generalized modeling can be leveraged as described here to develop a warning signal of critical transitions in the context of systemic inflammation. This validates the novel methodology for the estimation of stability based only on measurements of some state variables of a larger system without making any other assumptions about data availability or model structure. Furthermore, this shows that generalized models can provide warning signals even when they are fit to data generated by much more complex and higher dimensional systems.
Fig. 3. Translation from data to a warning signal.
From bottom to top, the three plots show: (1) pro-inflammatory signaling (P), with the line representing the detailed model output and the dots representing discrete samples every half hour; (2) the numerical derivative of P calculated with the backwards difference method; and (3) the maximum eigenvalue of the generalized model. Vertical lines between P and dP/dt indicate that the backwards difference method was used to estimate each derivative, taking into account the current time point and the previous time point only. Then, all of these values over a 10 hour window are used to estimate a single warning signal for the current time point. Thus, all of the vertical lines show all of the data that is used to produce the warning signal at a particular time point.
In addition to the simplest two-variable generalized model including only pro- and anti-inflammatory signaling, several different generalized models were evaluated, all containing the common motifs of negative feedback between pro- and anti-inflammatory signaling and a self-stimulatory positive feedback loop in pro-inflammatory signaling. In all of the evaluated models, the patterns of increases in the eigenvalues were largely similar, as shown in Fig. 4. This illustrates that the results presented here are not dependent on even a specific generalized model structure, as long as they contain the relevant motifs. The generalized model eigenvalues were also compared in Fig. 4 to the eigenvalues of the detailed model. This confirms that the patterns of changes in the estimated eigenvalues begin at roughly the same time as is observed in the eigenvalues of the underlying system.
Fig. 4. Comparison of eigenvalues from generalized models and from the underlying model.
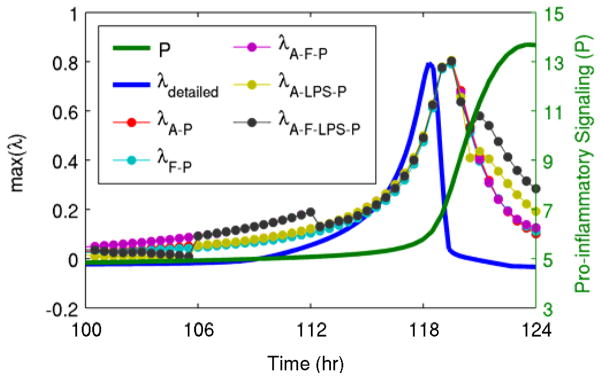
Shown here are eigenvalues estimated from all of the different generalized models (λi where i is the variables contained in the generalized model, as shown in Fig. 2), the eigenvalue calculated directly from the detailed model (λdetailed), and a state variable of the system (pro-inflammatory signaling, P). The estimated eigenvalues track the real eigenvalue, and they all clearly move before pro-inflammatory signaling enters its abrupt transition towards the persistent heightened inflammatory state.
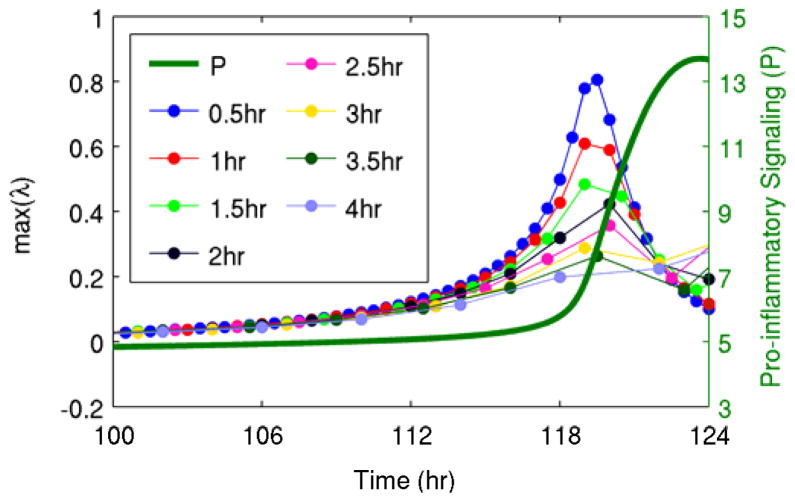
The results discussed above all used data sampled every 30 minutes from the detailed model. Fig. 5 illustrates that even lower frequency data can still be transformed into a predictive warning signal through the methods applied here. Although as the sampling rate decreases there was clearly a decrease in performance, in terms of deviation of the eigenvalue from baseline prior to the transition, there were still clear patterns in the trajectories of the eigenvalues up to a sampling period of approximately 4 hours.
Fig. 5. Effect of sampling frequency on predictions.
Warning signals were calculated from data sampled at periods ranging from 0.5 hr to 4 hr based on the generalized model containing only pro-inflammatory signaling (P) and anti-inflammatory signaling (A). Predictive value is maximized as sampling frequency increases.
To study the implications of early detection of a critical transition, we investigated an intervention applied when signs of a transition are apparent either in the eigenvalue warning signal or directly in the state variables of the model. Fig. 6 shows the effects of removing the inflammatory instigator at these two time points. The earlier intervention driven by the early warning signal restored homeostasis, but the later intervention after the system had already begun to move to the heightened inflammatory state was not sufficient to avert the transition, ultimately leaving the system in a persistent inflammatory state even in the absence of an inflammatory instigator. The presence of a critical time window between the time when markers of an impending transition are apparent and the “point of no return” where intervention does not successfully restore homeostasis underscores the importance of identifying warning signals as early as possible.
Fig. 6. Intervention performed based on the warning signal or the magnitude of state variables.
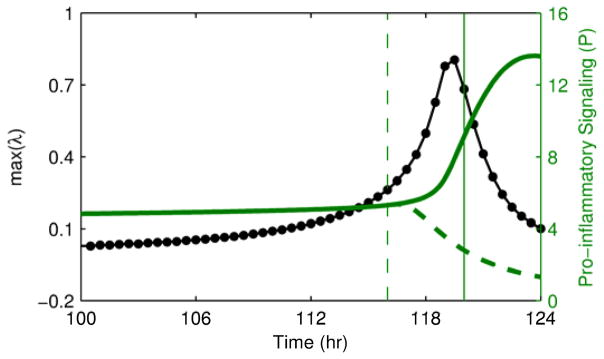
Intervention to remove the bacterial load is performed either at 116 hr when the warning signal is clearly elevated (dashed lines) or at 120 hr after the state variables of the system have clearly begun to transition (solid lines). The earlier intervention is able to restore homeostasis, but the later intervention after the transition has already begun is not sufficient to restore homeostasis.
4. Discussion
A key innovation here lies at the intersection of data and modeling. If very high resolution and low noise data was available, no model would be necessary to predict transitions as traditional statistical and signal processing approaches could be utilized (Scheffer et al., 2009). Conversely, if a perfect computational model was available, then it could simply be simulated forward to predict the future even without any data. As shown by Lade and Gross, combining relatively limited data with a simple model based on high-level network structure can result in informative predictions of forthcoming transitions (Lade and Gross, 2012). In addition to investigating a novel application in systemic inflammation, we extended this technique in two important ways. First, we established that the dimensionality of the underlying system (a detailed model of systemic inflammation) does not need to be the same as the dimensionality of the generalized model derived from the high-level network structure. This is important because it shows that the high-level network structure of a significantly more complex system is sufficient to predict transitions, which is critical in any application to real data generated by a much more complex biological system. Second, we derived predictive estimates of the stability of the system based only on data from the state variables, rather than assuming knowledge or measurability of internal production and degradation rates.
In our underlying model of systemic inflammation, bacterial load (LPS) drives the inflammatory response, and transitions were provoked by gradually increasing this variable. Yet even generalized models that do not include LPS still captured the loss of stability and movement between steady states driven by the self-stimulatory pro-inflammatory feedback loop, which is shown in Fig. 4 by the similar results produced regardless of whether LPS was included or excluded. This highlights that appropriate analysis of internal components of the inflammatory response can reveal a universal dynamics-based marker of the risk of transition, independent of the specific cue. This is an important conclusion because in a clinical setting the ultimate source of inflammation might not be known, or it might be difficult to quantify, or there could be multiple inflammatory instigators such as an injury and a subsequent infection. Because internal dynamics of the inflammatory response on its own contain sufficient information to predict transitions, similar dynamics would be expected in any gradually deteriorating inflammatory condition.
A high-level overview of the process for translating data into a warning signal is shown in Fig. 3. In this example, the generalized model contained only variables representing pro- and anti-inflammatory signaling. Of course, there is no single biomarker that precisely corresponds to these terms. Thus, a significant challenge remains in determining how to reconcile data from a much higher dimensional system with a simple generalized model. One approach is through high-dimensional data analysis. Clusters of gene expression values could be used to define the state variables of a generalized model, similar to how we previously leveraged microarray data from peripheral blood leukocytes to infer levels of pro- and anti-inflammatory signaling (Foteinou et al., 2009a). Similarly, principal components analysis (PCA) has been applied to cytokine data, which can be used to identify key aggregate drivers of inflammation in a reduced dimensional space (Nieman et al., 2012). Based on these types of approaches, one can imagine the inputs to a generalized model being high-level markers of system function rather than raw data of individual biomarkers.
Another important issue in terms of the data input into a generalized model is sampling frequency. Other than through noninvasive metrics like ECG and EEG, which would not be sufficient to assess the inflammatory state of a patient to the extent necessary for the proposed computational methods, high frequency data is generally not available. As shown in Fig. 5, performance increases as the sampling frequency decreases, but even with a relatively large sampling frequency, there is still predictive value in the eigenvalues. Depending on the speed of transition from one state to another, the required sampling frequency would likely change, and factors such as biological or experimental noise could alter requirements. However, the salient point is that sampling at reasonable rates has the potential to provide predictive information when evaluated in the context of a generalized model.
The concept of making predictions based on fairly simple models calibrated based on limited data is particularly important from a translational perspective. Systems biology represents an especially challenging field in terms of data availability. In general, complex systems biology models (including the detailed model of systemic inflammation discussed here) are not uniquely identifiable from available experimental data (Gutenkunst et al., 2007). The implication of this is that there may be multiple formulations of a model, in terms of both structure and parametrization, which can equally well fit a dataset, thus presenting a challenge in predictive applications of models. However, even this realization understates the true scope of the problem. A systems biology model may be fit to experimental data generated from multiple subjects under multiple different conditions, which is typically quite difficult as described above. A translational model must be fit to data generated from a single subject in a single condition, which is a far more difficult problem. Dynamics-based analysis of limited data in the context of a simple model has the potential to overcome these challenges by minimizing data required to predict transitions.
The identification of early warning signals preceding a transition is particularly useful if it provides sufficient time for intervention to potentially avert an undesirable regime shift (Biggs et al., 2009). For instance, if a warning signal for the onset of a disease was identified, but earlier treatment did not improve clinical outcomes, it would be of minor importance. The ultimate goal is not to simply detect a transition so that a patient could be more closely monitored and more rapidly treated, it is to detect a transition in sufficient time that the transition can be entirely averted through an appropriate intervention. In this regard, the results in Fig. 6 are interesting as they show the potential for precisely this type of prediction by the presence of a critical time window between the identification of an early warning signal and the “point of no return”. This presents the opportunity for earlier intervention to restore homeostasis, whereas an identical intervention would be unsuccessful at a later time point after the state variables of the system have begun to visibly move towards the unhealthy steady state.
The broad goal of data-driven prediction of the future state of patients is not new; ICU scoring systems have been designed and widely applied for this purpose. We draw a distinction between these traditional metrics, typically derived from simple combinations of commonly available clinical and demographic information, and newer dynamics-based methods that leverage advances in data collection towards more fine-grained predictions of imminent events. One class of approaches is based on the information content provided by very high dimensional measurements such as microarrays. Cobb et al. used microarrays to identify the onset of ventilator-associated pneumonia in trauma patients by identifying a subset of informative genes and using principal component analysis (PCA) to evaluate the movement of these genes from a normal recovering state to a pathological state representing pneumonia (Cobb et al., 2009). The identification of patients moving to different states in principal component space is similar to the concept of identifying transitions in physiological state space. This relationship is made more explicit in the work by Chen et al. which attempts to identify “dynamical network biomarkers” (small clusters of genes representing components that change early in the transition between steady states) driven by a theoretical foundation based on statistical approaches towards identifying bifurcations in systems with multiple steady states (Chen et al., 2012). These microarray-based approaches are significantly different than the method proposed here in that they require high-dimensional measurements and they do not assume any a priori network structures to inform their predictions. High throughput measurements have also shown the potential to allow for the identification of changes in dynamics preceding transitions in other domains; for instance, high-resolution imaging revealed spatial patterns in ventilation driven by bistability and competition between short-range and long-range interactions (Venegas et al., 2005).
In addition to techniques applying dynamical analysis of high throughput data to predicting physiological transitions, data that can be feasibly acquired in a very high frequency manner has also been found to be useful. One useful type of analysis in this regard is heart rate variability (HRV) derived from ECG data, which has been shown to be predictive of the onset of neonatal sepsis (Moorman et al., 2011) and potentially also sepsis in adults (Ahmad et al., 2009). Although the precise mechanistic origins of HRV are uncertain, it has been hypothesized that the characteristic patterns in HRV preceding the onset of sepsis may be the outcome of a dynamical system undergoing a bifurcation (Flower et al., 2010). If this is true, it lends credence to the hypothesis that stability analysis has a role in predicting this type of bifurcation in patient state. There has also been progress in the analysis of EEG data for predicting the onset of epileptic seizures. Despite challenges in validating preliminary studies and translating seizure prediction to clinical practice, appropriate analyses of this high-frequency data have shown the ability to reveal predictive information (Mormann et al., 2007). In total, experimental techniques that allow for either more frequent sampling or simultaneous measurements of large numbers of features enable dynamics-based approaches towards predicting future developments in patients’ states.
Significant challenges remain in model-based prediction of critical transitions between physiological steady states. Homeostasis, in reality, is not simply a single fixed point. There are both random and deterministic patterns in homeostasis. Circadian rhythms are a prominent source of homeostatic variability. Although circadian rhythms are often suppressed in critically ill patients (Lowry, 2009; Mundigler et al., 2002), there is still a need to very accurately distinguish between movement that is part of a healthy circadian rhythm and a pathological transition between steady states. Generalized models of periodic systems have been studied (Kuehn and Gross, 2011), but not yet applied in the prediction of critical transitions. Random noise is another confounding factor which makes the estimation of partial derivatives from limited data more difficult, although appropriate smoothing of the data may be sufficient to retain predictive power (Lade and Gross, 2012).
Current scientific literature contains examples of improved mathematical techniques for identifying critical transitions from limited data as well as novel experimental techniques to generate more and better physiological data. This convergence between theory and experimentation makes the prospect of predicting transitions between physiological steady states more and more plausible as time goes on, with potential applications in a wide range of systems. The work presented here represents a step forward towards achieving these translational goals in conditions related to systemic inflammation.
Supplementary Material
Highlights.
We predicted critical transitions between steady states in inflammation.
We made predictions based on data from a detailed model of systemic inflammation.
Smaller, high-level models were applied to evaluate stability.
These models required minimal data and assumptions.
Predicting transitions allowed for earlier and more successful interventions.
Acknowledgments
IPA acknowledges support from NIH GM082974. JDS and SEC are supported, in part, from NIH GM34695.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Jeremy D. Scheff, Email: jdscheff@gmail.com.
Steve E. Calvano, Email: calvanst@umdnj.edu.
Ioannis P. Androulakis, Email: yannis@rci.rutgers.edu.
References
- Ahmad S, Ramsay T, Huebsch L, Flanagan S, McDiarmid S, Batkin I, McIntyre L, Sundaresan SR, Maziak DE, Shamji FM, Hebert P, Fergusson D, Tinmouth A, Seely AJ. Continuous multi-parameter heart rate variability analysis heralds onset of sepsis in adults. PLoS One. 2009;4:e6642. doi: 10.1371/journal.pone.0006642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andreasen AS, Krabbe KS, Krogh-Madsen R, Taudorf S, Pedersen BK, Moller K. Human endotoxemia as a model of systemic inflammation. Curr Med Chem. 2008;15:1697–705. doi: 10.2174/092986708784872393. [DOI] [PubMed] [Google Scholar]
- Angus DC, Linde-Zwirble WT, Lidicker J, Clermont G, Carcillo J, Pinsky MR. Epidemiology of severe sepsis in the United States: analysis of incidence, outcome, and associated costs of care. Crit Care Med. 2001;29:1303–10. doi: 10.1097/00003246-200107000-00002. [DOI] [PubMed] [Google Scholar]
- Biggs R, Carpenter SR, Brock WA. Turning back from the brink: detecting an impending regime shift in time to avert it. Proc Natl Acad Sci U S A. 2009;106:826–31. doi: 10.1073/pnas.0811729106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchman TG. Physiologic stability and physiologic state. J Trauma. 1996;41:599–605. doi: 10.1097/00005373-199610000-00002. [DOI] [PubMed] [Google Scholar]
- Buchman TG. Novel representation of physiologic states during critical illness and recovery. Crit Care. 2010;14:127. doi: 10.1186/cc8868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter SR, Cole JJ, Pace ML, Batt R, Brock WA, Cline T, Coloso J, Hodgson JR, Kitchell JF, Seekell DA, Smith L, Weidel B. Early warnings of regime shifts: a whole-ecosystem experiment. Science. 2011;332:1079–82. doi: 10.1126/science.1203672. [DOI] [PubMed] [Google Scholar]
- Chen L, Liu R, Liu ZP, Li M, Aihara K. Detecting early-warning signals for sudden deterioration of complex diseases by dynamical network biomarkers. Sci Rep. 2012;2:342. doi: 10.1038/srep00342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cobb JP, Moore EE, Hayden DL, Minei JP, Cuschieri J, Yang J, Li Q, Lin N, Brownstein BH, Hennessy L, Mason PH, Schierding WS, Dixon DJ, Tompkins RG, Warren HS, Schoenfeld DA, Maier RV. Validation of the riboleukogram to detect ventilator-associated pneumonia after severe injury. Ann Surg. 2009;250:531–9. doi: 10.1097/SLA.0b013e3181b8fbd5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MJ. Use of models in identification and prediction of physiology in critically ill surgical patients. Br J Surg. 2012;99:487–93. doi: 10.1002/bjs.7798. [DOI] [PubMed] [Google Scholar]
- Dakos V, Carpenter SR, Brock WA, Ellison AM, Guttal V, Ives AR, Kefi S, Livina V, Seekell DA, van Nes EH, Scheffer M. Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS One. 2012;7:e41010. doi: 10.1371/journal.pone.0041010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flower AA, Moorman JR, Lake DE, Delos JB. Periodic heart rate decelerations in premature infants. Exp Biol Med (Maywood) 2010;235:531–8. doi: 10.1258/ebm.2010.009336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foteinou PT, Calvano SE, Lowry SF, Androulakis IP. Modeling endotoxin-induced systemic inflammation using an indirect response approach. Math Biosci. 2009a;217:27–42. doi: 10.1016/j.mbs.2008.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foteinou PT, Calvano SE, Lowry SF, Androulakis IP. In silico simulation of corticosteroids effect on an NFkB- dependent physicochemical model of systemic inflammation. PLoS One. 2009b;4:e4706. doi: 10.1371/journal.pone.0004706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foteinou PT, Calvano SE, Lowry SF, Androulakis IP. Multiscale model for the assessment of autonomic dysfunction in human endotoxemia. Physiol Genomics. 2010;42:5–19. doi: 10.1152/physiolgenomics.00184.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foteinou PT, Calvano SE, Lowry SF, Androulakis IP. A physiological model for autonomic heart rate regulation in human endotoxemia. Shock. 2011;35:229–39. doi: 10.1097/SHK.0b013e318200032b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross T, Feudel U. Generalized models as a universal approach to the analysis of nonlinear dynamical systems. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;73:016205. doi: 10.1103/PhysRevE.73.016205. [DOI] [PubMed] [Google Scholar]
- Gutenkunst RN, Waterfall JJ, Casey FP, Brown KS, Myers CR, Sethna JP. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput Biol. 2007;3:1871–78. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haimovich B, Reddell MT, Calvano JE, Calvano SE, Macor MM, Coyle SM, Lowry SF. A novel model of common Toll-like receptor 4- and injury-induced transcriptional themes in human leukocytes. Crit Care. 2010;14:R177. doi: 10.1186/cc9283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuehn C. A mathematical framework for critical transitions: Bifurcations, fast-slow systems and stochastic dynamics. Physica D. 2011;240:1020–35. [Google Scholar]
- Kuehn C, Gross T. Nonlocal generalized models of predator-prey systems. 2011 http://arxiv.org/abs/1105.3662.
- Kuehn C, Siegmund S, Gross T. Dynamical analysis of evolution equations in generalized models. IMA J Appl Math 2012 [Google Scholar]
- Lade SJ, Gross T. Early warning signals for critical transitions: a generalized modeling approach. PLoS Comput Biol. 2012;8:e1002360. doi: 10.1371/journal.pcbi.1002360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowry SF. Human endotoxemia: a model for mechanistic insight and therapeutic targeting. Shock. 2005;24(Suppl 1):94–100. doi: 10.1097/01.shk.0000191340.23907.a1. [DOI] [PubMed] [Google Scholar]
- Lowry SF. The stressed host response to infection: the disruptive signals and rhythms of systemic inflammation. Surg Clin North Am. 2009;89:311–26. vii. doi: 10.1016/j.suc.2008.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moorman JR, Carlo WA, Kattwinkel J, Schelonka RL, Porcelli PJ, Navarrete CT, Bancalari E, Aschner JL, Whit Walker M, Perez JA, Palmer C, Stukenborg GJ, Lake DE, Michael O’Shea T. Mortality reduction by heart rate characteristic monitoring in very low birth weight neonates: a randomized trial. J Pediatr. 2011;159:900–6. e1. doi: 10.1016/j.jpeds.2011.06.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mormann F, Andrzejak RG, Elger CE, Lehnertz K. Seizure prediction: the long and winding road. Brain. 2007;130:314–33. doi: 10.1093/brain/awl241. [DOI] [PubMed] [Google Scholar]
- Mundigler G, Delle-Karth G, Koreny M, Zehetgruber M, Steindl-Munda P, Marktl W, Ferti L, Siostrzonek P. Impaired circadian rhythm of melatonin secretion in sedated critically ill patients with severe sepsis. Crit Care Med. 2002;30:536–40. doi: 10.1097/00003246-200203000-00007. [DOI] [PubMed] [Google Scholar]
- Nieman G, Brown D, Sarkar J, Kubiak B, Ziraldo C, Dutta-Moscato J, Vieau C, Barclay D, Gatto L, Maier K, Constantine G, Billiar TR, Zamora R, Mi Q, Chang S, Vodovotz Y. A two-compartment mathematical model of endotoxin-induced inflammatory and physiologic alterations in swine. Crit Care Med. 2012;40:1052–63. doi: 10.1097/CCM.0b013e31823e986a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ridley S. The recognition and early management of critical illness. Ann R Coll Surg Engl. 2005;87:315–22. doi: 10.1308/003588405X60669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheff JD, Calvano SE, Lowry SF, Androulakis IP. Modeling the influence of circadian rhythms on the acute inflammatory response. J Theor Biol. 2010;264:1068–76. doi: 10.1016/j.jtbi.2010.03.026. [DOI] [PubMed] [Google Scholar]
- Scheff JD, Mavroudis PD, Calvano SE, Lowry SF, Androulakis IP. Modeling autonomic regulation of cardiac function and heart rate variability in human endotoxemia. Physiol Genomics. 2011;43:951–64. doi: 10.1152/physiolgenomics.00040.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheffer M, Bascompte J, Brock WA, Brovkin V, Carpenter SR, Dakos V, Held H, van Nes EH, Rietkerk M, Sugihara G. Early-warning signals for critical transitions. Nature. 2009;461:53–9. doi: 10.1038/nature08227. [DOI] [PubMed] [Google Scholar]
- Shanker BA, Coyle SM, Reddell MT, Choi CW, Calvano J, Macor MA, Calvano SE, Lowry SF. Modeling the human injury response. Journal of the American College of Surgeons. 2010;211:S53–S54. [Google Scholar]
- Venegas JG, Winkler T, Musch G, Vidal Melo MF, Layfield D, Tgavalekos N, Fischman AJ, Callahan RJ, Bellani G, Harris RS. Self-organized patchiness in asthma as a prelude to catastrophic shifts. Nature. 2005;434:777–82. doi: 10.1038/nature03490. [DOI] [PubMed] [Google Scholar]
- Vodovotz Y, Constantine G, Rubin J, Csete M, Voit EO, An G. Mechanistic simulations of inflammation: current state and future prospects. Math Biosci. 2009;217:1–10. doi: 10.1016/j.mbs.2008.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.