Two-dimensional Raman-terahertz spectroscopy of water

Significance

The discussion about the structure of water becomes increasingly more controversial, and appears to be stuck because the major techniques used to study it (small-angle X-ray scattering emphasizing the structure, multidimensional infrared spectroscopy emphasizing the dynamics, and molecular dynamics simulations using questionable force fields) do not seem to provide mutually converging results. This calls for a different experimental approach, which we offer here with 2D Raman-terahertz spectroscopy. The work extends multidimensional vibrational spectroscopy into the far-IR regime where thermally excited soft modes are found that are directly responsible for molecular dynamics (in contrast with the high-frequency spectator modes investigated in 2D-IR spectroscopy, which per se are quiet at room temperature and sense the environment only indirectly).

Abstract

Two-dimensional Raman-terahertz (THz) spectroscopy is presented as a multidimensional spectroscopy directly in the far-IR regime. The method is used to explore the dynamics of the collective intermolecular modes of liquid water at ambient temperatures that emerge from the hydrogen-bond networks water forming. Two-dimensional Raman-THz spectroscopy interrogates these modes twice and as such can elucidate couplings and inhomogeneities of the various degrees of freedoms. An echo in the 2D Raman-THz response is indeed identified, indicating that a heterogeneous distribution of hydrogen-bond networks exists, albeit only on a very short 100-fs timescale. This timescale appears to be too short to be compatible with more extended, persistent structures assumed within a two-state model of water.

Water forms local structures due to the directionality of hydrogen bonding, and it is generally accepted that the emerging hydrogen-bond network is ultimately responsible for the many anomalies in the macroscopic thermodynamic properties of water (1). The consequences of that statement are however still discussed in an extremely controversial manner (2–11). For example, an increasing scattering amplitude for small angles in X-ray scattering experiments of room-temperature water has been interpreted in terms of the so-called “two-state model” of water with patches of a low-density liquid (LDL) and a high-density (HDL) liquid (5), whereas other researchers have interpreted essentially the same experimental result as continuous––in contrast with bimodal––density fluctuations, as they are expected from the isothermal compressibility (6). From a theoretical point of view, the hypothesized liquid-to-liquid phase transition in the deeply supercooled regime is discussed as either separating two metastable thermodynamic states of the liquid (2, 3, 8, 10) or as an artifact from nonequilibrated molecular dynamics simulations (7, 11). These two problems are related because two-state behavior at ambient temperatures is thought to be a reminiscence of the liquid-to-liquid phase transition in the deeply supercooled regime. It is currently not clear whether a liquid-to-liquid phase transition exists [neither for computer models (2, 3, 7, 8, 10, 11) nor for real water], and even if it does exist, it is not clear whether two-state behavior survives into ambient conditions. To provide unique experimental input to these types of questions, we present a 2D spectroscopy directly in the low-frequency terahertz (THz) regime, where the intermolecular motions of water are detected. The method can elucidate the heterogeneity and lifetimes of the hydrogen-bond networks of liquid water.

In contrast with any X-ray experiment performed so far (4–6), all of which take essentially an instantaneous snapshot (10), multidimensional IR spectroscopies (12–17), as well as related hole-burning or photon echo experiments (18–21), interrogate the molecular system at least twice and thus can deduce time correlations of interconverting structures. These experiments have been performed on the OH (or its deuterated version OD) intramolecular stretch vibration of water, which serves as a local sensor making use of the fact that its frequency is a sensitive probe of the strength of hydrogen bonding to the environment (22–24). Due to the multiple interactions with the sample, these spectroscopic techniques can reveal the inhomogeneous broadening of the OH or OD stretch vibration and thus the heterogeneity in hydrogen-bond strengths. Water as a liquid is of course not static, as such the inhomogeneous broadening is not static, but it is nevertheless meaningful to define an inhomogeneity on a certain timescale. It is very well established from these IR experiments that the OH or OD stretch vibration of liquid water is inhomogeneously broadened on an ∼1-ps timescale, which is interpreted as the typical lifetime of the hydrogen bonds.

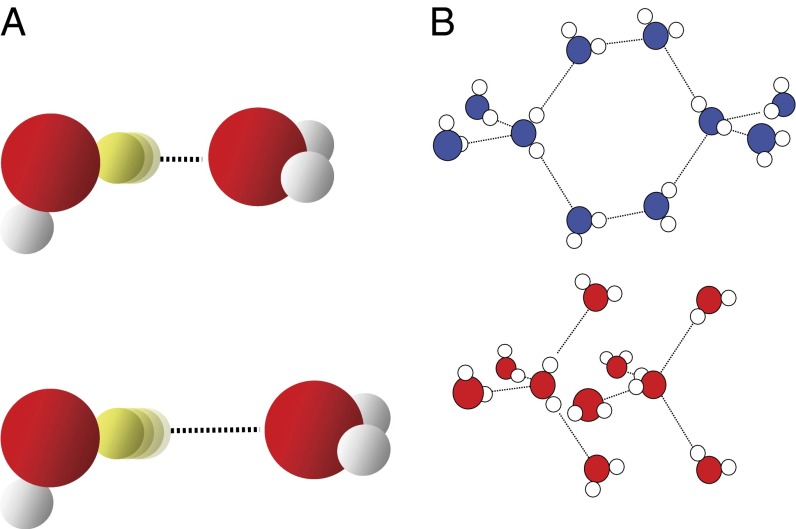
At this point, we need to introduce the concept of hierarchy of inhomogeneities. To that end, consider water dimers with short and long hydrogen bonds shown in Fig. 1A. The length or strength of a hydrogen bond modulates the OH stretch potential and as such the OH stretch vibrational frequency (22–24). The nonlinear experiments mentioned above (12–21) would thus interpret the OH stretch vibration as inhomogeneously broadened. However, now consider these two structures to be just the turning points of a lower-frequency intermolecular hydrogen-bond stretch vibration. If the water dimers were in the gas phase, literally as depicted in Fig. 1A, that hydrogen-bond stretch vibration per se would be perfectly homogeneous, and yet, a nonlinear IR experiment on the OH stretch vibration would misinterpret the system as inhomogeneously broadened on the timescale of the hydrogen-bond stretch vibration. Indeed, the hydrogen-bond stretch vibration has been observed as modulation in photon echo experiments on the OH stretch vibration (21) as well as in related simulation works (22, 23). When we talk about inhomogeneous water structures, we have in mind more extended hydrogen-bond networks, as for example those proposed for LDL and HDL water (Fig. 1B) (3). These hydrogen-bond networks will not necessarily differ greatly with respect to the OH stretch vibrations, but might with respect to the collective intermolecular modes, which include the hydrogen-bond stretch vibration at about 6 THz (i.e., 200 cm⁻¹) and the hydrogen-bond bend vibration at about 2 THz (i.e., 60 cm⁻¹), the latter of which has been shown to extend over three solvation shells by ab initio molecular dynamics (MD) simulations (25). Both 1D-Raman (26–31) and 1D-THz (27, 32) spectroscopy in this low-frequency range have been used extensively to study pure water as well as water with various solutes. In fact, a recent 1D-Raman experiment of supercooled water has been fitted in terms of two spectrally distinguishable components underneath the 200-cm⁻¹ band (31), which coincide with corresponding bands in high- and low-density amorphous ice (33). The fitting was performed using a line-shape analysis (which is not trivial including mode coupling theory) (31), but to unambiguously unravel that type of inhomogeneity, one needs a multidimensional spectroscopy of the low-frequency intermolecular modes directly.

Fig. 1.

Hierarchy of inhomogeneities. (A) Two configurations of a single hydrogen bond and (B) two extended hydrogen-bond networks proposed to explain LDL (Upper) and HDL (Lower) water (3).

With exactly that objective in mind, 2D Raman spectroscopy was proposed by Tanimura and Mukamel quite some time ago (34). That proposal initiated a great deal of theoretical (35–42) work. The experimental implementation, however, turned out to be exceptionally difficult (43–48), because cascaded third-order processes contaminate the desired fifth-order Raman signal (49). The fifth-order Raman signal could be isolated for certain liquids like CS₂ or formamide (44–48), but not yet for water due to its very weak Raman cross-section. On the other hand, 2D THz spectroscopy has also been demonstrated (50, 51), but due to the limited THz pulse energies that are currently available it is so far applicable only to low-lying strong electronic resonances with huge collective transition dipoles. Based on MD simulations, we have recently proposed a hybrid 2D Raman-THz spectroscopy (52, 53), which circumvents the technological limitations of both 2D Raman and 2D THz spectroscopy.

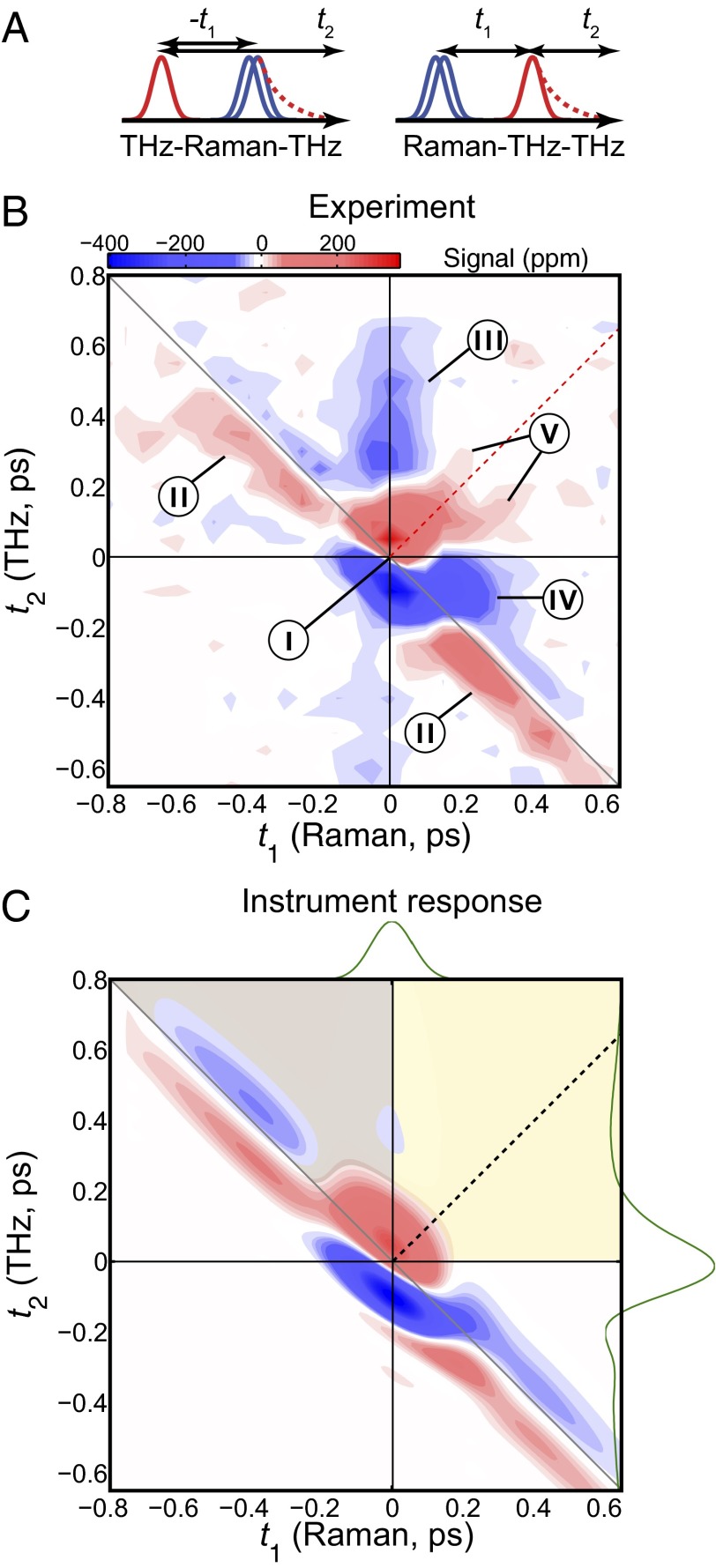
In 2D Raman-THz spectroscopy, two short laser pulses hit the sample: a nonresonant 800-nm pulse and a resonant half-cycle THz pulse. The first laser pulse excites a coherence of an intermolecular vibrational mode through either a Raman or a direct THz interaction, depending on which of these pulses hits the sample first. After time t₁, the second pulse (THz or Raman, respectively) interrogates the molecular system a second time, and the resulting coherence state is read out at time 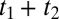by the emission of a THz field. We will refer to the two possibilities as the Raman-THz-THz and THz-Raman-THz pulse sequences, respectively (Fig. 2A). Both pulse sequences, as well as the Raman-Raman-Raman pulse sequence of 2D Raman spectroscopy (34), may in principle induce the same coherence pathways, albeit with varying probabilities due to the different selection rules of Raman and THz interactions (53). The most significant aspect of any of these pulse sequences is the switching of coherences induced by the second pulse, which ultimately allows one to correlate various degrees of freedom with each other. Most importantly in the context of the discussion above, if the spectrum of collective intermolecular modes is inhomogeneously broadened due to hydrogen-bond network patterns that are stable on the timescale of the experiment, the second pulse may rephase the coherence induced by the first pulse, giving rise to an echo (39).

Fig. 2.

Two-dimensional Raman-THz response of water. (A) Pulse sequences and (B) the experimental 2D Raman-THz signal of water. The intensity scale is given in parts per million (ppm) with respect to the maximum of the THz pulse field transmitted through the water sample. The red dotted line indicates the diagonal 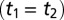, where an echo is potentially expected. The origin 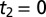is defined as the peak of the transmitted THz pulse, which is also measured during scanning. The origin 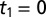has been adjusted to fit with the instrument response function. Labels I–V indicate features discussed in the text. (C) The IRF. 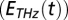Raman and input THz pulses have been determined experimentally and are shown as green lines on the top and left side, respectively (see SI Materials and Methods for details). The black dotted line indicates the diagonal, the gray shaded area is where the THz-Raman-THz sequence is expected, and the yellow-shaded area is where the Raman-THz-THz sequence is expected.

Results

In the present work, we measured the 2D Raman-THz response of liquid water at ambient conditions. Conceptually, our experimental setup is not different from an optical-pump-THz-probe experiment (54, 55), just that the Raman pump pulse is nonresonant and as such excites a vibrational coherence. The setup had to be optimized for a high detection sensitivity (the peak of the emitted third-order field is only 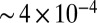of that of the input THz pulse) and low dispersion for a clean instrument response function (IRF; see Materials and Methods for details). The half-cycle THz pulses with a duration of ∼140 fs (i.e., the FWHM of the positive spike) peak at ∼1.4 THz and extend from ∼0.3 THz to ∼6 THz (200 cm⁻¹) with an almost flat phase across the spectrum (Fig. S1A), and thus cover the hydrogen-bond bend mode at 60 cm⁻¹ and a significant part of the hydrogen-bond stretch mode at 200 cm⁻¹. They however miss the librational band at 600 cm⁻¹. The Raman pump pulses with a length of 110 fs FWHM (Fig. S1B) cover a somewhat larger frequency range up to ∼9 THz (300 cm⁻¹).

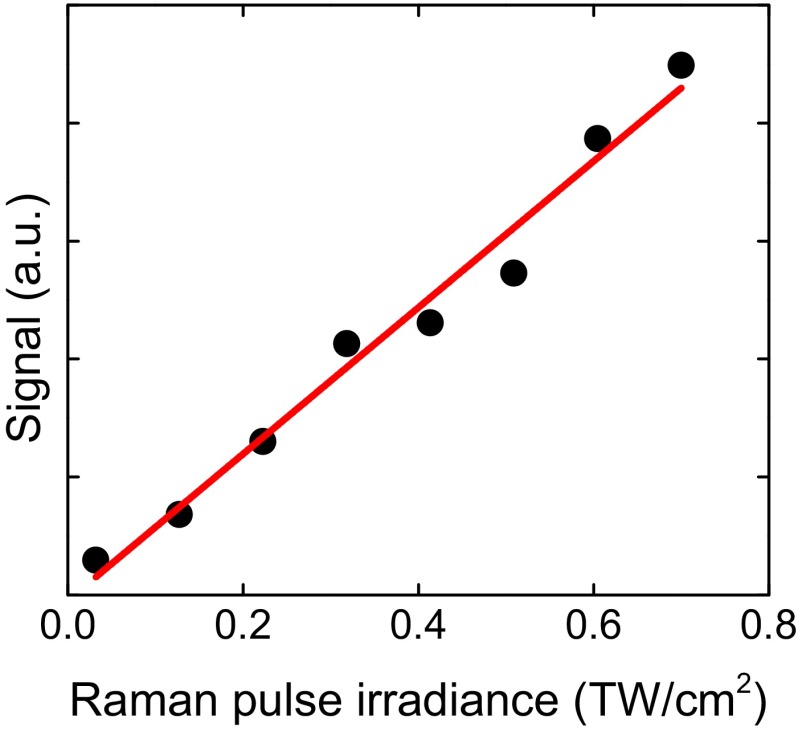
Fig. 2B shows the 2D Raman-THz response of liquid water, which reveals a rich set of features with good signal-to-noise ratio. Before discussing the 2D Raman-THz signal in detail, we need to investigate its dependence on the Raman pump-pulse irradiance. The high irradiance required to obtain a measurable signal is a major concern because it may photoionize water and lead to the generation of solvated electrons, which in turn may interact with the sample and/or with the probing THz pulses and lead to an unwanted signal. As the generation of solvated electrons is a multiphoton process, its appearance depends highly nonlinearly on pump-pulse intensity. The 2D Raman-THz signal, in contrast, has two field interactions with the Raman pulse and therefore should depend only linearly on the Raman pulse intensity. We thus critically verified the linearity of the signal by varying the Raman pulse intensity with an adjustable neutral density filter. The result in Fig. 3 indeed reveals a linear behavior in a regime below ca. 1 TW/cm², indicating that the signal is the desired 2D Raman-THz response. When increasing the Raman pump-pulse irradiance beyond that regime, we do observe a signal that depends nonlinearly on the pump irradiance (Fig. S2A) and looks qualitatively very different from the Raman signal. This signal is due to the solvated electrons upon photoionization of water with a threshold of above 1 TW/cm² for 800-nm pulses (as a side remark, we note that photoionization of neat water probed by THz radiation is in itself an interesting result, which will be investigated in detail in a separate publication). We also explored the polarization dependence of the signal. Whereas the 2D Raman-THz signal in the linear regime has a pronounced polarization effect (Fig. S2B), as expected for a Raman effect, the solvated electron signal at higher pump fluency is polarization independent, because the solvated electron is essentially spherical. We thus conclude that it is possible to detect the 2D Raman-THz signal that is not contaminated by the presence of solvated electrons in the water sample. The 2D Raman-THz response of Fig. 2B has been measured at a pump irradiance of 0.6 TW/cm², which is safely within the linear regime.

Fig. 3.

Raman-pulse irradiance dependency of the peak of the 2D Raman-THz signal.

For the 2D Raman-THz response shown in Fig. 2B, we control two delay stages in the experimental setup (Materials and Methods): Delay 1 scans the delay between the Raman and THz pulses at the sample t₁, and delay 2 scans the delay between the THz input pulse at the sample and the emitted field t₂. The two possible pulse sequences for the 2D Raman-THz signal (53) are shown in Fig. 2A. In the experiment we scan t₁ from negative to positive times, which switches the signal from the THz-Raman-THz sequence to the Raman-THz-THz sequence. The time t₂ is defined as the delay between the THz input pulse and the emitted field, and not necessarily between the second pulse and the emitted field, so that 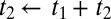for . 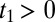Therefore, the Raman-THz-THz sequence appears in the upper-right quadrant with and 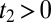(shaded in yellow in Fig. 2B), whereas the THz-Raman-THz sequence appears in the upper triangle of the upper-left quadrant with 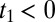and 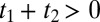(shaded in gray in Fig. 2B).

The signal extends beyond these regions, because the molecular response function 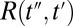is convoluted with laser pulses that are not infinitesimally short:

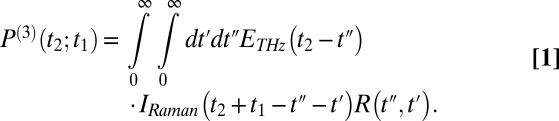Here, 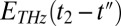is the THz pulse in the sample, 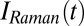the intensity profile of the Raman pump pulse, and t₁ accounts for the experimentally controlled delay time between the peaks of the two pulses (Materials and Methods). The molecular response function 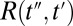is the property we ultimately want to measure because it contains the molecular information, and also because it can be compared with all-atom MD simulations (52, 53). To extract 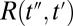, we need to precisely know the input THz and Raman pulses entering Eq. 1, as well as how the emitted field propagates to the detection crystal (56) (Fig. S3). For the latter, we describe the generated third-order field as a time derivative of the third-order polarization:

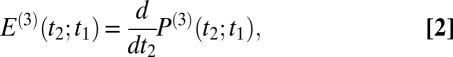which is a good approximation for the most simple case when dispersion and absorption can be neglected and the process is quasi–phase-matched (57, 58). We subsequently introduce the effect of dispersion and absorption of the water jet via a linear transfer function in the frequency domain. That transfer function can be combined with those of the imaging optics and the detection crystal (56, 59), revealing a total transfer function 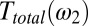, with which we obtain for the detected field

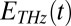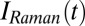The input pulses and , as well as the transfer function 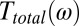, have been determined experimentally, as discussed in detail in SI Materials and Methods (Figs. S1, S4, and S5). Whereas methods to invert Eqs. 1–3 have been worked out (56, 58), we chose here a forward strategy, i.e., simulate the measured signal from a given response function 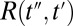, so future theoretical work can still be compared with our experiment.

Evaluating Eqs. 1–3 for a hypothetical instantaneous response function 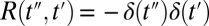reveals the IRF (Fig. 2C) of the setup, for which the integrals in the convolution Eq. 1 disappear:

The third-order polarization will then be a product of the two pulses, which extends along the antidiagonal in the 2D representation of Fig. 2C due to the argument 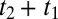in 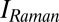, reflecting the arrangement of delay lines in the experimental setup (Materials and Methods). The time derivative Eq. 2 is responsible for the minus–plus (blue–red) pattern in the IRF in the t₂ direction. Eq. 3 stretches it toward positive t₂ (because T_total is causal) with only a little bit of ringing (which is the reward for keeping dispersion low in the thin sample jet and generation and detection crystals as well as the high-aperture imaging optics). Note that the IRF stays quite narrow in the diagonal direction with 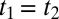, because the Raman pump pulse is significantly shorter than the THz pulse and because it is clean without wings (Fig. S1 and the pulses shown in green in Fig. 2C). This feature is a manifestation of the fact that the time resolution of an optical-pump-THz-probe experiment is not limited by the THz pulse length, but rather by the pump pulse and the bandwidth of the gated detection process (58).

Discussion

Certain parts of the experimental data (Fig. 2B) very closely resemble the IRF (Fig. 2C), indicating that we can determine the laser pulses and the transfer function with high accuracy. Any feature in the experimental data that is observed also in the IRF, i.e., in particular the spikes around 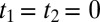labeled as “I” in Fig. 2B and the antidiagonal ridge labeled as “II,” originates from a part of the water response that is much faster than our laser pulses. Presumably, this fast response is due to the electronic polarizability as well as librational motion of water with a typical frequency of 600 cm⁻¹. In contrast, any feature beyond the IRF originates from water response that is slow enough to be observed with our time resolution. Three such features labeled III–V can indeed be identified. Features III and IV extend along the positive t₁ and t₂ axes, and the simulation results from ref. 52 suggest that these features essentially reflect the 1D Raman and 1D THz responses, respectively. The long time relaxation tail of the 1D-Raman response decays on a typical timescale of 350 fs at room temperature (albeit in a nonexponential manner) (26), in reasonable agreement with the decay of features III. The long time relaxation tail of the 1D-THz response, on the other hand, decays much slower with 8 ps (27). Due to the time derivative in Eq. 2, we are very insensitive to such slow processes, so feature IV probably reflects some of the oscillatory contribution of the 1D-THz response. It has also been shown in ref. 52 that the 2D response is not just a simple product of these 1D responses; as such, the 2D response contains additional information.

In this regard, the most interesting is feature V, which extends along the diagonal 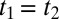in the upper-right quadrant and contains additional substructure. Fig. 4 highlights that feature by showing a cut along the diagonal with the decay of the experimental data (red) being slower than that of the IRF (black). The diagonal 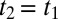is where an echo is expected. Echoes appear when a multimode system gets synchronized twice by two perturbations separated by a time t₁. Whenever the character of the various modes persists for sufficiently long time and thus keeps a memory about their oscillation frequency, as they do for a heterogeneous set of oscillators, an echo is emitted at 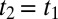when the modes rephase upon a second perturbation. That is, the various modes run out of phase during time t₁, and rephase during time t₂ because the second perturbation may “invert the coherence.” As such, echoes are indicative for inhomogeneous broadening. The process of de- and rephasing is relatively intuitive to visualize in the case of the spins echo (Hahn echo) (60) as well as for electronic and vibrational photon echoes (21, 61–63), but the concept is much more general; for example, echoes upon multiple temperature jumps have been proposed as well (64, 65). Also in the context of 2D Raman spectroscopy, echoes have been discussed extensively (36, 39, 40). In comparison with conventional photon echo spectroscopy (21, 61–63), it is less obvious to identify the coherence pathways that invert the coherence upon the second pulse, but they do exist (39). Traces of a photon echo indeed appear in simulations of the 2D Raman spectroscopy of water as a ridge along the diagonal, but only when approximating the signal with instantaneous or quenched normal modes (figure 3 in ref. 36). The mechanism of the flow of coherence pathways is the same for 2D Raman and 2D Raman-THz spectroscopy, albeit with different selection rules. We therefore propose that feature V is related to an echo, which in contrast with the discussion of ref. 53 would actually be more evident for the Raman-THz-THz pulse sequence. Note, however, that the response functions reported in refs. 52, 53, based on a simple nonpolarizable point charge water model, cannot reproduce the experimental results, for reasons that are currently not clear.

Fig. 4.

Cuts along the diagonal for the Raman-THz-THz pulse sequence, red for the experimental data and black for the IRF. The data beyond 0.3 ps give an idea of the signal-to-noise ratio.

With that in mind, we turn to a discussion of the implications of these results in the context of the introduction. The appearance of an echo hints toward an inhomogeneous distribution among the collective intermolecular hydrogen-bond modes. Certainly, verifying this interpretation needs further theoretical attention, but if it turns out to be correct, this inhomogeneity would live for only a few hundred femtoseconds, in fair agreement with conclusions drawn from 3D-IR spectroscopy of the OD stretch vibration of water (17). In particular, it would live significantly shorter than the typical lifetime of a single hydrogen bond of about 1 ps, which has been concluded from 2D-IR and related experiments on the OH-stretch (or OD-stretch) vibration (12–21). Not unreasonably, the lifetime of a single hydrogen bond seems to be an upper limit for the lifetime of more extended hydrogen-bond networks. In ref. 25, the 200-cm⁻¹ band has been dissected into the various hydrogen-bond stretching modes of a tetrahedral water cluster, which is the most common structural motive in liquid water up to the first solvation shell. Three distinguishable subbands have been identified, a situation which would indeed give rise to an echo. If the lifetime of a single hydrogen bond is 1 ps, then the lifetime of a tetrahedral water cluster with four hydrogen bonds can be as short as 250 fs, assuming that the various hydrogen bonds evolve statistically independently from each other. That simple estimate reveals a timescale that is in good agreement with the echo decay time we observe in Fig. 4. In essence, the low-frequency modes are quite fragile.

The 100-fs timescale appears to be too short to be compatible with more extended, persistent structures assumed within a two-state model of water, as they have been deduced from X-ray scattering experiments (5). Either such extended structures do not exist at room temperature, or their low-frequency intermolecular spectra are so similar that they cannot be distinguished spectroscopically. Simulation work along the lines of refs. 52, 53 will be able to answer questions of that kind.

In conclusion, we believe that 2D Raman-THz spectroscopy, which we have shown to be experimentally accessible with good signal-to-noise ratio (Fig. 2B), is the most decisive spectroscopy as of today of the intermolecular structure and dynamics of liquid water. In combination with refined computer models of water, it will lead to a better understanding of the microscopic structure of water. Shorter Raman and THz pulses would certainly be desirable in an improved instrument using, e.g., a plasma generation and detection scheme (66) to fully cover the 200-cm⁻¹- band as well as the librational band. Furthermore, the 2D Raman-THz response of supercooled water would be rewarding because the dynamics is going to be slower and thus easier to measure (16), because two-state behavior––if it exists at all––will be more pronounced, and because evidence for the existence of two subbands underneath the hydrogen-bond stretching band at 200 cm⁻¹ has recently been given by 1D-Raman spectroscopy (31). Finally, an extension of this work to study solute–water interactions will be most interesting; for example, proteins (32) or salts (29) have been shown to modify the THz or Raman water spectrum, respectively.

Materials and Methods

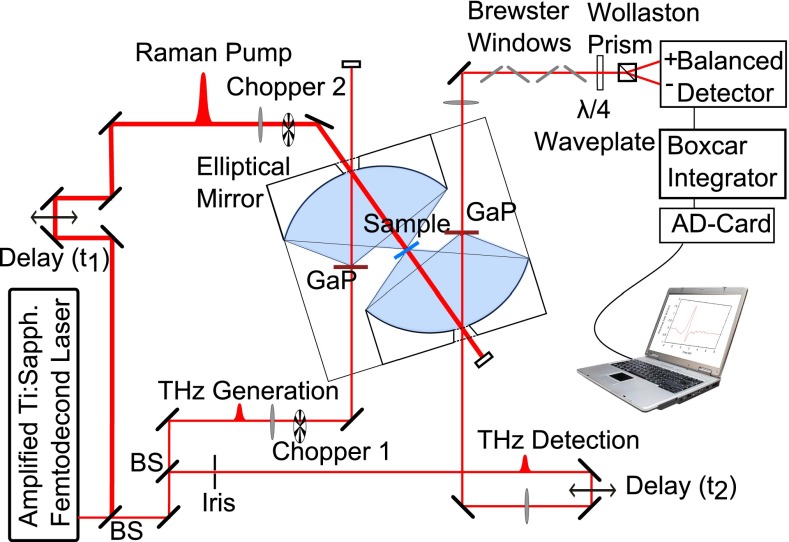
The setup used in the 2D Raman-THz experiment is essentially a standard optical-pump–THz-probe spectrometer (Fig. 5) (54). A commercial Ti:sapphire oscillator and a chirped-pulse amplifier (Spectra Physics) delivered 110-fs, 800-nm pulses at 5-kHz repetition rate. With beamsplitters, a small portion of the laser output was split in two parts that are used to generate and detect the THz pulses by optical rectification and electrooptic sampling, respectively (55). We used two identical 0.1-mm-thick (110) GaP crystals for both processes. Pulses with 10 μJ of energy were focused onto the generation crystal with a spot size of 50 μm (intensity just below the damage threshold). The THz pulses from the GaP generation crystal were collected and focused onto the sample and then onto the detection crystal by two custom-made elliptical aluminum mirrors (2f = 83 mm). This arrangement has a numerical aperture of about 1 and provides a near-diffraction limited spot size of 200 μm for the THz field at the sample and at the detection crystal. The detecting 800-nm beam passed through an iris for spatial mode cleaning, and was subsequently coupled to the detecting crystal via an optical delay stage (t₂) and through a small hole in the second elliptical mirror. It then passed through four ZnSe Brewster-angle windows, a quarter-wave plate, and a Wollaston polarizer followed by two balanced photodiodes detecting the difference between s- and p polarizations in the measuring 800-nm beam. The sensitivity of the electrooptic detection was enhanced by introducing the four properly mounted ZnSe Brewster windows before the quarter-wave plate. This arrangement increases the ratio between the measured signal and the amount of light on the detector (the details of this detection enhancement will be discussed in a separate publication). The photodiode signals were then amplified, integrated in a boxcar integrator, and recorded in a computer on a single-shot basis.

Fig. 5.

2D Raman-THz experimental setup.

Approximately 200 μJ per pulse of the laser output was used as Raman pump pulses, which were passed through an optical delay stage controlling t₁. The Raman pulses were focused with a lens (f = 1 m) and coupled onto the sample collinearly with the THz pulses through a small hole in the first elliptical mirror. The spot size at the sample was adjusted to about 250 μm by keeping the focus ∼8 cm after the sample. An autocorrelation measurement (using an AC-1PS autocorrelator from UVisIR Inc.) and a Gaussian fit with an FWHM of about 150 fs of the Raman pulse are shown in Fig. S1B. Assuming Gaussian pulses, this corresponds to a pulse duration of ∼110 fs FWHM. Importantly, the Raman pulses are very clean with essentially no wings. If wings were present, they would show up in the diagonal cut of the IRF in Fig. 4. The same pulse was also used to generate the THz pulse in the first GaP crystal.

The Raman pump pulses were modulated at half of the laser frequency and the THz creation pulses at a quarter of the laser frequency using two optical choppers. Electrooptic sampling directly measures the THz field rather than its intensity. The transmitted THz field and the generated 2D Raman-THz field are additive and thus the 2D Raman-THz signal could be calculated as a difference between pumped and unpumped sample:

All four types of data were recorded independently so that the THz pulse itself was also measured constantly during scanning:

The setup was optimized for a high detection sensitivity to be able to measure the very small 2D Raman-THz signal. Further, we optimized the setup for low dispersion to obtain as short and clean an IRF as possible (Fig. 2C). Measures to achieve a high sensitivity include the high repetition rate of the laser system (5 kHz), the ZnSe Brewster windows, high numerical aperture optics, careful positioning of the crystals and water sample at the foci of the setup, as well as the long scanning time for the 2D data set of Fig. 2B of about 2 wk. The IRF was optimized by using thin 100-μm GaP crystals, which give an almost perfect half-cycle THz pulse with hardly any ringing (Fig. S1A) that would have complicated the discussion of the difference between IRF and water response significantly (Figs. 2 and 4). GaP produces significantly less THz light than the more commonly used ZnTe, making it harder to measure the small signal, but we considered the cleanness of the pulses to be most important. Finally, the high-aperture optics proves to be relevant as well because it provides a very flat transmission function down to quite low frequencies of ∼0.3 THz (Fig. S5B). We verified that the signal is not contaminated by a 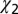-response from the water-jet surfaces.

The water sample (triple-distilled water) flowed in a windowless 40-μm-thick gravity-driven jet to avoid any extra artifacts from windows as well as any accumulative thermal effects in the excitation volume. The arrival time of the THz pulse Eq. S6 was used as a measure of the thickness of that jet. Modulation of the thickness of the jet during the time of data scanning due to water evaporation, which changed the water level in the reservoir and hence the pressure of the water delivered to the jet, was controlled by continuously adding small amounts of water with a syringe pump. The THz section of the setup was sealed in a nitrogen-purged box to remove water vapor. All measurements were performed at room temperature.