Optimal control of gene expression for fast proteome adaptation to environmental change

Significance

For rapid growth in different environments, bacterial cells must perpetually adapt their enzyme levels to efficiently metabolize different sets of nutrients in different surroundings. When environmental shifts are frequent and swift, the bacteria must rapidly adjust the levels of all their different proteins—their proteome. We have theoretically identified the best gene-expression strategy for rapid proteome adjustment upon environmental change and found simple, general descriptions for the dynamic change of the proteome composition and the adaptation time following such optimal strategy. Our work predicts important aspects of bacterial physiology and connects it with the population genetics and evolution of bacterial populations. Our theory is relevant to understanding antibiotic resistance and the development of strategies for maximal biomass production.

Abstract

Bacterial populations growing in a changing world must adjust their proteome composition in response to alterations in the environment. Rapid proteome responses to growth medium changes are expected to increase the average growth rate and fitness value of these populations. Little is known about the dynamics of proteome change, e.g., whether bacteria use optimal strategies of gene expression for rapid proteome adjustments and if there are lower bounds to the time of proteome adaptation in response to growth medium changes. To begin answering these types of questions, we modeled growing bacteria as stoichiometrically coupled networks of metabolic pathways. These are balanced during steady-state growth in a constant environment but are initially unbalanced after rapid medium shifts due to a shortage of enzymes required at higher concentrations in the new environment. We identified an optimal strategy for rapid proteome adjustment in the absence of protein degradation and found a lower bound to the time of proteome adaptation after medium shifts. This minimal time is determined by the ratio between the Kullback–Leibler distance from the pre- to the postshift proteome and the postshift steady-state growth rate. The dynamics of optimally controlled proteome adaptation has a simple analytical solution. We used detailed numerical modeling to demonstrate that realistic bacterial control systems can emulate this optimal strategy for rapid proteome adaptation. Our results may provide a conceptual link between the physiology and population genetics of growing bacteria.

A challenging problem in bacterial physiology is to understand how bacteria adapt to changes in nutritional supply to grow rapidly in different environments (1). More than 50 y ago, the remarkable observation was made that the cell mass and intracellular composition of protein, RNA, and DNA appeared to be determined by the steady-state growth rate of bacterial population rather than by the nutritional composition of the growth medium (2). The work of Schaechter et al. (2) and subsequent seminal works on DNA replication (e.g., ref. 3) led to the concept of growth rate-dependent control of physiological parameters (4), later shown to be an approximation (1, 5). These early observations along with later determinations of the varying components of bacterial cells growing in changing environments (e.g., ref. 5) have contributed greatly to today’s quantitative bacterial physiology (ref. 6 and references therein).

The linear relation between growth rate and RNA content found by Schaechter et al. (2) implies that the growth rate is a linear function of the ribosome content of growing bacteria (4, 5). To this first “growth law” have recently been added complementary growth laws (6), suggesting partitioning of the bacterial proteome in three functionally distinct sectors: (i) ribosomal proteins and auxiliary translation factors, (ii) enzymes for nutrient uptake and metabolism, and (iii) a fixed fraction independent of growth condition (6).

Bacterial cells continually import nutrients from the environment and convert them to intracellular metabolites, including biomass precursors like amino acids and nucleotides. The transformation of nutrients to intracellular metabolites is carried out in a large network of enzyme-catalyzed reactions (7) with rates determined by the abundance of enzyme molecules and the concentrations of their substrates and products. Formation of biomass requires rates of supply of its precursors at fixed molar ratios (7) implying stoichiometric coupling of the reaction flows in the metabolic network of the cell (8).

During the last decade, quantitative bacteriology has benefited greatly from successful reconstruction of metabolic networks at the genome scale based on whole genome sequences and biochemical and enzymatic data (9). Computational modeling of such networks has been used to predict phenotypic responses to environmental changes (9, 10). Descriptions of proteome dynamics are mainly based on coarse-grained models (7, 11–13) and these types of approaches have recently culminated in an in silico model of the whole Glycoplasma genitalium cell (14). Eventually, such modeling efforts may be extended to reproduce important aspects of the adaptation dynamics of bacterial cells (15).

Ehrenberg and Kurland (16) emphasized the Darwinian aspect of bacterial growth by formulating criteria for optimal proteome composition to achieve maximal growth rate and, thus, fitness value of bacterial populations thriving in different environments. Among these criteria is the demand for stoichiometrically balanced metabolic pathways, the choice of an optimal rather than maximal accuracy of tRNA selection in genetic code translation, and strong selection pressure to maximize the ratio between kinetic efficiency and peptide investment in all enzymes of the bacterial cell.

The starting point of the present work is the notion that there is strong selection pressure not only for rapid steady-state growth rate of bacteria but also for rapid adaptation of the bacterial proteome to environmental change. This notion leads to two major questions: First, what would be the optimal gene-expression strategy for minimal adaptation time after an environmental shift? Second, can such an optimal gene-expression strategy be emulated by the control systems of real bacteria?

To answer these and related questions, we model bacterial metabolism as a large network of stoichiometrically coupled flows (8, 17) in which the set of currently rate-limiting components determines the varying growth rate during bacterial adaptation to an environmental shift. Applying control theory (18, 19), we demonstrate that the time of adaptation for an initially unbalanced proteome to a new environment is minimized when all intracellular protein synthesis is devoted to expression of the rate-limiting components of the proteome. This optimal strategy leads to simple, analytical expressions for proteome dynamics during adaptation, and the minimal proteome adjustment time is given by the Kullback–Leibler distance (20) from the pre- to the postshift proteome divided by the postadaptation growth rate. We use detailed numerical modeling of the repressor-controlled metabolic pathways for amino acid synthesis (8, 17) to demonstrate that realistic bacterial control systems can indeed emulate the on–off optimal strategy for rapid proteome adaptation to environmental shifts, provided that the feedback loops have sufficiently high sensitivity amplification (21).

At the end of this report, we discuss extensions of the present theory to include fitness maximization of populations growing in a perpetually changing world and putative roles of protein degradation for swift proteome adaptation.

Results

We consider a bacterial population that grows in a preshift environment with steady-state rate 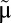. At time 0 the environment changes abruptly (1, 5) and the growth rate initially adopts the postshift value μ(0). At this point the cell population starts adapting to the new growth medium: its proteome composition changes and the growth rate gradually increases toward its steady-state value, 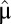, as determined by the quality of the postshift medium (1, 5). To quantify the speed of adaptation, we define a proteome adaptation time, 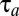, from the integral

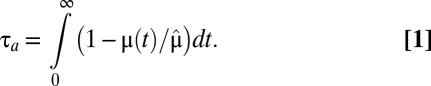Its meaning follows from the observation that the long-term biomass increase in the postshift medium will be a factor of 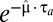smaller than if the bacterial population had been fully adapted with growth rate, 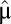, immediately after the environmental shift. For bacteria living in a changing world, long adaptation times therefore lead to reduced fitness value, suggesting strong selection pressure for small 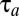-values. What then would be the optimal gene-expression strategy for fast proteome reorganization that minimizes the time of adaptation to the new environment? This question is addressed in the next section, where we develop a quantitative model for proteome reorganization in response to environmental change.

Proteome Rearrangement by Selective Gene Expression and Dilution.

To model proteome response to medium change, we partition the bacterial proteome in enzyme blocks, E_i, so that each block in the network of metabolic pathways contains sets of coregulated enzymes and their auxiliary protein factors (8). In the absence of protein degradation, the time derivative, 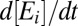, of the concentration, 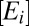, of a block, E_i, is determined by the rate of its synthesis by ribosomes and its dilution by volume increase (16). The rate of synthesis of a block depends on the fraction, u_i, of ribosomes devoted to its production, the total ribosome concentration, 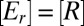, the average speed, v, of peptide elongation on ribosomes and the number, N_i, of amino acid residues in the block (8). The enzyme-block concentration, 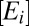, is diluted by volume growth with the current growth rate, . The proteome block dynamics can now be described by a set of ordinary, nonlinear, differential equations:

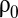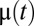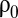When the proteome density, , defined as the total number of amino acid residues per cell volume, is constant, the current growth rate, , is given by the total rate of amino acid residue incorporation into peptide chains () normalized to (1, 16):

where

We now replace the enzyme-block concentrations, 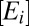, by their corresponding block-mass fractions in the proteome, x_i (22):

Using the relation between the growth rate, 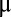, and the protein synthesis (Eq. 3) and replacing the enzyme-block concentrations, 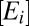, by the mass fractions, 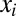, we can rewrite Eq. 2 in the simple form:

Up to this point, our description of proteome dynamics has been general. We now take advantage of the observation that bacterial metabolism can be approximated as a large network of stoichiometrically coupled flows (8, 17). In this flow model, the growth rate of an adapting cell is determined by the set of rate-limiting enzyme blocks, identified as those with minimal and equal ratios between their current, 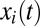, and final, 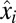, mass fractions (see SI section Growth Rate and Proteome Composition for details). In this approximation, the current growth rate is given as

Here 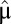is the postadaptation growth rate and the ratio

is a current mass fraction normalized to its postadaptation value. The main assumption in the derivation of Eq. 7 is that currently rate-limiting enzyme blocks (with minimal q value) operate at their maximal postadaptation speed also during adaptation (SI section Growth Rate and Proteome Composition). In contrast, the enzyme (or ribosome) blocks present in excess operate at varying and submaximal rates as determined by the rate-limiting flows. For example, if the ribosome block has excess capacity for protein synthesis in relation to the rate of amino acid synthesis, the peptide elongation rate, 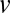, is determined by the rate-limiting supply of amino acid and not the maximal postadaptation rate of the ribosome.

With the growth rate expressed as in Eq. 7, the adaptation time τ_a in Eq. 1 becomes:

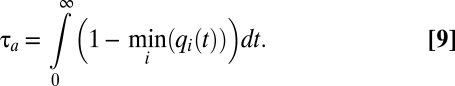This relation shows that in the framework of the flow model, the adaptation time is determined by the adaptation dynamics of the proteome components with the minimal q value. Using Eqs. 6 and 7, we obtain an equation system for dynamics of 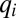values as

with the initial conditions 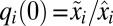, where 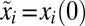represents the preshift proteome mass fractions (see Table S1 for the list of the variables used in equations).

The description of the dynamics of proteome adaptation by Eq. 10 is complete when the gene-expression components, 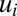, are known as, for example, functions of the current q_i values. In our search for a strategy that minimizes 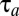in Eq. 9, we derive in the section On–Off-Controlled Proteome Adaptation an analytical solution to Eq. 10 in the case when all gene expression is directed to the synthesis of the rate-limiting enzyme blocks.

On–Off-Controlled Proteome Adaptation.

According to Eq. 7, the set of proteome components with the smallest 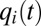value determines the current growth rate, 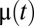. Directing all protein synthetic activity to this rate-limiting set would therefore lead to a rapid increase in the growth rate and thus to rapid adaptation. Such a gene-expression strategy could be viewed as being caused by the action of feedback loops ascribing u_i values of gene expression in response to the current set of q_i values of the proteome. 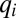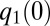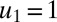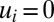According to such a strategy and assuming that enzyme block 1 has the smallest value, , at time 0, all protein synthesis is directed to block 1, meaning that and when 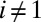in Eq. 10. Now, only 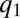increases by block 1 synthesis, whereas all other 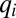values decrease by dilution. At a later time, 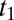, the increasing 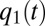value becomes equal to the decreasing, next-smallest 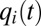value, say 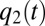, at which point these two enzyme blocks are equally rate limiting: 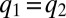. Then, all protein synthesis is partitioned to blocks 1 and 2 in such a way that 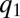remains equal to 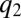, i.e., with 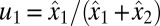and 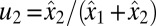. At a time 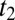, 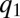and 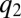become equal to 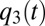of the third-most rate-limiting block. Then, all protein synthesis is partitioned to blocks 1, 2, and 3 in such a way that they remain equally rate limiting until their q_i values become equal to the fourth smallest 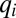value, and so on (see Fig. S1 for a graphic illustration of this strategy). With continuation of this procedure, more and more cell components become equally rate limiting and protein synthesis becomes more and more distributed among the enzyme blocks until after a finite time, T_adj, proteome adaptation is complete. From that point, the cells grow with the postadaptation rate 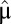, all mass fractions have their postadaptation values 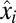, and all 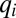values are equal to 1. By this strategy, proteome rearrangement is governed by on–off control, i.e., all available protein synthesis is directed toward a subset of growth-limiting enzyme blocks (their synthesis is fully on), whereas the mass fractions of all other protein blocks decrease by dilution (their synthesis is fully off). In this case there is an analytical solution to Eq. 10 (illustrated in Fig. S2) and the adaptation time, 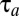, is given by (see SI section Adaptation Time in the On-Off Strategy)

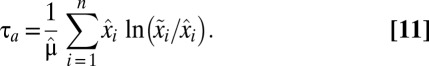It follows from Eq. 11 that 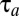is fully determined by the postadaptation growth rate, , and the Kullback–Leibler distance (20), 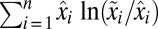, from the preshift (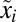) to the postshift (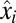) proteome with the block-mass fractions interpreted as probabilities of finding the different blocks in the proteome (Discussion). It is seen that the adaptation time 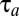is dominated by terms with large postshift mass fractions, 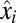, and small ratios between pre- and postshift mass fractions, 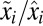. When the proteome contains a maintenance component with mass fraction 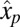that remains unaltered throughout the adaptation period (6), Eq. 11 remains valid, provided that 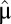is replaced by 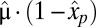(Eq. S2.27).

With the 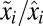ratios numbered according to magnitude (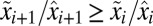) the time, 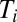, at which the synthesis of block i is turned on is given by (SI section Adaptation Time in the On-Off Strategy):

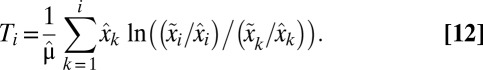The on–off strategy leads to a fully adapted postshift proteome at a finite time, 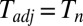, given by:

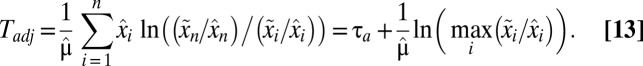At this point it is clear that the on–off adaptation strategy confers analytically tractable proteome dynamics (SI section Adaptation Time in the On-Off Strategy) and simple expressions for the adaptation time, , in Eq. 11 and the adjustment time, T_adj, in Eq. 13. However, the question if the on–off strategy minimizes these times remains unanswered. In the section On–Off Control Minimizes the Proteome Adaptation Time we use control theory (18, 23) to show that, indeed, the on–off strategy minimizes both 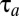and T_adj, although another strategy conferring equally small adjustment and adaptation times may exist. Readers less interested in the formal proof of optimality of the on–off strategy may skip this section.

On–Off Control Minimizes the Proteome Adaptation Time.

To prove that the adaptation time, 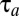, and adjustment time, T_adj, are minimized by the on–off strategy, we take advantage of control theoretical results regarding optimal value functions (23). An optimal value function, 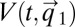, is defined as an integral over a function :

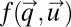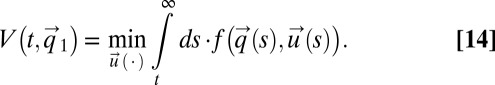This integral is minimized by the choice of an optimal strategy vector, 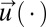with components u_i. In our special case, the integrand in Eq. 14 is given by 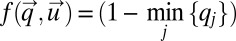. The components, q_i, of the vector 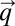obey the differential equation 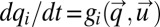with the initial condition 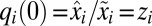. Furthermore, according to Eq. 10. As neithe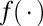r nor 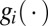depend explicitly on the time, t, it follows that also 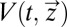in Eq. 14 lacks explicit time dependence and is fully determined by the initial condition 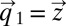(18), so that we can write 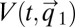= 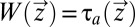where τ_a is defined by Eq. 11. In a time-independent case such as this, 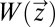is an optimal value function only if it satisfies the time-independent Hamilton–Jacobi–Bellman (HJB) equation (18)

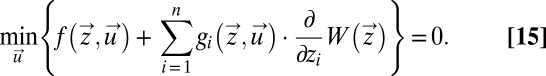When the adaptation time in Eq. 11, considered as an optimal value function

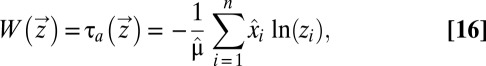is inserted in Eq. 15, we should obtain

Eq. 17 can be simplified to (see SI section Proof of the Optimality of the On–Off Strategy)

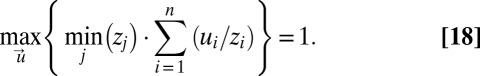Because the sum of the gene-expression fractions u_i is 1, the left side of Eq. 18 is maximal and equal to 1 only when u_i = 0 for all 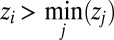. From this follows that the HJB Eq. 17 is 0 with 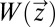from Eq. 16 and 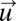determined by the on–off strategy. This proves that the on–off strategy minimizes the integral in Eq. 9 and, thus, that there is no smaller adaptation time than 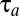given by Eq. 11. A similar proof can be used to show that also the proteome adjustment time, , in Eq. 13 is minimized by the on–off adaptation strategy.

Repressor-Based Control of Adaptation.

In this section we investigate if realistic control systems for bacterial gene expression can emulate the on–off strategy during adaptation and confer adaptation times close to those resulting from the ideal on–off control of gene expression. For this, the cells would have to direct most of their protein synthetic activity to production of the currently rate-limiting set of enzymes. We note already at this point that any rate-limiting metabolic flow in the cell can, in principle, be identified by a high concentration of its substrate or low concentration of its product metabolite. Accordingly, when substrate or product metabolites are used as signal molecules for repressor- or activator-controlled transcription, gene expression is expected to be partitioned roughly according to the prescriptions of optimal on–off control. To provide a quantitative basis for this intuitive reasoning, we perform detailed numerical modeling of the adaptation behavior of well characterized control systems of the metabolic pathways for amino acid production and consumption in protein synthesis (8, 17) (Fig. S3). The amino acid biosynthetic genes are controlled by repressors, ribosome-dependent attenuation of transcription or both, as in the trp operon case (see ref. 8 and references therein). The sensitivity of repressor control increases with the increasing number of subunits per repressor (8, 24), and intracellular synthesis of amino acids is product inhibited (25–27). Here, we focus on repressor control, but note that the attenuation mechanism has similar properties (see ref. 8 and references therein). Previous numerical modeling of the amino acid synthetic pathways (8, 17) is here extended to include feedback control of ribosome synthesis, making the description of the dynamics of the translation part of the bacterial proteome complete (see Fig. S3 and Methods for details).

To simulate the adaptation behavior of a bacterial population, we assume that it first grows exponentially in an amino acid-supplemented medium. Here, the concentration of the ribosome block is high, but the concentrations of amino acid-synthesizing enzyme blocks are low. Adaptation of the proteome after a rapid shift to an amino acid lacking medium is simulated numerically in the cases of repressor control or is derived analytically from the ideal on–off strategy. 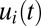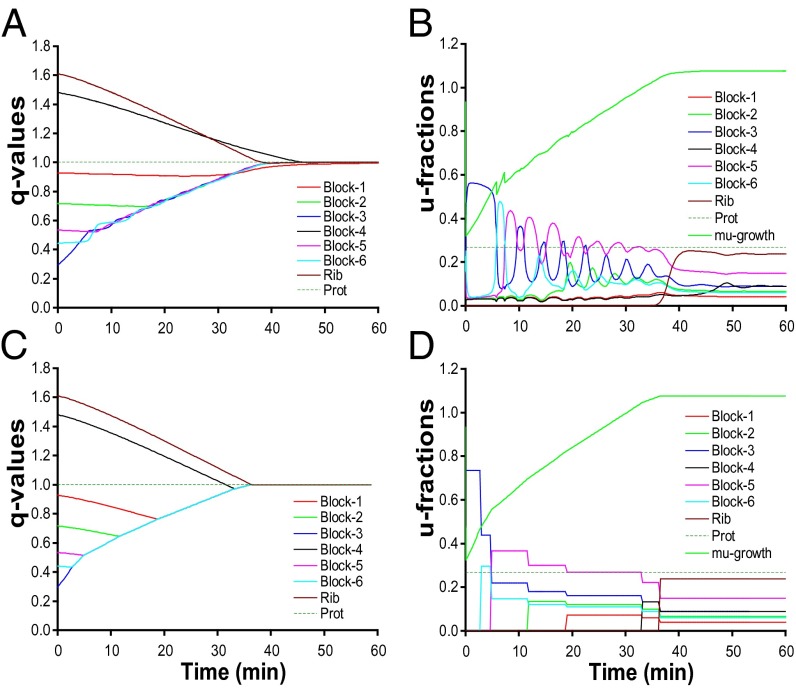In the case of monomeric repressor control, the expression components of the amino acid synthetic enzymes, , and the growth rate, 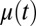, are shown in Fig. 1B and the endpoint-normalized mass fractions, 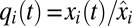, of the amino acid synthetic and ribosome blocks are shown in Fig. 1A. In the case of ideal on–off control, the parameters , and 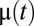are shown in Fig. 1D and the 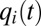dynamics in Fig. 1C. In both cases, adaptation starts at the same preshift proteome composition 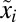and ends at the same postshift proteome composition 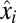and growth rate 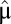. The adaptation time, 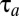, is 669 s in the monomeric repressor case and 589 s in the on–off control case as calculated from Eq. 11. Monomeric repressor control confers, in other words, a 14% slower adaptation than ideal on–off control. The time evolution of the proteome (compare Fig. 1 A and C) and the growth rate (compare Fig. 1 B and D) appear similar in the momeric repressor and on–off cases, but the gene-expression components, 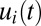, differ. In the case of on–off control, the 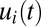components evolve in a regular manner, remaining constant in time intervals where the set of rate-limiting enzyme blocks is unaltered (Fig. 1D). In the repressor case, in contrast, the 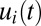components display large-amplitude oscillations over time (compare Fig. 1 B and D).

Fig. 1.

Comparison of adaptation dynamics of the cell proteome when gene expression is regulated by monomeric repressors (A and B) or by on–off control (C and D). A and C show proteome adaptation as the dynamics of the end-point normalized mass fractions q_i(t) of enzyme and ribosome blocks. “Prot” refers to a maintenance proteome component, the mass fraction of which remains constant during adaptation. The dynamics of the u_i parameters for repressor control is shown in B and for on–off control in D.

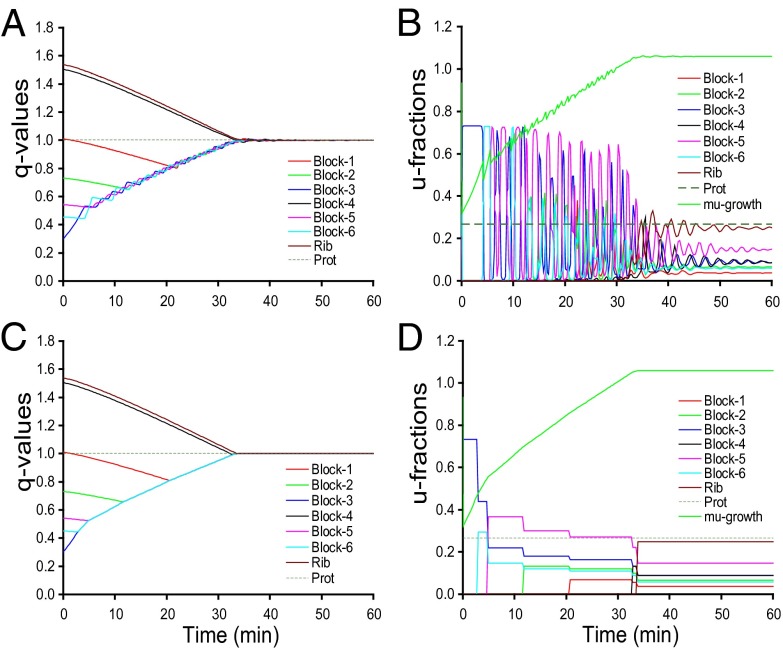
In Fig. 2, we show similar scenarios as in Fig. 1 but with tetrameric repressors, promoting significantly higher sensitivity of regulation than their monomeric counterparts (8, 24). In the tetrameric repressor case, the adaptation time is 557 s and only about 1% longer than the adaptation time of 554 s in the corresponding ideal on-off case. Apart from a small, oscillatory ripple, growth rate and proteome evolution are almost identical in the tetrameric repressor and on–off regulated cases. At the same time, the oscillations in the 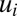components are even more pronounced in the tetrameric than in the monomeric repressor case (compare Figs. 1B and 2B). In the case of dimeric repressors, the dynamics of the 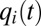and 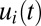components is much more similar to that of tetrameric than monomeric repressors (Fig. S4). The proteome adaptation time ( 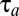= 580 s) is, as in the tetrameric repressor case, about 1% longer in the dimeric repressor case than that in the ideal on–off case ( 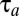= 575 s).

Fig. 2.

The same as in Fig. 1, but with the adaptation dynamics of the proteome regulated by tetrameric repressors (A and B) compared with regulation by ideal on–off control (C and D).

Discussion

In this work, we have modeled proteome reorganization after environmental shifts by considering the bacterium as a network of stoichiometrically coupled metabolic flows (8, 17). The network is balanced during steady-state growth in the pre- and postshift states but unbalanced during adaptation due to shortage of enzymes required at higher concentrations in the postshift environment. We define a proteome adaptation time, 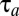(Eq. 1), and use control theory (18, 19) to demonstrate that is minimized when all available ribosomal activity is devoted to synthesis of the set of currently rate-limiting proteome components. This on–off strategy allows for analytical solutions to the proteome dynamics (section Adaptation Time in the On-Off Strategy in Supporting Information), a simple expression for the finite time, T_adj, at which proteome adjustment is complete (Eq. 13) and a remarkably simple sum of terms for the minimal proteome adaptation time (Eq. 11).

We note that the sum in Eq. 11 for minimal 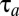can be interpreted as the Kullback–Leibler distance (20) between the distributions of the preshift (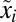) and postshift (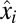) mass fractions taken as probabilities to find component i in the proteome. Accordingly, the minimal shift time is obtained by dividing the Kullback–Leibler distance by the postadaptation growth rate 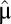, suggesting that the Kullback–Leibler distance may be a natural measure of divergence between proteome compositions under different growth conditions.

The main hypothesis of the present work is that real bacterial populations emulate the on–off strategy of gene expression to confer rapid proteome adaptation to environmental changes. Eventually this hypothesis must be settled by quantitative monitoring of proteome dynamics, e.g., by mass spectrometry (28) or ribosomal profiling through deep sequencing (29). Here, we have probed this hypothesis and some of its underlying assumptions by comparing its predictions with results from detailed numeric modeling of intracellular protein synthesis (section Repressor-Based Control of Adaptation). This approach serves a twofold purpose. First, it tests the realism of the flow model for proteome dynamics (Eq. 10) in which the presence of metabolite intermediates is implicit by comparing its predictions with those from a much more detailed model in which the presence of such metabolites (amino acids and aminoacyl-tRNAs) is explicit. Second, it reveals the extent to which repressor systems of a cell can emulate the on–off gene-expression strategy, rigorously proven here to be optimal for rapid proteome adaptation within the framework of the flow model.

In the case of monomeric repressors with their relatively low sensitivity to amino acid concentration (8, 24), the time of adaptation in response to a down-shift in medium quality is 14% longer than that predicted by Eq. 11 for on–off strategy of gene expression. However, in the case of dimeric or tetrameric repressors, with their relatively high sensitivity to amino acid concentration (8, 24), the adaptation time is only about 1% longer than that predicted by the optimal on–off strategy. In the case of tetrameric repressor control, gene expression displays apparently chaotic behavior with high frequency oscillations of large amplitude (Fig. 2B) in sharp contrast to the case of optimal on–off strategy where gene expression is regular (Fig. 2D). Despite this and apart from high-frequency ripples of small amplitude, the proteome dynamics (Fig. 2A) under repressor control is very similar to that obtained for the flow model (Fig. 2C). These results suggest that predictions of proteome dynamics and adaptation times based on the optimal on–off strategy may give excellent approximations for the proteome dynamics of real adapting cells despite large oscillations in their gene expression (Fig. 2B). The origin of these oscillations can be traced to the extreme sensitivity of amino acid pools to small deviations from perfect flow balancing between several, rate-limiting amino acid synthetic pathways (17). Because, however, the deviations from perfect flow balance are very small (17), the oscillations in protein synthesis are small and the repressor-regulated gene expression faithfully reproduces the proteome dynamics and growth rate during the adaptation phase. Moreover, the application of a numeric filter (sliding time average over a 4-min window) to suppress the rapid oscillations in gene expression in Fig. 2B reveals that the averaged levels of gene expression under repressor control are very similar to those prescribed by the ideal on–off strategy (Fig. S5). This means that in a coarse-grained sense repressor regulation may indeed emulate the optimal on–off strategy.

Our modeling results also suggest that optimal regulation for rapid proteome adaptation may critically depend on the sensitivity of the metabolite sensing control systems. Rapid proteome adaptation is conferred much more efficiently by dimeric and tetrameric than by monomeric repressors. This is in line with the observation that most bacterial repressors and activators exist as dimers, which when promoter bound may further oligomerise (30, 31), or as free tetramers (32) and even hexamers (33).

According to Eq. 11, the minimal proteome adaptation time, 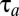, is sensitive to large ratios, 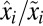, between post- and preshift mass fractions of proteome components. In cases when the postshift mass fraction, 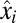, is much larger than its preshift counterpart, 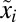, the adaptation time would be significantly reduced if preshift 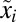were kept at a level above its stoichiometric balance point. At the same time, this would necessarily lead to a reduced growth rate in the preshift state by the burden of redundant protein mass. For bacteria living in a perpetually changing world, fitness maximization requires maximization of a growth rate that is averaged over the times spent in different habitats and during adaptation periods. An optimal strategy would be to balance the growth rate loss due to redundant proteins in one habitat to the gain in the rapidity of adaptation as conditions change (34). Indeed, the experimental finding that the ribosome concentration supersedes what is required for balanced growth in very poor media may be one example of such a strategy (see ref. 1 and references therein). Eventually, when the condition improves the adaptation to rapid growth is much faster than from a preshift population with much lower concentration of ribosomes. There may also be significant phenotypic diversity in the proteome composition of an isogenic bacterial population due to stochastic fluctuations in protein copy numbers (see ref. 35 and references therein). Cells with preshift proteome compositions close to their ideal postshift values will then adapt much faster than the total population as described by Eq. 11. Putting the present theory in population-genetic context may make it possible to quantitatively predict the optimal levels of redundant proteins or an optimal level of phenotypic diversity (36) in populations thriving under perpetually changing conditions.

The adaptation time in Eq. 11 has been derived without taking intracellular protein degradation into account. It is, however, clear that protein degradation may contribute favorably to proteome adaptation, not the least in the case of a down-shift from an amino acid-proficient to an amino acid-deficient medium (Figs. 1 and 2). Here, specific degradation of non–rate-limiting enzymes could provide a source of amino acids for the synthesis of rate-limiting enzymes, thereby speeding up adaptation. It is, however, not clear how such selective protein degradation would be controlled. Also, in the case of uniform protein degradation, the adaptation time limit given by Eq. 11 can be transcended. In this relatively simple case, proteome dynamics obeys a slightly modified version of Eq. 10, and a similar on–off strategy for control of enzyme-block expression as in the present case appears to minimize the adaptation time.

One important role of theory in physics has been to consider the performance limits of physical systems, with Carnot’s limit cycles for the steam engine as an early example. Expression (11) for the minimal possible adaptation time and the corresponding analytical solution to equation system (10) provide a principally similar tool to gauge the performance of cell regulatory circuits during bacterial adaptation. Therefore, similar limit approaches may, indeed, become increasingly important in the theoretical biology of the future.

Methods

We use a detailed model for cell adaptation based on the control systems for amino acid synthetic operons (8, 17). This model, depicted in Fig. S3, is naturally partitioned into three modules: (i) synthesis of intracellular protein components, (ii) synthesis of amino acids and aminoacylation of tRNAs, and (iii) feedback control of the synthesis of intracellular proteome components.

• i) The dynamics of the concentrations of the enzyme and ribosome blocks is described by Eqs. 2–5. To calculate the growth rate 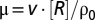, we assumed that the ribosomes have an average peptide elongation rate v, determined by the concentrations, 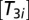, of ternary complexes composed of aminoacyl-tRNAs (AA-tRNAs), elongation factor Tu (EF-Tu), and GTP (8):

  

• Here, 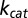is the maximal peptide-elongation speed of the ribosomes, 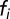is the fraction of amino acid i in the proteome, is the K_m value for the interaction of a ternary complex with the ribosome. We assume that the concentration of EF-Tu in the cell is high enough to cover all AA-tRNAs, so that the concentrations of 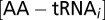and 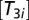are equal, explaining the second equality in Eq. 19.

• ii) Each enzyme block, E_i, synthesizes an amino acid, AA_i, with the rate 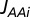. This amino acid is attached to its cognate tRNA(s) by an aminoacyl-tRNA synthetase (RS) operating at the rate 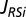; AA-tRNA_i is then consumed in protein synthesis with the rate . For a detailed description of the equations governing the dynamics of the AA_i and AA-tRNA_i pools, see section Detailed Model for Cell Adaptation in Supporting Information.

• iii) The fraction, 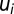, of ribosomes devoted to the synthesis of enzyme block E_i is determined by the concentration of the mRNA transcribed from the E_i-encoding operon. To simplify, we assume that each mRNA concentration is proportional to its rate of synthesis, 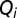. Here, we only consider repressor-regulated amino acid-producing operons, and assume (8) that each Q_i value is determined by the fraction of repressor-free operator. The latter depends on the current AA_i concentration. Concerning control of ribosome synthesis, our model mimics the ppGpp-based feedback control of ribosomal RNA synthesis (8, 17). For details on the Q_i calculation, see section Detailed Model for Cell Adaptation in Supporting Information. The value of Q_m+1 for maintenance proteins (6) is chosen so as to ensure a constant fraction u_p of ribosomes devoted to its synthesis. With the Q_i values proportional to the concentrations of the corresponding mRNAs, 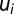fractions of the ribosomes translating these mRNAs are given by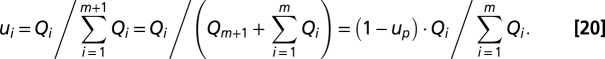

  

• The value of was set to 0.266 in our model calculations. Thus, the Q_i values completely determine the 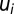parameters making the description of proteome dynamics by Eq. 2 complete.