Torsion Profiling of Proteins Using Magnetic Particles

Abstract

We report a method to profile the torsional spring properties of proteins as a function of the angle of rotation. The torque is applied by superparamagnetic particles and has been calibrated while taking account of the magnetization dynamics of the particles. We record and compare the torsional profiles of single Protein G-Immunoglobulin G (IgG) and IgG-IgG complexes, sandwiched between a substrate and a superparamagnetic particle, for torques in the range between 0.5 × 10³ and 5 × 10³ pN·nm. Both molecular systems show torsional stiffening for increasing rotation angle, but the elastic and inelastic torsion stiffnesses are remarkably different. We interpret the results in terms of the structural properties of the molecules. The torsion profiling technique opens new dimensions for research on biomolecular characterization and for research on bio-nanomechanical structure-function relationships.

Introduction

The structural properties of proteins are intimately linked to their biological function. An important way to reveal structural molecular properties is by characterizing the response to mechanical stress or strain. Mechanical forces and/or torques have been applied to single biomolecules by techniques such as AFM (1), micropipettes (2), optical tweezers (3,4), and magnetic tweezers (5,6). The majority of studies have focused on the stretching and twisting properties of DNA (7–9), with and without DNA-binding molecules (5). Proteins have been studied under stretching forces, revealing characteristic conformational changes induced by the unfolding and refolding of protein domains (5,10–12). However, proteins have hardly been studied under torque and twist. Torque has been applied to multiprotein fibers (13), but the torsional properties of single proteins have not yet been investigated.

Recently we have demonstrated that magnetic tweezers can be used to measure the torsional deformation of a single protein pair (14). The torsional constant of a Protein G–Immunoglobulin G (IgG) complex was quantified, under the assumption of a constant magnetic moment in the particle. We will find in this article that a static moment only occurs at low field values and that it is important to take account of the magnetization dynamics in the particles.

In this article, we demonstrate how we can uncouple the torque calibration from measuring the magnetic moment of the particles. The calibration method takes account of the dynamic magnetization of the particles, so it is applicable for a wide range of fields and torque values. We reveal that markedly different torsional moduli exist for different protein complexes. We also record torsion profiles, i.e., we measure the dependence of the torsional modulus on the angle over which a protein complex is twisted. More specifically, the torsion profiles of two protein complexes are studied, which are schematically shown in Fig. 1 a, i.e., a Protein G-immunoglobulin G complex (Protein G–IgG) and an immunoglobulin G–immunoglobulin G complex (IgG–IgG). In the Protein G–IgG complex, Protein G binds specifically (15) to the crystallizable (Fc) part of the mouse IgG antibody. The IgG–IgG complex consists of a goat anti-mouse IgG that binds to the crystallizable part (Fc) of the mouse IgG.

Figure 1.

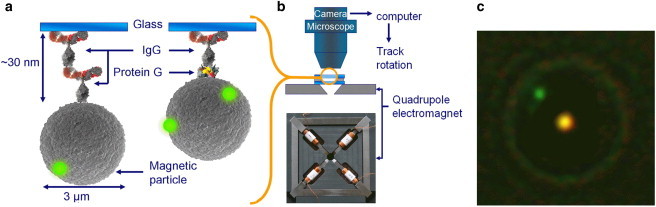
Setup for rotational actuation of particles and proteins. (a) Magnetic particles are bound to a glass substrate by means of the Protein G–IgG complex or the IgG–IgG complex. (b) Inside a fluid cell, the particles are actuated by a rotating magnetic field generated by a quadrupole electromagnet with slanted (45°) soft-iron pole tips. (c) The particle orientation is visualized by means of attached small green fluorescent spheres. The bright spot at the center of the particle is an artifact due to the applied bright-field light. The bright spot is exploited to track the particle center.

Materials and Methods

The experimental setup is schematically shown in Fig. 1 a. Superparamagnetic particles (M-270 carboxylated; 2.8 μm diameter; from Dynal Invitrogen, Carlsbad, CA) were coated with one of the target proteins (either Recombinant Protein G or Goat anti-Mouse IgG; Merck, Whitehouse Station, NJ), and streptavidin (Merck). The latter allows the attachment of fluorescent nanoparticles as optical tags to present a clearly visualized rotation of the magnetic particle. Fluorescent nanotags (FluoSpheres, biotinylated, yellow/green, 0.2 μm diameter) were purchased from Invitrogen (Carlsbad, CA). The coated magnetic particles were attached to primary antibodies (monoclonal Mouse-IgG; Merck) which were physisorbed on a glass substrate (18 × 18 mm² coverslips; VWR international, Radnor, PA). To reduce nonspecific binding, the glass surfaces were coated with casein (Sigma-Aldrich, St. Louis, MO).

The coating of the magnetic particles with Protein G or Goat IgG and streptavidin was done competitively using EDC-NHS coupling chemistry. The surface of the magnetic particles containing carboxylic groups was activated using EDC (1-ethyl-3-(3-dimethylaminopropyl) carbodiimide), and subsequently stabilized using NHS (N-hydroxysuccinimide). The activation buffer was removed, and a 50 mM MES buffer containing Protein G or Goat IgG and streptavidin was added to allow for reaction of the activated particle surface with the amine end-groups of the proteins. After 2 h of incubation time, ethanolamine was added to quench the reaction. The presence of both streptavidin and Protein G or Goat anti-Mouse IgG was confirmed by the enzyme-linked immunosorbent assay, using either biotin-HRP or Protein G-HRP. Chemiluminescence was measured using a standard well-plate reader (Fluoroskan Ascent FL; Thermo Fisher Scientific, Waltham, MA). Particles were stored in PBS (phosphate-buffered saline) buffer containing 0.02% Tween-20 and 10 mg/mL BSA (bovine serum albumin).

To allow us to track rotation accurately, fluorescent nanotags were attached to the magnetic particles. A quantity of 5 μL of demineralized water containing fluorescent nanotags (2 × 10¹⁰ particles/mL) was added to a 100 μL PBS solution containing magnetic particles (100 μL 2 × 10⁷ particles/mL). Binding of the labels was induced by means of centrifugation (for 5 min at 13,400 rpm in a microcentrifuge; Eppendorf Minispin, Hamburg, Germany). The particles were redispersed by means of vortexing.

Before torsion experiments, glass slides were rinsed and washed with isopropanol. After drying, a circular fluid chamber was made by means of an imaging spacer. Then, for unbound particle experiments, the surface was blocked with casein by incubating a 100 μL droplet of PBS containing 100 mg/mL casein for 1 h. After incubation, the sample was washed with PBS and dried. In the case of bound particle experiments, the blocking step was preceded by the incubation of 100 μL 50 nM Mouse IgG in PBS. After incubation, the sample was washed with PBS and subsequently the substrate was blocked with casein.

Different protocols were followed for experiments on unbound and bound particles. In case of unbound particle experiments, a 10 μL particle solution was loaded in a fluid cell. The fluid cell was closed by means of another glass slide and placed under the microscope and onto the magnetic setup. The particles were allowed to sediment onto the substrate by the force of gravity for 2 min. In the case of bound particle experiments, a 10 μL particle solution was pipetted onto a washed glass cover slide. Subsequently, an unclosed fluid cell with adsorbed Mouse IgG was put on the droplet to make a closed cell. In this way, the incubation of the magnetic particles on the treated substrate was not initiated yet. The fluid cell was then turned upside down and placed onto the magnetic setup, which was set to generate a static horizontal magnetic field of 1 mT. After 5 min incubation, the fluid cell was reverted to let the force of gravity pull on the particles and remove unbound particles from the glass substrate.

Magnetic particles were actuated by means of a quadrupole electromagnet (Fig. 1 b) which generates an in-plane rotating magnetic field (0.1–36 mT) with a negligible downward field gradient (1 T/m at 10 mT). Particle images were acquired at ∼30 frames per s using an electron-multiplying charge-coupled device camera (Luca-S; Andor Technology, Belfast, Ireland) which was mounted onto a microscope ((Leica DM6000M; Leica Microsystems, Wetzlar, Germany) with a 63× water immersion objective. The total magnification of the sample was 1260×. For excitation of the fluorescent particles, a mercury lamp was used in combination with a model No. L5 filter cube (Leica Microsystems). The sample was excited in reflective mode, and unfiltered bright-field light (halogen lamp) was applied in transmitted mode. The intensity of the bright-field light was adjusted such that in the recorded images both the fluorescent tag(s) and the magnetic particle are visible, e.g., as shown in Fig. 1 c. Images were analyzed using customized software developed in MATLAB (The MathWorks, Natick, MA). More specifically, combining magnetic particle center tracking and fluorescent particle tracking on the edge of the magnetic particle, the orientation of the magnetic particle can be determined for each frame with an accuracy of 2°.

It should be noted that due to the random labeling with fluorescent nanoparticles, only magnetic particles could be considered containing one or more fluorescent nanoparticles on their side (as seen from the camera). This enabled us to analyze only a small fraction of all magnetic particles bound to the substrate, i.e., ∼5%. In case a fluorescent nanoparticle was observed in the center of the magnetic particle, it was excluded, as the fluorescent nanoparticle may then be responsible for the (nonspecific) binding.

Results and Discussion

Torque calibration using unbound particles

The torque on the superparamagnetic particles was quantified by measuring the rotation frequency of unbound particles in solution in an applied rotating magnetic field. The particle rotation frequency was measured for different field strengths and field rotation frequencies (Fig. 2 a). Magnetic particles are observed to keep up with the magnetic field rotation up to a breakdown frequency. Above the breakdown frequency, the average particle rotation frequency declines and a wiggling behavior is observed as shown in Fig. 2 b. In a repetitive fashion, particles rotate in the same direction as the magnetic field for some time, thereafter slow down, rotate backward shortly, and then rotate along with the rotating field again. The origin of the breakdown is that the magnetic torque cannot overcome the viscous drag that comes along with synchronous rotation of the particle with the field.

Figure 2.

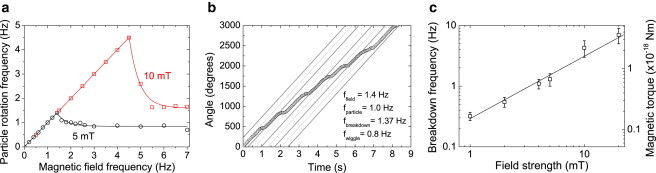
Quantification of the applied magnetic torque from unbound particle actuation. (a) The rotation frequency of an unbound particle as a function of the rotation frequency of the applied magnetic field, for field strengths of 5 mT and 10 mT. The particle continuously follows the magnetic field up to the breakdown frequency. (b) Above the breakdown frequency, the particle rotation frequency decreases due to remagnetization of the particle magnetic moment (characterized by the wiggles). The orientation of the magnetic field is plotted (shaded lines) and phase-shifted by multiples of 180° to show that the particle follows the magnetic field (5 mT) with a phase-lag of 180°. (c) At the breakdown frequency, i.e., right before the particle remagnetizes, the magnetic torque can be determined from the hydrodynamic drag.

A breakdown frequency and wiggling behavior have also been observed by Janssen et al. (16) for a slightly different type of superparamagnetic particles, namely Dynal M-280 particles (diameter of 2.8 μm; Dynal Biotech, Invitrogen), for fields up to 2 mT. The wiggling frequency appeared to correspond to the difference between the field rotation frequency and the net particle rotation rate, which means that every wiggle period corresponds to one full rotation of the field relative to the magnetic particle. This observation proves that at low fields the magnetic torque is dominantly generated by a magnetic moment that has a fixed orientation inside the particle. In later experiments on M-270 particles at higher fields, Janssen et al. (14) observed a switching of the magnetization in the particles, but the dynamic properties were not quantified in detail.

We have studied the magnetic properties of the M-270 particles by recording the breakdown frequency and wiggling behavior at different field strengths. For field strengths below 5 mT, we observe the same behavior as reported by Janssen et al. (16), i.e., every wiggle corresponds to one full rotation of the field relative to the magnetic particle. However, above 5 mT we observe a different behavior, as plotted in Fig. 2 b. The wiggling frequency equals twice the difference between the field rotation frequency and the net particle rotation rate. Therefore, two wiggling cycles occur during one rotation of the field with respect to the particle. In other words, the particle is dragged along with the field twice during one relative field rotation. This proves that the magnetic moment of the particle reorients during one relative field rotation. At fields above 5 mT, the magnetic moment of the particle becomes dynamic and has two preferential magnetization directions, indicating a dominant uniaxial magnetic anisotropy of the magnetic particles.

An important consequence of the dynamic magnetic moment is that the size of the magnetic moment can no longer be directly determined from the breakdown frequency, because the angle difference between the moment and field becomes uncertain. As we will show later in this article, the remagnetization of the magnetic moment already occurs at a phase-difference ≪ 90°. Therefore, a calibration method is needed that is compatible with a dynamic magnetization and that is independent of the magnetization details. We propose to calibrate the torque at the condition of maximum torque. The maximum torque value can be quantified at the breakdown frequency of an unbound particle on a surface. At the breakdown frequency the maximum magnetic torque, τ_m,max, is equal to the Stokes drag,

$${\tau }_{m,\text{max}}=8\pi C_{\text{drag}}{C}_{\text{BR}}\eta R^3{\omega }_{\text{BD}},$$ (1)

with η the dynamic viscosity of the solution, R the radius of the particle, and ω_BD the angular velocity at the breakdown frequency. Due to the vicinity of a substrate, a correction factor C_drag is required for the effective drag coefficient. For a rotating particle on a surface the factor has been numerically estimated (14) to be C_drag = 1.22. In addition, a factor C_BR has been included to account for the effect of rotational Brownian motion on the measured breakdown frequencies. The factor C_BR was obtained from numerically simulating the unbound rotating particle behavior, which is discussed in more detail in Section S1 in the Supporting Material. The equation of motion was solved using a forward Euler method with and without Brownian rotation included (17). Including Brownian rotation in the simulations is found to reduce the particle breakdown frequency. However, the relative difference between the maximum torque deduced from the maximum angular velocity with and without Brownian rotation is nearly independent of the magnitude of the field in a range between 5 and 30 mT. Consequently we can use a constant Brownian rotation correction factor: C_BR = 1.16 × 0.05.

With Eq. 1. we can calculate the maximum magnetic torque that can be applied on a particle without having any knowledge about its magnetic microstructure, which is very convenient. Now we want to determine if this maximum magnetic torque calibration method, performed on freely rotating particles in solution, is a suitable predictor for the maximum magnetic torque in a bound-particle twisting experiment. We want to determine the particle-to-particle variation of the maximum magnetic torque within one batch of particles.

For the Dynal M-270 particles used in our experiments, the accuracy of the measured torque was investigated for a single particle by studying the angle at which remagnetization occurs in subsequent rotation cycles. We observed a torque variation with a standard deviation of <4% (see Fig. S8 in the Supporting Material). The particle-to-particle variation in remagnetization angle was found to be ∼10% (also see Fig. S8). This indicates that remagnetization occurs at a relatively well-defined angle.

For these particles, we have experimentally determined the maximum magnetic torque at different field strengths, as shown in Fig. 2 c. The breakdown frequency at each field strength was measured for different particles, and a particle-to-particle variation is found with a standard variation of 28% in the reached maximum torque (see Section S2 in the Supporting Material).

It is interesting to note that Klaue and Seidel (18) reported a much larger particle-to particle variation of the maximum magnetic torque (∼55%) on similar particles (2.8 μm, M-280 Dynal). We also measured a large particle-to-particle variation (∼70%) of the permanent moment of M-280 particles (16). Interestingly, the M-270 particles exhibit much smaller sustainable torques at the same field strengths (∼10-fold lower), with a smaller variation (∼28%). For the M-280 particles, Klaue and Seidel found a saturation in the applicable torque (corresponding to overcoming the coercive field) at a field strength of ∼150 mT. In our experiments with the M-270 particles, the coercive field is already overcome at a field strength of 5 mT, which indicates that the internal magnetic structure is very different. Finally, it should be noted that these particles are produced for their superparamagnetic properties (i.e., a high magnetic susceptibility) and that the remanescence and coercive field, which are studied here, are neither specified nor controlled by the supplier.

In summary, the maximum magnetic torque of the M-270 particles used in our experiments has a particle-to-particle variation of ∼28% and has a linear dependence on the magnetic field strength, which gives a convenient relationship to predict the magnetic torque in experiments with particles that are biologically bound to a surface.

Bond discrimination

We are interested in studying the torsion profiles of single protein complexes. Therefore conditions need to be created in which single protein complexes bind the magnetic particles to the surface. We have optimized the experimental conditions by studying particle binding for low densities of Mouse IgG adsorbed on the glass substrate. Assuming that the antibody adsorption process is a random process governed by Poisson statistics, the incubation concentration is optimal if a significant fraction of the functionalized magnetic particles does not bind during incubation on the functionalized surface. In that case, there are bound particles but the probability for multiple bonds (i.e., with more than one protein complex forming a bond between the particle and the substrate) is relatively small (see Section S4 in the Supporting Material). We have determined the fraction of particles that bind after incubation for different Mouse IgG incubation concentrations (see Fig. S5) and have derived an optimal incubation concentration of 50 nM Mouse IgG.

To validate experimentally whether single specific bonds are obtained at this incubation concentration, we have measured the bond strengths between the particles and the substrate. We carried out a series of bond dissociation assays with specific magnetic forces applied on the particles, as previously described in Jacob et al. (19). Analyzing the number of particles leaving the substrate as a function of time, allows a determination of the dissociation rate constant (k_off) that is specific for the bond. The extrapolated dissociation rate at zero force corresponds to the thermal dissociation rate that can be validated by surface plasmon resonance (SPR). In our experiments with Protein G-coated particles and IgG on the substrate (see Section S5 in the Supporting Material), three different populations of bound particles were identified: nonspecifically bound particles that are weakly bound; specifically bound particles presumably corresponding to a single protein complex; and particles with a strong bond that most likely resemble multiple specific and/or nonspecific bonds. The k_off value found for the single protein complex fraction was found equal within the error margins to the k_off obtained from an SPR experiment with exactly the same proteins. Consequently, single specific bonds are indeed formed using our method and these may thus be probed rotationally. By applying a rotating magnetic field, we also observe three distinct types of behavior, namely particles rotating continuously; particles that are completely immobile; and particles that exhibit an oscillatory behavior. For a given single magnetic particle, we cannot determine to which group it belongs by a dissociation measurement, since dissociation is a statistical single-event process. However, on an ensemble level we can compare populations in terms of bond strength and response in a rotating magnetic field. In view of our data we conclude that the intermediately strong bound particles (i.e., single specific bonds) correspond to the particles exhibiting an oscillatory behavior in a rotating field.

To study the population properties further, we characterized nonspecific bonds in a rotating field, by analyzing particles bound to a nonfunctionalized casein-blocked substrate. On this control substrate, we mainly observe continuously rotating or completely immobile particles, and we conclude that these behaviors correspond to nonspecific bonds. On a rare occasion, we also observed a particle exhibiting an oscillatory behavior as plotted in Fig. 3 a. We observe that the angular range over which the particle rotates drifts over time. In contrast, the oscillatory behavior of particles on a functionalized surface is regular and reproducible, as shown in Fig. 3, b and c. For specifically bound particles we measure a periodic movement with a constant angular range. From these observations we conclude that specific bonds between the particle and the substrate, in a rotating magnetic field, generate an oscillatory behavior of the bound particle over a constant angular range.

Figure 3.

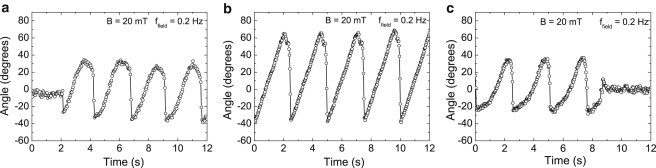
Discrimination of nonspecific and single or multiple specific biological bonds based on the rotational particle response to a rotating magnetic field. (a) Oscillatory behavior of a nonspecifically bound particle in a control experiment. (b and c) Oscillatory behavior of particles bound to the glass substrate by means of the Protein G–IgG complex. The behavior plotted in panel b is the largest rotation observed and attributed to a single specific bond, whereas the behavior in panel c corresponds to a particle bound by multiple bonds.

In addition to separating specific and nonspecific bonds, the rotating field also makes a distinction between single and multiple bonds. An increased amount of specific bonds between particle and substrate will increase the torsional rigidity of the total effective bond between the particle and the substrate. The increased torsional rigidity should result in a smaller angular excursion of the particle at the same applied torque. Consequently, single bonds can be identified as the bonds that exhibit the largest excursion in a rotating magnetic field. For the incubated concentration of Mouse IgG on the substrate, and assuming the adsorbed antibody distribution to be governed by Poisson statistics, we estimate the fraction of single specific bonds to be ∼80% of all formed specific bonds (single or multiple). For more details on the estimate, we refer to Section S4 in the Supporting Material. Comparing this to our experiments, we mostly observe oscillations over an angular range of ∼110°, at a field strength of 20 mT (Fig. 3 b). For a much smaller fraction of particles the amplitude is ∼60° or less (Fig. 3 c). Quantitatively, out of 11 particles observed to exhibit oscillatory behavior, we find that 64 ± 18% exhibits the larger excursion, and 36 ± 18% to the smaller excursion. Therefore, we attribute the oscillation results as in Fig. 3 b to single protein complexes that are sandwiched between a magnetic particle and the substrate.

Protein G–IgG torsion profile

We have analyzed the rotational behavior of particles bound to the substrate by one Protein G–IgG complex. In Fig. 4 a, the typical response is shown of such particles to a rotating magnetic field (20 mT), first in the clockwise and subsequently, after a short pause, in the anti-clockwise direction. The angular orientation of the magnetic field is plotted as well as the particle angle with respect to its zero-field state.

Figure 4.

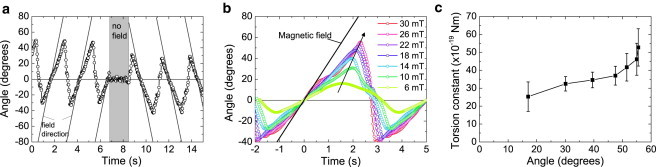
Torsion profile of the Protein G–IgG complex sandwiched between a particle and the glass substrate. (a) The particle orientation as a function of time in a magnetic field rotating in the anti-clockwise direction and in the clockwise direction, respectively. (Solid lines) Orientation of the magnetic field, which is turned off from t = 7 s to t = 8.5 s. (b) The rotational response measured at different field strengths. (c) From the maximum angular excursion, i.e., when the particle starts to remagnetize, the torsional spring constant is determined at the corresponding twisting angle.

In a rotating magnetic field, the particles are observed to exhibit a sawtoothlike behavior, of which the frequency is twice the field frequency due to the remagnetization of the particles. When the magnetic field is turned off, the particles rotate back to a well-defined angle, which we call the equilibrium angle. We find that this angle does not show hysteresis under any type of magnetic actuation that we can apply (up to 30 mT). In addition, both for clockwise and anticlockwise rotations, the particles cross the equilibrium orientation together with the field orientation. These observations indicate that the response of the bound particles to the applied rotational deformations is fully elastic. We attribute this behavior to the protein complex sandwiched between the particle and the substrate. When rotated from its equilibrium angle by a magnetic torque, an opposing molecular torque appears due to the twisting of the sandwiched protein complex. The molecular torque causes the magnetic moment to lag behind the field. At a certain angle difference between moment and field a remagnetization occurs, which effectively reverses the direction of the magnetic torque. As a result, molecular torque and magnetic torque act in the same direction, and the particle moves back and rotates beyond the equilibrium angle to find a new balance between the magnetic torque and the again-opposing molecular torque. Note that from Fig. 4 a, it can be deduced that the angular difference between the particle magnetic moment and the magnetic field is 35 ± 2° when the remagnetization occurs. The fact that this angle is well below 90° indicates that the particle magnetic moment consists of a distribution of magnetic moments rather than a single moment. Furthermore, the fact that the remagnetization angle is well above zero degrees indicates that the moment distribution has granularity. As presented in Section S6 in the Supporting Material, the remagnetization angle is found to decrease for increasing field strength, which can be explained by the smaller relative angle difference that is required to overcome the coercive field at higher field strengths. In addition, a particle-to-particle variation is found of ∼10% in remagnetization angle, which is slightly smaller than the found particle-to-particle variation in ferromagnetic properties. See Section S6 in the Supporting Material for further details.

To quantify the torsion properties of the Protein G–IgG complex, we can use the maximum-torque calibration that was performed on unbound particles (see Fig. 2 c). The bound particles are in a maximum-torque condition at their maximum angle of excursion. In the maximum-torque condition the effective magnetic moment remagnetizes and therefore the angle between the magnetic moment and the magnetic field and consequently the applied torque that is exerted onto the particle are well defined. For the unbound particles in solution, the counteracting torque is due to the hydrodynamic drag. For bound particles the counteracting torque is dominated by the molecular deformation. To model the molecular torque, we assume that the sandwiched protein complex acts as a torsional spring. The corresponding torsional spring constant k(θ) can then be determined by balancing the torques at the maximum angular excursion,

$${\tau }_{m,\max }\left(B\right)=8\pi C_{\text{drag}}\eta R^3\frac{\text{d}{\theta }_{\max }}{\text{d}t}+k\left({\theta }_{\max }\right){\theta }_{\max },$$ (2)

with B the field strength at which the maximum magnetic torque was determined (see Fig. 2 c). The viscous drag is negligible in the experiments with bound particles, as proven by the data in Fig. 4 a (the field crosses the particle orientation at θ ≅ 0; see also Fig. S9). Using Eq. 2. we can determine the torsional spring constant for the Protein G-IgG complex, and at a field strength of B = 22 mT we find a torsional spring constant of k = (4.3 ± 1.3) × 10³ pN·nm/rad. As is shown in Section S8 in the Supporting Material, a variation in the measured torsion constant is found of ∼30%. This variation is rather small and comparable to the variation found in the magnetic torque. We assume that the antibodies are coupled to the substrate at random orientation, caused by the nonspecific attachment process. Still the variation of torsion constants is small. We attribute the small variation to the fact that only a few orientations allow for binding of a Protein G to the Fc region of the antibodies and consequently the number of possible configurations becomes rather confined.

The values for the torsional spring constant can be compared to the results reported in Janssen et al. (14). In that article we assumed an angular difference of 90° between field and moment upon remagnetization, yielding a torsional spring constant of k = (1.5 ± 0.3) × 10³ pN·nm/rad. From the results in this article we know that the molecular spring constant is, in fact, approximately a factor of three higher, because the angle difference between the field and moment upon remagnetization is 35 ± 2° rather than 90°.

A completely independent method to determine the torsional spring constant is by analyzing the thermally induced angular fluctuations of a bound particle in the absence of a constraining field. This method has been used in the literature to determine the torsion stiffness of dsDNA (8,9). We investigated the applicability of this method for our relatively stiff protein system using the data presented in Fig. 4 a. In Section S9 in the Supporting Material, we show that the distribution of observed angles indeed resembles a Gaussian distribution. From its width, we determine the torsional spring constant to be k = (5.5 ± 0.8) × 10³ pN·nm/rad. It should be noted that the relatively small amplitudes of the oscillations, which are only slightly above the accuracy of the angle-tracking algorithm, limit the accuracy of this analysis. Furthermore, a small history-dependent remanent field of the pole tips (∼0.3 mT) can also influence the angular fluctuations and may give a systematic error. Nevertheless, the estimated value for the torsional spring constant is remarkably similar to the value found from magnetic actuation on the same particle.

An important difference between actuated particle rotation to obtain the torsional constant and the analysis of thermal fluctuations is the ability of the former to determine the dependence of the torsional spring constant on the twisting angle, as is shown in Fig. 4 c by varying the magnetic field strength (see Fig. 4 b). Interestingly, for the probed angular range, the protein complex exhibits nonlinear torsional stiffening. To our knowledge, this is the first reported angle-dependent measurement of the torsional spring constant of protein molecules, which we refer to as a torsion profile.

IgG–IgG torsion profile

To determine the molecule-dependence of the torsion profile, we have also studied the twisting behavior of the IgG–IgG complex. Fig. 5 shows the torsion profile of the IgG–IgG complex. We again observe an oscillatory behavior when a rotating magnetic field is applied (see Fig. 5 a). However, the maximum excursion is much larger than for the Protein G–IgG complex, for the same applied field strength and magnetic torque. Furthermore, there is no well-defined equilibrium position in absence of a magnetic field. Apparently the molecular torque is too small to overcome small energy barriers in the rotational energy landscape, which may be attributed either to inelastic deformations of the protein complex itself or to rotational irregularities of particle-surface interactions. As the rotational behavior in both the clockwise and the anticlockwise direction is similar, the equilibrium angle is assumed to be exactly in the center of the reached angular range. Using Eq. 2, we have determined the torsion constant at several twisting angles (see Fig. 5, b and c). The torsion constant of IgG–IgG is found to be 5.5 ± 1.6 times lower than the torsion constant of Protein G–IgG. As with the Protein G–IgG complex we observe an increased stiffness for increased twisting angles of the IgG–IgG complex. For the IgG–IgG complex, a variation in determined torsional stiffness is found of ∼40% (see Section S8 in the Supporting Material), being slightly larger than the variation found for the Protein G–IgG complex.

Figure 5.

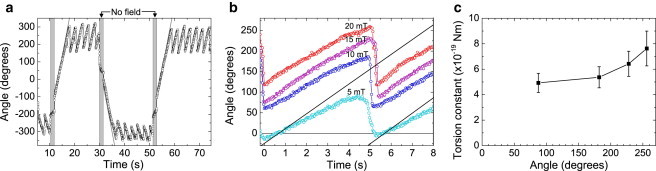
Torsion profile of the IgG–IgG complex sandwiched between a particle and the glass substrate. (a) The particle orientation as a function of time in a magnetic field rotating in the anti-clockwise direction and in the clockwise direction. (Solid lines) Orientation of the magnetic field for the first cycle. (Shaded zones) Time when the magnetic field is turned off. (b) The rotational response measured at different field strengths. (c) From the maximum angular excursion, i.e., when the particle starts to remagnetize, the torsional spring constant is determined at the corresponding twisting angle.

The calculation of the torsional modulus of a protein complex requires a detailed molecular model. As a first approximation we use a continuum approach to extract an estimated Young’s modulus from the experiments. To take account of the influence of length on the stiffness of the system, we convert the torsion constant to the torsional modulus (20) by multiplying it with the length of the twisted system. The dimensions of IgG (21) are reported to be 14.5 nm × 8.5 nm × 4 nm. We estimate the size of Protein G to be ∼3 nm in all directions (22). If we assume the length of the complex to be 17.5 nm and 29 nm for, respectively, the Protein G–IgG complex and the IgG–IgG complex, the torsional moduli are, respectively, (6 ± 2) × 10⁻²⁶ N·m² and (2 ± 0.8) ×10⁻²⁶ N·m². In other words, the torsional constants as well as the torsional moduli of the two protein systems are clearly different.

Finally, it is interesting to consider the energy stored in a protein complex upon twisting. In our experiments, the maximum torque reaches 4 × 10⁻¹⁸ N·m·rad⁻¹ and with a typical twist angle on the order of radians, the stored energy can be estimated as several hundreds of k_BT! Unfortunately, no literature exists on energy storage in proteins by twisting, therefore we compare the stored energy with typical energies required to unfold proteins upon stretching. Force-extension curves on proteins such as individual (titin) immunoglobulin domains (1), have been shown to unfold at forces of typically a few hundreds of pN and show extensions of several tens of nm, which also corresponds to a stored energy of several hundreds of k_BT. We conclude that the energy required to twist proteins is of the same order of magnitude as the energy required for protein stretching. Note, however, that these are order-of-magnitude estimates. A more detailed comparison is only possible once the force-distance and torque-angle relationships are measured and compared in detail.

Conclusions

In this study, we have revealed what we believe to be a novel way to calibrate the torque on magnetic particles in a rotating magnetic field and we have applied the method to quantify the angle-dependent torsion properties of individual protein complexes. The maximum-torque calibration method takes account of the dynamic particle magnetization and is independent of the micromagnetic properties of the particles. We have demonstrated that the calibration method allows the measurement of protein torsion profiles, i.e., measurements of the angle-dependent torsion constants of protein complexes sandwiched between a particle and a substrate. We have quantified the torsion properties of Protein G–IgG and IgG–IgG complexes, revealing similarities (reproducibility, torsional stiffening) and remarkable differences (magnitude of the torsion constants, inelastic properties).

The precision of the torque calibration method is presently determined by particle-to-particle variations. For the M-270 particles the precision is ∼25%. It will be interesting to evaluate particles of different manufacturers with the aim of improving the precision of the applied torque.

We have observed that the applied rotating field discriminates qualitatively how particles are bound to a substrate. Specific bonds give repetitive oscillatory particle motion while nonspecific bonds give free rotation, no rotation, or oscillatory motion with a drifting angular range. Such a discrimination of bond types is interesting for application in biosensors, because in high-sensitivity biosensing it is very important to be able to distinguish between specific and nonspecific binding (16,23,24).

In our experiments we have not observed the rupture of biological bonds by torque application. The applied torque (4 × 10⁻¹⁸ N·m/rad) sets a lower limit for the torque required to break a Protein G–IgG and IgG–IgG bond by rotational deformation. It will be interesting to further investigate potential bond rupture by torsional stress, e.g., by employing particles with larger magnetic moments and larger torques.

Furthermore, a systematic torsion-profiling study on proteins with well-known structures may provide detailed insights into the functioning of those structures. It may become possible to attribute the torsional response to secondary structures (α-helices, β-sheets, etc.) of the protein. In addition, structure-function relationships can be investigated, e.g., by measuring the response of molecules with helicity to torque or by studying the biochemical activity (dissociation constant, enzymatic activity, etc.) under torsional stress loading.

We conclude that the torsion-profiling technique described in this article opens new dimensions for research in biomolecular characterization, the field of biosensing, and examination of bio-nanomechanical structure-function relationships.