Effects of Interactions with the GroEL Cavity on Protein Folding Rates

Abstract

Encapsulation of proteins in chaperonins is an important mechanism by which the cell prevents the accumulation of misfolded species in the cytosol. However, results from theory and simulation for repulsive cavities appear to be inconsistent with recent experimental results showing, if anything, a slowdown in folding rate for encapsulated Rhodanese. We study the folding of Rhodanese in GroEL, using coarse-grained molecular simulations of the complete system including chaperonin and substrate protein. We find that, by approximating the substrate:GroEL interactions as repulsive, we obtain a strong acceleration in rate of between one and two orders of magnitude; a similar result is obtained by representing the chaperonin as a simple spherical cavity. Remarkably, however, we find that using a carefully parameterized, sequence-based potential to capture specific residue-residue interactions between Rhodanese and the GroEL cavity walls induces a very strong reduction of the folding rates. The effect of the interactions is large enough to completely offset the effects of confinement, such that folding in some cases can be even slower than that of the unconfined protein. The origin of the slowdown appears to be stabilization—relative to repulsive confinement—of the unfolded state through binding to the cavity walls, rather than a reduction of the diffusion coefficient along the folding coordinate.

Introduction

The majority of small proteins are able to fold spontaneously to their native, functionally relevant state. However, there are many proteins for which correct folding is greatly assisted by chaperones (1–4), a group of proteins responsible for protecting and aiding nascent and misfolded proteins to adopt their native state while preventing aggregation (5–8). Chaperonins are an important class of chaperones that are able to encapsulate substrate proteins, isolating them from the surrounding environment. Hydrolysis of ATP is used to drive the chaperonins through a sequence of states that favor folding over competing aggregation and misfolding pathways (9). The best characterized of the chaperonins is GroEL, a 60-kDa complex present in bacterial cells, consisting of two heptameric rings stacked back-to-back, each with a cavity 60–70 Å in diameter (10) in which folding is mediated by ATP-driven conformational changes to its structure and repeated binding with the co-chaperonin GroES (11–13).

There is still some debate over the exact mechanism by which GroEL acts to enhance the yield of correctly folded proteins. The two main hypotheses are the passive-cage (or Anfinsen cage) (14,15) and iterative-annealing models (16). The passive-cage model considers that the primary role of the chaperonin cavity is to protect against aggregation in the cytosol, and that it does not actively influence folding (17). In vitro experiments have shown that protection from aggregation by GroEL can effectively enhance the folding yield of substrate (14,15). The iterative annealing model proposes that repeated binding and unbinding of the partially folded substrate is critical for the protein to achieve the native state, via denaturation of transient misfolded or partially folded states (18).

The mechanism of GroEL has been the subject of many theoretical (19–22) and simulation (23–31) studies. Most of these have focused on the physical effects of confinement on folding: the reduction in entropy of the unfolded chain due to simple volume exclusion by the cavity is expected to stabilize the folded state and lower the barrier for folding, both of which would be expected to be advantageous for chaperonin function. Indeed, simulations of coarse-grained models have demonstrated this effect (23,24,26,27,29,32), and experimental support comes from the effect of GroEL mutations which alter the cavity volume (33). However, atomistic simulations with explicit solvent suggest a more complex picture (28,30,31,34): it has been found that introducing a confining potential may actually destabilize a protein when solvent is explicitly included (28). Explicit solvent simulations of mini-proteins confined within polar and nonpolar cavities have shown these, respectively, to destabilize and stabilize the folded state (30), while confinement between attractive walls has been shown to stabilize folded over misfolded states (31).

In contrast to theoretical predictions based on excluded volume, recent experiments by Hofmann et al. (35) using single-molecule spectroscopy showed that, if anything, Rhodanese folding was slowed down by encapsulation within a single-ring variant of GroEL (SR1), which does not undergo ATP-dependent cycling. These results suggest that simple repulsive confinement models, while capturing the important—and clearly relevant—excluded volume effect of encapsulation, are missing qualitatively relevant effects on the folding inside GroEL, even in the absence of ATP turnover. In this work, we aim to understand the effect of interactions with the cavity wall on the folding of Rhodanese in GroEL. Our aim is to include, as completely as possible, the sequence-specific interactions between substrate and chaperonin. The most realistic method for inclusion of such physical interactions is via all-atom simulations with explicit solvent, but obtaining folding events with such simulations is far out of reach for such a large system. Therefore, we tackle the problem using a hierarchy of coarse-grained folding models, in which we ultimately explicitly include all residues of the GroEL, GroES, and Rhodanese, together with a sequence-based, transferable potential. Consistent with earlier results using simplified models, we find that the effect of the volume excluded by the chaperonin is to accelerate folding; however, introduction of realistic interactions between the walls of the cavity and the chaperonin results in a slowdown of folding to an extent that can completely offset and even overcome the excluded volume effect. In our model, we show that the dependence of the diffusion coefficient for the folding coordinate on introduction of attractive interactions with the cavity is relatively modest. Rather, slowdown due to attractive interactions arises from the unfolded state being stabilized by binding to the walls of the cavity. We also explore how the interactions with the cavity depend on the sequence composition of the cavity walls, and we observe occasional excursions of parts of the unfolded Rhodanese chain outside the cavity—consistent with experimental results using anti-Rhodanese antibodies.

Methods

Details of folding simulations

All molecular simulations were performed with an α-carbon representation of the proteins, using a modified version of the GROMACS 4.0.5 program (36). Langevin dynamics simulations were run with a timestep of 15 fs and a friction coefficient of 0.2 ps⁻¹. Bond lengths were constrained to their initial values using the LINCS algorithm (37). Simulations were run at a temperature of 340 K, chosen to observe folding events on a practical timescale for the particular coarse model of Rhodanese used.

A pairwise-additive potential was used to describe the whole system. The potential for intramolecular residue pairs in Rhodanese was derived from the experimental structure (PDB:1RHS (38)) using the Gō model of Karanicolas and Brooks (39). Nonbonded interactions between pairs of residues in GroEL/GroES were treated with the transferable Kim-Hummer (KH) binding potential (40). Pair interactions between the GroEL and Rhodanese were treated either using this transferable binding potential, or with a repulsive potential (representing two different confinement scenarios). However, while the simulation temperature of 340 K was chosen based on the folding time of the Gō model, the KH model was parameterized at 300 K. We accordingly scaled all the KH pair energies such that the correct statistical weights would be obtained from simulations at 340 K. The chaperonin coordinates were taken from the structure of single-ring GroEL bound by GroES and ADP, with the cavity in the open conformation (PDB:1SX4 (10)). The GroEL and GroES residues present in this experimental structure were treated as rigid in the simulations. The C-terminal tail residues (526–550) of GroEL, missing from the crystal structure, were added in an initial linear conformation, and were allowed to move in the simulation. The bonded energy terms (bonds, angles, dihedrals) for these tails were taken from the Karanicolas and Brooks Gō model (with native bond lengths and angles being, respectively, 3.8 Å and 84.3°).

For the unconfined folding simulations, Rhodanese was initialized in an extended conformation. For the confined simulations, including those in GroEL, unfolded yet sufficiently compact conformations of Rhodanese were produced by performing high-temperature simulations in the repulsive sphere (described below). Ten of the resulting structures were then inserted into the repulsive GroEL cavity and steepest-descent minimization was performed to prevent overlaps, resulting in initial sets of coordinates for the folding runs.

The final simulations were run for 6 μs and coordinates were output every 15 ps. All timescales were subsequently scaled by a factor of 100 to account for the low viscosity used in the simulations.

Repulsive cavity

The repulsive spherical cavity required for reproducing confinement effects was implemented via the addition of a repulsive potential of the form

$$V\left(r_i\right)=\epsilon {\left(\frac{\sigma }{r_i-R-\sigma }\right)}^{12}$$ (1)

to the total residue potential, where r_i is the radial position of residue i; ε is 2.4 kcal/mol, which is the energy scale; R is 35 Å is the cavity radius; and σ is 6 Å is the range of interaction.

Hybrid pair potential

Accurate simulation of Rhodanese-GroEL interactions beyond those that were purely repulsive required the adoption of a more realistic multiprotein binding model. The Kim-Hummer model is a transferable, coarse-grained potential designed to reproduce equilibrium dissociation constants of weak protein-protein binding using a contact energy based on the Miyazawa-Jernigan matrix, together with a screened electrostatic potential (40). Specifically, the contact energy ϵ_ij between residue types i and j is given by ϵ_ij = λ(m_ij − ϵ₀) in which m_ij is the Miyazawa-Jernigan contact energy (41), λ = 0.159 and ϵ₀ = −2.27 k_BT. According to the model, the interactions between Rhodanese and GroEL residues then become a sum of Lennard-Jones and electrostatic terms:

$$V_{ij}^{\text{LR}}\left(r_{ij}\right)=u_{ij}^{\text{LJ}}\left(r_{ij}\right)+u_{ij}^{\text{EL}}\left(r_{ij}\right).$$ (2)

Residue pairs which interact favorably, i.e., for which ϵ_ij < 0, had an attractive form of $u_{ij}^{\text{LJ}}$ (standard 12-6 Lennard-Jones potential), whereas unfavorable interactions were described by a modified Lennard-Jones potential with a long-range repulsion (40). The electrostatic interactions were defined as a Debye-Hückel potential that models the screening effect of solvent with a monovalent salt concentration of ∼100 mM,

$$u_{ij}^{\text{EL}}=\frac{q_i{q}_j{e}^{-r/\eta }}{4\pi Dr},$$ (3)

where D is 80; η is 10 Å; and q_i is the charge (in e) on residue i.

Definitions of parameters Q and θ

For calculation of Q from the simulation coordinate data, we first define the degree of nativeness for each pair of residues that forms a contact,

$$q_{ij}={\left(1+\text{exp}\left[\beta \left(r_{ij}-r_{ij}^{\left(0\right)}\right)\right]\right)}^{-1},$$ (4)

where β defines the steepness of the contact formation curve, set to 2 Å⁻¹ and $r_{ij}^{\left(0\right)}$ is the separation of the residues in the native structure. Then the total fraction of native contacts is

$$Q=\frac{1}{N_Q}\sum _{i,j}^{\text{contacts}}{q}_{ij},$$ (5)

where N_Q is the total number of native contacts in the polypeptide.

The fraction of residues in contact with GroEL, θ(t), was defined as N_c(t)/N_r, where N_c(t) is the number of Rhodanese residues within 8 Å of at least one GroEL residue at time t and N_r is the total number of Rhodanese residues.

Calculation of diffusion coefficient

We calculated position-dependent diffusion coefficients and free energies in the unfolded state by using a previously described Bayesian method (42). We used data from umbrella sampling simulations in the unfolded state in which the bias V(Q) = (k/2)(Q – Q₀)² was added to the potential, with k = 2870 kcal/mol and Q₀ = 0.15. The Q range sampled was divided into 20 bins, and the propagators p(j,Δt|i,0) for moving from bin i to bin j after a lag of Δt were estimated by counting transitions from the simulation data. A lag time of Δt = 1.5 ns was used, chosen sufficiently long that the estimated diffusion coefficients were approximately independent of the lag. A smoothening prior of 0.1 ms⁻¹ was used to ensure the continuity of the calculated diffusion coefficients (42).

Results

In our models, we represent each residue of both the Rhodanese, and (where present) SR1-GroEL:GroES, by a bead centered on the Cα carbon, as depicted in Fig. 1. For the full Rhodanese:GroEL:GroES system, this reduces the total number of particles from 67,647 atoms to 4801 coarse beads. Although this is still a large system for folding simulations, the coarse-graining is sufficient that it is computationally feasible to sample multiple folding events. The folding of the unencapsulated Rhodanese was described using a structure-based potential (39), which has been successfully used to described folding, misfolding, and coupled folding and binding (39,43–45). We first perform multiple simulations of the protein folding, starting from the unfolded state, for 6 μs each. Langevin dynamics with a low friction coefficient of $0.2{\text{ps}}^{-1}$ was used, resulting in an acceleration of the dynamics by a factor of ∼100 relative to water viscosity (46). All times and rates reported below have accordingly been scaled by this factor.

Figure 1.

Structures of Rhodanese and GroEL:GroES at Cα resolution. N-terminal (blue) and C-terminal (red) domains of Rhodanese; (yellow) intervening linker. A slice through GroEL:GroES is shown (GroES, light blue; GroEL, orange/gray). Disordered C-termini (not resolved in crystal structure) are shown (pink).

In isolation, the folding of the N- and C-terminal subdomains of Rhodanese is approximately independent, with each domain folding in a cooperative fashion. This can be seen from the fraction of native contacts, Q(t), in Fig. 2, which shows a sharp increase associated with the folding of each domain. Note, however, that it is also evident from these trajectories that Rhodanese folding is not strictly two-state, with the population of several intermediate states. This is qualitatively consistent with experimental folding studies on Rhodanese, which suggested that the slow folding of Rhodanese can be attributed to the presence of at least three intermediates, one of which is particularly prone to aggregation (47,48). To simplify the analysis, however, we have applied a two-state approximation, where we define the folded and unfolded states as being centered at Q = 0.8 and Q = 0.2, respectively. A similar two-state approximation was made in interpreting the single-molecule FRET experiments (35).

Figure 2.

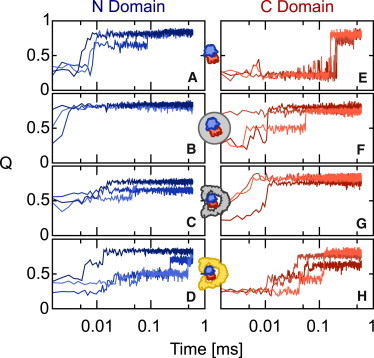
The fraction of native contacts, Q(t), for the N domain (A–D) and the C domain (E–H) of Rhodanese under the different confinement scenarios; unconfined (A and E); spherical confinement (B and F); repulsive GroEL (C and G); and KH GroEL (D and H). Three trajectories are shown in each case (varying colors).

Effect of confinement and interactions with chaperonin

To describe the effect of the chaperonin on folding, we have adopted a hierarchy of models in which progressively more detail is included in the simulation. The first effect that must be considered, and is undoubtedly present for any confined protein, is the effect of the volume excluded by the chaperone. We initially model this using a simple spherical repulsive cavity, similar to that adopted in many previous studies (23–25,27,29). Folding simulations of Rhodanese in a spherical cavity of 70 Å diameter (chosen to have a similar volume to the interior of GroEL) were run, resulting in a strong acceleration of the folding of both domains, relative to the unconfined case (representative folding trajectories are monitored by Q in Fig. 2, B and F). Such an acceleration is to be expected in general because of the destabilization by confinement of the unfolded state of the 293-residue protein, relative to the more compact folding transition states.

Next, we considered a more detailed model for the chaperonin, in which each residue of the GroEL and GroES is explicitly represented. To make the simulations more computationally accessible, most residues of the GroEL and GroES were frozen in the simulations, with the exception of the disordered C-terminal tail residues of the seven GroEL domains, i.e., residues 526–550, which are missing in the crystal structure. While the bonding of the tail residues in the GroEL was described by similar energy terms to those in the structure-based model (39), nonbonded interactions of the tail residues with each other and with the GroEL were treated with the transferable, sequence-based Kim-Hummer (KH) potential (40). Therefore, we made no assumptions about specific structure in the disordered tails.

Using this model for the GroEL, Rhodanese was included in two ways:

In the first method, all interactions between the GroEL and Rhodanese were given by a short-range repulsive potential. While this is similar to the repulsive spherical cavity, it is also an important reference because it provides a precise representation of the excluded volume effect due to the chaperonin.

In the second method, GroEL:Rhodanese interactions were treated with the KH potential. This is an empirically parameterized binding potential, optimized to reproduce binding affinities for protein:protein interactions in the micromolar to millimolar range (40), and should therefore provide a realistic representation of the interaction strengths between substrate and chaperonin possible in the context of a coarse-grained model. The potential includes both explicit screened electrostatic interactions, as well as a residue-residue contact potential, which is either attractive or repulsive depending on the identity of the residue pairs. Rhodanese-Rhodanese interactions were always treated by the same structure-based potential. The electrostatic interactions were included for all charged residue pairs in both the confined and unconfined scenarios.

Trajectories for the folding of Rhodanese in the repulsive and interacting GroEL are shown in Fig. 2, C, and G, and Fig. 2, D and H, respectively. As might be expected, the repulsive GroEL produces similar results to the simple spherical cavity—justifying the use of such cavities to model excluded volume effects in previous studies. However, the results with the inclusion of the full interaction potential are in striking contrast with the repulsive GroEL, or spherical cavity, and in fact bear more resemblance to the unconfined folding. To better quantify the folding rate in the different scenarios, we have determined average rates over 10 folding trajectories in each case, summarized in Fig. 3 A, by fitting a single exponential function to the average 〈Q(t)〉 over all simulations (Fig. 3 B). These confirm the picture obtained from the coarse-grained trajectories: confinement in either a repulsive sphere, or repulsive GroEL model, results in an increase of folding rate by 1–2 orders of magnitude. Inclusion of the attractive interactions, however, causes a dramatic slowdown of both domains, such that the folding rates are again comparable to those for the unconfined protein. A similar slowdown of C-terminal folding was observed experimentally for Rhodanese (35), and an even stronger retardation of folding has been observed for the 64-residue chymotrypsin inhibitor 2 (49). We note that the folding rates of both domains are accelerated by a similar factor in the repulsive spherical cavity, but for the repulsive GroEL, the C domain is accelerated more, which may be due to GroEL having a stronger confinement effect than the spherical cavity.

Figure 3.

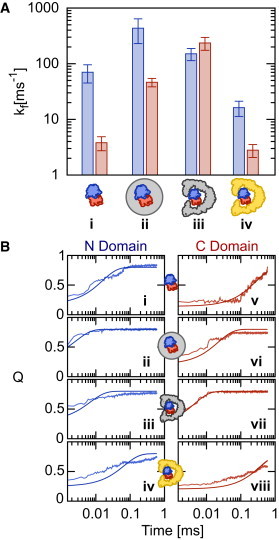
(A) Rhodanese folding rates for the N domain (blue) and C domain (red) under conditions of (i) no confinement; (ii) spherical confinement; (iii) repulsive GroEL; and (iv) KH GroEL. (B) Single-exponential fits made to ensemble-averaged trajectories 〈Q(t)〉 from which rate estimates were made.

An important question, given that the folding is clearly not two-state, is whether the process monitored by single-molecule FRET is the same as that monitored by the fraction of native contacts. We first address this by assuming a scenario in which the main contribution to the experimental signal is the change in FRET efficiency. We have calculated the average efficiency over all the trajectories, 〈E(t)〉, in an analogous fashion to the calculation of 〈Q(t)〉 above. We assume that the motion of the chain is slow relative to the fluorescence lifetime of the donor, and that the chromophores sample all possible relative orientations isotropically, so that

$$E\left(R\right)\approx {\left(1+{\left(\frac{R}{R_0}\right)}^6\right)}^{-1},$$

where R is the instantaneous distance between the C^α carbons of the residues to which the chromophores are attached and R₀ is the Förster radius, taken to be 5.4 nm for the chromophores used. We find a relatively small overall change in efficiency, particularly for the N domain, but the signal can be fitted by the exponential decay with the same rate coefficient as that fitted to the Q trajectories (see Fig. S1 in the Supporting Material). In the case of the C domain in GroEL, there is also a fast phase which corresponds to binding to the GroEL cavity, which we excluded from the fit.

In practice, however, most of the change in experimental signal comes not from the change in FRET efficiency, but from the overall difference in quantum yield (or brightness) between the folded and unfolded states (35). In the unfolded state, it appears that both donor and acceptor are strongly quenched by exposed tryptophan residues. When the protein folds, these are buried, leading to a large increase in the total number of detected photons. While it would be difficult to model quantitatively this quenching effect, because the burial of the large tryptophan side-chains (which form many contacts) is likely to be highly correlated with the global Q, it may be that Q is not a bad proxy for the experimental signal after all.

Origin of slowdown

Comparing the rates in the repulsive GroEL reference system with those in the interacting GroEL, we find that the C-terminus appears to be more strongly affected by switching on the attractive interactions, being slowed by around two orders of magnitude, versus just over one order of magnitude for the N-terminus. We can gain some insight into the effect of interactions between GroEL and substrate by monitoring, for each domain, the fraction of Rhodanese residues forming contacts with GroEL, θ(t), and correlating this with the fraction of native Rhodanese contacts, Q(t) (Fig. 4). This indicates that, in general, the unfolded Rhodanese forms a large number of contacts with the cavity wall, and that formation of native contacts occurs concomitantly with the breaking of contacts between Rhodanese residues and the cavity wall. This is in contrast to the situation for repulsive GroEL, where the number of contacts formed is negligible (see Fig. S2). The formation of strong contacts with the cavity wall suggests that the slowdown in folding rate is due to stabilization of the unfolded state, relative to the situation of repulsive confinement. The net result is that the folding rates in the attractive cavity are comparable to those of the unconfined protein.

Figure 4.

Contact formation with chaperonin cavity. (Upper) The fraction of native contacts Q(t) (blue, N domain; red, C domain) and the fraction of residues forming contacts with GroEL θ(t) (gray) trajectories for three example trajectories folding inside the interacting GroEL. (Lower) A snapshot of Rhodanese (N-domain in blue, linker in yellow, and C domain in red) bound to GroEL from the KH cavity simulation; note that the GroEL (in pink) has been cut away to reveal the substrate.

An alternative mechanism for the reduction of rate would be a lowering of the diffusion coefficient due to sticking to the cavity wall. We have calculated the effective position-dependent diffusion coefficients and free energies along Q in the unfolded state from umbrella sampling runs using a previously described Bayesian method (42). Note that the reported free energies include the umbrella potential. Note, also, however, that as protein folding can be modeled as one-dimensional diffusion, addition of this potential is not expected to modify the diffusion coefficient, and indeed, we have found this to be accurate for small model systems (50). We find relatively small differences in diffusion coefficient, with values of ∼3 ms⁻¹ for the unconfined Rhodanese, and values of ∼1 ms⁻¹ for Rhodanese confined in either the repulsive or attractive GroEL (Fig. 5). Thus, the primary effect is of confinement reducing the diffusion along Q (presumably due to the restrictions imposed on chain movement by the cavity). The change in rate is therefore unlikely to arise from variation of the diffusion coefficient, given that the largest variation of D due to interactions with the cavity would be expected in the unfolded state. While a change in D may play a role for an atomistic model with more sources of friction (e.g., hydrogen bonds) (51), a change in barrier height appears to be sufficient to explain our results. We note that although the relative balance between the nativelike Gō interactions driving folding and the interactions with the cavity walls has been set in a somewhat ad hoc way in our simulations, this should not affect this conclusion, as an increase of barrier height would be expected due to stabilization of the unfolded state regardless of the original barrier height.

Figure 5.

Position-dependent diffusion coefficients (upper) and free energies (lower) for unfolded Rhodanese. (Left) Unconfined; (center) confined in repulsive GroEL; (right) confined in GroEL interacting with Kim-Hummer potential.

Because of the nature of our model of GroEL:Rhodanese interaction, we can address the sequence-specific effects which give rise to a higher affinity of the C-terminus for the cavity wall. Although the folds of the N- and C-terminal domains are highly similar (Cα-RMSD 1.65 Å for alignment of residues in secondary structure (52)), their sequences are highly dissimilar (13% sequence identity), suggesting that interactions with the cavity may differ for the two domains. To determine the magnitude of the Rhodanese:GroEL interactions, we calculated the average total interaction energy between Rhodanese and GroEL and the average number of contacts made by each domain with the cavity wall in simulations of unfolded Rhodanese. We used the same umbrella sampling runs as used for the calculation of the diffusion coefficient, above, to enhance sampling of the unfolded state. The average energy per cavity contact for the N domain was 0.12 kcal mol⁻¹, much smaller than that for the C domain, 0.27 kcal mol⁻¹. The energies per residue were 0.07 and 0.12 kcal mol⁻¹ for the N and C domains, respectively. The results suggest that the C domain makes stronger contacts with GroEL when compared with the N domain and therefore spends more time bound to the cavity wall.

Partial escape of Rhodanese from the GroEL cavity

An interesting phenomenon observed in the simulations with the attractive GroEL is that a portion of the unfolded Rhodanese termini transiently escapes from the GroEL interior through channels in the side of the barrel. Note, however, that, on the time scale of our simulations, we did not observe escape through the disordered termini at the base, as has also been proposed (53). To quantify the extent to which this escape occurs, we define Rhodanese residues to be outside GroEL if they reside outside a cone defined by x² + y² = (a + bz)² where a and b were determined to be 45.3 Å and 0.27 respectively, by fitting to the Cα coordinates from the GroEL structure. In Fig. 6, we show histograms of the fraction of Rhodanese outside the chaperonin and the distribution of the exterior residues on z. It is not clear whether these partial escape events may be related to the mechanism of the chaperonin, but it is possible that reducing the amount of chain inside the cavity may lower the frustration from nonnative contacts toward forming the correct folded structure. We note that there is some empirical support for a partial escape of the substrate, from experiments using anti-Rhodanese antibodies to detect the exterior portion of the chain (54).

Figure 6.

Excursions of unfolded Rhodanese outside GroEL cavity. (A) The probability density for Rhodanese residues found outside the cavity along z from the base (z = −65 Å) to the tip (z = 45 Å) of GroEL and (B) the probability density of the fraction of Rhodanese residues outside the cavity, f_outside. (C) An example of a portion of the Rhodanese chain outside the chaperonin, taken from the simulations with the KH cavity, with GroEL cut away to show also the interior portion of the chain; color scheme as in Fig. 4.

Discussion

We have shown that the inclusion of sequence-specific interactions between GroEL and the substrate Rhodanese is an important factor in determining folding rates in the chaperonin, comparable in magnitude to the volume exclusion due to confinement, but with the opposite effect on the rate. While confinement in an appropriately sized repulsive spherical cavity captures quite well the excluded volume effects of the chaperonin on the folding rate, it is necessary to incorporate more realistic physical interactions with the cavity to obtain results comparable to experiment. The origin of the slowdown is stabilization of the unfolded state, rather than interactions with the cavity wall. We expect this observation to be fairly generally applicable to GroEL substrates and other model substrates, and not an extreme example. This is because the hydrophobicity of the Rhodanese sequence is quite typical of that of real substrates or model proteins (55).

One aspect in which our results differ from experiment, is that the order of folding of N- and C-terminal domains is reversed, with the N-terminus folding faster than C in simulations, but slower than C in experiments. This appears to reflect a relatively subtle balance between the native interaction strengths of the two domains: having similar structure, their relative folding rates are predominantly affected by domain stability (56). We found that, by decreasing the native contact energies of the N domain by 5% and increasing those of the C domain by 5%, their order of folding can indeed be reversed (see Fig. S3); however, this order of folding should not affect our conclusions regarding the effect of the chaperonin on folding rates. We note the fact that, in the rescaled model, the unconfined N-domain folds more slowly that the C-domain, while the C-domain is slowed more by the interactions with the GroEL—which opens the possibility that encapsulation could reverse the order of folding. We have also focused on relative folding rates, rather than an absolute comparison of our folding rates with those from experiment. The coarse-graining methods employed in our simulations result in a smoothing of the energy landscape, as a result of the reduction in degrees of freedom and the removal of nonnative interactions within Rhodanese. This permits folding events to be observed within reasonable timescales, with the result that our calculated folding rates were much larger than those observed experimentally, even after rescaling for frictional effects.

In this work, we have focused on folding of already-encapsulated proteins. Although ATP-dependent turnover is certainly important, interactions with the chaperonin cavity are always present and need to be accounted for. We have shown that encapsulation in the GroEL cavity slows down the folding of Rhodanese using a coarse-grained, yet complete, structural model of SR1 GroEL/ES and a transferable potential for modeling interprotein binding, corroborating the results from single-molecule experiments (35). Although attractive interactions theoretically stabilize protein oligomers in confinement (57), the effect on stability and kinetics of protein folding is more complex. Using a simple model cavity with attractive walls, Betancourt and Thirumalai found an interesting “turnover” (23) in folding rate with the strength of interaction: a weak interaction initially increased the folding rate, but then stronger interactions slowed it down again, resulting in an optimal interaction strength which maximized the folding rate (a similar effect has been observed for protein-protein interactions in the presence of attractive crowders (58)). Weak interactions initially stabilize more folded structures (including the folding transition state) because these are able to form more contacts at a lower entropic cost; however, once the interactions become sufficiently strong, the unfolded state is ultimately able to form more contacts with the cavity wall and is consequently stabilized. The turnover in folding rate motivated the suggestion that the interactions with the chaperonin may have been optimized so as to maximize folding rate (23). Our results (and the experiments on Rhodanese folding) suggest that, at least for GroEL and Rhodanese, the interactions are sufficiently strong that they fall in the regime where folding is slowed down—not just relative to confinement in a repulsive cavity, but even relative to the unconfined protein. This naturally prompts one to ask what the role of such interactions might be. One possibility is that they are unavoidable and bounded by the range of possible interaction strengths between polypeptide chains. To investigate the range of possible interactions, we considered three putative GroEL variants in which we replaced all coarse residues of the chaperonin with one of tryptophan, serine, or glutamic acid, representing hydrophobic, polar, and charged surfaces, respectively. While such variants could never exist in reality, they provide a measure of the extremes of interaction strength accessible to protein sequences. We calculate the fraction of the unfolded protein which is bound in each case, obtaining fractions bound of 0.82, 0.19, and 0.17, for GroEL lined with Trp, Ser, and Glu, respectively, compared to 0.47 for the real GroEL. This suggests that, in fact, a considerable range of interaction strength is possible within the available sequence space. Thus, the interactions may not have been tuned to maximize folding rate; rather, they may confer some advantage for substrate folding. Studies using simplified models have shown that indeed, weakly hydrophobic interactions can assist the correct folding of proteins with frustrated energy landscapes (23,27).

What are the implications for the mechanism of action of GroEL? The fact that the folding is in fact slowed by interactions with the cavity wall suggests that, in the case of Rhodanese, the primary function of the chaperonin is to sequester the protein to avoid aggregation before it is folded or to prevent misfolding, rather than to accelerate folding. However, it is certainly possible that an iterative annealing mechanism may be important in other cases. Including the possibility of iterative annealing in the context of such a coarse-grained model would therefore be interesting to address in future work.