The Control of Global Brain Dynamics: Opposing Actions of Frontoparietal Control and Default Mode Networks on Attention

Abstract

Understanding how dynamic changes in brain activity control behavior is a major challenge of cognitive neuroscience. Here, we consider the brain as a complex dynamic system and define two measures of brain dynamics: the synchrony of brain activity, measured by the spatial coherence of the BOLD signal across regions of the brain; and metastability, which we define as the extent to which synchrony varies over time. We investigate the relationship among brain network activity, metastability, and cognitive state in humans, testing the hypothesis that global metastability is “tuned” by network interactions. We study the following two conditions: (1) an attentionally demanding choice reaction time task (CRT); and (2) an unconstrained “rest” state. Functional MRI demonstrated increased synchrony, and decreased metastability was associated with increased activity within the frontoparietal control/dorsal attention network (FPCN/DAN) activity and decreased default mode network (DMN) activity during the CRT compared with rest. Using a computational model of neural dynamics that is constrained by white matter structure to test whether simulated changes in FPCN/DAN and DMN activity produce similar effects, we demonstate that activation of the FPCN/DAN increases global synchrony and decreases metastability. DMN activation had the opposite effects. These results suggest that the balance of activity in the FPCN/DAN and DMN might control global metastability, providing a mechanistic explanation of how attentional state is shifted between an unfocused/exploratory mode characterized by high metastability, and a focused/constrained mode characterized by low metastability.

Introduction

Understanding how cognition emerges from neural activity requires a description of the dynamic interactions between brain regions. Intrinsic functional connectivity networks (ICNs), reflecting underlying patterns of structural connectivity, have previously been described (Honey et al., 2009; Smith et al., 2009). However, network activity is dependent on behavioral context, dynamically reconfiguring over time (Fox et al., 2005). Therefore, the investigation of brain networks needs to consider not only the structural connections that constrain functional interactions, but also dynamic changes in functional interactions.

One approach is to consider the brain as a complex dynamic system (Beggs and Plenz, 2003; Beggs, 2008; Kitzbichler et al., 2009; Chialvo, 2010; Shanahan, 2012). Metastability, which we here define as the tendency to move endogenously between transient attractor-like states, is an important property of such systems (Friston, 1997; Tsuda, 2001; Shanahan, 2010a; Kelso, 2012). According to one hypothesis, increased metastability in the brain allows more flexible dynamic interactions between regions, whereas reductions in metastability may accompany persistent, more stable states (Shanahan, 2010b).

The relationship between brain network metastability and cognition is unclear. High metastability may facilitate transitions between a large repertoire of network configurations, allowing an exploratory cognitive state and the efficient response to changing external events (Werner, 2007; Deco et al., 2009; Fritz et al., 2010). In contrast, once a specific behavior is needed, for example in response to a perceived threat, networks supporting a focused response should be stable over time, corresponding to a reduction in the metastability of the system. This study explores the idea that changes in whole-brain metastability go hand in hand with shifts between unfocused, exploratory, or “resting” states and focused attentionally demanding states.

These broadly opposed cognitive states (exploratory vs focused) are associated with functional differences in well established ICNs. Activity in frontoparietal control networks (FPCNs) and dorsal attention networks (DANs) is high when attention is directed externally (Corbetta and Shulman, 2002; Vincent et al., 2008; Spreng et al., 2010; Fornito et al., 2012), associated with the reduction in activity within the default mode network (DMN) (Singh and Fawcett, 2008). These networks show anticorrelated activity over time, which may be important for efficient cognitive function (Werner, 2007; Kelly et al., 2008; Deco et al., 2011; Shanahan, 2012).

We investigated the relationship between brain activity and global dynamics (particularly a measure of the variability in the spatial coherence over time that we use as a proxy for metastability) in two behavioral states, as follows: (1) an attentionally demanding task [the choice reaction time task (CRT)]; and (2) an unconstrained resting state. Figure 1 presents a high-level schematic of our approach, in which computational simulations complement empirical neuroimaging data. We first recorded functional MRI data during both the performance of the CRT and with the subject at rest (Fig. 1A). We then simulated the neural dynamics arising in these distinct cognitive states using a computational model of brain function consisting of a network of Kuramoto oscillators (Kuramoto, 1984), constrained by the white matter connectivity of the brain (Fig. 2A). Previous work has demonstrated that patterns of fMRI activity measured within the DMN can be simulated by similar computational models (Cabral et al., 2011).

Figure 1.

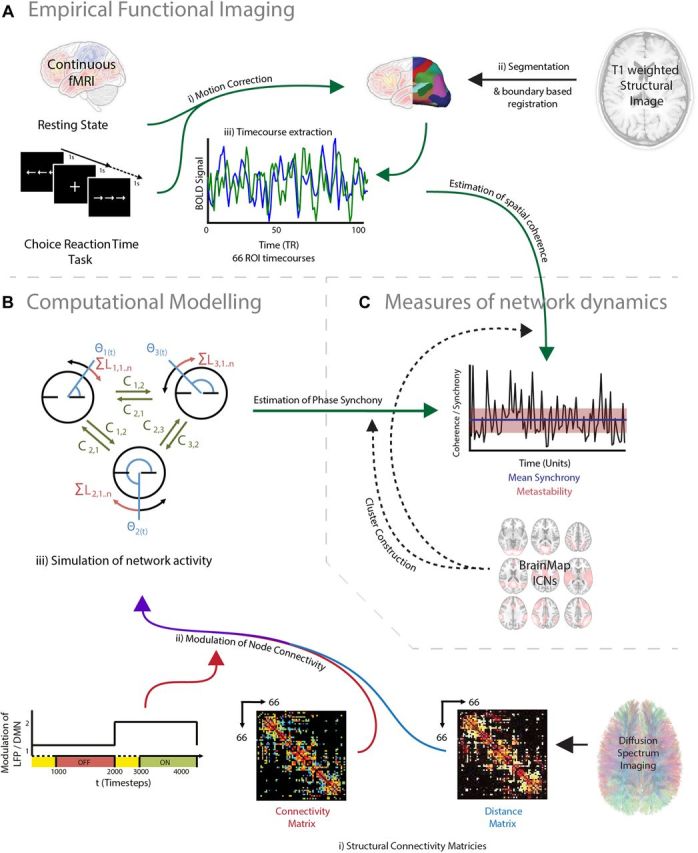
Overview of experimental design. A, fMRI was used to estimate global measures of network dynamics during task or rest. Example time courses are extracted from the right precentral gyrus (blue) and the left precuneus (green). B, We used a computational model to simulate neural dynamics using dynamic systems framework constrained by structural connectivity. C, We used analysis of the coherence of empirical fMRI data, and the phase output of the computational model to compare the global dynamics of empirical data and the dynamics of a computational model constrained by structural connectivity and activation of specific regions of the brain. The example demonstrates spatial coherence over time of empirical data during the choice reaction time task.

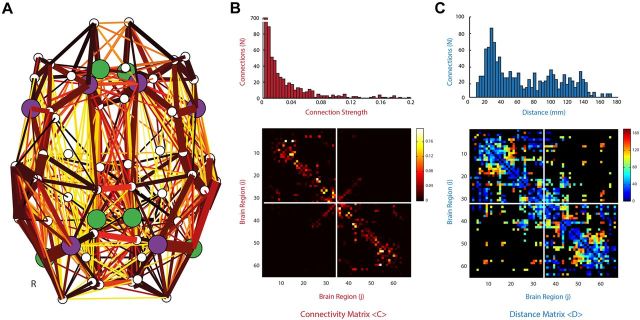
Figure 2.

Structural overview of the computational model. A, Graphic overview of the 66 region structural connectivity matrices used in the Kuramoto oscillator system. B, Thickness of connecting vertices represents the strength of connections according to the connectivity matrix. C, Hotter colors represent longer connections, according to the distance matrix. Regions are sorted according to the regions shown in Table 1. Nodes comprising the FPCN/DAN are highlighted in purple. Nodes comprising the DMN are highlighted in green.

We tested the hypothesis that the CRT would be associated with decreased metastability, whereas the unconstrained rest state would be associated with the reverse pattern. As expected, we found this change both in the simulated data and empirical data (using proxy measures for network dynamics), providing converging empirical and theoretical evidence for global changes in network dynamics relevant to cognitive control.

Materials and Methods

Empirical functional data

Subjects.

Sixteen subjects (8 females; mean age, 28 years) underwent functional MRI while performing (1) a continuous version of the CRT, and (2) a rest scan where there was no explicit task. In addition, 24 separate neurologically healthy subjects (8 males; mean age, 35.0 years) took part in a further fMRI study where the CRT was interleaved with rest in a blocked design. Data from this second study were used to functionally localize regions more active during the CRT or during rest. All participants gave written consent, were checked for contraindications to MRI scanning, and had no history of significant neurological or psychiatric illness. The Hammersmith, Queen Charlotte's & Chelsea research ethics committee awarded ethical approval for the study.

Image acquisition protocols.

Functional MRI data were acquired using a Phillips Intera 3.0 tesla MRI scanner using standard protocols. Earplugs and padded headphones were used to protect participants' hearing during the scanning procedure. Standard T1-weighted structural images were also acquired for coregistration and segmentation of functional data.

Stimulus design.

During the CRT task, an initial fixation cross was presented for 350 ms. The fixation cross was followed by a left or right response cue arrow to which subjects were instructed to respond as quickly and as accurately as possible with a button press with the right or left index finger. Each trial was presented for 1000 ms, with an interstimulus interval of 1000 ms during which the fixation cross was displayed on screen. Trials were repeated continuously for the duration of the functional acquisition. There was no rest period, jitter in the intertrial interval, or other baseline task during the continuous run. As such, dynamics during this task were not due to alternating between rest and task or different task demands. During the 5 min resting-state run, participants were asked to lie still in the scanner with their eyes closed and were not asked to perform any task in particular.

Analysis of functional imaging data.

Preprocessing of functional data involved realignment of EPI images to remove the coarse effects of motion between scans using the FMRIB motion correction tool MCFLIRT (Jenkinson et al., 2002; Smith et al., 2004; Fig. 1A). T1 images for each subject were segmented into 66 regions homologous with those characterized in the Hagmann human cortical connectivity datasets using the Desikan-Killiany Freesurfer atlas (Dale et al., 1999; Desikan et al., 2006; Hagmann et al., 2008; Table 1). The segmented T1 images were registered to the motion-corrected data using boundary-based registration (Greve and Fischl, 2009). Mean BOLD time series for each cortical region were extracted for both the continuous CRT and resting-state scans. We bandpass filtered the data between 0.01 and 0.15, and then regressed out a six-direction motion parameter model estimated by MCFLIRT (Jenkinson et al., 2002; Smith et al., 2004) and time series-sampled from regions of white matter and CSF to reduce physiological and movement confounds. Analyses were either calculated on all regions simultaneously (global) or within specific predefined intrinsic connectivity networks (local). The ICNs were estimated by projecting the resting state-independent components corresponding to putative brain networks (rather than non-neural noise) from Smith et al. (2009) onto the 66 regions of interest. A region was classified as part of a specific ICN if the mean value from the independent component was within z > 1.64 (nominal p > 0.05). The ICNs were labeled according to the study by Smith et al. (2009): primary and secondary visual, dorsal attention, default mode, motor, auditory, salience, and right and left lateralized frontoparietal networks. (5) Given the relatively few time points in the fMRI time series, rather than measuring signal coherence using techniques such as wavelet coherence (Kitzbichler et al., 2009; Chang and Glover, 2010), we define a proxy measure of metastability as the variability in spatial coherence of the signal globally or locally (within a network) over time according to the following equation:

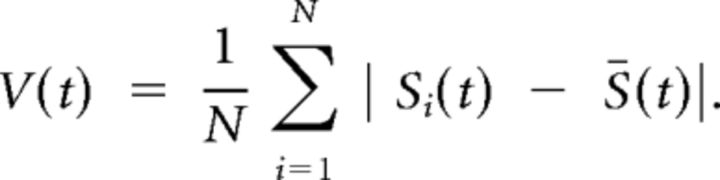Where V is the spatial coherence of a group of N regions at each time point (either of all 66 for global measures or a specific subset for local coherence within an ICN), S_i is the signal for an individual region of the brain (see above), and S̄ is the mean of all considered time courses. We define our proxy measure of metastability as σV, the SD of V across time and our proxy measure of synchrony as the reciprocal of mean spatial variance across time, 1/V̄.

Table 1.

List of network nodes and corresponding Talairach centroids for each region

Label		Brain region	Centroid*
Right	Left		Left	Right
1	66	Entorhinal cortex	[−24.00, −9.00, −24.33]	[26.00, −7.00, −26.50]
2	65	Parahippocampal gyrus	[−24.33, −32.50, −11.00]	[27.33, −30.50, −12.33]
3	64	Temporal pole	[−31.25, 10.75, −30.50]	[32.67, 14.33, −29.67]
4	63	Frontal pole	[−10.00, 62.50, −6.00]	[9.00, 63.00, −8.00]
5	62	Fusiform gyrus	[−35.32, −45.50, −13.18]	[36.00, −45.82, −13.55]
6	61	Transverse temporal cortex	[−43.25, −22.25, 10.25]	[43.67, −20.33, 9.67]
7	60	Lateral occipital cortex	[−27.09, −88.14, 4.09]	[29.53, −87.42, 5.16]
8	59	Superior parietal cortex	[−22.59, −59.00, 45.41]	[24.85, −58.37, 46.04]
9	58	Inferior temporal cortex	[−49.65, −33.59, −17.59]	[50.53, −28.79, −18.74]
10	57	Inferior parietal cortex	[−36.72, −65.68, 29.56]	[43.93, −60.43, 29.07]
11	56	Supramarginal gyrus	[−50.42, −36.53, 31.68]	[51.88, −31.00, 31.44]
12	55	Bank of the superior temporal sulcus	[−51.00, −44.40, 6.80]	[50.71, −38.43, 5.14]
13	54	Middle temporal cortex	[−50.47, −30.32, −5.79]	[56.65, −23.90, −10.60]
14	53	Superior temporal cortex	[−52.83, −15.62, −1.17]	[53.32, −11.18, −2.79]
15	52	Postcentral gyrus	[−40.93, −22.73, 44.83]	[43.87, −20.39, 43.03]
16	51	Precentral gyrus	[−38.00, −9.14, 41.19]	[38.67, −7.97, 41.22]
17	50	Caudal middle frontal cortex	[−34.38, 14.23, 40.69]	[35.31, 13.15, 41.92]
18	49	Pars opercularis	[−44.36, 15.91, 14.00]	[45.60, 16.10, 13.70]
19	48	Pars triangularis	[−42.57, 32.43, 2.86]	[44.50, 31.88, 4.00]
20	47	Rostral middle frontal gyrus	[−34.05, 40.42, 16.95]	[33.77, 42.50, 15.77]
21	46	Pars orbitalis	[−40.33, 43.67, −8.67]	[39.83, 44.17, −8.50]
22	45	Lateral orbitofrontal gyrus	[−22.50, 33.70, −10.80]	[22.37, 32.26, −13.00]
23	44	Caudal anterior cingulate cortex	[−7.25, 17.50, 29.50]	[6.50, 21.25, 27.50]
24	43	Rostral anterior cingulate cortex	[−6.75, 37.50, 2.00]	[7.75, 35.75, 3.00]
25	42	Superior frontal gyrus	[−13.26, 28.88, 37.76]	[13.78, 30.02, 38.41]
26	41	Medial orbitofrontal gyrus	[−7.58, 37.50, −13.33]	[7.25, 38.25, −12.50]
27	40	Lingual gyrus	[−14.44, −65.56, 0.06]	[16.00, −65.47, −0.24]
28	39	Pericalcarine cortex	[−11.11, −78.89, 10.56]	[13.90, −77.50, 10.10]
29	38	Cuneus	[−7.13, −80.38, 22.50]	[10.40, −78.80, 22.10]
30	37	Paracentral lobule	[−8.36, −28.36, 54.64]	[10.50, −26.83, 53.50]
31	36	Isthmus of the cingulate cortex	[−8.63, −44.63, 23.00]	[11.00, −43.75, 22.50]
32	35	Precuneus	[−10.22, −52.48, 37.65]	[13.39, −56.04, 36.30]
33	34	Posterior cingulate cortex	[−6.71, −16.29, 36.71]	[8.71, −14.57, 36.57]

Nodes comprising the FPCN/DAN are highlighted in bold type. Nodes comprising DMN are highlighted in italic type.

*Data are given as Talairach coordinates [x, y, z].

Functional localizer.

Given the absence of a baseline condition for the continuous functional CRT and rest datasets described above, we were not able to use these to demonstrate the neural systems activated in the different states. Therefore, a blocked design MRI dataset interleaving CRT and rest was used to functionally localize the networks within the brain that are activated during CRT > rest, and rest > CRT. These data and analysis of the CRT data were the same as for the healthy control CRT dataset described by Bonnelle et al. (2011).

Computational modeling

Empirical structural connectivity.

The computational simulation is based on connectivity matrices describing the strength 〈C〉 and length 〈L〉 of white matter connections among 66 cortical regions defined using tractography of diffusion spectrum imaging (Fig. 1B). The network constructed by these matrices is illustrated in Figure 2A. These matrices, initially described by Hagmann et al. (2008), have been subsequently used in Kuramoto model regimes similar to those that we propose here to demonstrate the emergent properties of resting-state functional connectivity (Cabral et al., 2011). See Hagmann et al. (2008) for details of the methodology used to define these structural connectivity matrices.

Simulation of network activity.

The activity of each of the 66 brain regions (which we define here as a node) is represented in our model as the phase of a single-phase oscillator over time (Kuramoto, 1984; Acèbron et al., 2005; Cumin and Unsworth, 2007; Breakspear et al., 2010; Shanahan, 2010a; Cabral et al., 2011). Each node is connected to all other nodes within the system according to empirical connectivity matrices (see above). The phase at each node over time θ_i(t), is described by the dynamic Kuramoto oscillator equation (Kuramoto, 1984; Acèbron et al., 2005):

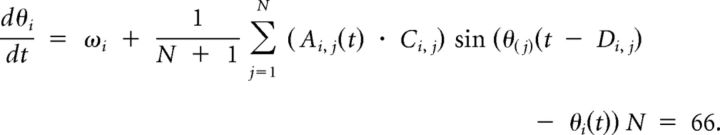The natural frequency ω defines the phase change of an uncoupled node per time step. The connectivity matrix 〈C〉 is determined by the empirical strength of white matter connections. The distance matrix 〈D〉, determined by the empirical length connections between regions, imposes time delay on phase interactions between nodes. This is analogous to simulation of a delay caused by neural conduction between regions of the brain. The time-dependent activity matrix 〈A〉(t) determines the functional state of the network (e.g., whether any regions have simulated activation; see below). In addition, two scaling factors were defined, for the distance and coupling matrices. The behavior of the Kuramoto model with respect to global metastability and synchrony by modulation of these factors has been explored previously (Shanahan, 2010a; Cabral et al., 2011). Using a grid-search approach, we set the values of these parameters within the model so as to maximize global synchrony and metastability, within a model where 〈A〉(t) is a unit matrix (i.e., a matrix with all elements equal to one). Recent work (Cabral et al., 2011; Haimovici, 2013) suggests that biologically realistic functional connectivity networks emerge from dynamic computational simulations when they maximize equivalent measures as metastability.

Simulation of cognitive states.

To simulate activation of a particular network of brain regions implicated in a particular cognitive state (e.g., the DAN/FPCN), the efferent connection strengths from the network nodes to other nodes was increased (although qualitatively similar results were achieved when bilateral—afferent and efferent—connections were modulated; Table 1). This simple manipulation was sufficient to change the global dynamics and produce qualitatively similar changes to those observed with the empirical time series.

In the simple Kuramoto oscillator model, simulating different cognitive states involves modulating the effective connectivity between oscillators. If a given brain region is more active, this is assumed to result in increased influence over connected regions. In the model, this is determined by the activity matrix, 〈A〉(t). The simulations presented here run for 4000 time steps. During the first 2000 time steps, 〈A〉(t) is a unit matrix—〈A〉(t)_{i, j} = 1 (Fig. 1B, OFF). During the final 2000 time steps, we simulated the activation of specific cognitive networks (e.g., the DMN) by selecting nodes of the specific network (e.g., posterior cingulate cortex, inferior parietal lobe) and increasing by a range of factors between 1.1 and 3 〈A〉(t), one of the two connecting edges, so as to increase the “outgoing” connectivity of these regions, according to the undirected connectivity matrix 〈C〉 (Fig. 1B, ON). To allow for the starting effects and extraneous effects of sudden manipulation of the model, we discarded the first 1000 time steps of each phase of the simulation. Pilot simulations indicated that similar results were found for a range of modulation values. By including the OFF (baseline state), we can investigate the effect of different states on synchrony and metastability (i.e., whether simulated activation increase or decrease these measures). Here we consider simulated activity within the FPCN/DAN by modulating nodes representing the bilateral inferior frontal gyrus, superior frontal gyrus, and superior parietal lobules (Fig. 2A, purple); and the DMN by modulating nodes representing bilateral inferior parietal, and anterior and posterior cingulate (Fig. 2A, green).

The first 20 time steps of both the ON and OFF periods were discarded to allow for the evolution of stable network dynamics. Measurements of network synchrony and metastability (see below) were calculated for both the ON and OFF periods to determine the change from baseline.

Measures of global and local network dynamics.

To evaluate measures of network dynamics within the computational model, we evaluated the phase history of the computational model either across all oscillators, or for clusters of oscillators defined as part of different intrinsic connectivity networks (see above), using the order parameters R(t) and Φ(t), jointly defined by:

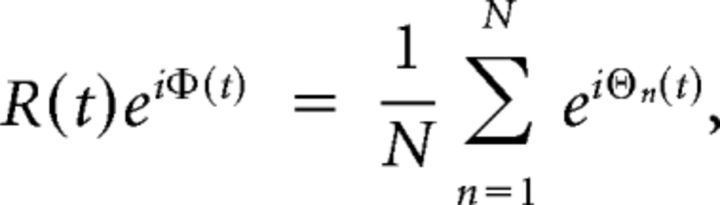where N is the total number of oscillators within the network or ICN (Fig. 1C). The level of synchrony between simulated time series from different oscillators is described by R(t), in terms of how coherently phase changes over time (Shanahan, 2010a; Cabral et al., 2011). During fully synchronous behavior, R(t) = 1 and 0, where phase across all phase time series is fully asynchronous. The global phase of the entire population of phase time series is described by Φ(t). We measure global dynamics in terms of mean global synchrony across the entire simulated time series (R̄), and global metastability as the variance σ_R of global network synchrony across the same period (Shanahan, 2010a; Cabral et al., 2011).

Results

The choice reaction time task activates the frontoparietal control network and deactivates the default mode network

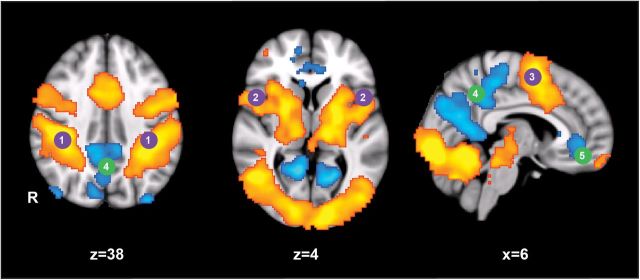
Consistent with the existing literature (Bonnelle et al., 2011; Sharp et al., 2011), performance of the CRT during fMRI was associated with significant activation in visual, somatosensory, and motor regions of the brain, as well as bilateral parts of the FPCN/DAN and the DAN (Fig. 3, purple). This comprised activation in the following areas: (1) bilateral superior parietal lobule; (2) the frontal operculum and pars opercularis; and (3) the posterior superior frontal gyrus. As expected, parts of the DMN were deactivated relative to rest during performance of the CRT. These included the anterior and posterior portions of the cingulate gyrus.

Figure 3.

Standard fMRI analysis of CRT task. Regions of the brain active during the choice reaction time task using standardized fMRI subtraction analysis. CRT > rest (orange-red); rest > CRT (blue). 1, Superior parietal lobule; 2, inferior frontal gyrus–pars opercularis; 3, posterior portion of the superior frontal gyrus; 4, anterior cingulate gyrus; 5, posterior cingulate gyrus. Cluster corrected p < 0.01, z = 2.3, n = 26.

Global and local dynamics of empirical data in different cognitive states

To assess the global dynamics of the brain during the CRT task and rest, we collected fMRI data during continuous performance of the CRT task and a separate resting fMRI run. We sampled BOLD time series from 66 different regions of the brain, and assessed the metastability and synchrony across all regions of the brain or within subsets of regions that form intrinsic connectivity networks (see Materials and Methods). Figure 4 shows the group results of global and within-network variability across time for both CRT and REST. Figure 5 illustrates the difference between CRT and rest on global and local dynamics in a single subject, with noticeably greater variability in the measure of synchrony over time. Across all the subjects, performance of the CRT was associated with a mean reduction in global metastability, compared with rest (t₍₁₅₎ = −3.18; p < 0.01) and an increase in global synchrony (t₍₁₅₎ = 3.02; p < 0.01).

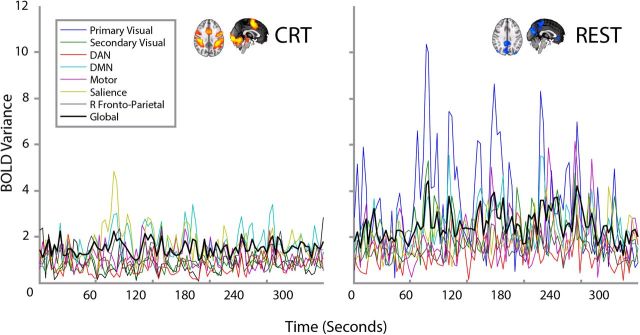
Figure 4.

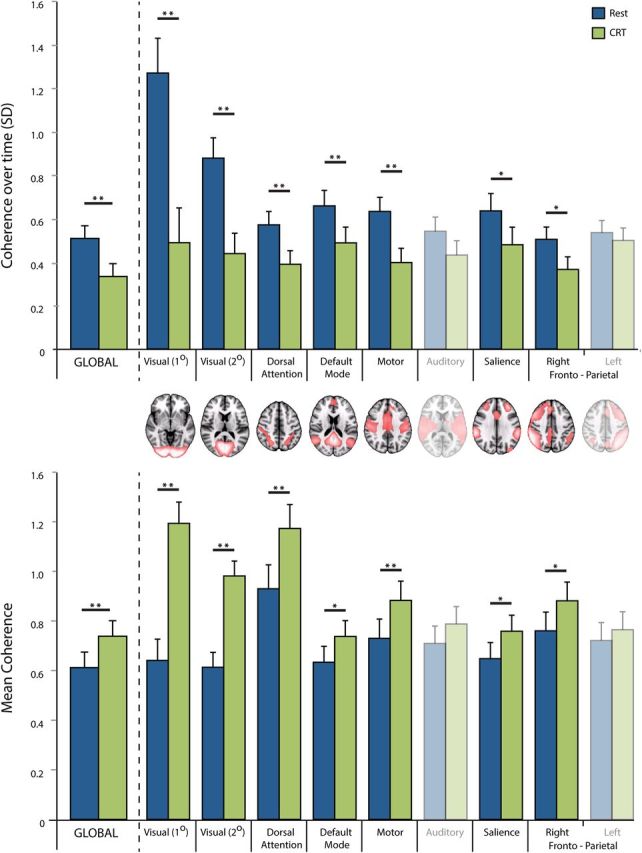
Measures of variability in coherence over time (top) and mean coherence (bottom) between CRT (in green) and rest (in blue), for continuous BOLD fMRI data. Single asterisks show differences that are statistically significant at p < 0.05 (two-tailed t test); double asterisk is significant at p < 0.01; n = 16. Error bars indicate ±1 SEM.

Figure 5.

Results from a single illustrative subject. The global (i.e., all 66 regions) and local (i.e., specific ICNs) time series of synchrony during the CRT (on the left) or at rest (on the right). Greater variability in synchrony (i.e., our definition of metastability) can be seen at rest.

To explore dynamics within ICNs, we also performed a task × ICN repeated-measures ANOVA for metastability and synchrony using networks defined by ICA (Fig. 5). For metastability, there was a significant main effect of task (F_(1,15) = 17.65; p < 0.01) and ICN (F_(2,30) = 21.16; p < 0.001), and an interaction between task and ICN (F_(2,27) = 20.327; p < 0.001). For synchrony, there was a significant main effect of task (F_(1,15) = 17.43; p < 0.01) and ICN (F_(3,49) = 26.2; p < 0.001), and an interaction between task and ICN (F_(3,39) = 26.94; p < 0.001). Post hoc t tests demonstrated significant decreases in metastability within specific ICNs, corresponding to primary visual (t₍₁₅₎ = −5.22; p < 0.001), secondary visual (t₍₁₅₎ = −5.87; p < 0.001), and motor areas of the brain (t₍₁₅₎ = −4.09; p < 0.001), including dorsal attention (t₍₁₅₎ = −2.98; p < 0.01), default mode (t₍₁₅₎ = −3.08; p < 0.001), salience (t₍₁₅₎ = −2.19; p < 0.05), and right frontoparietal control networks (t₍₁₅₎ = −2.73; p < 0.05).

In the previous analysis, the 66 regional time series were not variance normalized before calculating metastability and synchrony. However, qualitatively similar (although weaker) results were found with variance normalization, as follows: metastability was significantly reduced during CRT compared with rest both globally (t₍₁₅₎ = 2.23; p < 0.05) and within the motor network (t₍₁₅₎ = 4.99; p < 0.001). Global synchrony was significantly increased during CRT compared with rest (t₍₁₅₎ = 3.02; p < 0.01), as was local synchrony within the dorsal attention (t₍₁₅₎ = 3.22; p < 0.01), default mode (t₍₁₅₎ = −2.75; p < 0.05), salience (t₍₁₅₎ = 2.51; p < 0.05), and right frontoparietal control networks (t₍₁₅₎ = 2.51; p < 0.05).

Performance on the CRT task was highly consistent across subjects, as expected based on previous findings in neurologically healthy participants (Bonnelle et al., 2011; Sharp et al., 2011). Mean accuracy on the task was very high (97.7 ± 0.02%), and mean reaction time was fast and consistent across subjects (0.45 ± 0.061 s). Given this lack of variability, we did not expect reliable relationships between individual variability and measures of metastability. However, there was a negative correlation between metastability during CRT in the DMN and the SD of the reaction time (r₁₆ = −0.57; p < 0.05), but this does not survive Bonferroni correction.

There was no difference in head movement between the two conditions (mean relative motion per TR was 0.076 mm at rest and 0.075 mm during the CRT task; t₍₁₅₎ = 0.18; n.s.). Therefore, the differences in metastability and synchrony are highly unlikely to be due to artifacts resulting from head motion between the two conditions.

Computational modeling of cognitive network activation

To complement the empirical analysis, the dynamic systems model allowed us to simulate the effects of increased activity in the FPCN/DAN and the DMN on global metastability and synchrony. The model involved 66 Kuramoto oscillators (1 corresponding to each segmented brain region) coupled together according to a human white matter tractography atlas (Figs. 1, 2). Either the baseline state or FPCN/DAN or DMN active states were simulated and measures of dynamics calculated.

Dynamics were explored globally and locally within clusters of nodes of the model, defined in the same way as the empirical data. We then ran a task × cluster repeated-measures ANOVA for metastability and synchrony (Fig. 6A), mirroring the empirical data. For metastability, there was a significant main effect of task (F_(1,15) = 2022; p < 0.001) and ICN (F_(2,16) = 20476; p < 0.001), and an interaction between task and ICN (F_(2,27) = 1946.38; p < 0.001). For synchrony, there was a significant main effect of task (F_(1,15) = 7288.45; p < 0.001) and ICN (F_(2,22) = 47446.51; p < 0.001), and an interaction between task and ICN (F_(2,26) = 3864.95; p < 0.001).

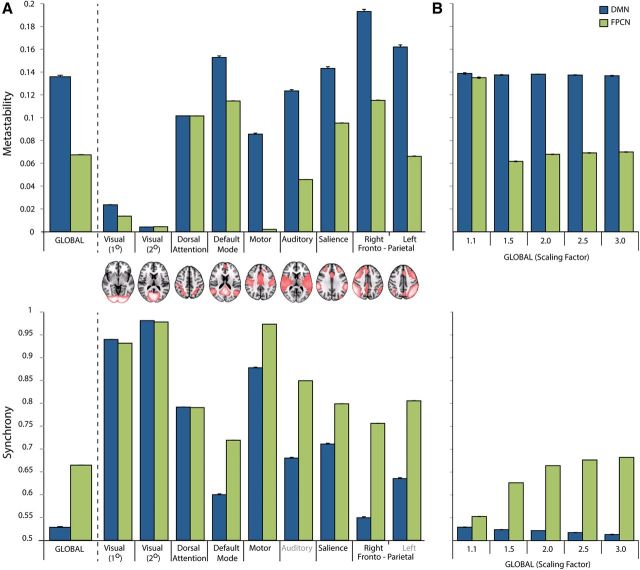
Figure 6.

Global and local measures of metastability (top) and synchrony (bottom) from the simulations of FPCN/DAN (associated with the CRT task; green) or DMN (associated with the rest state; blue). Results are averaged across 15 different simulations. A, Local measures of network dynamics within ICNs during simulation of FPCN/DAN or DMN activation with a scaling factor of 2. B, Global changes in dynamics for a range of different scaling factors. Error bars indicate ±1 SEM.

Post hoc t tests demonstrated that global metastability was significantly reduced during CRT compared with rest (t₍₁₅₎ = −46.16; p < 0.001). Significant decreases in metastability were also seen in clusters of oscillators corresponding to primary visual (t₍₁₅₎ = −45.82; p < 0.001), default mode (t₍₁₅₎ = −26.39; p < 0.001), salience (t₍₁₅₎ = −32.14; p < 0.001), motor (t₍₁₅₎ = −92.84; p < 0.001), auditory (t₍₁₅₎ = −67.75; p < 0.001), and left (t₍₁₅₎ = −46.16; p < 0.001) and right (t₍₁₅₎ = −37.39; p < 0.001) frontoparietal networks. In contrast, metastability increased within clusters of oscillators representing secondary visual areas of the brain (t₍₁₅₎ = 89.70; p < 0.001), although this result had a very small magnitude compared with the other clusters of oscillators.

A significant increase in global network synchrony occurred during simulated activation of the FPCN/DAN, compared with similar activation of the DMN (t₍₁₅₎ = −82.37; p < 0.001). This was associated with decreases in synchrony within the default mode (t₍₁₅₎ = −69.25; p < 0.001), salience (t₍₁₅₎ = −47.91; p < 0.001), motor (t₍₁₅₎ = −69.25; p < 0.001), auditory (t₍₁₅₎ = −101.05; p < 0.001) and left (t₍₁₅₎ = −82.37; p < 0.001) and right (t₍₁₅₎ = −87.03; p < 0.001) frontoparietal networks. In contrast, synchrony decreased with task within clusters of oscillators representing the dorsal attention network (t₍₁₅₎ = 4.74; p < 0.001), and primary (t₍₁₅₎ = 34.86; p < 0.001) and secondary (t₍₁₅₎ = 391.88; p < 0.001) visual areas of the brain; although, the magnitude of the effects for all three of these clusters was very small compared with those of the other ICNs.

The reported effects were found by doubling the coupling of oscillators involved in the DMN or the FPCN/DAN. The effects are consistent using a range of different factors to modulate the couplings between regions. Factors of 1.1, 1.5, 2.5, and 3 demonstrated similar changes in network synchrony and metastability (although they differed in the magnitude of their effects) (Fig. 6B).

To better understand why there are differential effects of the DMN or FPCN/DAN on dynamics in the computational model, we studied how the graphs changed. Modulating the FPCN/DAN altered the connectivity of 160 edges of the network (mean connection strength, 0.007 ± 0.017; mean distance, 77.49 ± 41.51 mm). Whereas modulating nodes representing the DMN altered connectivity along 118 edges of the network (mean connection strength, 0.016 ± 0.032; mean distance, 56.37 ± 33.79 mm). The distributions in both strengths and lengths of connections between the FPCN/DAN and the DMN were significantly different (Kolmogorov-Smirnov test: strengths, p < 0.005; lengths, p < 0.001; Fig. 7).

Figure 7.

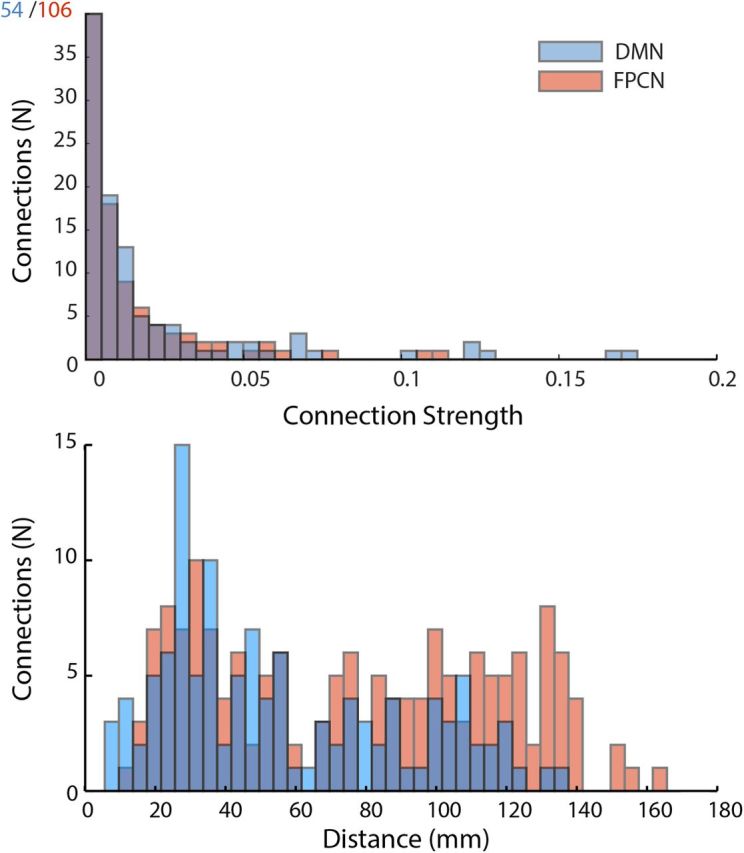
Overview of connectivity of the connectivity strength (top) and length (bottom) of edges projecting from nodes modulated during simulated activation of either the DMN (blue) or the FPCN (red).

Discussion

Here we use computational modeling and human neuroimaging to show how measures of whole-brain dynamics vary depending on the behavioral state and how this may be a consequence of the effective network organization of the brain. As expected, when subjects performed an attentionally demanding task that requires an external focus of attention, activity in the FPCN/DAN increased and activity in the DMN decreased (Fox et al., 2009; Spreng et al., 2010; Sharp et al., 2011). These relative changes in network activity were accompanied by a global increase in spatial coherence over time and a reduction in the variance of spatial coherence over time (our proxy empirical measures of synchrony and metastability). The same pattern of results was also found across the majority of specific ICNs, suggesting that the effect is global. These findings support the proposal that more stable neural dynamics emerge during periods of consistent and focused behavior. Our computational simulation results show the same qualitative pattern as the empirical results, providing a possible mechanistic explanation of how this global change in brain activity might be controlled. The simulations suggest that increasing activity in the FPCN/DAN produced a reduction of global metastability and increased synchrony. In contrast, increased activity in the DMN produced increased metastability and reduced synchrony. Across most ICNs, there was the same pattern of local decreases in metastability and increased synchrony with the CRT task, mirroring the empirical results (although there was a small subset of ICNs with the opposite pattern, albeit with a very small effect size compared with the other ICNs).

Our converging computational and empirical work suggests that global neural dynamics are “tuned” by varying levels of activity within the FPCN and DMN, which have the effect of shifting the system into a more or less metastable state. This is consistent with theoretical and experimental work suggesting that the brain exists in a critical state, at a “tipping point” between order and disorder. The scaling parameters used in the simulations were chosen to simultaneously maximize both metastability and synchrony, features that would be consistent with a critical system (Beggs and Plenz, 2003; Kitzbichler et al., 2009; Chialvo, 2010; Shanahan, 2012; Haimovici, 2013). Critical systems balance the competing demands of information propagation around a system with the need to maintain stable functional long- and short-scale connections (Beggs and Plenz, 2003; Beggs, 2008). Therefore, tuning of criticality within the brain by selective activation of functional networks may increase or decrease the information capacity of the system depending on the behavioral context. For example, at rest with activated DMN, the information capacity of the system is maximized at the expense of network stability, while during active attentional states, FPCN/DAN activation results in increased stability of the network, but reduced information capacity.

The DMN is typically more active during stimulus-independent thought, and when maintaining a broad attentional state (Buckner et al., 2008; Zhang and Raichle, 2010; Bonnelle et al., 2011; Sharp et al., 2011). Common to these types of behavior is the lack of behavioral focus, which could be thought of as “releasing” neural activity, thereby allowing it to take on multiple different network configurations over time. This variability in network configuration would result in relatively low synchrony and increased metastability when measured across the whole brain. In contrast, to efficiently perform a task like the CRT, a consistent neural configuration of visual, motor, and prefrontal cortical activity needs to be maintained over time. This would allow an individual to maintain their attention on the task, and prevent behavioral interference from internal thoughts or competing sensory stimuli that are irrelevant to task performance. This consistent network activity would result in relatively high synchrony and low metastability. This mapping between cognitive processes and whole-brain dynamics is in marked contrast to many theories of cognition that propose a discrete coupling between a region or network of brain regions and a specific cognitive ability.

The work here suggests that the FPCN/DAN can influence sustained attention through stabilization (reduced metastability and increased synchrony) of the temporal dynamics of the whole system. Similarly, the simulation of DMN activation provides a possible mechanistic explanation of the functional role of the DMN, in “permitting” the system to move into a more unconstrained state. In this state, the brain shows higher metastability and lower synchrony, exhibiting more labile dynamics, spontaneously passing between different states that would facilitate both mind wandering and maintaining a broad attentional cognitive state.

One of the most striking findings from the computational work is that differential effects on global metastability and synchrony can emerge from the same type of connection strength increase in the two networks. As the underlying connections and initial strengths in the model are based on white matter tract structure, this provides evidence that the network connections are “hard wired” to produce these different actions on network dynamics. This shows how flexible changes in large-scale network dynamics could be produced by increased effective connectivity in two opposing networks, in the absence of any long-distance inhibitory network connections. Therefore, the model provides a putative mechanistic explanation of how network topology (i.e., a functional constraint imposed by structural connectivity) relates to functional global dynamics. Although the simulated DMN and the simulated FPCN/DAN conditions both involved modulating the connectivity from equal numbers of nodes (three bilateral pairs of cortical regions), the distributions of the affected connections are different. Specifically, the connections from the DMN are predominantly strong, short-range connections, whereas the FPCN/DAN (Fig. 7) are longer and weaker connections. These results suggest that increasing long-range, weaker connections may enhance the overall stability of the network, whereas increasing the effect of shorter, stronger connections has a much smaller effect and may reduce network stability. Future computational and empirical work is needed to explore precisely how these graph-theoretical measures can explain the contrasting effects of different networks on global brain dynamics.

There are a number of limitations to the work. The computational model we have used is obviously a simplification of real brain function. For example, the simulation is built on a relatively (compared with the brain) low-dimensional connectivity matrix of 66 regions. The constraints inherent in streamline tractography using diffusion MR mean that the matrix is not directed, but instead all connections are bidirectional. In addition, long-distance connections in the connectivity matrix (e.g., interhemispheric pathways) may be difficult to resolve accurately as uncertainty in streamline location introduced by factors such as crossing fibers, increases with the length of the streamline (Jones, 2010a,b). At the level of individual nodes, we also assume all nodes to be equivalent, and differences in known cytoarchitecture are not modeled. These limitations mean that precise, quantitative comparisons between the simulations and the brain were not expected. Equally, these limitations may reduce the power of graph-theoretical interpretation the modeling results (see above). Difficulties with the measurement of BOLD fMRI signals such as partial volume effects, regional differences in vascular reactivity, or susceptibility artifacts also make precise quantitative comparisons challenging. The effects of these limitations are likely to be most pronounced on dynamics within small clusters of regions, where inaccuracies with empirical measurement of tracts and BOLD signal will have a larger effect.

However, despite these limitations, the simulation provides important insights into the relationship among the structure of the brain, patterns of functional activity, and cognition. It is striking that qualitatively similar relationships between network activity and global brain dynamics can be observed, even though the model contains no constraints about the functional roles of the regions involved (e.g., the model does not “know” that DMN regions are more active at rest). The work demonstrates how such a simple model can, at least at the level of global network dynamics, replicate the broad task-evoked changes in BOLD seen with fMRI, even though the model is based on nothing more than the network topology (i.e., the structural connections within the brain).

The simulations described are only one way of exploring the interaction between nodes. In the present model, all connections are excitatory, whereas, in reality, the function of individual connections is also defined by the receptors at the synapse (Palomero-Gallagher et al., 2009), and the neuromodulatory effect of neurotransmitters such as dopamine or serotonin is not modeled. Equally, while the Kuramoto model that we used operates only at one fast scale, constrained by the range of natural frequencies selected for each node, we have not explored whether the effects demonstrated by our network simulations are present in empirical data at multiple different scales (e.g., affecting the fast gamma band measured with EEG and the slow components of the BOLD signal measured with fMRI). Therefore, it is clear that future work should examine the types of dynamics revealed by our simulations in a range of empirical neuroimaging data at a range of spatial and temporal scales, using models capable of simulating a wider range of neural and cognitive data, should incorporate far more biological constraints including both region-specific neural characteristics as well as, for example, integrating patterns of neurotransmitter pathways and receptor densities (Amunts et al., 2000; Palomero-Gallagher et al., 2009).

Together, the work shows how changes in the balance of activity between key brain networks could shift attentional state between an unfocused/exploratory mode characterized by high metastability and a focused/constrained mode with low metastability. We propose that the balance of activity between the FPCN and the DMN acts to tune global brain metastability, which influences how consistent brain network activity is over time.