Fractionating the neural correlates of individual working memory components underlying arithmetic problem solving skills in children

Graphical abstract

Highlights

• •Developmental role of working memory (WM) components in arithmetic examined.
• •Visuo-spatial and central executive strongest predictors of arithmetic ability in children.
• •Individual WM components associated with distinct patterns of brain response.
• •Concordance between cognitive and neural fractionation of WM during arithmetic.

Abstract

Baddeley and Hitch's multi-component working memory (WM) model has played an enduring and influential role in our understanding of cognitive abilities. Very little is known, however, about the neural basis of this multi-component WM model and the differential role each component plays in mediating arithmetic problem solving abilities in children. Here, we investigate the neural basis of the central executive (CE), phonological (PL) and visuo-spatial (VS) components of WM during a demanding mental arithmetic task in 7–9 year old children (N = 74). The VS component was the strongest predictor of math ability in children and was associated with increased arithmetic complexity-related responses in left dorsolateral and right ventrolateral prefrontal cortices as well as bilateral intra-parietal sulcus and supramarginal gyrus in posterior parietal cortex. Critically, VS, CE and PL abilities were associated with largely distinct patterns of brain response. Overlap between VS and CE components was observed in left supramarginal gyrus and no overlap was observed between VS and PL components. Our findings point to a central role of visuo-spatial WM during arithmetic problem-solving in young grade-school children and highlight the usefulness of the multi-component Baddeley and Hitch WM model in fractionating the neural correlates of arithmetic problem solving during development.

1. Introduction

Working memory (WM) is now increasingly considered to be an important factor in the development of mathematical cognition in general (LeFevre et al., 2005, Raghubar et al., 2010) and arithmetic problem solving skills in particular (Geary et al., 2004, Imbo and Vandierendonck, 2008, Raghubar et al., 2010). A long line of research in adults has established that complex arithmetic problem solving tasks require active maintenance and manipulation of task relevant visuo-spatial and phonological information in WM (Hitch, 1978, LeFevre et al., 2005). In contrast, how different components of WM contribute to the development of arithmetic skills is poorly understood. Baddeley and Hitch's multi-component WM model offers a powerful approach for studying this question. This model has played a prominent role in our understanding of the fundamental constituents of general cognitive abilities (Baddeley, 1986, Baddeley, 1996, Baddeley, 2003, Baddeley, 2012, Baddeley and Hitch, 1974). Only a few behavioral studies have, however, used such models to examine how different components of WM contribute to arithmetic problem solving skills in children (LeFevre et al., 2005, Raghubar et al., 2010). Emerging behavioral data suggest that individual WM components make unique contributions to the development of arithmetic problem solving skills (De Smedt et al., 2009, Meyer et al., 2010, Simmons et al., 2012). Whether individual WM components rely on different brain systems during arithmetic problem solving is currently not known.

Baddeley and Hitch's multicomponent WM model includes a central executive (CE) responsible for high level control, monitoring and task switching, along with subordinate phonological (PL) and visuo-spatial (VS) components for short term storage and maintenance of verbal and visuo-spatial information (Baddeley, 2012). Behavioral studies have suggested that each WM component plays a different role in arithmetic problem solving. The CE is required for the complex arithmetic procedures of carrying and borrowing (Imbo et al., 2007). The phonological loop is used for active maintenance of intermediate results (Trbovich and LeFevre, 2003). And finally, the visuo-spatial sketchpad is involved in the solution of multi digit operations (Heathcote, 1994), single digit subtraction problems (Lee and Kang, 2002), and has been connected to the representation of quantities in the format of an internal mental number line representation (Rotzer et al., 2009). In children specifically, CE predicts performance on single-digit addition tasks in 5–8 year old children (De Smedt et al., 2009, Meyer et al., 2010, Simmons et al., 2012). Geary et al. (2012) found that starting in grade 1, higher CE scores predicted faster transitions from counting (e.g., 6 + 5 = 6 + 1 + 1 + 1 +1 + 1 = 11) to a more sophisticated decomposition strategy (e.g., 6 + 5 = 5 + 5 + 1 = 10 + 1 = 11). Simmons et al. (2012) found a trend for PL ability predicting multiplication performance in 7–8 year olds and other studies have demonstrated a link between PL ability and math performance tests including word problems in grade 2 (De Smedt et al., 2009, Meyer et al., 2010). VS ability has been found to predict magnitude judgment and number writing skills in 5–8 year old children (Simmons et al., 2012), and arithmetic performance in 6–8 year old children (De Smedt et al., 2009, Meyer et al., 2010).

In contrast to behavioral studies, brain imaging studies of arithmetic cognition in children have not directly examined the role of individual WM components. For the most part, the role of WM has been surmised based on greater prefrontal cortex engagement in children (Cantlon et al., 2009, Grabner et al., 2009, Ischebeck et al., 2007, Rivera et al., 2005). Two recent brain imaging studies have indirectly addressed the link between WM abilities and numerical problem solving skills. Dumontheil and Klingberg (2012) found that activity in the intra-parietal sulcus during a visuo-spatial WM task predicted arithmetic performance two years later in a sample of 6–16 year old children and adolescents. Rotzer et al. (2009) found that compared to typically developing controls, children with low math ability had lower VS abilities as well as lower activity levels in the right inferior frontal gyrus, right anterior intra-parietal sulcus, and right insula during a visuo-spatial WM task. While these studies have provided some evidence for the differential influence of WM components in numerical problem solving abilities in children, their precise neural representations remain unknown. Critically, no previous brain imaging studies have simultaneously examined the role of the three WM components in children's problem solving abilities.

Here we use an individual differences approach to fractionate the neural correlates of individual WM components underlying arithmetic problem solving skills in children. Our central goal is to test the hypothesis that the CE, VS and PL play distinct roles in problem solving. To the extent that these core components of WM engage different brain areas our findings would provide novel support for theories which posit that CE, VS and PL encapsulate distinct cognitive processes. The period encompassing ages 7–9 years is a time of significant developmental change in the acquisition of single digit addition skills as evidenced by shifts from unsophisticated to mature strategy use (Siegler et al., 1995, Siegler and Shrager, 1984) and by dynamic shifts in the role of different WM components (De Smedt et al., 2009, Meyer et al., 2010), making it an ideal period for investigating this question. Based on previous behavioral studies in children, we predicted that VS and CE would emerge as the strongest behavioral predictors of basic arithmetic skills. Studies in patients with brain lesions have emphasized dissociations linking the CE to the lateral prefrontal cortex (Baddeley et al., 1997), the PL to the inferior frontal cortex and supramarginal gyrus (Vallar and Papagno, 2002), and the VS to ventral occipito-temporal and dorsal posterior parietal cortex (Della Sala and Logie, 2002). A recent meta-analysis of verbal and visual WM tasks has pointed to a common fronto-parietal network active across different domains, with differential activation of Broca's area for verbal tasks, premotor cortex for object and location tasks, posterior lateral PFC for maintenance of items in WM and anterior lateral PFC for maintaining task set (Rottschy et al., 2012).

Extrapolating from these WM studies, we hypothesized that the CE, PL and VS components would engage distinct brain systems during arithmetic problem solving. In parallel with the hypothesized behavioral results, we further predicted that VS and CE components would strongly modulate brain activity in distinct fronto-parietal regions, while PL effects would be generally weak.

2. Methods

2.1. Participants

Seventy-four participants (40 female, 34 male) were recruited from a wide range of schools in the San Francisco Bay Area using mailings to schools and postings at libraries and community groups. Our theoretical focus on variability in working memory recruitment during complex arithmetic task performance dictated a tightly constrained focus on 7–9 year old participants (M = 7.8 years, SD = 0.7). All participants were right-handed (Oldfield, 1971) and reported no history of psychiatric illness or medication use. All participants completed the Wechsler Abbreviated Scale of Intelligence (Wechsler, 1999) and met the inclusion criterion of full-scale IQ above 80. Informed consent was obtained from the legal guardian of the child, and all study protocols were approved by the Stanford University Institutional Review Board.

2.2. Cognitive assessments

2.2.1. Mathematical abilities

Numerical Operation and Mathematical Reasoning subtests of the WIAT-II (Wechsler, 2001) were used to assess domain-wide mathematical proficiency. Numerical Operations is a pencil-and-paper test that measures number writing and identification, rote counting, number production, and simple addition, subtraction, multiplication, and division calculations. Age-appropriate examples include horizontally presented problems such as 4 − 2 = ? and vertically presented problems such as 37 + 54 = ?. Mathematical Reasoning is a verbal problem-solving test that measures counting, geometric shape identification, and single and multi-step word problem-solving involving time, money, and measurement with both verbal and visual prompts. This test also includes problem solving with whole numbers, fractions and decimals, graph interpretation, mathematical pattern identification, and solution of statistics and probability problems. Age selected examples include presentation of a drawing of a dime coupled with verbal presentation of the question: “How many pennies does it take to equal the value of one dime?”. A probability problem asks: “If you flipped a coin ten times, how many times would the coin be most likely to land on heads?”.

2.2.2. Working memory

Three subtests of the Working Memory Test Battery for Children (WMTB-C; Pickering and Gathercole, 2001) were used to assess central executive, phonological, and visuo-spatial ability. Central executive ability was assessed using Counting Recall wherein participants sequentially counted aloud arrays of 4–7 dots on cards of progressively increasing sequence length, and then recited the totals for each card in the order that the cards appeared in the sequence. For each test, the score was determined by the total number of trials successfully completed before the participant failed to produce the correct sequence three times at a given span level. Each span level consisted of 6 possible trials. Phonological capacity was assessed using Digit Recall wherein participants were presented with incrementally larger digit strings and then asked to immediately reproduce the string. Visuo-spatial ability was assessed using a variant of the Corsi block tapping task called Block Recall wherein the assessor tapped out progressively longer sequences of block patterns in a staggered three-dimensional 9 block array; participants were asked to immediately reproduce the sequence. For both tasks, the inter stimulus interval was approximately 1 second in duration.

2.3. Brain imaging

2.3.1. Experimental procedures

The fMRI experiment consisted of blocks of: (1) Complex addition, (2) Control addition, (3) Number identification and (4) Passive fixation. For Complex addition, participants were presented with an equation involving two addends and asked to indicate via button box, if the proposed answer was correct or incorrect (e.g., “3 + 4 = 8″). One operand ranged from 2 to 9, the other from 2 to 5 (tie problems, such as “5 + 5 = 10″, were excluded), and half of the trials were presented as correct equations. Incorrect answers deviated by ±1 or ±2 from the correct sum (Ashcraft and Battaglia, 1978). Control addition was based on the same task model as Complex however, one addend was always 1 (e.g., 3 + 1 = 4). Our use of this task was based on pilot studies, which suggested that children are consistently faster on these problems compared to the Complex addition problems (Ashkenazi et al., 2012, Cho et al., 2012, Rosenberg-Lee et al., 2011). Furthermore, children show less strategy variability for “N + 1″ problems, thus serving as ideal control problems for our study (Baroody, 1985, Barrouillet and Lépine, 2005, Siegler, 1987). In the number identification task, arithmetic symbols were replaced by irrelevant keyboard characters (e.g., “4 o 5 @ 7”) and participants were asked to assess if “5” was among the presented digits. Finally, in the Passive fixation task, the symbol “*” appeared at the center of the screen and participants were asked to focus their attention on it. To aid children's performance, specific task instructions appeared below each problem. During the Complex and Control addition tasks, the word “Solve” appeared below the problem. In the number identification task, the word “Find” appeared on the screen, and during the passive fixation trials, the word “Look” appeared on the screen. Stimuli were presented in a block fMRI design in order to optimize signal detection (Friston et al., 1999). In each task, stimuli were displayed for 5 s with an inter-trial interval of 500 ms. There were 18 trials of each task condition, broken up into 4 blocks of 4 or 5 trials, thus each block lasted either 22 or 27.5 s. The order of the blocks was randomized across participants with the following constraints: in every set of 4 blocks, all of the conditions were presented and the Complex and Control addition task blocks were always separated by either a Find or a Passive fixation block; all other orders of addition and non-addition task conditions were equally likely. The total length of the experimental run was 6 min and 36 s. A verification, rather than verbal production, format was used in the scanner because overt verbal responses can result in significant head movement in children resulting in unusable fMRI data.

2.3.2. Stimulus presentation

The task was programed using E-Prime (Psychology Software Tools, Inc., Pittsburgh, PA) on a PC running Windows XP. The onsets of the fMRI scan and experimental task were synchronized using a TTL pulse delivered to the scanner timing microprocessor board from a serial response box connected to the computer. Stimuli were presented visually at the center of a screen using a custom-built magnet compatible projection system. The temporal precision of stimulus presentation and response onset detection was accurate to approximately ±1 ms.

2.3.3. fMRI data acquisition

Images were acquired on a 3T GE Signa scanner (General Electric, Milwaukee, WI) using a custom-built head coil at Stanford University's Richard M. Lucas Center for Imaging. Head movement was minimized during the scan by cushions placed around the participant's head. A total of 29 axial slices (4.0 mm thickness, 0.5 mm skip) parallel to the AC-PC line and covering the whole brain were imaged with a temporal resolution of 2 s using a T2* weighted gradient echo spiral in-out pulse sequence (Glover and Lai, 1998) with the following parameters: TR = 2 s, TE = 30 ms, flip angle = 80°, 1 interleave. The field of view was 20 cm, and the matrix size was 64 × 64, providing an in-plane spatial resolution of 3.125 mm. To reduce blurring and signal loss from field inhomogeneity, an automated high-order shimming method based on spiral acquisitions was used before acquiring functional MRI scans (Kim et al., 2002).

2.3.4. fMRI preprocessing

fMRI data were analyzed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm/). The first 5 volumes were not analyzed to allow for T1 equilibration. A linear shim correction was applied separately for each slice during reconstruction (Glover and Lai, 1998). Images were realigned to the first scan to correct for motion and slice acquisition timing. Following procedures used in AFNI Despike (Cox, 1996), deviant volumes resulting from spikes in movement greater than 0.5 voxels (1.56 mm) (translational displacement computed as the square root of sum of the x, y, z plane) or spikes in the global signal greater than 5% were then interpolated using the two adjacent scans. No participant had greater than 15% of volumes interpolated. Images were spatially normalized to standard MNI space using the echo-planar imaging template provided with SPM8, resampled every 2 mm using trilinear sinc interpolation, and smoothed with a 6 mm full-width half-maximum Gaussian kernel to decrease spatial noise prior to statistical analysis. Mean average motion over x, y, and z planes for all subjects was 1.0 mm (SD = 0.8) and unidirectional motion was: x (M = 0.5 mm, SD = 0.5 mm), y (M = 0.9, SD = 0.9), and z (M = 1.5, SD = 1.0).

2.3.5. Individual subject and group analyses

Task-related brain activation was identified using the general linear model implemented in SPM8. In the individual subject analyses, interpolated volumes flagged at the preprocessing stage were de-weighted. For the mathematical cognition task, brain activity related to each task condition was modeled using boxcar functions corresponding to the block length and convolved with a canonical hemodynamic response function and a temporal dispersion derivative to account for voxel-wise latency differences in hemodynamic response. Low-frequency drifts at each voxel were removed using a high-pass filter (0.5 cycle/min). Serial correlations were accounted for by modeling the fMRI time series as a first-degree autoregressive process. Voxel-wise t-statistics maps contrasting Complex and Control addition problems were generated for each participant. For group analyses, contrast images corresponding to the Complex minus Control addition tasks were analyzed using a random effects analysis. To preserve shared variance among the three WM measures the contrast images for Complex minus Control were examined using three separate ANCOVA models including one for CE, PL and VS. Single sample t-tests were used to identify significant clusters of activity in separate whole brain analyses; in order to fully characterize WM-related effects, results from the regression analyses were not masked by task-related activation. For all analyses, significant activation clusters were determined using a height threshold of p < 0.01, with cluster correction for multiple comparisons within a gray matter mask at p < 0.05 (k = 100 voxels) determined using Monte Carlo simulations implemented in MatLab using methods similar to AFNI's AlphaSim program (Forman et al., 1995, Ward, 2000).

3. Results

3.1. Cognitive assessments

Raw and standardized scores for WIAT-II mathematical subtests and the WMTB-C measures of working memory components are presented in Table 1. Averages for all scores were in the normal range, with the exception of central executive (CE). Due to our tight age range (7–9) and lack of correlations between age and the raw working memory measures (all p > .1), all subsequent analyses were performed using these values rather than standardized scores. We analyzed zero-order correlations between multiple component WM scores and assessments of math ability to avoid elimination of shared variance consistent with the main fMRI correlational analyses. Correlations between the behavioral measures are presented in Table 2. Each of the three WM measures was significantly correlated with all of the standardized measures of math achievement, with the exception of PL ability and Numerical Operations.

Table 1.

Raw and standardized cognitive assessment scores.

Measure	Raw		Standardized
	M	SD	M	SD
Full-scale IQ	–	–	111	12.5
WIAT-II
Numerical Operations	17	4.3	105	15.3
Mathematical Reasoning	35	6.0	110	13.8
WMTB-C
Central executive	18	5.1	84	18.7
Phonological	28	3.7	106	15.5
Visuo-spatial	24	2.7	95	10.8

Note: WIAT-II = Wechsler Individual Achievement Test-Second Edition; WMTB-C = Working Memory Test Battery for Children.

Table 2.

Correlation between cognitive measures.

Variables	Mathematical Reasoning	Central executive	Phonological	Visuo-spatial
Numerical Operations	.61***	.26*	.08	.44***
Mathematical Reasoning		.37***	.26*	.25*
Central executive			.39***	.14
Phonological				−.02

df = 72.

^*p < .05.

^***p ≤ .001.

3.2. Brain imaging

3.2.1. Behavioral performance

In-scanner behavioral performance was analyzed using participant's median reaction time (RT) and accuracy. Overall, average correct RT was 2572 ms (SD = 552) and average accuracy was 83% (SD = 12). Paired samples t-tests indicated that performance on Complex problems was slower (2843 ms, SD = 621) and less accurate (77%, SD = 16) than compared to Control problems (2366 ms, SD = 554; 88%, SD = 12; t (73) = 8.3, SE = 57, p < .001 and t (73) = -5.9, SE = 1.7, p < .001, respectively). Following the analytical model of our core imaging analyses, Complex minus Control accuracy and median RT were analyzed as zero-order correlations with each WM component. In contrast to correlations to the more behaviorally sensitive measures included in the assessments of math ability, all scanner task behavior correlations were non-significant, p > .5.

3.2.2. Arithmetic task activation

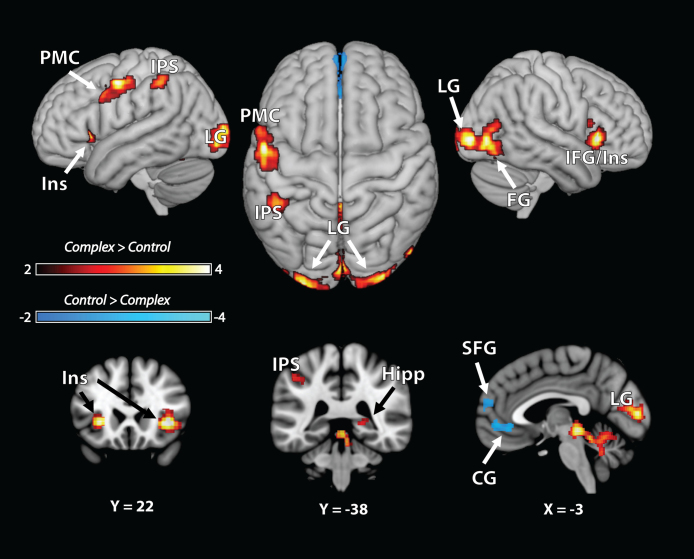
We first examined overall levels of activation independent of WM. Overall arithmetic complexity related activation (Complex minus Control) was detected in a distributed set of brain regions including bilateral lingual gyrus, bilateral fusiform gyrus, bilateral insula, left intra-parietal sulcus and left pre-motor cortex (Table 3 and Fig. 1). Task-related deactivation was observed in bilateral paracingulate cortex, anterior cingulate cortex and right frontal pole.

Table 3.

Peak activation for whole brain analysis of Complex task performance.

Region	Cluster size (voxels)	Peak T-score	Peak MNI coordinates (mm)
			X	Y	Z
Complex > Control
B lingual gyrus	6188	5.57	16	−84	6
R fusiform gyrus			38	−68	−12
R insula cortex	610	4.36	38	22	0
L pre-motor cortex	409	4.13	−54	−6	48
L insula cortex	279	4.00	−28	22	2
L supramarginal gyrus/intra-parietal sulcus	209	3.30	−44	−44	46
Control > Complex
B paracingulate/anterior cingulate cortex	224	3.12	−4	48	−4
R frontal pole/paracingulate cortex	157	2.93	2	56	18

Note: p < .01, non-parametric FWE p < .05. B = bilateral. R = right; L = left.

Fig. 1.

Arithmetic complexity-related brain activation. Significant group-level activations for the contrast of Complex–Control were detected in bilateral anterior insula, right inferior frontal gyrus, left premotor cortex, right posterior hippocampus, bilateral lingual and fusiform gyri, and left intra-parietal sulcus. Deactivation was detected only in the ventromedial prefrontal cortex. Complex addition problems were of the form x + y = z with one operand from 2 to 9 and the other from 2 to 5; the Control problems had the same format except that x or y was set to 1. PMC, premotor cortex; Ins, insula; IPS, intra-parietal sulcus; LG, lingual gyrus; FG, fusiform gyrus; IFG, inferior frontal gyrus; SFG, superior frontal gyrus; CG, cingulate gyrus; LG, lingual gyrus; Hipp, hippocampus (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).

3.2.3. Relation between arithmetic task activation and individual WM scores

Regression analysis was used to investigate the relation between arithmetic complexity related brain activation and CE, PL, and VS ability scores. We performed three separate regression analyses, one for each subcomponent, in order to preserve the shared variance between WM measures. This allowed us to detect functional dissociations as well as overlap across the three WM measures. This approach is key to our research questions assessing the uniqueness and overlap of WM components during arithmetic verification problem solving. The neuroimaging results are presented below in order of their rank-order for prediction of math achievement: VS, CE, and lastly, PL.

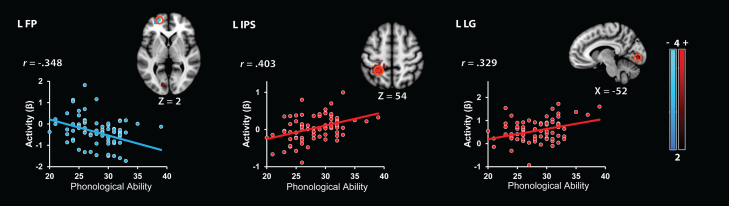
3.2.3.1. VS

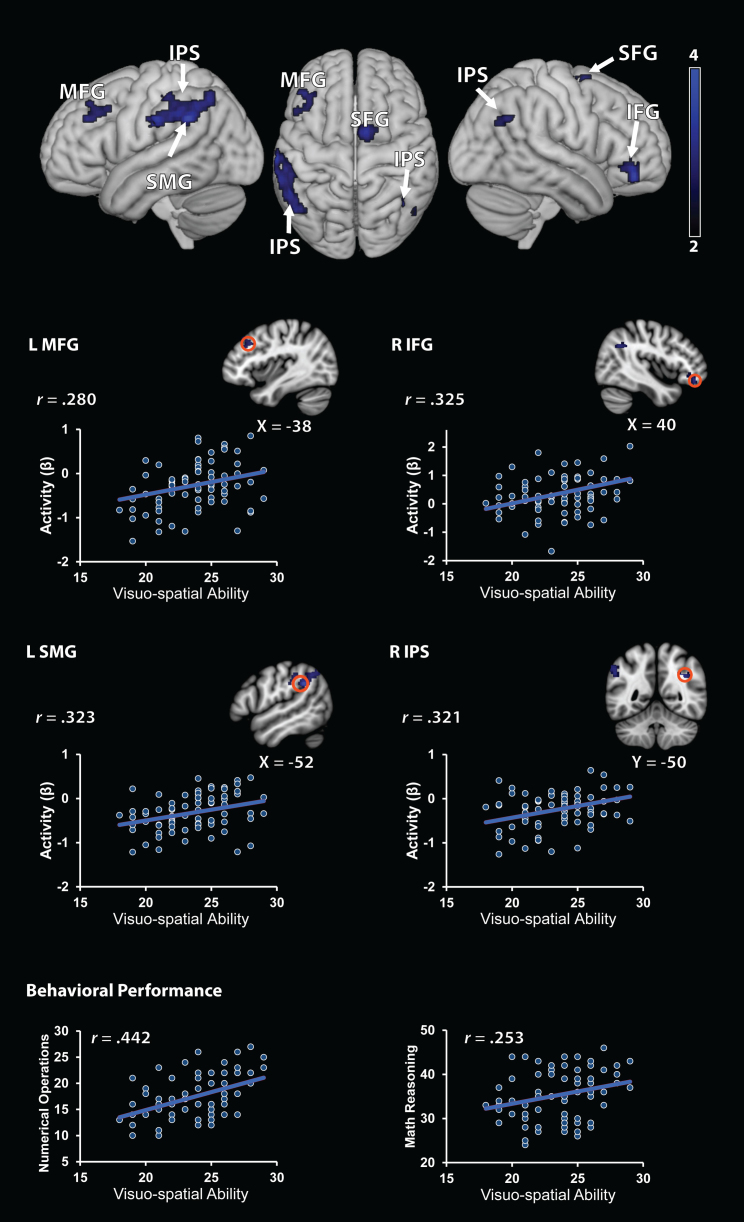
The VS component of WM was associated with task-related activation in left supramarginal gyrus, left posterior intra-parietal sulcus, right angular gyrus, left middle frontal gyrus (dorsolateral prefrontal cortex), left inferior frontal gyrus (ventrolateral prefrontal cortex), and the medial aspects of the superior frontal gyrus (Table 4 and Fig. 2). No brain regions showed negative correlations with VS ability.

Table 4.

Brain areas associated with visuo-spatial component of working memory.

Region	Cluster size (voxels)	Peak T-score	Peak MNI coordinates (mm)
			X	Y	Z
L supramarginal/angular gyrus	707	3.79	−52	−46	32
L inferior frontal gyrus	150	3.67	40	42	−14
R superior frontal gyrus	103	3.29	8	2	64
R intra-parietal sulcus (posterior)	156	3.20	38	−50	32
L middle frontal gyrus	134	2.97	−42	34	32

Note: p < .01, non-parametric FWE p < .05. R = right. L = left. No significant deactivation was observed.

Fig. 2.

Brain areas associated with visuo-spatial component of working memory. Individual differences in visuo-spatial ability emerged as the strongest and most consistent predictor of behavior and brain response during arithmetic problem solving. Increased arithmetic complexity-related brain responses were located in left dorsolateral and right ventrolateral prefrontal cortex, as well as bilateral posterior parietal cortex including intra-parietal sulcus. MFG, middle frontal gyrus; IPS, intra-parietal sulcus; SMG, supramarginal gyrus; SFG, superior frontal gyrus; IFG, inferior frontal gyrus. Bottom panel: regions of interest depicted as orange open circles (radius: 6 mm). Scatter plots are based on functional clusters identified using whole-brain regression analysis, and are provided for the purpose of visualization. L, left; R, right. Behavioral Performance: for comparison, plots of cognitive assessments of math and visuo-spatial ability. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.2.3.2. CE

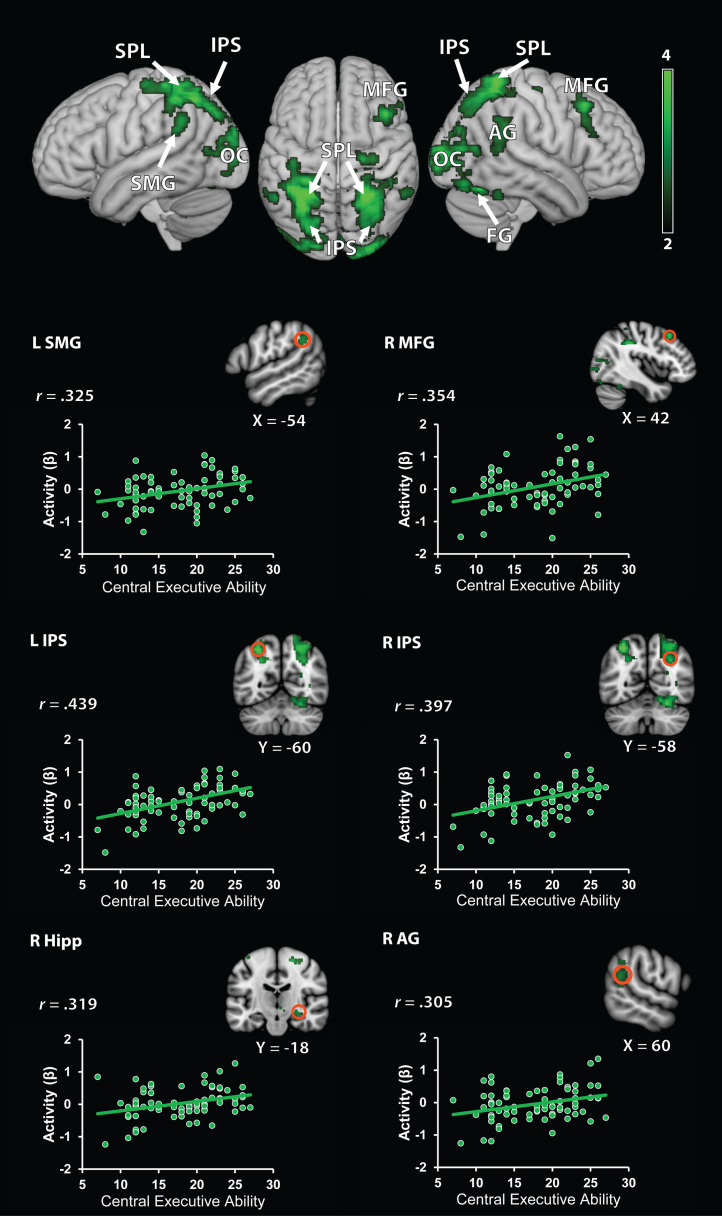
The CE component of WM was associated with task-related activation in bilateral superior parietal lobule, bilateral intra-parietal sulcus, bilateral occipital cortex and fusiform gyrus, left supramarginal gyrus, right angular gyrus, right middle frontal gyrus (dorsolateral prefrontal cortex), and right hippocampus (Table 5 and Fig. 3). No brain regions showed negative correlations with CE ability.

Table 5.

Brain areas associated with the central executive component of working memory.

Region	Cluster size (voxels)	Peak T-score	Peak MNI coordinates (mm)
			X	Y	Z
L superior parietal lobule	10,651	4.69	−28	−48	52
R superior parietal lobule		4.49	26	−50	68
L cuneus/superior occipital cortex		4.26	−20	−82	28
R occipital cortex		4.07	16	−88	14
R fusiform gyrus		4.04	26	−64	−20
R cuneus		3.39	30	−62	38
R angular gyrus		2.98	58	−46	24
R middle frontal gyrus	259	3.74	42	22	46
R hippocampus	183	3.27	30	−18	−10
R pre-motor cortex	115	3.23	22	−18	60
L supramarginal gyrus	160	3.18	−54	−50	34
R brain stem	182	3.12	6	−22	−6
R fusiform gyrus	116	3.00	40	−48	−26

Note: p < .01, non-parametric FWE p < .05. R = right. L = left. No significant deactivation was observed. Sub-peaks for the large posterior cluster (first in table) were chosen at distance 32 mm apart.

Fig. 3.

Brain areas associated with the central executive component of working memory. Central executive ability was correlated with distributed brain areas including dorsolateral prefrontal cortex, posterior parietal cortex, and hippocampus during arithmetic problem solving. SPL, superior parietal lobule; SMG, supramarginal gyrus; IPS, intra-parietal sulcus; MFG, middle frontal gyrus; AG, angular gyrus; FG, fusiform gyrus; OC, occipital cortex. Bottom panel: regions of interest depicted as orange open circles (radius: 6 mm). Scatter plots are based on functional clusters identified using whole-brain regression analysis, and are provided for the purpose of visualization. L, left; R, right. Behavioral Performance: for comparison, plots of cognitive assessments of math and visuo-spatial ability. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.2.3.3. PL

The PL component of WM was associated with task-related activation in left anterior intra-parietal sulcus and lingual gyrus (Table 6 and Fig. 4). PL ability was negatively correlated with task-related activation in the left frontal pole.

Table 6.

Brain areas associated with the phonological component of working memory.

Region	Cluster size (voxels)	Peak T-score	Peak MNI coordinates (mm)
			X	Y	Z
Positive correlations
L intra-parietal sulcus	329	4.28	−24	−46	54
L lingual gyrus	129	3.50	−8	−86	−2
L superior occipital cortex	269	3.46	−22	−74	32
Negative correlations
L frontal pole	151	3.53	−20	56	2

Note: p < .01, non-parametric FWE p < .05. L = left.

Fig. 4.

Brain areas associated with the phonological component of working memory. Negative correlations were observed in the frontal pole (FP). Positive correlates were detected in left anterior intra-parietal sulcus (IPS) and lingual gyrus (LG). Regions of interest depicted as open orange circles (radius: 6 mm). Scatter plots are based on functional clusters identified using whole-brain regression analysis, and are provided for the purpose of visualization.

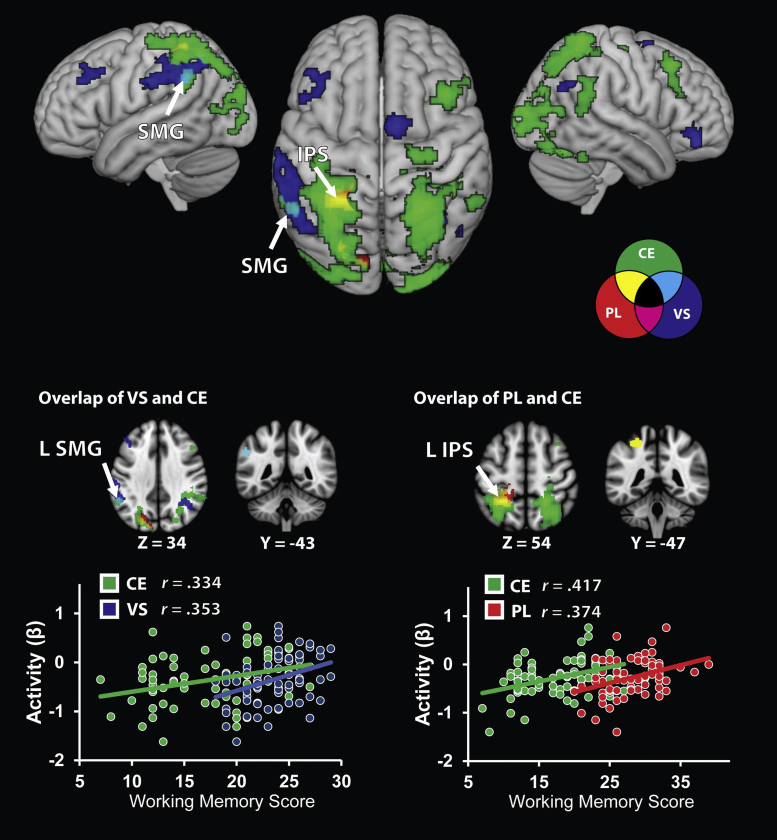
3.2.4. Functional dissociations and overlap between WM components

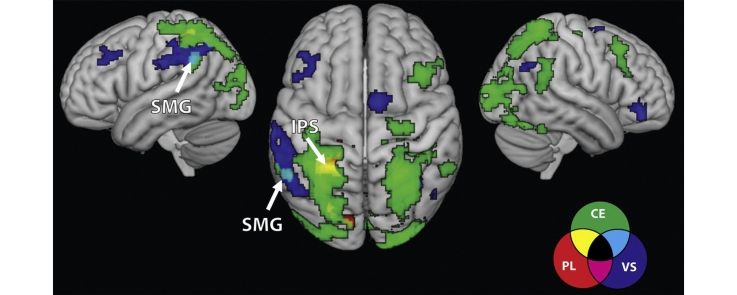
Fig. 5 shows brain areas that demonstrated distinct and overlapping arithmetic task-related activation associated with each WM component. Only two circumscribed regions of overlap were observed. First, overlap between VS and CE related activation was observed in the left supramarginal gyrus. Second, overlap between CE and PL related activation was observed in left anterior intra-parietal sulcus. No overlap was observed between brain responses associated with VS and PL ability.

Fig. 5.

Functional dissociations and overlap between brain areas associated with each of the three components of working memory. Overlap between central executive (CE) and visuo-spatial (VS) components was observed only in left supramarginal gyrus (SMG), overlap between CE and phonological (PL) components was observed only in the left intra-parietal sulcus (IPS) and no overlap was observed between VS and PL components. Negative correlation between activity and PL ability is not depicted (see Fig. 4). No overlap for VS and PL (magenta) was observed. Bottom panel: coronal slices depict regions of interest selected as overlap in correlations of activity and individual working memory components. Scatter plots are based on functional clusters identified using whole-brain regression analysis, and are provided for the purpose of visualization. L, left.

4. Discussion

Behavioral models of cognitive skill development have emphasized the separate roles of different WM components. Here we examined whether CE, VS and PL, the key components of WM, map onto distinct patterns of brain activity during arithmetic verification problem solving. We are aware of no prior studies examining individual differences in multiple components of WM ability associated with problem solving in adults or children, thus, a priori, both positive and negative correlations might have been possible: positive correlations could reflect appropriate engagement of task relevant processes and negative correlations could represent inefficient processing. It is therefore noteworthy that, with the exception of the left frontal pole involvement in PL, no brain areas in our study showed negative correlations with the CE and VS. This finding emphasizes the facilitating effects of increased WM capacity via increased cortical engagement during early arithmetic development.

Our study revealed a striking functional dissociation in arithmetic-related brain activity associated with each individual WM component. The VS, CE and PL components of WM were associated with distinct patterns of task-related brain activation in prefrontal, posterior parietal and inferior temporal cortices. Notably, the VS and CE were associated with distinct prefrontal-parietal circuits known to be involved in WM. In contrast, the effects of PL were generally weak both at the behavioral and neural levels. Notably, no brain regions showed overlap across all three components. Interestingly, all pairwise overlap was localized to left posterior parietal cortex. The effects of VS and CE overlapped in the left supramarginal gyrus, whereas the CE and PL showed overlap in left anterior intra-parietal sulcus. Collectively these results are the first demonstration of distinct patterns of brain activity related to multi-component WM in children as well as the first convincing demonstration of tripartite WM dissociation over multiple functional systems underlying arithmetic cognition in children. Below, we discuss the implication of our results for a number of extant hypotheses concerning the role of multiple WM components in children's arithmetic cognition including the fundamental role of VS ability in numerical problem solving.

4.1. Differential role of visuo-spatial working memory underlying problem solving in children

Behaviorally, VS ability emerged as the strongest predictor of math skills. Greater VS ability was associated with better performance on Numerical Operations and Math Reasoning, two standardized measures of math ability from the WIAT-II. The largest correlation obtained between any math and WM measure was between VS ability and Numerical Operations ability (r = .44), a standardized measure of arithmetic proficiency based on numerical calculations and fact retrieval without any linguistic demands. For Mathematical Reasoning, which involves word-based math problem solving, VS ability was the second ranking predictor compared to CE.

VS abilities were also strongly correlated with brain responses during arithmetic problem solving. Individual differences in VS ability were associated with increased task-related brain responses in left dorsolateral and right ventrolateral prefrontal cortex, as well as bilateral intra-parietal sulcus and supramarginal gyrus in the posterior parietal cortex. These responses were largely specific to VS ability, as overlap between the VS and CE components was observed only in a circumscribed cluster of voxels in left supramarginal gyrus; no overlap was observed between VS and PL abilities in any brain region.

Multiple lines of evidence in children have pointed to overlapping patterns of activation of fronto-parietal regions in VS WM and arithmetic problem solving (Kaufmann et al., 2011, Klingberg, 2006, Klingberg et al., 2002, Kwon et al., 2002, Rivera et al., 2005, Rotzer et al., 2009). A core theme in these studies is that fronto-parietal circuits are involved in both VS WM and arithmetic tasks. Evidence for direct links between visuo-spatial WM and arithmetic is also beginning to accumulate; Dumontheil and Klingberg (2012) found that activity level in the intra-parietal sulcus of the posterior parietal cortex during a visuo-spatial WM task predicted arithmetic performance two years later. Rotzer et al. (2009) found that compared to controls, children with low math ability had lower visuo-spatial WM performance and lower levels of activity in the right inferior frontal gyrus, right intra-parietal sulcus, and right insula during VS WM task performance. Taken together, these findings provide important new insights into the role of the VS component of WM in numerical problem solving in young children and they provide further evidence for direct links between the two domains. Our results complement these findings by demonstrating that children with greater visuo-spatial WM capacity engage frontal and parietal regions to a greater extent than children with lower visuo-spatial WM capacity.

4.2. VS, CE and PL components of WM are associated with distinct brain responses

Our findings demonstrate that CE, VS and PL are associated with distinct patterns of brain response, and provide new evidence to substantiate the Baddeley model of working memory in a developmental context (Baddeley, 2012). We observed a striking functional dissociation between brain regions associated with each individual WM component. Importantly, the VS and PL components showed no overlap and the CE was the only component that showed overlap with each of the other two components; this feature of the data also supports the Baddeley and Hitch model as PL and VS are characterized as distinct subordinate systems under the control of the CE. Finally, it is noteworthy that overlap between the CE and the two other components were observed only in the posterior parietal cortex, suggesting that this region is an important locus for the integration of information in WM during arithmetic problem solving (Ansari, 2008, Dehaene et al., 2003, Kawashima et al., 2004, Kucian et al., 2008, Menon et al., 2000, Rivera et al., 2005, Rosenberg-Lee et al., 2011). Although both the VS and CE ability were each associated with activation in multiple prefrontal and parietal areas, there was no overlap between these components except in the ventral aspects of the left supramarginal gyrus. Notably, core prefrontal regions associated with the VS and CE showed no overlap; this dissociation of WM-related functional activity is consistent with cognitive conceptualizations of fractionated WM (Baddeley, 2012) and suggest that behavioral models separating the contribution of these three WM components are fundamentally related to neural function during an arithmetic task. The greater involvement of distinct prefrontal and parietal cortices in children with higher CE ability is consistent with behavioral and neuroimaging studies which have suggested that skill acquisition in the developmental window studied here is characterized by greater reliance on control mechanisms that facilitate controlled retrieval and the inhibition of irrelevant math facts or operations (Chen and Siegler, 2000, Cho et al., 2012, Geary, 2004). Indeed, Bailey et al. (2012) recently showed that CE capacity in first graders (age 6) was predictive of ability to retrieve facts from memory in later grades. In contrast to the VS and CE components, PL was not associated with increases in brain responses in any prefrontal cortex regions. PL ability was associated with greater responses in circumscribed regions of the superior parietal lobule that overlapped with brain areas that were correlated with the CE. Our findings suggest a pattern of largely distinct brain responses associated with each WM component.

4.3. Multi-component WM and problem solving skills in children

Although the role of multi-component WM in children's arithmetic problem solving has been examined in several previous behavioral studies, no consensus has yet emerged for the differential roles of importance of the three components (Geary, 2004, Raghubar et al., 2010). Findings from our study support the fundamental explanatory properties of Baddeley and Hitch's tripartite model of WM (Baddeley, 2012, Logie, 2011) in the domain of children's arithmetic cognition and highlight largely distinct neural processes correlated with each component. Additionally, our study also highlights a specific role of VS ability both at the behavioral and neural levels. This prominent role of VS ability in both behavioral and brain measures of performance is consistent with models of arithmetic that emphasize spatial number line representation of quantity (Ashkenazi and Henik, 2010, Ashkenazi et al., 2013, Dehaene et al., 2003, Rotzer et al., 2009). The link between quantity and space requires domain-general VS processes (de Hevia and Spelke, 2010, Dehaene et al., 2003); one central example for the support systems that link number and space is visuo-spatial WM (De Smedt et al., 2009, Geary and Hoard, 2001, Holmes and Adams, 2006, Meyer et al., 2010, Rasmussen and Bisanz, 2005). During the initial stages of arithmetic knowledge acquisition children use these mental number line representations along with visuo-spatial WM to help solve problems and build domain-specific representations (de Hevia and Spelke, 2010, Rasmussen and Bisanz, 2005).

In addition to the interesting findings for the role of VS abilities in complex problem solving, the current paradigm afforded simultaneous examination of the role of CE processes during this period of arithmetic skill development. Increased fronto-parietal recruitment helps explain why better CE ability leads to better long term retrieval of facts (Bailey et al., 2012, Geary et al., 2012) despite the proximal importance of VS ability and dovetails with other behavioral data showing that more successful attempts at early executive intensive non-retrieval strategies leads to higher correct retrieval later in development (Ashcraft, 1982, Groen and Parkman, 1972, Siegler et al., 1995, Siegler and Shrager, 1984). Overlap in VS and CE correlations in the left supramarginal gyrus represents another intriguing aspect of our findings. Although multiple parietal regions were engaged during our task, only the supramarginal gyrus showed overlap between the CE and VS components. This ventral subdivision of the posterior parietal cortex is typically engaged by cognitive tasks that require manipulation of the contents of WM (Kwon et al., 2002). In contrast, the dorsal aspects of the parietal cortex, including the IPS, have generally been implicated in visual short term memory (Todd and Marois, 2005), spatial attention (Knops et al., 2009, Silk et al., 2010) and semantic representations of quantity (Cohen Kadosh et al., 2008, Hubbard et al., 2005). Behavioral research has suggested that the visuo-spatial store is supported by the more general attentional resources of the CE component of WM (Alloway et al., 2006, Thompson et al., 2006). Our study provides partial, but not full, support for this view and identifies the left supramarginal gyrus as a locus of this interaction. It is, however, important to note that this was the only brain area where the VS and CE showed prominent overlap, suggesting that the two components largely operate independently.

Previous studies of numerical cognition have reported an anterior to posterior shift in activation with development (Kawashima et al., 2004, Kucian et al., 2008, Rivera et al., 2005). Within the posterior parietal cortex, at least two studies of arithmetic have reported greater activity in older subjects in the left supramarginal gyrus (Rivera et al., 2005, Rosenberg-Lee et al., 2011). These results suggest that in math cognition, this area may be a key locus for the intersection of development and individual differences in working memory, but further research is needed to fully elucidate this relationship. In the present study we used a verification task which did not require a verbal response, whether a verbal production task involves greater engagement of the PL remains to be investigated. Finally, the current data suggest future possibilities for some integration between developmental models of arithmetic cognition that emphasize the importance of central executive processes and those that emphasize spatial-number related hypotheses by demonstrating connections to both, generalized over separate cortical areas during this important window in the development of cognitive arithmetic skill.

5. Conclusions

We examined Baddeley and Hitch's multi-component WM in the context of arithmetic problem solving abilities in children. We used a combination of neuropsychological assessments of math ability and working memory, and functional neuroimaging, within the context of a single well-controlled cognitive task involving arithmetic problem solving. We found a striking concordance between cognitively derived fractionation of WM and arithmetic complexity-related functional brain activity. This suggests that multi-component WM as a model of arithmetic development explains fundamental relationships that are manifest at the level of neural activity. Our findings point to a central role for VS abilities during ages 7–9, an important stage in the development of math abilities in children. Finally, it is noteworthy that the VS and PL components showed no overlap in brain activation and the CE was the only component that showed overlap with each of the other two components, consistent with the Baddeley and Hitch model which places PL and VS as distinct subordinate systems under the control of the CE. Overlap between the CE and the two other WM components was observed in the posterior parietal cortex, suggesting that this region is a locus for integration of information in WM during arithmetic problem solving in children. Further studies are needed to examine how brain systems associated with each WM component interact dynamically to support arithmetic problem solving and skill development in young children.

Conflicts of interest

The authors declare they have no conflicts of interest.