Polarization distance: a framework for modelling object detection by polarization vision systems

Abstract

The discrimination of polarized light is widespread in the natural world. Its use for specific, large-field tasks, such as navigation and the detection of water bodies, has been well documented. Some species of cephalopod and crustacean have polarization receptors distributed across the whole visual field and are thought to use polarized light cues for object detection. Both object-based polarization vision systems and large field detectors rely, at least initially, on an orthogonal, two-channel receptor organization. This may increase to three-directional analysis at subsequent interneuronal levels. In object-based and some of the large-field tasks, the dominant e-vector detection axes are often aligned (through eye, head and body stabilization mechanisms) horizontally and vertically relative to the outside world. We develop Bernard and Wehner's 1977 model of polarization receptor dynamics to apply it to the detection and discrimination of polarized objects against differently polarized backgrounds. We propose a measure of ‘polarization distance’ (roughly analogous to ‘colour distance’) for estimating the discriminability of objects in polarized light, and conclude that horizontal/vertical arrays are optimally designed for detecting differences in the degree, and not the e-vector axis, of polarized light under natural conditions.

1. Introduction

Imagine trying to find an apple in a tree with leaves that constantly change colour as they flutter in the wind. This analogy illustrates a terrestrial problem in the polarized light realm. Objects such as waxy leaves or insect cuticle may reflect or internally produce polarized light. Unlike most colour information, polarization often changes substantially with the orientation of an object. Both e-vector axis and degree of reflected polarized light can be affected by an object's position and orientation relative to the sun and the viewer. This relative lack of information constancy may be why object-based polarization vision seems to be comparatively rare on land, where objects tend to be swamped by high levels of background ‘polarization pollution’ [1]. It also helps to explain some of the visual adaptations in terrestrial animals that deliberately destroy or minimize polarization sensitivity [2]. In aquatic environments, however, animals do use this modality, sometimes with very high acuity, for detecting objects around them [3–6].

The absence of air underwater creates a fundamental optical difference between terrestrial and aquatic environments. Objects underwater have far lower levels of reflected polarized light owing to the low refractive index difference between water and the object's surface. Instead of a jumble of e-vector information, the underwater world is either low-polarization (when reefs, algae and other objects form the background) or dominated by a constant, mostly horizontal linearly polarized background (from particle scatter in the water column) [7,8]. Here, object-based polarization vision can, in theory, be used to great effect to increase the contrast between objects and the homogeneously polarized or unpolarized background. In the cephalopods and some crustaceans, this modality has been exploited for communication, with the development of polarized body patterns [9–11].

Our division between worlds above and below water is to some extent exaggerated: there are insect species, butterflies for example, that appear to use polarization for communication [12]. Interestingly, these signals are given by forest shade dwellers, a terrestrial situation with minimized specular reflection from leaves and other shiny surfaces [13]. Also both the polarized pattern in the sky and reflections from water surfaces provide reliable sources of polarization information on land, cues that are known to be used by a variety of animals for several different tasks [1]. However, the general differences, we note, are frequently overlooked and this paper is an exploration of the polarization potential of both aquatic and terrestrial environments, bearing in mind that, as ever in biology, there are exceptions to some of the suggested ‘rules’.

For example, object-based polarization vision can be useful in terrestrial environments that provide relatively constant gradients of polarized light, such as forest shade as just noted. Alternatively, open intertidal mudflats are also, visually, relatively simple, consisting of a flat, highly reflective (and therefore horizontally polarized) ground surface topped with a constant celestial polarization field [14]. It is unsurprising, therefore, to find that intertidal invertebrates have some of the most sensitive polarization vision systems found to date [5].

These object-based polarization vision systems differ from those found in many invertebrates that restrict their effort to certain, usually upward-directed (dorsal rim, DR) areas of the visual field. The task for the DR is to mediate specific behavioural actions such as navigation, orientation or habitat location relative to the celestial polarization sky patterns [1,15,16]. Such systems have been investigated extensively (reviewed by [2]), and so we focus our attention on the relatively poorly understood problem of polarized object detection.

To detect objects against a background, the light sensitive part of the eye must be able to register a contrast in brightness, colour and/or polarization. The underlying cellular dynamics of the photoreceptors and their neural connections are key elements in understanding how this contrast is perceived. Most vision systems are thought to employ neural opponency mechanisms to compare the activity of different photoreceptors [15,17], and subsequently the activity of different parts of the visual field. For colour discrimination tasks, a useful framework for predicting which colour differences are detectable is to calculate a measure of ‘colour distance’ based on the light environment, the spectral sensitivities of the various colour receptors and the spectral properties of viewed objects [18]. Inspired by such colour vision models, and by the earlier work of Bernard & Wehner [19] on the parallels between colour and polarization vision systems, we present a framework for predicting the visual contrast available for object detection in polarization scenes. We calculate a measure of ‘polarization distance’ that can be used to predict just-notable-differences (JNDs) between polarized objects and their backgrounds. This is done for two-channel polarization systems that are in some ways equivalent to dichromatic colour vision (potential applications to three channel systems are explored in the electronic supplementary material). In other ways, there are fundamental differences between colour and polarization models (for example, the axial nature of the e-vector of light), and we explore those differences further here.

2. Two-channel polarization vision

To illustrate the concept of polarization distance, we present a model of the simplest and probably the most common mechanism for object-based polarization vision systems, a two-channel orthogonal photoreceptor set (oriented perpendicularly to each other and to the direction of incoming light) connected by a single type of first-order opponent interneuron. This can either be thought of in terms of single photoreceptors that carry orthogonal detectors, arrays of photoreceptors (e.g. the cephalopods [20]) or even whole eyes (e.g. spiders [21]) that possess orthogonal sensitivities between them. Most of those animals known to use polarized light for object-based tasks, notably crustaceans, cephalopods and insects, but probably also some vertebrates, are thought to use such a system. Indeed, both crustaceans and cephalopods appear to go to great lengths of anatomical organization to retain a purely two-channel orthogonal system, at least to the level of the first interneuron [20,22,23]. What lies beyond the initial processing of polarization information is known relatively well for some insects [24–26] and for the crayfish [27]. For the model, and for the remainder of the paper, we will assume that the object and background differ only in their linear degree and/or e-vector axis of polarization, with brightness and hue remaining constant. Such visual systems are not expected to be sensitive to circularly polarized light so ellipticity was ignored in the model. However, the principles can easily be extended to incorporate this if necessary (e.g. for stomatopod crustaceans [28]). Bernard & Wehner [19] examined the similarities between the three variables in colour vision; intensity, hue and saturation, and the three variables in polarization; intensity, e-vector axis and degree. That approach is expanded upon in this analysis. All simulations were run in Matlab [29], code available on request.

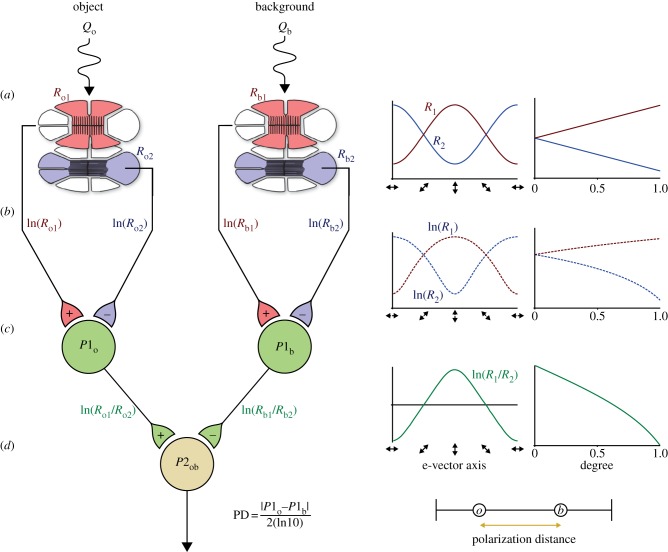
First, we consider the sensitivity characteristics of the orthogonal photoreceptor array (figure 1a). In this case, receptor R₁ is sensitive to vertically polarized light, and receptor R₂ to horizontally polarized light. Because of the axial nature of the absorption characteristics of microvilli (the membranes bearing the dichroic visual pigment [30]), the sensitivity of these receptors (R) can be modelled by Bernard & Wehner's [19] cosine function (figure 1a, right),

2.1

where Ø is the e-vector axis, Ø_max is the receptor orientation for maximal sensitivity, d is the degree of polarization of incoming light and S_p is the level of effective polarization sensitivity of each photoreceptor.

Figure 1.

Schematic of the two-channel polarization model. (a) Polarized light from an object and the background are detected by two receptors in different parts of the eye. Each receptor is composed of two sets of orthogonally oriented receptor cells, vertical (red) and horizontal (blue). Receptor activity is modulated by changes in e-vector axis and degree of polarized light (graphs right). (b) Signals from each set of receptor cells are passed via an opponent system to interneurons, which show inhibitory/excitatory responses. (c) Polarization distance is calculated as a normalized measure of relative P1 interneuron activity (d).

The signals from these two receptors are then carried to the first level of processing by nerve axons with a receptor potential approximated by the natural log of receptor activity (figure 1b). Vertical and horizontal inputs then combine through opponent connections to the first level interneuron P1 (figure 1c). Interneuron P1 therefore has the following activity profile:

2.2

where R₁ and R₂ are equivalent to R for each receptor orientation.

To compare the contrast between an object and the background, the activity of two P1 interneurons, one viewing the object (P1_obj) and one viewing the background (P1_bgd), need to be compared. Our measure of polarization distance (PD) models the difference between these two interneurons as a further level of opponency

2.3

in which the absolute difference in interneuron activity (P1) from the object (_obj) and background (_bgd) is normalized to a standard value from a system with high polarization sensitivity (in this case S_p = 10, i.e. is normalized to 2(ln10); figure 1d),

The highest contrast available to a two-channel system occurs when the object and background are fully linearly polarized with orthogonal e-vector axes matching the orientations of the two receptors. So an object that is vertically polarized, viewed against a horizontally polarized background, yields a polarization distance close to 1 (figure 2a). As the difference in e-vector axis or degree of polarization decreases, so too does the polarization distance value (figure 2b,d).

Figure 2.

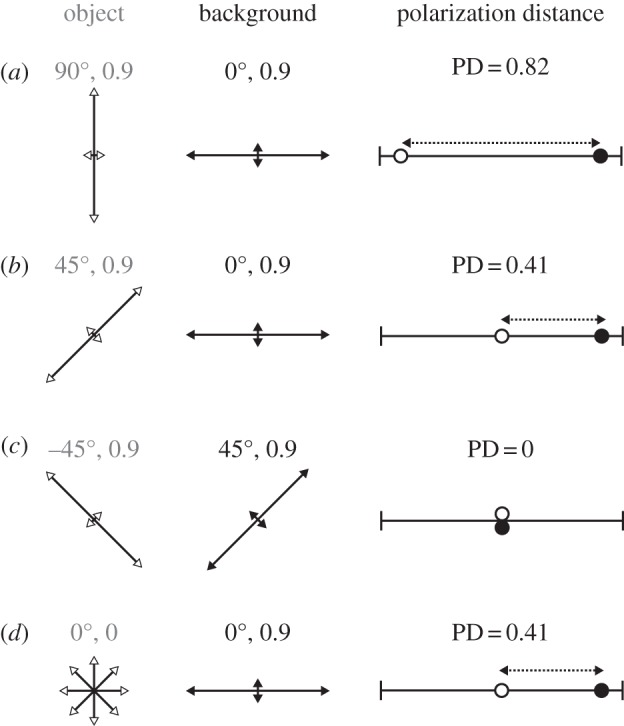
(a–d) Example polarized object (white arrows) viewed against a background (black arrows) and their associated two-channel polarization distance. Arrow orientation and length encode polarized light e-vector axis and degree of polarization, respectively. Calculations assume an underlying polarization sensitivity (S_p) of 10.

Bernard & Wehner [19] noted that two-channel polarization systems are vulnerable to a number of null points and confounds for various e-vector axes and degree conditions. For example, fully polarized light with e-vector axes at −45° or 45° are indistinguishable from each other or from unpolarized light of the same intensity. Our measure of polarization distance captures these null points, with diagonally orthogonal object and background polarized cues registering a polarization distance of 0 (figure 2c).

Using the model, we can predict how polarization distance varies across a range of different polarized object and background conditions. For example, changing object e-vector axis when viewed against a horizontally polarized background produces a simple single peak relationship in polarization distance, with maxima when the object is orthogonal to the background and minima when the object matches the background (figure 3a, solid line). This relationship changes when background e-vector is different from the axes of the receptor array. For example, for a background of 30°, a bimodal relationship occurs with maxima at 90° as well as a secondary peak around 0°. Minima are now located at 30° (matching the background) and at −30° (figure 3a, dashed line). So an object with an e-vector of −30° is essentially indistinguishable (has a polarization distance of 0) from a background of 30°. Similarly, an object of −45° would blend in to a background of 45°, despite an e-vector difference of 90° (figure 3a, dotted line). This symmetrical insensitivity across the receptor axes of sensitivity was noted by Bernard & Wehner [19] and is a well-known theoretical property of two-channel polarization vision systems. Note that, because e-vector is an axial measurement, 0°, −180° and 180° are equivalent, as are −90° and 90°.

Figure 3.

Effect of changing various parameters of polarized light on polarization distance. For each panel, some parameters are varied (a) object and background e-vector axis, (b) object e-vector and polarization sensitivity, (c) object and background degree of polarized light, and (d) object e-vector and degree of polarized light) and some remain constant (specified in inset text). For (d), polarization distance relative to a background with an e-vector of 30° and degree 0.5 (star) is represented by contour lines (ranging from 0 to 0.55). The small square illustrates a single stimulus that differs in polarization properties but which should be indistinguishable from the background. Unless otherwise stated, all graphs are calculated for a visual system with S_p = 10.

Polarization contrast vision is also affected by the sensitivity (S_p) of the animal's visual system. In our case, we have used S_p = 10 as a normalization factor for calculating polarization distance. So an animal with S_p = 10 has a maximal polarization distance of 1 when viewing a fully polarized vertically orthogonal object on a horizontally polarized background (figure 3b, solid line). As S_p becomes weaker (S_p = 5 and 2), so too does the contrast between polarized object and background (figure 3b, dashed and dotted lines). Changes in object and/or background degree of polarization also produce predictable changes in polarization contrast. As object degree of polarization increases, polarization distance also increases in a roughly linear manner (figure 3c).

Finally, the clear degeneracy between the degree and e-vector of polarized light, from the perspective of a two-channel polarization vision system, is illustrated in figure 3d. In this case, objects are viewed against a fixed 30°, 50% polarized background (figure 3d, star). Contour lines indicate combinations of object e-vector angle and degree that produce the same polarization distance. For example, the PD = 0 contour line indicates all polarized objects that are indistinguishable from the background. So a fully polarized object with an e-vector of 38° (figure 3d, square) produces a contrast of zero in the animal's visual system as a 30°, 50% polarized background, and so on.

A number of additional considerations for the design of the two-channel model are explored in the electronic supplementary material, S1.

3. Modelling discrimination thresholds

Just as for colour vision, measuring and modelling discrimination thresholds in the polarization realm is important for understanding the capabilities and limitations of object-based vision systems. These thresholds can be estimated either by modelling noise levels in the receptor and neuron photo-transduction cascade [18], or by measuring the capabilities of particular vision systems in associative learning [3,4,31,32] or innate response [5,6,22,33] experiments. Previous behavioural studies have tended to produce a single measure of difference in e-vector axis as an estimate of the capability of a given polarization vision system [3,5]. However, as we have discussed above, sensitivity to different e-vector axes varies according to absolute e-vector axis and degree of polarization. Polarization distance can therefore be a useful tool to predict how discriminable various polarized objects appear against a given background, and so can predict how JNDs should vary across different polarization conditions. JNDs are behavioural measures, again usually associated with colour, but are now also becoming possible to assign to polarization vision [3,5,6,34].

Once a discrimination threshold (and therefore JND) has been estimated, polarization distance can be used to model how this threshold should vary across different object/background polarization conditions for a suggested visual processing system. For example, in a previous experiment, we measured the discrimination threshold for the fiddler crab as a difference in e-vector angle of 3.2° [5]. The exact liquid crystal display polarization properties of the background were: e-vector = 32.0°; linear degree = 0.95; and of the just-notable looming object: e-vector = 29.8°; linear degree = 0.93. This equates to an orthogonal two-channel polarization distance measure of 0.022 (derived from equations (2.1)–(2.3), assuming S_p = 10). We can then predict the discrimination curve for a range of example backgrounds over all possible object polarization states (figure 4). In these graphs, those objects falling within the grey areas have e-vector and linear degree of polarization properties that render them indistinguishable from the example background (represented by a star in each panel).

Figure 4.

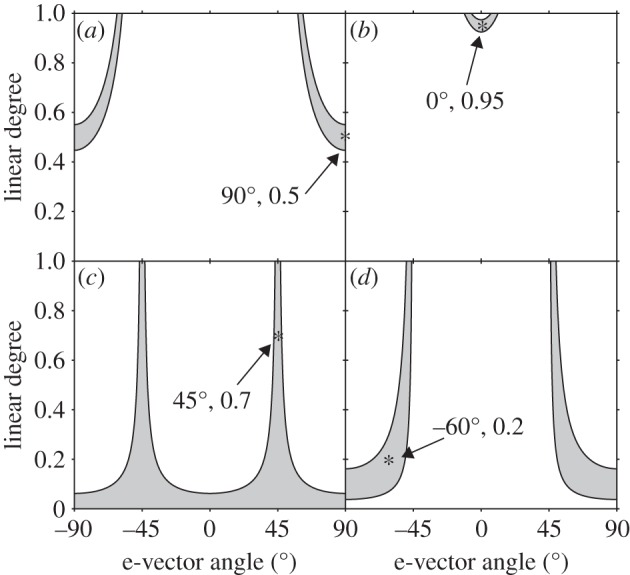
Predicted discrimination curves for the fiddler crab Uca vomeris. The star represents the polarization properties of four example backgrounds (a–d). E-vector axis and degree of polarization for an object viewed against this background are represented on x- and y-axes, respectively. Grey shaded areas indicate all object polarization properties that fall below the measured JND of the fiddler crab, and so are predicted to be indistinguishable to the fiddler crab.

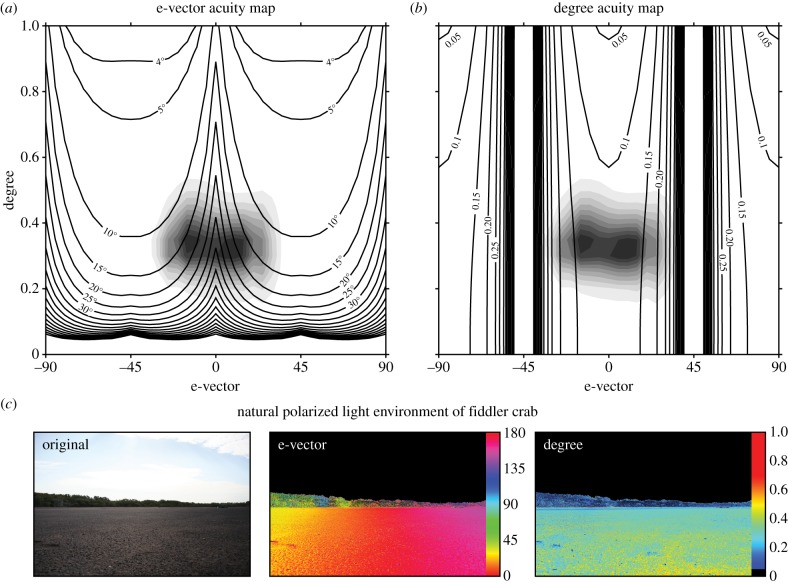
Given that the model allows us to estimate polarization JNDs for any linear polarization condition, we can now go on to make inferences about what type of signals are best designed for stimulating a given visual system in a given environment. For example, using our fiddler crab JND polarization distance of 0.022, we can solve the previous equations to find JNDs for all linear polarization conditions. Figure 5 presents e-vector and degree acuity maps, in which the black contours represent the JND value for e-vector (a) or degree (b), with all other parameters remaining the same between the background and the object. For the fiddler crab's orthogonal receptor system, e-vector acuity is the strongest around background e-vectors of –45° and 45°. By contrast, the animal is most sensitive to differences in the degree of polarized light around 0° and 90°, matching the axes of the underlying receptor system. The ground-level environment of the fiddler crab (against which it needs to discriminate conspecifics) tends to be dominated by horizontal, or near horizontal polarized light reflected from the mudflat (figure 5a,b—grey shaded contours and figure 5c—mudflat polarimetry). This corresponds to the area of maximum acuity for degree of polarized light, but minimum acuity for e-vector axis of polarized light. One explanation for this could be that the horizontal/vertical receptor array is primarily a sensor tuned to detect the differences in the degree of polarized light in a horizontally polarized world, rather than being designed to discriminate small differences in e-vector axis.

Figure 5.

Polarization acuity maps for the fiddler crab Uca vomeris. Black contour lines indicate the JND value for object e-vector (a) and degree (b) for all background linear polarization conditions. For (a) object degree is 1, and for (b) object e-vector axis is 90°. Note that the clustering of vertical contour lines in (b) indicates a steep decline in acuity towards the ±45° region. Shaded contours indicate the distribution of polarized light in the natural environment of the fiddler crab. These mudflat contours lie in the low e-vector acuity region in (a) and the high degree acuity region in (b). (c) Image polarimetry of a mudflat scene viewed in the direction of the sun (at around 45° above the horizon), from which the shaded contours in (a,b) are calculated. Note that in (c,d) all values less than 5% polarized have been assigned the colour black.

4. Polarimetry

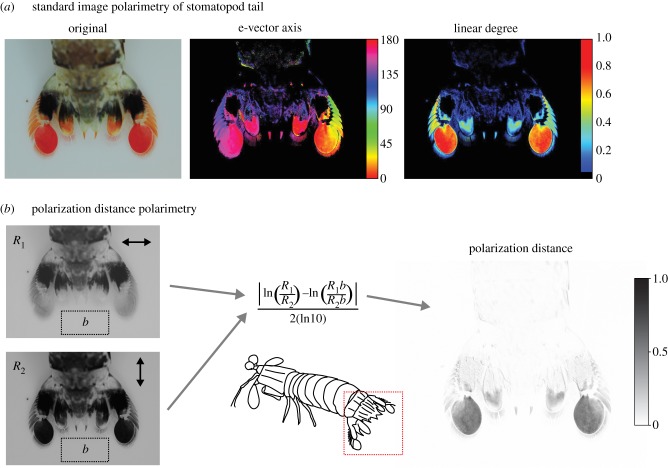
Image polarimetry is the process of reconstructing the polarization properties of visual scenes from a series of images taken through a range of different polarization filters. The differential contrast between these images can be used to calculate the Stokes parameters [35], and hence the e-vector axis and degree of polarized light at each location in the scene (e.g. figure 6a). To fully represent the linear polarization properties of a scene, a minimum of three photographs are required, taken through linear polarizers angled at 0°, 45° and 90°.

Figure 6.

Polarization distance in image polarimetry for the tail of a stomatopod Odontodactylus latirostris. (a) Example of standard image polarimetry. E-vector axis (middle) and degree (right) of polarized light were calculated from four original images (one of which is shown on the left) taken through linear polaroid filters at 0°, 45° and 90°. Note that any areas with a degree of polarized light less than 5% are assigned black. (b) Photographs taken through horizontal and vertical linear polaroid filters (left) are first filtered to match a polarization sensitivity S_p of 10 (see text for calculation) and then used to compute polarization distance (right) for all pixels relative to the background area b (left dotted rectangle). In this example, the uropods of the stomatopod are highly linearly polarized, and so have a large polarization distance (grey) relative to the unpolarized background (white).

To better understand the information available to an orthogonal two-channel polarization vision system, we can adapt polarimetry techniques to use our measure of polarization distance. To do this, two images of a scene are required, each one taken through a linear polarization filter parallel to the modelled receptor orientation. In our example (figure 6b), the tail of a stomatopod (Odontodactylus latirostris) has been photographed through a horizontal and vertical polaroid filter. The green channel is extracted from the image (as this most closely represents the spectral sensitivity of a broad spectrum polarization receptor) and each pixel value is converted to an estimate of receptor activity R for a given polarization sensitivity S_p as follows:

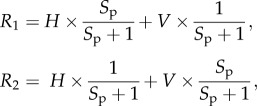4.1

where H and V are the original horizontal and vertically polarized images. In this example, we used an S_p of 10.

These estimates of receptor activity are then inserted into our polarization distance equation (figure 6b, centre). Note that a measure of polarization distance by necessity compares two regions of an image, so in this example, the stomatopod tail is compared with a background region below (figure 6b, dotted rectangle). The uropods of this species are highly linearly polarized and so stand out as dark regions in the polarimetry image (figure 6b, right). The final image therefore approximates the contrast available in the early stages of visual processing for an animal (such as a cuttlefish) with an orthogonal two-channel polarization vision system.

5. Conclusion

The use of polarization vision by some animals for detecting objects in the environment has opened the need for biologically meaningful measures of discrimination. We extended upon previous models of polarization-sensitive photoreceptors and interneurons to develop the concept of polarization distance, a measure roughly analogous to colour distance. By applying this model to orthogonal two-channel polarization vision systems we conclude that the degree of polarized light is likely to be more useful and reliable than the e-vector axis, which relies on the geometry of objects and source of illumination. We suggest that, for a constantly horizontally polarized environment such as underwater or on two-dimensional mudflats, a two-channel system with polarization sensitivity oriented horizontally and vertically is optimally designed for detecting objects differing in their degree, and not the e-vector of polarized light. Furthermore, careful eye alignment, as observed in fiddler crabs and cuttlefish, suggests (among other tasks) the strong importance of maintaining a horizontal/vertical receptor alignment with the external world. In such visual systems, the polarization distance framework allows researchers to identify null points of discrimination and generate testable predictions for polarization sensitivity to controlled stimuli. Finally, the possibility of three or more channel polarization vision systems should not be discounted, but even stomatopods appear to use multiple two-channel systems rather than three (see the electronic supplementary material, S2 for an extended discussion of three channel systems).

Funding statement

The authors were supported by funding from the Asian Office of Aerospace Research and Development, the Air Force Office of Scientific Research, and the Australian Research Council.