Preference patterns for skewed gambles in rhesus monkeys

Abstract

While standard models of risky choice account for the first and second statistical moments of reward outcome distributions (mean and variance, respectively), they often ignore the third moment, skewness. Determining a decision-maker's attitude about skewness is useful because it can help constrain process models of the mental steps involved in risky choice. We measured three rhesus monkeys’ preferences for gambles whose outcome distributions had almost identical means and variances but differed in skewness. We tested five distributions of skewness: strong negative, weak negative, normal, weak positive and strong positive. Monkeys preferred positively skewed gambles to negatively skewed ones and preferred strongly skewed and normal (i.e. unskewed) gambles to weakly skewed ones. This pattern of preferences cannot be explained solely by monotonic deformations of the utility curve or any other popular single account, but can be accounted for by multiple interacting factors.

1. Introduction

Human and animal decision-makers prefer gambles with greater expected values to those with lesser expected values. In other words, we prefer outcome distributions with higher means. We are also sensitive to outcome distribution variance [1]. Preference patterns that depend on outcome mean and variance have driven the development of many successful models of risky choice, including the concept of nonlinear utility, prospect theory, decision-by-sampling, aspirational weighting and regret aversion [1–6].

In addition to mean and variance, the first and second statistical moments of outcome distributions, gambles are characterized by a third moment, skewness, which describes the asymmetry in variance of a distribution around its mean. Positively skewed distributions have a long or heavy tail greater than the mean, whereas negatively skewed distributions have a long or heavy tail less than the mean (illustrated in figure 1a). Skewness, variance and mean are orthogonal measures, and thus can vary independently. Thus, a positively skewed gamble may offer the chance of particularly large rewards, whereas a negatively skewed gamble may offer the chance of particularly small rewards, even if the expected values and variances of the gambles are matched.

Figure 1.

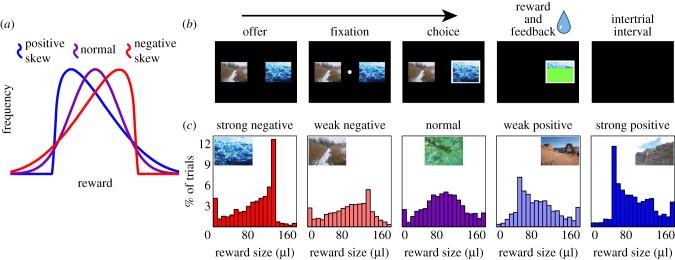
Skewness illustration and task design. (a) Illustrations of reward outcome distributions for positively skewed (blue), negatively skewed (red) and normal distributions (purple). (b) Randomly chosen nature photographs associated with each of a random pair of gambles were displayed for 500 ms. Then, a fixation dot would appear, requiring a 100 ms fixation to progress to the choice phase. Monkeys chose their preferred gamble by fixating on it for 200 ms, after which the gamble was resolved. Trials were separated by 1 s. (c) Histograms showing actual reward outcome distributions and photographs associated with the five gambles.

Knowing a decision-maker's skewness preferences can constrain models of mental processes that determine risky choices. For example, axiomatic approaches that rely on nonlinear value transformations [5] predict that risk-seeking decision-makers should prefer any positively skewed distribution to a negatively skewed one with the same mean and variance. By contrast, sampling models predict that preferences will regress towards the median, and that risk-seekers should therefore prefer negatively skewed distributions because they have higher medians [6].

The small number of previous investigations into the effects of skewness on risk preferences has suggested a preference for positive skewness [7,8], and that changes in skewness may affect preferences for variance [9,10]. However, all previous studies used discrete (rather than continuous) outcome gambles, which are susceptible to anchoring and other biases, and choices based on description, which are sensitive to editing and other biases [11]. Moreover, no previous study has examined preferences for skewness sign and strength in the same study, meaning that they lacked the sensitivity to detect nonlinear preference patterns that could falsify simple utility-based accounts of risk attitudes.

We measured decision-makers’ attitudes towards skewed distributions with closely matched means and variances. We used rhesus monkeys (Macaca mulatta) because they have very stable risk preferences (typically, strong risk-seekingness), fine sensitivity to small differences in reward size, excellent capacity for learning and a willingness to perform thousands of trials with minimal satiation effects [12].

2. Material and methods

Three rhesus monkeys served as subjects. Visual stimuli were photographs on a computer monitor in front of the animal (figure 1b). Stimuli were controlled by Matlab with Psychtoolbox and Eyelink Toolbox. A solenoid valve controlled the delivery duration of fluid rewards. Every trial monkeys chose between two different options selected randomly from a set of nine. These included four differently sized riskless rewards (107, 160, 213 and 267 μl) and five gambles with reward sizes drawn from variously skewed distributions. Although riskless options are potentially interesting, monkeys almost always chose them over the gambles, almost certainly owing to their higher expected values. Therefore, we do not describe their results further. Eye positions were sampled by a camera system (SR Research, Osgoode, Ontario, Canada). A small mount maintained head position during performance.

Each gamble was associated with an emotionally neutral nature photograph containing no humans, animals or food (figure 1c). The gambles offered a water reward whose size varied from 0 to 160 μl. The reward size on a given trial was determined by a random number generator (the function pearsrnd in Matlab's Statistics Toolbox). For the five gambles, this function used the same mean, variance and kurtosis terms (0.5, 0.25 and 3, respectively), and used five different skewness terms (−1, −0.5, 0, 0.5 and 1, respectively) to generate a multiplier. Because pearsrnd distributions are technically infinite in extent, we truncated its output at 0 and 1, effectively truncating reward sizes at 0 and 160 μl. In practice, fewer than 5% of outcomes were truncated for any of the five gambles; however, this process did lead to slight differences in mean and variance of the gambles (see the electronic supplementary material, table S1). All data are freely available on figshare: http://dx.doi.org/10.6084/m9.figshare.827292 [13].

(a). Task timeline

Options were presented simultaneously for 500 ms and monkeys were allowed to freely inspect them. Then, a central fixation dot appeared; monkeys could fixate on it for 100 ms to initiate the choice phase. Gaze directed to either option resulted in a white outline. Monkeys selected options by maintaining gaze on them for 200 ms. Following selection, the unchosen option disappeared, the gamble was resolved and reward was dispensed. In addition to the reward, a secondary feedback was shown for gamble choices: the photograph corresponding to the chosen gamble was overlaid for 500 ms with a green rectangle whose size was linearly proportional to the received reward size. Trials were separated by a 1 s interval.

(b). Precautions against false positive results

To reduce the likelihood of inadvertent p-hacking, and thus of erroneous false positive results, we designed the task and chose the size of the dataset (10 000 trials per monkey) and subject pool (three monkeys) before data collection began. Confidence intervals were calculated with the Clopper–Pearson method for binomial data with two tails and a significance threshold of α = 0.05.

3. Results

On each trial, monkeys chose between two gambles (figure 1b). The probability density functions of these gambles had nearly identical means, variance and kurtosis, but differed strongly in skewness (strong negative skewness, weak negative, normal, weak positive or strong positive; see the electronic supplementary material, table S1). No substantial trial-to-trial effects were observed in two of the monkeys; weak effects were observed in subject B for risk-seekingness, but not for skewness choices (see the electronic supplementary material).

(a). Preference for positive skewness over negative skewness

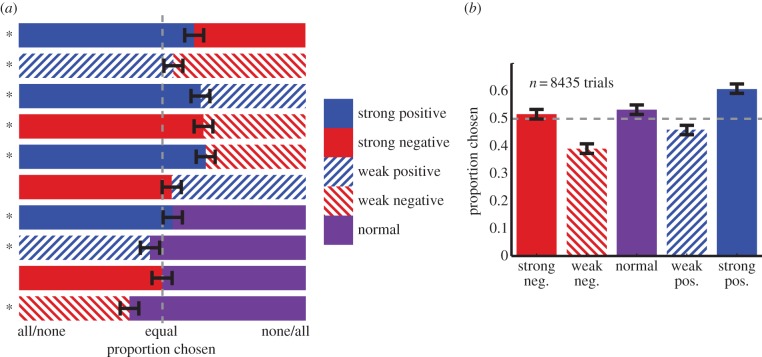
In these analyses, n refers to the number of trials in which each option pair occurred. All three monkeys preferred positive to negatively skewed gambles (monkey B: 54.56%, n = 1140, p = 0.0023; monkey H: 55.59%, n = 1083, p < 0.001; monkey J: 59.09%, n = 1166, p < 0.0001). When choosing between the two weakly skewed options, one monkey preferred positive skewness; the other two were indifferent (H: 61.13%, n = 282, p < 0.0001; p > 0.5 for the others). All three preferred positive skewness when considering strongly skewed options only (B: 57.91%, n = 278, p = 0.0098; H: 61.65%, n = 279, p < 0.001; J: 64.0%, n = 275, p < 0.0001). These results indicate that these monkeys prefer positive to negative skewness (figure 2a,b).

Figure 2.

Preferences of the average monkey. (a) Average preferences within each gamble pairing (±Clopper–Pearson interval; see §2). (b) Pairwise preferences for each gamble collapsing across all alternatives (±Clopper–Pearson interval).

(b). Preference for strong skewness over weak skewness

All three monkeys preferred strongly skewed options to weakly skewed ones (B: 57.5%, n = 1134, p < 0.0001; H: 63.94%, n = 1065, p < 0.0001; J: 62.6%, n = 1115, p < 0.0001). This bias for strong skewness was observed in the positive skewness domain (B: 56.07%, n = 280, p = 0.0484; H: 60.82%, n = 268, p < 0.0001; J: 72.83%, n = 276, p < 0.0001) and in the negative skewness domain (B: 65.81%, n = 272, p < 0.0001; H: 68.12%, n = 276, p < 0.0001; J: 58.89%, n = 270, p = 0.0041). These results indicate that these monkeys prefer strong to weak skewness, regardless of sign.

(c). Preference for normally distributed options

The skewness strength data suggest these monkeys may have a U-shaped preference function for skewness; if so, normal distributions ought to be least preferred overall. However, this does not appear to be the case. Two of the three monkeys preferred normal distributions to weakly skewed ones (B: 58.99, n = 595, p < 0.0001; H: 64.1%, n = 546, p < 0.0001). The third monkey did not have a significant preference either way (J: 51.11%, n = 585, p = 0.6189).

4. Discussion

We investigated whether monkeys are sensitive to differences in skewness for reward outcome distributions that are closely matched in mean and variance. Our three subjects consistently preferred strongly skewed gambles, positively skewed gambles and normally distributed gambles. These results confirm that our subjects can distinguish between continuous outcome distributions that differ only in skewness, and that they have consistent preferences for differently skewed gambles with similar means and variances. Our findings therefore suggest that preference models that only account for mean and variance ignore higher-level determiners of risky choice. To our knowledge, this study represents the first investigation of reward preferences for skewness involving full (i.e. non-discrete) reward distributions. Full distributions are less susceptible to anchoring effects and are more closely analogous to many real-world examples of skewed outcome distributions, for example investment returns.

The simplest models of risky choice hold that decision-makers subject outcomes to a nonlinear (but monotonic) utility reweighting [5,14]. Such approaches predict a monotonic preference function for skewness: risk-seekers should prefer positive skewness and the risk-averse should prefer negative skewness. We did not find a linear ordering of preference for skewness. Our results therefore show that monkeys’ risk preferences cannot be explained by any monotonic (i.e. convex or concave) utility transform. These data are also inconsistent with the simplest sampling models, which would predict that preferences should track medians rather than means [6,15]. They also are inconsistent with single threshold models like aspiration theory [4] and risk-sensitive foraging theory [16]: although a specific threshold could promote positive skewness seeking, it could not lead to preferences for strong over weak skewness in both positive and negative domains. Finally, our data are inconsistent with entropy reduction models of risky choice; these would predict an inverse U-shaped preference pattern, because entropy per choice is maximal with normal distributions and declines with skewness [17].

While each of these possibilities is insufficient on its own to explain our data, they are consistent with the idea that risk preferences are determined by multiple competing influences. For example, our observations are consistent with a three-factor model comprised: (i) a linear preference for positive skew, which might be due to an aspiration theory-like reward threshold, (ii) a U-shaped preference for skewness, which might reflect a preference for a wider range between highest and lowest deciles of outcomes and (iii) a narrower inverse U-shaped preference for normality which could result from entropy-seeking. Thus, our results are consistent with the idea that our decisions reflect the outcome of multiple ‘tools’ drawn from a heuristic toolbox, which are selected and combined during choice [18,19]. We anticipate that future studies will provide further behavioral and neural support for multi-factor models of risky choice in animals.

All animal procedures were approved by the University of Rochester Animal Care and Use Committee and were conducted in compliance with the Public Health Service's Guide for the Care and Use of Animals.

Funding statement

This research was supported by an R00 (NIDA 027718) and an NSF CAREER Award (1253576) to B.Y.H.