Marathon performance in relation to body fat percentage and training indices in recreational male runners

Abstract

Background

The purpose of this study was to investigate the effect of anthropometric characteristics and training indices on marathon race times in recreational male marathoners.

Methods

Training and anthropometric characteristics were collected for a large cohort of recreational male runners (n = 126) participating in the Basel marathon in Switzerland between 2010 and 2011.

Results

Among the parameters investigated, marathon performance time was found to be affected by mean running speed and the mean weekly distance run during the training period prior to the race and by body fat percentage. The effect of body fat percentage became significant as it exceeded a certain limiting value; for a relatively low body fat percentage, marathon performance time correlated only with training indices.

Conclusion

Marathon race time may be predicted (r = 0.81) for recreational male runners by the following equation: marathon race time (minutes) = 11.03 + 98.46 exp(−0.0053 mean weekly training distance [km/week]) + 0.387 mean training pace (sec/km) + 0.1 exp(0.23 body fat percentage [%]). The marathon race time results were valid over a range of 165–266 minutes.

Introduction

It is well known that for endurance sports like marathon running, characteristics such as maximal oxygen uptake (VO_2max), lactate threshold, and the energy cost of running play key roles in performance.1 Measurements of these variables are generally reserved for high-level distance runners. The increasing number of recreational runners participating in major running events, including the marathons held in New York, Chicago, London, and Berlin, suggested a need to develop analyses that relate race performance to variables easily detected or self-monitored, like training characteristics. Several studies in the last 30 years have shown that a combination of physiological, anthropometric, and training characteristics can predict performance in long-distance running.2–8

Measurement of physiological parameters such as VO_2max and ventilatory and lactate thresholds typically involves expensive laboratory facilities and requires a measurement protocol assuring the same test conditions for the entire cohort of athletes. A method to predict race performance based on training and anthropometric indices may be an attractive and inexpensive alternative to metabolic testing for the increasing numbers of noncompetitive runners in marathon events.

The aim of this study was two-fold. The first aim was to identify training and anthropometric variables contributing significantly to the prediction of final marathon (performance) time. The second aim was to develop a correlation giving marathon performance time as a function of the main predictive factors through multiple nonlinear regression analysis. This correlation can be used by amateur runners before the race to assess their expected performance in relation to their training level and anthropometric characteristics.

Subjects and methods

The organizers of the Basel marathon in Switzerland invited all male participants in the races held in 2010 and 2011 to participate in the planned investigation via an electronic newsletter distributed three months before the start of the marathon. In order to increase the sample size, the data were collected over two consecutive years. No criteria for inclusion or exclusion were applied for participation in the study. Training and anthropometric characteristics as independent variables were determined prerace and bivariately and multivariately correlated, with marathon race times as the dependent variable.

Subjects

Of 691starters, 126 European men were interested in participating in the study. The number of interested women was too low to compare with men. Before the race, the participants were informed of the procedure and gave their informed written consent. The study was approved by the institutional review board of the Canton of St Gallen, Switzerland. All interested athletes were subelite recreational runners. An elite athlete is defined here as a runner earning a living from trophy money and sponsorship. All participants in this study completed the race distance of 42.195 km within 5.5 hours, which was the time limit set by the organizer. Two male runners finished within the top three finishers. The athletes started at 10.15 am and had to complete two laps. In both years, the weather conditions were comparable. In 2010, the temperature at the start of the race was 17.5°C, with a relative humidity of 88%. By 2 pm, the temperature had risen to 23.9°C and the relative humidity had decreased to 60%. Wind speed was 1 m/sec at the start of the race and had increased to 2 m/sec by 2 pm. In 2011, the temperature was 16.9°C at the start of the race, with a relative humidity of 83%. By 2 pm, temperature had increased to 23.5°C and the relative humidity had decreased to 66%. Wind speed was 1 m/sec at the start of the race and remained unchanged at 2 pm. The organizer provided food and fluids at several aid stations.

Training records

In the three months between registration for the study and the start of the marathon, each athlete kept a training diary recording all training units with distance and duration per unit. Table 1 summarizes the training variables, including the mean, standard deviation, and range, ie, the weekly distance run (K), number of workouts per week (N_w), mean distance per workout (K_w), mean duration of workouts (T_w) and running speed during training sessions (V). The training pace (P) is related to the training speed by the simple equation P = 3600/V, with V expressed in km/hour and P expressed in sec/km. The number of years as an active runner was also recorded.

Table 1.

Training characteristics self-reported by the complete database of athletes (n = 126)

	Mean	SD	Range
Mean training distance run per week (km)	44.7	24.7	7.5–150.0
Mean number of workouts per week	3.7	1.6	1–11
Mean distance run per workout (km)	14.2	6.6	5–40
Mean duration of workouts (minutes)	72.5	20.4	30–145
Mean running speed during training (km/hour)	11.1	1.4	7.5–15.5
Period as active runner (years)	10.5	9.4	0.5–35.0

Abbreviation: SD, standard deviation.

Anthropometric measurements

Weight, height, limb circumferences, and skinfold thickness were recorded by the same investigator on the afternoon of the day before each race. One trained investigator took all the anthropometric measurements. A Beurer® BF15 scale (Beurer GmbH, Ulm, Germany) was used to measure body mass to the nearest 0.1 kg. A stadiometer (Tanita HR 001 Portable Height Measure, Tanita Europe, Amsterdam, The Netherlands) was used to measure body height to the nearest 0.01 m. The body mass index of each athlete was calculated using body mass and body height (kg/m²). The same investigator measured limb circumferences and skinfold thickness on the right arm, torso, and leg in all cases. Skinfold thickness was measured using a skinfold calliper (GPM-Hautfaltenmessgerät, Siber and Hegner, Zurich, Switzerland). All skinfolds were measured to the nearest 0.2 mm. The skinfold calliper measured with a pressure of 0.1 mPa ± 5% over the whole measuring range. All measurements were taken three times and the mean was used for calculations. Skinfold thickness was measured after 4 seconds.9 A reliability check was conducted on 27 male runners.10 The intraclass correlation within the two investigators was excellent for all anatomical sites measured and for the summary measurements of skinfold thickness. Agreement tended to be higher within than between investigators, and showed good reliability, with an intraclass correlation of 0.99 (95% confidence interval 0.99–1.00) for the summary measurements of skinfold thickness between investigators. The intraclass correlations for investigator 1 versus investigator 1 and for investigator 2 versus investigator 2 for single skinfold thickness measurements were between 0.98 and 0.99, respectively. For the sum of seven and eight skinfolds, the respective intraclass correlations were 0.99 and 1.00. For the sum of eight skinfolds for investigator 1, the bias (ie, average difference between investigator 1 and investigator 2) was −0.515 mm, the standard deviation of the average difference was 1.492 mm, and the 95% limits of agreement were between −3.439 mm and 2.409 mm.

Limb circumferences were measured using a nonelastic tape measure (KaWe CE, Kirchner und Welhelm, Asperg, Germany) to the nearest 0.1 cm. The circumference of the upper arm was measured at the mid arm, the circumference of the thigh was taken at the mid thigh, and the circumference of the calf was measured at the mid calf. Body fat percentage (BF) was estimated using the equation BF = 0.465 + 0.180(Σ7SF) − 0.0002406(Σ7SF)2 + 0.0661(age), where Σ7SF is the sum of the thicknesses of the pectoral, mid axilla, triceps, subscapular, abdomen, suprailiac, and front thigh skinfold. 11 The predicted residual sum of squares r² was high (0.90) and the standard error of estimate of the predicted residual sum of squares was excellent (2.2% at the mean) for the equation when applied to a sample of 160 men.

Skeletal muscle mass (SMM) was estimated using the anthropometric equation: SMM = Ht × (0.00744 × CAG² + 0.00088 × CTG² + 0.00441 × CCG²) + 2.4 × gender − 0.048 × age + race + 7.8, where Ht is body height, CAG is skinfold-corrected upper arm girth, CTG is skinfold-corrected thigh girth, CCG is skinfold-corrected calf girth, and gender = 1 for male; age is expressed in years; race = 0 for white men and 1 for black men.12 The limb circumferences (C_limb) crrected for subcutaneous adipose tissue thickness. The skinfold caliper measurement (S) was assumed to be twice the subcutaneous adipose tissue thickness. The corrected muscle (including bone) circumferences (C_m) were calculated as C_m=C_limb − π S. For dimensional consistency, corrected muscle circumferences were squared and multiplied by body height to obtain a three-dimensional skeletal muscle mass measurement.12 This anthropometric equation was validated using magnetic resonance imaging to determine skeletal muscle mass. There was a high correlation between the predicted skeletal muscle mass and the skeletal muscle mass measured by magnetic resonance imaging (r² = 0.83, P < 0.0001, standard error of estimate = 2.9 kg). The correlation between the difference in measured and predicted skeletal muscle mass and the actual measured skeletal muscle mass was highly significant (r² = 0.90, P = 0.009). A summary of the anthropometric variables investigated (with mean, standard deviation, and range) is provided in Table 2.

Table 2.

Anthropometric variables for the complete database of athletes (n = 126)

	Mean	SD	Range
Age (years)	42.8	10.8	18–72
Body mass (kg)	73.9	8.1	57.7–106.0
Body stature (m)	1.78	0.06	1.64–1.94
Body mass index (kg/m2)	23.4	2.2	18.6–33.5
Length of leg (cm)	85.5	4.2	74.0–98.0
Circumference of upper arm (cm)	29.2	1.9	23.5–34.5
Circumference of thigh (cm)	55.0	2.6	45.0–63.0
Circumference of calf (cm)	37.9	2.3	32.3–49.4
Pectoral skinfold (mm)	8.2	3.0	2.8–16.4
Mid-axilla skinfold (mm)	9.7	2.9	4.4–17.2
Triceps skinfold (mm)	7.9	2.6	3.4–19.2
Subscapular skinfold (mm)	10.5	4.0	4.6–31.2
Abdominal skinfold (mm)	15.4	6.9	4.8–38.0
Suprailiac skinfold (mm)	18.4	7.1	5.4–39.2
Front thigh skinfold (mm)	12.1	4.9	3.8–28.6
Medial calf skinfold (mm)	6.2	2.4	2.0–15.0
Body fat (%)	16.3	5.6	8.5–25.5
Skeletal muscle mass (kg)	38.4	3.3	27.5–49.0

Abbreviation: SD, standard deviation.

Refinement of input database

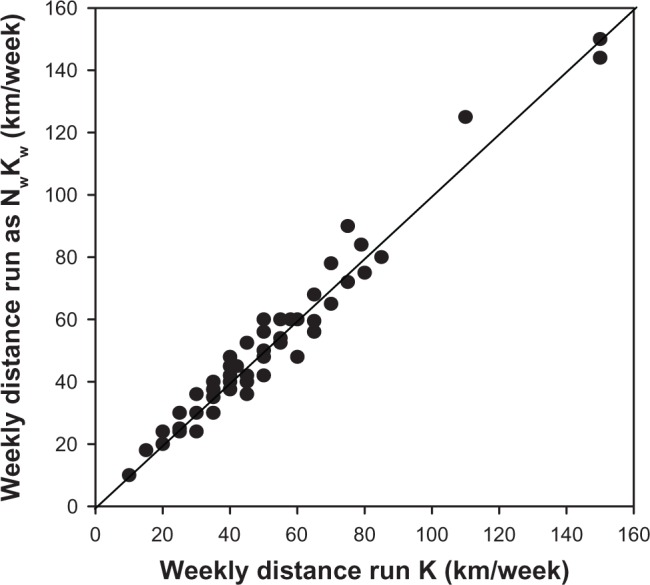
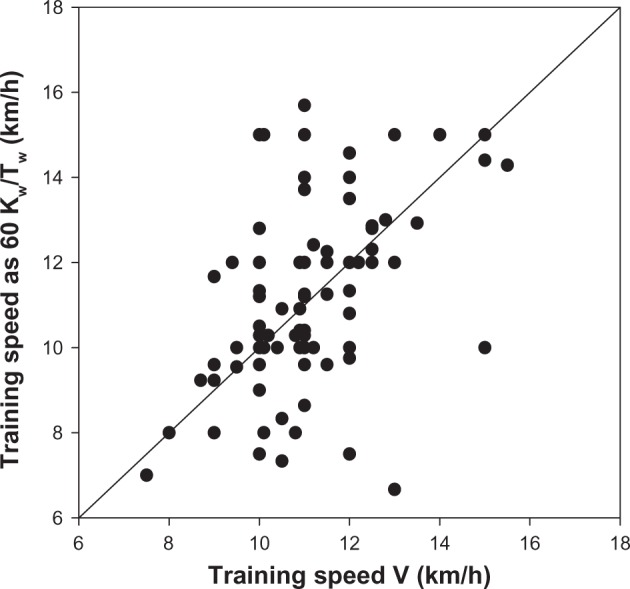
High quality of self-reported training variables is crucial for reliable statistical analysis of data and to give an accurate prediction of marathon performance time. Runners reported in their fies the average weekly distance run (K) as well as the mean number of workouts per week (N_w) and the mean distance run per workout (K_w). Clearly, for the reported data to be correct, the equation must be: K = N_w × K_w. Moreover, runners were asked to report their mean training velocity (V) as well as the mean duration of workouts (T_w). Again, for the reported data to be correct, V K_w, and T_w must obey the relationship: V = 60 × K_w/T_w, with V in km/hour, K_w in km, and T_w in minutes. Figures 1 and 2 show the comparisons between the pairs of variables (N_w × K_w, K) and (60 × K_w/T_w, V) for the full data sample (n = 126). The accuracy of the self-reported data can be deduced from the distance of points from the line of perfect agreement. Many points are relatively distant from this line. A possible criterion that can be used to exclude bias is to eliminate from the database all data which deviates from the perfect agreement line by more than ±20% for mean weekly distance run and ±15% for mean training speed. A stricter selection criterion was chosen for V, because this is the main variable predictive of marathon performance time. Figures 3 and 4 report data which obey both the selection criteria imposed on the full database. The number of runners from whom data were obtained is therefore reduced from 126 to 51.

Figure 1.

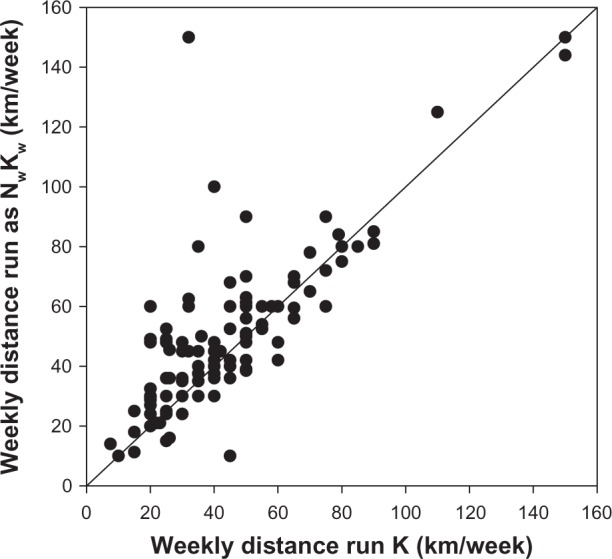
Analysis of self-reported weekly training distance data for full sample (n = 126).

Abbreviations: K, mean weekly distance run; N_w, mean number of workouts per week; K_w, mean distance run per workout.

Figure 2.

Analysis of self-reported training speed data for full sample (n = 126).

Abbreviations: V, mean training velocity; K_w, mean distance run per workout; T_w, mean duration of workouts.

Figure 3.

Self-reported weekly training distance for the reduced sample (n = 51).

Abbreviations: K, mean weekly distance run; N_w, mean number of workouts per week; K_w, mean distance run per workout.

Figure 4.

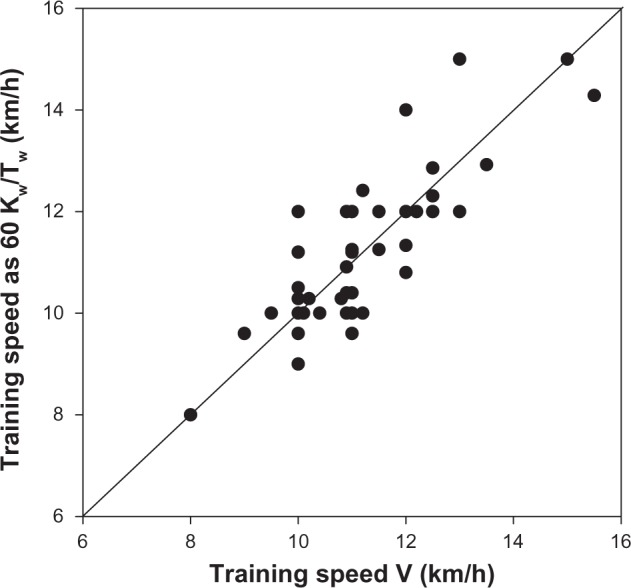
Self-reported training speed for the reduced sample (n = 51).

Abbreviations: V, mean training velocity; K_w, mean distance run per workout; T_w, mean duration of workouts.

Further refinement was done in view of the following points of concern. First, runners declaring a distance run of less than 30 km/week were excluded from the study because this distance is not reliable for marathon training. These subjects are very likely to have underestimated the real distance run. Second, runners competing in the race without a regular pace were also dropped from the study. It is well known that wide variation in velocity during a marathon implies an energy expenditure well above that required for a race performed at a regular pace.

In order to assess the regularity of pace during the race, we compared the times required to complete the first and second half of the race as reported in the official results for the Basel marathon 2010 and 2011. Runners performing their race with a difference in the time required to run the first and second halves of the marathon of more than 10 minutes were removed from the database. In the paper reported by Tanda,7 this criterion was more selective, with a maximum tolerance of only four minutes.

In view of the abovementioned issues, the input database was then reduced to 25 sets of input data. These 25 subjects correctly declared, with a certain degree of approximation, their training data and were able to run the race without marked changes in pace.

Anthropometric measurements for all the athletes were measured the day before the race. Refinement of the input data for the relationship between marathon performance time and anthropometric variables was not related to the self-reported training indices but only to the quality of race performance. Again, runners performing their race with a difference of more than 10 minutes in the time required to run the first and second halves of the marathon were not included. As a consequence, the database for the anthropometric indices was reduced to 52 sets of input data.

In conclusion, the following input data were considered: for the relationship between marathon performance time and training indices, there were 25 subjects who correctly reported K and V and ran the race at a regular pace. For the relationship between marathon performance time and anthropometric indices, there were 52 subjects who ran the race at a regular pace, regardless of the accuracy of self-reported training data.

Statistical analysis

Standard software for regression analysis of data according to different shapes (eg, linear and nonlinear, such as polynomial, exponential, and power) of the mathematical correlating function was used to correlate training and anthropometric variables with the effective marathon performance time recorded for the athletes included in each database. To evaluate the accuracy of a given regression curve, the standard error of estimate and the correlation coefficient r were considered. The standard error of estimate quantifies the spread of datum points around the regression curve. This was computed as $\sqrt{\Sigma {(Y-Y^{\prime })}^2/(n-n_p),}$ where Y is the actual score, Y′ is the score predicted from the regression model, n is the number of datum points, and n_p is the number of parameters (constants, exponents) included in the regression model.

The correlation coefficient r is given by $\sqrt{\left(\Sigma {(\overline{Y}-Y)}^2-\Sigma {(Y-Y^{\prime })}^2\right)/\Sigma {(\overline{Y}-Y)}^2}$, where $\overline{Y}$ is the mean of the Y values and each sum includes the total number n of data. For a perfect fit, the standard error of the estimate is expected to approach zero and the correlation coefficient r to approach unity. Conversely, too large values for the standard error of estimate or values of r relatively far from unity are considered as indicators of poor quality of correlation. For each selected training and anthropometric variable, the best curve of regression with marathon performance time was obtained among the several regression models provided by the curve fitting software. The best predictive factors for marathon performance time were then identified from a comparative analysis on the basis of respective values of the standard error of estimate and r. Finally, a multiple nonlinear regression analysis was used to determine the relationship giving marathon performance time as a function of the best predictive factors.

Results

After refinement of the input data, two distinct databases were considered and formed by n = 25 (ie, database for training indices) and n = 52 (ie, database for anthropometric indices). By processing the selected input database, the mean training distance run per week, K (km/week), mean training speed, V (km/hour), and body fat percentage, BF (%) were found to be strongly correlated with marathon performance time (in minutes), as reported in Table 3. It is worth noting that mean training pace, P (sec/km) can be considered in place of V (km/hour), with P = 3600/V. Table 3 shows a good quality of correlation between marathon performance time and all three indices, with a correlation coefficient r of between 0.49 and 0.76. These results support the effort to find a relationship which includes all the three variables, ie, K, V (or P), and BF.

Table 3.

Relationship for MPT versus training and anthropometric indices for reduced data sample (n = 25 for training indices and n = 52 for anthropometric indices)

	Shape of regression curve	Correlation coefficient (r)	SEE (minutes)
MPT versus K	Exponential decay	0.49	22.9
MPT versus V (or P)	Linear	0.76	16.6
MPT versus BF	Linear	0.60	18.3

Abbreviations: MPT, marathon performance time; K, mean weekly training distance; V, mean training velocity; P, mean training pace; BF, body fat percentage; SEE, standard error of the estimate.

A correlation between marathon performance time and the predictive variables (K, P, and BF) was found by processing the reduced data sample of 25 athletes who submitted reliable self-reported training data and ran the marathon without excessive variation in race pace. According to this set of data, marathon performance time (MPT) can be predicted by the following equation:

$$\text{MPT}=(42.195/60)(17.1+140.0\exp [-0.0053\text{\hspace{0.17em}K}]+0.55\text{\hspace{0.17em}P)+(exp[0.23{BF-10}}-1\text{]}$$ (1)

with marathon performance time in minutes.

The predicted marathon pace P_m (in sec/km), given by P_m = (60/42.195) MPT, can be readily obtained from equation (1):

$${\mathrm{P}}_{\mathrm{m}}=17.1+140.0\exp (-0.0053\text{\hspace{0.17em}K})+0.55\text{\hspace{0.17em}P}+\text{1.422\hspace{0.17em}(exp[0.23{BF-10}]}-1)$$ (2)

After a few mathematical passages, equations (1) and (2) can be rewritten as:

$$\text{MPT}=11.03+98.46\exp (-0.0053\text{\hspace{0.17em}K})+0.387\text{\hspace{0.17em}P}+\text{0.1\hspace{0.17em}}\exp (0.23\text{\hspace{0.17em}BF})$$ (1’)

$${\mathrm{P}}_{\mathrm{m}}=15.68+140.0\exp (-0.0053\text{\hspace{0.17em}K})+0.55\text{\hspace{0.17em}P}+\text{0.142\hspace{0.17em}}\exp (0.23\text{\hspace{0.17em}BF})$$ (2’)

with marathon performance time in minutes, P_m and P in sec/km, K in km/week, and BF as a percentage.

The range of validity is K = 30–150 km/week, P = 232– 400 sec/km (V = 9–15.5 km/hour), BF = 9.3%–25.5%, and marathon performance time = 165–266 minutes (P_m = 234–378 sec/km). Values for marathon performance time predicted by equation (1’) are reported in Figure 5 versus the recorded marathon performance times, together with the line of perfect agreement. Points are centered around the line of perfect agreement with a standard error of estimate of 14.3 minutes. The correlation coefficient r is 0.81.

Figure 5.

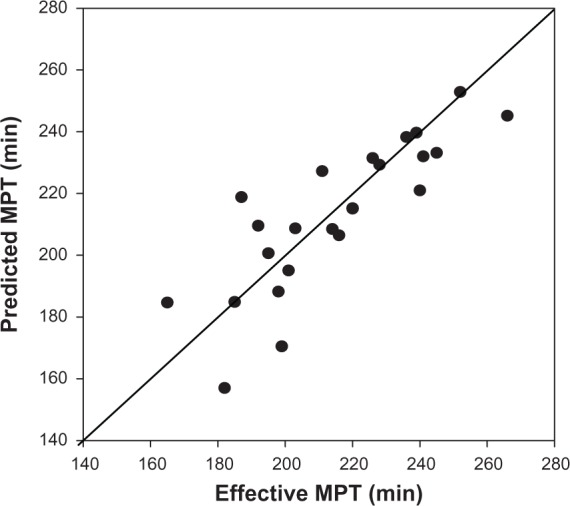
Marathon performance time predicted by equation (1) versus actual marathon performance time.

Note: Solid line represents perfect agreement. SEE = 14.3 minutes.

Abbreviations: MPT, marathon performance time; SEE, standard error of the estimate.

Discussion

Marathon performance has recently been found to be related to training indices7 and training and anthropometric characteristics.8 According to these investigations, two relationships can be used to predict marathon performance time:

$$\text{MPT}=(42.195/60)(17.1+140.0\exp [-0.0053\text{\hspace{0.17em}K}]+0.55\text{\hspace{0.17em}P})$$ (3)

according to Tanda,7 sample n = 46, range of validity for marathon performance time = 167–216 minutes, and standard error of estimate = 4 minutes.

$$\text{MPT}=326.3+2.394\text{\hspace{0.17em}BF}–12.06\text{\hspace{0.17em}V}$$ (4)

according to Barandun et al,8 sample n = 126, range of validity for marathon performance time = 165–350 minutes, and standard error of estimate = 24 minutes.

Units used in equations (3) and (4) are as follows: marathon performance time in minutes, mean weekly distance run (K) in km/week, mean training pace (P) in sec/km, BF as a percentage, and mean training velocity (V) in km/hour (P [sec/km] = 3600/V [km/hour]). Both studies recognized mean training speed or pace as the best predictor of marathon performance time. It should be noted that other training indices, such as mean distance per workout, maximum distance run per week, number of workouts per week, and number or previous marathons run, were not found to be predictive of marathon performance time.7,8

Firstly, equations (3) and (4) were applied to the entire database consisting of 126 sets of data as shown in Figure 6. The standard error of estimate is relatively large for both equations, but body fat percentage and training speed (equation 4) seem to correlate with marathon performance time better than weekly distance run and training pace (equation 3). To provide further evidence, the standard error of estimate and correlation coefficient for the relationships of marathon performance time versus K, V (or P), and BF were calculated and are reported in Table 4. The training speed emerges as the best predictor (highest r, lowest standard error of estimate), whereas the weekly distance run appears to be poorly correlated with MPT. Next, attention was focused on the 41 runners who finished the race within 220 minutes, in order to be consistent with the range of validity of equation (3). The results are reported in Figure 7, showing that the standard error of estimate for equation (3) is markedly reduced, while the standard error of estimate for equation (4) remains approximately the same. It can be argued that the weekly distance run and training pace are the best predictor variables for faster runners.

Figure 6.

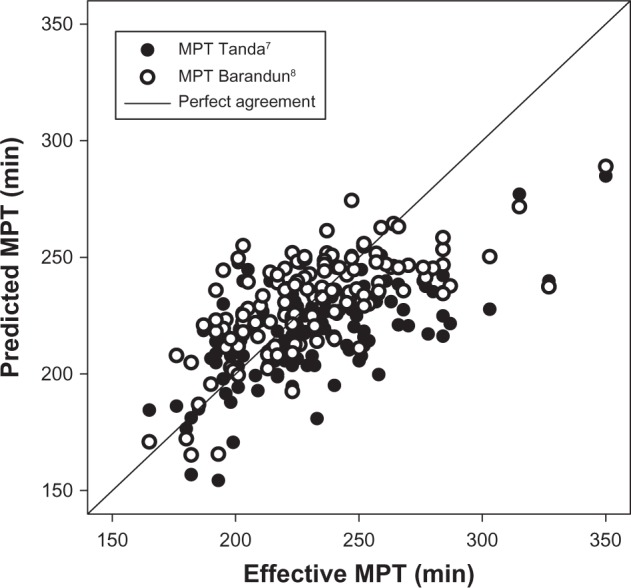
Comparison of marathon performance time predicted from equation (3)7 and equation (4)8 for the full sample data (n = 126).

Notes: SEE = 28.4 minutes (equation 3) and 23.7 minutes (equation 4).

Abbreviations: MPT, marathon performance time; SEE, standard error of the estimate.

Table 4.

Relationships for MPT versus training and anthropometric indices for full data sample (n = 126)

Full data sample	Shape of regression curve	Correlation coefficient (r)	SEE (minutes)
MPT versus K	Linear or exponential decay	0.30	30.3
MPT versus V (or P)	Linear	0.61	25.2
MPT versus BF	Linear	0.44	28.5

Abbreviations: MPT, marathon performance time; K, mean weekly training distance; V, mean training velocity; P, mean training pace; BF, body fat percentage; SEE, standard error of the estimate.

Figure 7.

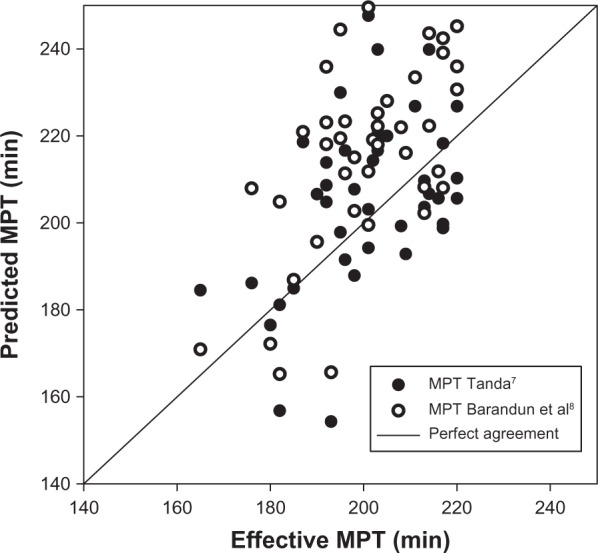
Comparison of marathon performance time predicted from equation (3)7 and equation (4)8 for runners completing the race within 3 hours and 40 minutes (n = 41).

Note: SEE = 18.5 minutes (equation 3) and 23.6 minutes (equation 4).

Abbreviations: MPT, marathon performance time; SEE, standard error of the estimate.

Finally, equations (3) and (4) were applied to the selected database (n = 25), obtained after refinement of the training data. The results are shown in Figure 8, where the predicted MPT values are plotted as a function of the effective MPT values. Both relationships have a standard error of estimate close to 17 minutes, which is significantly lower than that obtained by processing of the full input data, but MPT predicted by equation (4) is overestimated. MPT values given by equation (3) and applied to the sample reported by Tanda7 (n = 46) are also reported. It is noteworthy that equation (3) was found by processing very accurate training data accumulated over the eight-week period preceding the race, and that the number of subjects was small (n = 22, ie, similar to the actual input database) but the number of considered races was larger (n = 46, because of some subjects running more than one marathon and providing a training diary for each race). The standard error of estimate in equation (3) was only 4.0 minutes and body mass index, not considered in the relationship, was found to have a negative effect on the accuracy of prediction. Indeed, when only subjects having a body mass index lower than 23 are considered (BF was not reported in the Tanda paper7) the standard error of estimate was reduced to 3.5 minutes. This finding indicates that an anthropometric characteristic such as body mass index or body fat percentage could play a role in the prediction of MPT.

Figure 8.

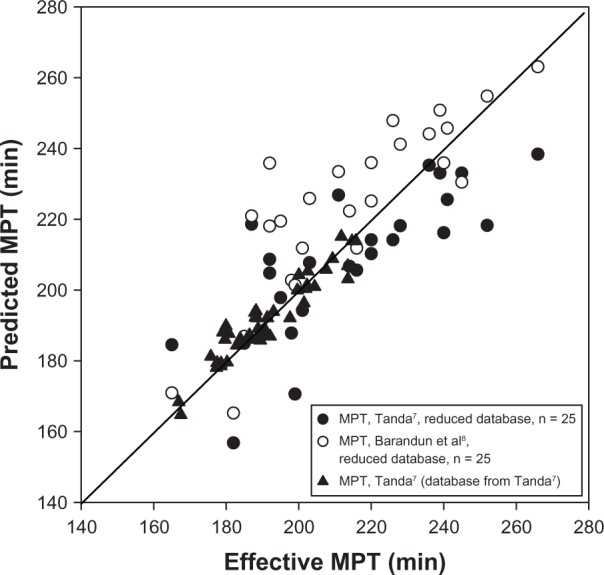
Marathon performance time predicted from equation (3) and equation (4) versus actual marathon performance time for the reduced sample data (n = 25).

Notes: Marathon performance time predicted from equation (3) using the database from Tanda7 (n = 46) are included.

Abbreviation: MPT, marathon performance time.

Indeed, application of equation (3) to the present database (n = 25) shows that relatively low BF (<13%–14%) was a good predictor of MPT in these runners, regardless of the value for BF. Conversely, as BF increases to a critical value of around 17%–18%, equation (3) gives predicted MPT values typically lower than the actual ones. For a BF of about 20%, MPT is underestimated by about 10 minutes, and for a BF of 25%, MPT is underestimated by more than 30 minutes. This observation suggested that a correction factor (C_BF) should be introduced into equation (3) to take into account the effect of BF as follows:

$${\text{C}}_{\text{BF}}=(\exp [a\left\{\text{BF-10}\right\}]-1)$$ (5)

where a is a parameter deduced by the regression analysis of MPT underestimation values (given by equation 3) versus BF values. From data processing, it was found that a = 0.23; for BF lower than 13%, the effect of the correction factor given by equation (5) is negligible (less than one minute of MPT). Conversely, as BF increases, the C_BF increases exponentially, as documented in the experimental data. Therefore, the proposed relationship for MPT as shown in equation (1’), was modeled on the structural basis of equation (3), here implemented with a correction term (equation 5) taking into account the effect of BF.

These results show a good correlation between MPT and the identified parameters of body fat percentage, weekly training distance run, and mean training speed or pace. The accuracy of this predictive correlation for MPT is strongly dependent on the quality of the self-reported training data. For instance, excessive rounding off of approximations or the absence of a global positioning system device to measure the workout distance run could lead to serious errors in data processing. The lack of reliability of some of the self-reported training data is a major limitation of this study, albeit mitigated by refinement of the input data. For future research, the collection of additional and very precise training data provided by marathon runners could lead to a further improvement of the predictive correlation for MPT.

Conclusion

Body fat percentage and training indices such as mean training pace and mean weekly distance run in the period before the race are good predictors of MPT for recreational male runners. Mean training pace emerged as the most important parameter affecting MPT. A correlation giving MPT as a function of mean training pace, mean weekly distance run, and body fat percentage was developed:

MPT (minutes) = 11.03 + 98.46 exp(−0.0053 K[km/week]) + 0.387 P(sec/km) + 0.1 exp(0.23 BF [%])(standard error of estimate = 14.3 minutes, r = 0.81)

The influence of BF becomes significant when it exceeds a certain limiting value; for relatively low BF values, MPT is only correlated with training indices. Only MPT results for athletes performing the race at a regular pace (ie, without excessive variation in the time taken to run the first and second halves of the marathon) can be considered in research to find a reliable correlation between MPT and training and/or anthropometric characteristics.