Abstract
In this article, an approximate analytical solution of flow and heat transfer for a viscoelastic fluid in an axisymmetric channel with porous wall is presented. The solution is obtained through the use of a powerful method known as Optimal Homotopy Asymptotic Method (OHAM). We obtained the approximate analytical solution for dimensionless velocity and temperature for various parameters. The influence and effect of different parameters on dimensionless velocity, temperature, friction factor, and rate of heat transfer are presented graphically. We also compared our solution with those obtained by other methods and it is found that OHAM solution is better than the other methods considered. This shows that OHAM is reliable for use to solve strongly nonlinear problems in heat transfer phenomena.
Introduction
In recent years a great deal of focus has been devoted to non-Newtonian fluid flow and heat transfer because of various applications in various fields of science and engineering. In this regard there has been increased interest in flow and heat transfer problem involving viscoelastic fluids. The mathematical modeling of channel flow of viscoelastic fluid and related heat transfer problems (e.g. hot rolling, extrusion of plastic) have been the focus of considerable research works [1]–[9]. Obtaining velocity and temperature distribution from the mathematical model in an efficient and reliable manner is highly important.
The flow through a porous medium has many applications in science and engineering. For instance in ground water hydrology, reservoir engineering, petroleum engineering, chemical engineering, chemical reactors to agriculture irrigation and drainage and the recovery of crude oil from the pores of the reservoir rocks [10]–[12].
In particular, the characteristics of heat transfer in the case of porous medium is of high importance due to its wide range applications in for example, heat exchangers, transport of heated or cooled fluids, micro-electronic cooling, chemical processing equipment, and porous burners, etc. Many researchers have investigated such phenomena. Example include Trimis [13] who has shown that porous media can be very useful within many applications in energy and heat-engineering and Bassam and Abu-Hijleh [14] who have examined heat transfer from a 2D backward facing step with different porous segments and analyzed the effect of these layers on local and overall Nusselt numbers. Nield and Kuznetsov [15] have analyzed the interaction of two porous layers with the same porosity and permeability but different thermal conductivity effects in forced convection and Nemoda et al. [16] studied a porous burner and surface burner numerically with different heat conductivity and power of burners. Pilevne and Aydin [17] have investigated forced convection in axisymmetric channel with different porous layers.
Many analytical methods like homotopy perturbation method (HPM) [18]–[19], Adomian decomposition method (ADM) [20]–[21], homotopy analysis method (HAM) [22] have been successfully applied for different heat transfer phenomena.
Optimal homotopy asymptotic method (OHAM) is an approximate (or semi) analytical technique that is straightforward to use and does not require the existence of any small or large parameter.
The basic idea of optimal homotopy asymptotic method was initially introduced by Marinca and Herisanu [23]. OHAM reduces the size of the computational domain and can be applied to wide variety of problems. OHAM is a consistent analytical tool and it has already been successfully applied to a number of nonlinear differential equations arising in science and engineering. OHAM has been used to study steady flow of a fourth-grade fluid flow through a porous medium [23], oscillators with discontinuities and fractional-power restoring force [24], periodic solutions for the motion of a particle on a rotating parabola [25], thin film flow of a fourth-grade fluid [26], nonlinear heat transfer equations [27], and nonlinear problem in elasticity [28].
By means of OHAM, Islam et al. [29] investigated Couette and Poiseuille flows of a third grade fluid with heat transfer analysis, Idrees et al. [30] analyzed the KDV equation and Mohsen et al. [31] studied viscous flow in a semi porous channel with uniform magnetic field. Ghoreishi et al. [32] provided a comparative study for nth-order integro-differential equations, Mabood et al. [33], [34] investigated heat transfer in hollow sphere and analyzed boundary layer flow, Khan et al. [35] studied thin film flow in porous medium. Babaelahi et al. [36] examined the viscoelastic boundary layer fluid flow over a stretching sheet.
In this paper, optimal homotopy asymptotic method is utilized in order to study the flow and heat transfer of a viscoelastic fluid in an axisymmetric channel with porous wall and the influence of various parameters on the dimensionless velocity and temperature.
Problem Formulation
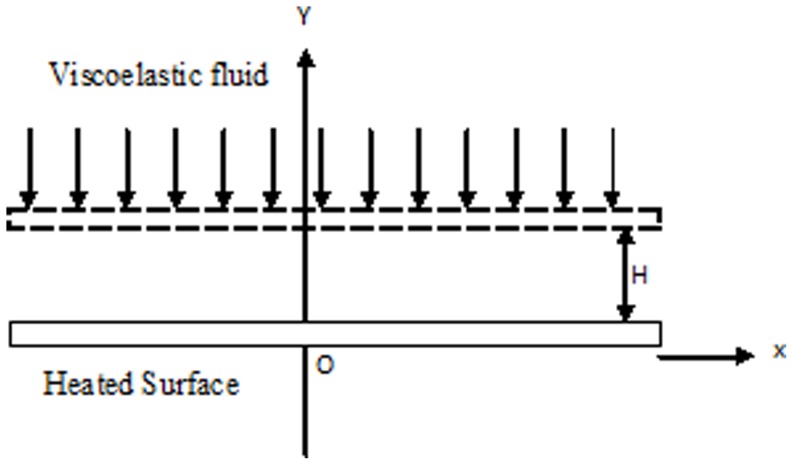
We consider the phenomena of flow and heat transfer of a viscoelastic fluid in a channel. The schematic diagram is presented in Fig. 1. The x-axis is parallel to the surface of disc and z-axis is normal on it. The porous disc of the channel is placed at Y = +H. The wall that coincides with x-axis is externally heated and other perforated wall viscoelastic fluid is injected consistently in a way to keep cool the heated surface. In this regard, we follow the approach of [9].
Figure 1. Schematic diagram of the problem.
We assume that the flow field is stagnation flow with injection. The flow of viscoelastic fluid is considered to be steady, axisymmetric and two-dimensional. The governing equations for the flow and heat transfer are [8]:
| (1) |
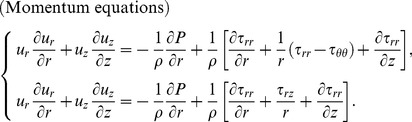 |
(2) |
| (3) |
The boundary conditions for Eqs. (1) – (3) are:
| (4) |
Where 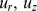 are the velocity components along in
are the velocity components along in  and
and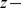 directions, respectively.
directions, respectively. 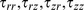 be the components of stress matrix,
be the components of stress matrix, 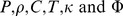 are pressure, density, specific heat, temperature, thermal conductivity and dissipation function respectively, and the dissipation function and stress components are defined as [8]:
are pressure, density, specific heat, temperature, thermal conductivity and dissipation function respectively, and the dissipation function and stress components are defined as [8]:
| (5) |
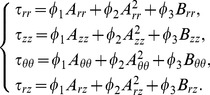 |
(6) |
The similarity solution for Eqs. (1) – (3) with boundary conditions Eq. (4), the dimensionless similarity variables [8]:
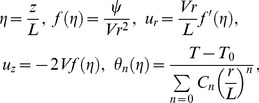 |
(7) |
where prime denotes differentiation with respect to 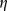 .
.
Using Eq. (7) and eliminating the pressure term, Eqs. (1) – (3) reduced to the following ordinary differential equations or similarity equations.
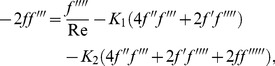 |
(8) |
| (9) |
where 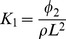 ,
, are cross viscosity parameters, Re is the Reynolds number and Pr is the Prandtl number. Using Eq. (7) the boundary conditions (Eq. (4)) can be transformed for the considered problem are:
are cross viscosity parameters, Re is the Reynolds number and Pr is the Prandtl number. Using Eq. (7) the boundary conditions (Eq. (4)) can be transformed for the considered problem are:
| (10) |
| (11) |
The above system of Eqs. (8) – (9) with boundary conditions Eqs. (10) – (11) were studied by Kurtcebe and Erim [8] for K2 = 0. In this paper, we reconsider these equations as:
| (12) |
| (13) |
and solve by means of optimal homotopy asymptotic method.
Quantities of physical interest are the local friction factor, and the local Nusselt number. Physically, 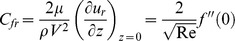 represents the friction factor, and
represents the friction factor, and 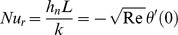 defines the heat transfer rate.
defines the heat transfer rate.
Basic Principles of OHAM
We review the basic principles of OHAM as expounded in [27]–[28], [34]–[35] and other papers in the following steps:
(i) Let us consider the following differential equation:
| (14) |
where  is problem domain,
is problem domain, 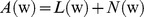 , where
, where  and
and 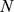 are linear and nonlinear operators respectively,
are linear and nonlinear operators respectively, 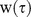 is an unknown function and
is an unknown function and 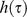 is a known function,
is a known function,
(ii) Construct an optimal homotopy equation as follows:
| (15) |
where is an embedding parameter,
is an embedding parameter,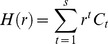 is an auxiliary function on which the convergence of the solution is dependent. The auxiliary function
is an auxiliary function on which the convergence of the solution is dependent. The auxiliary function 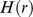 serves also to adjust the convergence domain as well as control the convergence region.
serves also to adjust the convergence domain as well as control the convergence region.
(iii) If 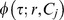 is expanded in a Taylor’s series about
is expanded in a Taylor’s series about  , the following an approximate solution is obtained:
, the following an approximate solution is obtained:
| (16) |
It has been observed by previous researchers that the convergence of the series Eq. (16) depends upon 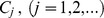 . If it is convergent then:
. If it is convergent then:
| (17) |
is obtained.
(iv) Substituting Eq. (17) in Eq. (14), results in the following residual:
| (18) |
If 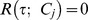 , then
, then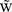 will be the exact solution although for nonlinear problems this will not usually be the case. For determining
will be the exact solution although for nonlinear problems this will not usually be the case. For determining 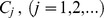 methods such as Galerkin’s method or the method of least squares can be utilized.
methods such as Galerkin’s method or the method of least squares can be utilized.
(v) Substitution of these constants into Eq. (17) results in the approximate solution.
Solution of the problem via OHAM
According to the OHAM, Eqs. (12) – (13) can be written as:
| (19) |
| (20) |
where primes denote differentiation with respect to 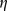 .
.
We consider 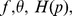 and
and 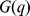 as follows:
as follows:
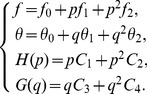 |
(21) |
Using Eq. (21) in Eqs. (19–20) and after simplification as well as rearranging the terms based on the powers of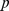 and
and 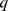 , we obtain zeroth, first, and second order problems are:
, we obtain zeroth, first, and second order problems are:
Zeroth order problem:
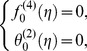 |
(22) |
with boundary conditions:
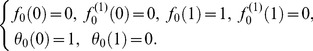 |
(23) |
Its solution is:
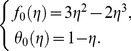 |
(24) |
First order problem:
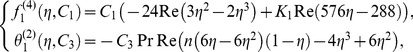 |
(25) |
with boundary conditions:
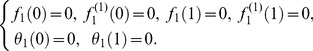 |
(26) |
Its solution is:
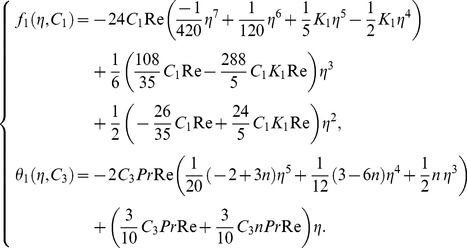 |
(27) |
and so on …
Set 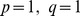 , to obtain the three terms solution using OHAM for dimensionless velocity and temperature profile as:
, to obtain the three terms solution using OHAM for dimensionless velocity and temperature profile as:
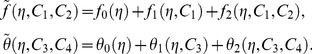 |
(28) |
The method of least squares is used to obtain the convergence-control parameters 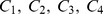 in Eq. (28), i.e.
in Eq. (28), i.e.
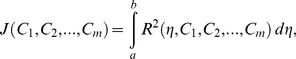 |
(29) |
where 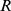 is the residual,
is the residual,
| (30) |
In case of 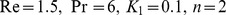 , then the values of
, then the values of 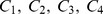 are given below:
are given below: 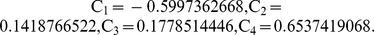
Results and Discussion
In this paper, we have successfully employed OHAM to obtain the approximate analytical solutions of flow and heat transfer problem for viscoelastic fluid in a channel with porous wall. Various values of different controlling parameters for both dimensionless velocity and temperature profiles are obtained. The approximate analytical solution for dimensionless velocity and temperature using OHAM are compared with those obtained by HAM [9] and numerical shooting method [9] shown in Tables 1 and 2. These results indicate that OHAM is a feasible and efficient technique for problems arising in heat transfer although more studies need to be conducted. Percentage of error is calculated for obtained OHAM solutions in Tables 1–2. The percentages reflect that our solution is more accurate than HAM [9] solution.
Table 1. Comparison of 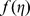 values using different methods.
values using different methods.

|
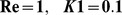
|
||||
| OHAM (Present results) | NM [9] | HAM [9] | % error HAM | % error OHAM | |
| 0.0 | 0 | 0 | 0 | 0 | 0 |
| 0.1 | 0.3021760 | 0.3021792 | 0.03021752 | 0.00132371 | 0.00105897 |
| 0.2 | 0.11348615 | 0.11348995 | 0.11348557 | 0.00385937 | 0.00334831 |
| 0.3 | 0.23672114 | 0.23672600 | 0.23671190 | 0.00595625 | 0.00205300 |
| 0.4 | 0.38448353 | 0.38449935 | 0.38448227 | 0.00444214 | 0.00411444 |
| 0.5 | 0.54036989 | 0.54036906 | 0.54037008 | 0.00018876 | 0.00015359 |
| 0.6 | 0.68889001 | 0.68889398 | 0.68891470 | 0.00203772 | 0.00057628 |
| 0.7 | 0.81730234 | 0.81729920 | 0.81731584 | 0.00203597 | 0.00038419 |
| 0.8 | 0.91604548 | 0.91604363 | 0.91604691 | 0.00035806 | 0.00020195 |
| 0.9 | 0.97845326 | 0.97845350 | 0.97845308 | 0.00004292 | 0.00001242 |
| 1.0 | 1 | 1 | 1 | 0 | 0 |
Table 2. Comparison of 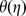 values using different methods.
values using different methods.

|
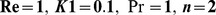
|
||||
| OHAM (Present results) | NM [9] | HAM [9] | % error HAM | % error OHAM | |
| 0.0 | 1 | 1 | 1 | 0 | 0 |
| 0.1 | 0.82706311 | 0.82706323 | 0.82706690 | 0.0004437 | 0.0000145 |
| 0.2 | 0.66453625 | 0.66453256 | 0.66453855 | 0.0009013 | 0.0005552 |
| 0.3 | 0.51925531 | 0.51925353 | 0.51925913 | 0.0010784 | 0.0003428 |
| 0.4 | 0.39448602 | 0.39448392 | 0.39448742 | 0.0008872 | 0.0005323 |
| 0.5 | 0.29052119 | 0.29051950 | 0.29052246 | 0.0010188 | 0.0005817 |
| 0.6 | 0.20561711 | 0.20561368 | 0.20561841 | 0.0023004 | 0.0016681 |
| 0.7 | 0.13697446 | 0.13697040 | 0.13697661 | 0.0045338 | 0.0029641 |
| 0.8 | 0.08156221 | 0.08156009 | 0.08156599 | 0.0072339 | 0.0025993 |
| 0.9 | 0.03663756 | 0.03663979 | 0.03664378 | 0.0108898 | 0.0060862 |
| 1.0 | 0 | 0 | 0 | 0 | 0 |
The influence and effect of different parameters on velocity and temperature are displayed in Figs. 2 and 3. In Figs 2(a) and (b), the effect of parameters 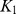 and
and 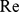 on the dimensionless velocity are displayed while keeping fixed values of parameters
on the dimensionless velocity are displayed while keeping fixed values of parameters  and
and 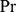 . It is observed that the dimensionless velocity at the center of the channel increases with an increase in
. It is observed that the dimensionless velocity at the center of the channel increases with an increase in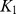 . The dimensionless velocity also increases with Reynolds number inside the channel. In Fig. 3(a), the effects of
. The dimensionless velocity also increases with Reynolds number inside the channel. In Fig. 3(a), the effects of 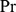 and
and  on the dimensionless temperature are displayed for different values of
on the dimensionless temperature are displayed for different values of 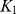 and
and 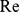 . It is found that the dimensionless temperature decreases inside the thermal boundary layer with increasing
. It is found that the dimensionless temperature decreases inside the thermal boundary layer with increasing  and
and 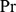 . The effects of
. The effects of 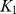 on the dimensionless temperature are found to be negligible whereas the dimensionless temperature decreases with an increase in the Reynolds number. In Fig. 4 we present and highlight the influence of Reynolds and cross viscosity parameter on skin-friction factor. It is notice that skin-friction factor coefficient increases linearly with an increase in
on the dimensionless temperature are found to be negligible whereas the dimensionless temperature decreases with an increase in the Reynolds number. In Fig. 4 we present and highlight the influence of Reynolds and cross viscosity parameter on skin-friction factor. It is notice that skin-friction factor coefficient increases linearly with an increase in 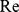 and the opposite nature of skin-friction factor can be observed with the increases in cross viscosity parameter
and the opposite nature of skin-friction factor can be observed with the increases in cross viscosity parameter 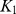 . The variation of the Nusselt number (representing the dimensionless heat transfer rate at the surface) is presented for different parameters in Figs. 5–6. Fig. 5 depicts the behavior of heat transfer rates against Reynolds and Prandtl numbers. A monotonic increase in heat transfer rate is observed for increasing values in both parameters. Fig. 6 shows the heat transfer rate against Reynolds and for different fluids according to power law index
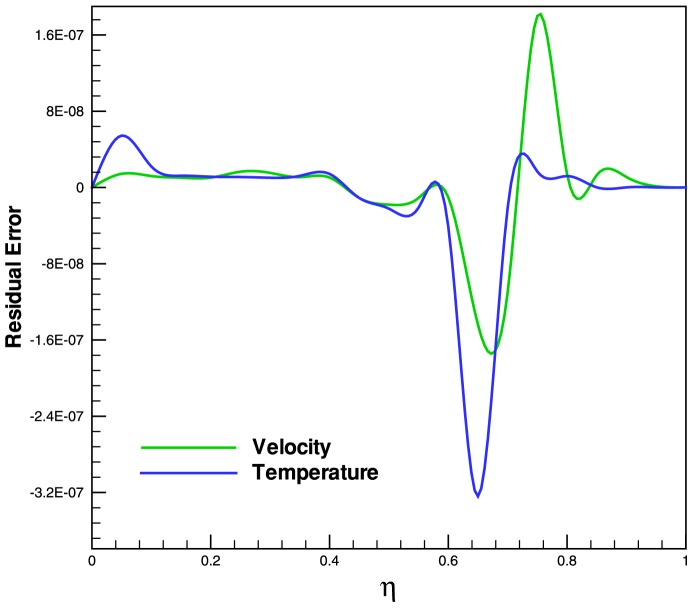
. The variation of the Nusselt number (representing the dimensionless heat transfer rate at the surface) is presented for different parameters in Figs. 5–6. Fig. 5 depicts the behavior of heat transfer rates against Reynolds and Prandtl numbers. A monotonic increase in heat transfer rate is observed for increasing values in both parameters. Fig. 6 shows the heat transfer rate against Reynolds and for different fluids according to power law index 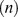 . The heat transfer rate increases with the increase in power law index, which indicate that the non-isothermal surface generate higher heat transfer rates. Finally, Fig. 7 shows the residual error for both dimensionless velocity and temperature profiles.
. The heat transfer rate increases with the increase in power law index, which indicate that the non-isothermal surface generate higher heat transfer rates. Finally, Fig. 7 shows the residual error for both dimensionless velocity and temperature profiles.
Figure 2. Effects of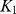 on dimensionless velocity profile for different values of Reynolds number.
on dimensionless velocity profile for different values of Reynolds number.
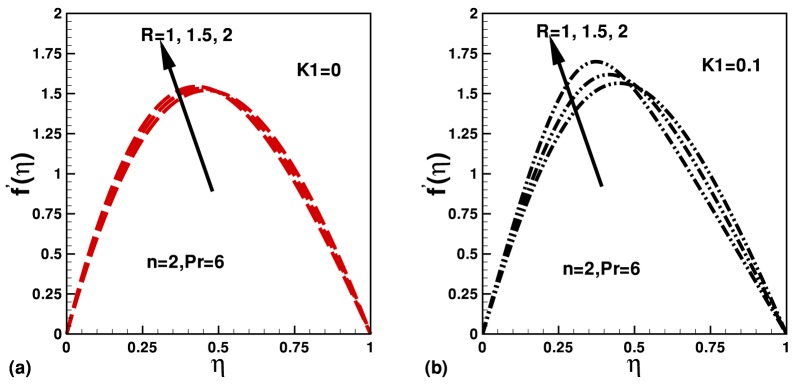
Figure 3. Variation of dimensionless temperature with transverse distance for different values of parameters.
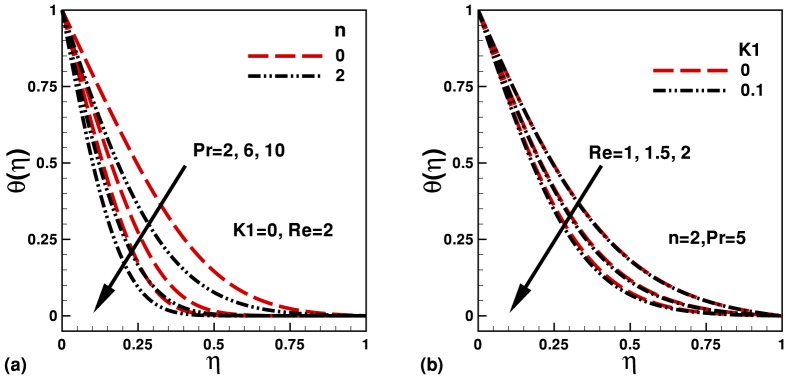
Figure 4. Variation of skin friction coefficient with Reynolds number and different value of .
.
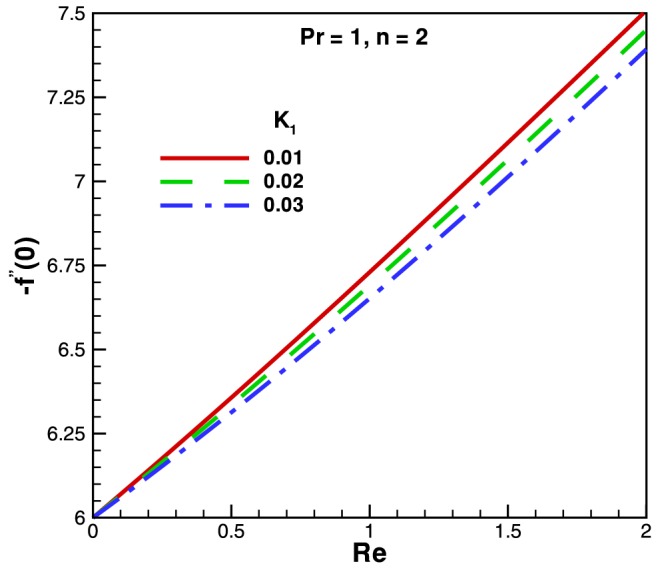
Figure 5. Variation of heat transfer rates with Reynolds number and different values of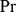 .
.
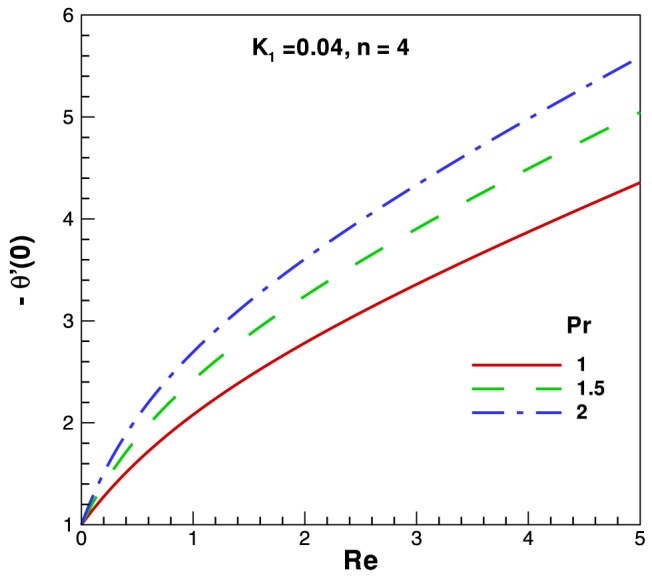
Figure 6. Variation of heat transfer rates with Reynolds number and different values of .
.
Figure 7. Residual Error of dimensionless velocity and temperature profiles at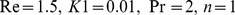 .
.
Conclusion
In this paper, OHAM is successfully employed in order to obtain an approximate solution for flow and heat transfer of viscoelastic fluid in a channel. Effects of different controlling parameters on dimensionless velocity, temperature, skin-friction as well as Nusselt number are investigated. The present OHAM results are compared with existing numerical and HAM result and a good agreement is observed with both methods. These comparisons show that OHAM is an effective technique for the solution of nonlinear problems in heat transfer. We can draw the following conclusion:
The dimensionless temperature directly proportional to Reynolds number
The skin-friction factor increases monotonically with Reynolds number
Rate of heat transfer increases with increase in Prandtl number
Funding Statement
The authors have no support or funding to report.
References
- 1. Rivlin RS, Ericksen JL (1955) Stress–deformation relations for isotropic materials. J Ration Mech Anal 4: 323–425. [Google Scholar]
- 2. Yuan SW, Finkelstein AB (1956) Laminar pipe flow with injection and suction through a porous wall. Trans ASME 78: 719–724. [Google Scholar]
- 3. White JL, Metzner AB (1965) Constitutive equations for viscoelastic fluids with application to rapid external flows AIChE J. 11(2): 324–330. [Google Scholar]
- 4. Terill RM (1965) Laminar flow in a uniformly porous channel with large injection. Aeronautics Q 16: 322–32. [Google Scholar]
- 5.Debruge LL, Han LS (1972) Heat transfer in a channel with a porous wall for turbine cooling application. J Heat Transfer Trans ASME 385–90.
- 6. Shin S, Ahn HH, Cho YI, Sohn CH (1999) Heat transfer behavior of a temperature dependent non-Newtonian fluid with Reiner–Rivlin model in a 2:1 rectangular duct. Int J Heat Mass Transfer 42: 2935–42. [Google Scholar]
- 7. Akcay M, Yukselen A (1999) Drag reduction of a non-Newtonian fluid by fluid injection on a moving wall. Arch Appl Mech 69: 215–25. [Google Scholar]
- 8. Kurtcebe C, Erim MZ (2002) Heat transfer of a non-Newtonian viscoinelastic fluid in an axisymmetric channel with a porous wall for turbine cooling application. Int Comm Heat Mass Transfer 29(7): 971–82. [Google Scholar]
- 9. Esmaeilpour M, Domairry G, Sadoughi N, Davodi AG (2010) Homotopy analysis method for the heat transfer of a non-Newtonian fluid flow in an axisymmetric channel with a porous wall. Commun Nonlinear Sci Numer Simul 15: 2424–30. [Google Scholar]
- 10. Islam S, Mohyuddin MR, Zhou CY (2008) Few exact solutions of non-Newtonian fluid in porous medium with hall effect. Journal of Porous Media 11(7): 669–80. [Google Scholar]
- 11. Islam S, Zhou CY (2007) Certain inverse solutions of a second-grade MHD aligned fluid flow in a porous medium. Journal of Porous Media 10(4): 401–8. [Google Scholar]
- 12. Vafai K, Tien CL (1981) Boundary and inertia effects on flow and heat transfer in porous media. Int J Heat Mass Transfer 24(2): 195–203. [Google Scholar]
- 13.Trimis D (2000) Stabilized combustion in porous media-applications of the porous burner tecnology in energy and heat-engineering. Fluids Conference and Exhibit, Denver.
- 14. Bassam K (2000) Abu-Hijleh (2000) Heat transfer from a 2D backward facing step with isotropic porous floor segments. Int J Heat Mass Transfer 43: 2727–37. [Google Scholar]
- 15. Nield DA, Kuznetsov AV, Xiong M (2000) Effect of heterogeneity in forced convection in a porous medium: parallel plate channel or circular duct. Int J Heat Mass Transfer 43: 4119–34. [Google Scholar]
- 16. Nemoda S, Trimis D, Zivkovic G (2004) Numerical simulation of porous burners and hole plate surface burners. Thermal Science 8(1): 3–17. [Google Scholar]
- 17. Pilevne E, Aydin M (2006) Forced convection in a variable section axisymmetric channel with different porous layers and heat generation. Proc 4th WSEAS Int conf on Heat Transfer. Thermal Engineering and Environment. Elounda Greece 21–23: 287–91. [Google Scholar]
- 18. Khan ZH, Gul R, Khan WA (2008) Effect of variable thermal conductivity on heat transfer from a hollow sphere with heat generation using homotopy perturbation method. Proceedings of HT2008. ASME heat transfer summer conf collocated with the Fluids Engineering, Energy Sustainability and 3rd Energy Nanotechnology Conf. 1: 301–9. [Google Scholar]
- 19. Gul R, Khan ZH, Khan WA (2008) Heat transfer from solids with variable thermal conductivity and uniform internal heat generation using homotopy perturbation method. ASME 2008 heat transfer summer conf collocated with the Fluids Engineering Energy Sustainability and 3rd Energy Nanotechnology Conferences Heat Transfer 1: 311–9. [Google Scholar]
- 20. Khan ZH, Gul R, Khan WA (2008) Application of Adomian decomposition method for sumudu transform. NUST Journal of Engineering Sciences 1(1): 40–44. [Google Scholar]
- 21. Kechil SA, Hashim I (2007) Non-perturbative solution of free-convective boundary-layer equation by Adomian decomposition method. Physics Lett A 363(1–2): 110–4. [Google Scholar]
- 22. Abbasbandy S (2006) The application of homotopy analysis method to nonlinear equations arising in heat transfer. Physics Lett A 360: 109–13. [Google Scholar]
- 23. Marinca V, Herisanu N, Bota C, Marinca B (2009) An optimal homotopy asymptotic method applied to the steady flow of fourth-grade fluid past a porous plate. Appl Math Lett 22: 245–51. [Google Scholar]
- 24. Herisanu N, Marinca V (2010) Accurate analytical solutions to oscillators with discontinuities and fractional-power restoring force by means of the optimal homotopy asymptotic method. Comp Math Appl 60: 1607–15. [Google Scholar]
- 25. Marinca V, Herisanu N (2010) Determination of periodic solutions for the motion of a particle on a rotating parabola by means of the optimal homotopy asymptotic method. Journal of Sound and Vibration 329: 1450–1459. [Google Scholar]
- 26. Marinca V, Herisanu N, Nemes I (2008) Optimal homotopy asymptotic method with application to thin film flow. Central European Journal of Physics 6: 648–53. [Google Scholar]
- 27. Marinca V, Herisanu N (2008) An optimal homotopy asymptotic method for solving nonlinear equations arising in heat transfer. Int Commun Heat Mass Transfer 35: 710–5. [Google Scholar]
- 28.Marinca V, Herisanu N (2011) Nonlinear dynamical systems in engineering. Some Approximate Approaches. Springer, Verlag.
- 29. Islam S, Shah RA, Ali I (2010) Optimal homotopy asymptotic solutions of Couette and Poiseuille flows of a third grade fluid with heat transfer analysis. Int J Nonlinear Sci Numer Simul 11(6): 389–400. [Google Scholar]
- 30. Idrees M, Islam S, Tirmizi SIA, Haq S (2012) Application of the optimal homotopy asymptotic method for the solution of the Korteweg–de Vries equation. Mathematical and Computer Modelling 55: 1324–33. [Google Scholar]
- 31. Mohsen S, Hamid RA, Domairry D, Hashim I (2012) Investigation of the laminar viscous flow in a semi-porous channel in the presence of uniform magnetic field using optimal homotopy asymptotic method. Sains Malaysiana 41(10): 1281–5. [Google Scholar]
- 32. Ghoreishi M, Ismail AIM, Alomari AK (2011) Comparison between homotopy analysis method and optimal homotopy asymptotic method for nth-order integro-differential equation. Math Meth Appl Sci 34: 1833–42. [Google Scholar]
- 33.Mabood F, Khan WA, Ismail AIM (2013) Application of optimal homotopy asymptotic method for heat transfer in hollow sphere with robin boundary conditions. Heat Transfer-Asian Research In press.
- 34.Mabood F, Khan WA, Ismail AIM (2013) Solution of nonlinear boundary layer equation for flat plate via optimal homotopy asymptotic method. Heat Transfer-Asian Research In press
- 35. Khan N, Mahmood T, Hashmi MS (2013) OHAM solution for thin film flow of a third order fluid through porous medium over an inclined plane. Heat Transfer Research 44(8): 1–13. [Google Scholar]
- 36. Babaelahi M, Domairry G, Joneidi AA (2010) Viscoelastic MHD flow boundary layer over a stretching surface with viscous and ohmic dissipations. Meccanica 45(6): 817–27. [Google Scholar]