Axial Super Resolution Topography of Focal Adhesion by Confocal Microscopy

Abstract

The protein organization within focal adhesions has been studied by state-of-the-art super resolution methods because of its thin structure, well below diffraction limit. However, to achieve high axial resolution, most of the current approaches rely on either sophisticated optics or diligent sample preparation, limiting their application. In this report we present a phasor-based method that can be applied to fluorescent samples to determine the precise axial position of proteins using a conventional confocal microscope. We demonstrate that with about 4,000 photon counts collected along a z-scan, axial localization precision close to 10 nm is achievable. We show that, with within 10 nm, the axial location of paxillin, FAK, and talin is similar at focal adhesion sites, while F-actin shows a sharp increase in height towards the cell center. We further demonstrated the live imaging capability of this method. With the advantage of simple data acquisition and no special instrument requirement, this approach could have wide dissemination and application potentials.

INTRODUCTION

Fluorescence microscopy provides high specificity and live imaging capabilities that makes it an invaluable tool to study biomolecular distribution and dynamics. However, the application of fluorescence microscopy is hindered in many areas of biology by the limitation imposed by the diffraction limit unless super-resolution methods are used. Even so, super-resolution methods can be problematic when the resolution is needed in the axial direction. Light diffraction limits the smallest focal volume into which light can be focused, that is, the point spread function (PSF), to ~200 nm in the lateral image plane and about three times worse along the optical axis. This resolution is approximately the size of an intracellular organelle and thus is inadequate for dissecting the inner architecture of many subcellular structures.

Recently, several fluorescence microscopy techniques have been introduced to improve the axial resolution beyond the diffraction limit. Several approaches have been implemented to measure the axial profile of the PSF as the readout for the fluorophore axial position. In the biplane FPALM method (Juette et al., 2008), a beam splitter separates the image of single molecules into two channels that focused at different axial planes ~350 nm apart. The axial position of the single molecule could then be determined by comparing the peak widths in the two axial planes. In the astigmatic approach (Huang et al., 2008a,b), a cylindrical lens is introduced along the imaging path to defocus the light beam along one direction, which generates the ellipticity of the image as a function of the axial position. The ellipticity for each molecule was then used as z-coordinate read-outs. While these techniques allow axial resolution improvement on relatively simplified optical setups, their axial resolutions, however, are still typically in the range of sub-100 nm.

Through the implementation of interference principle, several novel fluorescence-imaging techniques have achieved axial resolution close to 10-nm scale, comparable to the thickness of cellular membrane (7–10 nm). The combination of PALM and interferometry approach by dual-objective design (Kanchanawong et al., 2010; Shtengel et al., 2009) has been described with 10–15 nm full width half maximum in the vertical axis. This approach has been used to dissect the nanoscale focal adhesion structure (Kanchanawong et al., 2010). A recent modification of fluorescence interference contrast microscopy termed scanning angle interference microscopy (Paszek et al., 2012) also showed similar axial resolution. Furthermore, this method has the capability of achieving live cell imaging.

Although these super resolution methods have provided biological images with stunning details along the optical axis, the requirement of sophisticated optical devices or intensive sample preparation/calibration protocols limit their application and dissemination. For PALM-based systems, in addition to the limitation of photo-activatable compounds in terms of biocompatibility and switching performance, the requirement of long data acquisition time hampers its applicability to dynamical studies. On the other hand, the scheme of scanning angle interference microscopy (Paszek et al., 2012) which utilized TIRF-based imaging, restricted the detection thickness to ~100 nm. Furthermore, the need of reflective substrate and intensive calibration also complicate the experimental setup.

Similar to the concept of biplane and astigmatic approaches described previously (Huang et al. 2008a,b; Juette et al., 2008), in this report we propose to exploit the PSF under a confocal microscopy setup to extract the molecule position with a precision in the 10 nm range. Along the optical axis, the PSF shape can be approximated by a Gaussian, in which the center-of-mass corresponds to the position of the fluorescent molecule. Hence, by taking z-stack images using a confocal microscope with step size smaller than the PSF, in principle it is possible to determine the position of a fluorophore with a precision better than the diffraction limit by calculating the center-of-mass of the intensity profile. In this article, we aim to localize thin layers of molecules, which is a common situation encountered in many biological systems.

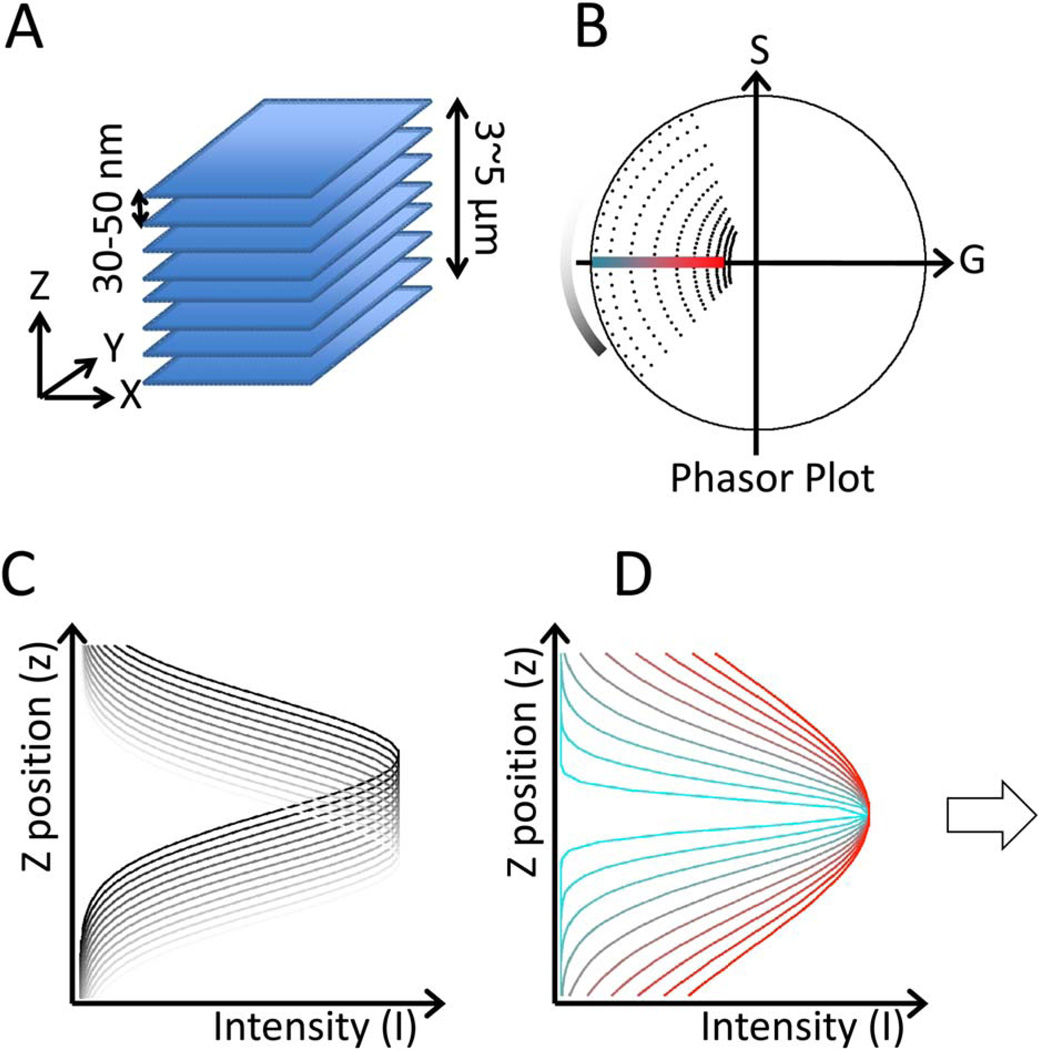
To efficiently determine the center-of-mass of the intensity profile, we applied the phasor approach, taking advantage of the fact that no prior assumption is needed about the shape of the PSF and of its robustness against noise. The phasor approach has been shown to be a powerful tool to resolve lifetime imaging data (Digman et al., 2008; Hinde et al., 2012; James et al., 2011; Stringari et al. 2011) as well as spectrum image data (Fereidouni et al., 2012), demonstrating the versatility of the phasor representation for imaging analysis. In this work we implemented the phasor method for axial center of mass determination through the analysis of the phasor first harmonic value. By transforming the intensity profile along the axial direction to a phasor vector, the angle of the vector correlates to the intensity center position, and the length of the vector gives us the information about the thickness of the fluorescent layer convoluted with the PSF (Fig. 1). Because in the Fourier domain a convolution reduces to the sum of angles, we have a simple method to determine the thickness of layers. The phasor approach can be applied to the each pixel of a z-stack by transforming the axial intensity profile at each pixel to a point in the phasor diagram, and then reconstructing the axial topography according to each pixel’s phasor angle (Fig. 1B).

Fig. 1.

Phasor transformation approach to determine axial super resolution topography. (A) An object is scanned at different focal planes to produce a z-stack. The slices separation is about 50 nm. (B) The phasor transformation maps the position and width of the Gaussian shape intensity profile (C) The colors (black to white for the z-position) indicate the relative placement in the phasor plot in which the angle is directly related to the original position. (D) The width of the intensity profile (colored in red to blue) maps into the modulus of the phasor; the smaller the width, the larger is the modulus. By selecting points in the plot at the same phase angle we can determine which part of the sample is at a give height. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

We demonstrate the proposed method by measuring the axial position of several focal adhesion-related proteins (paxillin, FAK, talin, and F-actin) at focal adhesion sites. Our results are comparable to a previously reported study using interferometric PALM (Kanchanawong et al. 2010). Furthermore, we show the dynamics of F-actin axial topography at a cell border with axial super resolution. This example not only demonstrates the live imaging capability of this approach, but also shows that the axial super resolution topography may carry distinct information that is obscured in intensity-based 3D image reconstruction.

The z-phasor approach is conceptually different from current super resolution methods based on the localization of single molecules in 3D. In our method we localize layers of molecules without the molecules blinking or being photoactivated which yields high precision center-of-mass localization of the layer along the axial axis. It also offers an alternative way for 3D data representation in contrast to common intensity-based 3D image reconstruction. As the approach is based on off-the-shelf commercial confocal microscope and conventional fluorescent imaging sample preparation, we expect this method to be easily applied to other biological systems, and also in conjunction with super-resolution techniques.

MATERIALS AND METHODS

Cell Culture Preparation

HEK 293 cell line (ATCC, CRL-1573) and CHO-K1 cell line (ATCC, CCL-61) were used for the experiments. Cells were cultured in Dulbecco’s modified Eagle’s medium (DMEM) with high glucose (Sigma, St. Louis, MO) and supplemented with 10% (v/v) fetal bovine serum at 37°C in a 5% CO₂ humidity incubator. Cells were pleated on MatTek 35-mm glass-bottom dishes coated with 5 µg of Fibronectin-Rhodamine (Cytoskeleton, Denver, CO). One day before imaging, cells were transfected with paxillin-EGFP (C-terminal linked), FAK-EGFP, talin-EGFP (N-terminal linked), or Lifeact-EGFP (Ibidi, Verona, WI) using Lipofectamine 2000 (Invitrogen, Carlsbad, CA) according to manufacturer’s protocol.

Microscope Setup

Confocal z-stacks were collected by an Olympus FV1000 confocal microscope (Olympus, Japan) using the standard Olympus FV software. A 60× water super apochromatic objective was used. We used lasers with excitation wavelength at 488 and 543 nm simultaneously to excite GFP and Rhodamine. The signal was split using a 560 nm band pass dichroic. The emission of GFP and Rhodamine were collected with 505–525 nm bandpass filter and 560–600 nm bandpass filter, respectively. Z-stack images were obtained with 256 × 256 pixels in the x–y plane with pixel size of 50 nm, and 50 nm step size along the axial axis with 80–100 slices in total, depending on the sample thickness.

Phasor Algorithm

We calculate the first harmonic of the cosine–sine Fourier transform to extract the center-of-mass information, as depicted in Figure 1. The intensity profile along the axial direction for each x–y coordinate, I_x,y(z), is transformed into a point in the phasor plot with S and G coordinates defined by the equations below:

$$S_{x,y}(\mathrm{\omega })=\frac{{\int }_0^L{I}_{x,y}(z)\text{sin}(\mathrm{\omega }z)\mathrm{d}z}{{\int }_0^L{I}_{x,y}(z)\mathrm{d}z}$$ (1)

$$G_{x,y}(\mathrm{\omega })=\frac{{\int }_0^L{I}_{x,y}(z)\cos (\mathrm{\omega }z)\mathrm{d}z}{{\int }_0^L{I}_{x,y}(z)\mathrm{d}z}$$ (2)

In Eqs. (1) (2) ω = 2πL where L is the total span of the z-stack along the z axial direction. For each phasor coordinate value, we define the angle ϕ and the modulus M of the phasor as

$$\mathrm{\varphi }={\text{tan}}^{-1}\left(\frac{S}{G}\right)$$ (3)

$$M=\surd (G^2+S^2)$$ (4)

As shown in Figure 1, the angle ϕ is linearly dependent on the position of the peak in the intensity profile I_x,y(z):

$$Z\text{center}=\frac{\mathrm{\varphi }\times L}{2\pi }$$ (5)

Each pixel of the z-stack gives a point in the phasor plot, and the angle ϕ for each phasor value is used to reconstruct the axial topography of the layer containing the fluorescent molecules.

Calibration Using a Reference Surface

To calibrate possible tilt of the microscope slide and to provide the height calibration that enables the comparison across different measurements and fields of view, we cultured cells on fibronectin–Rhodamine-coated imaging dishes; the signal from fibronectin and Rhodamine is used to define the zero position across the field of view. The fibronectin–Rhodamine z-stack data are phasor-transformed and the corresponding heights for each pixel are calculated using Eqs. (1) and (2). A plane with a given inclination and tilt was then fit to the measured fibronectin–Rhodamine topography and defined as zero height per each pixel of the image. This correction for inclination and tilt was applied to each image of the same stack. The phasor transform, surface calibration, and data plotting were integrated in the SimFCS program available at www.lfd.uci.edu.

RESULTS

Demonstration of the Phasor Approach Using a Single 2 µm Bead Immobilized on a Glass Surface

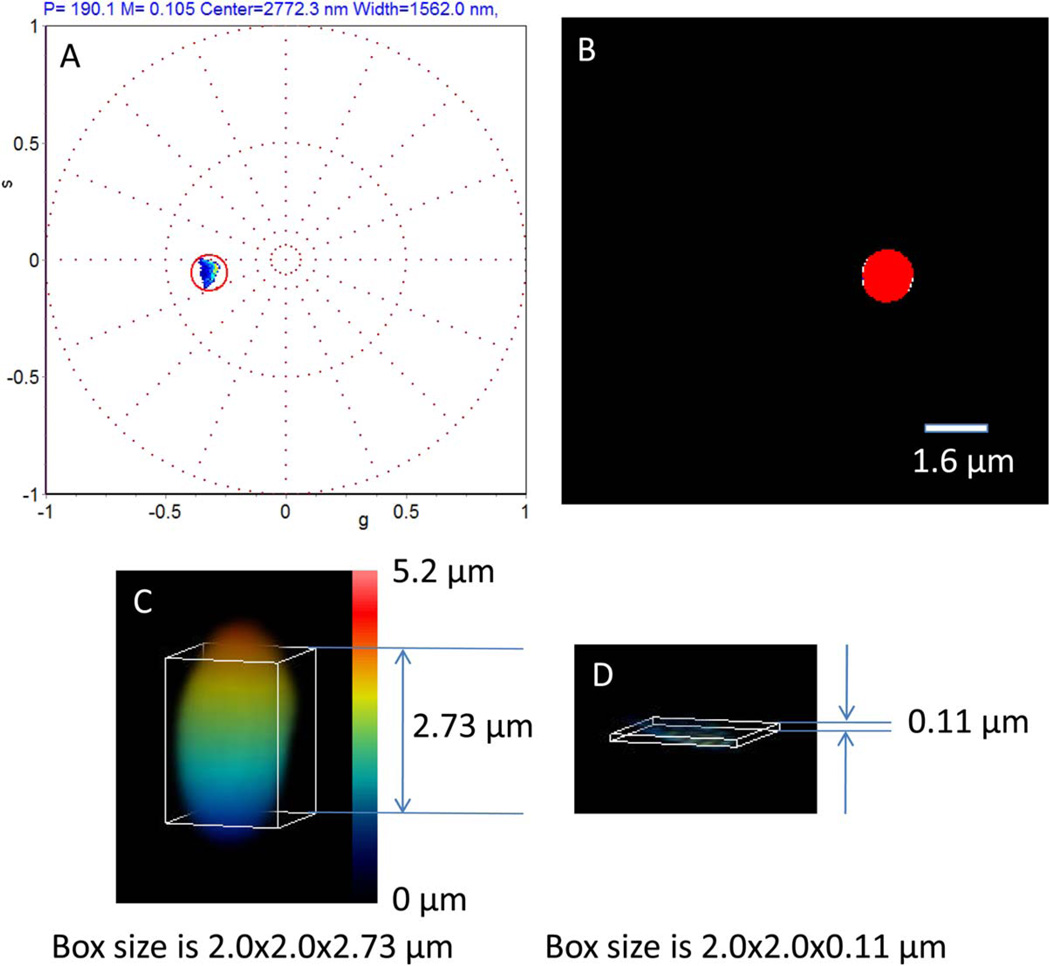
A single bead was imaged using a stack of 106 slices in the z-direction with 50 nm step size. In Figure 2A we show the phasor plot, with a single cluster at about 2,772 nm with respect to the beginning of the z-stack. This cluster contains about 68% of the total image intensity and the phasor in this cluster correspond to the bead as shown in Figure 2B. The 3D reconstruction using an isosurface that encompass about 68% if the total intensity is shown in Figure 2C. The size of this isosurface is about 2 µm in the x–y plane but it is longer than expected in the z-plane, presumable because of the larger size of the PSF in the axial direction. The reconstruction of the center of mass of the fluorescence intensity using the phasor approach is shown in Figure 2D with a very narrow distribution of about 110 nm in the axial direction as shown in Figure 2D. This example illustrates the basic difference between the 3D-isosurface reconstruction and the phasor reconstruction of the center of mass of the fluorescence distribution in the axial direction. Note that the information of the overall width of the fluorescence distribution is not lost because the modulus of the cluster of phasors is located at a position corresponding to a width of approximately 1,562 nm as shown in Figure 2A.

Fig. 2.

Difference between 3D reconstruction by intensity isosurface and the phasor determination of the center of mass of the fluorescence distribution of a 2 µm bead. A 2 µm bead was scanned at 50 nm per z-slice for a total height of 5.2 µm. (A) The phasor plot was constructed as described in Figure 1. The phasor distribution extends on a very narrow region as shown by the red circle. The diameter of the circle is 60 nm. (B) In the image projection image all the points in the red circle correspond to 68% of the intensity distribution and they are painted in red. (C) 3D reconstruction using intensity isosurface at the intensity that corresponds to 68% of the intensity histogram of the entire z-stack. The bead has the correct size in th x-y plane but it appears taller in the z-direction. (D) Selection of the points in the phasor plot in the red circle shows a very narrow distribution of heights (about 110 nm). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Localization Accuracy of the Phasor Center of Mass Determination

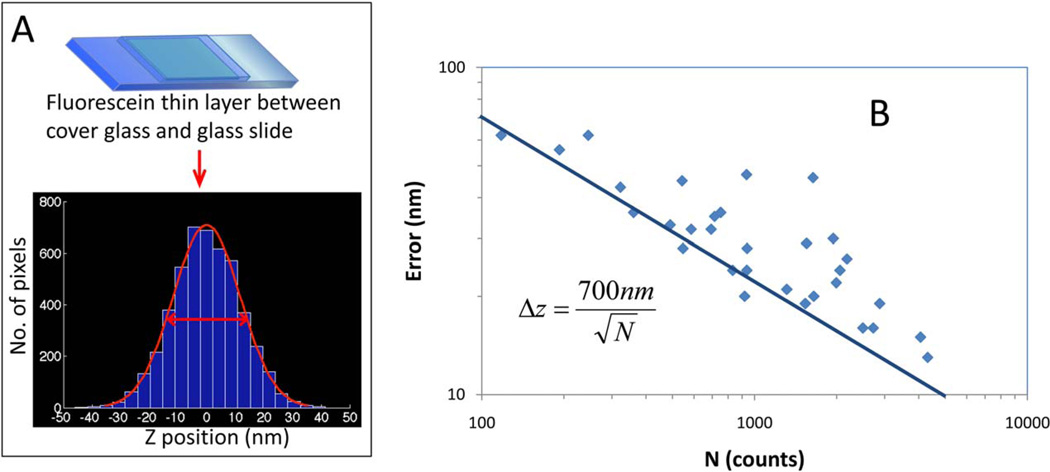
In order to estimate the localization precision of the phasor-based approach using a conventional confocal microscope (Olympus FV1000), we measured a thin layer of fluorescein solution between a coverglass and a glass slide (Fig. 3A), which should simulate a uniform flat layer of fluorophores. Z-stack confocal images were taken across the fluorescein thin layer with step size of 50 nm, and the center-of-mass axial position of each pixel was calculated by the phasor approach method. The standard deviation of the histogram of axial positions of each pixel measured across the image was used as a measure of localization precision. The laser power was then changed and the measurement was repeated several times. Figure 3B shows the relationship between the error deviation of the axial position of pixels and the total photon counts collected along one axial scan at a pixel. The localization accuracy scales approximately as the inverse square root of the number of photons detected and shows that a pixel in which the z-scan has a total number of photons of about 4,000 has an uncertainty in the localization of the center of mass of the layer of about 10 nm.

Fig. 3.

Estimation of the localization error using a fluorescein thin layer. (A) To estimate the localization precision by the phasor approach, we measured a thin layer of fluorescein between coverglass and glass slide, which represents a flat surface. Z-stacks of 256 × 256 pixels × 100 pixels (x, y, and z) with 50 nm/pixel in each direction were acquired with different laser power. The data were then phasor transformed to calculate the axial position for each x-y pixel. For each condition, we estimated the standard deviation of the pixel axial position distribution. (B) The standard deviation of the pixel axial position is inversely proportional to the square root of the number of photons detected. The solid line represents the theoretical curve for the equation shown in the panel. In ideal condition about 5,000 photons collected in a pixel along the z-scan are needed to recover the center of mass of the fluorescence distribution with an error of 10 nm. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Focal Adhesion Proteins Axial Position Determined by the Z-Phasor Method

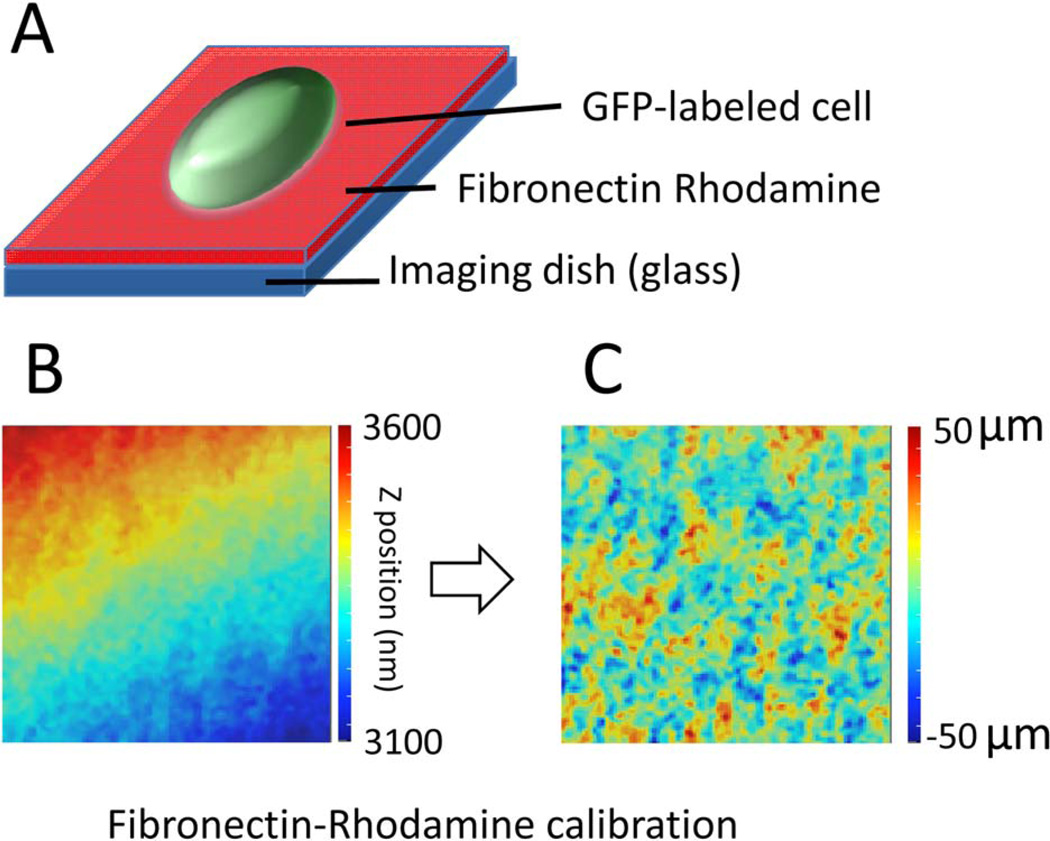
To compare the relative axial position of several focal adhesion proteins, we cultured different GFP-labeled CHO-K1 cells on fibronectin–Rhodamine coated imaging dishes (Fig. 4A). Z-stack images of focal adhesions were taken with step size of 50 nm. Both fluorescence signal from the proteins and Rhodamine were acquired simultaneously and the data were phasor-transformed as described in Material and Methods. The surface fit of the fibronectin–Rhodamine layer defines the 0 height position at each pixel and it provides the baseline for the comparison across samples. Figure 2B shows that the tilt and inclination can be substantial, with a total span in the field of view up to 500 nm. After correction, the fibronectin–rhodamine layer appears flat on the average with local deviations smaller that 50 nm. Here, we don’t correct for systematic difference in focus because of the use of two colors, but we use the red color as our zero reference level and for the correction of the tilt of the slide. Because all proteins we describe here are emitting in the same green channel we believe that the relative comparison should not be affected by the potential systematic error because of the use of the two different colors.

Fig. 4.

Correction for the inclination and tilt of the microscope slide. (A) In order to compare the axial position across samples, EGFP-paxillin labeled cells were cultured on top of fibronectin–Rhodamine coated image dishes, where the rhodamine layer serves as an internal calibration. The image stack was acquired with two channels for EGFP and Rhodamine signals, simultaneously. (B) Using the measurement from fibronectin–Rhodamine, we measured the inclination and tilt of the slide surface. (C) These values were used to correct the position of the sample in the green channel for each pixel of the field of view. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

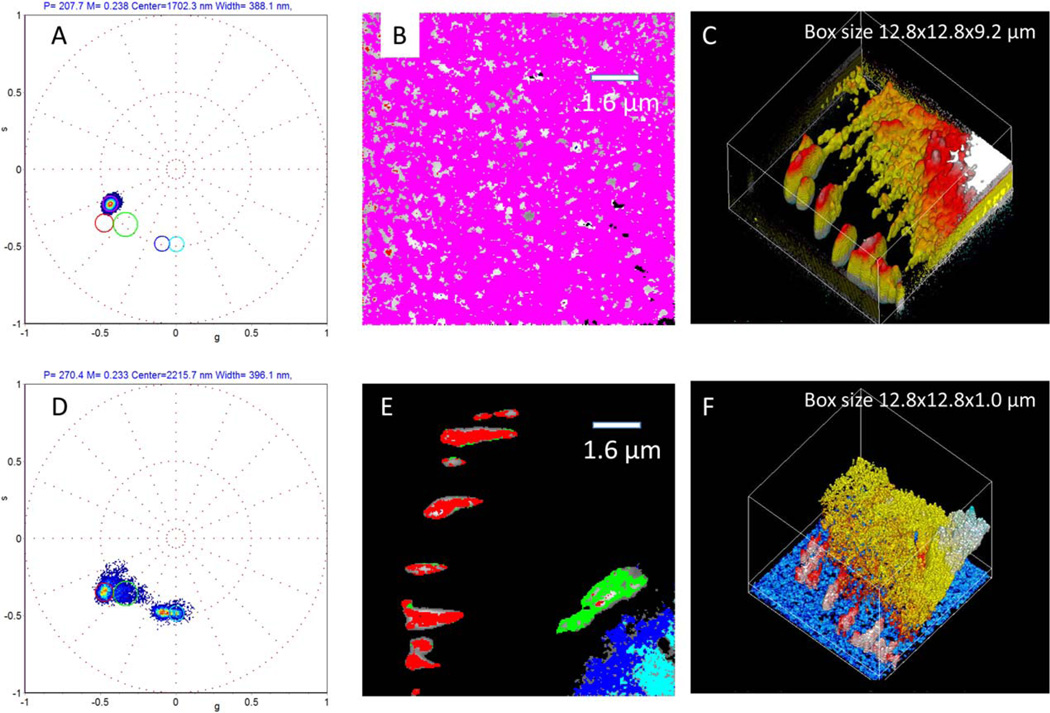
In Figure 5 we compare the representation of the same z-stack dataset by conventional intensity-based 3D reconstruction (Fig. 4C) and phasor-transformed axial topography (Fig. 4F) of a CHO-k1 cell expressing paxillin–EGFP. In Figure 5A we show the narrow cluster distribution of the fibronectin layer and in Figure 5B we show the layer is narrow and flat after the tilt correction. In Figure 5C we show the 3D isosurface reconstruction. Because the focal adhesions are very bright, it is difficult to choose the appropriate isosurface level for the entire image. Furthermore in this example, it was very difficult to determine the center-of-mass difference using intensity-based 3D reconstruction (Fig. 5C); the overall scale of the box in the 3D reconstruction is 9.2 µm in the z-direction. Instead using the phasor-transformed axial topography, distinct regions with different axial position and thickness can be separated even when the height difference between the layers is well below the size of the PSF. The location of the layer of paxillin-EGFP at focal adhesions is close to the surface (blue), in contrast to the higher center-of-mass axial positions of paxillin in the cytoplasm which is towards cell center (yellow to red). Reciprocally, we can select regions in the phasor plot (Fig. 5D) and paint the original image based on height, thus providing segmentation based on pixels with similar axial positions (Fig. 5E). As shown in Figure 5D, we recognize three distinct regions in the phasor plot that corresponds to separate areas of a cell (Fig. 5E). The mean axial position of each region can be determined with high precision based on the average angle ϕ of the selected region in the phasor plot. These values are given in the caption of Figure 5. Figure 5F shows the axial topography of paxillin-EGFP distribution after calibration using the fibronectin-Rhodamine layer (shown in blue in Fig– 5F). The size of the box in the z-direction is only 1 µm and we can easily follow the various layers were paxillin is located.

Fig. 5.

Determination of the z-position of a layer of paxillin-EGFP molecules in focal adhesions. (A) Phasor plot of the fibronectin–rhodamine layer on the glass-surface. The position as well as the width of the layer can be determined from the position of the phasor cluster in the magenta cursor. After correction of the inclination and tilt as described in Figure 4, the rhodamine layer average location is at 1,702 nm. (B) points in the projection image selected by the magenta cursor. (C) Isosurface 3D reconstruction of this sample. Note that the focal adhesions appear very broad and that the box in panel C has a z-range of 9.2 µm. (D) the phasor plot of the same sample. We can identify at least four clusters indicated by the colored cursors (red at 1,770 nm, green at 1,858 nm, blue at 2,126 nm and cyan at 2,215 nm. Note also that the clusters are narrower than the rhodamine layer, in part because of the different wavelength of excitation and emission of the two channels. (E) The colored cursors selects clearly distinct feature of the image. The focal adhesion can be identified with the red cursor and perhaps the green cursor, while the rest of the signal arises from cytoplasmic paxillin EGFP. (F) the location of the paxillin-EGFP layers using the information from the phasor plot. Note that the box z-range for this panel is 1 µm. The paxillin layers are well visible in the phasor-reconstructed image while the 3D isosurface reconstruction does not follow the surface but the intensity isosurface. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

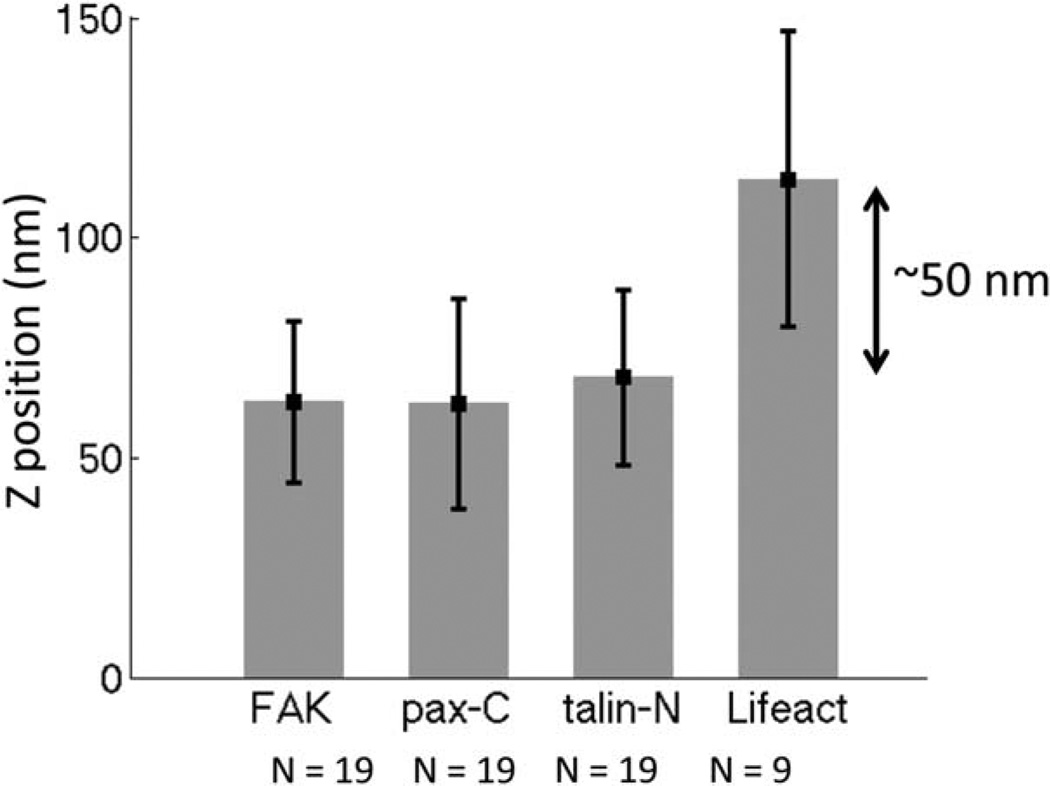
Using the z-phasor approach, we measured the axial position of paxillin-EGFP, FAK-EGFP, talin-EGFP, and Lifeact-EGFP at focal adhesions in multiple cells (Fig. 6). The number of cells measured is given in Figure 6. The position determination for these proteins obtained with the phasor approach is comparable to the result obtained by the interferometric PALM method (Kanchanawong et al., 2010) in terms of relative position, in which FAK, paxillin-C terminal, and talin-N terminal are within 10 nm difference, and F-actin occupies the position ~50 nm above. However, we notice the slight difference in terms of absolute position of all proteins (20 nm higher in our measurement), which may be because of the difference in the zero position calibration. In Kanchanawong et al.’s work (2010), the baseline was determined by the gold beads on the glass dish while in our experimental setup we used the fibronectin–Rhodamine center-of-mass as the baseline. As we mention, we have not accounted for a potential difference of the focus of the two different colors.

Fig. 6.

Focal adhesion proteins axial position determined by phasor approach. We compared the axial position of FAK, paxillin-C terminal, talin-N terminal, and F-actin (Lifeact label) at focal adhesions. The overall result is comparable to the measurement by interferometric PALM method (Kanchanawong et al., 2010) in terms of relative position, in which FAK, paxillin-C terminal and talin-N terminal are within 10 nm difference, and F-actin occupies the position ~50 nm above.

Actin Axial Topography Dynamics

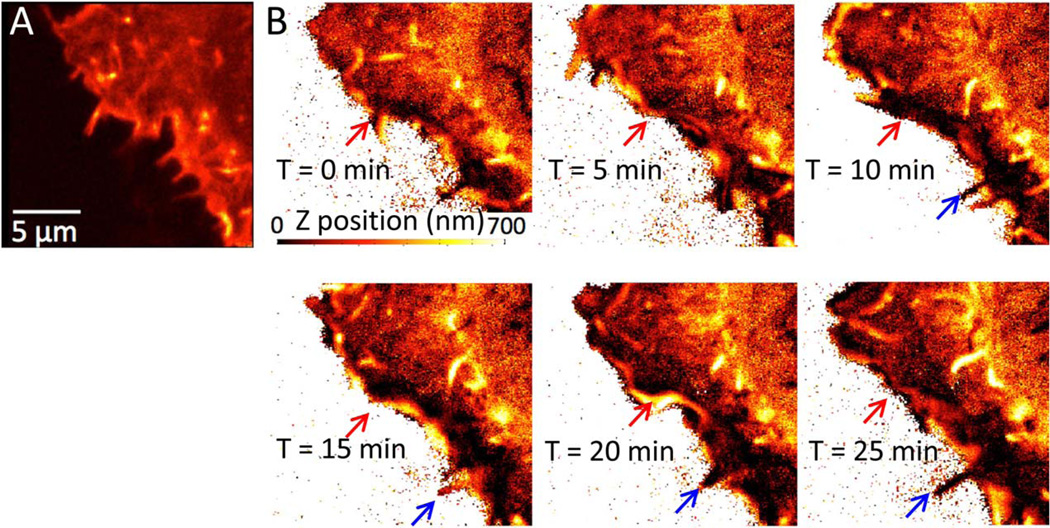
We further investigated the live cell imaging capability of the z-phasor method by imaging the dynamics of F-actin in the lamellipodia of a HEK 293 cell (Fig. 7). Z-stack time series images were taken over half an hour. Because GFP and fibronectin–Rhodamine signals were recorded simultaneously for all acquisitions, potential overall sample drift over the time course of the experiment were taken into account, and we were able to observe F-actin axial position changes with high precision. In contrast to the intensity-based image representation (Fig. 7A), after phasor-transformation, the F-actin axial position changes can be detected during membrane ruffling as indicated by the red arrows in Figure 7B. Filopodia appearing at different heights were also observed. One example of filopodia growing along the fibronectin surface is indicated by blue arrows (Fig. 7B).

Fig. 7.

Actin axial topography dynamics at cell border. A HEK-293 cell transfected with Lifeact-EGFP to label F-actin was imaged over 25 min. (A) Intensity image shows high F-actin concentration at filopodia. (B) The phasor transformed axial topography shows distinct axial position of filopodia and lamellipodia. The topographic map changes with time because of membrane ruffling as indicated by red arrows. Blue arrows indicate an example of filopodia growing along the fibronectin surface. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

DISCUSSION

In this article, we present an axial super resolution topography method based on the phasor transformation of z-stacks obtained with a conventional confocal microscope. Because of its simplicity of implementation and no specific fluorophore requirement, the method may be useful for biological research in need for live imaging with high axial resolution. Furthermore, there is no restriction on sample depth or thickness besides the restriction posed by the working distance of the objective used. This is in contrast with methods based on interference or dual-objective setup that limit the sample thickness to less than 1 µm.

In addition to the ease of implementation, the z-phasor method which is based on a fluorescence intensity center-of-mass determination provides several advantages. First, the fit-free, fast calculation nature of phasor transformation is computationally inexpensive, and the only parameters needed are the z step size of the image stack and the total z-range. The detailed model of the PSF shape is not necessary provide that the PSF is relatively symmetrical along the axial direction. Second, because the phasor calculation integrates the signal along the axial axis, it yields higher accuracy and noise tolerance compared to super resolution through biplane and astigmatic approaches, which generally use one or two sections of the PSF to estimate the axial position (Huang et al., 2008a,b; Juette et al., 2008). Furthermore, the phasor techniques that were previously developed for fluorescence lifetime measurement (Digman et al., 2008; Hinde et al., 2012; James et al., 2011; Stringari et al. 2011) can be readily applied, including the reciprocal mapping feature as demonstrated in Figures 2B and 5F.

The phasor approach also provides a different way to reconstruct 3D images. Conventionally, 3D image data are reconstructed by intensity isosurfaces. However, for many structures, the fluorescence intensity varies along the surface and also in the interior and the isointensity surface could not show the structure position accurately. The center-of-mass representation as determined by the phase of the phasor is independent on the intensity (in the same way as fluorescence lifetime is independent on the concentration of the fluorophore) and it can provide the position of the surface correctly even if the density of fluorophores changes along the surface. For very small structures, by focusing on positional information, the method can be advantageous over the conventional 3D reconstruction. In addition, it is possible to combine the information of the angle of the phasor vector that determines the center of mass and the modulus of the vector that determines the thickness to perform image reconstruction.

As with other super resolution methods, the localization accuracy limitation of the z-phasor approach is governed by the number of photons collected, as shown in Figure 3. When working with live samples, the acquisition speed, photo-toxicity, and desired accuracy all need to be taken into consideration. For EGFP-labeled live cells, we used low laser power for excitation to minimize photo-bleaching while still acquiring about 500–1,000 photons per z-scan at the pixels of interest which according to the graph in Figure 3 results in an error in the determination of the center of mass of about 30–20 nm., respectively. As described in Eq. (4), the phasor transformation provides a linear relationship between the phasor vector angle ϕ and the center-of-mass position. It holds true only if the entire Gaussian shape is covered in the acquisition, namely the z-scan must cover the entire object to be measured.

The phasor approach to determine the position of a surface can also be applied to multi-color acquisition. In the experiments described in this work we used two-color acquisition (EGFP green and fibronectin–Rhodamine red), where the Rhodamine is used for establishing the zero at each pixel location. To compare two or more protein localizations within a cell simultaneously, one can perform dual transfection and apply the same two-color approach to calculate the relative distances between two labeled protein species. However, the chromatic aberration from the objective and the possible laser alignment mismatch need to be taken into account. The experiments presented in this report were acquired with an apochromatic objective that minimizes the chromatic aberration and the rhodamine layer was only used as a term of comparison between different samples and for correcting the tilt of the microscope slide.

We show in the example in Figure 7F-actin dynamics with time resolution in the minutes range. By reducing the field of view, or by performing x–z scans, the time resolution can be in the seconds scale. Furthermore, by oscillating the laser beam along the z-axis, we could reach millisecond time scale at one pixel and this type of acquisition might be suitable to perform real-time “surface tracking.” This idea is similar, in the principle, to the nSPIRO method (Lanzano and Gratton 2012) in which the beam fast oscillation is utilized to determine the fluorophore position.

In this article, we mainly used the first harmonic for the phasor transformation to determine the center-of-mass position of the fluorescent layer. As protein organizations may have more complex features than a monolayer, additional analysis may be needed to retrieve this detailed information. Assuming that there are two layers of fluorophores at different axial positions, performing the phasor transformation with the first harmonic gives us the weighted average center position of these two layers. One possible way to retrieve the relative distance of the two layers is by analyzing the Fourier spectrum of the intensity profile that will show at higher harmonics the interference pattern because of the two layers. This problem is similar to the decomposition of lifetime decays using the phasor approach. In the lifetime case, the use of higher harmonics is needed to resolve multiple exponentials. However, higher harmonics have more noise and more counts will be needed to use this approach.

In conclusion, in this article, we present an axial super resolution topography method based on data acquired in a conventional confocal microscopy and employing the phasor transformation algorithm that has already wide dissemination and application for FLIM and spectral analysis. Although the results shown in this report were obtained in 2D cell cultures, this method can be applied to cells cultured in 3D matrix to study their protein organizations, which may not be easily reachable by other super resolution methods.