Quantitative measurement of intracellular transport of nanocarriers by spatio-temporal image correlation spectroscopy

Abstract

Spatio-temporal image correlation spectroscopy (STICS) is a powerful technique for assessing the nature of particle motion in complex systems although it has been rarely used to investigate the intracellular dynamics of nanocarriers so far. Here we introduce a method to characterize the mode of motion of nanocarriers and to quantify their transport parameters on different length scales from single-cell to subcellular level. Using this strategy we were able to study the mechanisms responsible for the intracellular transport of DOTAP-DOPC/DNA and DC-Chol-DOPE/DNA lipoplexes in CHO-K1 live cells. Measurement of both diffusion coefficients and velocity vectors (magnitude and direction) averaged over regions of the cell revealed the presence of distinct modes of motion. Lipoplexes diffused slowly on the cell surface (diffusion coefficient, D ≈ 0.003 µm²/s). In the cytosol, the lipoplexes’ motion was characterized by active transport with average velocity ν ≈ 0.03 µm/s and random motion. The method permitted us to generate intracellular transport map showing several regions of concerted motion of lipoplexes.

1. Introduction

Nanocarriers offer unique possibilities to overcome cellular barriers in order to improve the delivery of various drugs and gene nanomedicines [1–3]. A fundamental step towards the design of nanocarriers is the complete knowledge of the delivery mechanisms such as cellular uptake, cytoplasmic transport, endosomal escape, and nuclear localization. Even though important steps in this direction have been taken, the key issue of specifically how nanocarriers travel through the cytoplasm remains largely unknown. Thus, there is scope to use and develop methods that allow us to investigate the hurdles impeding drug and gene delivery [4–9].

Here we introduce a strategy based on spatio-temporal image correlation spectroscopy (STICS) [10,11] that allows us to characterize the intracellular mode of motion of nanocarriers and to quantify their transport parameters on different length scales from single-cell to subcellular level. Except for few reports in which it was used to investigate the Golgi trafficking [12], intracellular trafficking of vesicles [13] and polymer/DNA complexes (polyplexes) [14], STICS has poorly been considered as a tool to study the intracellular transport of gene nanocarriers. By its nature, the STICS technique measures an ensemble of particles and can report average values but not their distribution, as can be done by SPT [15–19]. The STICS method is a powerful tool for determining the average kinetic behavior of multiple intracellularly moving nanocarriers and allows us to extract a great amount of data due to its high statistics (all particles are counted, irrespective of their brightness). Using this strategy we could study the mechanisms responsible for the intracellular transport of lipoplexes in CHO-K1 live cells. This mammalian cell line was chosen due to its common use in biomedical research for transfection, expression, and large-scale recombinant protein production. Likewise, two frequently used lipoplex formulations were chosen. The first formulation was the widely used system made of the cationic lipid 1,2-dioleoyl-3-trimethylammonium-propane (DOTAP) and the zwitterionic lipid dioleoylphosphocholine (DOPC). The second one was the binary system made of the cationic 3β-[N-(N,N-dimethylaminoethane)-carbamoyl] cholesterol (DC-Chol) and the zwitterionic helper lipid dioleoylphosphatidylethanolamine (DOPE). Using STICS we have measured the effective diffusion constants and transport velocities of DOTAP-DOPC/DNA and DC-Chol-DOPE/DNA lipoplexes to understand how they behave when introduced to cells; specifically, how they are transported to the cell nucleus. Most importantly, due to the ability of correlation techniques to analyze distinct regions of interest (ROIs) in a confocal image [10, 11, 20–23], STICS allowed us to investigate the motion of particles within different subcellular regions, thus revealing the presence of distinct local dynamics. Taking advantage of these distinct features here we introduced a detailed procedure to study the intracellular mode of motion of nanocarriers by STICS without adopting any a priori fitting model. Measurement of both diffusion coefficients and velocity vectors (magnitude and direction) averaged over regions of the cell revealed the existence of distinct modes of motion. Lipoplexes diffused slowly on the plasma membrane surface (diffusion coefficient, D ≈ 0.003 µm²/s). In the cytosol, the lipoplexes’ motion was characterized by active transport with average velocity |ν| ≈ 0.03 µm/s and random motion. The method permits us to generate intracellular flow mapping of moving nanoparticles showing several regions with concerted motion that appears to be directed towards the nucleus, though further statistical analysis would be needed to show that this is the mechanism contributing to the eventual nuclear destination.

2. Experimental section

2.1 Liposomes and lipoplexes preparation

The cationic lipids 1,2-dioleoyl-3- trimethylammonium-propane (DOTAP) and 3β-[N-(N’,N’-dimethylaminoethane)-carbamoyl]-cholesterol (DC-Chol) and the zwitterionic helper lipids dioleoylphosphocholine (DOPC) and dioleoylphosphatidylethanolamine (DOPE) were purchased from Avanti Polar Lipids (Alabaster, AL) and used without further purification for the preparation of DC-Chol-DOPE and DOTAP-DOPC cationic liposomes (CLs). In brief, the binary lipid mixtures, at molar fractions of neutral lipid in the bilayer φ=neutral/(neutral+cationic) (mol/mol) = 0.5 were first dissolved in chloroform and subsequently left to evaporate under vacuum for at least 24 h. The obtained lipid films were then hydrated with Nanopure water until a final concentration of ~ 1 mg/ml. Sonication to clarity was needed to obtain unilamellar CLs. For size and ζ-potential measurements experiments, calf thymus (CT) DNA (Sigma-Aldrich, St. Louis, MO) was used. For confocal laser scanning microscopy (CLSM) experiments, Cy3-labeled 2.7-kbp plasmid DNA (Mirus Bio Corporation, Madison, WI) was used. In order to form binary lipoplexes (DOTAP-DOPC/pDNA or DC-Chol-DOPE/pDNA) ready for administration to CHO-K1 cells, 100 µl of phosphate buffered saline (PBS) were added to a 5 µl dispersion containing binary CLs (5 µl of DOTAP-DOPC or 5 µl of DC-Chol-DOPE). The same amount of buffer was added to 1 µl of plasmid DNA (pDNA). These solutions were subsequently left to equilibrate for a few minutes. Then, the pDNA solution was poured in the liposome dispersion (cationic lipid/DNA charge ratio (mol/mol), ρ≈3) and after 20 minutes the complexes were ready to use. For size and ζ-potential measurements samples were prepared by mixing an adequate amounts of the CT DNA solutions to suitable volumes of liposome dispersions, so as to obtain samples at a fixed ρ≈3.

2.2 Size and ζ-Potential Measurements

All size and ζ-potential measurements were made on a Zetasizer Nano ZS90 (Malvern, U.K.) at 25 °C with a scattering angle of 90°. Sizing measurements were made on the neat vesicle dispersions, whereas the samples were diluted 1:10 with distilled water for the ζ-potential experiments to obtain reliable and accurate measurements. For all of the samples investigated, the data show a unimodal distribution and represent the average of at least five different measurements carried out for each sample. More extensive experimental details can be found in the literature [23].

2.3 Cell culture and transfection

CHO-K1 cells were purchased from American Type Culture Collection (CCL-61 ATCC) and were grown in Ham’s F12K medium supplemented with 10% of Fetal Bovine Serum (FBS) at 37°C and in 5% CO₂. Cells were split every 2–4 days to maintain monolayer coverage. On the day of transfection, the culture medium was removed, and cells were washed three times with PBS before adding lipoplexes in a total medium volume of about 2 ml. After administration, 4 hours of incubation allowed complete internalization of the complexes (data not reported). To eliminate non internalized and freely diffusing complexes, the medium was then replaced with the measurement medium, i.e. DMEM depleted of phenol red.

2.4 CLSM Experiments

Confocal microscopy experiments were carried out using a Fluoview FV-1000 (Olympus, Tokyo, Japan) microscope. The excitation source was a 543nm HeNe laser. More details about the experimental setup can be found elsewhere [20]. Following the practical guidelines by Kolin and Wiseman [11], the experiments were carried out at 37°C and were controlled by a data acquisition software (FV10-ASW, Olympus, Tokyo, Japan). For each region of interest, at least 50 raster scanned images of 256 × 256 pixels were acquired. The pixel size was set equal to 0.1–0.25 µm/pixel, while the pixel dwell time was set equal to 8–20 µs/pixel. Due to the slow dynamics of the complexes, the time resolution (i.e. the distance in time between two subsequent frames) was set equal to the frame acquisition time plus a delay time on the order of 1–5 seconds (Δt in the following). Data were analyzed by a custom-made data acquisition software (SimFCS, Laboratory for Fluorescence Dynamics, Irvine, CA -downloadable from www.lfd.uci.edu) and an additional custom-made Matlab (The Math Works, Natick, MA) program.

2.5 STICS Data Analysis

The raw data for image correlation analyses is an image series which is the fluorescence intensity, recorded as a function of space and time, i(x, y, t). It is possible to define a generalized spatio-temporal correlation function (single detection channel) [10, 11]:

$$\mathrm{g}(\mathrm{\xi },\mathrm{\eta },\mathrm{\tau })=\frac{\langle \mathrm{\delta }\mathrm{i}(\mathrm{x},\mathrm{y},\mathrm{t})\mathrm{\delta }\mathrm{i}(\mathrm{x}+\mathrm{\xi },\mathrm{y}+\mathrm{\eta },\mathrm{t}+\mathrm{\tau })\rangle }{{\langle \mathrm{i}(\mathrm{x},\mathrm{y},\mathrm{t})\rangle }_{\mathrm{t}}{\langle \mathrm{i}(\mathrm{x},\mathrm{y},\mathrm{t}+\mathrm{\tau })\rangle }_{\mathrm{t}+\mathrm{\tau }}}$$ (1)

where δi(x, y, t)=i(x, y, t)-<i(x, y, t)>_t is the intensity fluctuation at image pixel position (x, y) and time t, the angular brackets in the denominator represent spatial ensemble averaging over images at time t and t+τ in the time series, and the numerator is also an ensemble average over all pixel fluctuations in pairs of images separated by a time-lag of τ. An image series is discrete in both space and time, so a discrete approximation of the temporal generalized function (equation (1)) is defined as follows:

$$\mathrm{g}\text{'}(\mathrm{\xi },\mathrm{\eta },\mathrm{\tau })=\frac{1}{\mathrm{N}-\frac{\mathrm{\tau }}{\mathrm{\Delta }t}}\sum _{\mathrm{k}=1}^{\mathrm{N}-\frac{\mathrm{\tau }}{\mathrm{\Delta }t}}\frac{1}{\text{XY}}\sum _{\mathrm{x}=\mathrm{\delta }\mathrm{x}}^{\delta \mathrm{x}\cdot \mathrm{X}}\sum _{\mathrm{y}=\mathrm{\delta }\mathrm{y}}^{\mathrm{\delta }\mathrm{y}\cdot \mathrm{Y}}\frac{\langle \mathrm{\delta }\mathrm{i}(\mathrm{x},\mathrm{y},\mathrm{\Delta }\mathrm{t})\mathrm{\delta }\mathrm{i}(\mathrm{x}+\mathrm{\xi },\mathrm{y}+\mathrm{\eta },\mathrm{k}\cdot \mathrm{\Delta }\mathrm{t}+\mathrm{\tau })\rangle }{{\langle \mathrm{i}(\mathrm{x},\mathrm{y},\mathrm{k}\cdot \mathrm{\Delta }\mathrm{t})\rangle }_{\mathrm{k}\cdot \mathrm{\Delta }\mathrm{t}}{\langle \mathrm{i}(\mathrm{x},\mathrm{y},\mathrm{k}\cdot \mathrm{\Delta }\mathrm{t}+\mathrm{\tau })\rangle }_{\mathrm{k}\cdot \mathrm{\Delta }\mathrm{t}+\mathrm{\tau }}}$$ (2)

where X and Y are the number of pixels spanning the region being analyzed (e.g. X=Y=16, 32, 64, 128, 256,… pixels), N is the number of images in the image series (e.g. N=50 in our experimental data), k is a dummy variable, Δt is the time resolution and δx=δy is the pixel size. Different ROI sizes allow us to investigate the biological system at different scales. In fact, due to the anisotropy of cells, decreasing the ROI size allows us to gain local dynamical information. To perform the STICS analysis, the lipoplex must remain inside the ROI for all the experimental times, otherwise it will affect the time correlation functions analogously to photobleaching (see the Results section for further details). The minimum achievable ROI size, ROI_min, is therefore dictated mainly by the dynamics of the system. From local dynamical parameters of lipoplex investigated by SPT [17–19], we can provide an estimate of ROI_min~ 10 µm (see supplementary data for a detailed calculation). Considering an average pixel size of about 0.2 µm, the ROI must be greater than 32 × 32 pixels (6.4 × 6.4 µm² ). Hence, we decided to set the minimum value for X equal to 64 pixels. To reduce computation times, equation (2) is typically calculated using Fast Fourier Transform methods rather than by direct calculation. Prior to calculation of the correlation function (equation (2)), it is necessary to apply an immobile population filtering algorithm to detect only moving complexes [10]. A corrected pixel intensity (i_new) is obtained by subtracting the average intensity for each pixel time trace from the original pixel intensity (i_old). At single pixel location (x, y) the immobile filtered intensity could be defined as follows:

$${\mathrm{i}}_{\text{new}}(\mathrm{x},\mathrm{y},\mathrm{k})={\mathrm{i}}_{\text{old}}(\mathrm{x},\mathrm{y},\mathrm{k})-\frac{1}{\mathrm{N}}\sum _{\mathrm{k}=0}^{\mathrm{N}-1}{\mathrm{i}}_{\text{old}}(\mathrm{x},\mathrm{y},\mathrm{k})+\mathrm{a}$$ (3)

where the summation is over discrete image frames (k) so the subtracted term is effectively the time average through the image series of the intensity at image pixel location (x,y), and the scalar term a is the average image intensity of the entire stack. It is added to all pixels for each image of the entire stack to avoid average image intensities near zero and consequent wide oscillations of the correlation functions (equation (2)) [20–22]. The STICS function calculated by equations (2) and (3) is then fit to the analytical model derived for the mode of motion present in the analyzed ROI of the sample. In the presence of flow, the STICS correlation function could be fitted to a 2D Gaussian which moves from the spatial zero-lags as a function of time lag τ. The two-dimensional velocity of the sample is determined by tracking the center of the moving peak at each time lag. Linear regressions of the x- and y-coordinates of the peak position as a function of time yield the x- and y-components of the velocity (obviously, under the assumption of uniform motion). Instead, from the heights of the 2D Gaussian curves we can determine the two-dimensional diffusion coefficient and velocity (if flow is present). In fact, in the case of single population that undergoes Brownian diffusion, the temporal intensity correlation function (i.e. equation (1) with ξ=η=0) could be fitted to:

$$\mathrm{g}(0,0,\mathrm{\tau })=\mathrm{g}(0,0,0){(1+\frac{\mathrm{\tau }}{{\mathrm{\tau }}_{\mathrm{d}}})}^{-1}{[1+\frac{\langle {{\mathrm{\omega }}_0}^2\rangle }{{{\mathrm{\omega }}_{\mathrm{z}}}^2}\frac{\mathrm{\tau }}{{\mathrm{\tau }}_{\mathrm{d}}}]}^{-\frac{1}{2}}+{\mathrm{g}}_{\infty }$$ (4)

where g(0,0,0) is the zero-lags amplitude, g _∞ is the longtime offset, <ω₀²>/ω_z² is the ratio between the average radial and axial beam radii, and the characteristic diffusion time τ_d is related to the diffusion coefficient, D by:

$$\mathrm{D}=\frac{\langle {\mathrm{\omega }}_0^2\rangle }{4{\mathrm{\tau }}_{\mathrm{d}}}$$ (5)

The mean e⁻² radius, <ω₀²>, for a particular analysis is usually determined by fitting the spatial autocorrelation function (i.e. equation (1) with τ=0) of each image to a 2D Gaussian and finding the average value of <ω₀²> for the time series. In the case of single population that simultaneously undergoes Brownian diffusion and flow, the fitting function becomes:

$$\mathrm{g}(0,0,\mathrm{\tau })=\mathrm{g}(0,0,0){(1+\frac{\mathrm{\tau }}{{\mathrm{\tau }}_{\mathrm{d}}})}^{-1}{[1+\frac{\langle {{\mathrm{\omega }}_0}^2\rangle }{{{\mathrm{\omega }}_{\mathrm{z}}}^2}\frac{\mathrm{\tau }}{{\mathrm{\tau }}_{\mathrm{d}}}]}^{-\frac{1}{2}}\text{exp}\{-{\left(\frac{\left|\nu \right|\mathrm{\tau }}{\langle {\mathrm{\omega }}_0^2\rangle }\right)}^2{(1+\frac{\mathrm{\tau }}{{\mathrm{\tau }}_{\mathrm{d}}})}^{-1}{[1+\frac{\langle {{\mathrm{\omega }}_0}^2\rangle }{{{\mathrm{\omega }}_{\mathrm{z}}}^2}\frac{\mathrm{\tau }}{{\mathrm{\tau }}_{\mathrm{d}}}]}^{-\frac{1}{2}}\}+{\mathrm{g}}_{\infty }$$ (6)

where |ν| is the two-dimensional velocity, that in principle should be equal to the one obtained by tracking the moving peak. To determine the diffusion coefficient, equation (5) still holds. Due to the contribution of shot-noise to the numerator of equation (1) only at zero-lag (both spatial and temporal, i.e. ξ=η=τ=0), all the fits in this analysis are performed excluding the zero-lag amplitude. More details about the STICS theory can be found elsewhere [10, 11].

3. Results

3.1 Size and ζ-potential

Size and ζ-potential measurements showed thatboth DOTAP-DOPC/DNA and DC-Chol-DOPE/DNA lipoplexes are positively charged aggregates with low colloidal dimensions (table 1). Charge and size dimensions are suitable for the purpose of delivering genes in live cells [4–8].

Table 1.

Average hydrodynamic diameter, D, and ζ-potential, ζ_P, of DOTAP-DOPC/DNA and DC-Chol-DOPE/DNA lipoplexes. Standard deviations are also reported.

	D [nm]	ζP[mV]
DOTAP-DOPC/DNA	214±30	48.8±2.0
DC-Chol-DOPE/DNA	190±20	51.0±1.5

3.2 STICS

3.2.1 STICS analysis on 256 × 256 pixels images

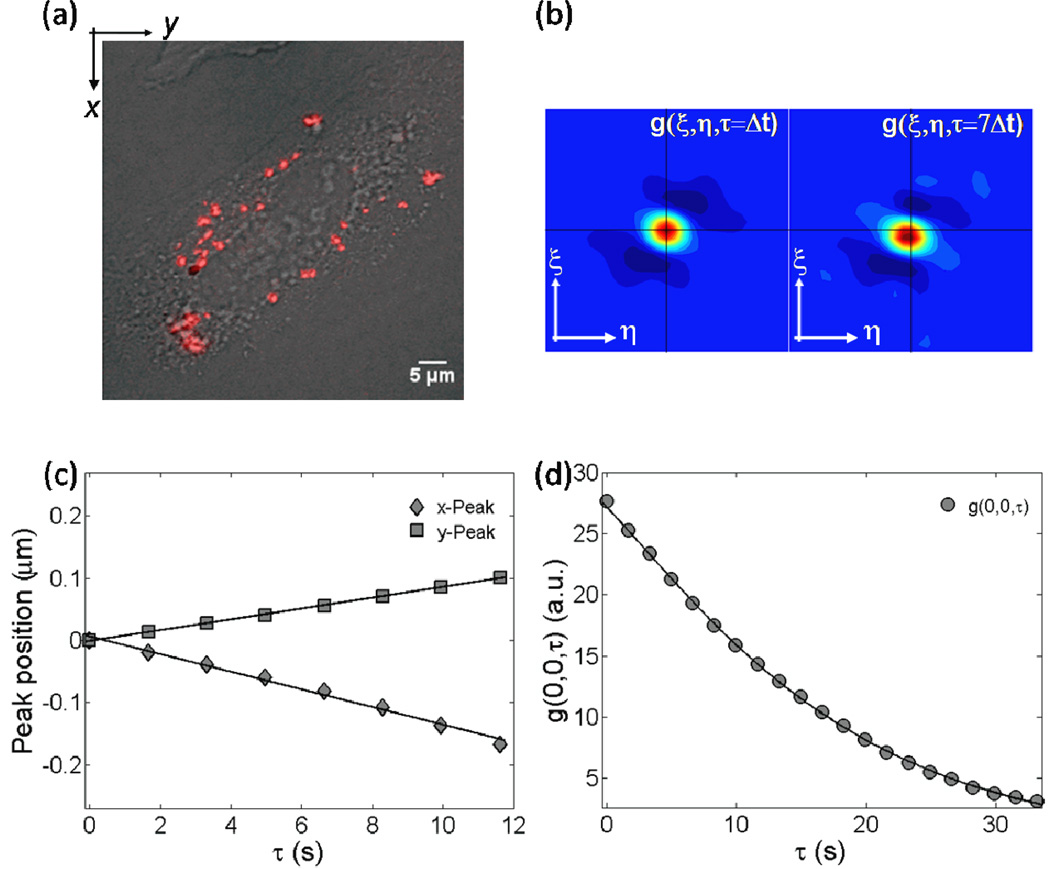
Figure 1 shows the steps of our analysis, for a representative time series of DC-Chol-DOPE/DNA lipoplexes. Figure 1a is the superimposition of lipoplexes fluorescence image (the first image of the temporal stack) on top of the corresponding CHO-K1 cell Nomarski image. First, we followed the peak position of the 2D Gaussian fit to the calculated STICS curves (equation (2)). Such procedure does not require any a priori knowledge about the mode of motion of lipoplex particles and, importantly, it is not affected by photobleaching [24]. This necessary first step introduces the major difference between our novel STICS approach and the STICS study of polyplexes performed by Kulkarni et al [14]. If some particles have moved between frames, the correlation function is going to change depending on the kind of microscopic motion undergone by the particles [10, 11]. In the case of Brownian diffusion, confined diffusion and randomly oriented transport, lipoplexes will tend to exit the correlation area in a symmetric fashion. Thus, the Gaussian peak will stay centered at (0, 0), but its value will decrease with time [10, 11]. On the other side, if the particles are on average flowing uniformly, the spatial correlation Gaussian peak value will be shifted to lag positions (ξ= -ν_x×Δt; η= -ν_y×Δt) where ν_x and ν_y are the x and y velocities of the particles and the amplitude of the peak could decrease due to photobleaching [24]. The most frequent situation we found is schematically reported in figure 1b where contour plots of the raw STICS curves at τ=Δt and τ=7Δt are reported. As shown in figure 1b, the STICS peak moves with time (the horizontal black line is inserted to follow easily the peak shift). The change of peak position measures the net resultant directed component of flow direction and speed of particle population. In principle, findings of figure 1b might indicate either that, on average, lipoplexes have been actively transported in the cytosol [11,14] or that a global motion of the cell has occurred. However, comparing the first and last Nomarski images of the temporal stack, we can exclude the global motion of the cell (see the representative figure S1 in the supplementary data). After motion categorization, one can quantitatively determine the velocities of lipoplexes as explained in figure 1c where the change of the x- and y- coordinates of the 2D Gaussian peak position as a function of the delay time τ are shown. As described in the experimental section, the slope of the fitting line represents the velocities (ν_STICS) along the x- and y- directions. Fitting for the x- and y-peak displacements provides an estimate of ν_x = −0.0142±0.0010µm/s and ν_y= 0.0100±0.0020µm/s. The next step was to compare the velocities along the x- and y- directions with those one can obtain from the temporal autocorrelation trace g(0, 0, τ) [10]. As a consequence of the motion categorization of lipoplexes as directed, the raw temporal image correlation (TICS) function (figure 1d, filled circles) was fitted (solid line) by equation (6). From the fitting procedure the dynamical parameters, i.e. the velocity, ν_TICS, and the diffusion coefficient, D_TICS, were obtained (|ν_TICS| = 0.0300±0.0040 µm/s, D_TICS = 0.0011±0.0005 µm²/s). We observe that the average values of ν_STICS and ν_TICS were slightly different from each other (table 2). Such difference may arise from a weak photobleaching contribution [24]. We have calculated the bleaching decay constant k from the average image intensity, obtaining k = (0.0013±0.0007) s⁻¹ and k = (0.004±0.003) s⁻¹ for DOTAP-DOPC/DNA and DC-Chol-DOPE/DNA complexes respectively. However, even if we do not apply any correction, the average values are in good agreement with each other within their experimental standard deviations. By applying the same analysis, we found that, within experimental errors, the motion of DOTAP-DOPC/DNA lipoplexes was as fast as that of DC-Chol-DOPE/DNA ones (table 2).

Figure 1.

Steps of the STICS analysis: (a) superimposition of lipoplexes fluorescence image (the first image of the temporal stack) on top of the corresponding CHO-K1 cell Nomarski image; (b) the contour plots of the raw STICS curves at τ=Δt and τ=7Δt (the horizontal black line helps follow the motion of the STICS peak position); (c) the x- and y-coordinates (filled diamonds and squares, respectively) of the 2D Gaussian peak position as a function of the delay time τ. Solid line is the best linear fit to the data. From the slope of the linear fits, the velocities (ν_STICS) along the x- and y- directions could be calculated; (d) the raw temporal image correlation function (circles) and the related fit (solid line) using equation (6) to obtain the dynamical parameters, i.e. the velocity ν_TICS and the diffusion coefficient D_TICS.

Table 2.

Average dynamical parameters obtained from the linear fitting of the peak position (ν_STICS) and from the temporal image correlation function using equation (6) (ν_TICS and D_TICS) (from at least 10 temporal stacks of 256 × 256 pixels images). Standard deviations are also reported.

	νSTICS[µm/s]	νTICS[µm/s]	DTICS[µm2/s]
DOTAP-DOPC/DNA	0.010±0.009	0.023±0.011	0.0010±0.0008
DC-Chol-DOPE/DNA	0.030±0.015	0.022±0.007	0.0010±0.0007

3.2.2 STICS analysis on 128 × 128 pixels images

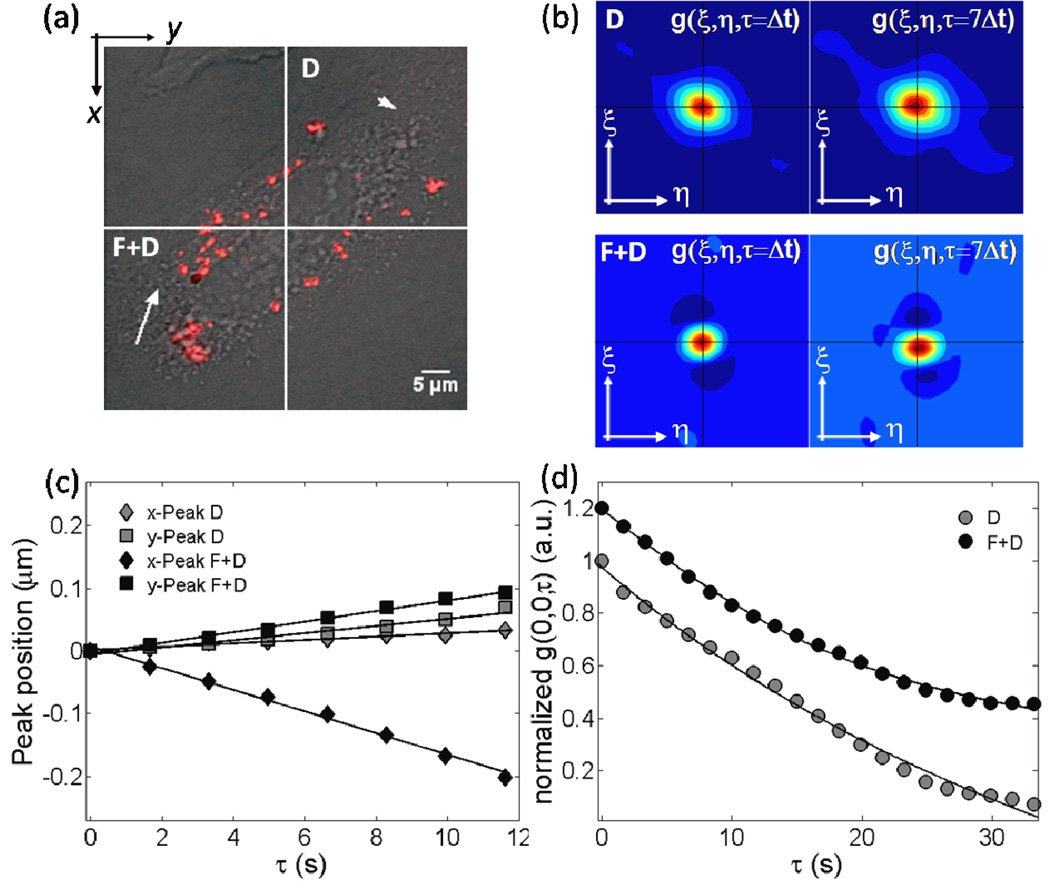
Since reducing the ROI size allows one to detect different scale processes, we applied the same procedure to 128 × 128 pixels images. The simplest option was to consider the four ROIs of 128 × 128 pixels obtained from the division of the original image (figure 2a). Figure 2 shows the steps of our analysis as proposed in figure 1, performed in two out of these four ROIs. Figure 2b shows the contour plots of the raw STICS curves at τ=Δt and τ=7Δt; the top and bottom plots refer to the top-right and bottom-left 128× 128 pixels ROIs of figure 2a, respectively. Again, fitting for the x- and y-peak displacements provides an estimate of ν_x and ν_y (figure 2c). The velocity vectors are inserted in the corresponding ROI of figure 2a (white arrows).

Figure 2.

Division of figure 1a into four ROIs as small as 128 × 128 pixels each (a). The steps of our analysis as proposed in figure 1, but restricted only to the top-right and bottom-left ROIs.(b) contour plots of the raw STICS curves at τ=Δt and τ=7Δt; the top and bottom plots refer to the top-right and bottom-left 128× 128 pixels ROIs of (a), respectively. (c) thex- and y-coordinates (filled diamonds and squares, respectively) of the 2D Gaussian peak position as a function of the delay time τ. Solid line is the best linear fit to the data. From the slope of the linear fits, the velocities (ν_STICS) along the x- and y- directions could be calculated. From them, we can classify the top-right and bottom-left ROIs motion as diffusion (D) and flow and diffusion (F+D), respectively. The division in four smaller ROIs allows mapping of the lipoplex flow field; the velocity vectors are inserted in the corresponding ROI (white arrows). (d) fitting for the raw temporal image correlation functions (filled circles) using the proper theoretical model (equations (4) and (6) for D and F+D, respectively).

The x- and y- components of velocity in the top-right ROI are smaller than the values obtained by Hebert et al [10] in the simulations of pure diffusion motion (ν_x= 0.006±0.001 µm/s and ν_y= 0.007±0.006 µm/s). For the sake of clarity it should be underlined that velocity less or equal to the resolution limit of the STICS technique does not guarantee the motion is Brownian diffusion. For instance, if confined diffusion or randomly oriented transport would be present, the STICS peak might not appreciably move with time. Anyway, previous SPT studies have shown that diffusion and active transport are the main intracellular modes of motion of nanocarriers [18, 27]. According to this consideration lack of concerted velocity allowed us to categorize the lipoplex motion in this ROI as being diffusion (thus labeled as “D”), while considering as directed motion in other analyzed ROI (labeled as “F+D”). Lastly, figure 2d shows the raw temporal image correlation functions (filled circles); the previous motion classification allows us to fit the data with the proper theoretical function (equations (4) and equation (6) for D and F+D, respectively), avoiding the imposition of any a priori specific model. From the fitting procedure the dynamical parameters, i.e. the velocity, ν_TICS, and the diffusion coefficient, D_TICS, were obtained (D_TICS = 0.005 3±0.0006 µm²/s for the diffusion region and |ν_TICS|= 0.0315±0.0090µm/s, D_TICS = 0.0017±0.0009 µm²/s for the directed diffusion region).

3.2.3 STICS analysis on 64 × 64 pixels images

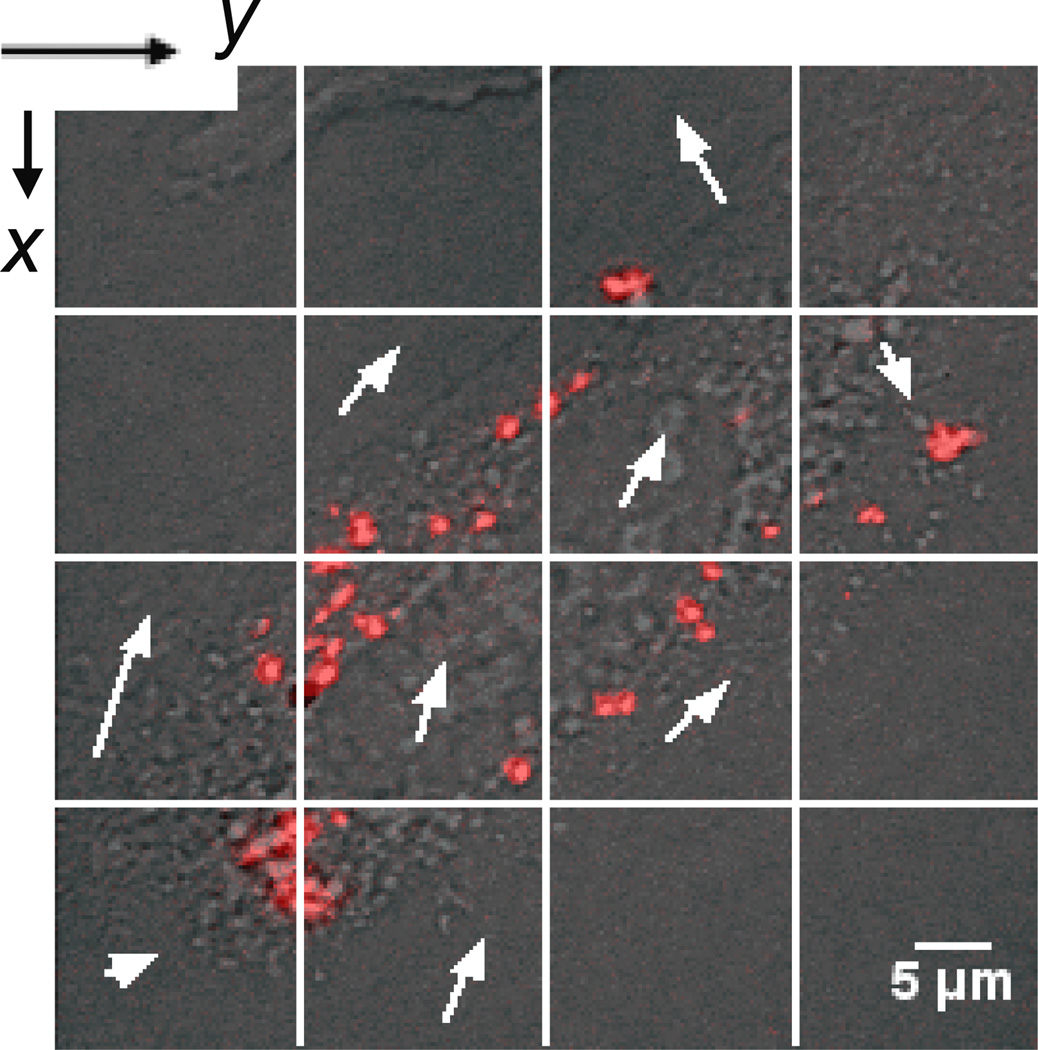
Dividing the image into ROIs as small as 64 × 64 pixels and performing spatio-temporal correlation analysis in each of them separately allows mapping of the flow field (figure 3) [28]. Even if all the vectors (white arrows) have different magnitudes and directions, it is clear that the directed motion of lipoplexes approximately takes place along the major axis of cell. We focused our analysis to specific 64 × 64 pixels ROIs that we classified as being 'inside the cytoplasm' or 'close to cell borders'. We applied the procedure to all subcellular regions considered (more than 20 for each type, more than 100 lipoplexes). The most frequent situation we found is reported in the representative figure S2 that describes the analysis carried out for an 'inside the cytoplasm' subcellular region (indicated by a white edge square in figure S2a). The 2D Gaussian fit to the calculated STICS curves was found to move with time (figure S2b) thus confirming that the motion of lipoplexes in the cytosol is mainly directed. Fitting for the x- and y-peak displacements (figure S2c) provides an estimate of ν_x= −0.0230±0.0020 µm/s and ν_y = 0.0054±0.0007 µm/s (|ν_STICS| = 0.0240±0.0063 µm/s). Instead, fitting of the temporal image correlation using the flow and diffusion model (equation (6)) provides an estimate of |ν_TICS| = 0.0390±0.0020 µm/s and D_TICS = 0.0053±0.0008 µm²/s. For both DC-Chol-DOPE/DNA and DOTAP-DOPC/DNA lipoplexes it is possible to notice again slight differences between ν_STICS and ν_TICS possibly due to photobleaching. We observe that the average values (Intracellular active transport in table 3) are of the same order of magnitude of those obtained from the analysis of the 256 ×256 pixels image (figure 1). On the other hand, in some less frequent cases, we found in ‘inside the cytoplasm’ subcellular regions that the 2D Gaussian fit to the calculated STICS curves did practically not move with time (figure S3 in the supplementary data). As done in section 3.2.2, we can conclude that these ROIs display mainly diffusion-like motion [11]. Our findings are in excellent agreement with those of recent SPT studies showing that the intracellular lipoplex motion is either directed or Brownian with active transportation being definitely more frequent than Brownian diffusion. Thus, we proceed by fitting the temporal correlation function using the purely diffusive model (equation (4)) and the obtained value are reported in table 3. Lastly, we were interested to explore the motion of lipoplexes when near either plasma or nuclear membranes. Figure S4 in the supplementary data shows the analysis performed in a ROI 'close to a cell border', indicated by a white edge square in figure S4a. The correlation functions appear symmetric and at the origin, typical of diffusive-like behavior [10]. This result is in very good agreement with the recent tracking results reported by Chen et al [30] showing that, before moving into the cytosol, nanoparticles undergo slow membrane diffusion on the cell surface with an extremely low velocity. Then, we proceed by fitting the temporal correlation function using the proper diffusive model (equation (4)), without any a priori knowledge on the motion. We obtain therefore the diffusion coefficient D_TICS = 0.0037±0.0009 µm²/s. The average dynamical parameters obtained from these diffusive ROIs of both DOTAP-DOPC/DNA and DC-Chol-DOPE/DNA lipoplexes are listed in table 3 (Membrane diffusion).

Figure 3.

Division of figure 1a into sixteen ROIs as small as 64 × 64 pixels each. Fitting for the x- and y-displacements of the 2D Gaussian peak as a function of the delay time τ allows to obtain the velocity vector. Applying it to all the subcellular regions considered, the lipoplex flow field is obtained (white arrows).

Table 3.

Average dynamical parameters obtained from the linear fitting of the peak position (ν_STICS) and from the temporal image correlation function using equation (4) (*) or equation (6) (#) (ν_TICS and D_TICS) for complexes ‘close to a membrane’ or ‘inside the cell’, respectively (from at least 10 temporal stacks of 64 × 64 pixels images). Standard deviations are also reported.

	Mode of motion	νSTICS[µm/s]	νTICS[µm/s]	DTICS[µm2/s]
	Intracellular active transport#	0.040±0.011	0.041±0.017	0.0030±0.0010
DOTAP-DOPC/DNA	Intracellular diffusion*	0.004±0.001	---	0.0007±0.0006
	Membrane diffusion*	0.0040±0.0020	---	0.0025±0.0008
	Intracellular active transport#	0.029±0.022	0.036±0.017	0.0028±0.0022
DC-Chol-DOPE/DNA	Intracellular diffusion*	0.005±0.004	---	0.0021±0.0015
	Membrane diffusion*	0.005±0.003	---	0.0024±0.0016

4. Discussion

The issue of how lipoplexes move through the cytoplasm remains largely unknown. Measuring these dynamics, particularly transport parameters such as diffusion coefficient and velocity, is considered a fundamental step for understanding how such delivery methods compare with fast moving viruses and how to boost their transfection efficiency (TE). Recent advancements into efficient tracking algorithms combined with increased computing speed and parallel processing capabilities have made SPT the most frequent option to study the intracellular dynamics of nanocarriers. Here we have used the STICS approach for analyzing aspects of lipid-mediated gene delivery. To the best of our knowledge, this is the first time that STICS has been applied to study the intracellular dynamics of lipoplexes at the single-cell level.

The procedure we introduced, as schematically explained in figure 1, consisted of two steps: i) motion categorization; ii) measurement of diffusion coefficients and velocity vectors (magnitude and direction). First we applied the STICS analysis to 256 × 256 pixels images (each confocal image contained a single cell). Both the global cell dynamics and the motion of particles influence the correlation analysis. Since we were simply interested in the intracellular dynamics of lipoplexes, first we paid attention to exclude that the cell or its organelles move during image acquisition (figure S1 in the supplementary data). The STICS analysis in 256 × 256 pixels images showed that the average motion of lipoplexes is directed. Remarkably, the results of our STICS analysis are in very good agreement with the findings of recent SPT studies [17–19, 25–27] showing that lipoplexes are actively transported by cytoskeleton networks with typical velocity, ν, varying between ≈ 0.02 and ≈0.2 µm/s depending on several factors such as the lipid species and the particle size. In those studies, the velocity component is generally assumed as an estimation of the activity of the microtubule motors as the lipoplex cargoes are transported through the cytoplasm. However, locally in the cell, the motion of gene nanocarriers can be different from active transport [27]. Therefore, it is mandatory to find ways to extract the maximum possible information from the available data. The most general case is a combination of diffusion, flow, and immobile populations [10–11, 14]. The possibility to use correlation analysis to distinguish between such different sub-populations strictly depends on their relative contribution to overall transport. Thus, we asked whether STICS could be able to discriminate between different local dynamics of lipoplexes. After removing the contribution of immobile particles from the correlation analysis, two different situations can occur [10]. First, if the diffusing population is fast compared to the directional flow, then its effects on the flow correlation peaks will be short-term as the central Gaussian will decay quickly. Second, if the diffusing population is slow, it can be considered as quasi-immobile and its intensity is also going to be mostly eliminated by the same Fourier-filtering used to remove the contribution of steady particles [10]. Simulations performed by Herbert et al [10] showed that the STICS analysis is still valid when the characteristic diffusion time, τ_d, is about five times faster or slower than the flow characteristic time, τ_f. When the diffusion time is neither fast nor slow compared to flow, the STICS analysis is less accurate. Given the dynamical parameters of lipoplexes [27] we could estimate that their characteristic τ_D is more than ten times larger than τ_F confirming that STICS can distinguish between coexisting diffusion and flow populations (see supplementary data for a detailed calculation). To elucidate the existence of local lipoplex dynamics, we therefore segmented the cells in 4 boxes as small as 128 × 128 pixels. This approach allowed us to obtain more accurate and detailed results than those one can obtain when 256 × 256 pixels images are considered [10, 22]. Indeed, the existence of a diffusive-like process (figure 2) with characteristic diffusion coefficient, D≈10⁻³µm/s², was clearly demonstrated. Then we segmented the cells into 16 boxes of 64 × 64 pixels. This allowed us to figure out that the coexistence of active motion and diffusion is a general feature of intracellular transport of lipoplexes. According to recent literature [14, 27], we also observe that the active transport is definitely more frequent than diffusion.

Dividing the confocal image into 16 regions and performing spatio-temporal correlation analysis in each segment separately allowed achieving detailed information of local dynamics of lipoplexes. Assembling the results from all image segments resulted in the depiction of a map of diffusion coefficients and a flow map (figure 3). Remarkably, STICS analysis shows that there is a net flux of lipoplexes directed along the long axis of the cell (figure 3, arrows), with the average flow rate of 0.03 µm/s and 0.04 µm/s for DOTAP-DOPC/DNA and DC-Chol-DOPE/DNA lipoplexes respectively. The internal distribution of cytoskeletal filaments produces an elongated shape of CHO cells, as proved by fluorescently labeling both actin and microtubule filaments in figure S5. This makes the lipoplexes accumulate and move mostly along the principal axis (figure 3). When specific 64 × 64 pixels ROIs in the cell were considered (figure S2 and figure S3) the STICS analysis allowed us to detect three different kinds of local motion: intracellular active motion, intracellular diffusion and diffusion in the proximity of cell borders. While active motion and diffusion exhibited transport dynamical parameters similar to those found in previous analyses (table 3), diffusion in the proximity of cell borders deserves a comment. When in proximity to the plasma membrane or the nuclear membrane (figure S4), lipoplex motion was always categorized as diffusion and lipoplexes were found to move slowly with an extremely low average velocity (_STICS<0.005 µm/s). This result is in very good agreement with the recent tracking findings reported by Chen et al [30] showing that, before moving into the cytosol, nanoparticles undergo slow membrane diffusion on the cell surface with an extremely low velocity.

5. Conclusions

Despite the increased application of nanomaterials in diagnostics and therapeutics, the interactions of nanoparticles with subcellular structures in living cells remain unclear [31]. In this work, we have introduced a method to characterize the mode of motion of nanocarriers and to quantify their transport parameters on different length scales from single-cell to subcellular level. In order to avoid any a priori assignment of the type of motion, we decided not to obtain the dynamic parameters by fitting directly the temporal image correlation function, but to classify first the region of interests according to the STICS velocities we obtained. Using this strategy we were able to study the mechanisms responsible for the intracellular transport of DOTAP-DOPC/DNA and DC-Chol-DOPE/DNA complexes in CHO-K1 live cells. When lipoplexes were actively transported, velocity values averaged ≈0.03–0.04 µm/s while approached zero for diffusion. On the other side, when lipoplexes were in the proximity of either the plasma membrane or the nuclear membrane, their mode of motion was always classified as diffusion. From such analyses, we conclude that STICS is useful and powerful for determining the average kinetic behavior of multiple intracellularly moving lipoplexes. The STICS analysis allows us to extract a large amount of data on a statistically broader basis. The transport characteristics of modified lipoplexes (e.g. after interaction with biological fluids such as human plasma [32–35]) and the relative importance of transport within the full pathway of delivery is currently under investigation. Since there is no limitation on the kind of nanocarriers that can be investigated, lessons learned from this work will inform future nanocarrier design for enhanced drug and gene delivery.