Neural representation of orientation relative to gravity in the macaque cerebellum

Summary

A fundamental challenge for maintaining spatial orientation and interacting with the world is knowledge of our orientation relative to gravity, i.e. tilt. Sensing gravity is complicated because of Einstein’s equivalence principle, where gravitational and translational accelerations are physically indistinguishable. Theory has proposed that this ambiguity is solved by tracking head tilt through multisensory integration. Here we identify a group of Purkinje cells in the caudal cerebellar vermis with responses that reflect an estimate of head tilt. These tilt-selective cells are complementary to translation-selective Purkinje cells, such that their population activities sum to the net gravito-inertial acceleration encoded by the otolith organs, as predicted by theory. These findings reflect the remarkable ability of the cerebellum for neural computation and provide novel quantitative evidence for a neural representation of gravity, whose calculation relies on long-postulated theoretical concepts such as internal models and Bayesian priors.

Introduction

Sensing and coping with gravity, as well as understanding how living organisms adapt to it, has been an alluring challenge and a topic of great fascination to scientists. Multiple studies have indeed documented the importance of sensing gravity for both motor planning and sensory perception (Gaveau et al. 2011; MacNeilage et al. 2007; Senot et al. 2012; Zago and Lacquaniti 2005). Sensing gravity is complicated, however, because gravitational and translational accelerations are physically indistinguishable (‘equivalence principle’; Einstein, 1907). As a result, the otolith organs in the inner ear, which are linear acceleration sensors, carry inherently ambiguous information and respond similarly to both head tilt relative to gravity (Gravitational Acceleration, GA) and translation (Translational Acceleration, TA; Figure 1A). Theorists have proposed that this ambiguity is resolved as follows: because tilt movements are rotations, the brain can construct an internal estimate of head tilt using rotation cues from the semicircular canals in the inner ear and the visual system (Angelaki et al. 1999; Bos and Bles 2002; Green and Angelaki 2007a; Green et al. 2005; Laurens et al. 2011; Laurens and Droulez 2007; Laurens and Angelaki 2011; Mayne 1974 (pp534–540); Merfeld 1995; Merfeld et al. 1999; 2001; 2005; Zupan et al. 2002). The tilt-induced activation of the otolith organs can be then subtracted from their raw signal to extract a translational acceleration signal.

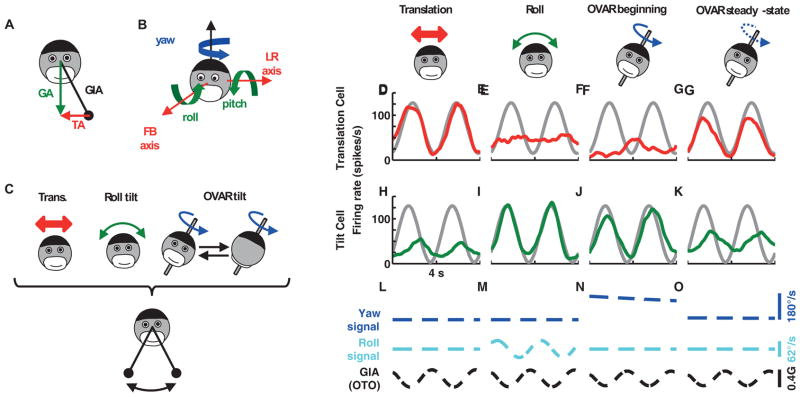
Figure 1. Tilt and translation protocols and responses from example cells.

(A) Equivalence principle: the otolith organs are sensitive to the gravito-inertial acceleration (GIA), which is equal to the difference between the gravity vector (GA) and the translational acceleration (TA). (B) Naming conventions of the head’s translation and rotation axes. (C) Representation of the motion protocols used in this study. The GIA stimulus along the LR axis, represented by a swinging pendulum (bottom), is identical during the 3 protocols (translation, tilt, OVAR). (D–O) responses from a translation-selective cell (red) and a tilt-selective cell (green) during (D), (H) left-right (LR) translation, (E), (I) roll tilt, (F), (G), (J), (K) constant velocity off-vertical axis rotation (OVAR). (L), (M), (N) and (O) illustrate the corresponding yaw velocity (detected by horizontal canals, blue), roll velocity (detected by vertical canals, cyan) and GIA along the LR axis (detected by otolith organs, OTO; black). Gray curves: fit to the LR translation response (shown in D, translation cell) or the roll tilt response (shown in I, tilt cell). We compared the cell’s OVAR modulation to the gray response, and computed a gain ratio (see Experimental Procedures): F: G_trans=0.2, ϕ_trans=156°; G: G_trans=0.9, ϕ_trans=12°; J: G_tilt=0.9, ϕ_tilt=−27°; K: G_tilt=0.4, ϕ_tilt=−86°. Note that the two cells were chosen to have a negligible response to pitch and FB translation, such that these components could be ignored (for illustrative purposes only; all data were analyzed using a vectorial approach; see Experimental Procedures). OVAR beginning shows 3–7s after motion onset. OVAR steady-state illustrates 51–55s (translation cell) or 63–67s (tilt cell) after motion onset. Additional response profiles can be found in Figure S1.

In support of this theory, neurons selective to translation have been identified in the vestibular and cerebellar nuclei (Angelaki et al. 2004; Shaikh et al. 2005a, b), in Purkinje cells of the caudal vermis (Yakusheva et al. 2007), in the ventral posterior thalamus (Meng et al. 2007) and in cortical areas (Liu and Angelaki 2009; Liu et al. 2011). In contrast, surprisingly little is known about the neural correlates of a ‘gravity signal’. Its existence has been supported by behavioral and neuroimaging studies (Indovina et al. 2005; Merfeld et al. 1999), but solid evidence for an explicit tilt signal has yet to be identified in single neuron and population responses. Modulation of vestibular and cerebellar neurons during roll and pitch tilt has been described previously and these responses have been attributed to convergence of signals from the otolith organs and the semicircular canals (Zhou et al. 2006; Fushiki and Barmack 1997; Yakhnitsa and Barmack 2006). However, that these neurons actually encode an internal estimate of tilt relative to gravity has never been tested explicitly.

Here we provide the first quantitative evidence that the activity of a subpopulation of Purkinje cells in the caudal cerebellar vermis (nodulus/uvula, NU) encodes a neural estimate of head tilt relative to gravity and that this is done through an internal model (Mayne 1974 (pp534–540); Merfeld 1995; Laurens and Droulez 2007; Laurens and Angelaki 2011). In order to reach this conclusion, we recorded Purkinje cell responses during constant velocity rotation around a tilted axis (Off-Vertical Axis Rotation, OVAR). Because OVAR is a dynamic tilt stimulus (e.g. the head tilts periodically from left ear down to right ear down, see Figure 1C), comparable to sinusoidal tilt (e.g. roll in Figure 1C) but performed through a fundamentally different movement (constant velocity rotation in yaw instead of oscillation in roll of pitch, see Figure 1B for definitions of the rotation and translation axes), we could demonstrate that these cells encode head tilt during arbitrary rotations in space. Furthermore, it is known that OVAR induces an illusion of translation (Denise et al. 1988; Wood et al. 2007; Vingerhoets et al. 2006; 2007) which develops gradually and which can be predicted based on the internal tilt signal and physical laws. We show that this illusion is apparent in the responses from a ‘translation-selective’ group of Purkinje cells (Angelaki et al. 2004; Yakusheva et al. 2007). Remarkably, the population activity from the ‘tilt-selective’ cells predicts the responses of ‘translation-selective’ cells, reflecting the physical relationships between gravitational and translational accelerations described by Einstein (1907). Finally, we also demonstrate in tilt-selective neurons the neural correlates of the ‘somatogravic’ illusion, which is a perception of tilt experienced during sustained linear acceleration, a well-known cause of disorientation (Graybiel and Clark 1965; Curthoys 1996; Seidman and Paige 1996; Merfeld et al. 2001; Clément et al. 2002; Merfeld et al. 2005). These results show how theoretical concepts can be identified in both single neuron and population activity.

Results

The otolith organs sense tilt (gravitational acceleration GA). However, they are also sensitive to translational acceleration (TA) (Angelaki et al. 2004): like a head-fixed pendulum (see Figure 1C, bottom), afferents from the otolith organs encode net gravito-inertial acceleration (GIA), (Figure 1A):

$$\text{GIA}=\text{GA}-\text{TA}$$ (eq. 1)

Unlike otolith afferents, many Purkinje cells in the caudal cerebellar vermis (nodulus/uvula, NU) respond during translation in darkness (Figure 1D), but not during an equivalent (same GIA) tilt stimulus (Figure 1E). Another group of Purkinje cells respond during tilt (Figure 1I), but show little modulation during 0.5Hz translation (Figure 1H; see also Figure S1). On the basis of these responses, Purkinje cells were classified as ‘translation-selective’ (Figure 2; red, 81/211, 38%), ‘tilt-selective’ (green, 71/211, 34%) or ‘GIA-selective’ (black, 20/211, 10%). Another 39 cells (19%, gray) that were not significantly fitted by any one model were classified as ‘composite’ (see Angelaki et al. 2004 and Experimental Procedures for details).

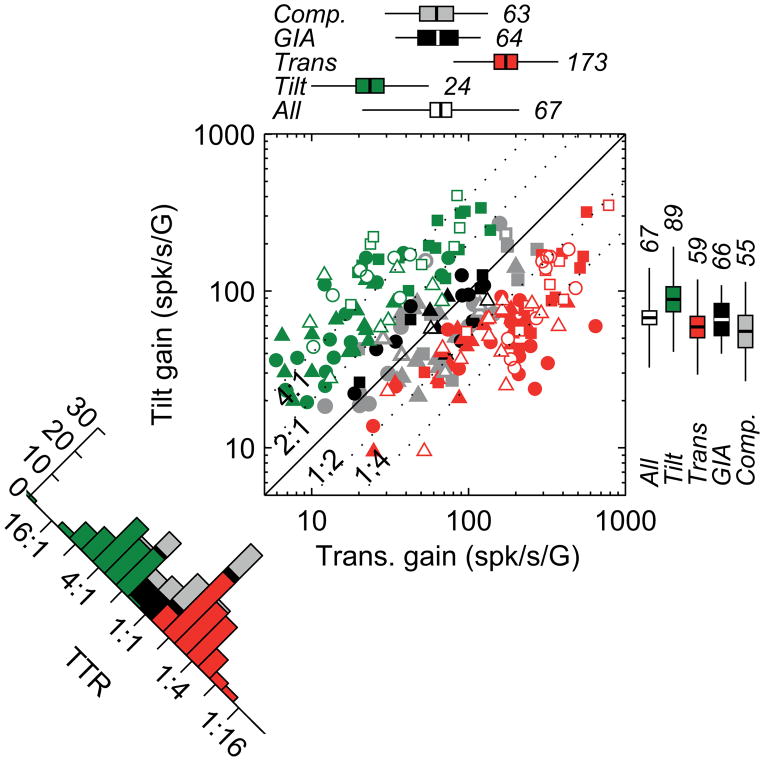
Figure 2. Population summary of tilt and translation responses.

The scatter plot shows tilt versus translation gain, with each symbol corresponding to a single neuron, color-coded according to cell classification type (green: tilt-selective cells; red: translation-selective cells; black: GIA-selective cells; grey: composite cells). Different symbols are used for different animals (squares: animal V; circles: animal T; triangles: animal K). Open symbols represent putative Purkinje cells and filled symbols represent confirmed Purkinje cells (see Experimental Procedures). Reconstructed positions of recorded cells in stereotaxic coordinates are illustrated in Figure S3. Boxplots on top and side represent geometric mean (numbers and lines inside box), 95% confidence intervals (box) and SD (lines). The histogram on the lower left shows the distribution of the tilt-translation ratio (TTR). The TTR histogram had two peaks and differed significantly from both a uniform (p_uniform < 0.001) and a Gaussian (p_Gaussian = 0.001) distribution, whereas it was not different from a bimodal distribution (p_bimodal = 0.2). The analysis identifying tilt-selective, translation-selective, GIA-selective and composite cells is based on the assumption of linearity (see Experimental Procedures), which is fulfilled (Figure S7). Additional response properties (preferred directions and phases) can be found in Figure S2; the reconstructed position of the cells is shown in Figures S3.

Translation-selective Purkinje cells may respond to lateral motion (as in Figure 1D), forward/backward motion or combinations thereof (Figure S2). Similarly, tilt-selective Purkinje cells may respond to roll (as in Figure 1I), pitch or combinations thereof (Figure S2). When tilt gain (expressed relative to G=9.81m/s²) is plotted versus translation gain on a cell-by-cell basis, tilt- and translation-selective cells lie above and below the diagonal, respectively (Figure 2, green and red symbols), whereas GIA and composite cells tend to lie close to the diagonal (Figure 2, black and gray symbols). Tilt-selective cells were generally less responsive overall than translation-selective cells (boxplots on top and right of the scatter plot show mean gain, SD and 95% confidence intervals). A ‘Tilt/Translation Ratio’ (TTR), which quantifies the cells’ relative gain to tilt vs. translation, showed a bimodal distribution (Figure 2, lower-left histogram along the diagonal, see legend). Thus, tilt- and translation-selective cells represent two distinct subpopulations, rather than the two sides of a single-peaked continuous distribution, and GIA-selective cells are relatively rare in the NU. Tilt cells were encountered more medially (p=0.02, Spearman’s rank correlation) and anterior (p<0.001, Spearman’s rank correlation) than translation-selective cells, suggesting they might be more prevalent in the medial nodulus (see Figure S3).

Significant modulation during tilt was also previously reported in both the vestibular nuclei (Zhou et al. 2006) and NU (Fushiki and Barmack 1997; Yakhnitsa and Barmack 2006). However, tilt movements like those in Figure 1I are sinusoidal rotations, which are directly sensed by the vertical semicircular canals. On the basis of sinusoidal pitch/roll motion paradigms only, it is unclear whether ‘tilt-selective’ cells trivially represent vertical canal activation (e.g., as concluded by Fushiki and Barmack 1997; Yakhnitsa and Barmack 2006), rather than tilt relative to gravity more generally. In order to determine whether tilt-selective Purkinje cell responses indeed represent an internal estimate of gravity, we used a different 0.5Hz tilt stimulus that does not activate the vertical canals: constant velocity rotation in darkness about an axis that is tilted 10° (off-vertical-axis rotation, OVAR; Figure 3A) at 180°/s. OVAR causes the head to alternate between left-ear-down (LED) and right-ear-down (RED) orientations (Figure 3B), thus mimicking 0.5Hz roll tilt (Figure 3C, bottom). As the head also moves through nose-up (NU) and nose-down (ND) orientations (Figure 3B), it also mimics pitch tilt (Figure 3C, top). Importantly, unlike actual roll/pitch tilts that activate vertical canals sinusoidally, the OVAR constant velocity rotation activates the horizontal semicircular canals only. According to the internal model hypothesis, the brain should keep track of tilt relative to gravity during any type of movement, independently of the rotation axis (Laurens et al. 2011). Thus, if indeed tilt-selective Purkinje cell activity reflects an internal estimate of tilt, their response during 180°/s OVAR should be identical to that during 0.5Hz pitch/roll tilt.

Figure 3. Decomposition of the OVAR stimulus into actual tilt and erroneous translation signals (see also Figure 1).

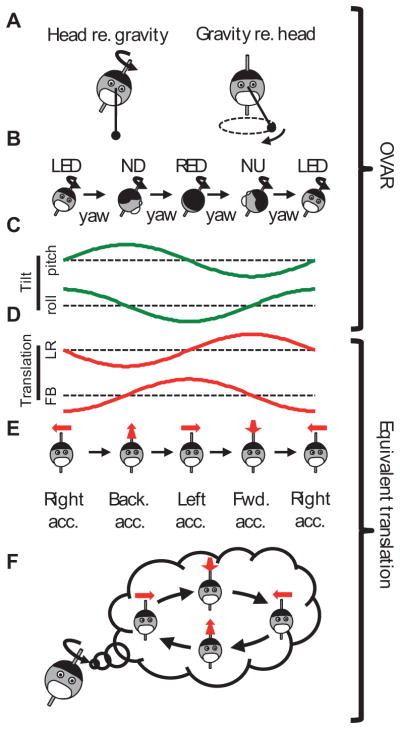
(A)–(C) real motion (tilt), (D)–(F) corresponding erroneous translation. (A) During OVAR, the head rotates around a tilted axis (left). In an egocentric frame of reference, the gravity vector rotates around the head (right). (B) During OVAR, the head passes though the Left-Ear-Down (LED), Nose-Down (ND), Right-Ear-Down (RED) and Nose-Up (NU) orientations successively. (C) Pitch and roll oscillations corresponding to the head trajectory in B. (D) Forward-backward (FB) and leftward-rightward (LR) oscillations generating the same otolith activation as in C. (E) Erroneous translational acceleration corresponding to the head orientations represented in B. (F) Illusion of translation along a circular trajectory during steady-state OVAR in humans, obtained by following the pattern of acceleration illusions in E (Vingerhoets et al. 2006; 2007).

In line with this hypothesis, the example tilt cell’s response amplitude during OVAR (Figure 1J; green; see Movie S1) was 90% of its amplitude during roll (gray lines in Figure 1H–K represent fits to the data in Figure 1I; see Experimental Procedures). Note that, in Figure 1H–K, we chose a cell which doesn’t respond to pitch. Therefore, the pitch tilt component during OVAR (Figure 3C) can be ignored for simplicity in this example (but it was taken into account in all analyses; see Experimental Procedures).

Results from 37 tilt Purkinje cells are summarized in Figure 4A (green symbols). Early during constant velocity OVAR (2–4s in Figure 4A; note that 0–2s is the acceleration period from 0 to 180°/s), there was no significant difference between OVAR and tilt modulation amplitude (p=0.66, Wilcoxon signed rank test). The two responses were correlated, with a slope of 0.90 (green band, 95% confidence interval: [0.73,1.07], p≪0.001). Thus, tilt-selective Purkinje cells modulated during OVAR similarly as during pitch/roll tilt, despite the different nature of the rotation movement used to generate the motion. On the basis of this result, one can rule out the hypothesis that these cells respond to an activation of the vertical semicircular canals only, since vertical canals are not active during this type of rotation. Furthermore, the activation of the horizontal canals is continuous during OVAR (Figure 1N) but the response of the cells is sinusoidal (Figure 1J). This could not occur if these cells simply relayed angular velocity signal from the semicircular canals. Therefore, this result demonstrates that these cells are indeed combining a constant velocity rotation signal and a cyclic GIA signal into a cyclic tilt signal (Figure 4; see also Figure S4 and Theory in Supplementary Materials).

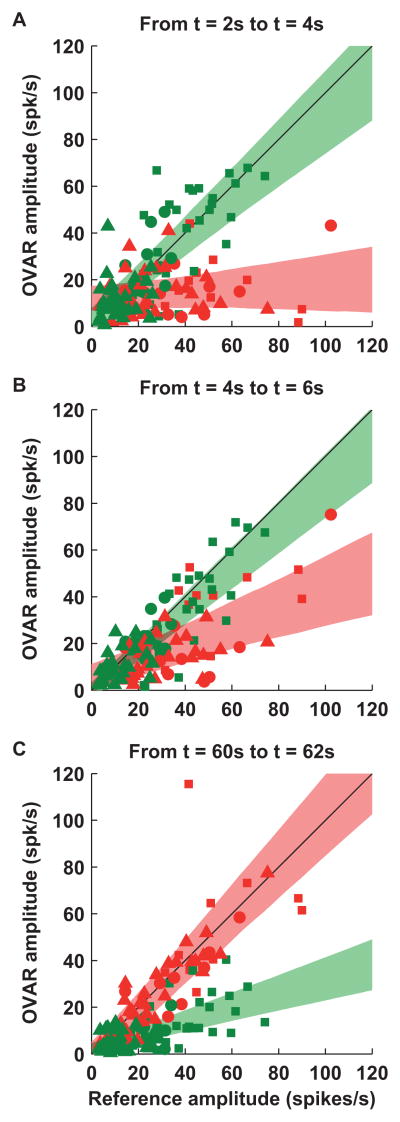
Figure 4. Comparison of the response during OVAR with the ‘rereference’ response during tilt or translation on a cell-by-cell basis.

Modulation amplitude during OVAR at (A) t=2–4s, (B) t=4–6s and (C) t=60–62s after motion onset is plotted versus tilt (for tilt-selective Purkinje cells, n=37, green) or translation (for translation-selective cells, n=27, red) reference amplitude (i.e. the response amplitude expected in response to a tilt or translation stimulus equivalent to OVAR; see Experimental Procedures; e.g., gray lines in Figure 1D–O). Two data points are shown per cell (corresponding to the two rotation directions; see Experimental Procedures). Linear regressions were performed, with the 95% confidence intervals represented by green and red bands. Different symbols are used for different animals (squares: animal V; circles: animal T; triangles: animal K). Phase values are illustrated in Figure S4. Reconstructed positions of recorded cells in stereotaxic coordinates are illustrated in Figure S3.

A similar correlation (slope: 0.88 [0.75,1.00], p≪0.001) was also seen during the next OVAR cycle (4–6s, Figure 4B, green band and green symbols), although OVAR response amplitude was slightly smaller than tilt response amplitude (p=0.011, Wilcoxon signed rank test). This decline continued as constant velocity was maintained, as illustrated during steady-state for the example tilt cell in Figure 1K (OVAR amplitude was 40% of tilt amplitude). Across the tilt cell population (Figure 4C, green symbols), responses during steady state OVAR were significantly attenuated compared to tilt responses (p≪0.001, Wicoxon signed rank test) and the regression slope dropped to 0.31 [0.22, 0.4]. Thus, the ability of these neurons to encode tilt relative to gravity broke down during steady-state OVAR, although it did not decline to zero.

This decline is explained by the sensory signals present during each stimulus (Figure 1L–O). During constant velocity rotation, canal-driven rotation signals are initially accurate (Figure 1N, ‘Yaw canals’) but decay over time and fail to encode the rotation in the steady-state (Figure 1O and Suppl. Materials: Theory). In fact, the pattern of canal and otolith organ activation during steady-state OVAR is identical to that during translation (compare Figure 1O and 1M). As a result, the absence of any (horizontal or vertical) canal activation during steady-state OVAR prevents tilt-selective Purkinje cells from computing an accurate estimate of gravity.

What happens during steady-state OVAR is further illustrated in Figure 3D–F. According to Einstein’s equivalence principle, LED tilt and rightward acceleration activate the otolith organs identically, while RED tilt is equivalent to a leftward acceleration. Thus, the roll component of the stimulus can be interpreted as leftward-rightward (LR) translation and the pitch motion can be interpreted as forward-backward (FB) translation (Figure 3C, D). Such combination of LR and FB motion would correspond to a circular path (Figure 3F), in line with human perception during steady-state OVAR (Denise et al. 1988; Wood et al. 2007; Vingerhoets et al. 2006; 2007).

If an erroneous translation signal is generated during steady-state OVAR, one would expect responses of translation-selective Purkinje cells to show reciprocal changes to the activation pattern seen in tilt-selective neurons. Indeed, as illustrated by the example cell (Figure 1F, G; Movie S2) and summary data (Figure 4, red symbols and red bands), translation-selective cell responses were negligible at the beginning of OVAR (Figure 4A: Slope=0.07 [−0.05,0.18]), but gradually built-up (Figure 4B: Slope=0.36 [0.22,0.50]) and in steady-state became indistinguishable from translation responses (Figure 4C: Slope=1.03 [0.87,1.20]; p=0.18, Wilcoxon rank test).

These conclusions were supported further by decoding tilt- and translation-selective population responses (see Experimental Procedures). As illustrated in Figure 5A, upon rotation onset, the gain of the gravitational acceleration (GA) signal encoded by the tilt-selective population (GA signal, green) was high (G_tilt=0.76), with an average phase close to 0°. After this initial peak, the decoded GA signal decayed to an average of G_tilt=0.17, while simultaneously acquiring a phase lag of ϕ_tilt = −47°. Symmetrically, the gain of the translation-selective population response (TA signal; Figure 5B, red) increased from near zero at OVAR onset to G_trans = 0.86 during steady-state. This pattern of responsiveness was consistent across animals (Figures S4, S5).

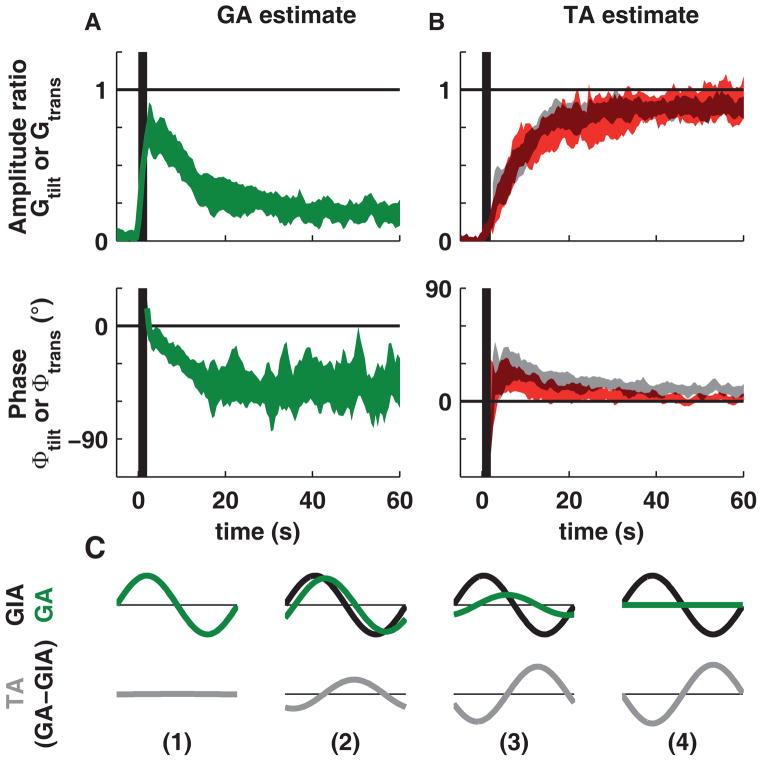
Figure 5. Time course of the decoded gravitational (GA) and translational (TA) acceleration estimates.

Average gain ratio (G_tilt and G_trans) and phase difference (ϕ_tilt and ϕ_trans) of the OVAR responses (relative to the reference) of (A) tilt-selective cells (green, n=37) and (B) translation-selective cells (red, n=27) as a function of time. Responses are shown as bands illustrating 95% confidence intervals (computed using bootstrapping). Note that the steady-state tilt response, G_tilt, is significantly different from zero. These average population responses can be interpreted as decoded internal TA and GA estimates expressed relative to the GIA (GA) or –GIA (TA), such that (G_tilt =1, ϕ_tilt =0) corresponds to a correct perception of tilt and (G_trans =1, ϕ_trans =0) to a complete illusion of translation (see C). The grey bands on panel B show the TA estimate predicted by solving the equation (GIA = GA−TA). Vertical black bands mark the acceleration period when rotation velocity ramps up from 0 to 180°/s (see Experimental Procedures). Data from individual animals are illustrated in Figure S5. (C) Illustration of the predicted TA signal. The upper panels show the GIA (black) and GA (green) estimates in four conditions (1: correct perception of tilt, 2–3: the perception of tilt decreases and lags, similar to OVAR at t=5s and in the steady-state, 4: no perception of tilt). The predicted TA signal (TA = GA-GIA) is shown in the last row (gray). The TA signal in (4), corresponding to a complete illusion of translation, is used as a reference (G_trans =1, ϕ_trans =0) in (B). Note that the predicted TA signal has a phase lead in (2) compared to (4); this is similar to the phase lead of the TA signal at t=5s. This data is shown for each animal separately in Figure S5.

One of the most fundamental assumptions of the internal model hypothesis is that the brain uses an internal model of eq. 1, and these data allow testing of this hypothesis directly. Recall that we have treated the two neuronal population responses independently: translation-selective cells were used to decode the TA signal, and tilt-selective cells were used to decode the GA signal in Figure 5A, B. However, if these two population responses indeed reflect the internal model computations, then the decoded signals should follow eq. 1 precisely. We tested this prediction by using this equation to predict the decoded TA signal on the basis of the GA signal, i.e. TA = GA−GIA (as illustrated in Figure 5C). Remarkably, the TA prediction computed from the tilt Purkinje cell population activity (Figure 5B, grey bands) is indistinguishable from the TA signal carried by the population of translation Purkinje cells (overlapping 95% confidence intervals in Figure 5B, gray vs. red).

In order to provide additional insight about the interpretation of these results, we simulated the internal estimates of tilt and translation (Figure 6; see Suppl. Materials: Theory and Simulations for a complete description) with a previously established model (Laurens and Angelaki 2011). This model encompasses the same assumptions as previous work (Bos and Bles 2002; Laurens and Droulez 2007; Merfeld 1995; Zupan et al. 2002); i.e., that a GA estimate is computed by integrating angular velocity signals provided by the semicircular canals and that this estimate is used to extract the TA estimate from the GIA. In addition, the computation of GA includes a ‘somatogravic’ feedback loop (Graybiel and Clark 1965; Curthoys 1996; Seidman and Paige 1996) (Figure 6; see also Suppl. Materials: Theory and Simulations), which continuously aligns the GIA towards the GA through a feedback loop. The effect of this feedback is that the GIA is used as a default GA estimate at low frequencies (Merfeld 1995; Bos and Bles 2002; Zupan et al. 2002; Laurens and Angelaki 2011). This additional influence was recently formalized mathematically as a Bayesian prior that reflects the experience that it is more likely we are stationary (but potentially tilted) than accelerating in the world (Laurens and Droulez 2007; Laurens and Angelaki 2011). This prior strengthens the internal estimate of tilt by dominating the GA estimate when reliable rotation cues are missing and improves the noise-driven drift that is produced when angular velocity signals are integrated (Laurens and Angelaki 2011). The similarity between the model’s simulations (Figure 6) and the signals decoded from the tilt- and translation-selective neuronal populations (Figure 4, 5) provides strong support for the theoretical framework of the internal model hypothesis.

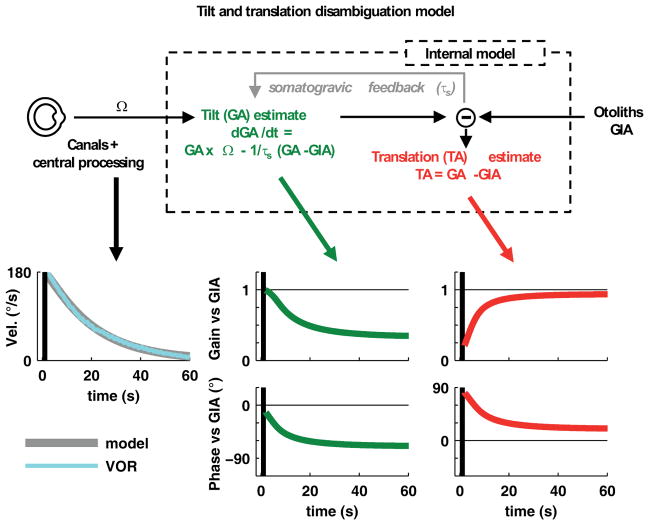
Figure 6. Simplified model of tilt-translation disambiguation.

An internal estimate of gravity (tilt) is computed by multisensory integration of canal and otolith cues (details of the central processing of angular velocity, Ω, are not represented in this figure (see Laurens and Angelaki 2011). An important component of this model is a ‘somatogravic’ feedback, which slowly aligns the GA estimate with the GIA and corrects the errors that would otherwise be introduced because of inaccurate rotation estimates. The time course of the simulated rotation (Ω), gravity (GA) and translation (TA) signals are shown in grey, green and red, respectively (bottom traces), using τ_s=0.9s. Vertical black bands mark the acceleration period as in Fig. 5. The model time constant was determined by fitting horizontal eye velocity of the rotational VOR (cyan), averaged across all animals. The model predicts how the initially correct tilt signal decreases (to G_tilt ≈ 0.33) and acquires a phase lag (ϕ_tilt ≈ −70°), as predicted by equation S8 (see Suppl. Materials: Theory), and how the acceleration signal increases during OVAR (to G_trans ≈ 0.94 and ϕ_trans ≈ 20°).

Notably, one property of the decoded GA signal is remarkably consistent with theory: In agreement with the non-zero slope of tilt responses in Figure 4C (green symbols; green bands) and the fact that the confidence intervals of G_tilt formed a narrow band clearly distinct from 0 in Figure 5A, the simulated gravity estimate from the model also asymptotes at a non-zero gain and phase values during steady-state (Figure 6). This is in line with human perception, reporting a reduced but continuous tilt sensation during steady-state OVAR (Denise et al. 1988; Wood et al. 2007; Vingerhoets et al. 2006; 2007). This steady-state tilt estimate arises, despite the absence of canal activation (Figure 1O), because of the ‘somatogravic’ feedback described above. Although the effect of this feedback is higher at low frequencies, it is appreciable at 0.5Hz.

In addition to contributing to the GA estimate during steady state OVAR (Figure 5A), the somatogravic effect is also responsible for the modulation of tilt-selective cells during translation (Figures 7A, B and S6), in particular at low frequencies. According to theory, the GIA oscillates slowly during low-frequency translation and therefore the tilt estimate has time to fully develop (Figure 7B, upper panel). In contrast, at high frequencies, the somatogravic effect never fully develops as the GIA swings rapidly from one direction to the other (Figure 7B, lower panel; note the similarity with Figure 1H, K). Thus, as expected from a low-pass filter (see Suppl. Materials: Theory), the tilt estimate during translation is predicted to (1) be larger in magnitude at lower frequencies and (2) to lag the GIA increasingly more at higher frequencies. Under the assumption that tilt-selective Purkinje cells indeed represent an internal estimate of gravity according to the model in Figure 6, the effects of this feedback should also be evident in the responses of tilt-selective neurons during translation at different frequencies.

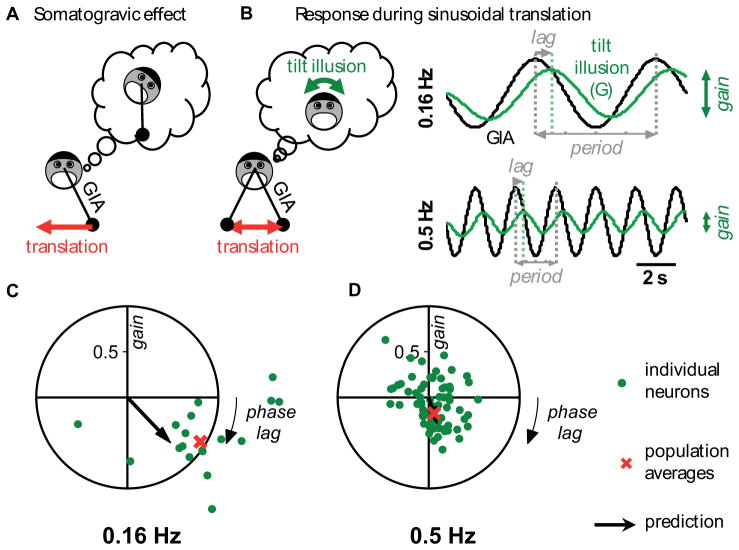
Figure 7. Responses of tilt-selective Purkinje cells during translation at two frequencies and comparison with somatogravic feedback predictions.

(A) Somatogravic effect: a constant acceleration is interpreted as tilt. (B) illustration and simulation of the tilt illusion attributable to the somatogravic feedback during sinusoidal translation at 0.16 Hz (top) and 0.5 Hz (bottom). (C), (D) measured normalized response, h_soma = h_trans/h_tilt, shown as polar plots where the radius illustrates its gain and the polar angle its phase (see Experimental Procedures). Green dots: response of individual cells (0.16 Hz: n=18; 0.5 Hz: n = 71 cells). Red cross: average response of the tilt cell population, computed by linear regression (see Experimental Procedures). Black arrow: response predicted by the model. These data are also shown as gain vs. frequency plots in Figure S6.

The results of this analysis are shown in the scatter plots of Figure 7C–D (see also Figure S6), where each data point represents a cell’s response to translation, normalized by its response to tilt (see Experimental Procedures). During 0.16 Hz translation, the normalized response of NU tilt-selective cells (n = 18 cells) has an average gain of 0.94 and a phase difference of −31° (negative phase numbers represent lags; Figure 7C, red cross). This means that these cells respond to the translation stimulus almost as if it were a tilt stimulus, i.e., nearly with the same amplitude, and with a small phase lag. This population mean corresponds closely to the effect of the somatogravic feedback in the model with τ_s = 0.9s (gain=0.7, phase lag = −45°; Figure 7C, black arrow head). At 0.5 Hz (n = 71 cells), the normalized population response was much weaker, with an average gain of 0.19 and an average phase lag of −71° (Figure 7D). These values are close to the responses of tilt-selective cells during steady-state OVAR (Figure 5A). For comparison, the model predicts a gain of 0.33 and a phase lag of −70°. These results provide further support of the hypothesis that the translation and OVAR modulation of tilt-selective cells in the cerebellar cortex reflects the somatogravic effect.

These findings, in terms of both single cell responses (Figure 4, 7) and population averages (Figure 5), strongly support the hypotheses that (1) tilt-selective Purkinje cells in the caudal vermis carry an internal estimate of gravitational acceleration computed using both horizontal and vertical semicircular canal cues; (2) GA- and TA-population activities are complementary to each other, such that their net sum equals GIA; and (3) the tilt population activity during steady-state OVAR (Figure 5A) and low frequency sinusoidal translation (Figure 7) is consistent with a neural correlate of another theoretical prediction, the somatogravic effect.

Discussion

Theory has proposed that the brain solves a fundamental sensory motion ambiguity by constructing an internal estimate of head tilt relative to gravity through multisensory integration and neural computation (Mayne 1974, Merfeld et al. 1999; Indovina et al. 2005; Laurens and Droulez 2007; Laurens et al. 2011). Despite accumulating evidence in support of this framework from theoretical and behavioral studies, its neural correlates have remained a mystery. We have shown here that a subpopulation of Purkinje cells in the caudal cerebellar vermis selective to tilt encode this long-postulated signal.

In addition, tilt-selective and translation-selective Purkinje cells are complementary to each other, such that their population activity sums to the net gravito-inertial acceleration encoded by the otolith organs, as predicted by theory (Laurens and Angelaki 2011; Merfeld 1995; Merfeld et al. 1999; Zupan et al. 2002). We have also shown that the tilt signal encoded by the population of tilt-selective cells is subject to the well-known somatogravic effect (Graybiel and Clark 1965; Curthoys 1996; Seidman and Paige 1996), which has been modeled as a Bayesian prior centered on zero translational acceleration, reflecting the experience that it is more likely to be stationary but potentially tilted than accelerating in the world (Laurens and Droulez 2007). This prior has been hypothesized to compensate for sensory inaccuracies and improve the noise-driven drift that is produced when angular velocity signals are integrated (Laurens and Angelaki 2011).

Put together, these finding provide a direct demonstration that neuronal populations in the macaque cerebellum encode internal tilt and translation signals, whose computation follows precisely the long-postulated (Mayne 1974, pp534–540) concept of internal model. One of the most remarkable properties of tilt-selective cells is their ability to keep encoding tilt relative to gravity, regardless of the type of rotation that caused this orientation change. The paradigms used in this study illustrate how fundamentally different types of movements (sinusoidal rotation around one axis or constant velocity rotation around another axis) can bring the head to the same position. In order to track the motion of the head/body in space, the brain must have the ability to integrate information about any type of rotation in space. This task is conceptually easy for a mathematician (e.g. eq. S1 in Suppl. Materials) and the present findings demonstrate that neuronal circuits also have the ability to perform similar three-dimensional spatio-temporal operations.

An accurate estimate of spatial orientation is primordial for everyday life. Tilt and translation signals must be correctly computed not only for generating motor commands (Gaveau et al. 2011; Senot et al. 2012; Zago and Lacquaniti 2005; Merfeld et al. 1999; Indovina et al. 2005), but also for avoiding illusions, loosing balance and causing disorientation (Merfeld et al. 2005; Laurens and Angelaki 2011). The fact that the output of this long hypothesized internal model is found in cerebellar Purkinje cells supports a link between the cerebellum and internal models (Wolpert et al.1998; Vercher et al., 2003; Cullen et al. 2011; Green and Angelaki 2007b). Although internal models are typically linked with motor control, the present results suggest a potential role of the cerebellum in sensory functions.

Experimental Procedures

Experimental Setup

Three male rhesus monkeys (Maccaca mulatta) were implanted with a circular delrin ring to immobilize the head, scleral search coils to measure eye movements and a delrin platform for neural recordings (Meng et al. 2005; Shaikh et al. 2005a, b). Experimental procedures were in accordance with US National Institutes of Health guidelines and approved by the Institutional Animal Studies Committee.

During experiments the monkeys were comfortably seated in a primate chair secured inside the inner gimbal of a vestibular stimulator composed of a three-axis rotator mounted on a 2 m linear sled (Acutronics Inc., Pittsburgh, PA). Animals were positioned such that all three rotation axes (yaw, pitch, and roll) were aligned with the center of the head and the stereotaxic-horizontal plane was earth-horizontal. To avoid visual cues, motion stimuli were presented in a dark room. The eye coil signals and stimuli were filtered (200Hz; 6-pole Bessel) and digitized at a rate of 833.33 Hz (model 1401, CED, 16-bit resolution; Cambridge Electronics Design, Cambridge, UK).

Purkinje cells in the nodulus (lobule 10) and ventral uvula (lobule 9c, d) (collectively referred to here as ‘NU’) were recorded extracellularly using epoxy coated tungsten microelectrodes (9–12 MΩ impedance; FHC, Bowdoinham, ME). Neuronal data was acquired using an analog channel of the 1401 (33 KHz) and analyzed offline using custom Matlab (Mathworks) scripts to extract spike timing from the raw neuronal data. We sorted spikes manually based on spike statistics (amplitude, peak velocity) and principal component analysis (PCA). Specifically, we plotted the amplitude of each spike versus the peak value of the derivative of the spike waveform. When a neuron is well isolated, its spikes appear as a well separated cloud of dots, whose borders were drawn manually. Furthermore, the waveforms of all detected spikes (from −0.5 ms to 1 ms following spike onset) were fed through a PCA. We computed PCA scores of all spikes along the two first components and plotted them. In this graph, well-isolated neurons also appear as a distinct cloud of dots whose border was drawn by hand. As a final product, we only kept spikes which appeared in both clouds of dots. This procedure is adequate for identifying well-isolated neurons and extracting their spikes in a rapid and robust manner.

The cerebellar nuclei (CN), vestibular nuclei (VN) and NU were identified using stereotaxic coordinates relative to the abducens nuclei (see Shaikh et al. 2005a, b; Yakusheva et al. 2007; 2008; 2010 for details). All responses were recorded from the Purkinje cell layer, where both simple spikes (SS) and complex spikes (CS) could be heard in the audio monitor. We recorded from any spontaneously active cell, without pre-screening whether the neuron modulated to any particular stimulus. Most recorded neurons (162 out of 229 cells recorded in total and 147 out of 211 cells with significant responses, see Cell Classification) were identified as Purkinje cells offline by showing that recorded SS activity paused for at least 10 ms after the occurrence of a CS (e.g., see Figure 1 of Yakusheva et al. 2010). There were no differences between identified- and putative-Purkinje cells during either tilt/translation or OVAR stimuli, thus the two groups have been presented together in the main text. Reconstruction of recording cell location has been illustrated in Figure S3.

Classification Tilt/translation Protocol

To independently manipulate gravitational, translational and net gravito-inertial accelerations (i.e. GA, TA and GIA), all well isolated neurons were first tested using combinations of 0.5 Hz tilt (±11.5°, 36°/s) and translation (0.2 G, where G = 9.81 m/s²) stimuli (for details, see Angelaki et al. 1999; 2004; Yakusheva et al. 2007; 2008; 2010) (Figures 1 and S1). These stimuli consisted of either pure tilt (‘tilt’), pure translation (‘translation’) or combined translation and tilt (‘tilt−translation’ and ‘tilt+translation’) (Figure S1). Each cell was characterized at a minimum of two stimulus directions; e.g. leftward-rightward (LR) translation/roll tilt, forward-backward (FB) translation/pitch tilt, and/or half-way in-between these directions (see Figure 1B for definitions). If neural isolation was maintained, its activity was also recorded during the same protocols, using a frequency of 0.16 Hz and peak amplitude of 0.1 G (i.e., ±0.98 m translation or ±5.6° tilt).

Off-vertical axis rotation (OVAR)

Purkinje cells identified as ‘tilt-selective’ or ‘translation-selective’ using the classification protocol (see Cell Classification) were then tested during OVAR (Figures 1C and 3A, B). The animals were first tilted 10° in an orientation chosen randomly between nose-up, nose-down, left-ear-down and right-ear-down and then rotated for 80s in yaw at ±180°/s (90°/s²; thus, it took 2s until constant velocity was reached). This stimulus generates a rotating gravity vector with a magnitude of 0.17 G (= sin 10°) in the horizontal plane of the head (Figure 3A). Because rotation is at constant velocity, this stimulus delivers a 0.5 Hz oscillation of a ±0.17 G linear acceleration along the LR and FB axes (Figure 3C–E). Thus, OVAR and classification tilt/translation stimuli had approximately matched sinusoidally-varying GIA signals (i.e., same frequency and similar peak accelerations). Because the tilt angle during OVAR was limited to 10° due to mechanical limitations of our system, the intensity of the linear acceleration stimulus was somewhat lower during OVAR than during tilt/translation (0.17 G vs 0.2 G). We compensated for this by scaling response gains by a factor of 0.2/0.17.

Cell Classification

Neuronal activity was expressed as spike density (SPD), using a 50 ms standard deviation Gaussian kernel. Each cycle was subsequently fitted with a sinusoidal function to determine the gain and phase of the cell’s response on each cycle, which were expressed with complex numbers. This created the neuron’s response matrix X_obs, matched to the stimulus matrix S = [s_p, s_r, s_FB and s_LR], for pitch (s_p), roll (s_r), FB (s_FB) and LR (s_LR) acceleration components, respectively (expressed in units of G).

The most general (‘composite’) model assumes X_obs ≈ H_comp· S′ ≈ h_p*s_p + h_r*s_r + h_FB*s_FB + h_LR*s_LR, where h_p, h_r, h_FB and h_LR are the neuron’s response gain and phase to pitch tilt, roll tilt, FB and LR acceleration. Once best estimates for h_p, h_r, h_FB and h_LR were obtained using multiple linear regression, preferred direction, gain and phase for tilt and translation were computed as in previous studies (Angelaki 1991; Angelaki et al. 1992), with the following conventions for the preferred direction: pitch or FB = 0° and roll or LR = 90°.

In addition to the composite model, which assumes no a priori relationship between the four parameters, three 1^st-order models were also considered: (i) A ‘tilt’ model assumes that the neuron responds to tilt only, and that its modulation during translation should be 0, i.e. h_FB = h_LR = 0; (ii) A ‘translation’ model assumes that the neuron responds to translation only, and that its modulation during tilt should be 0, i.e. h_p = h_r = 0; and (iii) A ‘net gravito-inertial acceleration (GIA)’ model assumes that h_p = h_FB and h_r= h_LR. Goodness of fit of these models was determined based on the coefficient of determination, R², between the model’s prediction and the observed activity.

The composite model generally provided a good fit to the cells’ responses (the median and quartiles of the coefficient of determination were 0.75, 0.54 and 0.85, respectively), as illustrated in Figure S7, which plots the model’s prediction (in terms of both gain and phase) as a function of the experimentally measured gain and phase of all cells during translation (Figure S7A), tilt (Figure S7B), tilt-translation (Figure S7C) and tilt+translation (Figure S7D). This comparison also demonstrates the validity of the main assumption of this analysis, i.e., signals interact linearly in predicting cell responses.

Because we recorded from all well-isolated neurons, regardless of whether they appeared on-line to modulate or not, it was important to set an off-line statistical criterion to weed out cells unresponsive to these stimuli. To exclude cells with very low modulation compared to the inter-cycle variability, cells for which the composite model couldn’t explain more than 25% of the variance of the cell’s activity (i.e. R²_comp < 0.25) were considered ‘unresponsive’ and were withdrawn from further analysis. Out of 229 recordings, 211 cells passed this criterion and were considered ‘significantly modulated’ (Figure S7A–D, filled symbols). The remaining 18 neurons were considered ‘unresponsive’ and were excluded from further analysis (Figure S7A–D, open symbols)

We classified Purkinje cells as tilt-selective, translation-selective or GIA-selective by quantifying whether one of the 1^st-order models fitted the cell’s activity significantly (p<0.05) better than the others, based on a bootstrap procedure (1000 samples; Efron and Tibshirani 1991). If no 1^st-order model fitted the cell’s responses significantly better than the others (39 out of 211 cells), then it was classified as composite. There was no significant difference in the distribution of response types between the three animals (χ² test, 6 dof, p = 0.4): numbers of translation-selective, tilt-selective, GIA-selective and composite cells were as follows: animal V: 21/22/4/8; animal T: 25/25/10/11; animal K: 35/24/6/20, respectively.

By design because of the larger number of free parameters, the composite model always provides similar or higher (never lower) R² values than the best first-order model (Figure S7E). The ratio between the R² values of the composite and best first-order models is shown in Figure S7F–I. Typically, this ratio was smaller for translation-, tilt- and GIA-selective neurons (<1.1 for 105/172 cells, i.e. 61% and <1.3 for 161/192, i.e. 94%) than composite neurons (>1.1 for all cells and >1.3 for 27/39 cells, i.e. 69%). This indicates that the classification procedure doesn’t incorrectly classify composite cells with high R² ratio as translation-, tilt- or GIA-selective cells. Note that the few composite cells (12/39, 31%) with ratios smaller than 1.3 could represent first-order cells without a significant difference between first-order models. Thus, if anything, composite cells might have been overestimated as compared to first-order cells, a fact that does not present a problem in the present analyses. Also note that the first-order models were used for the purpose of classification (i.e., does a cell respond significantly more to tilt, or to translation, or to GIA?), and not to describe the cells’ responses accurately. In fact, all analyses (e.g. computing the cells’ responses to tilt and translation as well as the reference response) were performed based on the full, composite, model.

Statistical testing for bimodality of a distribution

We used a chi square test to determine whether a set of measurements follow a uniform, Gaussian or bimodal distribution, as follows: First, we fitted the cumulative distribution of the measured data with a uniform, a cumulative Gaussian distribution or the sum of two cumulative Gaussian distributions, using a gradient ascent method. Then we broke data into 10 bins. The limits of these bins were adapted so that 1/10th of the cells would be expected to fall into each bin according to the distribution being tested. We then counted the number of data points actually falling in these bins and tested whether they were significantly different from the fitted distributions using a χ² test with p-k-1 degrees of freedom, where p=10 is the number of bins and k is the number of parameters used in the fitting procedure; i.e., 0 for the uniform, 2 for the Gaussian (average and standard deviation) and 5 for the sum of two Gaussians (2 averages, 2 standard deviations and one weighting coefficient). This procedure was performed sequentially: if the observed distribution was different from a uniform distribution, then we tested the Gaussian model and then the bimodal distribution model. The p-values obtained when testing the uniform, Gaussian and bimodal model were denoted p_uniform, p_gaussian and p_bimodal, respectively.

Analysis of off-vertical axis rotation responses

Responses to OVAR were analyzed using a 2s sliding window by fitting the cell’s SPD with a rectified sinusoidal function, resulting in response matrixes y^CW(t) and y^CCW(t), for clockwise (CW) and counterclockwise (CCW) rotations, respectively. Our goal was to test how well OVAR responses can be predicted from the cell’s modulation during tilt and translation stimuli. Specifically for tilt-selective cells, we computed ‘predicted’ OVAR responses from the cell’s tilt properties, as z(t) = h_p·s_p(t) + h_r·s_r(t). For translation-selective cells, we computed ‘predicted’ OVAR responses as if the motion was interpreted as a corresponding translation, z(t) = h_FB·s_FB(t) + h_LR·s_LR(t) = h_FB·s_p(t) + h_LR·s_r(t). Figure 4 shows scatter plots of the amplitude of y^CW and y^CCW (actual OVAR responses, see above) versus the corresponding amplitude and phase of the prediction, z^CW and z^CCW (2 data points per cell).

The ratio y(t)/z(t), which can be expressed as the amplitude ratio (G_tilt and G_trans) and phase difference (Φ_tilt and Φ_trans) and is shown in Figure 5 as a function of time, was computed across the two populations of tilt-selective and translation-selective cells, respectively, using linear regression. If tilt-selective cells encode an internal gravity estimate, then G_tilt and Φ_tilt can be interpreted as the gain and phase of the GA estimate compared to a correct perception of tilt. Similarly, G_trans and Φ_trans represent the gain and phase of the internal estimate of translation. The 95% confidence intervals for G _tilt, Φ_tilt, G_trans and Φ_trans were computed using a bootstrap analysis (1000 samples, Efton and Tibashiarani 1991).

Comparison between data and predictions based on somatogravic feedback

If the otolith organs alone are stimulated (i.e., without simultaneous canal activation, e.g., during translation-only motion), then, according to the model of Figure 6, the somatogravic effect alone will drive the GA estimate with a transfer function:

$${\mathrm{h}}_{\text{soma}}=1/(1+\mathrm{i}.\mathrm{\omega }.{\mathrm{T}}_{\mathrm{s}})$$

This can be tested by considering the response of tilt-selective cells during sinusoidal translation and during steady-state OVAR. If h_tilt is the transfer function of a tilt-selective cell to tilt and if the somatogravic effect drives the tilt estimate during translation with a transfer function h_soma, then the response of a tilt-selective cell during translation and steady-state OVAR should be h_trans = h_tilt·h_soma. As a result, h_soma = h_trans/h_tilt. In order to test this prediction at the population level, we computed an average ratio h_trans/h_tilt by performing a linear regression between h_tilt and h_trans across all tilt-selective cells. This method was chosen for its similarity with the decoding of the GA signal in Figure 5 (alternatively, we computed the barycenter, i.e. the weighted average of the clouds of dots in Figure 7C, D, where the weights were equal to |h_tilt|; this other approach produced identical results). This analysis gave a population prediction for h_soma, which was then directly compared with the model simulations (Figure 7).

Highlights.

• A population of cerebellar Purkinje cells encodes head tilt relative to gravity.

• The sum of tilt and translation cell activities equals gravito-inertial acceleration.

• Tilt cells also encode an illusion of tilt induced by sustained linear acceleration.

• The cerebellum implements an internal model of the physical laws.