Selecting the Number of Principal Components in Functional Data

Abstract

Functional principal component analysis (FPCA) has become the most widely used dimension reduction tool for functional data analysis. We consider functional data measured at random, subject-specific time points, contaminated with measurement error, allowing for both sparse and dense functional data, and propose novel information criteria to select the number of principal component in such data. We propose a Bayesian information criterion based on marginal modeling that can consistently select the number of principal components for both sparse and dense functional data. For dense functional data, we also developed an Akaike information criterion (AIC) based on the expected Kullback-Leibler information under a Gaussian assumption. In connecting with factor analysis in multivariate time series data, we also consider the information criteria by Bai & Ng (2002) and show that they are still consistent for dense functional data, if a prescribed undersmoothing scheme is undertaken in the FPCA algorithm. We perform intensive simulation studies and show that the proposed information criteria vastly outperform existing methods for this type of data. Surprisingly, our empirical evidence shows that our information criteria proposed for dense functional data also perform well for sparse functional data. An empirical example using colon carcinogenesis data is also provided to illustrate the results.

1 Introduction

Advances in technology has made functional data (Ramsay and Silverman, 2005) increasingly available in many scientific fields, such as many longitudinal data in medical, biological research, electroencephalography (EEG) and functional magnetic resonance imaging (fMRI) data. There is tremendous research interest in functional data analysis (FDA) for the past decade. Among the newly developed methodology, functional principal component analysis (FPCA) has become the most widely used dimension reduction tool for functional data analysis. There is some existing work on selecting the number of functional principal components, but to the best of our knowledge, none of them were rigorously studied either theoretically or empirically. In this paper, we consider functional data that are observed at random, subject-specific observation times, allowing for both sparse and dense functional data. We propose novel information criteria to select the number of principal components, and investigate their theoretical and empirical performance.

There are two main streams of methods for FPCA, kernel based FPCA methods including Yao, Müller and Wang (2005a), Hall, Müller and Wang (2006), and spline based methods including Rice and Silverman (1991), James and Hastie (2001), and Zhou, Huang and Carroll (2008). Some applications of FPCA include Functional Generalized Linear Models, (Müller and Studtmüller, 2005; Yao, Müller and Wang, 2005b; Cai and Hall, 2005; Li, Wang and Carroll, 2010) and Functional Sliced Inverse Regression (Li and Hsing, 2010a).

At this point, the kernel based FPCA methods are better understood in terms of theoretical properties. This is due to the work of Hall and Hosseini-Nasab (2006), who proved various asymptotic expansions of the estimated eigenvalues and eigenfunction for dense functional data, and by Hall et al. (2006) who provided the optimal convergence rate of FPCA in sparse functional data. An important result of Hall et al. (2006) was that, although FPCA is applied to the covariance function estimated by a two dimensional smoother, when the bandwidths were properly tuned, estimating the eigenvalues is a semiparametric problem and enjoys a root n convergence rate, and estimating the eigenfunctions is a nonparametric problem with the convergence rate of a one dimensional smoother.

In the work on FDA mentioned above, functional data were classified as (a) dense functional data where the curves are densely sampled so that passing a smoother on each curve can effectively recover the true sample curves (Hall et al., 2006); and (b) sparse functional data where the number of observations per curve is bounded by a finite number and pooling all subjects together is required to obtain consistent estimates of the principal components (Yao et al., 2005a; Hall et al., 2006). There has been a gap in methodologies for dealing with these two types of data. Hall et al. (2006) showed that when the number of observations per curve diverges to ∞ with a rate of at least n^1/4, the pre-smoothing approach is justifiable and the errors in smoothing each individual curve are asymptotically negligible. However, in reality it is hard to decide when the observations are dense enough. In some longitudinal studies it is possible that we have dense observations on some subjects and sparse observations on the others. In view of these difficulties, Li and Hsing (2010b) studied all types of functional data in a unified framework, and derived a strong uniform convergence rate for FPCA, where the number of observations per curve can be of any rate relative to the sample size.

A common finding in the aforementioned work is that higher order principal components are much harder to estimate and harder to interpret. Because seeking sparse representation of the data is at the core of modern statistics, it is reasonable in many situations to model the high order principal components as noise. Therefore, selecting the number of principal components is an important model selection problem in almost all practical contexts of FDA. Yao et al. (2005a) proposed an AIC criterion for selecting the number of principal components in sparse functional data. However, so far there is no theoretical justification for this approach, and whether this criterion also works for dense functional data or the types of data in the grey zone between sparse and dense functional data remains unknown. Hall and Vial (2006) included theoretical discussion about the difficulty of selecting the number of principal components using a hypothesis testing approach. The bootstrap approach proposed by Hall and Vial provides a confidence lower bound υ̂_q for the “unconfounded noise variance”, and can provide some guidance in selecting the number of principal components. However, their approach is not a real model selection criterion, and one needs to watch the decreasing trend of υ̂_q and decide the cut point subjectively. The minimum description length (MDL) method by Poskitt and Sengarapillai (2011) is similar to Yao’s AIC in that each principal component is counted as one parameter, although of course the criteria are numerically different. We emphasize that, in reality, each principal component consists of one variance parameter and one nonparametric function. A main point of our paper is to justify how much penalty is needed in a model selection criterion, when selecting the number of nonparametric components in the data.

We approach this problem from three directions, with all approaches built upon the foundation of information criteria. In the marginal modeling approach, we focus on the decay rate of the estimated eigenvalues and develop a Bayesian Information Criterion (BIC) based selection method. The advantages of this approach include that it only uses existing outcomes from FPCA, namely the estimated eigenvalues and the residual variance, and that it is consistent for all types of functional data. As an alternative, we find that, with some additional assumptions, a modified Akaike Information Criterion (AIC) based on conditional likelihood could produce superior numerical outcomes. A referee pointed out to us that when the data are observed densely on a regular grid, where no kernel smoothing is necessary, there is some existing work in the econometrics literature based on a factor analysis model (Bai and Ng, 2002) to select the number of principal components. We study this class of information criteria in our setting and find out that they are still consistent if a specific undersmoothing scheme is carried out in the FPCA method. In addition, we also provide some discussion for the case that the true number of principal components diverges to infinity.

The remainder of the paper is organized as follows. In Section 2, we describe the data structure and the FPCA algorithm. In Sections 3.1 and 3.2, we propose and study the new marginal BIC and conditional AIC criteria, and we investigate the information criteria by Bai and Ng in Section 3.3. The proposed information criteria are tested by simulation studies in Section 4, and applied to an empirical example in Section 5. Some concluding remarks are given in Section 6, where we also provide discussion for the case that the true number of principal components diverges. All proofs are provided in the Supplementary Material.

2 Functional principal component analysis

2.1 Data structure and model assumptions

Let X(t) be functional data defined on a fixed interval T = [a, b], with mean function μ(t) and covariance function R(s, t) = cov{X(s), X(t)}. Suppose the covariance function has the eigen-decomposition $R(s,t)={\sum }_{j=1}^{\infty }{\omega }_j{\psi }_j(s){\psi }_j(t)$, where the ω_j are the nonnegative eigenvalues of R(·,·), which, without loss of generality, satisfy ω₁ ≥ ω₂ ≥ ⋯ > 0, and the ψ_j are the corresponding eigenfunctions.

Although, in theory, the spectral decomposition of the covariance function consists of infinite number of terms, to motivate practically useful information criteria, it is sensible to assume that there is a finite dimensional true model. Due to the nature of spectral decomposition, the higher order terms are less reliably assessed and their estimates tend to have high variation. Consequently, even though one could assume that there are an infinite number of components, unless the data size is very large, sensible variable selection criteria will still select a relatively small number of components – the first several that can be reasonably assessed. This phenomenon is reflected by the numerical outcomes reported in Table S.7 of the Supplementary Material, in which a much-improved performance of BIC is observed when the sample size increases to 2000. The performance of BIC is mostly determined by the accuracy of detecting non-zero eigenvalues and that this detection can be difficult for higher order terms. For the rest of the paper, except for Section 6.2, we assume that the spectral decomposition of R ends at a finite p terms, i.e. ω_j = 0 for j > p. Then the Karhunen-Loève expansion of X(t) is

$$X(t)-\mu (t)={\sum }_{j=1}^p{\xi }_j{\psi }_j(t),$$ (1)

where ξ_j = ∫ψ_j(t) {X(t) − μ(t)}dt has mean zero, with cov(ξ_j, ξ_j′) = I(j = j′)ω_j. Let p₀ be the true value of p.

Suppose we sample from n independent sample trajectories, X_i(·), i = 1, ⋯, n. It often happens that the observations contain additional random errors and instead we observe

$$W_{\mathit{ij}}=X_i(t_{\mathit{ij}})+U_{\mathit{ij}},j=1,\cdots ,m_i,$$ (2)

where U_ij are independent zero-mean errors, with $\mathrm{var}\{U_i(t)\}={\sigma }_u^2$ and the U_ij are also independent of X_i(·). Here the (t_ij) are random, subject-specific observation times. Suppose t_ij has a continuous density f₁(t) with support T. We adopt the framework in Li and Hsing (2010b) so that m_i can be of any rate relative to n. The only assumption on m_i is that all m_i ≥ 2, so that we can estimate the within-curve covariance matrix. In other words, we allow m_i to be bounded by a finite number as in sparse functional data, or diverging to ∞ as in dense functional data.

2.2 Functional principal component analysis

The functions μ(·) and R(·,·) can be estimated by local polynomial regression, and then ψ_k(·), ω_k and ${\sigma }_u^2$ can be estimated using the functional principal component analysis method proposed in Yao, et al. (2005a) and Hall, et al. (2006). We now briefly describe the method. We first estimate μ(·) by a local linear regression, μ̂(t) = â₀ where $({\widehat{a}}_0,{\widehat{a}}_1)={\mathrm{argmin}}_{a_0,a_1}{n}^{-1}{\sum }_{i=1}^n{m}_i^{-1}{\sum }_{j=1}^{m_i}{\{W_{\mathit{ij}}-a_0-a_1(t_{\mathit{ij}}-t)\}}^{2}K\{(t_{\mathit{ij}}-t)/h_{\mu }\}$, K(·) is a symmetric density function and h_μ is the bandwidth for estimating μ. Define C_XX (s, t) = E{X(s)X(t)} and M_i = (m_i − 1)m_i. We denote the bandwidth for estimating C_XX(·,·) by h_C and let Ĉ_XX (s, t) = b̂₀, where (b̂₀, b̂₁, b̂₂) minimizes

$$n^{-1}{\sum }_{i=1}^n{M}_i^{-1}{\sum }_{j=1}^{m_i}{\sum }_{k\ne j}{\{W_{\mathit{ij}}{W}_{\mathit{ik}}-b_0-b_1(t_{\mathit{ij}}-s)-b_2(t_{\mathit{ik}}-t)\}}^{2}K\left(\frac{t_{\mathit{ij}}-s}{h_C}\right)K\left(\frac{t_{\mathit{ik}}-t}{h_C}\right).$$

Then R̂(s, t) = Ĉ_XX (s, t) − μ̂(s)μ̂(t). In addition, (ω_k) and {ψ_k(·)} can be estimated from an eigenvalue decomposition of R̂(·,·) by discretization of the smoothed covariance function, see Rice and Silverman (1991) and Capra and Müller (1997). Let ${\sigma }_w^2(t)=\mathrm{var}\{W(t)\}=R(t,t)+{\sigma }_u^2$, and ${\widehat{\sigma }}_w^2(t)={\widehat{c}}_0-{\widehat{\mu }}^2(t)$, where, with a given bandwidth, h_σ, (ĉ₀, ĉ₁) minimizes $n^{-1}{\sum }_{i=1}^n{m}_i^{-1}{\sum }_{j=1}^{m_i}{\{W_{\mathit{ij}}^2-c_0-c_1(t_{\mathit{ij}}-t)\}}^{2}K\{(t_{\mathit{ij}}-t)/h_{\sigma }\}$. One possible estimator if ${\sigma }_u^2$ is

$${\stackrel{\sim }{\sigma }}_{u,\mathrm{I}}^2={(b-a)}^{-1}{\mathit{\int }}_a^b\{{\widehat{\sigma }}_w^2(t)-\widehat{R}(t,t)\}\mathit{dt}.$$ (3)

Define ω̂_k and ψ̂_k(·) to be the k^th eigenvalue and eigenfunction of R̂(s, t), respectively. Rates of convergence results for μ̂(·), R̂(·), ${\widehat{\sigma }}_w^2(·)$, ${\stackrel{\sim }{\sigma }}_{u,\mathrm{I}}^2$ and ψ̂_k(·) are described in the Supplementary Material, Section S.1.

3 Methodology

3.1 Marginal Bayesian Information Criterion

In a traditional regression setting with sample size n, parameter size p, and normally distributed errors of mean zero and variance ${\sigma }_u^2$, BIC is commonly defined as

$$\log ({\sigma }^2)+p\log (n)/n.$$

Considering the model equations (1) and (2), linking the current setup for each subject and then marginalizing over all subjects, we consider a generalized BIC criterion of the structure of

$$\log ({\widehat{\sigma }}_u^2)+P_n(p),$$ (4)

where ${\widehat{\sigma }}_u^2$ is an estimate of ${\sigma }_u^2$ by marginally pooling error information from all subjects and P_n(p) is a penalty term. Even though the concept behind our criterion has been motivated by the traditional BIC in regression setting, there are some marked differences. For example, the ξ_j in model (1) are random. As a result, marginally, there are not np parameters. Further, unlike the traditional regression problems, we do not need to estimate/predict ξ_j. Consequently, the number of parameters in a marginal analysis is not determined by the degrees of freedom of these unknown ξ_j. Inspired by standard BIC, we let the penalty be of the form P_n(p) = C_n,pp and then determine the rate of C_n,p.

Let ${\widehat{\sigma }}_{u,[p]}^2$ be the estimator of ${\widehat{\sigma }}_u^2$ based on the residuals after taking into account of the first p principal components. Define

$$R_{[p]}(s,t)={\sum }_{j=1}^p{\omega }_j{\psi }_j(s){\psi }_j(t),{\widehat{R}}_{[p]}(s,t)={\sum }_{j=1}^p{\widehat{\omega }}_j{\widehat{\psi }}_j(s){\widehat{\psi }}_j(t).$$

If p is the true number of principal components, then R_[p](s,t) = R(s,t). Since ${\mathit{\int }}_a^b{\widehat{\psi }}_k^2(t)\mathit{dt}=1$ for all k, we can estimate ${\sigma }_u^2$ by

$${\widehat{\sigma }}_{[p],\mathrm{marg}}^2=\frac{1}{b-a}\mathit{\int }\{{\widehat{\sigma }}_w^2(t)-{\widehat{R}}_{[p]}(t,t)\}\mathit{dt}=\frac{1}{b-a}\mathit{\int }{\widehat{\sigma }}_w^2(t)\mathit{dt}-\frac{1}{b-a}\sum _{k=1}^p{\widehat{\omega }}_k.$$ (5)

Replacing ${\widehat{\sigma }}_u^2$ by ${\widehat{\sigma }}_{[p],\mathrm{marg}}^2$ in (4), the new BIC criterion is given by

$$\mathrm{BIC}(p)=\log ({\widehat{\sigma }}_{[p],\mathrm{marg}}^2)+P_n(p).$$ (6)

That is, instead of estimating ${\widehat{\sigma }}_{u,[p]}^2$ from the estimated residuals, we will estimate it from a ‘marginal’ approach by pooling all subjects together. This way, we avoid estimating the principal component scores and dealing with the estimation errors in them.

Denote ∥·∥ as the L² functional norm, and define ${\gamma }_{\mathit{nk}}={\left(n^{-1}{\sum }_{i=1}^n{m}_i^{-k}\right)}^{-1}$, which is the k^th harmonic mean of the m_i’s. When m_i = m for all i, we have that γ_n1 = m and γ_n2 = m². For any bandwidth h, define

$$\begin{array}{lll}{\delta }_{n1}(h)& =& {[\{1+{(h{\gamma }_{n1})}^{-1}\}/n]}^{1/2},\\ {\delta }_{n2}(h)& =& {[\{1+{(h{\gamma }_{n1})}^{-1}+{(h^2{\gamma }_{n2})}^{-1}\}/n]}^{1/2}.\end{array}$$

We make the following assumptions.

• (C.1)The observations time t_ij ~ f₁(t), (t_ij, t_ij′) ~ f₂(t₁, t₂), where f₁ and f₂ are continuous density functions with bounds 0 < m_T ≤ f₁(t₁), f₂(t₁, t₂) ≤ M_T < ∞ for all t₁, t₂ ∈ T. Both f₁ and f₂ are differentiable with bounded (partial) derivatives.
• (C.2)The kernel function K(·) is a symmetric probability density function on [−1, 1], and is of bounded variation on [−1, 1]. Denote ${\nu }_2={\mathit{\int }}_{-1}^1{t}^{2}K(t)\mathit{dt}$.
• (C.3)μ(·) is twice differentiable and its second derivative is bounded on [a, b].
• (C.4)All second-order partial derivatives of R(s, t) exist and are bounded on [a, b]².
• (C.5) There exists C > 4 such that E(|U_ij|^C) + E{sup_t∈[a,b] |X(t)|^C} < ∞.
• (C.6)h_μ, h_C, h_σ, δ_n1(h_μ), δ_n2(h_C), δ_n1(h_σ) → 0 as n → ∞.
• (C.7)We have ω₁ > ω₂ > ⋯ > ω_p0 > 0 and ω_k = 0 for all k > p₀.

Let p̂ be the minimizer of BIC(p). The following theorem gives a sufficient condition for p̂ to be consistent to p₀.

Theorem 1

Make assumptions (C.1)-(C.7). Recall that P_n(p) is the penalty defined in (6), and define ${\delta }_n^{\ast }=h_{\mu }^2+{\delta }_{n1}(h_{\mu })+h_C^2+{\delta }_{n2}(h_C)$. Suppose the following conditions hold

1. for any p < p₀, pr[limsup_n→∞ {P_n(p₀) − P_n(p)} ≤ 0] = 1;

2. for any p > p₀, $\mathit{pr}[P_n(p)>P_n(p_0),{\mathrm{lim\; sup}}_{n\to \infty }{\delta }_n^{\ast }/\{P_n(p)-P_n(p_0)\}=0]=1$.

Then lim_n→∞pr(p̂ = p₀) = 1.

By Theorem 1, there is a large range of penalties that can result in a consistent BIC criterion. For example, let N = Σ_i m_i and recall that the penalty term P_n(p) = C_n,pp. If we let $C_{n,p}~\log (N){\delta }_n^{\ast }$, it is easy to verify that the conditions in Theorem 1 are satisfied.

We now derive a data-based version of P_n(p) that satisfies condition (i) and (ii). By Lemma S.1.1 in the Supplementary Material, ${\delta }_n^{\ast }$ is actually the L² convergence rate of R̂(·,·), which by Lemma S.1.3 in the Supplementary Material is also the bound for the null eigenvalues, {ω̂_k; k > p₀}. In reality, ∥R̂ − R∥ not only depends on ${\delta }_n^{\ast }$ but also on unknown constants depending on the true function R(·,·) and the distribution of W. To make the information criterion data-adaptive, we propose the following penalty

$$P_{n,\mathrm{adapt}}(p)=\log (N)p\Vert \widehat{R}-{\widehat{R}}_{[p]}\Vert /{\stackrel{\sim }{\sigma }}_{u,\mathrm{I}}^2.$$ (7)

Justification for (7) is given in the Supplementary Material, Section S.2.

3.2 Akaike Information Criterion based on conditional likelihood

The marginal BIC criterion can be computed by using outcomes from FPCA directly and it is consistent. However, its performances heavily rely on the precision in estimating ω_j, particularly when j is near the true number of principle components, p₀. It is known that the estimation of ω_j can deteriorate when j increases. In this subsection, we propose an alternative approach that, by having some additional conditions, allows us to take advantage of the use of likelihood. We consider the principal component scores as random effects, and proposed a new AIC criterion based on the conditional likelihood and estimated principal component scores. Such an approach is referred as conditional AIC in linear mixed models, see Claeskens and Hjort (2008). In an alternative context, Hurvich et al. (1998) proposed an AIC criterion for choosing the smoothing parameters in nonparametric smoothing. The FPCA method is to project the discrete longitudinal trajectories on some nonparametric functions (i.e. the eigenfunctions), and can thus be considered as simultaneously smoothing n curves. The AIC in the FPCA context is connected to that for the nonparametric smoothing problem, but the way of counting the effective number of parameters in the model will be different. Therefore, the penalty in our AIC will also be very different from that of the nonparametric smoothing problem.

Define W_i = (W_i1, …, W_i,mi)^T, μ_i = {μ(t_i1), ⋯, μ(t_i,mi)}^T and ψ_ik = {ψ_k(t_i1), ⋯, ψ_k(t_i,mi)}^T. Under the assumption that there are p non-zero eigenvalues, denote $X_{i,[p]}(t)=\mu (t)+{\sum }_{j=1}^p{\xi }_{\mathit{ip}}{\psi }_j(t)$, and X_i,[p] = {X_i,[p](t_i1), …, X_i,[p](t_i,mi)}^T = μ_i + Ψ_i,[p]ξ_i,[p], where Ψ_i,[p] = (ψ_i1, …, ψ_ip) and ξ_i,[p] = (ξ_i1, …, ξ_ip)^T. Under a Gaussian assumption, the conditional log likelihood of the observed data {W_i} given the principal component scores is

$$\begin{array}{lll}{\mathit{L}}_{n,\mathrm{cond}}(p,{\mathit{X}}_{[p]},{\sigma }_u^2)& =& {\sum }_{i=1}^n\left\{-(m_i/2)\log (2\pi {\sigma }_u^2)-{(2{\sigma }_u^2)}^{-1}{\Vert {\mathit{W}}_i-{\mathit{X}}_{i,[p]}\Vert }^2\right\}\\ & =& -(N/2)\log (2\pi {\sigma }_u^2)-{(2{\sigma }_u^2)}^{-1}{\sum }_{i=1}^n{\Vert {\mathit{W}}_i-{\mathit{\mu }}_i-{\mathrm{\Psi }}_{i,[p]}{\mathit{\xi }}_{i,[p]}\Vert }^2,\end{array}$$ (8)

where N = Σ_i m_i and ${\mathit{X}}_{[p]}={({\mathit{X}}_{1,[p]}^{\mathrm{T}},\dots ,{\mathit{X}}_{n,[p]}^{\mathrm{T}})}^{\mathrm{T}}$.

Following the method proposed by Yao et al. (2005a), we estimate the trajectories by

$${\widehat{X}}_{i,[p]}(t)=\widehat{\mu }(t)+{\sum }_{j=1}^p{\widehat{\xi }}_{ij}{\widehat{\psi }}_j(t),$$ (9)

where μ̂(·) and ψ̂_j(·) are the estimators described in Section 2. The estimated principal component scores, ξ̂_ij, are given by the principal component analysis through the conditional expectation (PACE) estimator by Yao et al. (2005a). Under the Gaussian model, the best linear unbiased predictor (BLUP) for ξ_i,[p] is ${\stackrel{\sim }{\mathit{\xi }}}_{i,[p]}={\mathrm{\Lambda }}_{[p]}{\mathrm{\Psi }}_{i,[p]}^{\mathrm{T}}{\sum }_{i,[p]}^{-1}({\mathit{W}}_i-{\mathit{\mu }}_i)$, where Λ_[p] = diag(ω₁, …, ω_p), ${\sum }_{i,[p]}={\mathrm{\Omega }}_{i,[p]}+{\sigma }_u^2{I}_{m_i}$ and ${\mathrm{\Omega }}_{i,[p]}={\mathrm{\Psi }}_{i,[p]}{\mathrm{\Lambda }}_{[p]}{\mathrm{\Psi }}_{i,[p]}^{\mathrm{T}}$. To estimate ξ̂_i,[p], the PACE estimator requires a pilot estimator of ${\sigma }_u^2$, for which we can use the integral estimator ${\stackrel{\sim }{\sigma }}_{u,\mathrm{I}}^2$ defined in (3). The PACE estimator is given by

$${\widehat{\mathit{\xi }}}_{i,[p]}={\widehat{\mathrm{\Lambda }}}_{[p]}{\widehat{\mathrm{\Psi }}}_{i,[p]}^{\mathrm{T}}{\widehat{\mathrm{\sum }}}_{i,[p]}^{-1}({\mathit{W}}_i-{\widehat{\mathit{\mu }}}_i),$$ (10)

where μ̂_i, Λ̂_[p] and Ψ̂_i,[p] are the estimates using the FPCA method described in Section 2, and ${\widehat{\mathrm{\sum }}}_{i,[p]}={\widehat{\mathrm{\Psi }}}_{i,[p]}{\widehat{\mathrm{\Lambda }}}_{[p]}{\widehat{\mathrm{\Psi }}}_{i,[p]}^{\mathrm{T}}+{\stackrel{\sim }{\sigma }}_{u,\mathrm{I}}^{2}I$.

To choose p, Yao et al. (2005a) proposed the pseudo AIC

$${\mathrm{AIC}}_{\mathrm{Yao}}(p)=L_{n,\mathrm{cond}}(p,{\widehat{\mathit{X}}}_{[p]},{\stackrel{\sim }{\sigma }}_{u,\mathrm{I}}^2)+p,$$ (11)

where X̂_[p] is the estimated value of X_[p] by interpolating the estimated trajectories defined in (9) on the subject-specific times. By adding a penalty p to the estimated conditional likelihood, Yao et al. essentially counted each principal component as one parameter.

To motivate our own AIC criterion, we consider dense functional data satisfying

$$m_i\asymp m\to \infty \mathrm{for\; all}i,\underset{i}{\sup }|m_i-m|/m\to 0.$$ (12)

We follow the spirit of the derivation of Hurvich and Tsai (1989), and define the Kullback-Leibler information to be

$$\mathrm{\Delta }(p,{\stackrel{\sim }{\mathit{X}}}_{[p]},{\stackrel{\sim }{\sigma }}^2)={\mathrm{E}}_F\{-2{\mathit{L}}_{n,\mathrm{cond}}(p,{\stackrel{\sim }{\mathit{X}}}_{[p]},{\stackrel{\sim }{\sigma }}^2)\},$$ (13)

for any fixed X̂_[p] and σ̂², where F is the true normal distribution given the true curves {X_i(·), i = 1, …, n}. Using similar derivations as in Hurvich and Tsai (1989), for any fixed parameters ${\stackrel{\sim }{\mathit{X}}}_{[p]}={\left\{{\stackrel{\sim }{\mathit{X}}}_{i,[p]}={\stackrel{\sim }{\mathit{\mu }}}_i+{\stackrel{\sim }{\mathrm{\Psi }}}_{i,[p]}{\stackrel{\sim }{\mathit{\xi }}}_{i,[p]}\right\}}_{i=1}^n$ and σ̂², we have

$$\begin{array}{lll}\mathrm{\Delta }(p,{\stackrel{\sim }{\mathit{X}}}_{[p]},{\stackrel{\sim }{\sigma }}^2)& =& N\log (2\pi {\stackrel{\sim }{\sigma }}^2)+\frac{1}{{\stackrel{\sim }{\sigma }}^2}\sum _{i=1}^n{\mathrm{E}}_F\Vert {\mathit{U}}_i+{\mathit{X}}_i-{\stackrel{\sim }{\mathit{X}}}_{i,[p]}\Vert \\ & =& N\log (2\pi {\stackrel{\sim }{\sigma }}^2)+N\frac{{\sigma }_u^2}{{\stackrel{\sim }{\sigma }}^2}+\frac{1}{{\stackrel{\sim }{\sigma }}^2}\sum _{i=1}^n{\Vert ({\mathit{\mu }}_i-{\stackrel{\sim }{\mathit{\mu }}}_i)+{\mathrm{\Psi }}_{i,[p_0]}{\mathit{\xi }}_{i,[p_0]}-{\stackrel{\sim }{\mathrm{\Psi }}}_{i,[p]}{\stackrel{\sim }{\mathit{\xi }}}_{i,[p]}\Vert }^2.\end{array}$$ (14)

By substituting in the FPCA and PACE estimators, the estimated variance under the model with p principal components is given by

$$\begin{array}{lll}{\widehat{\sigma }}_{[p]}^2& =& N^{-1}{\sum }_{i=1}^n{\Vert {\mathit{W}}_i-{\widehat{\mathit{\mu }}}_i-{\widehat{\mathrm{\Psi }}}_{i,[p]}{\widehat{\mathit{\xi }}}_{i,[p]}\Vert }^2=N^{-1}{\sum }_{i=1}^n{\Vert (I-{\widehat{\mathrm{\Omega }}}_{i,[p]}{\widehat{\mathrm{\sum }}}_{i,[p]}^{-1})({\mathit{W}}_i-{\widehat{\mathit{\mu }}}_i)\Vert }^2\\ & =& N^{-1}{\sum }_{i=1}^n{\Vert {\stackrel{\sim }{\sigma }}_{u,\mathrm{I}}^2{\widehat{\mathrm{\sum }}}_{i,[p]}^{-1}({\mathit{W}}_i-{\widehat{\mathit{\mu }}}_i)\Vert }^2.\end{array}$$

Then the Kullback-Leibler information for these estimators is

$$\mathrm{\Delta }(p,{\widehat{X}}_{[p]},{\widehat{\sigma }}_{[p]}^2)=N\log ({\widehat{\sigma }}_{[p]}^2)+{\mathit{A}}_n(p),$$ (15)

where ${\mathit{A}}_n(p)=N{\sigma }_u^2/{\widehat{\sigma }}_{[p]}^2+{\widehat{\sigma }}_{[p]}^{-2}{\sum }_{i=1}^n{\Vert {\mathit{\mu }}_i-\widehat{{\mathit{\mu }}_i}+{\mathrm{\Psi }}_{i,[p_0]}{\mathit{\xi }}_{i,[p_0]}-{\widehat{\mathrm{\Psi }}}_{i,[p]}{\widehat{\mathit{\xi }}}_{i,[p]}\Vert }^2$.

To derive the new AIC criterion, we need the following theoretical results to evaluate the expected Kullback-Leibler information. As discussed in Hurvich et al. (1998, page 275), in derivation of AIC, one needs to assume that the true model is included in the family of candidate models, and any model bias is ignored. For example, Hurvich et al. (1998) ignored the smoothing bias when developing AIC for nonparametric regressions. Following the same argument, we will ignore all the biases in μ̂(·) and ψ̂_k(·), and only take into account the variation in the estimators.

Proposition 1

Under assumptions (C.1)-(C.7), condition (12) and the additional assumption that n (h_μ + h_C) → ∞, ${\widehat{\sigma }}_{[p_0]}^2/{\sigma }_u^2=N^{-1}{\sum }_{i=1}^n{\sum }_{j=p_0+1}^{m_i}{\mathit{\chi }}_{\mathit{ij}}+R_n$, where the χ_ij are independent ${\chi }_1^2$ random variables and ${\mathit{R}}_n=O_p\{{\delta }_{n1}^2(h_{\mu })+{\delta }_{n1}^2(h_C)\}+o_p(n{N}^{-1})$. As a result, ${\widehat{\sigma }}_{[p_0]}\to {\sigma }_u^2$ in probability as n → ∞

The next proposition gives the asymptotic expansion for E{A_n(p₀)}.

Proposition 2

Under the same conditions as in Proposition 1, E{A_n(p₀)} = N + 2np₀ + o(n).

Thus, the expected Kullback-Leibler information is ${\mathrm{E}}_F\{\mathrm{\Delta }(p_0,{\widehat{X}}_{[p_0]},{\widehat{\sigma }}_{[p_0]}^2)\}={\mathrm{E}}_F\{N\log ({\stackrel{\sim }{\sigma }}_{[p_0]}^2)\}+N+2n{p}_0+o(n)$. This justifies defining AIC as

$$\mathrm{AIC}(p)=N\log ({\widehat{\sigma }}_{[p]}^2)+N+2\mathit{np}.$$ (16)

When m_i → ∞ and p is fixed, an intuitive interpretation for the proposed AIC in (16) is to consider FPCA as a linear regression on the observed data W_i − μ_i against covariates (ψ_i1,…, ψ_ip) for subject i, and consider the principal component scores as the subject-specific coefficients. By pooling n independent curves together and by adding up the individual AIC, we have a total of np regression parameters and the AIC in (16) coincides with that of a simple linear regression. The biggest difference between our AIC and that of Yao et al. in (11) is the way we count the number of parameters in the model.

3.3 Consistent information criteria

As pointed out by a referee, functional principal component analysis is closely related to factor models in econometrics, where there are some existing information criteria to choose the number of factors consistently (Bai and Ng, 2002). We stress that the data considered in the econometrics literature are multivariate time series data observed on regular time points, while we consider irregularly spaced functional data. The estimator and criteria proposed by Bai and Ng were based on matrix projections, while our FPCA method relies heavily on kernel smoothing and operator theory. As a result, deriving consistent model selection criteria for our problem is technically much more involved.

Inspired by Bai and Ng (2002), we consider two classes of information criteria:

$$\mathit{PC}(p)={\widehat{\sigma }}_{[p]}^2+{\mathit{pg}}_n,$$ (17)

$$\mathit{IC}(p)=\log \left({\widehat{\sigma }}_{[p]}^2\right)+{\mathit{pg}}_n,$$ (18)

where ${\widehat{\sigma }}_{[p]}^2$ is the error variance estimator used in our AIC (15) and g_n is a penalty. The estimator ${\widehat{\sigma }}_{[p]}^2$ in Bai and Ng (2002) was a mean squared error based on a simple regression, while our estimator is based on the PACE method involving kernel smoothing and BLUP.

For any p ≤ p₀, denote ψ_[p](t) = (ψ₁, …, ψ_p)^T (t), ψ_[p+1:p0] = (ψ_p+1, …, ψ_p0)^T (t), and define the inner product matrices ${\mathit{J}}_{1,p}=\mathit{\int }{\mathit{\psi }}_{[p]}(t){\mathit{\psi }}_{[p]}^T(t)f_1(t)\mathit{dt},{\mathit{J}}_{2,p}=\mathit{\int }{\mathit{\psi }}_{[p+1:p_0]}(t){\mathit{\psi }}_{[p+1:p_0]}^T(t)f_1(t)\mathit{dt}$ and ${\mathit{J}}_{12,p}=\mathit{\int }{\mathit{\psi }}_{[p]}(t){\mathit{\psi }}_{[p+1:p_0]}^T(t)f_1(t)\mathit{dt}$. Put Λ_[p+1:p0] = diag(ω_p+1, …, ω_p0), and

$$T_p=\mathrm{tr}\{\left(J_{2,p}-J_{12,p}^{\mathrm{T}}{J}_{1,p}^{-1}{J}_{12,p}\right){\mathrm{\Lambda }}_{[p+1:p_0]}\}.$$ (19)

Theorem 2

Suppose τ_p defined at (19) exists and is positive for all 0 ≤ p < p₀. Let p̂ be the minimizer of the information criteria defined in (17) or (18) among 0 ≤ p ≤ p_max with p_max > p₀ being a fixed search limit, and define ${\varrho }_n=h_{\mu }^2+h_C^2+h_{\sigma }^2+{\delta }_{n1}(h_{\mu })+{\delta }_{n2}(h_C)+{\delta }_{n1}^2(h_{\sigma })$. Under the assumptions (C.1) - (C.7) and condition (12), lim_n→∞ pr(p̂ = p₀) = 1 if the penalty function g_n satisfies (i) $g_n\stackrel{p}{\to }0$ and (ii) $g_n/(n/N+{\varrho }_n^2)\stackrel{p}{\to }\infty$.

In the factor analysis context, the penalty term in the information criteria proposed by Bai and Ng (2002) converges to 0 with a rate slower than $C_n^{-2}$, where C_n = min(m^1/2, n^1/2) translating to our notation. Their rate shows a sense of symmetry in the roles of m and n. Indeed, when the curves are observed on a regular grid, the data can be arranged into a n × m matrix W, the factor analysis can be carried out by a singular value decomposition of W, and hence the roles of m and n are symmetric. For the random design that we consider, we apply nonparametric smoothing along t, not among the subjects. Therefore, m and n play different roles in our rate. Not only does the smoothing make our derivation much more involved, but the fact the within-subject covariance matrices are defined on subject specific time points poses many theoretical challenges. Our proof uses many techniques from perturbation theory of random operators and matrices.

The following corollary shows that when the bandwidths are chosen properly, penalties similar to those in Bai and Ng (2002) can still lead to consistent information criteria.

Corollary 1

Suppose all conditions in Theorem 2 hold, and hμ ≍ max(n,m)^−c₁, h_C ≍ max(n,m)^−c₂, h_σ ≍ max(n,m)^−c₃, where 1/4 ≤ c₁, c₂ ≤ 1, 1/4 ≤ c₃ ≤ 3/2. Then p̂ that minimizes PC(p) or IC(p) is consistent if (i) $g_n\stackrel{p}{\to }0$ and (ii) $C_n^2{g}_n\stackrel{p}{\to }\infty$, where C_n = min(n^1/2, m^1/2) as defined in Bai and Ng (2002).

Bai and Ng (2002) proposed the following information criteria that satisfy the conditions in Corollary 1,

$$\begin{array}{lll}{\mathit{PC}}_{p1}(p)& =& {\widehat{\sigma }}_{[p]}^2+p{\widehat{\sigma }}_{\mathrm{pilot}}^2\left(\frac{n+m}{\mathit{nm}}\right)\log \left(\frac{\mathit{nm}}{n+m}\right),\\ {\mathit{PC}}_{p2}(p)& =& {\widehat{\sigma }}_{[p]}^2+p{\widehat{\sigma }}_{\mathrm{pilot}}^2\left(\frac{n+m}{\mathit{nm}}\right)\log \left(C_n^2\right),\\ {\mathit{PC}}_{p3}(p)& =& {\widehat{\sigma }}_{[p]}^2+p{\widehat{\sigma }}_{\mathrm{pilot}}^2\left\{\frac{\log (C_n^2)}{C_n^2}\right\},\\ {\mathit{IC}}_{p1}(p)& =& \log ({\widehat{\sigma }}_{[p]}^2)+p\left(\frac{n+m}{\mathit{nm}}\right)\log \left(\frac{\mathit{nm}}{n+m}\right),\\ {\mathit{IC}}_{p2}(p)& =& \log ({\widehat{\sigma }}_{[p]}^2)+p\left(\frac{n+m}{\mathit{nm}}\right)\log (C_n^2),\\ {\mathit{IC}}_{p3}(p)& =& \log ({\widehat{\sigma }}_{[p]}^2)+p\left\{\frac{\log (C_n^2)}{C_n^2}\right\},\end{array}$$ (20)

where ${\widehat{\sigma }}_{\mathrm{pilot}}^2$ is a pilot estimator for ${\sigma }_u^2$. In our setting, we can use ${\stackrel{\sim }{\sigma }}_{u,\mathrm{I}}^2$ defined at (3) in place of ${\widehat{\sigma }}_{\mathrm{pilot}}^2$, and replace m by either the arithmetic or the harmonic mean of m_i’s. Under the undersmoothing choices of bandwidths described in Corollary 1, all information criteria in (20) are consistent. One can easily see the similarity between the IC_p criteria and the AIC proposed in (16). In general, the IC_p criteria impose greater penalties to over-fitting than AIC. By comparing AIC with the conditions in Theorem 2 and other consistent criteria we developed, we can see the penalty term in AIC is a little bit small and that explains the non-vanishing chance of overfitting witnessed in our simulation studies, see Section 4.

4 Simulation Studies

4.1 Empirical performance of the proposed criteria

To illustrate the finite sample performance of the proposed methods, we performed various simulation studies. Let T = [0, 1], and suppose that the data are generated from the model (1) and (2). Let the observation time points T_ij ~ Uniform [0, 1], m_i = m for all i and $U_{\mathit{ij}}~\mathrm{Normal}(0,{\sigma }_u^2)$.

We consider the following five scenarios.

• Scenario I: Here the true mean function is μ(t) = 5(t − 0.6)², the number of principal components is p₀ = 3, the true eigenvalues are (ω₁, ω₂, ω₃) = (0.6, 0.3, 0.1), the variance of the error is ${\sigma }_u^2=0.2$ and the eigenfunctions are ψ₁(t) = 1, ${\psi }_2(t)=\sqrt{2}sin(2\pi t)$, ${\psi }_3(t)=\sqrt{2}cos(2\pi t)$. The principal component scores are generated from independent normal distributions, i.e. ξ_ij ~ Normal(0, ω_j). Here ${\omega }_3<{\sigma }_u^2$.

• Scenario II: The data are generated in the same way as in Scenario I, except that we replace the third eigenfunction by a rougher function ${\psi }_3^{\prime }(t)=\sqrt{2}cos(4\pi t)$ so that the covariance function is less smooth, and we let the principal component scores follow a skewed Gaussian mixture model. Specifically, ξ_ij has 1/3 probability of following a $\mathrm{Normal}(2\sqrt{{\omega }_j/3},{\omega }_j/3)$ distribution, and 2/3 probability of following $\mathrm{Normal}(-\sqrt{{\omega }_j/3},{\omega }_j)$, for j = 1, 2, 3.

• Scenario III: Set μ(t) = 12.5(t − 0.5)² − 1.25, ϕ₁(t) = 1, ${\varphi }_2(t)=\sqrt{2}cos(2\pi t)$, ${\varphi }_3(t)=\sqrt{2}sin(4\pi t)$, and (ω₁, ω₂, ω₃, σ₂) = (4.0, 2.0, 1.0, 0.5). The principal component scores are generated from a Gaussian distribution. Here ${\omega }_3>{\sigma }_u^2$.

• Scenario IV: The mean function, eigenvalues, eigenfunction and noise level are set to be the same as in Scenario III, but the ξ_ij’s are generated from a Gaussian mixture model similar to that in Scenario II.

• Scenario V: In this simulation, we set p₀ = 6, the true eigenvalues are (4.0, 3.5, 3.0, 2.5, 2.0, 1.5) and ${\sigma }_u^2=0.5$. We assume that the principal component scores are normal random variables and let the eigenfunctions be

  $$\begin{array}{l}{\psi }_1(t)=1;{\psi }_{2k}(t)=\sqrt{2}\sin (2k\pi t),\mathrm{for}k=1,2,3;\\ {\psi }_{2k+1}(t)=\sqrt{2}\cos (2k\pi t),\mathrm{for}k=1,2.\end{array}$$

In each simulation, we generated n = 200 trajectories from the models above, and compared the cases with m = 5, 10 and 50. The cases m = 5 and m = 50 may be viewed as representing sparse and dense functional data, respectively, whereas m = 10 represents scenarios between the two extremes. For each m, we apply the FPCA procedure to estimate $\{\mu (·),R(·,·),{\omega }_k,{\psi }_k(·),{\sigma }_w^2(t)\}$, then use the proposed information criteria to choose p. The simulation was then repeated 200 times for each scenario.

The performance of the estimators depends on the choice of bandwidths for μ(t), C(s, t) and ${\sigma }_w^2(t)$, and the optimal bandwidths vary with n and m. We picked the bandwidths that are slightly smaller than those minimizing the integrated mean squared error (IMSE) of the corresponding functions, since undersmoothing in functional principal component analysis was also advocated by Hall et al. (2006) and Li and Hsing (2010b).

We consider Yao’s AIC, MDL by Poskitt and Sengarapillai (2011), the proposed BIC and AIC in (6) and(16), and the criteria by Bai and Ng in (20). Yao’s AIC is calculated using the publicly available PACE package (http://anson.ucdavis.edu/mueller/data/pace.html), where all bandwidths are data-driven and selected by generalized cross-validation (GCV). The empirical distribution of p̂ under Scenarios I to IV are summarized in Tables 1-3. Since the true number of principal components p₀ is different in Scenario V, the distribution of p̂ is summarized in a separate Table 4.

Table 1.

When m = 5, displayed are the distributions of the number of selected principal components p̂ for all methods and across Scenarios I-IV. The true number of principal components is 3.

Scenario	Method	p̂ ≤ 1	p̂ = 2	p̂ = 3	p̂ = 4	p̂ ≥ 5
I	AICPACE	0.000	0.008	0.000	0.121	0.870
	AIC	0.000	0.405	0.580	0.010	0.005
	BIC	0.155	0.335	0.380	0.115	0.015
	PCp1	0.005	0.565	0.410	0.010	0.010
	ICp1	0.000	0.215	0.735	0.045	0.005
II	AICPACE	0.000	0.000	0.005	0.125	0.870
	AIC	0.000	0.205	0.630	0.155	0.010
	BIC	0.230	0.395	0.245	0.110	0.020
	PCp1	0.000	0.000	0.375	0.440	0.185
	ICp1	0.000	0.140	0.605	0.210	0.045
III	AICPACE	0.000	0.025	0.005	0.130	0.840
	AIC	0.000	0.035	0.720	0.170	0.075
	BIC	0.335	0.260	0.325	0.080	0.000
	PCp1	0.000	0.220	0.640	0.075	0.065
	ICp1	0.000	0.005	0.590	0.280	0.125
IV	AICPACE	0.000	0.015	0.015	0.145	0.825
	AIC	0.000	0.020	0.710	0.185	0.085
	BIC	0.315	0.180	0.410	0.070	0.025
	PCp1	0.000	0.160	0.640	0.095	0.105
	ICp1	0.000	0.015	0.560	0.260	0.165

Table 3.

For m = 50, displayed are the distributions of the number of selected principal components p̂ for all methods and across Scenarios I-IV. The true number of principal components is 3.

Scenario	Method	p̂ = 1	p̂ = 2	p̂ = 3	p̂ = 4	p̂ ≥ 5
I	AICPACE	0.000	0.000	0.000	0.000	1.000
	AIC	0.000	0.000	1.000	0.000	0.000
	BIC	0.000	0.000	0.830	0.150	0.020
	PCp1	0.000	0.000	1.000	0.000	0.000
	ICp1	0.000	0.000	1.000	0.000	0.000
II	AICPACE	0.000	0.000	0.000	0.000	1.000
	AIC	0.000	0.000	0.630	0.320	0.050
	BIC	0.000	0.000	0.795	0.185	0.020
	PCp1	0.000	0.000	0.955	0.045	0.000
	ICp1	0.000	0.000	0.945	0.055	0.000
III	AICPACE	0.000	0.000	0.000	0.000	1.000
	AIC	0.000	0.000	1.000	0.000	0.000
	BIC	0.000	0.000	0.775	0.200	0.025
	PCp1	0.000	0.000	1.000	0.000	0.000
	ICp1	0.000	0.000	1.000	0.000	0.000
IV	AICPACE	0.000	0.000	0.000	0.000	1.000
	AIC	0.000	0.000	0.945	0.055	0.000
	BIC	0.000	0.000	0.835	0.140	0.025
	PCp1	0.000	0.000	1.000	0.000	0.000
	ICp1	0.000	0.000	1.000	0.000	0.000

Table 4.

Distributions of the number of selected principal components p̂ for Scenario V. The true number of principal components is 6.

Scenario	Method	p̂ ≤ 4	p̂ = 5	p̂ = 6	p̂ = 7	p̂ ≥ 8
m=5	AICPACE	0.005	0.005	0.705	0.245	0.040
	AIC	0.165	0.330	0.470	0.035	0.000
	BIC	0.835	0.020	0.090	0.050	0.005
	PCp1	0.580	0.345	0.070	0.005	0.000
	ICp1	0.060	0.335	0.545	0.060	0.000
m=10	AICPACE	0.005	0.000	0.065	0.475	0.455
	AIC	0.000	0.000	0.570	0.280	0.15
	BIC	0.250	0.030	0.525	0.165	0.030
	PCp1	0.000	0.145	0.775	0.020	0.060
	ICp1	0.000	0.000	0.705	0.185	0.110
m=50	AICPACE	0.000	0.065	0.000	0.000	0.935
	AIC	0.000	0.000	0.260	0.405	0.335
	BIC	0.005	0.000	0.590	0.325	0.080
	PCp1	0.000	0.000	0.980	0.010	0.010
	ICp1	0.000	0.000	0.965	0.035	0.000

The proposed BIC method is based on the convergence rate results on the eigenvalues, and does not rely much on the distributional assumptions for X and U. From Tables 1-3, we see that BIC picks the correct number of principal components with high percentage in almost all scenarios, except for the cases where the data are sparse, i.e. m = 5. This phenomena is as expected, because it is harder to pick up the correct number of signals from sparse and noisy data.

Compared to BIC, the performance of the proposed AIC method is even more impressive. Although BIC is designed to be a consistent model selector, the AIC method selects the right number of principal component with a higher percentage in most of the cases we considered. This is partially due to the fact that AIC makes more use of the information from the likelihood. Even though the data are non-Gaussian in Scenario II and IV, the AIC still performs better than the BIC, and it shows that both the PACE method and the AIC method are quite robust against mild violation of the Gaussian Assumption. Even though the motivation and theoretical development for the AIC method described in Section 3.2 are for dense functional data, it performs surprisingly well for sparse data, such as the case m = 5.

There are six criteria in (20), and we find that the PC_p’s and the IC_p’s tend to perform similarly. To save journal space, we only provide the results for PC_p1 and IC_p1, and the results for the remaining criteria in (20) can be find in the expanded versions of Tables 1-4 in the Supplementary Material. As we can see, these criteria behave similar to the AIC, and they tend to do better only in a few occasions when AIC overestimates p.

For almost all scenarios considered, Yao’s AIC hardly ever picks the correct model, with the exception of Scenario V, m = 5, which will be discussed in more detail below. When the true number of principal components is 3, Yao’s AIC will normally chose a number greater than 5. This phenomenon becomes more severe when the data are dense. For example, when m = 50, Yao’s AIC almost always pick the maximum order considered, which is 15 in our simulations. The behavior of the MDL by Poskitt and Sengarapillai (2011) is similar to Yao’s AIC, and hence these results are only provided in Tables S.2 - S.5 in the Supplementary Material.

Scenario V, Table 4 is specially designed to check the performance of the proposed information criteria under the situations where we have a relatively large number of principal components. The proposed criteria worked reasonably well for m = 10 and 50, and performed much better than Yao’s AIC. The case of m = 5 under Scenario V is the only case in all of our simulations that Yao’s AIC picks the correct model more often than our criteria. With a closer look at the results, we find an explanation. The true covariance function under Scenario V is quite rough, and the GCV criterion in the PACE package chose a large bandwidth so that the local fluctuations on the true covariance surface are smoothed out. In other words, high frequency signals are smoothed out and treated as noise. In a typical run, the PACE estimates for the eigenvalues are (4.1736, 2.1350, 1.6697, 1.0009, 0.3978, 0.0476) which are far from the truth, (4.0, 3.5, 3.0, 2.5, 2.0, 1.5), and the estimated error variance is 6.519 in contrast to the truth ${\sigma }_u^2=0.5$. It is the combination of seriously underestimating the high order eigenvalues and small penalty in AIC that makes Yao’s criterion pick the correct number of principal components. Switching to our undersmoothing bandwidths, these estimates are improved but then Yao’s AIC will choose much larger values for p. This case also highlights the difficulty of FPCA when p is large but the data are sparse. Unless we have a very large sample size, estimation of these principal components is very difficult, and comparing the model selection procedures in such a case would not be meaningful.

4.2 Further Simulations

The Supplementary Material, Section S.4 contains further simulations, including (a) Expanded results with other model selectors in Tables S.2-S.5; (a) an examination of the sensitivity of the results to the bandwidth (Supplementary Table S.6); (c) the behavior of BIC with much larger sample size (Supplementary Table S.7); and (c) results when the value of m is not constant, i.e., m_i ≠ m for all i (Supplementary Table S.8).

5 Data analysis

The colon carcinogenesis data in our study have been analyzed in Li, Wang et al. (2007, 2010) and Baladandayuthapani et al. (2008). The biomarker of interest in this experiment is p27, which is a protein that inhibits cell cycle. We have 12 rats injected with carcinogen and sacrificed 24 hours after the injection. Beneath the colon tissue of the rats, there are pore structures called ‘colonic crypts’. A crypt typically contains 25 to 30 cells, lined up from the bottom to the top. The stem cells are at the bottom of the crypt, where daughter cells are generated. These daughter cells move towards the top as they mature. We sampled about 20 crypts from each of the 12 rats. The p27 expression level was measured for each cell within the sampled crypts. As previously noted in the literature (Morris et al. 2001, 2003), the p27 measurements, indexed by the relative cell location within the crypt, are natural functional data. We have m = 25-30 observations (cells) on each function. As in the previous analyses, we consider p27 in the logarithmic scale. By pooling data from the 12 rats, we have a total of n = 249 crypts (functions). In the literature, it has been noted that there is spatial correlation among the crypts within the same rat (Li et al., 2007, Baladandayuthapani et al., 2008). In this experiment, we sampled crypts sufficiently far apart so that the spatial correlations are negligible, and thus we can assume that the crypts are independent.

We perform the FPCA procedure as described in Section 2, with the bandwidths chosen by leave one curve out cross-validation. The estimated covariance function is given in the top panel of Figure 1. The estimated variance of measurement error by integration is σ̃_u,I = 0.103. In contrast, the top 3 eigenvalues are 0.8711, 0.0197 and 0.0053. Let k_n = max{k; ω̂_k > 0}, then the percentage of variation explained by the kth principal component is estimated by ${\widehat{\omega }}_k/({\sum }_{j=1}^{k_n}{\widehat{\omega }}_j)$. The percentage of variation explained by the first 7 principal components are (0.966, 0.022, 0.006, 0.003, 0.002, 0.001, 0.000).

Figure 1.

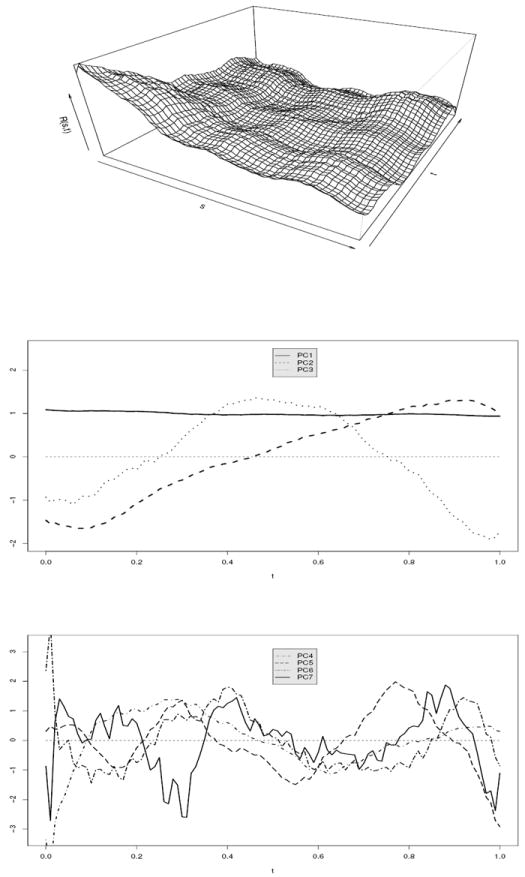
Functional principal component analysis for the colon carcinogenesis p27 data. Top panel: estimated covariance function; middle panel: the first 3 eigenfunctions; lower panel: eigenfunctions 4-7.

We apply the proposed AIC, adaptive BIC, the Bai and Ng criteria (20) and Yao’s AIC to the data. All of the proposed methods lead to p = 3 principal components, for which the corresponding eigenfunctions are shown in the middle panel Figure 1. As we can see, the first principal component is a constant over time, and the second and third eigenfunctions are essentially linear and quadratic functions. Eigenfunction 4 to 7 are shown in the bottom panel of Figure 1, and they are basically noises and are hard to interpret. We therefore can see that the variation among different crypts can be explained by random quadratic polynomials. Yao’s AIC, on the other hand, picked a much large number of principal components, with p = 9. This is due to the fact that a much smaller penalty is used in Yao’s AIC criterion. We have repeated the data analysis using other choices of bandwidths, and the results are the same.

6 Summary

6.1 Basic Summary

Choosing the number of principal components is a crucial step in functional data analysis. There have been some data-driven procedures proposed in the literature that can be used to choose the number of principal components, but these procedures have not been studied theoretically, nor were they tested numerically as extensively as in this paper.

To promote practically useful model selection criteria, we have assumed that there exists a finite dimensional true model. We found that the consistency of the model selection criteria depends on both the sample size n and the number of repeated measurements m on each curve. We proposed a marginal BIC criterion that is consistent for both dense and sparse functional data, which means m can be of any rate relative to n. In the framework of dense functional data, where both n and m diverge to infinity, we proposed a conditional Akaike information criterion, which is motivated by an asymptotic study of the expected Kullback-Leibler distance under Gaussian assumption.

Following the standard approach of Hurvich et al. (1998), we ignored smoothing biases in developing AIC. Our intensive simulation studies also confirm that bias plays a very small role in model selection. In our simulations in Section 4.2, we tried a wide range of bandwidths and thus increase or decrease the biases in the estimators, but the performance of AIC is almost the same. Intuitively, the models under different numbers of principal components are nested, for a fixed bandwidth the smoothing bias exists in all models that we compare, and therefore variation is a more decisive factor in model selection.

In view of the connection of FPCA with factor analysis in multivariate time series data, we revisited the information criteria proposed by Bai and Ng (2002). Even though our setting is fundamentally different, since we assumed that the observational times are random, and the FPCA estimators depend heavily on nonparametric smoothing and are much more complex than those in Bai and Ng, we show essentially similar information criteria can be constructed. Using perturbation theory of random operators and matrices, and under an under-smoothing scheme prescribed in Section 3.3, we showed that these information criteria are consistent when both n and m go to infinity.

6.2 Discussion of the case p₀ → ∞

Some processes considered as functional data are intrinsically infinite dimensional. In those cases, the assumption of p₀ being finite is a finite sample approximation. As the sample size n increases, we can afford to include more principal components in the model and data analysis. It is helpful to consider that the true dimension p_0n increases to infinity as a function of n. This setting was considered in the estimation of a functional linear model (Cai and Hall, 2006). To the best of our knowledge, no information criteria have been previously studied under this setting.

While allowing p_0n → ∞, the convergence rates for μ̂(t) and R̂(s, t) remain the same as those given in Lemma S.1.1 in the Supplementary Material, but the convergence rates for ψ̂_j(t) are affected by the spacing of the true eigenvalues. Following condition (4.2) in Cai and Hall (2006), we assume that for some positive constants C and α,

$$C^{-1}{j}^{-\alpha }\le {\omega }_j\le {\mathit{Cj}}^{-\alpha },{\omega }_j-{\omega }_{j+1}\ge C^{-1}{j}^{-1-\alpha },j=1,\dots ,p_{0n}.$$ (21)

To ensure that ${\sum }_j^{p_{0n}}{\omega }_j<\infty$, we assume that α > 1. Define the distances between the eigenvalues, δ_j = min_k≤j(ω_k − ω_k+1), which is no less than C⁻¹j^−1−α under condition (21). By the asymptotic expansion of ψ̂_j(t), see (2.8) in Hall and Hosseini-Nasab, 2006, one can show that the convergence rate of ψ̂_j is ${\delta }_j^{-1}$ times those in Lemma S.1.2 in the Supplementary Material, i.e.

$${\widehat{\psi }}_j(t)-{\psi }_j(t)=O_p\left[j^{\alpha +1}\times \left\{h_{\mu }^2+{\delta }_{n1}(h_{\mu })+h_C^2+{\delta }_{n1}(h_C)+{\delta }_{n2}^2(h_C)\right\}\right],j=1,\dots ,p_{0n}.$$

Assume that n, m, p_0n → ∞, $p_{0n}^{\alpha +1}{\varrho }_n\to 0$, and $p_{0n}^{\alpha +3}/min(n,m)\to 0$. Following the proof of Theorem 2, while taking into account the increasing estimation error in ψ̂_j(t) as j increases and the increasing dimensionality of the design matrix Ψ_i, we can show that

$${\widehat{\sigma }}_{[p]}^2=\{\begin{array}{ll}{\sigma }_u^2+{\tau }_p+O_p({\mathit{pm}}^{-1}+N^{-1/2})+o_p({\tau }_p+p^{\alpha +3}{\varrho }_n^2),& \mathrm{for}p<p_{0n};\\ {\widehat{\sigma }}_{[p_{0n}]}^2+O_p(m^{-1}+p_{0n}^{\alpha +3}{\varrho }_n^2),& \mathrm{for}p\ge p_{0n},\end{array}$$ (22)

where τ_p ≍ tr(Λ_[p+1:p0n]) is analogous to (19) and ϱ_n is as defined in Theorem 2. Since the eigenvalues are decaying to 0, the size of the signal τ_p ≍ p^−α as p increases to p_0n. In order to have some hope of choosing p_0n correctly, we need τ_p to be greater than the size of the estimation error, which implies that $p_{0n}^{2\alpha +3}{\varrho }_n^2\to 0$.

Now, consider the class of information criteria in Section 3.3. Suppose that p_0n increases slowly enough so that $p_{0n}^{2\alpha +3}/min(n,m)\to 0$, and that the penalty term satisfies τ_p/(pg_n) → ∞ for p < p_0n and ${\mathit{pg}}_n/(m^{-1}+p^{\alpha +3}{\varrho }_n^2)\to \infty$ for p > p_0n. Then we can show that the p̂ which minimizes PC(p) or IC(p) is consistent. These conditions translate to

$$p_{0n}^{\alpha +1}{g}_n\to 0,g_n/(p_{0n}^{-1}{m}^{-1}+p_{0n}^{\alpha +2}{\varrho }_n^2)\to \infty .$$ (23)

If p_0n = {min(m, n)}^β where 0 < β < 1/(2α+3), one can see that the criteria in (20) do not satisfy the conditions in (23) automatically and hence are not guaranteed to be consistent. An information criterion satisfying condition (23) requires a priori knowledge of the decay rate of the eigenvalues. Developing a data-adaptive information criterion that does not require such a priori knowledge is a challenging topic for future research.

Table 2.

When m = 10, displayed are the distributions of the number of selected principal components p̂ for all methods and across Scenarios I-IV. The true number of principal components is 3.

Scenario	Method	p̂ ≤ 1	p̂ = 2	p̂ = 3	p̂ = 4	p̂ ≥ 5
I	AICPACE	0.000	0.000	0.000	0.000	1.000
	AIC	0.000	0.005	0.980	0.015	0.000
	BIC	0.000	0.040	0.670	0.255	0.035
	PCp1	0.000	0.040	0.955	0.000	0.005
	ICp1	0.000	0.005	0.985	0.010	0.000
II	AICPACE	0.000	0.000	0.000	0.005	0.995
	AIC	0.000	0.000	0.710	0.260	0.030
	BIC	0.000	0.170	0.665	0.135	0.030
	PCp1	0.000	0.000	0.570	0.355	0.075
	ICp1	0.000	0.000	0.805	0.185	0.010
III	AICPACE	0.000	0.015	0.000	0.000	0.985
	AIC	0.000	0.000	0.580	0.400	0.020
	BIC	0.005	0.035	0.770	0.145	0.045
	PCp1	0.000	0.000	0.965	0.030	0.005
	ICp1	0.000	0.000	0.665	0.320	0.015
IV	AICPACE	0.000	0.000	0.000	0.000	1.000
	AIC	0.000	0.000	0.830	0.150	0.020
	BIC	0.010	0.005	0.775	0.190	0.020
	PCp1	0.000	0.000	0.920	0.045	0.035
	ICp1	0.000	0.000	0.900	0.085	0.015