Supervised calibration relies on the multisensory percept

SUMMARY

Multisensory plasticity enables us to dynamically adapt sensory cues to one another and to the environment. Without external feedback, “unsupervised” multisensory calibration reduces cue conflict in a manner largely independent of cue-reliability. But environmental feedback regarding cue-accuracy (“supervised”) also affects calibration. Here we measured the combined influence of cue-accuracy and cue-reliability on supervised multisensory calibration, using discrepant visual and vestibular motion stimuli. When the less-reliable cue was inaccurate, it alone got calibrated. However, when the more-reliable cue was inaccurate, cues were yoked and calibrated together in the same direction. Strikingly, the less-reliable cue shifted away from external feedback, becoming less accurate. A computational model in which supervised and unsupervised calibration work in parallel, where the former only relies on the multisensory percept, but the latter can calibrate cues individually, accounts for the observed behavior. In combination, they could ultimately achieve the optimal solution of both external accuracy and internal consistency.

INTRODUCTION

Multisensory plasticity enables us to dynamically adapt sensory cues to one another and to the environment, facilitating perceptual and behavioral calibration. Although most pronounced during development, plasticity is now believed to be a normal capacity of the nervous system throughout our lifespan (Pascual-Leone et al., 2005) Intriguingly, sensory cortices can functionally change to process other modalities (Merabet et al., 2005) with multisensory regions demonstrating the highest degree of plasticity (Fine, 2008). Sensory substitution devices and neuroprostheses aim to harness this intrinsic and ongoing capability of the nervous system in order to restore lost function, but fall short – likely due to our limited understanding of multisensory plasticity (Bubic et al., 2010).

The vestibular system is particularly well suited to study multisensory plasticity. Loss of vestibular function is initially debilitating, but the deficits rapidly diminish (Smith and Curthoys, 1989). A natural form of sensory substitution is thought to mediate the impressive behavioral recovery (Sadeghi et al., 2012). But multisensory plasticity is not limited to lesion or pathology: perturbation of environmental dynamics, e.g., in space or at sea, results in multisensory adaptation, with aftereffects and reverse adaptation evident upon returning to land (Black et al., 1995). Also, multisensory adaptation is believed to ameliorate motion sickness by reducing sensory conflict (Shupak and Gordon, 2006). But, despite its importance in normal and abnormal brain function, the rules governing multisensory plasticity are still a mystery.

Proficiency of multisensory perception can be assessed by two different properties: reliability and accuracy. Reliability (also known as precision) means that repeated exposure to the same stimulus consistently yields the same percept. It is measured by the inverse variance of the percept. Accuracy means that the perception truly represents the real-world physical property. It is measured by the bias of the percept in relation to the actual stimulus. An ideal sensor is both reliable (minimum variance) and accurate (unbiased). Similarly, reliable behavior represents a consistent response, while accuracy measures its “correctness” in the external world.

The prevalent theory of multisensory integration accounts for improved reliability (Yuille and Bülthoff, 1996; Ernst and Banks, 2002; van Beers et al., 2002; Knill and Pouget, 2004; Alais and Burr, 2004; Fetsch et al., 2009; Butler et al., 2010), but not for accuracy. Maintaining accuracy is a complex task. It requires simultaneous calibration of multimodal cues and their related behaviors to a changing environment (moving target), which is itself estimated from those cues. Recent studies suggest that the mechanisms underlying multisensory calibration are different from those of multisensory integration (Smeets et al., 2006; Ernst and Di Luca, 2011; Burr et al., 2011; Block and Bastian, 2011; Zaidel et al., 2011), but a comprehensive and quantitative understanding is missing.

We recently showed that multisensory calibration without external feedback (“unsupervised” calibration) acts to reduce or eliminate discrepancies between the cues, and is largely independent of cue reliability (Zaidel et al., 2011). This result is in line with the proposal that cue accuracy is more relevant than cue reliability for multisensory calibration (Gori et al., 2010; Ernst and Di Luca, 2011). This is especially important during development (Gori et al., 2012). But external feedback from the environment also affects multisensory calibration (Adams et al., 2010) especially when explicit and likely attributable to perception (e.g., wearing new glasses, a hearing aid, working with gloves, or due to sensory loss or perturbation). This may result in perceptual changes, behavioral changes, or both. Hence incorporating the effects of external feedback (“supervised” calibration) is required in order to fully understand multisensory calibration. Furthermore, since an interaction between reliability and accuracy is likely, manipulation of both in the same experiment is essential for a proper understanding of multisensory calibration.

Previous studies (including our own) have drawn conclusions from manipulating only one of these features, or assumed that cue reliability also reflects cue accuracy (e.g., testing calibration of a less reliable sense to vision). Some studies did dissociate accuracy from reliability (Knudsen and Knudsen, 1989a; Adams et al., 2001; van Beers et al., 2002) but did not measure reliability. Moreover, the results of these studies are conflicting; for example, Adams et al. found recalibration of the presumably more reliable cue, whereas Knudsen and Knudsen did not. Other studies have controlled reliability, but not accuracy (Burge et al., 2010; Zaidel et al., 2011). To the best of our knowledge, the present study is the first to systematically control both accuracy and reliability for multiple senses.

RESULTS

Multisensory calibration hypotheses

The ability to assess the accuracy of individual sensory cues would be beneficial for multisensory calibration, since it would allow targeted calibration of only the inaccurate cue. However, the extent to which the brain can accomplish this is unknown. Whether or not accuracy can be assessed for individual cues leads to very different calibration hypotheses. Specifically, if the mechanism of supervised calibration can correctly assess each individual cue’s accuracy, then one would expect targeted calibration of the inaccurate cue alone, regardless of reliability (optimal strategy). Alternatively, if supervised calibration can only assess accuracy for the combined cue, then individual cue accuracy would be unknown. Namely, if the combined cue is sensed to be inaccurate, there would be ambiguity regarding which single cue is responsible. In this case, cue reliability may come into play; this could result in suboptimal calibration. These ideas are implemented in the multisensory calibration models we consider here.

In Figure 1, we simulated two cues of heading direction, e.g. visual and vestibular, with a constant discrepancy between them (leftmost column). In accordance with the actual experiments, we simulated one cue as being more reliable, and the other, less reliable (red and blue shades, respectively). In the experiment, monkeys reported whether their heading direction was to the right or left with respect to straight ahead. Psychometric functions for heading discrimination (second column) represent the simulated proportion of rightward heading choices as a function of true heading; they take the form of cumulative Gaussian distributions. For each psychometric curve (cue-specific), the monkey’s representation of straight ahead is estimated from the point of subjective equality (PSE, equal rightward and leftward choice probability). The third column shows the distributions over the perceived heading for each cue, in response to a particular heading stimulus. Assuming a flat Bayesian prior and that PSE represents perceptual straight ahead, the bias in the perceived heading is equal in magnitude, but opposite in sign, to the corresponding PSE: when perception is biased to the left, the subject will make excessive leftward choices, and therefore the PSE will be shifted to the right.

Figure 1. Simulations of multisensory calibration.

Two cues for heading direction were generated with a constant heading discrepancy between them (stimulus schematics, leftmost column). One cue was made more reliable (red), and the other, less reliable (blue). For each cue, psychometric plots (cumulative Gaussian functions; second column) were simulated to represent the ratio of rightward choices as a function of heading direction. Each psychometric plot’s intersection with the horizontal dashed line marks its point of subjective equality (PSE, estimate of straight ahead). Corresponding probability distributions (third column) represent the perceived heading for each cue in response to a particular heading stimulus, with biases equal in magnitude, but opposite in sign, to the PSEs. Vertical dotted lines represent accurate perception, according to external feedback. Dark colors represent pre-calibration (baseline) behavior, lighter colors, post-calibration, and the connecting horizontal arrows mark the cues’ shifts. The time-course of calibration is presented in the rightmost column, with the vertical arrows demonstrating complete calibration (corresponding to the post-calibration psychometric and probability distribution plots). (A) During unsupervised calibration, the cues shift towards one-another, achieving internal consistency. For supervised calibration: (B) According to Model 1, only the inaccurate cue is calibrated, both when it is less reliable (top, blue) and more reliable (bottom, red). (C) According to Model 2, only the combined cue is used and thus both cues are calibrated according the combined cue (green).

During unsupervised calibration (Fig. 1A), no external feedback is provided. In this case, cue accuracy is unknown and there is no externally defined “straight ahead” (no depiction of accurate perception on the axes). However, discrepant sensory cues still undergo mutual calibration towards one another (Burge et al., 2010; Zaidel et al., 2011). The simulated cue calibration is depicted by the horizontal arrows, which mark the shifts from pre-calibration (darker colored curves) to post-calibration (lighter colored curves).

Unsupervised calibration presumably occurs in order to achieve “internal consistency”, that is, agreement between the different sensors (Burge et al., 2010). Previous work has shown that the ratio by which the individual cues are calibrated is not dependent on their reliabilities, but rather may reflect the underlying internal estimate of cue accuracy (Zaidel et al., 2011) such as a ‘prior’ regarding which cue is more likely to go out of calibration (Ernst and Di Luca, 2011). Hence, in this simulation, we arbitrarily used equal cue calibration rates, and thus the cues shifted by equal amounts. We portray here complete calibration, which leads to internal consistency (equality of post-calibration PSEs). More generally, calibration could be partial, for example due to the limited duration of an experiment. In this case, the cues will have shifted towards one another but not yet converged. Partial calibration is represented by the points along the curves in the rightmost column.

During supervised calibration, a ‘straight ahead’ stimulus (zero heading) is defined for each experimental condition (leftmost schemas, Fig. 1B and C). External feedback for rightward or leftward heading choices is then given according to this reference. Since there is a cue discrepancy, only one cue is actually congruent with feedback, and therefore accurate; the other cue is offset to the side, and thus feedback indicates that it is biased (inaccurate). In response, the cues’ psychometric curves can shift to attain better accuracy. These shifts may incorporate both perceptual changes and choice related changes (discussed further below). Thus ‘calibration’ refers here, generally, to the observed PSE shifts. We consider two models: in Model 1, supervised calibration has access to each individual cue’s noisy measurement (Fig. 1B); while in Model 2, supervised calibration relies only on the combined (multisensory) cue (Fig. 1C).

If supervised calibration has full access to each individual cue’s measurement (Model 1) then only the inaccurate cue should be calibrated, irrespective of cue reliability. The already accurate cue should on average not shift at all; it can have small fluctuations due to sensory noise, but these will be limited by the low rate of calibration, and feedback will subsequently bring it back. Consequently, in the simulation, we see that when the less reliable cue is initially inaccurate (top row, Fig. 1B), it alone shifts to become accurate (dark blue to light blue curves). The already accurate cue does not shift (light and dark red curves, superimposed). Also, when the more reliable cue is inaccurate and the less reliable cue, accurate (bottom row, Fig. 1B), once again, only the inaccurate cue shifts. Cue reliability is ignored.

By contrast, if only the combined cue is used by supervised calibration (Model 2), then individual cue accuracy cannot be assessed. Hence a viable calibration strategy would be to calibrate each individual cue in accordance with the combined cue’s inaccuracy (dark green, Fig. 1C). This would result in cue yoking, i.e. calibration of both cues together in the same direction until the post-calibration combined cue (light green) is accurate. Notably, in this case, the initially accurate cue will shift away from the external feedback, becoming inaccurate post calibration (red and blue in the top and bottom rows of Fig. 1C, respectively).

The strategy of Model 2 is dependent on relative reliabilities of the cues since the combined cue itself depends on these reliabilities. Namely, the combined cue bias, and resulting shifts, will be smaller when the more reliable cue is accurate (and the less reliable, inaccurate; top row, Fig. 1C) than when the less reliable cue is accurate (and the more reliable, inaccurate; bottom row, Fig. 1C). In Figure 1C we presented two examples with specific reliability ratios, however, these need not necessarily remain fixed. Rather, Model 2 is described by iterative equations (see Suppl. Experimental Procedures) and thus depends on the combined cue at any given time. Hence it generally incorporates any dynamic changes in cue reliabilities.

The strategy of Model 1, individual cue calibration, is ideal in that it converges monotonically to the solution in which both cues are individually accurate (rightmost column, Fig. 1B). In contrast, Model 2, with yoked cue calibration, is not ideal. An accurate cue is inadvertently shifted to become less accurate. In fact, although post-calibration the combined cue is accurate, neither cue is individually accurate. If, however, the supervised calibration system only has access to the combined cue, then yoked cue calibration would be the optimal calibration strategy, given the limited information. Namely, it converges monotonically to the solution in which the combined cue is accurate (rightmost column, Fig. 1C).

To discover the actual strategy that the brain uses for supervised multisensory calibration, we now analyze the data of visual and vestibular calibration from our heading discrimination experiments. In the experiments we manipulated cue accuracy by means of external feedback, and relative cue reliability through the coherence of the visual stimulus (as in Gu et al., 2008; Fetsch et al., 2009). Accordingly, we are able to characterize supervised multisensory calibration under the different scenarios of cue accuracy and relative cue reliability.

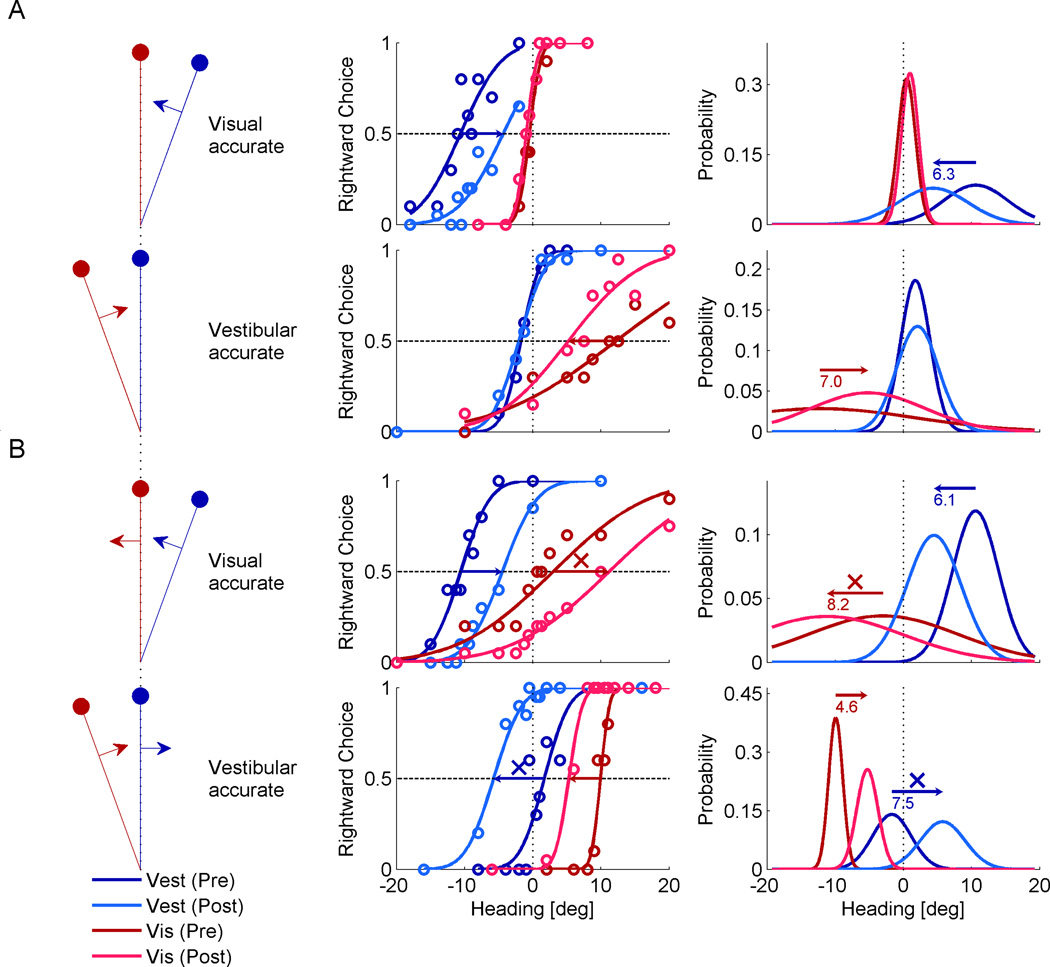
Supervised visual-vestibular calibration – examples

Four experimental sessions from one monkey are presented in Figure 2. The examples shown here all had a cue discrepancy of Δ = +10° (vestibular cue to the right; visual to the left) but results were similar, and in the opposite direction, for Δ = −10°. Here, the x-axis represents heading according to feedback. Hence, a cue which is in accordance with feedback (accurate) has a PSE of zero; and a cue which is offset from feedback experimentally, is by definition displaced on the x-axis. This manner of presentation allows visualizing which cues shift in accordance with feedback (towards 0) or away from feedback (away from 0).

Figure 2. Examples of supervised visual-vestibular calibration.

Four example sessions of supervised calibration are presented (each combination of the cues being more/less reliable and accurate/inaccurate). The heading discrepancy for all examples here was Δ = 10° (vestibular to the right of visual). Plotting conventions are similar to Figure 1, except that red colors represent the visual cue, and blue colors, the vestibular cue. Stimulus schematics (left column) indicate which of the discrepant cues was accurate (lies on vertical dotted line), according to external feedback. Psychometric data (circles, middle column) were fitted with cumulative Gaussian functions, and corresponding probability distributions were generated (right column). Horizontal arrows mark significant shifts of the cues, with the shift size in degrees presented below the arrows on the probability distribution plots. (A) When the more reliable cue was also accurate, only the other (less reliable and inaccurate cue) was calibrated. (B) When accuracy and reliability were dissociated (the less reliable cue was accurate), cue yoking was observed, i.e., both cues shifted together in the same direction. ‘X’ symbols mark shifts of the less reliable cue away from feedback, becoming less accurate.

Behavioral data (circle markers, middle column) were fit with cumulative Gaussian distributions. For each session, we measured visual (red) and vestibular (blue) calibration by the shift in the psychometric PSE from pre-calibration (darker colors) to post-calibration (lighter colors). We observe that when the visual cue was both more reliable and accurate (Fig. 2A, top row), it did not shift. However, the less reliable and inaccurate vestibular cue did. Similarly, when the vestibular cue was both more reliable and accurate (Fig. 2A, bottom row) it did not shift. However, the less reliable and inaccurate visual cue did.

By contrast, when accuracy and reliability were dissociated such that the less reliable cue was accurate and the more reliable cue inaccurate (Fig. 2B), a surprising form of calibration occurred: cues were yoked and shifted together. Specifically, when the vestibular cue was more reliable but inaccurate (top row in Fig. 2B) it was correctly calibrated to become more accurate (it shifted towards the dotted line). The less reliable and initially accurate visual cue was yoked to, and shifted in the same direction as the vestibular cue. It therefore wrongly shifted away from the external feedback, thus becoming less accurate (it shifted away from the dotted line). Similarly, when the visual cue was more reliable but inaccurate (bottom row in Fig. 2B), it was correctly calibrated to become more accurate. But the less reliable and initially accurate vestibular cue was yoked to, and shifted in the same direction as the visual cue, becoming less accurate.

Since this form of calibration caused an initially accurate cue to become inaccurate, it seems suboptimal. This latter result is particularly striking, since: i) we did not expect the less reliable cue to shift at all - it was already accurate and objectively did not need calibration. ii) If at all, one may have expected it to shift in the opposite direction – towards the more reliable cue, reducing the cue-conflict (like the barn owl; Knudsen and Knudsen, 1989a). Hence, when the less reliable cue was inaccurate, it shifted away from both feedback and the other cue!

Cue reliability and accuracy together influence multisensory calibration

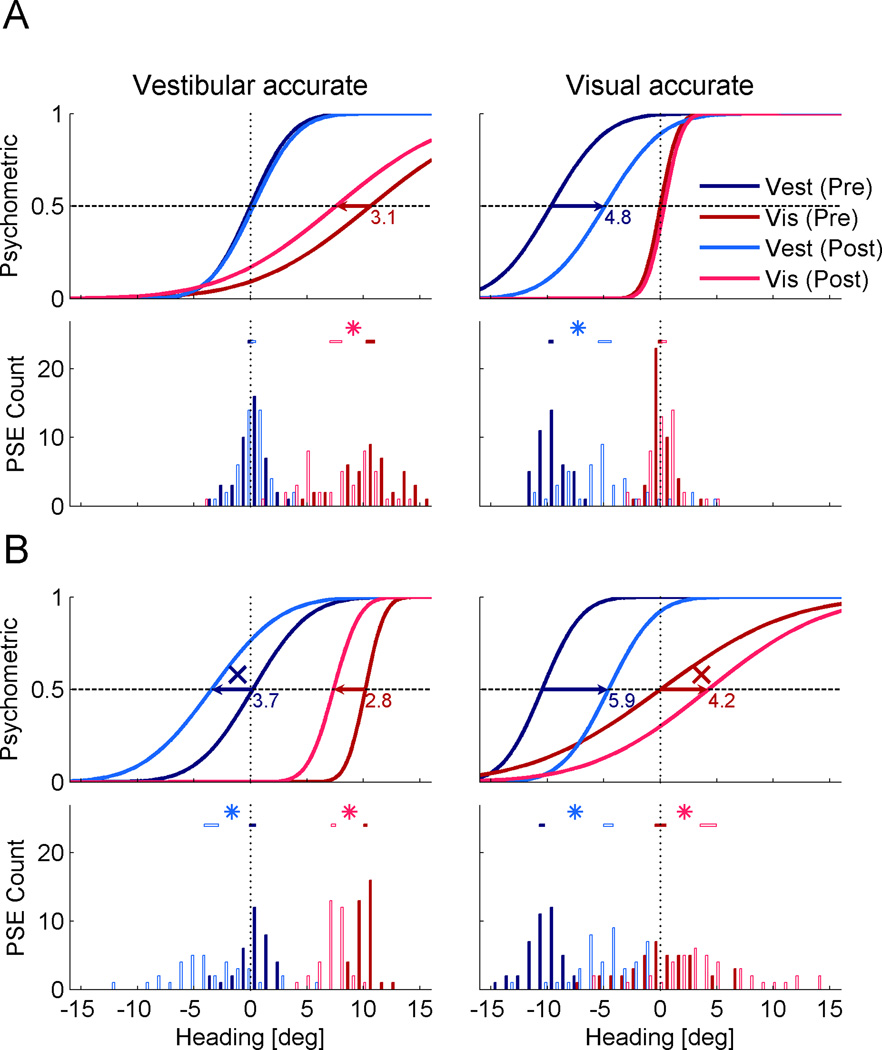
The qualitative differences observed between the examples in Figure 2A vs. 2B indicate that multisensory calibration is dependent on the configuration of cue accuracy and reliability. We now demonstrate that this ensues also at the population level. To do so, we calculated the population-averaged psychometric functions. This was done using the mean PSE and geometric mean threshold (standard deviation from the cumulative distribution fit) from all sessions of the five monkeys, in each condition. The population psychometric functions are displayed together with the PSE histograms in Figure 3.

Figure 3. Population shifts.

Population-averaged psychometric functions and PSE histograms are presented for each condition. All data are presented in the form of Δ = +10°, but also comprise data collected with Δ = −10° (the latter were flipped for pooling). Color conventions are the same as Figure 2. Significant shifts are marked by horizontal arrows on the psychometrics, and ‘*’ symbols between the PSE 95% confidence intervals (horizontal bars above the histograms). (A) When the more reliable cue was also accurate, only the other (less reliable and inaccurate cue) was calibrated. (B) When accuracy and reliability were dissociated (the less reliable cue was accurate) cue yoking was observed, i.e., both cues shifted together in the same direction. ‘X’ symbols mark shifts of the less reliable cue away from feedback, becoming less accurate. See also Supplemental Figure S1.

Here too, we observe that when the vestibular cue was both more reliable and accurate (Fig. 3A, left), only the visual cue shifted significantly. This is demonstrated by the absence of overlap between the visual pre- and post-calibration PSE 95% confidence intervals. The vestibular cue did not shift, and hence remained accurate. Similarly, when the visual cue was both more reliable and accurate (Fig. 3A, right) only the vestibular cue shifted significantly. The visual cue did not shift.

However, when external feedback was contingent on the less reliable cue, such that it was accurate, and the more reliable cue, inaccurate (Figure 3B), cue yoking was observed. Both cues shifted significantly, and in the same direction. The more reliable, but initially inaccurate, cue was correctly calibrated to become more accurate (visual cue in Fig. 3B, left and vestibular cue in Fig. 3B, right). However, the other, initially accurate but less reliable, cue was yoked to, and shifted with, the more reliable cue. Hence it wrongly shifted away from the external feedback, becoming less accurate (vestibular cue in Fig. 3B, left and visual cue in Fig. 3B, right).In the histograms (Fig. 3), the PSE distributions seem to be wider post-calibration. This probably reflects the addition of shift variability, since the actual post-calibration PSEs (not normalized to pre-calibration) are presented.

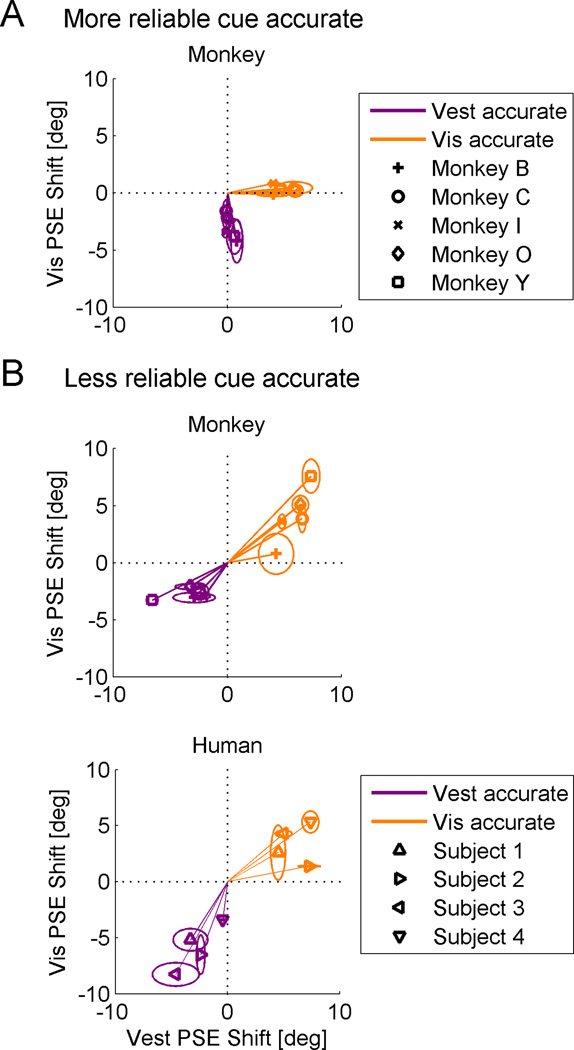
Cue shifts were then calculated for each session as the difference between the post- and pre-calibration PSEs (i.e., normalized to pre-calibration). In Figure 4 A and B (top plot) we compare the average cue shifts for each monkey, individually, across the different conditions. This demonstrates the same outcome as described above, but shows that the calibration strategy is robust and consistent across individual monkeys. For all monkeys, when the more reliable cue was accurate, it did not shift (Fig. 4A). Only the less reliable cue shifted. Hence, the data points lie along the axes. In contrast, when the less reliable cue was accurate (Fig. 4B, top plot), they do not. Rather, they indicate visual and vestibular shifts in the same direction - cue yoking (further analysis of monkey cue shifts and their dependence on reliability is presented in Suppl. Data and Fig. S1). In order to gain further insight into the phenomenon of cue yoking, we performed the same experiment in humans. Here, accuracy feedback was provided by auditory beeps and subjects were instructed to get as many trials as possible correct. We specifically tested the conditions in which we found cue yoking in the monkeys, i.e. when the less reliable cue was accurate.

Figure 4. Individual shifts.

Visual versus vestibular PSE shifts were plotted in the different conditions. Data for vestibular-accurate sessions are plotted in purple and data for visual-accurate sessions are plotted in orange. An ellipse around each data-point marks the standard error of the mean (SEM) calculated for each cue, individually. Data are presented in the form of Δ = +10°, but also comprise data collected with Δ = −10°. (A) When the more reliable cue was accurate, the data lie on the axes (dotted lines), indicating that only the inaccurate cue was calibrated. The accurate cue did not shift. (B) When the less reliable cue was accurate, the data lie in the quadrants of positive correlation, demonstrating cue yoking. Cue yoking was demonstrated for both monkeys (top plot, B) and humans (bottom plot, B).

Cue yoking in human subjects

Similar to the monkeys, humans also yoked their cues, namely the cues shifted in the same direction (as demonstrated by the location of the data in the upper right and lower left quadrants in Fig. 4B, bottom plot). Subjective reports after the experiments indicated varying levels of awareness: when the visual cue was more reliable, subjects were more aware that the feedback was ‘offset’ and reported consciously ‘correcting’ their responses in order to align them better with the feedback. When the vestibular cue was more reliable, subjects were less aware – mostly not noticing an offset (or unsure) and often postulating that post-calibration their cues were left unchanged (when in fact they were yoked).

The difference in awareness between visual more reliable versus vestibular more reliable sessions probably reflects the fact that, in the latter, the combined cue was less reliable (since only visual reliability was manipulated to control relative reliability) and thus a feedback offset was less discernible. Nonetheless, in both conditions calibration was similar and demonstrated cue yoking. Also, absence of subject awareness is not required to study calibration (e.g., in the classic visuomotor rotation, movement perturbation or prism adaptation experiments, subjects are typically also aware of the discrepancy).

Hence, while the yoked component of supervised calibration may incorporate perceptual shifts, it clearly seems to employ a cognitive or explicit strategy. This suggests that supervised calibration may utilize unique mechanisms; we address this in more depth below. From our data we are unable to quantitatively assess the extent to which remapping was perceptual versus choice related (i.e., occurred between perception and response). Disambiguating the two will require different methods, for instance magnitude estimation of heading direction. Similarly, while the supervised calibration hypotheses introduced above (Fig. 1) may imply perceptual calibration, they too can represent choice related calibration (also characterized by PSE shifts). The only difference would relate to the calibration rates (see Suppl. Experimental Procedures): for perceptual calibration, each cue shifts at its own rate; whereas for choice related calibration, the same rate should be expected for both cues. In our data, the vestibular cue demonstrates a significantly higher PSE shift rate vs. visual (see Suppl. Data). This seems to imply presence of perceptual calibration. However, in general, the PSE shifts in both the data and the models can represent perceptual shifts, choice related shifts, or a combination thereof. We now compare the monkey data to the models, in order to gain insight into what information is used during supervised calibration. We begin with a qualitative comparison, and continue thereafter with a quantitative model fit.

Yoked versus individual cue calibration models

When the less reliable cue was accurate, the data clearly demonstrate cue yoking (Figs. 2B, 3B and 4B). Therefore, the model of supervised individual cue calibration (Model 1, Fig 1B; which calls for calibration of only the inaccurate cue) does not seem feasible. However, also yoked cue calibration (Model 2, Fig. 1C) does not completely explain the results: i) according to Model 2, the cues should always shift in the same direction, by a proportional amount. This is not what we see (Fig. 4A). ii) It does not explain why, when the more reliable cue is accurate, we see a shift only for the other, inaccurate, cue (Model 2 predicts a significant shift for both cues). iii) Lastly, according to Model 2, both cues should shift more when the less reliable cue is accurate. However, the inaccurate cue seems to shift by roughly the same amount, regardless of reliability (Suppl. Fig. S1).

Therefore, neither Model 1 nor Model 2 accounts well for all the data. An initial impression is that when the more reliable cue was accurate, Model 1 best describes the data; whereas when the less reliable cue was accurate, Model 2 works best. It is possible to model these two scenarios separately. Accordingly, there could be a switching mechanism that chooses the appropriate strategy (Model 1 or Model 2) by context. However, a unifying model that can apply the same rules and explain the behavior for both would remove the need to infer context and select between multiple strategies. It would thus be more parsimonious.

To attain a more comprehensive theory for multisensory calibration, we need to address why cue yoking, as predicted by Model 2, is demonstrated at all. Namely, why (and when) would the combined cue be used for calibration? Ernst and Di Luca (2011) recently proposed a model for unsupervised calibration in which cues are calibrated towards one another according to the extent that they are not integrated. Namely, non-integrated cues will have a large discrepancy between their posterior estimates and thus calibrate at a faster rate than highly integrated cues. Their model allows for the whole range of integration (from segregation to complete integration). However, we find that a very high degree of integration is required in order to achieve calibration rates sufficiently low to account for our unsupervised calibration data (see Suppl. Experimental Procedures, and simulation results below). By extension, supervised calibration may thus also rely on the highly integrated cues, as proposed by Model 2.

Recently, Prsa et al. (2012) found that during rotational self-motion mainly the combined cue is relied upon for perceptual judgments. Based on this and the human reports of using an explicit strategy (above), we propose that Model 2 represents a more explicit, or conscious, component of supervised multisensory calibration. Accordingly, during supervised calibration, a highly integrated percept is used for comparison to external feedback, and thus cues are yoked in an effort to achieve external accuracy.

Interestingly, recent studies of visuomotor adaptation have also described the effects of an explicit strategy, and propose that it is superimposed on implicit adaptation (Mazzoni and Krakauer, 2006; Taylor and Ivry, 2011). In these studies, subjects were instructed, in a pointing task, to counter an introduced 45° visuomotor rotation using an explicit cognitive strategy – by moving to a marker located 45° away from the target. With this strategy, subjects were initially error-free. However, as training continued, the subjects progressively increased their offset, such that they were making errors (miscalibrated). The authors propose that this drift arises from superimposing implicit adaptation on the explicit strategy. Thus, Model 2 may represent only one aspect of multisensory calibration – a more explicit, supervised component. Perhaps, like in sensorimotor adaptation, here too there is a more implicit form of calibration simultaneously taking place - one that is not comparing external feedback to overt perception, but rather implicitly comparing the cues to one another.

We have already described a mechanism of unsupervised calibration for maintaining internal consistency (Zaidel et al., 2011). Thus it seems plausible to superimpose that component onto the supervised component from Model 2. This brings us to Model 3: a hybrid between yoked calibration for external accuracy (Model 2, supervised) and individual cue calibration for internal consistency (unsupervised). Note that this is not a hybrid of Models 1 and 2; but rather a hybrid of supervised (Model 2) and unsupervised calibration. Incorporating both components of supervised and unsupervised calibration, Model 3 has the potential to be a comprehensive framework for multisensory calibration. But does Model 3 account for the actual behavior observed in our data, in all the different conditions of cue accuracy and reliability?

Model 3: Simultaneous external-accuracy and internal-consistency calibration

We propose here a model in which supervised cue calibration for external accuracy, achieved by cue yoking, is superimposed with unsupervised cue calibration, for internal consistency. Although it may take a seemingly sub-optimal path (discussed further below), this hybrid model will ultimately converge on the externally accurate solution. Namely, only the inaccurate cue will have shifted to become accurate. Since, once the combined cue is externally accurate and the individual cues are internally consistent, both cues must also be externally accurate.

Since Model 3 converges on external accuracy, its endpoint is indistinguishable from Model 1. Both converge on the optimal solution. However, the route they take will be different. In Model 3, unlike in Model 1, the accurate cue will temporarily shift away from accuracy. Our data, presented above, represent the PSE-shift after 500 calibration trials and represent multisensory calibration after a finite number of trials. Hence they can expose this suboptimal shift and thus provide a widow into the mechanisms of multisensory calibration.

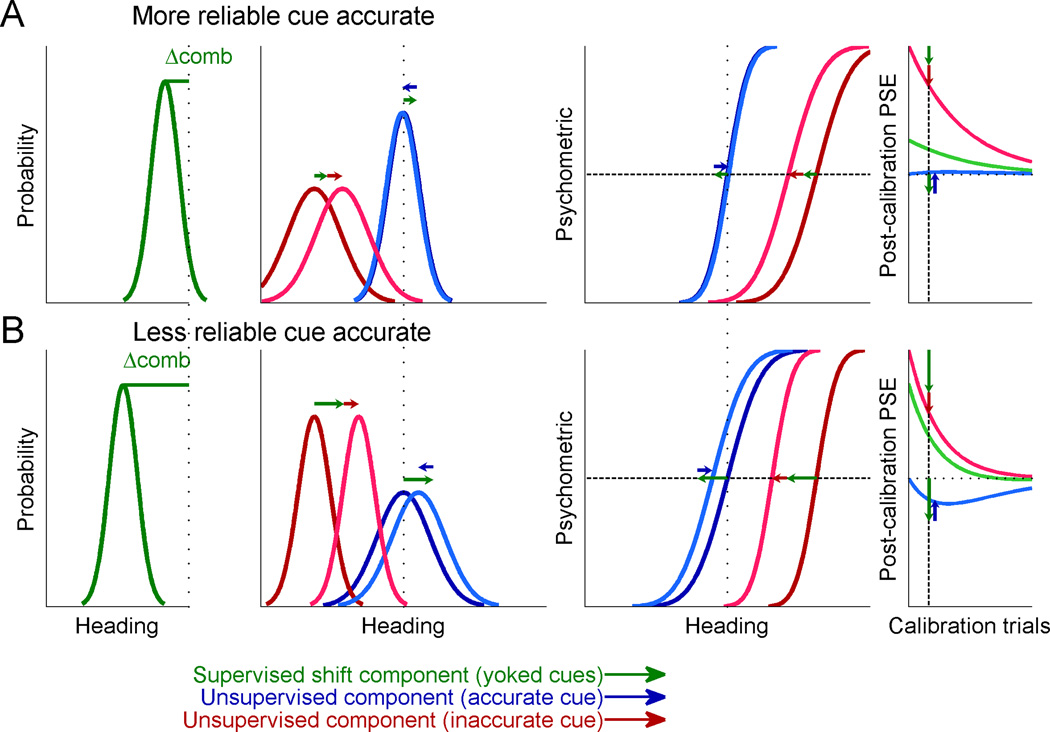
We present Model 3 in Figure 5. The post-calibration plots depicted are after 500 calibration trials (like the experiment) and thus represent partial calibration. Each cue shift is comprised of two components: the supervised, yoked, component (green arrows) and the unsupervised, individual, component (blue and red arrows for the accurate and inaccurate cue, respectively). The yoked component of the cues is always in the same direction, whereas the individual components are in opposite directions. The yoked and individual components for the inaccurate cue are always in the same direction and will therefore sum up. By contrast, the yoked and individual components for the accurate cue are always in opposite directions and will thus partially or fully cancel out. The extent of cancelling out depends on the components’ magnitudes.

Figure 5. Model 3 simulation.

Two cues for heading direction were generated with a constant heading discrepancy between them, and calibration was simulated according to Model 3. Pre-calibration, one cue was accurate (blue), and the other, biased (red) in relation to external feedback. Psychometric plots and probability density functions were generated similar to Figure 1. But here, post-calibration plots represent partial calibration, as depicted by the vertical dashed lines and arrows in the time-course plots (rightmost column). Green arrows represent the supervised, yoked, component, and blue and red arrows (for the accurate and inaccurate cue, respectively) represent the unsupervised, individual, component. (A) When the accurate cue was also more reliable, the combined cue bias was small (Δcomb; left column) and hence the yoked component was small. In total this resulted in a shift of the inaccurate but not accurate cue. (B) When accuracy and reliability were dissociated, the combined cue bias was large and hence the yoked component was dominant. This resulted in a shift of the accurate cue together with the inaccurate cue.

When the accurate cue is more reliable, the yoked component is small and thus more easily cancelled out by the individual cue component (blue probability density and psychometric curves in Fig 5A). However, when the accurate cue is less reliable, the yoked component will be larger and thus likely be dominant (blue curves in Fig. 5B). In contrast, the components of the inaccurate cue are summed in both cases, and thus the inaccurate cue will always shift to improve accuracy (red curves in Fig. 5A and B).

The rightmost column of Figure 5 demonstrates the post-calibration PSE as a function of calibration trials for the model. The vertical dashed line marks 500 trials, as used to collect data in this study, and used to create the post-calibration probability density and psychometric plots in this figure. It can be seen that if calibration is run for a long time, cues will ultimately reach external accuracy (curves asymptote to the horizontal dotted line, which marks accurate performance, according to external feedback). Also, Model 3 still captures the cue yoking observed in the data for the case in which the less reliable cue is accurate (Fig. 5B). But, when the more reliable cue is accurate, no cue yoking is observed (Fig. 5A), like in the data.

Model 4: Extended Ernst and Di Luca model

Extending the Ernst and Di Luca (2011) model to include external feedback in a manner consistent with their model (i.e., on the integrated ‘posterior’ cue) provides a model strikingly similar to Model 3. We call this Model 4 (see Suppl. Experimental Procedures). It too comprises an unsupervised term (according to their standard model) in addition to a supervised term which relies on the highly integrated cues. Thus Model 3 may represent a simplified subspace of Model 4, apart from a few small differences (one relating to unsupervised calibration; discussed further below).

Model comparison

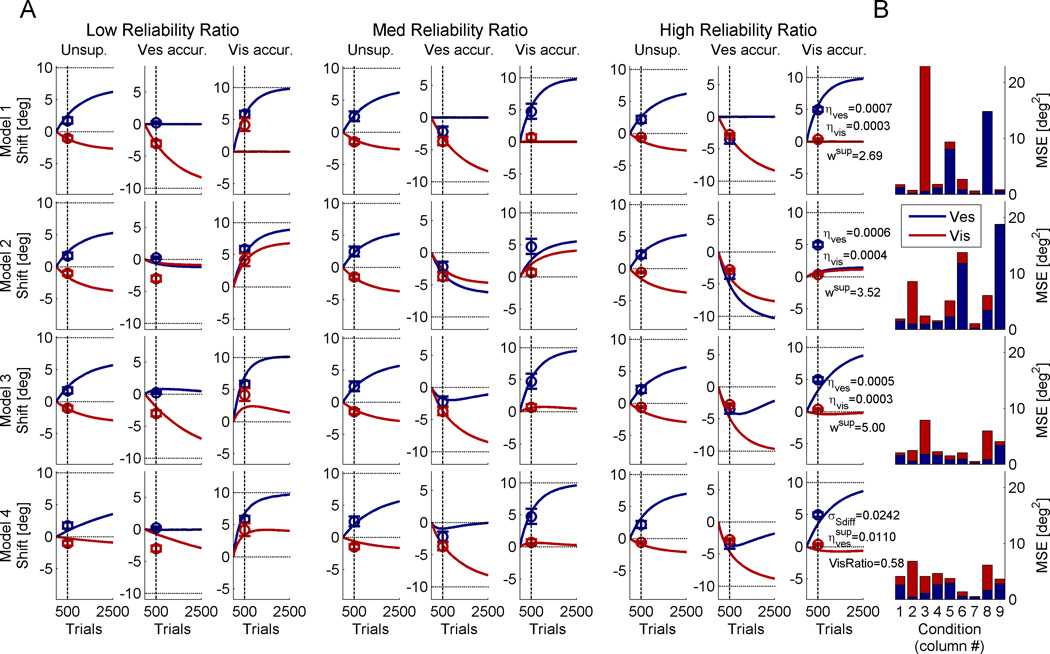
Figure 6 presents the model fits for all four models, averaged across monkeys. The models were fit at 500 calibration trials (vertical dashed lines, in accordance with data collection) but allowed to run for longer in order to see the extended dynamics of the models. Figure 6A shows the data (circle markers) and model predictions (solid curves) for each of the different conditions. While in the previous analyses and figures we focused on supervised calibration at the extremities (low and high reliability ratio), here, all conditions are presented, including the medium reliability ratio data and unsupervised calibration data (Zaidel et al., 2011). We note that also for the medium reliability ratio data, supervised calibration causes yoking, but to a lesser degree (vestibular cue in column 5 and visual cue in column 6).

Figure 6. Example model fit.

Circles mark the average visual and vestibular shifts and error bars represent the SEM (red and blue, respectively; in column 8, the blue circles are partially occluded by the red circles). The data were grouped (from left to right) by low, medium and high visual to vestibular reliability ratios. Each group comprises three columns which depict (from left to right) unsupervised calibration, vestibular accurate (supervised calibration), and visual accurate (supervised calibration). Solid curves represent the model simulations as a function of calibration trials, which were fit simultaneously to all the data at 500 trials (vertical dashed lines). Horizontal dotted lines mark the externally accurate solution. The model fit parameters are presented in column 9. (B) The model fits were assessed by the mean squared error (MSE) between the model simulations and the data, for each condition (red and blue, for visual and vestibular errors respectively). See also Supplemental Figures S2 and S3 for Model 3 and 4 fits for all monkeys.

As shown in Figure 6B, Models 3 and 4 produced the lowest mean squared errors between the model predictions and the data. To better understand the models’ performance, we now analyze them one at a time: In Model 1 (top row) the inaccurate cue shifts, and the accurate cue remains unchanged. Although Model 1 converges on the externally accurate solution (horizontal dotted lines), it does not account well for the data. This is especially evident when the less reliable cue is accurate and cue yoking is observed (columns 3 and 8; Figs. 6A and B). By definition, Model 1 cannot account for cue yoking. Model 2 (second row) displays cue yoking but also performs poorly, especially when cue yoking is not observed in the data (columns 2 and 9; Figs. 6A and B). It cannot account for both situations in which cues are and are not yoked, and hence results in large errors.

For Models 3 and 4, when the more reliable cue is accurate, only the inaccurate cue shifts (columns 2 and 9; Figs. 6A and B). But when the less reliable cue is accurate, cue yoking takes place (columns 3 and 8; Figs. 6A and B). Both Models 3 and 4 indicate that cue yoking is transient, and thus, the cues will ultimately converge on the externally accurate solution. We cannot test this latter hypothesis in our data due to the limited number of calibration trials and the unfeasibility of greatly extending this. However, support for this model can be found in the recent sensorimotor adaptation study by Taylor and Ivry (2011), which similarly showed miscalibration due to superimposed explicit and implicit components, and indeed found that increasing the number of adaptation trials reduced the miscalibration. Future validation of this predicted time-course is required. Model 3 and 4 fits for all the monkeys, individually, are presented in Supplemental Figures S2 and S3, respectively.

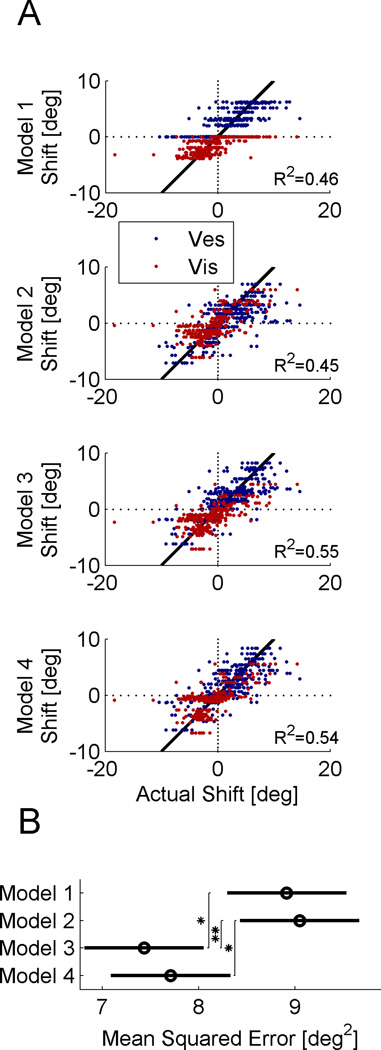
Figure 7 presents a model comparison summary for all the data (a total of 328 sessions from the 5 monkeys). Scatter plots of the model-predicted visual and vestibular shifts (red and blue, respectively) vs. the actual shifts are shown in Figure 7A. For a perfect model, the data points would lie along the diagonal black lines. Models 3 and 4 provide better data fits than Models 1 and 2, having higher R² values (see plot), which measures the fit to the diagonal. To compare the models statistically, we calculated the mean squared error across all the data (Fig. 7B). A 2-way ANOVA showed that the models are significantly different (p=0.0006).

Figure 7. Model fit comparison.

(A) Scatter plots demonstrate the model predicted vs. actual cue shifts (red and blue for visual and vestibular, respectively). The diagonal is marked by a solid black line, and represents a perfect model fit. R² values indicate the data fit to the diagonal. (B) Circles and horizontal bars mark the mean squared error and the Tukey-Kramer 95% confidence intervals, respectively (‘*’ indicates p<0.05; ‘**’ indicates p<0.01).

Using Tukey's honestly significant difference criterion, we found that Model 3 has a significantly smaller mean squared error than both Models 1 and 2 (p=0.012 and p=0.005, respectively). Model 4 was significantly better than Model 2 (p=0.028) and better than Model 1, but the latter did not reach our criterion for significance (p=0.060). These comparisons were made across all the data (according to the way the models were fit). However, if we were to compare only the supervised calibration fits, then Model 4 does do significantly better than both Models 1 and 2 (p=0.016 and p=0.008, respectively). Thus we attribute the lack of significance between Model 4 and Model 1 to the fact that Model 4 performs worse than the other models for unsupervised calibration (see Fig. 6B; specifically columns 1 and 4). This may relate to the fact that Model 4 (unlike Models 1–3) predicts that the unsupervised rate of calibration depends on the cue reliabilities (see Suppl. Experimental Procedures) whereas our unsupervised calibration data (fitted here) do not demonstrate that dependence (Zaidel et al., 2011). However, this may depend on task or species, since Burge et al. (2008) did find a dependence between reliability and the calibration rate of human reaching movements.

Finally, replacing Model 3 with a slightly different formulation, in line with choice related, as opposed to perceptual shifts (see Suppl. Experimental Procedures) resulted in performance and data fits indistinguishable from the standard Model 3 (mean squared error 7.44 ± 0.63 deg² vs. 7.43 ± 0.62 deg² for the standard Model 3; the latter presented in Fig. 7B). Thus, the extent to which supervised calibration is perceptual vs. choice related represents an interesting question for future studies.

DISCUSSION

In this study, we showed that supervised multisensory calibration is highly dependent on both cue accuracy and relative cue reliability. Through a seemingly suboptimal behavior, we were able to gain a better understanding of the underlying mechanisms of multisensory calibration. Specifically, our data indicate that in response to external feedback, supervised multisensory calibration relies only on the combined (multisensory) cue. These results seem to be in line with Prsa et al. (2012) who found that mainly the combined cue is relied upon for perceptual judgments during rotational self-motion. Our results do not require mandatory cue fusion; but rather indicate that the explicitly available combined cue is used during supervised calibration.

In contrast, during unsupervised multisensory calibration, which arises due to a cue discrepancy, cues are calibrated in opposite directions, towards one another (Burge et al., 2010; Zaidel et al., 2011). Individual cue calibration would not be possible without the ability to access the cues individually. Hence, for unsupervised calibration, individual visual and vestibular information is utilized. This seems to agree with Hillis et al. (2002) who showed that single cue information is not lost when different modalities are integrated. However, here (for self-motion perception) single cue information may only be available implicitly (Prsa et al., 2012). Together, these findings suggest more explicit vs. implicit mechanisms for supervised and unsupervised calibration, respectively. Also, they might indicate that the neural mechanisms of supervised and unsupervised calibration tap into different sensory representations (discussed further below).

In the supervised calibration experiments performed in this study, we manipulated cue accuracy through external feedback (and relative reliability) in the presence of a cue discrepancy. Modeling an unsupervised component (with access to the individual cues) superimposed on a supervised component (which relies only on the combined cue) best described the behavior. That individual cue information is used here for the unsupervised, but not supervised, component of multisensory calibration may stem from their different time-courses, and levels of processing. Unsupervised calibration arises from simultaneously presented, discrepant, cues. In contrast, supervised calibration relies on task feedback after the trial. Adams et al. (2010) showed that delayed and intermittent perceptual feedback is more important and efficient for multisensory calibration than continuous feedback. Our results of stronger supervised calibration are in line with this, and indicate that only the combined cue percept is used after the trial, perhaps highlighting a limitation of the brain. The more implicit process of unsupervised calibration may be slower and less efficient than supervised calibration, but it is able to compare cues to one another, probably due to their simultaneity.

We therefore suggest that unsupervised, and supervised, calibration differ in their purpose, mechanisms, and the information they utilize. The goal of unsupervised calibration is ‘internal consistency’. It achieves this by simultaneously comparing the cues to one another and calibrating them individually. By contrast, the goal of supervised calibration is ‘external accuracy’. It compares the combined cue percept to feedback from the environment, but lacks cue specific information. It therefore calibrates the underlying cues together (yoked) according to the combined cue error. Interestingly, it has been proposed that absence of multisensory integration during development may be to allow calibration of the sensory systems (Gori et al., 2012). This emphasizes the importance of this process, and also indicates that, with less cue integration, children may calibrate differently (perhaps better) in response to external feedback.

While unsupervised calibration is more implicit and thus likely to be perceptual, the supervised component seems to employ a more explicit mechanism. From our data and models we were unable to quantitatively assess how much of the supervised calibration was perceptual versus choice related. It is possible, for example, that supervised calibration targets the mapping between perception and action. This may explain why we found two different mechanisms, superimposed. This question provides an interesting next step, which should be addressed in future studies.

In combination, these two mechanisms of calibration (yoked calibration for external accuracy and individual cue calibration for internal consistency) can ultimately achieve external accuracy also for the individual cues. But the route to this ideal steady state may seem suboptimal. Adams et al. (2001) observed calibration of the inaccurate (but, in the context of their study, presumably more reliable) disparity cue. They say that the (presumably less reliable) texture cue remained accurate. However, the latter was not shown quantitatively, and calibration occurred over the course of days. Thus we do not know what happened to the less reliable cue in the short term. In our paradigm (<1 hour of calibration) we found cue yoking of the less reliable, to the more reliable cue. Our hybrid model is consistent with both results: it predicts cue yoking for the short term but convergence on the optimal solution after prolonged calibration. Hence, a strong characteristic of this hybrid model is suboptimal shifts after partial calibration, but optimal shifts eventually.

We find support for our proposal of two superimposed multisensory calibration mechanisms from recent studies of sensorimotor adaptation, which also describe separate perceptual and task-dependent components (Simani et al., 2007; Haith et al., 2008) and superimposed explicit and implicit mechanisms of adaptation (Mazzoni and Krakauer, 2006; Taylor and Ivry, 2011). Strikingly they too can cause miscalibration, which is reduced after longer adaptation (Mazzoni and Krakauer, 2006; Taylor and Ivry, 2011). Hence, although we focus here on multisensory calibration, this result is broad and spans multiple disciplines.

Unlike Adams et al. (2001), although long-term prism exposure in barn owls did achieve internal consistency, it did not achieve external accuracy - owls continued to make large errors even after months of continuous prism experience (Knudsen and Knudsen, 1989a; 1989b). Knudsen and Knudsen themselves determined that their results may reflect differences in species. Primates are capable of utilizing more complex (possibly cognitive and/or sensory) mechanisms. Also amphibians may be incapable of broad recalibration, since physical rotation of the eye by 180° or contralateral transplantation (after nerve regeneration) resulted in response behaviors that were opposite in direction to normal animals (Sperry, 1945).

When comparing the hybrid Model 3 to our data, it provided a significantly better fit than the non-hybrid models of multisensory calibration. Furthermore, it comprehensively accounts for multisensory calibration whether supervised or unsupervised (for the latter, the supervised term simply falls away) and for the different conditions of cue accuracy and reliability. The extended Ernst and Di Luca model (Model 4) was also a supervised-unsupervised hybrid, and similar to Model 3, converged on a solution whereby supervised calibration relies on a highly integrated percept. Thus Models 3 and 4 were very similar in concept and performance. Here, Model 3 performed marginally better due to its better account of our unsupervised data (Zaidel et al., 2011).

Heading perception involves several multisensory cortical regions, such as the dorsal medial superior temporal (MSTd), ventral intraparietal (VIP) and visual posterior sylvian (VPS) areas (Bremmer et al., 2002; Page and Duffy, 2003; Chen et al., 2011). Thus, the effects of multisensory calibration are likely to be evident cortically. But the mechanisms of calibration may also engage subcortical regions, such as the cerebellum and basal ganglia, both renowned for their roles in adaptation and learning (Raymond et al., 1996; Graybiel, 2005). Although traditionally associated with motor control, the cerebellum and basal ganglia are now believed to also be involved in non-motor tasks, including sensory processing and perceptual discrimination (Gao et al., 1996; Lee et al., 2005; Nagano-Saito et al., 2012) and they have been proposed to specialize in supervised, and reinforcement learning, respectively (Doya, 2000). Since “correct” feedback may be rewarding, they are both good candidates to mediate supervised multisensory calibration.

In conclusion, we presented here a first comprehensive analysis of multisensory calibration during manipulations of both cue reliability and accuracy. Our results indicate that two mechanisms of calibration work in parallel: unsupervised calibration has access to, and calibrates cues individually; whereas supervised calibration relies only on the combined cue, resulting in cue yoking. In combination, they could ultimately achieve the optimal solution of both internal consistency and external accuracy.

EXPERIMENTAL PROCEDURES

Details of the apparatus, stimuli and basic task design, previously published (Gu et al., 2008; Fetsch et al., 2009; Zaidel et al., 2011), are briefly summarized below together with the methods specific for this study. For further details please see the previous publications. For details of the models and human experimental methods please see Supplemental Experimental Procedures. The human study was approved by the internal review board at Baylor College of Medicine and subjects signed informed consent.

Monkeys and experiment protocol

Five male rhesus monkeys (Macaca mulatta) participated in the study. All procedures were approved by the Animal Studies Committee at Washington University, Saint Louis, MO (where the study began) and Baylor College of Medicine. Monkeys were head fixed and seated in a primate chair that was anchored to a motion platform (6DOF2000E; Moog, East Aurora, NY). Also mounted on the platform were a stereoscopic projector (Mirage 2000; Christie Digital Systems, Cypress, CA), a rear-projection screen and a magnetic field coil (CNC Engineering, Enfield, CT) for measuring eye movements (Judge et al., 1980). The projection screen (60 × 60 cm) was located ~30 cm in front of the eyes, subtending a visual angle of ~90° × 90°. Monkeys wore custom stereo glasses made from Wratten filters (red #29 and green #61, Kodak), which enabled rendering of the visual stimulus in three dimensions as red-green anaglyphs.

The monkeys’ task was to discriminate heading direction (two-alternative forced choice, right or left of straight ahead), after presentation of a single-interval stimulus. The monkeys were required to fixate on a central target during the stimulus, and then report their choice by making a saccade to one of two choice targets (right/left) illuminated at the end of the trial. The stimulus presented was either vestibular-only, visual-only or simultaneously combined vestibular and visual stimuli. The stimulus velocity followed a 4-sigma Gaussian profile with duration 1s and total displacement 13cm. Peak velocity was 0.35 m/s and peak acceleration was 1.4 m/s². Ten heading-directions were tested: five to each side. Heading angles were varied in small, logarithmically spaced, steps around straight ahead, and presented using the method of constant stimuli.

The optic flow simulated self-motion of the monkey through a random-dot cloud. Visual cue reliability was varied by manipulating the motion coherence of the optic flow pattern, i.e., percentage of dots moving coherently. Three levels of coherence were used: high (100% coherence), medium and low. Medium and low coherence values were monkey specific – determined such that the monkey’s visual threshold was comparable to and larger than his vestibular threshold, respectively. Vestibular reliability was fixed throughout the trials. For each session, the actual reliability ratio of the visual/vestibular cues, extracted from the data, was used for analysis (see section Data analysis below). Combined cue reliabilities were similar to those predicted theoretically by the individual cues (Suppl. Fig. S4).

At the end of a trial, monkeys were rewarded for a correct heading selection with a portion of water or juice. This provided the monkey with external feedback regarding cue accuracy. We assume that the monkey related to the feedback as accurate, insomuch as they needed to calibrate themselves to it. Hence a cue aligned to external feedback was considered externally accurate. Reward strategy thus provided the means to control cue accuracy. However, it had to be manipulated carefully in order not to interfere with the calibration, as described in detail below. Each experimental session comprised three consecutive blocks: pre-calibration, calibration and post-calibration:

The pre-calibration block comprised visual-only/vestibular-only/combined cues, interleaved. For some sessions the combined stimulus was excluded. The monkey was rewarded for correct choices 95% of the time and not rewarded for incorrect choices. The 95% correct reward rate was used in order to accustom the monkey to not getting rewarded all of the time, as was the case in the post-calibration block described below. This block was used to deduce the baseline bias and individual reliability (psychometric curve) of each modality for the monkeys. It comprised: 10 repetitions × 3 stimuli (visual-only/vestibular-only/combined) × 10 heading angles = 300 trials. When the combined stimulus was excluded, the block comprised 200 trials.

In the calibration block, only combined visual-vestibular cues were presented. A discrepancy of Δ = ±10° was introduced between the visual and vestibular cues for the entire duration of the block. The sign of Δ indicated the orientation of discrepancy: positive Δ represented an offset of the vestibular cue to the right and visual cue to the left; negative Δ indicated the reverse. During this block, reward was consistently contingent on one of the cues (visual or vestibular). The reward-contingent cue was considered externally accurate; the other, inaccurate. Only one discrepancy orientation (Δ) and reward contingency was used per session. This block typically comprised: 50 repetitions × 10 heading angles = 500 trials. The majority of sessions (75%) had 500 calibration trials exactly. Some sessions (25%) had more or less than 500 calibration trials (within ±100). No differences were noted for these data, and they were included with the rest.

During the post-calibration block, a shift of the individual (visual/vestibular) cues was measured by single-cue trials, interleaved with the combined-cue trials (with Δ = ±10° as in the calibration block). The combined-cue trials were run in the same way as in the calibration block. They were included in order to retain calibration, whilst it was measured. The probability of reward for single-cue trials worked slightly differently to the pre-calibration block, in order not to perturb the calibration: When the single-cue trial was at a heading angle, such that if it were a combined-cue trial the other modality would be to the same direction (right/left), the monkey was rewarded as in the pre-calibration block (95% probability reward for correct choices; no reward for incorrect). If however, the other modality would have been to the opposite side, a reward was given probabilistically (70%, no matter what the choice). This value was chosen since it roughly represents the correct choice rate in a normal heading discrimination task. This block typically comprised: 20 repetitions × 3 stimuli (visual-only/vestibular-only/combined) × 10 heading angles = 600 trials. At least 10 repetitions were required in this block for the session to be included in the study.

A typical session comprised ~1400 trials (~2.5 hours in total) and was run at high, medium or low coherence, with either positive/negative delta, and with either the visual or vestibular cue accurate. Unsupervised calibration data (from Zaidel et al., 2011) was also used in this study. These data were available for four of the five monkeys. Monkey I did not have unsupervised calibration data since he was not part of the previous study. In total N=328 experimental sessions from the five monkeys were analyzed in this study (116 vestibular accurate, supervised calibration; 102 visual accurate, supervised calibration; 110 unsupervised calibration). Data were sorted by low, medium and high visual to vestibular reliability ratio (RR) using the actual cue thresholds (see section Data analysis below), resulting in 121, 87 and 120 low, medium and high RR sessions, respectively.

Data analysis

Data analysis was performed with custom software using Matlab R2011b (The MathWorks, Natick, MA) and the psignifit toolbox for Matlab (version 2.5.6; Wichmann and Hill, 2001). Psychometric plots were defined as the proportion of rightward choices as a function of heading angle, and calculated by fitting the data with a cumulative Gaussian distribution function. For each experimental session, separate psychometric functions were constructed for visual and vestibular cues pre- and post-calibration. The psychophysical threshold and point of subjective equality (PSE) were the standard deviation (SD, σ) and mean (μ), respectively, deduced from the fitted distribution function. The PSE represents the heading angle of equal right/left choice proportion, i.e., perceived straight ahead, also known as the bias.

Visual/vestibular calibration was measured as the difference between the pre- and post-calibration PSEs. Post-calibration, the combined cue consisted of discrepant visual and vestibular stimuli (like during the calibration itself – see experiment protocol above). Hence it was different to the combined cue pre-calibration, which consisted of non-discrepant stimuli. This prohibited comparison between the pre- and post-calibration combined cue PSEs.

For 4 out of 656 monkey post-calibration psychometric functions (and 3 out of the 32, human) there was only one data-point that was not zero or one (there were none with only zeros and ones). This resulted from a large PSE shift to a region where the function was sparsely sampled. For these psychometric functions, it was difficult to determine the SD of the cumulative Gaussian fit. Hence, the pre-calibration SD was used as a Bayesian ‘prior’ for fitting the post-calibration psychometric function. The ‘prior’ was a raised cosine function which touched 0 at the 95% confidence limits of the pre-calibration SD.

The reliability ratio (RR) was defined as the ratio of visual to vestibular reliability and calculated for each session individually. Cue reliability was computed by taking the inverse of the threshold squared, using the geometric mean of the pre- and post-calibration thresholds extracted from the fitted psychometric curves. The data were divided into three RRs: low-RR (RR ≤ 2.5⁻¹), med-RR (2.5⁻¹< RR < 2.5) and high-RR (RR ≥ 2.5). For the human data we used slightly more relaxed boundaries of 2 and 2⁻¹. Since behavioral performance could change over time due to a ‘practice’ effect, we did not assume that RRs were equal across sessions with the same coherence. We therefore calculated the RR for each session individually.

For many analyses in the paper, we grouped the data by i) more reliable cue accurate and ii) less reliable cue accurate. The former comprise sessions of low-RR with vestibular accurate and high-RR with visual accurate. The latter comprise sessions of low-RR with visual accurate and high-RR with vestibular accurate.