Promises and limitations of hitchhiking mapping

Abstract

Building the connection between genetic and phenotypic variation is an important ‘work in progress’, and one that will enable proactive diagnosis and treatment in medicine, promote development of environment-targeted varieties in agriculture, and clarify the limits of species adaptation to changing environments in conservation. Quantitative trait loci (QTL) mapping and genome wide association (GWA) studies have recently been allied to an additional focus on ‘hitchhiking’ (HH) mapping — using changes in allele frequency due to artificial or natural selection. This older technique has been popularized by the falling costs of high throughput sequencing. Initial HH-resequensing experiments seem to have found many thousands of polymorphisms responding to selection. We argue that this interpretation appears too optimistic, and that the data might in fact be more consistent with dozens, rather than thousands, of loci under selection. We propose several developments required for sensible data analyses that will fully realize the great power of the HH technique, and outline ways of moving forward.

From QTL to hitchhiking mapping

Heritable differences among individuals are abundant in almost all populations and for nearly any phenotype. What kinds of genetic variants underlie this variation? What kinds of genes harbor these variants, and how are their effects linked to phenotype? Efforts to answer these questions date back to the early 20th century [1], and they became mainstream in quantitative genetics after [2] popularized the use of molecular markers. Thousands of QTL mapping projects have contributed superb advances. We now know that genes with major-effect mutations on a phenotype also harbor natural alleles with more moderate effects. We also have a reasonably good idea about the distribution of effects sizes for these mutations, and their role in new or fluctuating environments [3].

Major limitations of QTL mapping have also become clear [4]. These experiments are very tedious and labor intensive, as they require developing, genotyping, and maintaining hundreds of recombinant inbred genotypes or accessions. Because of this limitation, the precision of mapping is frequently limited to large regions of chromosomes rather than individual genes. The majority of experiments have ample ability to roughly map larger-effect QTLs. However, power for identifying alleles contributing to the phenotypic variation in more modest, though still sizable way, is substantially less impressive. Whenever a modest-effect allele is discovered, its contribution is typically overestimated (the so-called “winners’ curse” [5]). Some limitations have been overcome in simpler models, like yeast [6], but others persist. QTL analysis typically starts from crosses of two, or just a few accessions, thus most of natural variation remains untapped. Phenotypes are sometimes scored in individuals that are largely homozygous, thus causing concerns about effects of life history and behavioral phenotypes that strongly depend on inbreeding. Most of all, the task of moving from a large region to a causal polymorphism remains daunting in most systems.

Recently, an alternative mapping technique–to follow frequency changes at marker loci in selected populations– has been gaining popularity. It originally stems from the experiments of Dumouchel and Anderson [7] and Garnett and Falconer [8], and theoretical treatments of Thomson [9] and Thoday [10], but was first formalized as a mapping approach by Lebowitz et al. [11]. The idea is that selection changes the frequencies of molecular markers because they hitchhike (HH) with alleles of QTLs of the selected trait [12••], allowing inference of the linkage between the markers and QTLs. This is a very powerful approach, as QTLs with relatively small effects can be detected by genotyping a manageably small number of individuals. Initial experiments had involved crossing two accessions and applying multi-generation selection to their progeny [13,14]; these were then extended to mapping populations originating from a large number of isogenic founders [15] in Drosophila [13,16] and mice [14,17]. Those same ideas are applicable to any population under artificial selection, as long as a linkage map is available. Unlike QTL mapping, the technique is applicable to organisms in which controlled crosses are difficult to implement. Additionally, individuals remain largely heterozygous in the multi-founder case, removing the potential confounding of inbreeding depression. This has enabled a genetic dissection of life-history and behavioral characters [18•].

Resequencing and hitch-hiking mapping

Similar to QTL mapping, initial HH mapping relied on recombination breakpoints produced during the experiment, thereby limiting the mapping precision. This was necessary, as only a fraction of the genome could be measured and used as molecular markers, and selection could only be detected if linked to a marker. Recent advances in resequencing technology have greatly reduced this limitation. Researchers can now create a mapping population simply by sampling a large number of individuals in nature. Selection is then applied for several-to-hundreds of generations on replicate populations, and these populations (and preferably the starting population as well) are resequenced. Changes in frequency of most genomic polymorphisms are assayed (some loci and alleles remain difficult to annotate). Turner et al. [19] referred to this approach as “Evolve and Resequence” (E&R), as (in theory) the detection of neutral hitchhikers is no longer required. Here, we will term this technique HH-resequencing, or HHR, to emphasize the continuity of this approach with previous work. By what ever name, the approach seeks to combine the resolution of population genetic analysis of selection in natural populations (e.g. [20,21]) with the functional precision gained by applying selection to specific characters.

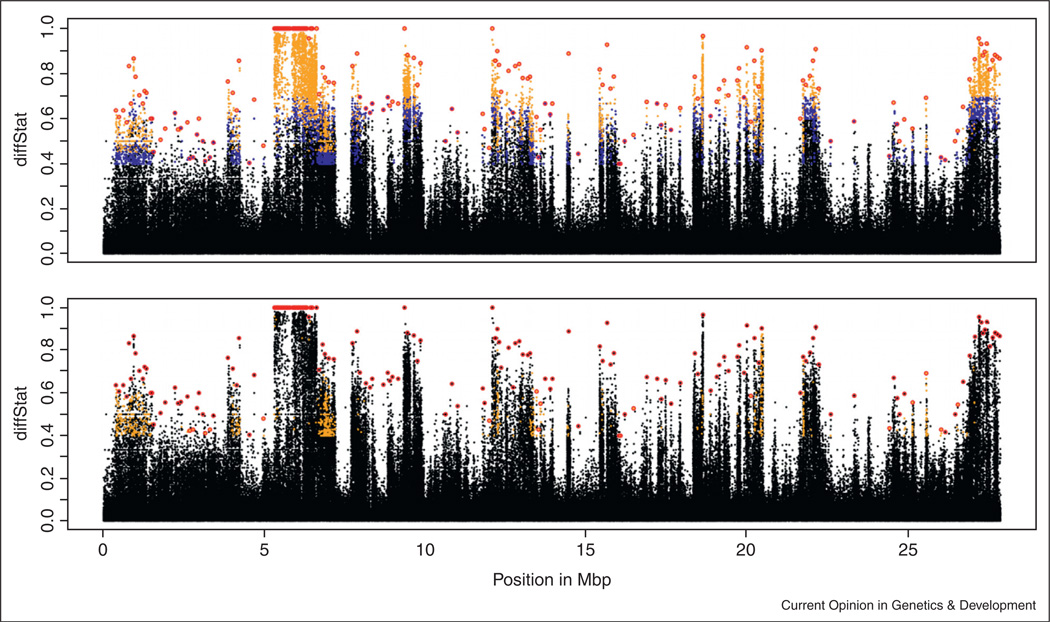
The power of early HHR efforts appears astounding. Turner et al. [22•] found 5205 genomic regions putatively responding to selection on body size. Is it possible that selection had acted on just a few polymorphisms, but many regions then appeared differentiated as they were in linkage disequilibrium (LD) with the selected loci? We examine Figure 1 to evaluate such a proposition. The responding polymorphisms appear well-spread over the genome and separated by those not exhibiting large changes in frequency. It thus appears that mapping had high precision, and that a very large number of QTL were found. Given that the extent of strong LD in natural fly populations is on the scale of ~100 base pairs in many genomic regions, such a ‘fine-grained’ selection response might be possible. However, to be conservative, Turner et al. [22•] identified 10 kb windows around strong-responding polymorphisms, and still found that 1236 genomic regions remained as putatively independent selection targets (see Figure 1). Likewise, OronzoterWengel et al. [23] adapted flies to different temperature and found on the order of 5000 polymorphisms responding to selection. Because of the rapid drop in LD around significant variants, they infer that this was caused by selection at many different loci. Turner and Miller [19] have observed 13,000 variants responding to selection (at an estimated 0.5% false discovery rate). Little was inferred about the number of causal loci vs. the proportion of significant variation caused by HH in this last case. However, when the data were combined with a genome-wide association study on the lines used to found the outbred population, results seemed consistent with a large number of causal variants [24].

Figure 1.

Differentiated polymorphisms on chromosome arm 3R, reproduced from Turner et al. [22•], Figure 4, with a following Figure Legend. The diffStat is shown for each variant that had higher or lower allele frequencies in the large-selected lines compared to the small-selected lines. Above: Color coding indicates significance: black = nonsignificant variants, blue = significant variants at the permissive FDR threshold (FDR < 10%); gold = significant variants at the restrictive FDR threshold (FDR < 5%); red = peak variants. Below: Color coding indicates estimated starting allele frequency: black = all variants, gold = variants with an average control frequency <0.05; red circles indicate peak variants, as in A. When 50 kb regions around strongest selected sites are assumed to be changing in frequency due to local hitch-hiking, the estimate for the number of selected polymorphisms is reduced to ~ 300. http://dx.doi.org/10.1371/journal.pgen.1001336.g004.

These inferences are dramatically different from the conclusions derived in more traditional QTL and GWA studies, in which a few polymorphisms of large effect are typically found [(3,but see 25)]. To reconcile this contradiction, one could postulate that the vast majority of differentiated polymorphisms were, in fact, affected by drift rather than selection. However, large population sizes relative to the number of generations (hundreds to thousands of individuals in tens to hundreds of generations) were used to minimize the effects of drift. Comparisons among replicated selected populations and/or extensive simulations of neutral polymorphisms experiencing drift rejected this simple conjecture in each case [19,22•,23].

Could it be that selection, in fact, had acted on each of thousands of polymorphisms, and changed the frequency of each of them? Back of the envelope calculations suggest this is not possible (see Box 1). Under this scenario, the strength of selection affecting each polymorphism should be on the order of 10⁻³. With a population size on the order of 10³, such a selection would be close to neutrality [4]. Furthermore, even if the populations were infinite in size, the allele frequency as a result of such a selection would change by only 10⁻³ in each direction of selection in the study of Turner et al. [22•] and by ~10⁻² in the experiments by Oronzo-terWengel et al. [23] and Turner and Miller [19]. These changes would simply be undetectable with the ~100× depth of sequencing these studies employed (and the commensurate sampling error involved in allele frequency estimates). We conclude that selection acting on each of thousands of polymorphisms exhibiting consistent differentiation between selected and base HHR populations cannot possibly be feasible.

Box 1.

Classical treatments in population genetics [4] have related an intensity of selection on phenotype, i, and an additive effect of a QTL scaled by phenotypic variation, a/σ_p, with the strength of selection on a QTL allele, s. For truncation selection, the relationship is simply:

$$s=i\times \left(\frac{a}{{\sigma }_p}\right)$$

Given a sensible assumption of 20% selection intensity and 50% heritability, what will the strength of selection be per polymorphism in the case of 5000 polymorphisms? The upper bound of selection is given by assuming that all polymorphisms have an equal effect: s = 0.2 × (1/sqrt(5000))/2 = 3 × 10⁻³. Let’s now calculate what change in allele frequency selection of such a strength would cause over the course of an HHR experiment selection. For additive genes with two alleles, Δq = s × q (1 − q)/W, where q is a lower frequency allele, and W is a mean fitness of population, here approximated as W~1.

Following Oronzo-terWengel et al. [23] who argued that most selected polymorphism are initially at lower frequency, we assume q = 0.05. Then, Δq = 3*10⁻³ * 0.05, that is, ~3*10⁻⁴ per generation. Assuming an infinite population size, and selection in both directions, the expected change over a dozen of generations in OronzoterWengel et al. [23] and Turner and Miller [19] is ~ 10⁻³; and over a hundred generations in Turner et al. [22•] is ~10⁻².

How many alleles could have responded to selection in these studies? Let us focus on the design of OronzoterWengel et al. [23]. Assume a 10% allele frequency change over the course of this experiment. A change of 1% per generation would require that the polymorphism accounts for approximately 5% of phenotypic variation, which means there could be no more than a few dozens of simultaneously selected polymorphisms of such an effect. This is an order to two orders of magnitude less than the number of polymorphisms apparently affected by selection. Note that while we focused on the three studies for illustrative purposes, there is a strong consistency with other HHR experiments [18•,26,27]. These striking inconsistencies require an explanation.

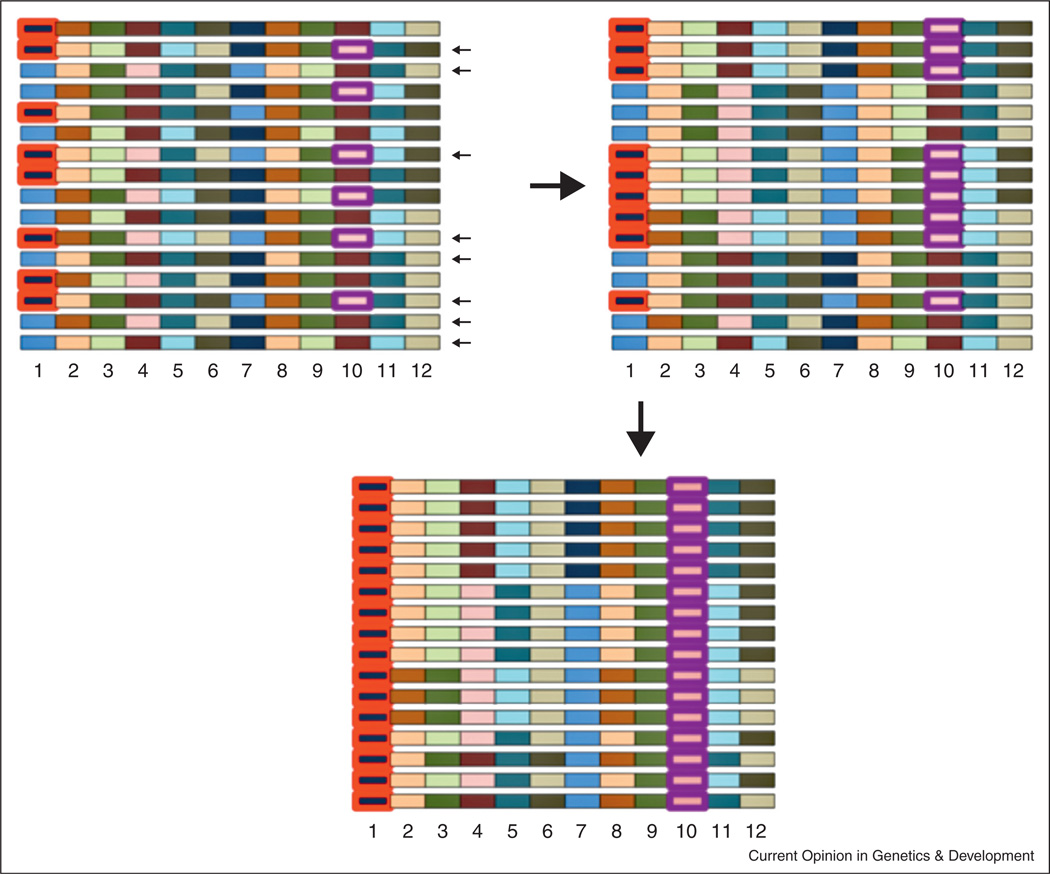
If not drift or population LD, what could be the force affecting the frequency of numerous polymorphisms in a way that is consistent between replicated selected and base populations? One straightforward potential explanation is a combination of local LD resulting from the evolutionary process in nature, and co-incindental long-range associations among these LD blocks resulting from stochastic sampling. For illustrative purposes, imagine 10 initial haplotypes sampled to establish a base HHR population in which 1000 markers were assayed. This immediately results in a massive amount of ‘sampling LD’ among polymorphisms. In a sense, each polymorphism segregating independently in the source population becomes — in the base population — statistically confounded with a hundred or so other polymorphisms. This confounding is randomly spread over the genome. Similar to QTL mapping and early HH mapping experiments [13,14,16,17], recombination during HHR experiments will progressively break down LD, increasing mapping precision. The sporadic, or sampling, LD shall–generally– decay in a similar way. However, this decay is more difficult to quantify. Furthermore, its’ degree is entirely unclear when strong polygenic selection is in place. In fact, such a selection could in principle ‘lock’ the sampling LD by eliminating recombination events among polymorphisms experiencing positive selection [28].

To see why, imagine that there are many modest effect, additive polymorphisms within a chromosome region, but few sampled haplotypes that contain the strongly selected combinations of these alleles. As a result, there may be few genealogies that connect a base and a selected HHR population (sequenced individuals may be decendents of a small fraction of founder individuals). These genealogies move selected alleles to high frequency, but they will likewise transport hundreds if not thousands of chance hitchhikers as well. These hitchhikers may appear to be separated by unaffected regions due to the combination of short range LD in nature and sampling among these short-range blocks in lab (Figure 2). Unless multiple base populations have been established independently, so that they do not share haplotypes, a large number of polymorphisms could be confounded through sampling LD and subsequent chance hitchhiking cannot be excluded. There could be, overall, dozens of the polymorphisms under selection in [18•,19,22•,23,26,27] and numerous hitch-hikers spread over the genome and rising in frequency in unison with causal polymorphisms.

Figure 2.

Sampling disequilibrium and its consequences in HHR mapping. A model or a natural population is shown on the top left. Each chromosome is conceptualized as a set of LD blocks, where LD is complete within each block but absent between blocks. There are 2 alleles (different colors) within each block (numbered 1–12). When a subset of chromosomes are sampled to found a population, sampling LD can associate non-adjacent LD blocks. For example, if the chromosomes indicated by small black arrows are sampled, the descendents would have LD between blocks 1 and 10 (top right). If one allele is then selected (circled in red), alleles at another locus can hitchhike (circled in purple). Because allele frequency between these blocks is changed less, this process could create many seemingly independent “peaks” along a chromosome despite only a subset of peaks containing a selected allele.

Overall, there seem to be both advantages and pitfalls of HH mapping in both evolve and resequence design and conceptually similar analyses of HH events in natural populations experiencing selection [20,21]. In the former case the size of sampled and selected populations is limiting, and in the latter similar limitations arise from demographic uncertainty.

Future progress in HHR

The problem above is not unlike the imprecision of more traditional QTL mapping, where numerous polymorphisms are confounded due to ‘localized’ LD. Here, the problem is exacerbated by confounding being ‘spread’ over the whole genome to create local false positives. The signal of selection is still there, but how can we localize its genomic targets? Burke et al. [26], Zhou et al. [27] and Remolina et al. [18•] have relied on summary statistics integrating the effects of thousands of polymorphisms to identify larger genomic regions under selection. For instance, a completed hard sweep is expected to produce low heterozygosity in the selected population, and a strong divergence from its base population [29]. In contrast, an incomplete sweep of an allele at low frequency in a base population can result in an increase of local heterozygosity in selected versus base populations. Remolina et al. [18•] proposed several tests based on these expectations, and relied on their overlap to identify a dozen genomic regions selection is likely acting upon. Applying such procedures might ameliorate the problem, but it seems possible that these signatures of selection both close and far from the selected site might be extremely similar (see [19] for some discussion). Haplotype-based tests may provide a resolution to this problem as well, as the LD of all polymorphisms could be compared at different stages of the experiment and included in the analysis. Haplotype data are very difficult to extract when exploiting the efficiency of pooled sequencing, but it may be possible in some situations [30]. Clearly, extensive simulations are required to establish experimental and analytical guidelines. Until then, we advise caution in estimating genetic complexity from a genomic response to selection without additional validation. The simulations will also contribute to optimizing experimental procedures, as there are unavoidable trade-offs such as population size and selection strength (e.g. [31]). Is it better to rely on a few generations of selection in several very large populations, perhaps even a single generation (e.g. [32])? This would be akin to a bulk segregant analysis, and would sacrifice the compounding power of repeated selection in favor of reduced sampling error. Would multi-generation recombination in the base population help to reduce the amount of sampling LD? These and other questions must be answered before investment in the HHR approach becomes substantial.

In conclusion, there is a great promise in HHR mapping: its power is remarkable, its precision is unclear. To fully realize this power, further simulation and theoretical work will be central in helping us interpret the experimental evolution data.