Forward- and Reverse-Traveling Waves in DP Phenomenology: Does Inverted Direction of Wave Propagation Occur in Classical Models?

Abstract

Recent basilar-membrane (BM) vibration experiments show that the phase slope of the distortion product (DP) in the cochlear region in which a backward-traveling wave is expected is negative, which is typical of a forward-traveling wave, according to the predictions of quasi-linear approximate solutions of classical 1-D transmission-line cochlear models. This phase behavior has been interpreted as suggesting a strong deviation from the “classical” models of the otoacoustic emission (OAE) generation and transmission. In this paper, the DP phase inversion phenomenon is approached from a conservative point of view. The DP phase is calculated in a classical cochlear model. The main conclusion is that deviations from the classical model are not necessary to account for the observed phase behavior.

INTRODUCTION

A lively debate has recently developed about the existence of slow transverse backward-traveling waves (TWs) along the BM at the frequency of distortion products (DPs) generated in the cochlea. The non-existence of backward TWs along the BM would require alternative generation and/or transmission mechanisms for the signals measurable in the ear canal as distortion product otoacoustic emissions (DPOAEs).

In a smooth cochlear model, without roughness, the DP generation would occur at the place x(f₂) where the overlap between the traveling waves (TW) of the two primaries f ₁ and f₂ is maximum. In this case the DP generation source is “wave-fixed”. An interesting implication of the Wentzel-Kramer-Brillouin (WKB) approach to the solution of the transmission-line models relates to the phase prediction of distortion products (DP). In scale-invariant models, in the case of wave-fixed sources, an approximately null phase gradient at the base of the cochlea is predicted or, in other words, the phase of the backward wave is independent of the primary frequencies, so long as their ratio f₂/f₁ is fixed, as we will implicitly assume in the following.

Assuming that the DP is observed instead at a fixed cochlear place x(f₀) between the base and x(f₂) and assuming a wave-fixed generation mechanism, the WKB perturbative approximation of a cochlear model based on a 1-D transmission line predicts a DP phase increasing with increasing f₂ in the case of the backward propagating wave that one would expect to observe between the generation place x(f₂) and the base. Conversely, a negative phase slope would be expected for any DP wave traveling forwards (i.e., towards the apex). In recent experiments on animals measuring the BM vibration at a fixed place x(f₀), de Boer et al. [2] reported a negative phase slope of the phase-frequency relation, consistent with previous experiments [3,5], which although differently designed, can be directly compared with the de Boer experiment under the scale-invariance hypothesis. The observation of a counterintuitive negative phase slope led the authors to coin the acronym IDWP (Inverted Direction of Wave Propagation). In a subsequent paper [1] the same authors interpreted the observed phenomenology as a consequence of the reduction or suppression of the backward TW in a cochlear region in which it should be expected to be dominant. They proposed that the reduction could be explained by the feed-forward nature of the active cochlear mechanism produced by the outer hair cells (OHCs), in which an OHC-mediated force on the BM amplifies in an asymmetric way the forward- and backward-traveling waves.

We prefer to define the phenomenon model-independently, as “negative phase slope” (NPS). In the calculations and in the numerical simulations presented in the present study, it is shown that the NPS phenomenon can be observed also assuming a more conservative point of view in which a feed-forward mechanism is not considered. The necessary conditions to observe the NPS have been explored, both in a classical active model [8] and in a fully nonlinear model [4,7], which has to be numerically solved in the time domain. The physical nature of the DP NPS phenomenon has not been completely clarified yet, but the main physical features of the cochlear model necessary to observe the phenomenon have been identified. A high stapes reflectivity seems to play a crucial role, together with active amplification and a broad distribution of the DP sources.

METHODS

The DP generation can be computed using perturbative techniques, adding the DP sources as perturbations in an underlying cochlear model that is linear and smooth. The Talmadge et al. model [8] provides a suitable framework for this study because its active “delayed stiffness” terms are linear. The Green’s function for the smooth cochlea in absence of reflections from the boundaries can be written as [6]:

$$G{(x\mid x^{\prime })}_{\infty }\propto \{\begin{array}{cc}{\psi }_l(x){\psi }_r(x^{\prime })& (x<x^{\prime });\\ {\psi }_r(x){\psi }_l(x^{\prime })& (x>x^{\prime }),\end{array}$$ (1)

where ψ_r,l are the basis functions representing respectively, waves moving forward and backward from/to the base and the location x along the BM:

$${\psi }_{r,l}(\omega ,x)\approx \sqrt{\frac{k(\omega ,0)}{k(\omega ,x)}}exp\left(\mp i{\int }_0^{x}k({\omega }_{\text{dp}},x^{″}){dx}^{″}\right).$$ (2)

As shown by Shera et al. [6, Eq. (B8)], Eq. (1) must be modified in presence of reflections. In particular, if reflections from the stapes are present, the expression for the Green’s function becomes:

$$G(x\mid x^{\prime })=G{(x\mid x^{\prime })}_{\infty }+R{\psi }_r(x){\psi }_r(x^{\prime }).$$ (3)

where R represents the stapes reflection coefficient. The DP source at frequency 2 f₁ – f₂ is assumed to be of the type

$$D({\omega }_1,{\omega }_2,x)=\gamma \rho ({\omega }_1,{\omega }_2){\xi }_r^2({\omega }_1,x){\xi }_r^{\ast }({\omega }_2,x),$$ (4)

where γ is the inverse of the Wronskian determinant of the right- and left-moving solutions and ξ (ω, x) represents the BM displacement due to the propagation of the right-moving traveling waves the frequencies of the primary tones:

$${\xi }_{r,l}(\omega ,x)\approx \frac{k^2(w,x)}{k^2(w,0)}{\psi }_{r,l}(\omega ,x).$$ (5)

The response to a source distributed along x as in Eq. (4) can be written as the convolution integral of the Green’s function with the function representing the source term itself. If the term coming from reflections is added to the Green’s function, the following expression is obtained for the pressure at the frequency of the DP, observed at a location basal with respect to the generation point x(f₂):

$$\begin{array}{l}{P}_d({\omega }_{\text{dp}},x)\propto {\int }_x^{\infty }d{x}^{\prime }\{{\psi }_r({\omega }_{\text{dp}},x^{\prime })D({\omega }_1,{\omega }_2,x^{\prime })\}{\psi }_l({\omega }_{\text{dp}},x)\\ +{\int }_0^{x}d{x}^{\prime }\{{\psi }_l({\omega }_{\text{dp}},x^{\prime })D({\omega }_1,{\omega }_2,x^{\prime })\}{\psi }_r({\omega }_{\text{dp}},x)\\ +{\int }_0^{\infty }d{x}^{\prime }\{{\psi }_r({\omega }_{\text{dp}},x^{\prime })D({\omega }_1,{\omega }_2,x^{\prime })\}{\psi }_r({\omega }_{\text{dp}},x).\end{array}$$ (6)

The term coming from G(x|x′)_∞ and that due to the reflection from the stapes are very similar to each other but they have the opposite resulting phase: the first represents a backward-traveling wave and the second a forward-traveling wave generated by the reflection at the stapes. If the reflectivity at the stapes is negligible, the calculation of P_d from Eq. (6) always gives a positive DP phase (for x < x′). But if R is sufficiently large the competition between the terms can produce different phase profiles. In particular, if the cochlea is active and the DP source is not point-like, the NPS phenomenon is predicted also by this “classical” model.

We employed a more sophisticated fully nonlinear model described elsewhere [4,7]. The solution of the cochlear equations was implemented in MATLAB, using an optimized version of the ode15s solver. The numerical solutions were performed in time domain with N = 1000 cochlear sections.

RESULTS

The physical circumstances under which the NPS can be observed have been studied in the case of a smooth linear model in which the DP generator is introduced as a perturbation by implementing Eq. (6) with the stapes reflectivity as a parameter. The model, including the values of all the parameters, is that discussed in [8], using as a free parameter only the passive quality factor Q of the model. A delayed stiffness [9] term is introduced in that model to obtain a tall and broad activity pattern.

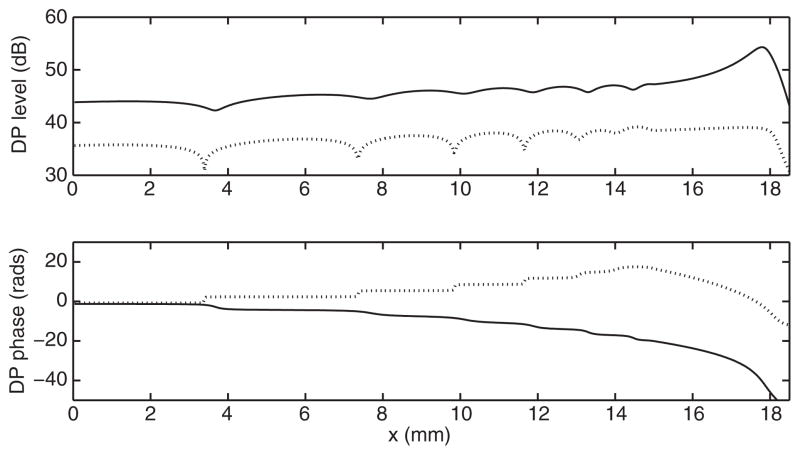
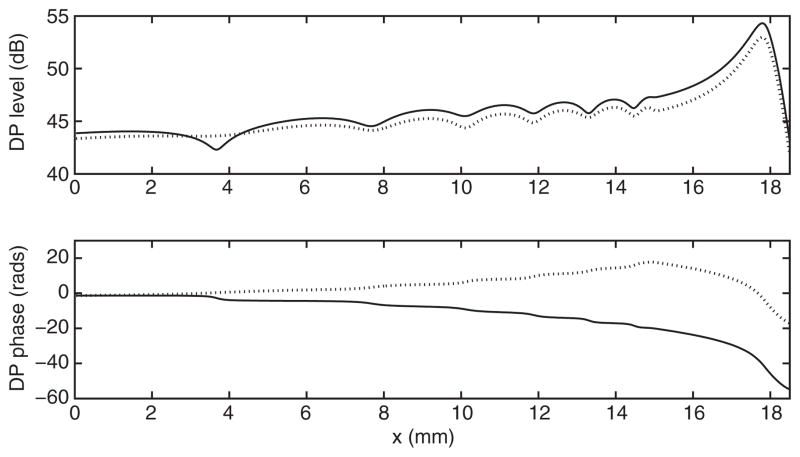
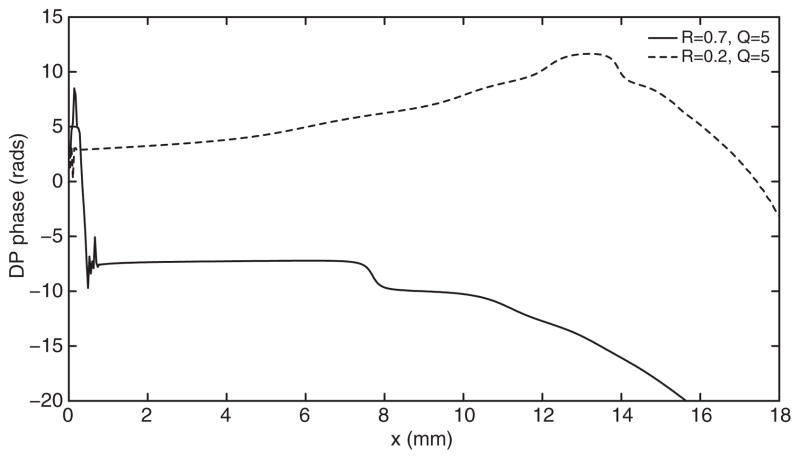
Figures 1 and 2 show the results obtained, respectively, by switching on/off the active delayed stiffness term and varying the stapes reflectivity R. The NPS phenomenon is not observed when the model is passive, unless unreasonably low values of the cochlear quality factor are assumed, which significantly expand the DP source towards the cochlear base. The cochlear activity, represented in the model of Fig. 1, by the Zweig anti-damping term seems therefore to play a crucial role in producing the NPS. Another essential role in the NPS is played by the stapes reflectivity: if the reflectivity is smaller than about 0.5 (in this model) the NPS is not observed even in the active model, as shown in Fig. 2. Also for the fully nonlinear diagonal anti-damping model [4,7], the high stapes reflectivity seems to be a necessary condition for the NPS, as it is shown in Fig. 3. The presence of a proper anti-damping term, pumping energy into the system when the wave passes through a negative damping region is not necessary in this model to observe the NPS. In fact, in this simulation, the maximum value of the anti-damping term (at low BM displacement levels) was a fraction (90%) of the passive damping.

FIGURE 1.

Amplitude and phase of the DP generated by f₁ = 2 kHz and f₂ = 1.22 f₁ in the case of an active (solid line) and passive (dotted line) model with Q = 25 and R = 1.

FIGURE 2.

Amplitude and phase of the DP generated by f₁ = 2 kHz and f₂ = 1.22 f₁ in the case of an active (solid line) and passive (dotted line) model with Q = 25 and R = 0.2.

FIGURE 3.

Phase of the DP generated by f₁ = 2 kHz and f₂ = 1.22 f₁ in the case of fully nonlinear numerical model with R = 0.7 (solid line) and R = 0.2 (dotted line).

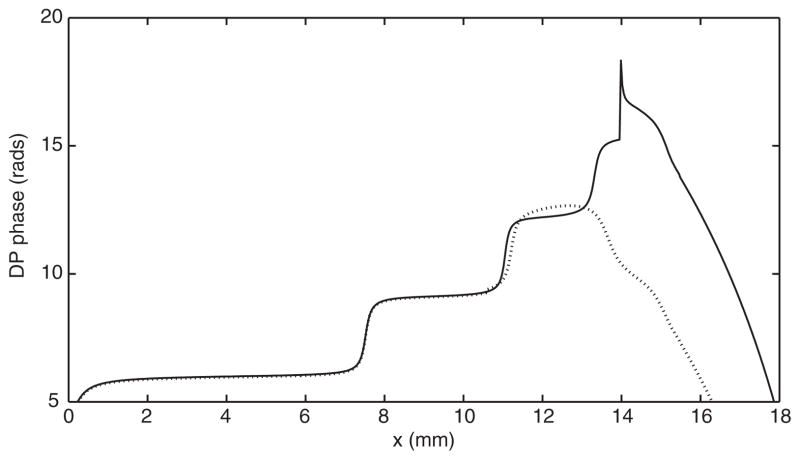
In the fully nonlinear model a crucial role for obtaining NPS seems to be played by the width of the DP source distribution. If the source is too localized around the x(f ₂) region, the NPS is not observed. To demonstrate this, the DP source was calculated from Eq. (4) by using the f₁ and f₂ profiles previously computed by the model and then it was directly injected in a region of variable width extending towards the base from the x(f ₂) location. As shown in Fig. 4, the turning point of the phase slope depends on the width of the injection region.

FIGURE 4.

Phase of the DP response produced by a DP source directly injected into the fully nonlinear model. The DP source extended from x(f₂ = 2–3kHz) (solid line) and x(f ₂ = 2–4.5kHz) (dotted line).

CONCLUSIONS

The NPS phenomenon can be observed also without invoking a feed-forward mechanism to enhance the forward-traveling wave with respect to the backward one. The physical circumstances necessary and sufficient to induce the non positive DP phase slope observed at a location between the generation place x(f₂) and the base seem to be: the wide distribution of the DP sources and the high stapes reflectivity. In a classical 1-D transmission line cochlear model [8] solved using a perturbative technique, the active nature of the model helps obtaining NPS for lower values of stapes reflectivity. The results have been confirmed using a fully nonlinear cochlear model, numerically solved in the time domain.