Intervention Effects for Students With Comorbid Forms of Learning Disability: Understanding the Needs of Nonresponders

Abstract

In this article, we considered evidence from our intervention research programs on whether students with learning disability (LD) in reading and mathematics (comorbid LD) respond differently to intervention, compared to students with reading LD alone (RD) or to students with mathematics LD alone (MD). The goal was to gain insight into whether comorbid disorder represents an LD subtype distinct from RD or from MD, which requires differentiated forms of intervention. Our analysis suggested that students with comorbid LD respond differently than those with MD, depending on the nature of mathematics intervention, and may therefore represent a distinctive subtype. By contrast, students with RD appear to respond to intervention in similar ways, regardless of whether they experience RD alone or in combination with MD. Results also suggest that distinctions between comorbid and single-order LD may depend on whether LD is defined in terms of lower- versus higher-order academic skill. Recommendations for future study are provided.

Randomized control studies create the basis for prescribing interventions to reduce the prevalence of learning disability (LD). In the primary grades, this is especially important for core components of the curriculum, which represent foundational competencies for future academic development and success in life: in reading, word-level skill and comprehension; in math, number combinations (i.e., addition and subtraction problems in the 0–18 range) and word problems. Across studies (see L. S. Fuchs, Fuchs, & Compton, 2012; O’Connor & Fuchs, in press), results demonstrate that students at risk for poor reading or mathematics development experience reliably and substantially more positive reading or mathematics outcomes if provided with tutoring of moderate intensity (i.e., conducted 3–4 times per week for 30–45 minutes per session for 12–20 weeks). Moreover, when at-risk students do not receive such preventative tutoring, the gap between their level of reading or mathematics performance and those of not-at-risk classmates widens, making it increasingly difficult for these children to profit from classroom instruction. By contrast, many at-risk students who receive high-quality tutoring make progress toward catching up to their classmates, and, for some of these children, the scaffolding provided through such short-term tutoring creates a strong foundation for them to experience long-term success with the school’s standard reading or mathematics program.

At the same time, as with any generally effective instructional program, not all students respond. In summarizing a program of research on the efficacy of mathematics tutoring, for example, L. S. Fuchs et al. (2012) estimated that the modal rate of unresponsiveness to well-designed mathematics tutoring programs, which were implemented with fidelity, was 4% of the general population. O’Connor and Fuchs (in press), D. Fuchs, Compton, Fuchs, Hamlett, and Lambert (2012), Torgesen (2000), and Wanzek and Vaughn (2009) have provided similar estimates for early reading intervention. This demonstrates the need for research to improve understanding about (a) what student characteristics are associated with unresponsiveness, so that lack of response may be predicted, and (b) how to design instruction that meets the needs of students who respond poorly to generally effective programs.

One hypothesis in the field of LD is that the comorbid presence of mathematics and reading difficulty is a student characteristic associated with distinctive profiles of academic deficits, with distinctive cognitive deficits, and with differentially poor response to intervention. Behavioral genetics research provides some support for the hypothesis that comorbidity may be distinct from single-order forms of LD (Willcutt et al., in press). Comorbidity for mathematics and reading difficulty is prevalent (Badian, 1999; Barbaresi, Katusic, Colligan, Weaver, & Jacobsen, 2005). Yet relatively little is understood about the nature of this condition. Some studies have examined profiles of reading difficulty with and without mathematics difficulty. Other studies have provided profiles of mathematics difficulty with and without reading difficulty. Few have examined all three disorders with a common set of methods. This is unfortunate because the cognitive profiles associated with comorbid disorder versus single-deficit forms of LD may differ.

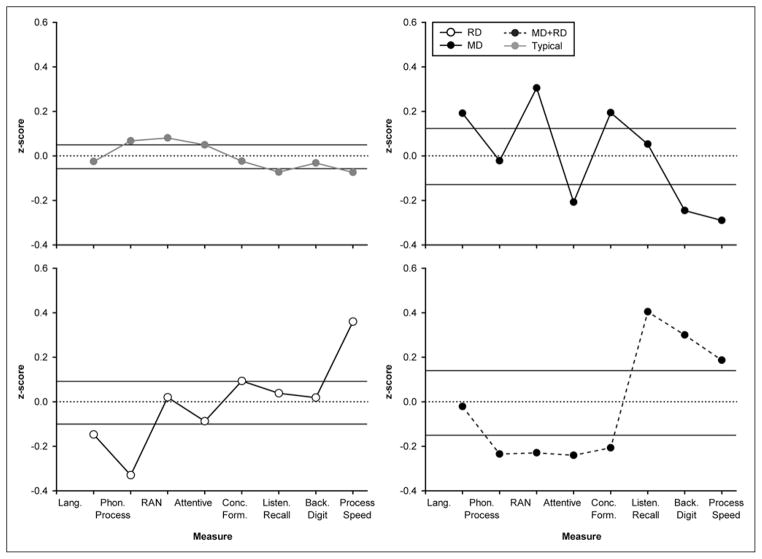
In Figure 1, we show cognitive profiles from an extant database for students we identified as having reading LD (RD; n = 65), mathematics LD (MD; n = 33), comorbid mathematics and reading LD (MD+RD; n = 25), or typical achievement (n = 424). Note that in the studies we describe in this article, children were identified with LD based on low achievement (typically < 25th percentile) using reading and/or mathematics measures we administered, and students with low IQ were excluded from participation. IQ–achievement discrepancies were not, however, employed to identify LD. Reliance on low achievement, with a low-IQ exclusion, is the predominant method for identifying LD within research studies at this time. Across the studies included in this article, the mean achievement levels of LD participants ranged between the 1st and 25th percentiles, with median performance across studies at the 13th percentile.

Figure 1.

Cognitive dimensions as a function of comorbidity status (RD vs. MD vs. MD+RD vs. typically developing; classifications based on word-level and calculation skill). Scores in left panel are not adjusted for each group’s grand mean across the eight cognitive dimensions; scores in right panel are adjusted. Lang. is oral language; Phon. Process. is phonological processing; Attentive is teacher ratings of attentive behavior; Conc. Form. is concept formation; Listen. Recall is listening recall span; Count. Recall is counting recall; Back. Digit is backward digit span; Process. Speed is processing speed. RD is students with reading disability; MD is students with mathematics disability; MD+RD is students with mathematics and reading disability; typical is typically developing students.

For each MD+RD, MD, RD, and typically developing child reflected in Figure 1, we assessed cognitive dimensions at the start of third grade, and we referenced performance on each cognitive dimension against a representative sample of 677 third graders; thus, the dimensions are on the same scale. We included measures of oral language (vocabulary, syntax, and listening comprehension), phonological processing (elision), rapid automatized naming (RAN-digits), teacher ratings of attentive behavior, concept formation, two forms of working memory (listening recall span and backward digit span), and processing speed (see Table 1 for measures). In the left panel of Figure 1, the profiles are not adjusted for each group’s overall level of performance; this panel illustrates how each group’s overall level of performance, across the dimensions, is low relative to typically developing children. For example, comorbid students are more than 1 standard deviation lower than typically developing children on oral language and 0.75 standard deviations lower on phonological processing. The display also shows that oral language and phonological processing, for example, represent important weaknesses for RD relative to students without RD, regardless of whether RD occurs with or without MD. Low performance on these dimensions is expected based on prior reading research (Compton, Fuchs, Fuchs, Lambert, & Hamlett, 2012; Morris et al., 1998).

Table 1.

Cognitive Dimension Measures.

Construct	Measure
Language
Vocabulary	Wechsler Abbreviated Scale of Intelligence, Vocabulary (Wechsler, 1999)
Syntax	Test of Language Development, Grammatic Closure (Newcomer & Hammill, 1988)
Listening comprehension	Woodcock Diagnostic Reading Battery, Listening Comprehension (Woodcock, 1997)
Phonological processing	Comprehensive Test of Phonological Processing (CTOPP), Elision, Sound Matching (Wagner, Torgesen, & Rashotte, 1999)
Rapid automatized naming	CTOPP, Rapid Digit Naming
Attentive behavior	Strengths/Weaknesses of ADHD, Symptoms & Normal Behavior (Swanson et al., 2004)
Concept formation	Woodcock–Johnson III (WJ-III), Concept Formation (Woodcock, McGrew, & Mather, 2001)
Working memory
Listening recall	Working Memory Test Battery for Children (WMTB-C), Listening Recall (Pickering & Gathercole, 2001)
Backward digit span	WMTB-C, Backward Digit Span
Processing speed	WJ-III, Visual Matching

By contrast, in the right panel of Figure 1, each group’s grand mean was centered at zero across the eight dimensions (i.e., the zero line for each group is that group’s grand average over eight dimensions), and the horizontal lines above and below zero represent a 95% confidence interval for that subtype. This makes it easier to detect differences in the shapes of the profiles for the three LD groups. For example, although oral language is severely deficient for comorbid students, other cognitive dimensions (phonological processing RAN, attentive behavior, and concept formation) contribute more to the shape of the MD+RD profile. By contrast, when MD occurs alone, oral language is a relative strength, and working memory (i.e., counting recall) and processing speed are relative weaknesses. Such strengths and limitations have previously been associated with calculation MD (L. S. Fuchs, Geary, Compton, Fuchs, Hamlett, & Bryant, 2010; L. S. Fuchs, Geary, Compton, Fuchs, Hamlett, Seethaler, et al., 2010; L. S. Fuchs, Fuchs, Stuebing, et al., 2008). Of interest, two dimensions appear uniquely associated with comorbid disorder (i.e., are outside the confidence band for comorbid but not for MD or RD): RAN and concept formation. This suggests MD+RD students present distinctive instructional needs. (Note that in the profiles shown in Figure 1, LD was defined in terms of lower-order skill: word-level skill for RD and calculation skill for MD. This is often the case in LD research. When classifications are instead formulated on the basis of higher-order skill [reading comprehension and word problems], a distinctive pattern of abilities for MD+RD remain, but contributors to the distinctive shape differ, one of which is oral language. We return to this point later.)

Distinctive profiles for MD+RD suggest the possibility that comorbidity represents a distinctive subtype of LD. Yet the most convincing evidence on the nature of comorbidity comes from experimental studies, in which groups of single-deficit versus comorbid students are randomly assigned to alternative forms of intervention designed to address hypothesized distinctions between comorbid and single-deficit learning difficulty. But few available studies have been prospectively designed to address hypothesized distinctions, even fewer with adequate power for detecting significant effects. In this article, we consider evidence from our intervention research programs on whether students with comorbid difficulty in reading and mathematics respond differently to intervention. The goal is to gain insight into whether comorbid disorder represents a subtype of LD distinct from RD or MD, which requires differentiated forms of intervention. We use these analyses to explore the comorbidity subtyping framework as a potential means for improving the field’s success in helping students with LD achieve stronger academic outcomes and to formulate questions for subsequent large-scale randomized control trials. We begin with mathematics, focusing on differential response as a function of comorbidity status on number combinations and then on word problems.

Does Responsiveness to Mathematics Intervention Differ as a Function of Comorbidity Status? MD Versus MD+RD

Comorbidity is an especially prominent idea in mathematics. In 1993, Geary proposed MD versus MD+RD as a potential scheme for subtyping mathematics disability. He hypothesized that because a key deficit associated with reading difficulty is phonological processing (Bruck, 1992) and because phonological processing deficits have been linked to difficulty with automatic retrieval of number combinations (e.g., L. S. Fuchs et al., 2005), students with MD+RD should experience greater difficulty with number combinations compared to MD students. In addition, given the language problems implicated in RD (e.g., Compton et al., 2012; D. Fuchs et al., 2012; also see Figure 1) and the transparent need to process language within word problems, another hypothesis is that students with MD+RD experience greater challenge than students with MD in developing competence with word problems.

Research suggests that, compared to students with comorbid disorder, children with MD use more efficient counting strategies to solve number combinations (Geary, Hamson, & Hoard, 2000; Jordan & Hanich, 2000) with faster retrieval times (Andersson & Lyxell, 2007; Hanich, Jordan, Kaplan, & Dick, 2001; Jordan & Montani, 1997) but comparable accuracy (Cirino, Ewing-Cobbs, Barnes, Fuchs, & Fletcher, 2007). However, the literature is inconsistent, with some studies showing that students with MD and those with MD+RD experience comparable deficits on number combinations (e.g., Jordan, Hanich, & Kaplan, 2003; Landerl, Bevan, & Butterworth, 2004; Micallef & Prior, 2004; Reikeras, 2006). Research on word problems more clearly reveals greater deficits for students with MD+RD compared to those with MD, even when problems are read aloud to students (e.g., L. S. Fuchs & Fuchs, 2002; Hanich et al., 2001).

In one of the largest and most direct analyses of whether students with MD and those with MD+RD present distinctive profiles of mathematics deficits, Cirino, Fuchs, Tolar, and Powell (2011) studied 266 students at the beginning of third grade, with 132 classified as MD+RD and 134 students as MD. Students were assessed on four types of mathematics performance: number combinations (i.e., addition and subtraction problems in the 0–18 range), word problems (i.e., narrative mathematics problems that describe combining two quantities, comparing two quantities, or a value that increases or decreases over time and require addition or subtraction, with or without regrouping, for solution), procedural calculations (i.e., adding and subtracting two-digit numbers, with and without regrouping), and math concepts (e.g., estimating answers to two-digit addition and subtraction problems; identifying place value of multidigit numbers). Multivariate profile analysis revealed a significant shape effect, indicating a distinctive pattern of mathematics skills for students with MD versus those with MD+RD. The strongest contributors to group discrimination were math concepts and word problems, where effect sizes (ESs) exceeded 0.60 in favor of the MD group. The MD and MD+RD groups performed more similarly on number combinations and procedural calculations.

This and the cognitive profile just presented suggest that a subtyping scheme involving MD versus MD+RD may help explain an important source of poor response to mathematics intervention and may be helpful for generating hypotheses about the nature of mathematics disability as well as its identification and treatment. As mentioned, most relevant studies have employed a cross-sectional causal-comparative design, as illustrated in Cirino et al. (2011). An alternative approach for studying the same issue is experimental, where students are stratified according to subtype and randomly assigned to various tutoring or control conditions, with the goal of determining whether the subtypes respond differentially to intervention. This design offers the basis for stronger, causal inference about the value of the subtyping scheme and may increase clarity about the nature of efficacious intervention for unresponsive students. Yet only a handful of studies have adopted this approach, and the sample sizes in those studies have generally been insufficiently large to detect statistical interactions between intervention condition and comorbidity status. For this reason, we synthesize available studies, each with a relatively small sample. The hope is that aggregating across these existing studies will provide new insights into whether mathematics difficulty, with and without comorbid reading difficulty, provides promise for understanding and addressing unresponsiveness to intervention.

Studies and Participants

We considered three prospectively designed randomized control trials examining the effects of intervention as a function of MD versus MD+RD status (L. S. Fuchs et al., 2009; L. S. Fuchs, Powell, et al., 2010; Powell, Fuchs, Fuchs, Cirino, & Fletcher, 2009). These studies, each of which was conducted in a separate year with a different sample, comprised a program of research with some common methodological features. In terms of sample, each study was conducted at third grade, with approximately half of each study’s sample in Nashville and the other half in Houston.

Also, in each study and at each site, a large number of children were screened at the start of the school year to identify the subset who met inclusion criteria. Participants had to perform below the 26th percentile on a measure of calculations, and when word problems were also targeted for intervention, students could qualify based on word-problem performance below the 26th percentile. This cut point was used because of its frequent use in the MD literature and because it yielded only 10% of these high-poverty metropolitan school populations. Students who met this mathematics entry criterion were also screened on a word-level reading measure. We excluded students who scored between the 25th and 40th percentiles in reading to create a buffer zone between MD students with and without RD. Those scoring at or above the 40th percentile on reading were classified as MD; those at or below the 25th percentile on reading were classified as MD+RD. We also excluded students with a standard score below 80 on both intelligence measure subtests because our interest was not in mental retardation.

Across studies, students were assigned to conditions in the same way, blocking on site, comorbidity status (MD vs. MD+RD), and type of screening difficulty (calculations, word problems, or both). In all studies, some pretreatment demographic and skill differences existed between students with MD and MD+RD (across intervention conditions). These differences were expected based on prior work and therefore bolster external validity: MD+RD students had more pervasive mathematics deficits or were more likely to repeat a grade or were more likely to receive special education. More important for internal validity, there were no interactions between comorbidity status and intervention condition (i.e., the pattern of demographic and pretest performance for MD vs. MD+RD was similar in each intervention condition).

In terms of tutoring, the studies also shared some methodological features. All sessions were audiotaped, and a random sample of tapes was coded to systematically represent tutors, treatments, and MD versus MD+RD students. Fidelity was high (> 95% of elements conducted) at both sites, for each intervention condition, and for MD and MD+RD subtypes. Also, there were no interactions that involved site. The final commonality was that for each mathematics construct, the same outcomes measures were used.

In the next analysis, we considered effects on number combinations and on word problems. Each study reported both types of outcomes, and each study incorporated intervention designed to enhance number combination skill (L. S. Fuchs et al., 2009; L. S. Fuchs, Powell, et al., 2010; Powell et al., 2009). Powell et al. (2009) focused only on number combinations intervention; the other two studies considered intervention designed to increase number combinations as well as intervention designed to increase word-problem performance. When considering number-combination outcomes, ESs aggregate outcomes for 422 students: 184 MD and 238 MD+RD. When considering word-problem outcomes, ESs aggregate outcomes for 283 students: 114 MD and 169 MD+RD.

Nature of Number Combination Intervention Conditions

The three studies collectively assessed three types of number combination intervention. Powell et al. (2009) and L. S. Fuchs et al. (2009) included intervention conditions focused on number combination practice that relied heavily on the use of a tutor-supervised computerized practice. For each trial, a complete problem and answer “flashed” briefly. The student stored this in short-term memory and typed the complete number combination. The assumption was that repeated pairings of a problem and its correct answer would help students commit the number combination to long-term memory. Typically developing students commit number combinations to long-term memory via repeated pairings, but those repeated pairings occur naturally with development of efficient counting and backup strategies (Geary, Widaman, Little, & Cormier, 1987; Goldman, Pellegrino, & Mertz, 1988; Groen & Parkman, 1972; Siegler, 1987). Given the deficiencies students with mathematics difficulty experience with counting and decomposition strategies (Geary et al., 1987), we were interested in a “direct route” for the reliable and efficient pairings just described. The tutor supplemented this computerized practice with flash cards and paper–pencil review.

In this practice, we embedded a focus on number knowledge to make practice meaningful. First, as students typed a number combination, a number line representation of the numbers in the problem appeared on the screen. Second, tutors provided explicit instruction. In the initial conceptual lessons, the focus was addition and subtraction concepts and adding and subtracting 0 and 1. The commutative property and the inverse relationship between addition and subtraction were also taught. Additional tutor-directed lessons occurred when a new number combination family was introduced. In these lessons, the tutor focused on how number sentences within the set are related. With tutor guidance, students experimented with constituting sets for a given number combination in multiple ways. We also incorporated lessons on decomposition strategies in relation to the 10 set and doubles.

The second approach for teaching number combinations was counting strategies, which were included in L. S. Fuchs et al. (2009) and L. S. Fuchs, Powell, et al. (2010). As noted, students with mathematics difficulty fail to develop sound number knowledge or efficient counting strategies; thus, they pair problems with answers slowly, taxing short-term memory and often producing incorrect answers. As a result, long-term representations for automatic retrieval fail to establish or are established incorrectly. We hoped that explicitly teaching counting strategies would help students develop fluency with number combinations and foster success in pairing problems with correct answers. Students were also taught that if they “just know” the number combination, they “pull it out of their head.” If not, they count up. Tutors taught students efficient counting strategies for addition (the min strategy) and for subtraction (the missing addend strategy). To help students develop fluency with these counting strategies, tutors used flash cards. When students answered a number combination incorrectly, tutors required them to “count up” to produce the correct answer before moving on. In this way, students were encouraged to count up as quickly and accurately as possible. At the end of 2 minutes, students counted the number of cards answered correctly and graphed the score. As in the other practice condition, explicit instruction on number knowledge was provided to make counting strategies meaningful. In L. S. Fuchs et al. (2009), counting strategies were combined with the computerized “flash” practice activity to provide 30 minutes of number combinations intervention.

In L. S. Fuchs, Powell, et al. (2010), counting strategies were combined with word-problem instruction—the third number combinations intervention. We refer to embedding counting strategies instruction within word-problem intervention as contextualized number combination intervention. Tutors taught counting strategies and provided flash-card practice, as just described. Of every session, 5 minutes was allocated to counting strategies. The other 25 minutes of each session, however, were devoted to word problems (see below), during which tutors required students to use counting strategies to derive answers to number combinations embedded in the word problems.

Word-Problem Intervention

Word-problem intervention relied on schema-broadening instruction (L. S. Fuchs et al., 2003; L. S. Fuchs et al., 2004; Fuchs, Fuchs, Craddock et al., 2008), in which students are taught to understand problems in terms of problem types (combine, compare, change), recognize defining features of each problem type, and represent the structure of each problem type with a metaequation. Before solving a problem, students RUN through it (Read the problem; Underline the question; Name the problem type). Students name the problem type using the defining features of each problem type. For example, for compare problems (e.g., John has 5 dogs. Mary has 3 cats. How many more animals does John have than Mary?), students identify whether two things are compared; if so, the metaequation is Bigger amount minus smaller amount equals Difference (B – s = D). They use the structure of the metaequation to solve the problem: place the unknown (x) and relevant numbers where they go in the equation; fill in signs; and solve for x, which can occur in any of the three slots of the equation (the missing number may be B, s, or D). For combine problems, the metaequation is Part 1 plus Part 2 equals Total (P1 + P2 = T). For change problems, the metaequation is Start amount plus/minus Change amount is End amount (St +/− C = E).

After the 2-week introductory unit addressing foundational skills (including how to solve simple standard and nonstandard equations with x standing for the unknown), three problem-type units are taught (combine, compare, and change). Cumulative review is incorporated throughout. To introduce a problem type, tutors begin with complete stories (no missing information), illustrating the problem type with concrete objects. They transition to two representations: first a graphic and then the metaequation. Students practice filling in numbers from complete stories into the slots of the graphic or equation. Then tutors provide instruction in using the metaequation to solve problems for that problem type, starting with x in the final slot and gradually introducing x in the first and second slots of the equation. Each lesson comprises four activities: review of previously taught foundational skills; the lesson, in which tutors introduce word-problem strategies and guide students through word problems while gradually decreasing support; a sorting game to provide practice recognizing defining features of and naming problem types; and an independent problem.

Differential Response on Number Combination Outcomes

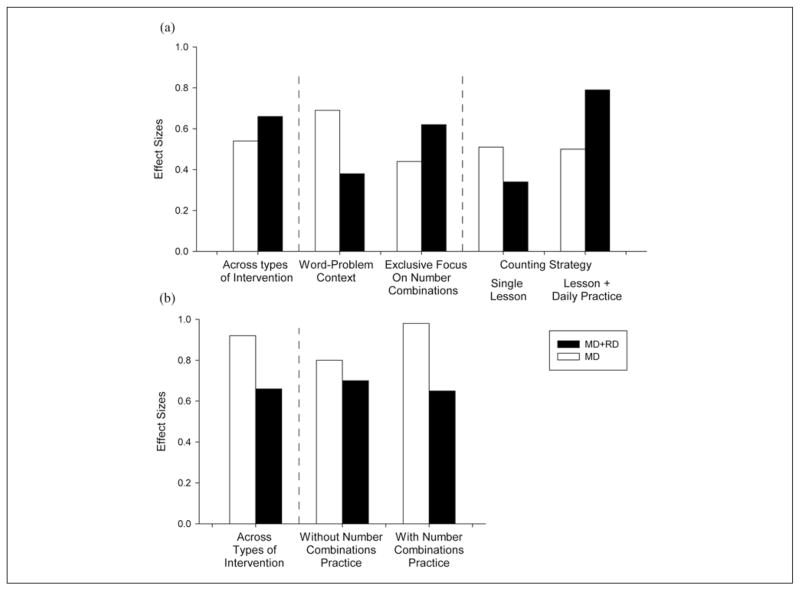
ESs for number combination outcomes are shown in Figure 3a. Across studies, overall response was similar for MD and MD+RD, with mean ESs, respectively, of 0.54 versus 0.66. This is consistent with the comparable performance reported in at least some causal comparative studies (e.g., Cirino et al., 2011; Jordan et al., 2003; Landerl et al., 2004; Micallef & Prior, 2004; Reikeras, 2006). More interesting, however, patterns in the data suggest that response may differ, depending on the nature of intervention.

Figure 3.

Effect sizes for number combination outcomes (a) and for word-problem outcomes (b) as a function of type of intervention and comorbidity status. MD is students with mathematics disability; MD+RD is students with mathematics and reading disability.

Contextualized versus decontextualized number combination intervention on number combination outcomes

The first pattern indicates varying outcomes for MD versus MD+RD when number combination intervention (a) is contextualized in word-problem instruction (with only 192 minutes allocated to number combination instruction over 48 sessions) versus (b) has an exclusive focus on number combinations intervention (with 1,200 minutes allocated to number combination instruction over 48 sessions). MD students enjoyed better number combination outcomes when number combination intervention was contextualized in word-problem instruction, with ESs of 0.69 versus 0.44. This advantage of 0.25 standard deviations for contextualized number combination intervention suggests that MD students take advantage of the word-problem context to strengthen performance on number combinations. By contrast, MD+RD students enjoyed superior number combination outcomes with decontextualized intervention that permitted an exclusive, more deliberate, and more intensive focus on number combinations. ESs were 0.38 versus 0.62, an advantage of 0.25 standard deviations for decontextualized intervention. MD+RD students’ greater challenges with oral language compared to MD (see Figure 1; ES = 0.53) may limit their opportunities for taking advantage of word problems to strengthen number combinations skill. Across MD and MD+RD, the ESs translate into a sizeable interaction of 0.50 standard deviations between number combination intervention approach and comorbidity status.

A single counting strategies lesson with versus without daily practice

The second pattern in the data concerns the amount of practice students need on number combinations. When we compared number combination intervention delivered without versus with daily timed practice in using counting strategies, MD students fared similarly in both conditions. ESs were 0.51 and 0.50. A single lesson on counting strategies, with encouragement for students to apply the strategies as needed, was as effective as daily practice designed to promote fluency with the strategies. But MD+RD students enjoyed a large advantage with daily practice, with ES of 0.34 versus 0.79. This again translates into an interaction of 0.50 standard deviations between number combination intervention approach and comorbidity status. It suggests the need for deliberate practice for MD+RD, but not MD students. This may be the result of MD+RD students’ greater challenges with phonological processing compared to MD (see Figure 1, ES = 0.74 and Figure 2), which underpins counting skill, which is in turn required for counting strategies.

Figure 2.

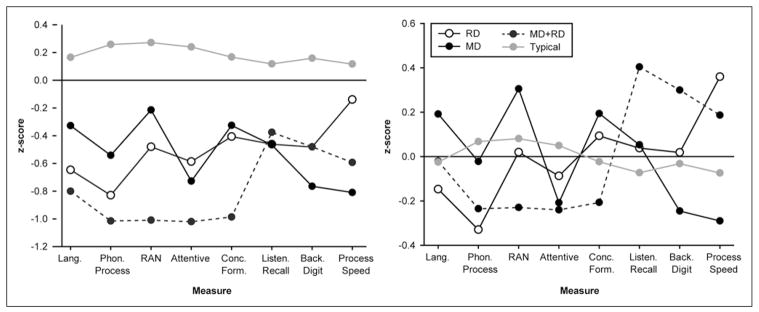
Cognitive profiles for RD vs. MD vs. MD+RD vs. typically developing, zero-centered and with a 95% confidence interval around that group’s grand mean superimposed on the graph (classifications based on word-level and calculation skill). Lang. is oral language; Phon. Process. is phonological processing; Attentive is teacher ratings of attentive behavior; Conc. Form. is concept formation; Listen. Recall is listening recall span; Count. Recall is counting recall; Back. Digit is backward digit span; Process. Speed is processing speed. RD is students with reading disability; MD is students with mathematics disability; MD+RD is students with mathematics and reading disability; typical is typically developing students.

Differential Response on Word-Problem Outcomes

ESs for number combination outcomes are shown in Figure 3b. Across studies, overall response was stronger for MD over MD+RD, with mean ESs of 0.92 versus 0.66. This advantage for MD on word problems is consistent with Cirino et al. (2011) and other studies (L. S. Fuchs & Fuchs, 2002; Hanich et al., 2001). More interesting, however, within word-problem intervention, number combination practice advantaged word-problem outcomes more for MD than for MD+RD. For MD, the mean ES on word-problem outcomes was 0.80 when number combination practice was excluded from word-problem intervention, but increased to 0.98 when number combination practice was included in word-problem intervention. This is an advantage of 0.18 standard deviations for MD students when word-problem intervention allocates as little as 5 minutes of every 30-minute session to number combinations. By contrast, for MD+RD, there was no advantage on word-problem outcomes for incorporating number combination practice in word-problem intervention. The mean ES for word-problem intervention without a focus on number combinations was 0.70; for word-problem intervention with a focus on number combinations, 0.65.

This interaction between instructional approach and comorbidity status on word-problem outcomes, of approximately one fourth of a standard deviation, is consistent with Jordan’s (2007) proposal that different mechanisms underlie word-problem deficits. That is, number combination deficits contribute to MD students’ difficulty with word problems, whereas other problems account for MD+RD students’ difficulty with word problems. The cognitive profiles presented earlier suggest two abilities may help explain MD+RD students’ difficulty with word problems: (a) oral language, which appears implicated in MD+RD but not MD (ES = 0.53, which increases when LD classifications are based on higher-order skill, which we discuss below) and (b) concept formation, which appears differentially problematic for MD+RD (ES = 0.81; also see Figure 2). The overall advantage for MD over MD+RD students on word-problem outcomes also suggests the need for a more intensive emphasis on word problems for comor-bid students.

Insights Into Comorbidity and Mathematics Intervention

These patterns in the data suggest that for MD, word-problem and number combination difficulty may be remediated efficiently with word-problem intervention that also teaches students counting strategies to solve number combinations. There is no such indication for MD+RD students. These students appear to require intervention that is more deliberate, sustained, and elaborated. This is the case for promoting number combination outcomes. It is also the case for enhancing word-problem outcomes. Clearly, larger-scale studies, powered to reveal intervention ESs as small as 0.25, are required. Such research might productively explore, for example, the following questions: Is word-problem intervention with a focus on oral language or concept formation more effective for MD+RD than for MD? And does incoming oral language ability or concept formation moderate the effects of intervention with and without an emphasis on oral language?

Word problems present important oral language and concept formation challenges for all students. These include, for example, underdeveloped representations of relational terminology and constructions (e.g., words such as more, less, older, younger) and discriminating relational vocabulary and constructions from confusable ones (e.g., Tom has 5 more marbles than Jill, as in compare problems, vs. Tom had 5 marbles and then he got 2 more, as in change problems); confusion with pronoun antecedents; and underdeveloped representations of vocabulary related to taxonomic relations at superordinate levels (e.g., 2 dogs + 3 cats = 5 animals; see McGregor, Newman, Reilly, & Capone, 2002). It is possible that word-problem intervention that focuses on these oral language or concept formation demands may be differentially effective for MD+RD and that treatment may moderate the relation between oral language ability or concept formation and learning.

We might pose similar questions about number combination intervention. For example, is strategic number combination practice designed to address the cognitive weaknesses associated with MD+RD but not MD (e.g., phonological processing deficits, as in Figures 1 and 2) more effective for MD+RD than MD? And do such cognitive abilities moderate the effects of intervention condition? This type of intervention by subtype study has the potential to provide productive directions for treatment and provide insights into the nature of MD versus MD+RD. Pending such studies on word problems and number combinations, we tentatively suggest that the mathematics intervention needs of students with MD differ from those with MD+RD. If so, it may be useful to screen for these subtypes and deliver intervention in different ways, perhaps at a more intensive level of the prevention system for MD+RD. In addition, the following questions arise: Can we provide reading comprehension instruction in the context of word problems, or is word-problem comprehension distinct from comprehension of other genres? Do MD and MD+RD respond differentially to intervention on other strands of math curriculum? And do MD+RD students require more “personalized” intervention in which teachers use ongoing progress monitoring and periodic diagnostic assessment to individualize programs?

Does Number Combination Intervention Enhance Reading Performance? RD Versus MD+RD

These findings raise another question: Given the multiple academic needs associated with comorbid disorder, in combination with the demand for these students to participate in the general education curriculum, can we configure intervention in efficient ways to simultaneously address more than one academic need? This question pertains to mathematics as well as reading. In this section, we turn our attention to reading, where researchers have allocated less attention to the issue of comorbidity. It is clear, however, that students with comorbid difficulty have more severe reading deficits compared to students with RD, even as comorbid students require additional intervention to address their mathematics difficulty. Moreover, at first grade, it is possible that two foundational component skills, word-level reading and number combinations, are linked via phonological processing—as suggested in Figure 1, as well as RAN. So it seems reasonable to ask whether intervention may be efficiently designed to address word-level skill and number combinations. We next summarize findings from a randomized control trial, in which we examined whether first-grade word-level reading intervention and number combination intervention may operate in synergistic ways to benefit reading development and whether such effects differ as a function of comorbidity status (RD vs. MD+RD).

Participants and Study Design

The study was conducted in 17 Nashville schools. Across two cohorts, we identified 300 first-grade students with high risk of RD in the following way. Teachers selected the lowest-performing students in their classes on reading. We then assessed these children on multiple reading measures, combining performance into a single factor score. The bottom half of the distribution was tested on the Vocabulary and Matrix Reasoning subtests of the Wechsler Abbreviated Scale of Intelligence, and only children with T-scores greater than or equal to 37 on either subtest were included. Finally, we included English language learners if they had achieved an Early Advanced proficiency score on the district assessment at end of kindergarten. Mathematics performance in the sample was allowed to vary.

We randomly assigned these children to a control group (no researcher-delivered intervention) or to one of two tutoring conditions: reading intervention alone (primarily at the word level) versus the same reading intervention combined with number combination intervention. Tutoring occurred three times per week for 20–24 weeks for 30–45 minutes per session. Attrition was similar across the three conditions, with 277 children remaining at the end of first grade. Fidelity of intervention implementation, on a random sample of audiotapes representing tutors, conditions, tutoring sessions, and children in similar ways, was comparable and strong. We designated RD as performance below the 25th percentile on a latent factor representing multiple pretest word-level reading scores. We classified MD+RD as concurrently performing below the 25th percentile on a calculations measure. Approximately equal numbers of the 277 students were RD and RD+MD in each condition.

Reading Intervention

Reading intervention focused on sight-word recognition, decoding, spelling, and fluency. Each lesson comprises seven activities. The first is practice on sight words that came from two sources: all sight words from a previous reading intervention (Al Otaiba & Fuchs, 2006; D. Fuchs, Compton, Fuchs, & Davis, 2008; D. Fuchs et al., 2001; McMaster, Fuchs, Fuchs, & Compton, 2005) and, to enlarge the pool, all words from the first and second grade levels of the school system’s core reading program. The combined corpus was 358 words, ordered in terms of importance by weighting them on two factors: the natural log-adjusted rank of the word in the Educator’s Word Frequency Guide (Zeno, 1995) and the natural log-adjusted number of vowels in the word. (We relied on these factors because they proved useful in predicting performance in a previous database.) In each lesson, 12 sight words are addressed. The tutor reads a word, and the student repeats it. This recurs twice, but if the child misses any word, the activity is repeated later in the lesson. Then, the student reads the words and earns a point for each word read correctly.

In the second activity, the student learns and practices sound–symbol correspondences. In addition to single phoneme–grapheme correspondences, tutors teach digraphs, vowel-consonant-E, phonograms (i.e., word families), the past tense (i.e., the sounds of –ed), and letters or digraphs representing multiple phonemes (e.g., y, ow). The tutor introduces each sound with its visual representation of the correspondence (e.g., snake for the /s/ sound). After introducing all new sound–symbol correspondences for that (lesson typically six or seven per lesson), the child pronounces the review sound–symbol correspondences. Then, the student identifies the sound for each letter, without the support of the visual representation.

The third activity is decoding, which relies on “tapping and sounding out.” The tutor points to each grapheme in a word, with dots shown under single-letter graphemes and lines under digraphs and vowel-consonant-E patterns. The tutor pronounces each sound, tapping each dot or line; then, reads each word slowly; finally, reads the word naturally. The student completes the same cycle. Once the student has read all words in this way, he or she reads each word independently and earns one point for every word read correctly without help. Fourth, the student uses tiles to spell words used during the decoding activity and several other decodable words already mastered. Each tile contains a single sound–symbol correspondence taught (digraphs and phonograms are written on a single tile). Following de Graaff, Bosman, Hasselman, and Verhoeven (2009), the tiles avoid students engaging in laborious writing.

Fifth, the student reads difficult sight words from the lesson story. The tutor reads these words; the student repeats them. Then, the tutor and student read a short section of a longer story. For this activity, 10 trade books were ordered in difficulty. The tutor reads the original trade book to the child on the initial day with that story; the student reads the text to the tutor from that trade book on the last day with that story. In the intervening days, sections of the trade book, reproduced on separate typed pages, are read aloud as follows. The tutor and student read aloud and at the same time from the section read the previous day. Then, the tutor reads a sentence on the day’s section, and the student immediately reads the same sentence, proceeding in this way through all sentences in the day’s section. Next, the tutor and student read the section together. Finally, the student reads the section twice independently. The tutor times these readings, encouraging faster reading the second time. If the student achieves that, he or she earns a point.

Seventh, students have 30 seconds to read as many words as possible from a sight word list, ordered from high to low frequency. Once the student reads a word correctly in three consecutive lessons, the word is removed from the list. The tutor awards one point for each word read correctly after the 30 seconds has elapsed. The tutor then provides corrective feedback using one of these strategies, depending on the word: reminding students sight words have to be memorized, using the word in a sentence, identifying salient letters that help pronunciation, or discussing the length of the word. At the end of the day’s lesson, the tutor awards a sticker if the child has demonstrated strong effort during that day’s lesson.

Number Combination Intervention

We relied on a modified version of counting strategies, in conjunction with number knowledge instruction to support understanding of the counting strategies and number combination principles. The modified counting strategies were designed to reduce the motor demands involved in the third-grade counting strategies described above. The tutor provides practice to support fluent use of these counting strategies and correct responding by requiring children to “know it or count” and requiring them to immediately correct errors using counting strategies.

Using the “Meet or Beat Your Score” activity, students have 90 seconds to answer flash cards. The student answers each problem presented correctly because, as soon as an error occurs, the tutor requires the student to use counting to correct the response. The 90 seconds continue to elapse as the student uses the counting procedure (as many times as needed). In this way, careful but quick responding increases the number of correct responses, which are counted and charted at the end of 90 seconds. Then, students have two chances to meet or beat that score.

Patterns in the Data

Based on this sample of first graders at high risk for RD, some of whom had concurrent MD, findings indicated the following. Across RD and MD+RD groups, reading intervention combined with number combination intervention produced reliably stronger number combination outcomes compared to reading intervention alone and compared to the control group. ESs were large (0.57 and 0.60). This is not surprising. Only number combination intervention was designed to enhance number combination outcomes. Effects on reading performance were more interesting. With pretreatment performance and effects of cohort controlled, students who received combined intervention (word-level reading intervention plus number combination intervention) outperformed students in the control group, with ESs of 0.56 and 0.39 on timed and untimed reading outcomes (across word and nonword measures), respectively. By contrast, children who received reading intervention alone did not reliably outperform students in the control group. Most interesting, improvement in number combinations fluency fully mediated group differences between the combined and reading-only interventions on both timed and untimed reading outcomes, and improvement in number combinations fluency partially mediated the difference between the combined intervention and control groups on the timed reading outcome.

That number combinations intervention should improve reading performance and that improvement in number combination fluency should mediate reading outcomes create the basis for hypothesizing that these lower-order reading and mathematics skills overlap in some important ways, that some of the same cognitive abilities contribute to both forms of academic competence. This was hypothesized by Geary (1993) and is suggested in some cognitive profiles involving students with comorbid disorder (e.g., Cirino et al., 2011). Some potentially implicated cognitive abilities are rapid naming and phonological processing (see Figures 1 and 2). In fact, as Koponen and Salmi (2011) reported, counting was a strong predictor of the covariance between word reading and calculation fluency, and kindergarten counting and rapid naming predicted reading as well as calculation fluency in Grades 2 and 3. After controlling for the effects of phonological awareness, counting uniquely accounted for 63% of the explained variance in number combination fluency; 11% in word reading fluency. RAN uniquely accounted for another 9% of explained variance in word-reading fluency (directly and indirectly through counting) and 9% in number combination fluency (indirectly through counting). Therefore, counting and RAN appear to predict word reading (as well as calculation fluency) among a sample with high prevalence of RD, and, in a representative sample, these associations remain even after controlling for the effects of verbal short-term memory and working memory.

At the same time, it is interesting to consider whether the effects of number combination intervention on word-level reading outcomes pertain across RD and MD+RD students or whether comorbidity status moderated these effects. In fact, we found no interaction between comorbidity status and condition, and ESs for RD versus MD+RD were not meaningfully different.

Insights Into Comorbidity and Reading Intervention

Additional insight into connections between word-reading and number combination fluency may be provided by studies that examine (a) whether improvement in RAN and phonological processing (as well as combination fluency) mediate the effects of word-level reading outcomes (and vice versa), (b) whether number combination intervention with word-level reading intervention is superior to number combination intervention alone in promoting number combination outcomes, and (c) whether phonological processing training improves number combination outcomes.

Studies with larger samples are also warranted on related questions assessing whether intervention on other aspects of reading and mathematics performance act in synergistic ways. For example, researchers might productively ask whether word-problem performance improves response to certain forms of reading comprehension instruction or whether reading comprehension performance improves in response to certain forms of word-problem instruction. At the same time, it is reassuring to find that comorbidity status did not moderate intervention effects. That is, RD and MD+RD students’ reading development benefited in similar ways from an intervention focus on mathematics. Pending additional studies on the effects of number combination intervention on reading outcomes, we tentatively suggest that the early word-level intervention needs of students with RD and RD+MD may be addressed more effectively by combining word-level reading intervention with number combination intervention. This also indicates the multifaceted needs of MD+RD children may be more efficiently addressed with intervention carefully designed to address cognitive limitations that contribute to reading as well as mathematics difficulty.

Caveats and Conclusion

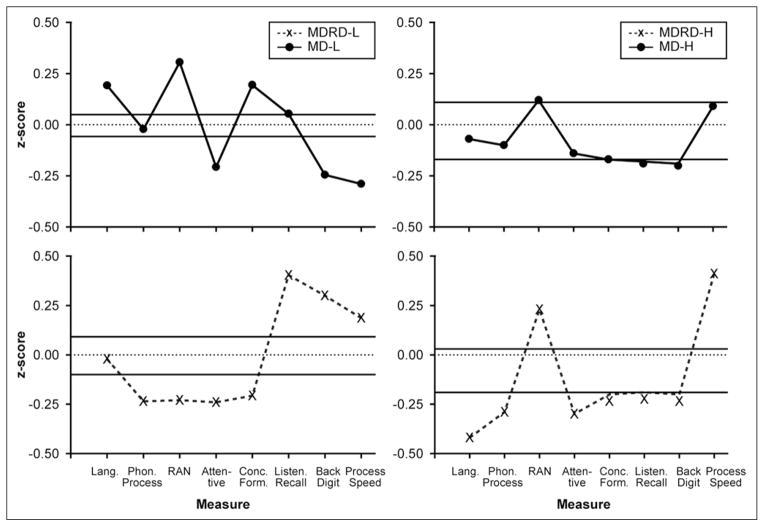
Before closing, we remind readers that the research discussed in this article, in combination with other available findings, constitutes a small literature for drawing conclusions about comorbidity as a framework for subtyping LD. We also note that LD classification in the mathematics and reading literatures (as reflected in comorbidity research) is commonly based exclusively on lower-order forms of academic competence (i.e., word-level and calculation skill; see Vukovic, Lesaux, & Siegel, 2010, for an exception). Given a lack of focus on higher-order comorbidity, for the present article, we examined cognitive profiles for lower- versus higher-order MD definitions. In Figure 4, the left panels show cognitive profiles for students with and without comorbidity, when LD is defined on lower-order skill (with 33 MD-L and 25 MD+RD-L). The right panels show students with and without comorbidity, when LD is defined instead on reading comprehension and word-problem skill (i.e., higher-order skill, with 42 MD-H and 36 MD+RD-H). Note that the left panels in Figure 4 are the same the right panels in Figure 2: both for lower-order MD definitions. We include them again in Figure 4 for ease of inspection. These left panels in Figure 4 show that oral language is a distinctive dimension of MDRD-L versus MD-L, because oral language is a strength for MD-L (relative to MD-L students’ other cognitive abilities). But on the right (with LD defined on higher-order skill), oral language is a distinctive dimension because oral language is a relative weakness for MDRD-H, but not for MD-H. In fact, oral language is the strongest contributor to the distinction between the two subtypes. So LC appears implicated in comorbid LD, but only when LD is defined on higher-order skill. These findings suggest the need for research on higher-order comorbidity.

Figure 4.

Cognitive profiles for lower-order MD definition (MD-L vs. MD+RD-L; left panels) and higher-order LD definition (MD-H vs. 36 MD+RD-H; right panels). Lang. is oral language; Phon. Process. is phonological processing; Attentive is teacher ratings of attentive behavior; Conc. Form. is concept formation; Listen. Recall is listening recall span; Count. Recall is counting recall; Back. Digit is backward digit span; Process. Speed is processing speed. MD-L is students with mathematics disability, defined as low calculation skill; MD+RD-L is students with mathematics and reading disability, defined as low calculation and low word-reading skill. MD-H is students with mathematics disability, defined as low word-problem skill; MD+RD-H is students with mathematics and reading disability, defined as low word-problem and low reading comprehension skill.

With these caveats in mind, we tentatively conclude that the comorbidity framework for subtyping LD may be more valid in mathematics than in reading. The mathematics studies presented in this article suggest that MD and MD+RD represent different forms of mathematics LD, with a distinctive pattern of cognitive abilities, which is reflected in varying response to alternative forms of mathematics intervention. On the other hand, the reading study suggests that comorbid and RD students respond in similar ways, at least when reading and number combination intervention is manipulated. This does not indicate RD and MD+RD are different forms of LD and does not provide support for distinguishing between instructional design for RD versus MD+RD. Even so, available studies are small for detecting interactions, and, as reflected in Figures 1, 2, and 4, comorbid disorder may be associated with a unique pattern of cognitive abilities. So additional intervention research is warranted, and some of those studies might contrast classifications based on lower- versus higher-order forms of reading and mathematics performance.

Comorbidity research is important because despite advances in the treatment of LD, direct skills instruction, the dominant, validated approach to intervention, fails to meet the needs of 25% to 40% of LD students (e.g., D. Fuchs et al., 2012; Fuchs, Fuchs, Craddock et al., 2008; L. S. Fuchs et al., 2012). Understanding student characteristics that distinguish single-deficit versus comorbid disorders and patterns of distinctive response to alternative forms of intervention may help explain such nonresponse. This in turn may provide insights for expanding the framework for intervention design and improving academic outcomes.