Protein kinetics: Structures of intermediates and reaction mechanism from time-resolved x-ray data

Abstract

We determine the number of authentic reaction intermediates in the later stages of the photocycle of photoactive yellow protein at room temperature, their atomic structures, and a consistent set of chemical kinetic mechanisms, by analysis of a set of time-dependent difference electron density maps spanning the time range from 5 μs to 100 ms. The successful fit of exponentials to right singular vectors derived from a singular value decomposition of the difference maps demonstrates that a chemical kinetic mechanism holds and that structurally distinct intermediates exist. We identify two time-independent difference maps, from which we refine the structures of the corresponding intermediates. We thus demonstrate how structures associated with intermediate states can be extracted from the experimental, time-dependent crystallographic data. Stoichiometric and structural constraints allow the exclusion of one kinetic mechanism proposed for the photocycle but retain other plausible candidate kinetic mechanisms.

The protein structures associated with short-lived intermediate states (ISs) that form and decay along a reaction pathway must be determined if the structural basis of function is to be fully understood. Models for such states are normally determined by physical or chemical trapping techniques designed both to greatly increase the lifetime of a particular state and to trap a structurally homogeneous species (1–4). However, the trapping techniques themselves may perturb the mechanism and the observed species may still not be structurally homogeneous (5). If homogeneous structures along the reaction path could be determined directly by using unmodified protein and reactants at near-physiological temperatures, the difficulties associated with trapping could be overcome.

The reaction pathway of a protein is typically described by a chemical kinetic mechanism populated by a reactant state, a set of ISs, and a product state. For such a mechanism to hold, the transit time of an individual molecule from each state to its neighboring state(s) must be short, compared with the lifetimes of the states themselves. That is, equilibration across all other degrees of freedom must be fast with respect to progress along the reaction pathway. The time scales of structural transitions in proteins range from picoseconds for side-chain relaxations (6) to several nanoseconds for protein backbone relaxations (7). Such protein-specific motions are thought to enable both the transitions between protein conformations or substates within a single state (8, 9), and those between ISs. If the lifetime of an IS is short compared with the time scales of protein-specific motions, a simple chemical kinetic mechanism (10) is unlikely to hold. If the converse is true, those distinct ISs that accumulate to sufficiently high concentration will be observable. If first-order reactions are considered, the rise and fall of the concentration of each state will be describable by a sum of exponentials.

With time-resolved Laue x-ray crystallography (11), we are able to collect accurate structure amplitudes to high resolution, covering the time scale from 100 ps to hours after reaction initiation (12). By comparing the structure amplitudes before initiation with those after a time delay, we obtain time-dependent difference electron density maps that provide a detailed picture of the structural changes as the reaction proceeds, without any trapping (13–18). However, whether or not a simple chemical mechanism holds, several ISs are likely to be populated at all time delays; the difference electron density features associated with each intermediate overlap in each map. Our goal is to identify the number of intermediates and obtain the time-independent structure of each. The time-dependent difference maps must therefore be separated into a small set of homogeneous, time-independent difference maps, one per intermediate. The initial stages of this separation are achieved by applying singular value decomposition (SVD) to the series of experimental, time-dependent difference maps (19). SVD analysis partitions the complete, time- and real space-dependent data matrix A into left singular vectors (lSVs) in matrix U, each of which contains time-independent structural information; right singular vectors (rSVs) in matrix V^T, each of which contains the time dependence of the corresponding lSV; and the SVs in the diagonal matrix S, which serve as weighting factors (19, 20), according to the equation A = USV^T.

Analysis of the rSVs determines whether or not they can be represented by a sum of exponentials. If so, a chemical kinetic mechanism is likely to hold, and the number of relaxation times is obtained directly (19, 20). This number imposes a powerful constraint on the mechanisms that are consistent with the data.

We demonstrate here, to our knowledge, the first application of SVD to experimental, time-resolved crystallographic data, and the extraction of time-independent intermediate structures. We investigate structural changes taking place in the photocycle of photoactive yellow protein (PYP) from Halorhodospira halophila (21). PYP is a blue light photoreceptor believed to be involved in the regulation of negative phototaxis (22) in various photosynthetic bacteria (23). Absorption of a photon of blue light triggers trans-to-cis isomerization of the chromophore of PYP, p-coumaric acid, and entry into a photocycle containing a series of at least six spectroscopically distinct states (24–28). The structures believed to be associated with three of these spectroscopic states have been characterized by physical trapping at cryogenic temperature (ref. 29; PDB ID code 3PYP), by establishing a photostationary state at room temperature (ref. 30; PDB ID code 2PYP), and by examination of a single time point in a pump-probe, time-resolved experiment at room temperature (ref. 31; PDB ID code 2PYR). A limited, time-dependent set of difference maps for PYP was subjected only to qualitative interpretation, and no intermediate structures could be extracted (15). Here, we quantitatively determine the structures of intermediates and identify plausible kinetic mechanisms from an entire time course of difference maps spanning the later stages of the photocycle of PYP.

Materials and Methods

Laue Data from PYP. Holo-PYP was expressed, purified, and crystallized as described (15). Typically, crystals of 110 μm in diameter and various lengths were used. The reaction was initiated by an intense 7 ns (full width at half maximum) laser flash of 485 nm wavelength from a neodymium:yttrium-aluminum-garnet pumped dye laser. The crystal structure was probed at 15 time delays by an intense polychromatic x-ray flash. All Laue data sets were collected at the BioCARS 14-ID beamline, Advanced Photon Source, Argonne National Laboratory (Argonne, IL), except 9 μs, 51 μs, and 8dk, which were taken from data cited in ref. 15. Raw data were reduced with laueview (32, 33). Data statistics are shown in Tables 1 and 2. Weighted difference maps, Δρ(t), were calculated according to data cited in refs. 15 and 19. Variation of photoactivation due to fluctuation of the laser power was taken into account by assuming a constant laser beam diameter and, hence, normalizing to a laser pulse energy of 4 mJ. Accordingly, the difference maps were multiplied before further analysis by a factor 4.0/E_laser. The factors for the 9- and 51-μs maps were found to be overestimated, because they appear as outliers in the rSV. Outliers were corrected as demonstrated (19). The correction factor for both the 9- and 51-μs maps was 1.3.

Table 1. Statistics of the time-dependent Laue data sets.

Values
Δt laser to x-ray	5 μs	9 μs	20 μs	51 μs	125 μs	250 μs	500 μs	850 μs	1 ms	2 ms	5 ms	7 ms	15 ms	30 ms	100 ms
dmin,a Å	1.85	1.6	1.85	1.6	1.9	1.7	1.7	1.75	1.8	1.7	1.9	1.8	1.7	1.6	1.6
X-ray sourceb	U	W	U	W	U	W	W	U	U	U	U	U	U	W	W
Detectorc	CCD	II	CCD	II	IP	IP	IP	CCD	IP	IP	IP	IP	CCD	IP	IP
ELaser,d mJ	3.2	2.2	3.2	2.2	4.2	4.5	4.5	2.6	4.2	4.5	4.5	3.6	3.6	4.5	4.5
Redundancye	6.8	9.9	6.5	9.7	8.4	6.6	7.3	9.1	8.5	9.1	9.5	8.0	12.3	8.1	9.3
Completeness,f %	83.0	80.0	81.4	80.0	82.1	87.9	87.3	85.3	81.5	87.0	88.1	80.8	88.5	86.9	87.5
∞-3.5 Å	97.0	92.2	95.3	93.4	98.6	97.8	97.0	98.0	97.6	98.3	99.0	96.5	99.0	97.9	97.7
Last shell	53.5	46.4	48.7	46.3	49.3	58.9	59.0	54.2	48.3	59.0	63.5	45.9	57.5	55.0	54.1
Rmerge,g %
on |F|	7.5	3.8	6.8	3.8	8.2	4.4	5.7	4.8	7.4	6.3	4.7	4.9	4.1	3.6	4.0
on |F|2	17.2	10.2	16.8	10.3	17.0	11.0	13.5	10.9	15.7	12.8	10.6	10.9	11.5	9.2	9.8
Reference darkh	1dk	2dk	1dk	2dk	3dk	4dk	4dk	5dk	6dk	6dk	6dk	5dk	7dk	4dk	4dk
Rscale,i %	14	15	13	15	9	16	13	7	9	7	8	9	7	8	8
〈|ΔF|〉j	31.0	20.6	27.0	21.8	20.7	26.5	23.3	13.2	17.8	13.6	12.7	15.0	11.8	13.2	10.8
〈 σ〈|Δ|〉 〉k	5.3	9.2	5.0	9.2	12.9	10.4	5.4	7.0	5.4	5.1	6.4	8.5	7.8	7.1	7.9
〈weight〉l	0.53	0.56	0.54	0.57	0.49	0.46	0.49	0.55	0.46	0.49	0.50	0.53	0.56	0.50	0.51

^aResolution limits at ≈50% completeness in the last-resolution shell (≈d_min + 0.1 Å). All difference maps calculated to 1.9-Å resolution.

^bW, wiggler, U, undulator.

^cCCD, ADSC Quantum-4 CCD detector; II, Thompson image intensified CCD detector; IP, MAR345 image plate detector.

^dEnergy of laser pulse.

^eCalculated from single reflections only.

^fCalculated from all reflections, including harmonics.

^gR_merge (|F|) = Σ ||F| - 〈|F|〉|/Σ |F| where 〈|F|〉 is the mean amplitude of multiple observations and symmetry measurements. R_merge (F²) = Σ ||F|² - 〈|F|²〉|/Σ |F|² where 〈|F|²〉 is the mean intensity of multiple observations and symmetry measurements.

^hDark data sets used to calculate difference maps; 6dk was also used for the 250- and 500-μs time points, because no dark data were collected on this crystal.

ⁱR_scale = Σ ||F_t|² - |F_D|²|/Σ |F_D|² after scaling of the time-dependent (|F_t|) to the dark (|F_D|) data sets.

^jMean of the absolute difference amplitudes.

^kMean error of the difference amplitude.

^lAverage weight for map calculation.

Table 2. Statistics of the dark Laue data sets.

	1dk	2dk	3dk	4dk	5dk	6dk	7dk
dmin,* Å	1.65	1.6	1.8	1.55	1.75	1.75	1.65
X-ray source†	U	W	U	W	U	U	U
Detector‡	CCD	II	IP	IP	IP	IP	CCD
Redundancy§	11.6	12.7	9.5	7.6	8.9	9.4	11.0
Completeness,¶ %	86.3	92.0	81.1	88.9	85.2	83.8	81.5
∞-3.5 Å	97.3	91.9	98.8	97.6	99.6	98.7	98.8
(last shell)	54.9	84.9	49.5	57.6	55.8	51.9	44.8
Rmerge,∥ %
on |F|	3.6	4.1	6.0	2.9	3.9	2.9	2.7
on |F|2	8.1	10.6	10.6	7.7	8.1	6.8	6.0

^*Resolution limits at ≈50% completeness in the last-resolution shell (≈d_min + 0.1 Å). All difference maps calculated to 1.9-Å resolution.

^†W, wiggler; U, undulator.

^‡CCD, ADSC Quantum-4 CCD detector; II, Thompson image-intensified CCD detector; IP, MAR345 image plate detector.

^§Calculated from single reflections only.

^¶Calculated from all reflections including harmonics

^∥R_merge(|F|) = Σ ||F| - 〈|F|〉|/Σ |F| where 〈|F|〉 is the mean amplitude of multiple observations and symmetry measurements. R_merge(F²) = Σ ||F|² - 〈|F|²〉|/Σ |F|² where 〈|F|²〉 is the mean intensity of multiple observations and symmetry measurements.

SVD-Driven Analysis. SVD flattening with phase recombination was performed with the time series of difference maps as outlined in ref. 19 with the following extensions. In the first round of phase improvement we used |Δρ| > 2σ for the SVD and gradually decreased this level in subsequent rounds to accept all grid points of the difference map. For the phase recombination, we used modified Laue amplitudes: |F|′ = |F_t| + (|F_D|^calc – |F_D|^obs), where |F_t| are the measured, time-dependent Laue amplitudes, |F_D|^calc are structure amplitudes calculated from the dark-state model (34), and |F_D|^obs are structure amplitudes collected without laser illumination, typically from the same crystal as |F_t|. Throughout, we used weighted difference amplitudes, w|ΔF_t| (15, 19). Difference maps Δρ(t)^svd from the last step of the iterative phase improvement established the data matrix A′, which was used for the final decomposition. The rSVs were fit by concentrations derived from candidate kinetic mechanisms. The candidate mechanisms were selected from the general mechanism, which accounts for the number of relaxation times observed. The time-independent difference maps Δρ_Ij were generated by projection, using the fitted concentrations (19).

Modeling the Structures of the Intermediates. Extrapolated electron density maps were used to model the structures of the intermediates. We calculated difference structure factors ΔF_Ij for each IS from a spherical volume of the time-independent difference map Δρ_Ij with radius 15 Å centered on atom C4 of the PYP chromophore. We added multiples of ΔF_Ij to the structure factors 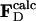to generate extrapolated structure factors: 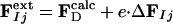. The factor e compensates for the missing scale in the rSV and for the occupancy values of the intermediates being <10%. It can be selected so that the map calculated from 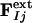does not contain negative features on the phenolate oxygen of pCA or on residues Arg-52 and Tyr-42. Conventional electron density maps for each intermediate, 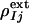, were calculated from 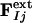. The atomic structures modeled into these maps were refined against the extrapolated amplitudes by using cns (35).

Posterior Analysis. Posterior analysis uses stoichiometric and structural constraints with the goal of identifying and excluding mechanisms that are incompatible with the data. The major difficulty is that a common scale is absent in the rSVs (36). The central idea of the posterior analysis is to restore a common or absolute scale by using calculated difference electron density values, which are equivalent to fractional concentration. This analysis can be performed after the structures of the intermediates are determined. Posterior analysis consists of two parts: computational and structural. Initially, the relaxation times are determined from the global analysis of the rSV. The rate coefficients can be uniquely determined only if the number of observed relaxation times is larger than or equal to the number of rate coefficients in the mechanism (37). This result is not normally the case. This situation may be resolved by putting the data on an absolute scale, which is equivalent to introducing stoichiometric constraints. Structural constraints can be introduced to allow a further level of discrimination. Thus, both the absolute values and the shapes of the functions which describe the time-dependent concentrations of the intermediates contribute to discrimination between the mechanisms (19).

The refined structures of the N intermediates (derived from the SVD analysis) and the dark state are used to derive structure factors F₁ ··· F_N and F_D and time-independent difference structure factors F₁–F_D, F₂–F_D ··· F_N–F_D. From these factors, N time-independent difference maps 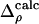are calculated. The time-dependent difference maps Δρ(t, k)^calc can then be determined on the absolute scale by using the concentrations c_n(t, k) of each intermediate, which depend on time t, on the candidate kinetic mechanism itself, and the rate coefficients k in the particular candidate mechanism (18). The observed difference maps Δρ(t)^svd were fit to the calculated difference maps Δρ(t, k)^calc at all time points t (t = 1···T) by using M map grid points in the entire protein region (Eq. 1). Minimization was achieved by varying the rate coefficients k.

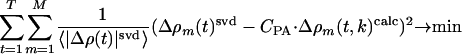[1]

The summation is evaluated at those points m, where the magnitude of the difference electron density in the observed and calculated difference maps exceeds 2σ or falls below –2σ. The fit is weighted by the average of the absolute difference electron density in the observed, SVD-flattened difference maps, 〈|Δρ(t)|^svd〉. C_PA corresponds to the fractional concentration of activated molecules at the beginning of our analysis and is equivalent to the constant of integration in the solutions to the coupled differential equations, which describe the mechanisms. C_PA was determined from the first two pairs of observed and calculated difference maps. The uncertainties of the fits were estimated for each time-point from the overall sigma values σ^svd in the observed, SVD-flattened maps (Eq. 2):

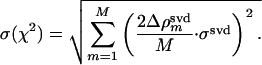[2]

If the assumed mechanism is incorrect, then the concentrations are also incorrectly determined and the Δρ(k, t)^calc do not fit the experimental, difference maps Δρ(t)^svd. That is, significant density remains in the time-dependent residual maps ΔΔρ(t, k) = Δρ(t)^svd – Δρ(k, t)^calc.

Results and Discussion

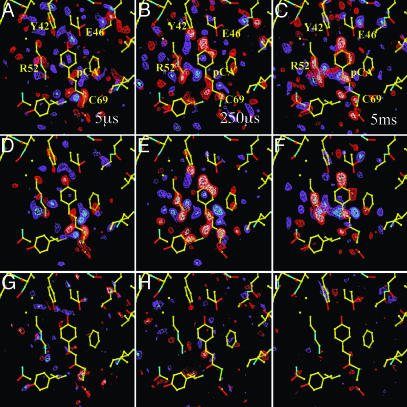
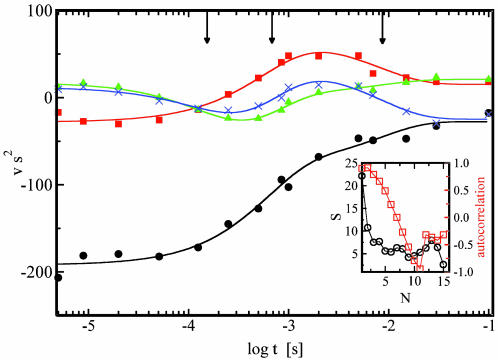
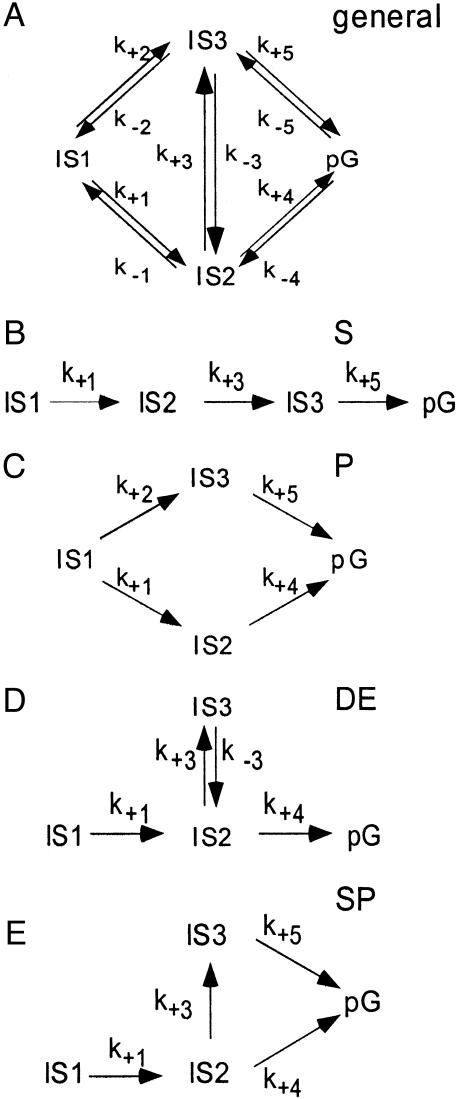
We probe the time-dependent evolution of structural changes in PYP by analyzing the 15 Laue data sets at time delays ranging from 5 μs to 100 ms after initiation of its photocycle by the ns laser pulse. The temporal array of the resulting 15 difference maps constitutes the data matrix A to be decomposed by SVD. From the 15 SVs and their associated lSVs and rSVs, only four contain significant structural signals by the criteria of Schmidt et al. (19). In Fig. 1, the experimental difference maps for three representative time delays are shown (Fig. 1 A–C) together with the corresponding SVD-flattened maps (19) reconstructed from the four significant lSVs (Fig. 1 D–F). Reconstruction with the remaining 11 lSVs displays only noise (Fig. 1 G–I) and thus confirms that signal is confined to the first four lSVs. The SVD procedure results in greatly reduced noise (compare the noise levels in the time-dependent, experimental time series and the SVD-derived time series provided by Fig. 6, which is published as supporting information on the PNAS web site). The four significant rSVs could be globally fitted by a sum of three exponentials with relaxation times of 170 μs, 620 μs, and 8.5 ms (Fig. 2). We draw two important conclusions: a simple chemical kinetic mechanism is likely to hold in this time domain; and the existence of three relaxation times shows that this mechanism must contain at least four states (Fig. 3). However, a consequence of the closely spaced relaxation times is that there is no time range within which the difference electron density is essentially constant and the underlying structure is homogeneous. Even a perfect trapping experiment would yield a heterogeneous mixture of structures. A structural interpretation is extremely difficult, unless the composite is separated into its pure, authentic components, which can be performed by fitting kinetic mechanisms to the rSVs (19).

Fig. 1.

The effect of SVD flattening. (A–C) Experimental, weighted difference electron density maps at representative time delays of 5 μs, 500 μs, and 2 ms, respectively. Contour level: red/white –2.5/–3.5 σ, blue/cyan 2.5/3.5 σ. (D–F) SVD-flattened difference electron density maps reconstituted with the first four significant singular vectors and values, lSV 1–4 at time delays as in A–C. Contour level: red/white –3/–4 σ, blue/cyan 3/4 σ. Yellow atomic structure: structure of the dark state, the chromophore pCA, and the residues Arg-52, Tyr-42, and Glu-46 are marked. (G–I) SVD-flattened difference electron density maps reconstituted with the 11 remaining singular vectors. Maps are at the same time points as in A–C and are reconstituted with the insignificant SVs and vectors, lSV 5–15. Contours on same sigma level as for D–F.

Fig. 2.

The time dependence of the rSVs. •, first rSV; ▪, second rSV; ▴, third rSV; X, fourth rSV; lines: global fit by a sum of three exponentials. Three relaxation times are marked by arrows. (Inset) Magnitude of the SVs, ○, and autocorrelation (AC), □, of rSVs.

Fig. 3.

The chemical, kinetic mechanisms. (A) General chemical, kinetic mechanism that generates three relaxation times. The state IS1 is the first observed intermediate after the illumination of the dark state pG. The activated molecules relax through two ISs, IS2, and IS3, to the dark state pG. The direct path from IS1 to the dark state pG is not considered. (B–E) Subsets of the general scheme compiled by setting certain rate coefficients to 0. (B) S, Irreversible, sequential mechanism. (C) P, Parallel mechanism. (D) DE, Mechanism with a dead end. (E) SP, Semiparallel mechanism.

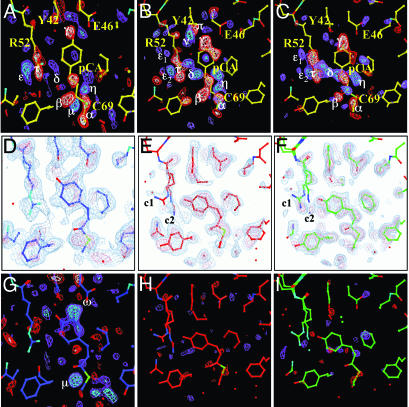
Four simpler candidate mechanisms (sequential, semiparallel, dead end, and parallel) are chosen from the general mechanism containing four states (Fig. 3A) by setting selected rate coefficients to 0. For each of the four candidate mechanisms, three time-independent difference maps, each associated with one of the ISs IS1, IS2, and IS3, can be obtained by fitting the remaining rate coefficients to the observed relaxation times, and identifying the contribution of all four lSVs to each state (see Eqs. 8–10 in ref. 19). We find that in this case, all four candidate mechanisms generate three qualitatively similar difference maps. That is, the maps do not distinguish between correct and incorrect candidate mechanisms. However, these maps do enable us to determine intermediate structure(s) by examining the three corresponding electron density maps calculated from extrapolated structure amplitudes. We find that the map representing the IS1 state populated between 5 and ≈200 μs does not represent a unique structure (Fig. 4D) and hence a unique atomic model could not be refined. When we tried to model a single chromophore conformation (blue in Fig. 4) into the electron density, the residual map (Fig. 4G) clearly showed the large features Ω and μ; we conclude that the chromophore conformation is heterogeneous. We believe that this heterogeneity is the result of the fact that the 5-μs time point occurs in the middle of the photocycle. An earlier intermediate with a different chromophore conformation may also contribute to the electron density. Indeed, there is both spectroscopic (27, 28) and structural (15) evidence of heterogeneity in this time range, associated with the pR spectroscopic state.

Fig. 4.

The time-independent density maps. (A–C) Time-independent difference electron densities Δρ of intermediates IS1, IS2, and IS3, respectively. Contour levels: red/white –4/–6 σ, blue/cyan 4/6 σ. Yellow atomic structure: structure of the dark state; blue, red, and green atomic structures: structures of the intermediates IS1, IS2, and IS3, respectively. The chromophore pCA, Cys-69, Arg-52, Tyr-42,and Glu-46 are marked in A. Difference electron density features in A–C: negative features α,β,γ and positive features μ, η, δ are associated with the chromophore; positive features ε, ε₁, ε₂ and negative feature τ are associated with Arg-52; features ν (positive) and π (negative) belong to Tyr-42. (D–F) Extrapolated, electron density maps used to model the intermediate structures IS1, IS2, and IS3, respectively. In D, the same residues as in A are marked; c1 and c2 in E and F refer to the two Arg-52 conformations. Contour levels: blue-tint 1.6 σ, pink-tint 3 σ. (G–I) 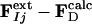residual maps. Contour level: red/white –3/–5 σ, blue/cyan 3/5 σ. Residual electron density features ω and π in G indicate an admixture (see text).

In contrast, the second, IS2, and third, IS3, states both arise from a unique structure and can be satisfactorily refined (Table 3). IS2 is significantly populated from 200 μsto ≈2 ms. Modeling it by a unique structure (Fig. 4E) results in a residual map (Fig. 4H) that displays only noise. In this structure, the very stable hydrogen bond network from Glu-46 and Tyr-42 to the phenolate oxygen of the transchromophore present in the ground state is broken and the cis chromophore is displaced toward the solvent. The phenolate oxygen most likely forms a new hydrogen bond to N_ε of Arg-52 (Fig. 4 B and E). Arg-52 has swung into the solvent (negative feature τ and positive feature ε; Fig. 4B) and displays two conformations c1 and c2 at nearly equal occupancy. Conformation c1 closely resembles that found in the photostationary state (30). Motion of Arg-52 causes structural changes in nearby residues. Thr-50 is hydrogen-bonded in the ground state to Tyr-42; when Thr 50 is displaced, Tyr-42 is pushed out of the plane (Fig. 4B, negative feature π and positive feature ν) and its O_ε1 atom is displaced by 1.2 Å. At the tail of the chromophore, very prominent negative difference electron density features are observed (feature β) also associated with trans-to-cis isomerization of the double bond in the tail.

Table 3. Refinement of the intermediate structures.

Refinement data	IS2	IS3
Factor e	7	11
Resolution, Å	1.9	1.9
Rwork,* %	24.5	24.2
Rfree,* %	28.9	25.9
NH2O	89	89

Factor e is defined and determined as described in Materials and Methods.

^*R_work/free = Σ ∥F^obs| -|F^calc∥/Σ|F^obs|,|F^obs| are the Laue amplitudes,|F^calc| are calculated from the atomic structure. R_free was determined from 5% of the data.

IS3 is the longest-lived IS and decays on the 10-ms time scale. It can also be satisfactorily refined with a single conformation (Fig. 4 C, F, and I). Although the two intermediates IS2 and IS3 are similar, several structural features distinguish them. The features π and ν in IS2 are nearly absent in IS3 (compare Fig. 4 B and C), which indicates that Tyr-42 has nearly reverted to the dark conformation. In IS3, residues around Arg-52 have changed their position and the prominent feature β near the chromophore carbonyl moiety is greatly reduced in magnitude. However, the phenolate ring is still displaced toward Arg-52 and remains hydrogen-bonded to it; and Arg-52 retains the two conformations c1 and c2, with nearly equal occupancy.

The structurally distinct intermediates IS2 and IS3 may account for the biphasic decay from a photostationary state (38). However, the structure of that state, which we designate I2-P (30), differs in detail from the present structures: in I2-P, the phenolate ring is further displaced toward Arg-52, which displays only the c1 conformation. Because the photostationary state accumulates the longest-lived intermediate, I2-P may represent an intermediate not populated to a significant extent in a pulsed experiment. We propose that the intermediates IS2 and IS3 correspond to the spectroscopically observed intermediates I₁′ and I₂ (21, 27), respectively. The relaxation times and the spectroscopically proposed structures (27) are in accordance with our results.

To identify one or more chemical kinetic mechanism(s) compatible with the data, we employ posterior analysis, which exploits the absolute scale of the crystallographic data (19). This approach is also useful for rejecting certain mechanisms that are incompatible with the data. Because we are unable to separate the admixture of structures in the difference map representing the IS1 state, two chromophore conformations with occupancy 0.5 each were modeled. We further assume that the mixture decays in parallel, which is reasonable because the difference electron density features of the mixture and the residual features (compare Fig. 4G) have roughly the same lifetimes. It is possible that if these assumptions are not valid, a different mechanism may fit the data better.

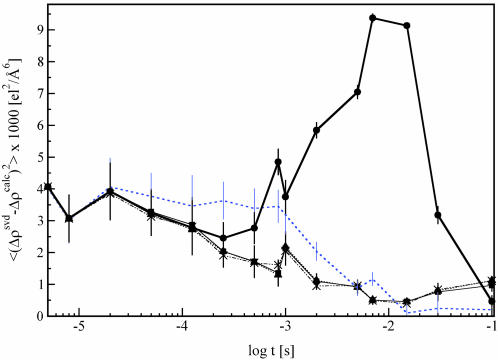
The structures of the intermediates and the dark state were used together with the candidate mechanisms to calculate time-dependent difference maps Δρ(k, t)^calc. These maps were compared with the observed, SVD-flattened difference maps Δρ(t)^svd. The extent of photoinitiation (factor C_PA in Eq. 1) was determined to be ≈14%. The rate coefficients k of the candidate mechanisms were refined (Table 4) to maximize agreement between the maps. The candidate mechanism S cannot fit the time dependence because Δρ(k, t)^calc deviates quantitatively and qualitatively from Δρ(t)^svd (Fig. 5); this mechanism must be discarded. However, the three candidate mechanisms (Fig. 3 C–E) each generate fits of similar quality and most importantly, the residual maps, Δρ(t)^svd – Δρ(k, t)^calc, contain no significant features. We infer that the three mechanisms (parallel, dead end, and semiparallel) are compatible with the present data and remain as plausible mechanisms (see also Figs. 7 and 8, which are published as supporting information on the PNAS web site).

Table 4. Rate coefficients (1/s) assigned to the mechanisms.

Rate coefficient	Sequential rates fixed	Sequential rates varied	Semiparallel	Dead end	Parallel
k+1	3,500	198	3,500	3,200	1,800
k+2	0	0	0	0	1,100
k+3	1,200	1.0 × 106	500	450	0
k-3	0	0	0	15	0
k+4	0	0	650	650	900
k+5	20	309	12	0	12

For mechanisms and the rate coefficients, see Fig. 3.

Fig. 5.

Fit result. Mean square deviation (χ²) of the calculated, time-dependent difference maps Δρ(t, k)^calc from the SVD-flattened difference maps Δρ(t)^svd plotted as a function of log time. Bold solid line and •, fit of sequential mechanism; rate coefficients fixed to physically meaningful values. Blue dotted line, no symbols; fit of sequential mechanism, thin solid line and ▪, fit of dead-end mechanism; dotted line and ▴, fit of semiparallel mechanism; dotted-dashed line and X, parallel mechanism.

Concluding Remarks. The SVD analysis of experimental, time-resolved crystallographic data on the photocycle of PYP has greatly reduced the noise, established that a chemical kinetic mechanism holds in this time range and permitted the identification of time-independent structural states. Posterior analysis of the SVD-flattened data demonstrates that one candidate mechanism is incompatible with the experimental data, but cannot distinguish among three remaining mechanisms. Authentic ISs within a reaction pathway can now be observed and structurally characterized. Knowledge of intermediate structures and the mechanisms that they populate will allow a deeper understanding of reactivity and macromolecular function at the atomic level.