Abstract
Purpose
This study examined the measurement invariance of responses to the patient-reported outcomes measurement information system (PROMIS) pain interference (PI) item bank. The original PROMIS calibration sample (Wave I) was augmented with a sample of persons recruited from the American Chronic Pain Association (ACPA) to increase the number of participants reporting higher levels of pain. Establishing measurement invariance of an item bank is essential for the valid interpretation of group differences in the latent concept being measured.
Methods
Multi-group confirmatory factor analysis (MG-CFA) was used to evaluate successive levels of measurement invariance: configural, metric, and scalar invariance.
Results
Support was found for configural and metric invariance of the PROMIS-PI, but not for scalar invariance.
Conclusions and recommendations
Based on our results of MG-CFA, we recommend retaining the original parameter estimates obtained by combining the community sample of Wave I and ACPA participants. Future studies should extend this study by examining measurement equivalence in an item response theory framework such as differential item functioning analysis.
Keywords: Factor analysis, Pain interference, Pain measurement, Patient outcome measures, Psychometrics
Introduction
Pain is one of the major distressing symptoms experienced by patients with numerous chronic and acute conditions, and pain interference is an important aspect of the pain experience [1]. Pain interference was among the first outcomes targeted in the National Institutes of Health’s (NIH) Patient-Reported Outcomes Measurement Information System (PROMIS) [2]. As defined in the PROMIS domain framework, pain interference refers to “consequences of pain on relevant aspects of persons’ lives and may include impact on social, cognitive, emotional, physical, and recreational activity as well as sleep and enjoyment of life [3].”
All PROMIS measures, including the PROMIS pain interference (PROMIS-PI), were developed as the banks of items calibrated to an item response theory (IRT) model. Data for the development of the first set of PROMIS measures were obtained by administering candidate items to a large sample comprised predominantly of an Internet panel of community participants (Wave I). The Wave I sample was quite large, but included few individuals with higher levels of pain. With IRT models, precise estimates of item parameters require not just large overall sample sizes, but adequate sample sizes in every response category [4]. To increase the number of observations in response categories indicating higher pain, the PROMIS Wave I sample was combined with data from the American Chronic Pain Association (ACPA) [2, 5–8].
Combining these data solved one challenge, but created a potential methodological issue. Whereas the ACPA data came from a clinical sample, the Wave I sample was predominately drawn from the community and a large portion of these were healthy. Researchers may be concerned that test score differences observed in different subgroups are due to measurement instrument problems rather than true differences in the trait being measured. This question can be answered by detecting a lack of measurement invariance. Measurement invariance means that the same construct is measured similarly across groups. Combining the Wave I and ACPA samples is appropriate only if the PROMIS-PI items are measurement invariant in the two groups. The purpose of this study was to examine measurement invariance of the PROMIS-PI using multi-group confirmatory factor analysis (MG-CFA).
Method
Participants
The PROMIS Wave I data included 19,601 participants recruited from YouGovPolimetrix and 1,532 were collected from research sites associated with the PROMIS network. Two data collection designs were utilized. In the “full bank” design, all 56 candidate PI items were administered. In the “block administration,” participants answered only 7-item subsets [2, 6–8]. The current study included only respondents from the full bank design.
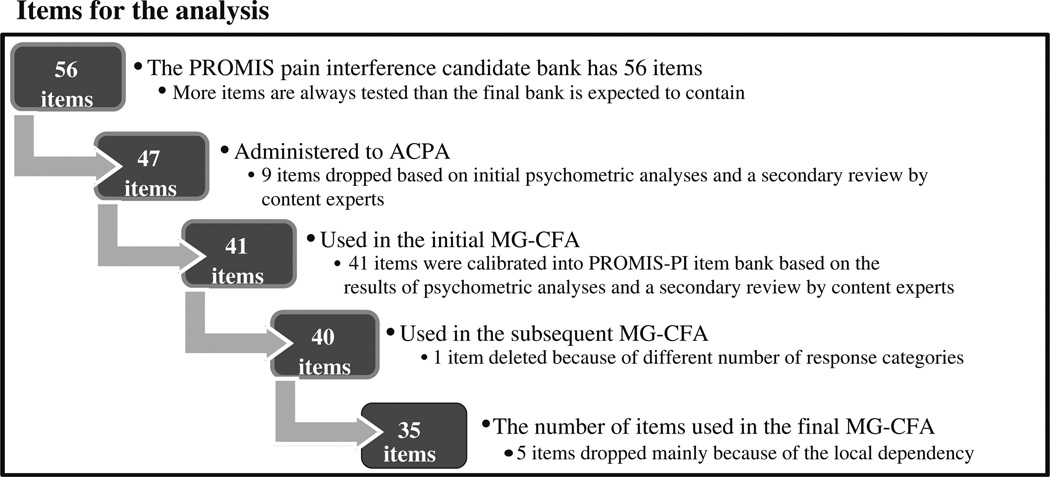
Before starting the ACPA data collection, nine items were removed from the candidate PROMIS-PI bank based on initial psychometric analyses following Wave I data collection and secondary review by content experts. Of the nine items removed, five were removed because of poor fit, three items were removed because they did not specifically mention pain, and one item was removed because of poor correlation with other items in the bank. This left a revised candidate item bank with 47 items (See Appendix). These were administered to ACPA participants who were 21 years of age or older and had at least one chronic pain condition for at least 3 months prior to the survey.
Note that only 41 items of the PROMIS-PI were analyzed across the two samples, WAVE I and ACPA, for the current study, because only 41 items were calibrated into the PROMIS-PI item bank based on the results of psychometric analyses and a secondary review by content experts. Furthermore, this study considered participants who had no missing item responses on these 41 items. Thus, a total of 754 PROMIS Wave I and 807 ACPA participants were included in the current study.
Measurement invariance
The first and weakest level of measurement invariance is configural invariance [9]. Configural invariance requires that the same pattern of item-factor loadings exists across group being compared, that is, the same items have nonzero loadings on the same factors. The next level, metric invariance [10], additionally requires that factor loadings are not statistically significantly different across groups. Scalar invariance [9, 11] requires configural and metric invariance and, additionally, invariant item intercepts across groups.
Analyses
To test measurement invariance using MG-CFA, Mplus 6.1 software [12] was used to estimate each model with weighted least squares mean and variance adjusted (WLSMV) estimation. Goodness of fit was evaluated using χ2, Comparative Fit Index (CFI) [13], Tucker–Lewis Index (TLI) [14], and root mean square error of approximation (RMSEA) [15, 16]. CFI and TLI values above 0.95 are preferable [17], and RMSEA values of less than 0.08 are considered to indicate fair fit [18]. In the MG-CFA approach, fit of a baseline model is compared to the fit of increasingly constrained models. Typically, the χ2 difference test is used to compare the fit of two nested models [17, 19, 20]. When the χ2 difference is not statistically significant, the researcher has evidence supporting the less parameterized model. Like the model fit χ2 test statistic, the χ2 difference test is sensitive to sample size. To account for this, we used an alpha level of 0.05 and also calculated Cheung’s and Rensvold’s ΔCFI index [21]. A difference of less than 0.01 in the ΔCFI index supports the less parameterized model [21, 22]. Model fit was only compared when both of the models of interest individually fit the data.
Measures
All 41 items administered to the Wave I and ACPA samples were rated on a 5-point scale ranging from 1 to 5. One item (PI9) was dropped because on this item, the two groups (ACPA and PROMIS Wave I) had a different number of response options, while MG-CFA requires that items administered to both groups have responses for the same number of response categories. ACPA participants endorsed only four response categories because nobody endorsed no interference in response to: How much did pain interfere with your day to day activities? PROMIS Wave I participants endorsed all five response categories. Thus, the choice was to collapse the first and second response category for the PROMIS Wave I sample or to drop the PI9 from the analyses. We chose to drop the item rather than recode the PROMIS Wave I responses.
The initial configural invariance model run with the remaining 40 items had unsatisfactory fit: χ2 (1,500, N = 1,561) = 22,919.14, p < .01, CFI = 0.90, TLI = 0.90, RMSEA = 0.135 (from 0.134 to 0.137). To improve model fit, we examined modification indices and residual correlations. The modification indices suggested adding correlated residuals to improve the model fit. However, doing so resulted in a non-positive latent variable matrix in our study [23]. Moreover, the larger values of modification indices suggested local dependence between items [24]. Instead of modifying the model by adding correlated residuals, we also examined the residual correlations with absolute values greater than 0.20 (suggesting the local dependency). Local independence means that after controlling for the trait level (i.e., pain interference), the response to any item is unrelated to any other item. Local dependence suggests that item responses are linked, that is, that the items are redundant. After examining modification indices, non-positive latent variable matrix, and the residual correlations, we decided to eliminate the following five items: (1) PI11 “How often did you feel emotionally tense because of your pain?”, (2) PI16 “How often did pain make you feel depressed?”, (3) PI42 “How often did pain prevent you from standing for more than one hour?”, (4) PI47 “How often did pain prevent you from standing for more than 30 min?”, and (5) PI55 “How often did pain prevent you from sitting for more than one hour?”. Thus, our final measurement invariance tests included only 35 PROMIS-PI items. Figure 1 illustrates a schematic flow of our item analysis for the current study.
Fig. 1.
A schematic flow of item analysis
Results
A total of 754 PROMIS Wave I (Men = 344 and Women = 410) and 807 ACPA (Men = 150 and Women = 654, missing = 3) participants were included in the current study (demographics in Table 1). Two datasets (ACPA and Wave I) were statistically different on age, t (1,554) = 3.627, p < .001, gender, χ2 (1, N = 1,558) = 130.67, p < .001, ethnicity, χ2 (1, N = 1,548) = 63.96, p < .001, marriage status, χ2 (2, N = 1,444) = 22.91, p < .001, and education, χ2 (4, N = 1,558) = 49.77, p < .001. Furthermore, an item specifically asking respondents to report current chronic conditions was only administered to the ACPA sample. The most frequently endorsed current chronic pain conditions were lower back pain, neck (or shoulder) pain, and other neuropathic pain (nerve damage) (See Table 2).
Table 1.
Demographics between the PROMIS Wave I and ACPA samples for pain interference
| PROMIS Wave I |
ACPA | |||
|---|---|---|---|---|
| Mean | SD (%) |
Mean | SD (%) |
|
| Age | 51.01 | 18.45 | 48.19 | 11.07 |
| Age group | N | % | N | % |
| 18–29 | 126 | 16.71 | 46 | 5.70 |
| 30–39 | 114 | 15.12 | 121 | 14.99 |
| 40–49 | 129 | 17.11 | 264 | 32.71 |
| 50–59 | 112 | 14.85 | 265 | 32.84 |
| 60–64 | 54 | 7.16 | 49 | 6.07 |
| 65–84 | 209 | 27.72 | 58 | 7.19 |
| 85+ | 7 | 0.93 | 2 | 0.25 |
| Missing | 3 | 0.40 | 2 | 0.25 |
| Gender | ||||
| Male | 344 | 45.62 | 150 | 18.59 |
| Female | 410 | 54.38 | 654 | 81.04 |
| Missing | – | – | 3 | 0.37 |
| Ethnicity | ||||
| White | 595 | 78.91 | 744 | 92.19 |
| Non-white | 155 | 20.56 | 54 | 6.69 |
| Missing | 4 | 0.53 | 9 | 1.12 |
| Marriage status | ||||
| Never-married | 135 | 17.90 | 64 | 7.92 |
| Married/living with partner in committed relationship | 487 | 64.59 | 484 | 59.98 |
| Separated/divorced/widowed | 132 | 17.51 | 142 | 17.60 |
| Missing | – | – | 117 | 14.50 |
| Education | ||||
| Less than high school grade | 17 | 2.26 | 18 | 2.23 |
| High school grade/GED | 111 | 14.72 | 131 | 16.23 |
| Some college/technical degree/AA | 249 | 33.02 | 382 | 47.34 |
| College degree (BA/BS) | 217 | 28.78 | 181 | 22.43 |
| Advanced degree (MA, PhD, MD) | 160 | 21.22 | 92 | 11.40 |
| Missing | – | – | 3 | 0.37 |
Table 2.
Current chronic pain condition(s) of the ACPA sample
| N | %a | |
|---|---|---|
| Migraine and/or other daily headache | 172 | 8.46 |
| Rheumatoid arthritis | 47 | 2.31 |
| Osteoarthritis | 150 | 7.38 |
| Pain related to cancer | 4 | 0.20 |
| Lower back pain | 444 | 21.84 |
| Neck or shoulder pain | 371 | 18.25 |
| Fibromyalgia | 296 | 14.56 |
| Other neuropathic pain (nerve damage) | 300 | 14.76 |
| Other | 248 | 12.20 |
| No chronic pain condition | 1 | 0.05 |
Participants can endorse up to three chronic pain conditions
Calculation based on the total endorsements (N = 2,033)
Confirmatory factor analysis
The CFA model run with the combined samples confirmed one latent factor χ2 (560, N = 1,561) = 8,795.562, p < .01, CFI = 0.991, TLI = 0.991, RMSEA = 0.097 (from 0.095 to 0.099).
Configural invariance
A configural invariance model (i.e., no across group equality constrains on any parameters) was tested across the two samples. The results supported configural invariance between the PROMIS and ACPA samples: χ2 (1,120, N = 1,561) = 10,481.76, p < .01, CFI = 0.96, TLI = 0.95, RMSEA = 0.103 (from 0.102 to 0.105) (See Table 3).
Table 3.
Results of testing measurement invariance of the pain interference items across PROMIS Wave I and ACPA samples using MG-CFA
| Invariance level | Overall fit indexes | Comparative fit indexes | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| χ2 | df | CFI | TLI | RMSEA | RMSEA 90 % CI | Model comparison | Δχ2 | Δdf | p | Δ CFI | |
| 1. Configural | 10,481.76 | 1,120 | 0.96 | 0.95 | 0.103 | 0.102 0.105 | 2 versus 1 | 1,422.39 | 35 | <.01 | Δ 0.00 |
| 2. Metric | 10,539.40 | 1,155 | 0.96 | 0.95 | 0.102 | 0.100 0.104 | n.a. | n.a. | n.a. | n.a. | n.a. |
| 3. Scalar | 24,484.92 | 1,295 | 0.89 | 0.90 | 0.151 | 0.150 0.153 | n.a. | n.a. | n.a. | n.a. | n.a. |
CFI comparative fit index, TLI Tucker–Lewis Index, RMSEA root mean square error of approximation, CI confidence interval, n.a. not applicable
Measurement invariance tests included 35 items after deleing PI9, PI11, PI16, PI42, PI47, and PI55 items from the initial 41 items
Metric invariance
The metric invariance model (i.e., equal constraints on unstandardized item-factor loadings across groups) also had good fit: χ2 (1,155, N = 1,561) = 10,539.40, p < .01, CFI = 0.96, TLI = 0.95, RMSEA = 0.102 (from 0.100 to 0.104). When we compared the fit of configural model (i.e., the same patterns of factor loading across groups) and metric (i.e., equal unstandardized factor loading values across groups) model, the χ2 difference test was statistically significant: Δχ2 (Δdf = 35) = 1,422.39, p < .01; A statistically significant decline in χ2 supporting some relationships among variables statistically differed PROMIS and ACPA samples. As noted above, the χ2 difference is sensitive when there are relatively larger sample sizes, so researches recommended CFI difference test for testing measurement invariance for a large sample size. Dissimilar to the χ2 difference test, the CFI difference test supported metric invariance (ΔCFI = 0.00) (See Table 3).
Scalar invariance
Next, we examined the PROMIS-PI for scalar invariance. The equivalence of thresholds across groups was not supported: χ2 (1,295, N = 1,561) = 24,484.92, p < .01, CFI = 0.89, TLI = 0.90, RMSEA = 0.151 (from 0.150 to 0.153). Since the scalar invariance model did not fit the data, model fit was not compared to test measurement invariance (See Table 3).
Discussion
We examined the measurement invariance of PROMIS-PI items across two qualitatively different samples using MG-CFA methods. There is currently no consensus regarding the level of invariance necessary before one can confidently compare scores across groups. Horn and McArdle [10] require metric invariance; Reise and Widman [25] require only partial-loading invariance (i.e., partial metric invariance); and Chen, Sousa, and West [26] require scalar invariance. Our analyses supported measurement invariance at the level of metric, but not scalar invariance.
Conclusions and recommendations
Had the PROMIS-PI been found to lack configural or metric invariance, a case could be made for re-calibrating the item bank or dropping items that function differently in the two groups. We found, however, that the PROMIS-PI met all but the strictest from of recommended measurement invariance for the comparison of scores across groups. This means that the instrument measures the same construct in both populations and the scores can be used to measure both healthy and clinical samples (such as those with chronic pain). Based on these results, we recommend using the original parameter estimates obtained from the combined sample of Wave I and ACPA participants. For clinicians, this finding means that the instrument can be scored and used as originally published.
The results of the study also suggest that the PROMIS pain interference bank includes items that are locally dependent. Local dependence results in biased parameter estimation [27, 28]. Thus, our results suggest that the PROMIS network should evaluate and address local dependency in the pain interference bank.
Future studies should extend our analyses by testing measurement invariance using an IRT framework. In IRT, lack of measurement equivalence occurs at the item level and is referred to as differential item functioning (DIF) [29]. Comparison of results based on MG-CFA used in this study and results based on IRT methods would further extend our understanding of the level of measurement invariance in the PROMIS-PI.
Acknowledgments
The project described was supported by Award Number 3U01AR052177-06S1 from the National Institute of Arthritis and Musculoskeletal and Skin Diseases. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Arthritis and Musculoskeletal and Skin Diseases or the National Institutes of Health.
Abbreviations
- ACPA
American Chronic Pain Association
- CFA
Confirmatory factor analysis
- IRT
Item response theory
- MG-CFA
Multi-group confirmatory factor analysis
- PI
Pain interference
- PROMIS
Patient-Reported Outcomes Measurement Information System
Appendix
See Table 4.
Table 4.
47 PROMIS pain interference items administered to the ACPA sample
| Item | Item stem |
|---|---|
| PAININ1 | How difficult was it for you to take in new information because of pain? |
| PAININ3 | How much did pain interfere with your enjoyment of life? |
| PAININ4 | How much did you worry about pain? |
| PAININ5 | How much did pain interfere with your ability to participate in leisure activities? |
| PAININ6 | How much did pain interfere with your close personal relationships? |
| PAININ8 | How much did pain interfere with your ability to concentrate? |
| PAININ9 | How much did pain interfere with your day to day activities? |
| PAININ10 | How much did pain interfere with your enjoyment of recreational activities? |
| PAININ11 | How often did you feel emotionally tense because of your pain? |
| PAININ12 | How much did pain interfere with the things you usually do for fun? |
| PAININ13 | How much did pain interfere with your family life? |
| PAININ14 | How much did pain interfere with doing your tasks away from home (e.g., getting groceries and running errands)? |
| PAININ16 | How often did pain make you feel depressed? |
| PAININ17 | How much did pain interfere with your relationships with other people? |
| PAININ18 | How much did pain interfere with your ability to work (include work at home)? |
| PAININ19 | How much did pain make it difficult to fall asleep? |
| PAININ20 | How much did pain feel like a burden to you? |
| PAININ22 | How much did pain interfere with work around the home? |
| PAININ24 | How often was pain distressing to you? |
| PAININ26 | How often did pain keep you from socializing with others? |
| PAININ28 | How often did you avoid trips that required sitting in a car/bus/train for more than two hours? |
| PAININ29 | How often was your pain so severe you could think of nothing else? |
| PAININ30 | How often did pain make it hard for you to walk more than 5 min at a time? |
| PAININ31 | How much did pain interfere with your ability to participate in social activities? |
| PAININ32 | How often did pain make you feel discouraged? |
| PAININ34 | How much did pain interfere with your household chores? |
| PAININ35 | How much did pain interfere with your ability to make trips from home that kept you gone for more than two hours? |
| PAININ36 | How much did pain interfere with your enjoyment of social activities? |
| PAININ37 | How often did pain make you feel anxious? |
| PAININ38 | How often did you avoid social activities because it might make you hurt more? |
| PAININ39 | How often did pain make simple tasks hard to complete? |
| PAININ40 | How often did pain prevent you from walking more than 1 mile? |
| PAININ41 | How often did you avoid trips that required sitting in a car/bus/train for more than 30 min? |
| PAININ42 | How often did pain prevent you from standing for more than one hour? |
| PAININ43 | How often did pain interfere with your ability to get a good night’s sleep? |
| PAININ44 | How often did you avoid trips that required sitting in a car/bus/train for more than one hour? |
| PAININ46 | How often did pain make it difficult for you to plan social activities? |
| PAININ47 | How often did pain prevent you from standing for more than 30 min? |
| PAININ48 | How much did pain interfere with your ability to do household chores? |
| PAININ49 | How much did pain interfere with your ability to remember things? |
| PAININ50 | How often did pain prevent you from sitting for more than 30 min? |
| PAININ51 | How often did pain prevent you from sitting for more than 10 min? |
| PAININ52 | How often was it hard to plan social activities because you didn’t know if you would be in pain? |
| PAININ53 | How often did pain restrict your social life to your home? |
| PAININ54 | How often did pain keep you from getting into a standing position? |
| PAININ55 | How often did pain prevent you from sitting for more than one hour? |
| PAININ56 | How irritable did you feel because of pain? |
Item names are based on their numbers in the original candidate item bank; therefore, PAININ1 is the first PROMIS pain interference item. For PROMIS pain interference items, the time frame is in the past 7 days
Contributor Information
Jiseon Kim, Department of Rehabilitation Medicine, University of Washington, Seattle, WA 98195, USA.
Hyewon Chung, Department of Education, Chungnam National University, 99, Daehak-ro, Yuseong-gu, Daejeon 305-764, Korea hyewonchung7@gmail.com.
Dagmar Amtmann, Department of Rehabilitation Medicine, University of Washington, Seattle, WA 98195, USA.
Dennis A. Revicki, Center for Health Outcomes Research, United BioSource Corporation, 7101 Wisconsin Ave., Suite 600, Bethesda, MD 20814, USA
Karon F. Cook, Department of Medical Social Sciences, Northwestern University, Feinberg School of Medicine, 625 N. Michigan Ave., Suite 2700, Chicago, IL 60611, USA
References
- 1.Dworkin RH, Turk DC, Farrar JT, Haythornthwaite JA, Jensen MP, Katz NP. Core outcome measures for chronic pain clinical trials: IMMPACT recommendations. Pain. 2005;113(1–2):9–19. doi: 10.1016/j.pain.2004.09.012. [DOI] [PubMed] [Google Scholar]
- 2.Amtmann D, Cook K, Jensen MP, Chen W-H, Choi S, Revicki D, et al. Development of a PROMIS item bank to measure pain interference. Pain. 2010;150(1):173–182. doi: 10.1016/j.pain.2010.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Riley W, Rothrock N, Bruce B, Christodolou C, Cook K, Hahn EA. Patient-reported outcomes measurement information system (PROMIS) domain names and definitions revisions: further assessment of content validity in IRT-derived item banks. Quality of Life Research. 2010;19(9):1311–1321. doi: 10.1007/s11136-010-9694-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Choi SW, Cook KF, Dodd BG. Parameter recovery for the partial credit model using MULTILOG. Journal of Outcome Measurement. 1997;1(2):114–142. [PubMed] [Google Scholar]
- 5.Samejima F. Estimation of latent ability using a response pattern of graded scores. Psychometrika Monograph Supplement. 1969;34( 4, Pt. 2, No 17) [Google Scholar]
- 6.Cella D, Riley W, Stone A, Rothrock N, Reeve B, Yount S, et al. Initial item banks and first wave testing of the patient–reported outcomes measurement information system (PROMIS) network: 2005–2008. Journal of Clinical Epidemiology. 2010;63(11):1179–1194. doi: 10.1016/j.jclinepi.2010.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liu HH, Cella D, Gershon R, Shen J, Morales LS, Riley W, et al. Representativeness of the PROMIS Internet panel. Journal of Clinical Epidemiology. 2010;63(11):1169–1178. doi: 10.1016/j.jclinepi.2009.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rothrock NE, Hays RD, Spritzer K, Yount SE, Riley W, Cella D. Relative to the general US population, chronic diseases are associated with poorer health–related quality of life as measured by the patient–reported outcomes measurement information system (PROMIS) Journal of Clinical Epidemiology. 2010;63(11):1195–1204. doi: 10.1016/j.jclinepi.2010.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Meredith W. Measurement invariance, factor analysis, and factorial invariance. Psychometrika. 1993;58(4):525–543. [Google Scholar]
- 10.Horn JL, McArdle JJ. A practical and theoretical guide to measurement invariance in aging research. Experimental Aging Research. 1992;18(3):117–144. doi: 10.1080/03610739208253916. [DOI] [PubMed] [Google Scholar]
- 11.Steenkamp EMJ, Baumgartner H. Assessing measurement invariance in cross-national consumer research. Journal of Consumer Research. 1998;25(1):78–90. [Google Scholar]
- 12.Muthén LK, Muthén BO. Mplus user’s guide. 6th ed. Los Angeles, CA: Muthén & Muthén; 1998–2010. [Google Scholar]
- 13.Bentler PM. Multivariate analysis with latent variables: Causal modeling. Annual Review of Psychology. 1980;31(1):419–456. [Google Scholar]
- 14.Tucker LR, Lewis C. A reliability coefficient for maximum likelihood factor analysis. Psychometrika. 1973;38:1–10. [Google Scholar]
- 15.Byrne BM. Structural equation modeling with LISREL, PRELIS, and SIMPLIS. Hillsdale, NJ: Lawrence Erlbaum; 1998. [Google Scholar]
- 16.Steiger JH, Lind JC. Statistically-based tests for the number of common factors. Paper presented at the annual spring meeting of the Psychometric Society; Iowa City, IA. 1980. [Google Scholar]
- 17.Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal. 1999;6(1):1–55. [Google Scholar]
- 18.Browne M, Cudeck R. Alternative ways of assessing model fit. In: Bollen K, Long J, editors. Testing structural equation models. London, England: Sage; 1993. pp. 136–162. [Google Scholar]
- 19.Marsh HW, Hau K, Wen Z. In search of golden rules: Comment on hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler’s (1999) findings. Structural Equation Modeling: A Multidisciplinary Journal. 2004;11(3):320–341. [Google Scholar]
- 20.Sivo SA, Fan X, Witta EL, Willse JT. The search for “optimal” cutoff properties: Fit index criteria in structural equation modeling. The Journal of Experimental Education. 2006;74(3):267–288. [Google Scholar]
- 21.Cheung GW, Rensvold RB. Evaluating goodness-of-fit indices for testing measurement invariance. Structural Equation Modeling: A Multidisciplinary Journal. 2002;9(2):233–255. [Google Scholar]
- 22.French BF, Finch WH. Confirmatory factor analytic procedures for the determination of measurement invariance. Structural Equation Modeling: A Multidisciplinary Journal. 2006;13(3):378–402. [Google Scholar]
- 23.Mora PA, Contrada RJ, Berkowitz A, Musumeci-Szabo T, Wisnivesky J, Halm EA. Measurement invariance of the mini asthma quality of life questionnaire across African–American and Latino adult asthma patients. Quality of Life Research. 2009;18(3):371–380. doi: 10.1007/s11136-009-9443-9. [DOI] [PubMed] [Google Scholar]
- 24.Hill CD, Edwards MC, Thissen D, Langer MM, Wirth RJ, Burwinkle TM, et al. Practical issues in the application of item response theory: A demonstration using items from the Pediatric Quality of Life Inventory™ (PedsQL™) 4.0 Generic Core Scales. Medical Care. 2007;45(5) Suppl 1:39–47. doi: 10.1097/01.mlr.0000259879.05499.eb. [DOI] [PubMed] [Google Scholar]
- 25.Reise SP, Widaman KF, Pugh RH. Confirmatory factor analysis and item response theory: Two approaches for exploring measurement. Psychological Bulletin. 1993;114(3):552–567. doi: 10.1037/0033-2909.114.3.552. [DOI] [PubMed] [Google Scholar]
- 26.Chen F, Sousa KH, West SG. Teacher’s corner: Testing measurement invariance of second-order factor models. Structural Equation Modeling: A Multidisciplinary Journal. 2005;12(3):471–492. [Google Scholar]
- 27.Yen WM. Scaling performance assessments: Strategies for managing local item dependence. Journal of Educational Measurement. 1993;30:187–213. [Google Scholar]
- 28.Steinberg L, Thissen D. Uses of item response theory and the testlet concept in the measurement of psychopathology. Psychological Methods. 1996;1:81–97. [Google Scholar]
- 29.Stark S, Chernshenko OS, Drasgow F. Detecting differential item functioning with confirmatory factor analysis and item response theory: Toward a unified strategy. Journal of Applied Psychology. 2006;91(6):1292–1306. doi: 10.1037/0021-9010.91.6.1292. [DOI] [PubMed] [Google Scholar]