Indirect Determination of Lactate Minimum Speed from a Single Maximal Performance in Young Swimmers

Abstract

This study aimed to generate equations for the indirect determination of lactate minimum (LM) intensity from short-distance maximal performances in 10- to 17-year-old swimmers. Seventy-one male (n = 41) and female (n = 30) competitive swimmers were divided into subgroups: one to generate predictive equations for LM (~70% of the sample), and the second to cross-validate the proposed equations (~30% of the sample). All participants swam maximally short-distance using front crawl stroke, and mean speed of the 100 (S100), 200 (S200), and 400 m (S400) performances were calculated in m·s^-1. The LM protocol was measured after an 8 min of passive recovery from the S200, consisting of five progressive 200 m performances (~80%, 84%, 88%, 92%, and 96% of S200). Multiple linear regressions generated predictive equations for LM from single performances (S100, S200, and S400), also considering as independent variables age, pubic hair index, body mass, height, and body fat. The relationships between variables were examined using standard error of estimate (SEE). Nevertheless, age, biological maturation and anthropometric variables did not contribute to explain LM. Further, for both genders, S200 was the best predictor for LM, contributing to 95% of LM variation in males and 81% in females. The generated equations were: “LM = 0.24 + 0.67 × S200” (adjusted R² = 0.95; SEE = 0.03 m·s^-1) for boys and “LM = 0.13 + 0.79 × S200” (adjusted R² = 0.81; SEE = 0.03 m·s^-1) for girls. The predicted LM did not differ from the measured LM during cross-validation analysis. A single performance was found to be a valid LM predictor in 10- to 17-year-old swimmers regardless of gender, age and biological maturation. Thus, this is a practical, non-invasive, and economical alternative to estimate the aerobic capacity in young swimmers.

Key Points.

• LM can be estimated from a single maximal swimming performance for boys and girls, regardless age, sexual maturity, anthropometrical and body composition parameters.

• For boys, S200 was the best LM predictor (LM = 0.24 + 0.67 x S200), explaining 95% of LM variation with great cross validation parameters.

• For girls, S200 was also the best LM predictor (LM = 0.13 + 0.79 x S200), explaining 81% of LM variation with great cross validation parameters.

Introduction

Indices of aerobic capacity are widely used in swimming to control, monitoring, and develop training programs (Fernandes et al., 2011; Greco and Denadai, 2005; Toubekis et al., 2011), however, most of these indices are determined invasively or during exhaustive tests that may interfere the training itself, discouraging coaches and swimmers to use it continually and thus, are not suitable for all age high level athletes, especially for children and adolescents regarding motivational aspects.

Lactate minimum (LM), for example, is a reproducible and valid index that estimates maximal blood lactate steady state (MLSS), nevertheless, despite the advantage of requiring only one day of assessment, the protocol is both exhaustive and invasive (Fernandes et al. , 2011; MacIntosh et al., 2002; Pardono et al., 2008; Ribeiro et al., 2003; Sotero et al., 2009). Determining critical swimming (CS) speed is also a valid, non-invasive method for evaluation of aerobic capacity in young swimmers, but a combination of two or more tests performed to exhaustion is required (Dekerle et al., 2002; di Prampero et al., 2008; Greco and Denadai, 2005; Toubekis et al., 2011 Toubekis et al., 2006; Zacca et al., 2010). On the other hand, a study by Sotero et al., 2009 showed that a single, non-invasive, 1600-m running performance could predict the running speed corresponding to LM speed in young men.

Thus, similarly, it would be useful for coaches and practitioners if LM swimming speed could be estimated using only one, non-invasive, short-distance maximal performance in children and adolescents. However, variables related to gender and biological maturation should be considered in the development of such a predictive equation. The processes of growth and development provide an increase in body size, modification of body composition and physiological characteristics during the puberty (Armstrong and McManus, 2011; Baxter-Jones et al., 2005; Malina et al., 2004; McManus and Armstrong, 2011; Rowland, 2005), which may affect the relationship between LM and maximal swimming performances.

Lätt et al., 2009 showed that physical, biomechanical, and physiological changes accompanying physical maturity influence swimming performance. Thus, the inclusion of age, sexual maturity, body mass, height, and body fat as independent variables could add some predictive power in the generated equation.

Therefore, the purpose of this study was to generate predictive equations for the indirect determination of swimming speed corresponding to LM in young male and female swimmers from short- distance maximal performances (i.e, 100, 200, and 400 m) and to examine what distance best correlates with LM intensity. It was hypothesized that, as in running, the LM swimming speed could be estimated from a single maximal swimming performance.

Methods

Subjects

Seventy- one 10- to 17-year-old young swimmers (41 males and 30 females) of regional and national competing level participated in this study. They were undertaking systematic exercise training for a minimum of two years with an average training volume of 35 km·wk^-1. Mean physical and training characteristics for each subgroup are shown in Table 1.

Table 1.

Physical and physiological characteristics of the subjects divided by subgroups and gender. Data are means (±SD).

Variables	M1 (n=29)	M2 (n=12)	F1 (n=21)	F2 (n=9)
Age (years)	13.6 (2.1)	14.3 (1.9 )	13.3 (2.0)	13.3 (2.6)
Body Mass (kg)	56.6 (16.4)	55.1 (12.1)	51.3 (9.3)	52.1 (13.5)
Height (m)	1.65 (.14)	1.66 (.10)	1.58 (.09)	1.57 (.10)
Body Fat (%)	14.2 (6.2)	13.0 (5.1)	23.4 (6.5) *	22.6 (6.0) †
Experience (years)	5.1 (3.4)	5.4 (3.2)	4.3 (2.3)	3.8 (2.9)
S100 (m·s-1)	1.33 (.19)	1.42 (.18)	1.20 (.10) *	1.23 (.09) †
S200 (m·s-1)	1.20 (.18)	1.27 (.18)	1.10 (.09) *	1.10 (.07) †
S400 (m·s-1)	1.12 (.17)	1.18 (.18)	1.03 (.10) *	1.03 (.08) †
LM(m·s-1)	1.04 (.12)	1.11 (.14)	1.00 (.08)	1.01 (.07)

M1 = Male subgroup 1; M2 = Male subgroup 2; F1 = Female subgroup 1; F2 = Female subgroup 2; S100 = average speed from 100-m maximal performance; S200 = average speed from 200-m maximal performance; S400 = average speed from 400-m maximal performance; LM = swimming speed corresponding to lactate minimum.

^* < 0.05 comparing F1 and M1;

^† p < 0.05 comparing F2 and M2.

Age was computed from date of birth and date of examination. Body fat was determined according to the equation by Slaughter et al., 1988, based on the sum of subscapular and triceps skinfold thicknesses, gender, race, and sexual maturity. All measurements were made by a single assessor to minimize possible errors. Sexual maturity was auto-assessed, visually, using the five levels of pubic hair developed by Tanner (1962). Written, informed consent was obtained from subjects and their parents, and ethical approval was granted by the Local Research Ethics Committee (# 121/2010).

Experimental design

After a visit to the laboratory for evaluation of anthropometric measures, the male (M) and female (F) participants were divided into subgroups 1 (M1 and F1), composed of 70% of the total sample, in order to generate predictive equations for LM, and subgroup 2 (M2 and F2), composed of 30% of the total sample, in order to cross-validate the proposed equations. The sample of each subgroup was randomly selected, controlled only by similar chronological age and sexual maturity in both subgroups.

Thereafter, following a standard warm-up, in random order, participants swam distances of 100, 200 and 400 m, at maximal speed, using the front crawl style, in a heated outdoor 50-m pool (25 ± 1°C). The protocol for the determination of LM occurred after an 8-min recovery period from the 200-m performance. The tests were performed over two weeks with a minimum interval of 48 h between each one. Participants were instructed to attend for testing well rested, nourished and hydrated. Participants were also instructed to abstain from caffeine and alcohol, and to refrain from strenuous exercise for 24 hours before testing.

Maximal performances of 100, 200, and 400 m

Each performance started with an impulse from the edge of the pool after a beep and the time taken to swim each distance was recorded using a manual chronometer. Thereafter, the mean speed of the 100-m (S100), 200-m (S200), and 400-m (S400) maximal performances were calculated in m·s^-1.

Swimming speed corresponding to lactate minimum

The incremental protocol for the determination of LM started after an 8-min recovery period from S200, which was used to elevate the blood lactate level. The incremental phase comprised five progressive performances of 200 m at intensities of about 80%, 84%, 88%, 92%, and 96% of S200, controlled by visual and audible signals, with 1-min intervals for blood sampling out of the pool (Fernandes et al., 2011; Ribeiro et al., 2003; Tegtbur et al., 1993).

Earlobe capillary blood samples (25 μL) were collected into a glass tube at the end of each stage of the incremental test and at the third, fifth, and seventh minute after lactatemia induction, during the passive recovery, to ensure that there was sufficient increase of lactate concentration. From these samples, blood lactate concentration was subsequently determined by electroenzymatic methods using an automated analyzer (YSI 2300 STAT, Ohio, USA).

The speed corresponding to LM was determined for each participant from the blood lactate concentrations (mmol·L^-1) and the swimming speed (m·s^-1) data obtained from the incremental swimming test. The data were fitted by a second-order polynomial regression curve and the speed corresponding to LM was considered the swimming speed at the minimum point of this curve (Pardono et al., 2008).

Statistical analyses

Data are presented as mean ± standard deviation (SD) and were analyzed using the Statistical Package for the Social Sciences 15.0 software (SPSS Inc., USA). The Shapiro-Wilk test was used to check the normality of the data distribution. The assumption of homogeneity of variance was tested using Levene’s test. Two-way analysis of variance (ANOVA) was used to assess the main effects of the subgroups and gender with statistical significance set at p < 0.05. Predictive equations for the indirect determination of the speed corresponding to LM (dependent variable) from S100, S200, and S400 were generated by multiple linear regressions from M1 and F1, and cross-validated on M2 and F2, respectively. Besides S100, S200, and S400, were considered as independent variables age, pubic hair index, body mass, height, and body fat. Stepwise method was used, in compliance with the presuppositions of collinearity (Tolerance and VIF), homoscedasticity and Durbin-Watson residuals autocorrelation. The relationships between variables were examined using Pearson’s correlation coefficient and standard error of estimate (SEE). Bland-Altman analysis was used to calculate the 95% limits of agreement (Mean difference ± 2 Standard deviation of the mean difference) during the cross-validation analysis, considering the normality of the differences distribution, the absence of significant difference between zero and mean difference values and the non-significant correlation between the mean values and differences (Bland and Altman, non-significant correlation between the mean values and differences (Bland and Altman,1986).

Results

Table 1 presents the physical and physiological characteristics for each gender, divided into subgroups 1 and 2. The ANOVA revealed a significant effect of gender on the body fat (p < 0.001), S100 (p < 0.001), S200 (p < 0. 001), and S400 (p = 0.003). The age, body mass, height, training experience and LM did not significantly differ between the genders (p >gt; 0.05). The male swimmers presented lower body fat and higher S100, S200, and S400 than the female swimmers. All these variables did not significantly differ between the subgroups 1 and 2 (p >gt; 0.05).

Table 2 presents the predictive equations for LM determined by stepwise multiple regression analysis. In relation to M1, the LM was significantly correlated with age (r = 0.63; p < 0.001), pubic hair index (r = 0.43; p = 0.019), body mass (r = 0.51; p = 0.005), and height (r = 0.52; p = 0.004), but not with body fat (r = -0.17; p =0.37). Nevertheless, these variables did not contribute to explain LM and the regression coefficients related to these variables were not different from zero (p >gt; 0.05). In relation to F1, all the independent variables (i.e., age, pubic hair index, body mass, height, and body fat) LM were not significantly correlated with LM (p >gt; 0.05), and therefore, did not contributed to explain LM. Thus, for both genders, only the variables S100, S200, and S400 alone contributed to explain LM. Further, for both genders, S200 was the best predictor for LM, contributing to explain 95% (male) and 81% (female) of the LM variation. Figure 1 depicts the relationships between S200 and LM for M1 (left) and F1 (right).

Table 2.

Relationship between swimming speed corresponding to lactate minimum (LM) and maximal swimming performance during 100 m (S100), 200 m (S200), and 400 m (S400).

Variables	Regression equation (m·s-1)	Correlation	Adjusted R2	SEE (m·s-1)
M1	LM = 0.28 + 0.58 × S100	.92 *	.84	.05
	LM = 0.24 + 0.67 × S200	.97 *	.95	.03
	LM = 0.29 + 0.67 × S400	.96 *	.91	.04
F1	LM = 0.15 + 0.71 × S100	.89 *	.79	.04
	LM = 0.13 + 0.79 × S200	.91 *	.81	.03
	LM = 0.34 + 0.64 × S400	.80 *	.62	.05

^* p< 0.001.

Figure 1.

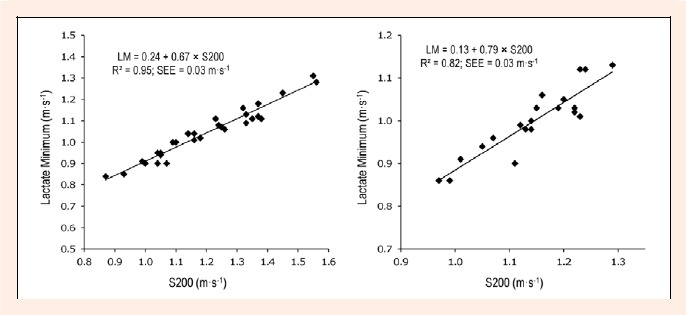
Relationships between average 200-m maximal performance (S200) and lactate minimum for male (left; n = 29) and female (right; n= 21) young swimmers. The continuous line represents the fitted regression line.

Table 3 presents the cross validation analyses. The predicted LM (LM_pred) did not differ from the measured LM for both groups (p >gt; 0.05). In fact, according to the 95% limits of agreement, the error in the prediction of LM would be about ± 8%.

Table 3.

Cross validation. Data are means (±SD).

Group	Variable	LMpred(m·s-1)	r	Diff (m·s-1)	Diff (%)	95% Limits of agreement (m·s-1)
M2	S100	1.10 (.11)	.91 ***	-.002 (.06)	-0.2 (5.6)	-.12 – .12
	S200	1.09 (.12)	.95 ***	.02 (.04)	1.4 (3.8)	-.07 – .11
	S400	1.08 (.12)	.94 ***	.03 (.05)	2.1 (4.2)	-.07 – .12
F2	S100	1.02 (.06)	.89 **	-.01 (.03)	-1.1 (3.2)	-.07 – .05
	S200	1.00 (.06)	.80 **	.01 (.04)	.9 (3.9)	-.07 – .09
	S400	1.00 (.05)	.80 *	.01 (.04)	1.0 (3.9)	-.07 – .09

Note. Values in m·s^-1. S100 = average speed from 100-m maximal performance; S200 = average speed from 200-m maximal performance; S400 = average speed from 400-m maximal performance; LM_pred = predicted lactate minimum.

^* p < 0.05;

^** p < 0.01;

^*** p < 0.001.

Discussion

The purpose of this study was to generate predictive equations for the indirect determination of swimming speed corresponding to LM in young male and female swimmers from short-distance maximal performances (i.e, 100, 200, and 400 m) and to examine what distance best correlates with the intensity corresponding to LM. The main finding was that the LM swimming speed can be estimated from a single maximal swimming performance in 10- to 17-year-old trained swimmers, regardless of age, sexual maturity, body mass, height, and body fat. Additionally, the S200 was the best predictor for LM in both male and female genders, contributing to explain 95% of LM variation in males and 81% in females.

CS is a method that can be used in young swimmers for the evaluation of aerobic capacity, but, although CS can be determined noninvasively, it needs a combination of two or more maximal effort tests for its determination (Dekerle et al., 2002; di Prampero et al., 2008; Greco and Denadai, 2005; Toubekis et al., 2006; 2011; Zacca et al., 2010). Another methodology proposed to predict aerobic capacity is a simple and effective 30-minute test. However, although this has proven effective in young swimmers (Costa et al., 2009; Oliveira et al., 2012) it would be extremely exhausting and monotonous. Further, direct determination of LM is invasive and requires a maximal exercise test to induce high blood lactate levels followed by submaximal performances (Pardono et al., 2008; Ribeiro et al., 2003; Tegtbur et al., 1993).

Given this, specific equations need to be developed to predict aerobic capacity which can be easily used in training, especially if they take into account the peculiarities of gender, age, and sexual maturation. Swimmers usually start systematic training and competitive participation before the onset of puberty at a relatively early age (Lätt et al., 2009). Further, the young athletes undergo great physiological, anthropometric and body composition modifications until they reach adulthood (Armstrong and McManus, 2011; Baxter-Jones et al., 2005; Malina et al., 2004; McManus and Armstrong, 2011).

Lätt et al., 2009 monitored male swimmers with an initial mean age of 13 years for 3 years and found that during this period, there were significant changes in physiological and body composition variables, which had a significant relationship to performance evolution. This result shows that during growth and development, young swimmers should not be subjected to the same evaluations as adults, since sensitivity is needed not only with regard to changes caused by the training itself, but also to the modifications caused by maturation.

Self-assessment of secondary sex characteristics is widely used in swimming to evaluate the biological maturity (Greco and Denadai, 2005; Lätt et al., 2009; Toubekis et al., 2011), especially for being a method of simple use, and because other methods require expensive equipment or longitudinal monitoring (Baxter-Jones et al., 2005). Although some studies have shown that children and adolescents can more easily identify pubic hair stages (Matsudo and Matsudo, 1994; Wacharasindhu et al., 2002), in swimmers it is interesting to compare these values with size of breasts stages in girls and size of genitalia in boys because some swimmers may shave the body. In the present study no difference were found between both analyses.

The equations presented in this study were different for males and females, although other factors such as age and sexual maturity did not contribute to LM determination. In addition, considering the high cost of laboratory tests and specialized personnel for LM determination, the generated predictive equations proved to be valid and practical for determining aerobic capacity intensities that can be used by swimming coaches to develop training programs. In fact, the S200 was the independent variable that best explained LM variation, irrespective of gender. Moreover, the prediction error was approximately 4% for confidence intervals of 68%.

The proposed equations can be easily applied by coaches for young swimmers, especially with regard to initial training and competitive participation in children who should not be treated as adult athletes. After determining the maximum 200-m swimming speed, during training or competitive event, the LM speed can be predicted and the result applied in several ways to develop training sessions according to competitive moments as suggested by Maglischo (2003, p.73- 89).

Conclusion

In summary, we concluded that LM swimming speed can be estimated from a single short-distance maximal performance in young swimmers. Additionally, the equations “LM = 0.24 + 0.67 × S200” for boys and “LM = 0.13 + 0.79 × S200” for girls, are valid and appropriate for LM prediction in 10- to 17-year-old trained swimmers, regardless of age and biological maturation, with explanatory power of 95% and 81%, respectively. Further studies are guaranteed to develop other predictive equations for different populations and different modes of exercise.

Biographies

Paulo V. MEZZAROBA

Employment

Associate Post-Graduate Program in Physical Education UEM/UEL, State University of Maringá, Brazil.

Degree

PhD student

Research interests

Exercise physiology, training

E-mail: paulomezzaroba@hotmail.com

Fabiana A. MACHADO

Employment

Department of Physical Education, State University of Maringá, Brazil. Associate Post-Graduate Program in Physical Education UEM/UEL, State University of Maringá, Brazil.

Degree

PhD

Research interests

Exercise physiology, training

E-mail: famachado_uem@hotmail.com