Bayesian Two-step Lasso Strategy for Biomarker Selection in Personalized Medicine Development for Time-to-Event Endpoints

Summary

Clinical trial designs for targeted therapy development are progressing toward the goal of personalized medicine. Motivated by the need of ongoing efforts to develop targeted agents for lung cancer patients, we propose a Bayesian two-step Lasso procedure for biomarker selection under the proportional hazards model. We seek to identify the key markers that are either prognostic or predictive with respect to treatment from a large number of biomarkers. In the first step of our two-step strategy, we use the Bayesian group Lasso to identify the important marker groups, wherein each group contains the main effect of a single marker and its interactions with treatments. Applying a loose selection criterion in the first step, the goal of first step is to screen out unimportant biomarkers. In the second step, we zoom in to select the individual markers and interactions between markers and treatments in order to identify prognostic or predictive markers using the Bayesian adaptive Lasso. Our strategy takes a full Bayesian approach and is built upon rapid advancement of Lasso methodologies with variable selection. The proposed method is generally applicable to the development of targeted therapies in clinical trials. Our simulation study demonstrates the good performance of the two-step Lasso: Important biomarkers can typically be selected with high probabilities, and unimportant markers can be effectively eliminated from the model.

1 Introduction

Cytotoxic chemotherapies continue to be the primary form of treatment for cancer. The treatment effects of cytotoxic agents come from their ability to eradicate rapidly dividing cancer cells. However, such detrimental effects are not specific to cancer cells, as rapidly dividing normal cells (e.g., hair or bone marrow) are often harmed by cytotoxic agents as well, and thus often results in side effects with varying severity. Historically, both the development and application of chemotherapy in treating cancer have been largely based on a specific cancer diagnosis, which is determined by the location and microscopic appearance (histology) of the tumor. Thus, patients diagnosed with cancer of the same classification are typically given the same treatment. Research has shown, however, that patients with similar tumor histologies may respond differently to the same chemotherapy. Hence, the administration of chemotherapy guided by a traditional tumor diagnosis may expose patients to excessive toxicity and result in unwanted side effects.

Unprecedented advances in life science, mainly during the last two decades, have revolutionized the landscape of cancer drug development via an exciting concept known as “personalized medicine”. The development of new molecularly targeted therapy is a major thrust to seize the promise held by personalized medicine. The new way for cancer drug development involves identifying specific regulators that play key roles in various processes of cancer biology, and developing molecularly targeted agents for these regulators to block signaling events associated with the growth of tumors. Unlike traditional approaches, personalized medicine uses novel diagnoses to screen for patients who are most likely to benefit from specific treatments based on an association between the molecular profiles of patients and the targeted effect of a specific therapy. This approach then assigns treatments that are individually tailored to patients according to their own molecular profiles.

As recognized in the Clinical Path Initiative, a program created by the U.S. Food and Drug Administration (FDA), one important component of targeted agent development is the identification and validation of biomarkers as molecular targets for patient screening and clinical endpoint evaluation. Current technological capabilities in genomics and proteomics allow researchers to quickly collect a large amount of biomarker information from patients in a cost-effective fashion. Therefore, the key issue in the design of clinical trials for personalized medicine is the ability to identify important and meaningful predictors from a pool of many possible variables.

Based on functions in diagnosis and treatment selection for cancer patients, biomarkers can be roughly classified into two categories: prognostic markers and predictive markers. Prognostic markers reflect a healthy status or a disease stage of a patient; they are associated with disease outcomes regardless of the treatment. One obvious prognostic biomarker is age. Older ages usually imply shorter survival times on all treatments. In prostate cancer, a common prognostic biomarker is the prostate-specific antigen (PSA), for which a higher value of PSA reflecting a larger tumor burden and, consequently, poor prognosis of a patient. On the other hand, biomarkers that can predict differential treatment efficacy in different marker groups are called predictive markers. For example, a high level of human epidermal growth factor receptor 2 (HER-2) is a predictive marker for trastuzumab, a targeted breast cancer therapy approved by the FDA. In the clinical trials for targeted therapy development, one primary goal is centered around the identification and validation of predictive and prognostic markers. In the linear model setting, treatment effects are usually characterized by a linear combination of treatment main effects, marker main effects, and marker–treatment interactions. In this case, a non-zero marker main effect represents a prognostic marker and a non-zero marker–treatment interaction signifies a predictive marker.

Our research is motivated by one of the first biopsy-based and biomarker-integrated clinical trials for targeted agent development at MD Anderson Cancer Center. The trial is referred to as BATTLE, which stands for “Biomarker-based Approaches of Targeted Therapy for Lung Cancer Elimination” as described in Zhou et al. (2008) and Kim et al. (2011). One of the main aims of the BATTLE trial is to establish a program for clinical trials with targeted therapy development. The BATTLE trial also seeks to identify molecular features in tumor tissues that correlate with tumor response and to discover new signaling pathways to be tested in future trials. Building from the success of the original BATTLE trial, several follow-up trials are being planed at MD Anderson Cancer Center with primary goals of validating the findings in the BATTLE trial and identifying biomarkers associated with treatment effects of novel combinations of targeted therapies. The selection of variables from numerous biomarkers is an important aspect of these new trials for targeted therapy development.

To embrace the demand of emerging targeted agent trials, we propose a two-step variable selection strategy for the time-to-event endpoint to identify important biomarkers, as the selected biomarkers can be subsequently used in the adaptive randomization procedure to assign more patients with better treatments based on patients’ marker profiles. Hence, the variable selection must be accurate and robust, meaning that the selected biomarkers should be able to provide good prediction and the selection should be stable against variation in the data. The least absolute shrinkage and selection operator (Lasso) proposed by Tibshirani (1996) and its various extensions are suited to this purpose, as Lasso can handle variable selection and parameter estimation simultaneously. Lasso is a natural choice of the statistical approach to targeted agent development, for which marker identification and treatment effect estimation are equally important. To better incorporate the variable selection process into the Bayesian adaptive design framework, we implement the Bayesian Lasso, which simplifies the selection of the tuning parameter and takes into consideration the uncertainty of variable selection. Our marker selection strategy consists of two sequential steps: Step 1 uses the Bayesian group Lasso to screen for biomarkers with either prognostic or predictive values for grouped variables (with each biomarker group as a selection unit); and step 2 applies the Bayesian adaptive Lasso for refined variable selection among the biomarkers identified in the first step. Our simulation study demonstrates that this Bayesian two-step Lasso strategy outperforms the usual one-step Lasso variable selection methods.

It often occurs in oncology trials that many participants have already failed at least one prior treatment, and the experimental new drug may be their only hope for effective disease control. One incentive for participation in a clinical trial is the potential of providing effective treatments to patients within the trial. To find effective treatments for each patient, biomarkers that can differentiate treatment effects among patients need to be identified. Lasso-type methods have been extensively developed in the context of variable selection, which offers a suitable tool for modeling covariate effects in targeted agent development. The combination of Lasso with Bayesian adaptive randomization can help us to achieve the goal of treating patients better, as we continue to learn from accumulating data to identify important biomarkers for treatment selection and progressively optimize patient allocation based on biomarker information.

The remainder of this paper is organized as follows. In Section 2, we provide an introduction to Lasso and its Bayesian implementation under the Cox proportional hazards model, and propose a Bayesian two-step Lasso strategy motivated by the need for biomarker identification for targeted agent development. In Section 3, we examine the performance of the Bayesian two-step Lasso method through simulation studies in terms of identifying both prognostic and predictive markers. We conclude with some discussions in Section 4.

2 Bayesian Two-step Lasso Strategy

2.1 Bayesian Cox’s Proportional Hazards Model

In clinical trials for targeted agent development, the time-to-event (TTE) outcomes, such as progression-free survival (PFS) or overall survival (OS), are typically the clinically meaningful endpoints. Unless a good short-term surrogate endpoint is available, the recommended primary endpoint is often PFS or OS. Under the Cox proportional hazards model (Cox, 1972) the hazard function for subject i with covariates X_i is given by

$$h(t\mid {\mathrm{X}}_i)=h_0\left(t\right)\exp \left({{\mathrm{X}}_i}^T\beta \right),$$ (1)

where h₀(t) is the baseline hazard function and β is a vector of unknown parameters. In an alternative formulation, model (1) can be viewed as a special case of a multiplicative intensity model based on the counting process (Clayton, 1991; and Fleming and Harrington, 1991). For subject i, i = 1, … , n, the counting process and the at-risk process are denoted by N_i(t) and Y_i(t) respectively, where N_i(t) represents the number of events in the time interval [0, t], and Y_i(t) = 1 if subject i has not experienced the event or has not been censored by time t, and Y_i(t) = 0 otherwise. The intensity process for subject i is given by

$$h(t\mid {\mathrm{X}}_i)=Y_i\left(t\right)h_0\left(t\right)\exp \left({{\mathrm{X}}_i}^T\beta \right),$$

for which we model the baseline cumulative hazard function $H_0\left(t\right)={\int }_0^t{h}_0\left(s\right)$ ds through a gamma process prior (Kalbfleisch, 1978). We partition the time axis into J segments based on the observed event times, and define the increment of the cumulative baseline hazard in (t_j–1, t_j] as $d{H}_{0j}={\int }_{t_{j-1}}^{t_j}{h}_0$ (s)ds. Then, the likelihood function can be written as

$$L(\beta ,H_0\mid D)=\underset{i=1}{\overset{n}{\Pi }}\underset{j=1}{\overset{J}{\Pi }}{\left\{Y_{ij}d{H}_{0j}\exp \left({{\mathrm{X}}_i}^T\beta \right)\right\}}^{\Delta N_{ij}}\exp \left\{-Y_{ij}d{H}_{0j}\exp \left({{\mathrm{X}}_i}^T\beta \right)\right\}$$ (2)

where H₀ = (H₀₁, … , H_0J), D denotes the observed data, ΔN_ij is the number of events in (t_j–1, t_j] for subject i, and Y_ij = 1 if subject i is at risk at time t_j, otherwise Y_ij = 0. The likelihood in (2) is equivalent to assuming that ΔN_ij, the increment of the counting process N_i(t) in (t_j–1, t_j], follows independent Poisson distributions with mean Y_ij dH_0j exp $\left({{\mathrm{X}}_i}^T\right)\beta$. The gamma process prior for the baseline cumulative hazard function can be expressed as

$$H_0~GP(c{H_0}^{\ast },c),$$

where c is a parameter to weigh the confidence about the prior information, and ${H_0}^{\ast }$ is the base measure which is an increasing function with ${H_0}^{\ast }\left(0\right)=0$. If we let ${H_0}^{\ast }\left(t\right)=rt$ where r is a prespecified hyperparameter, this leads to an exponential distribution for the survival time. The gamma process prior implies that the dH_0j ’s have independent gamma distributions,

$$d{H}_{0j}~\mathrm{Gamma}\left(c{H_0}^{\ast }(t_j-t_{j-1})c\right),j=1,\cdots ,J.$$ (3)

2.2 Bayesian Lasso

Lasso is essentially an L₁-penalized least square estimator. More specifically, let Y be a vector of responses of length n, and X be the design matrix of the covariates of dimension n × p, where p is the total number of predictors. The Lasso estimator is given by

$${\widehat{\beta }}_L=\underset{\beta }{\arg \min }\left\{l\left(\beta \right)+\lambda \sum _{j=1}^p\mid {\beta }_j\mid \right\},$$

where the least square objective function l(β) = (Y – Xβ)^T (Y – Xβ), λ is a tuning parameter, and the penalty function takes an L₁ norm. This is related to the ridge regression, in which the penalty takes an L₂ norm $\lambda {\sum }_{j=1}^p\mid {\beta }_j{\mid }^2$. To improve the performance of Lasso in various practical situations, many extensions of Lasso have been developed. As a remedy for inconsistent estimation of the large model parameters, Zou (2006) proposed the adaptive Lasso,

$${\widehat{\beta }}_A=\underset{\beta }{\arg \min }\left\{(\beta )+\lambda \sum _{j=1}^p\frac{\mid {\beta }_j\mid }{\mid {{\tilde{\beta }}_j}^{LS}\mid }\right\},$$

where ${{\tilde{\beta }}_j}^{LS}$ is the usual least square estimator of β_j without any penalty term. Yuan and Lin (2006) developed the group Lasso for selecting important factors that are grouped together,

$${\widehat{\beta }}_G=\underset{\beta }{\arg \min }\left\{l({\beta }_1,\cdots ,{\beta }_K)+\lambda \sum _{k=1}^K\Vert {\beta }_k\Vert G_k\right\},$$

where $l({\beta }_1,\cdots ,{\beta }_K)={\mathrm{Y}-{\sum }_{k=1}^T{\mathrm{X}}_k{\beta }_k)}^T(\mathrm{Y}-{\sum }_{k=1}^K{\mathrm{X}}_k{\beta }_k)$, K is the number of groups, β_k is a vector of β’s belonging to group k, $\Vert {\beta }_k{\Vert }_{\mathrm{G}k}={\left({{\beta }_k}^K{\mathrm{G}}_k\right)}^{1∕2}$ and G_k is a postive definite matrix. For convenience, G_k is often set to be the identity matrix. Different multiplication factors can be imposed on the group penalty function, especially when the dimensions of the predictor groups are different. The group Lasso facilitates the selection of predictor groups when the grouping information is known in advance.

The Lasso estimator is usually calculated at a grid of tuning parameters of λ, and a cross-validation procedure is subsequently used to select an appropriate λ. This often leads to a convex optimization problem, for which the least angle regression (Efron et al., 2004) is developed to compute the entire coefficient path at the cost of a full least square fit. Recently, the coordinate descent algorithm has been successfully applied to speed up the Lasso computation (Friedman et al., 2007).

In the Bayesian paradigm, Park and Casella (2008) formulated the Bayesian Lasso by assuming independent Laplace prior distributions for the β_j ’s,

$$\pi (\beta \mid {\sigma }^2)\propto \exp \left(-\frac{\lambda }{\sqrt{{\sigma }^2}}\sum _{j=1}^p\mid {\beta }_j\mid \right).$$

Laplace prior distributions can be generated using a scale mixture of normal distributions, with a gamma prior for λ² and an improper prior for σ² (Kyung et al., 2010),

$$\begin{array}{cc}\hfill \beta \mid {\sigma }^2,{\mathrm{D}}_{\tau }& ~N_p(0,{\sigma }^2{\mathrm{D}}_{\tau }),\hfill \\ \hfill {\mathrm{D}}_{\tau }& =\mathrm{diag}\{{\tau }_1^2,...,{\tau }_p^2\},\hfill \\ \hfill {\tau }_j^2\mid {\lambda }^2& \stackrel{i.i.d.}{~}\mathrm{Exponential}({\lambda }^2∕2),\hfill \\ \hfill {\lambda }^2& ~\mathrm{Gamma}(a,b),\hfill \\ \hfill \pi \left({\sigma }^2\right)& \propto 1∕{\sigma }^2,\hfill \end{array}$$

Similarly, the Bayesian group Lasso can be formulated as

$$\begin{array}{cc}\hfill {\beta }_k\mid {\sigma }^2,{\tau }_k^2& ~N_{m_k}(0,{\sigma }^2{\tau }_k^2{\mathbf{I}}_k),\hfill \\ \hfill {\tau }_k^2\mid {\lambda }^2& ~\mathrm{Gamma}\left(\frac{m_k+1}{2},\frac{{\lambda }^2}{2}\right),\hfill \\ \hfill {\lambda }^2& ~\mathrm{Gamma}(a,b),\hfill \\ \hfill \pi \left({\sigma }^2\right)& \propto 1∕{\sigma }^2,\hfill \end{array}$$

where m_k is the dimension of the kth group, I_k is the identity matrix of size m_k, and a and b are hyperparameters.

2.3 Bayesian Two-step Lasso Strategy

The Bayesian two-step Lasso procedure was motivated by the need of designing exploratory trials for targeted therapy development in lung cancer. The trial has two stages. In the first stage, patients can be equally randomized into treatments. At the end of stage one, additional exploratory biomarkers will be chosen through variable selection for adaptive randomization in the second stage. The trial design and conduct, including variable selection and adaptive randomization of patients, are all implemented in the Bayesian framework. The proposed Bayesian two-step Lasso procedure will be used for variable selection procedure at the end of stage one of the trial.

Without loss of generality, we consider three treatment arms: Treatment 0 corresponds to the standard (non-targeted) therapy serving as the control; and treatments 1 and 2 are the single or combined molecularly targeted agents, which leads to two treatment indicators with treatment 0 as the reference. Suppose that there are K biomarkers under investigation, from which we aim to identify the prognostic markers and predictive markers for clinical use. Let β_t1 be the main effect of treatment 1 (corresponding to covariate x_t1), β_t2 be that of treatment 2 (corresponding to covariate x_t2), and (β_m1, … , β_mk) be those of the K biomarkers (corresponding to covariates x_m1, … , x_mk). To determine which marker is predictive, we also include the interaction terms between each marker and the two treatment indicators. In particular, we denote β_1k and β_2k as the interaction effects between marker k and treatments 1 and 2, respectively. Therefore, the parameterization in model (1) can be written as

$$\begin{array}{cc}\hfill {\mathbf{X}}^T\beta =& {\beta }_{T1}{x}_{T1}+{\beta }_{T2}{x}_{T2}\hfill \\ \hfill & +{\beta }_{M1}{x}_{M1}+...+{\beta }_{MK}{x}_{MK}\hfill \\ \hfill & +{\beta }_{11}{x}_{T1}{x}_{M1}+{\beta }_{21}{x}_{T2}{x}_{M1}\hfill \\ \hfill & ⋮\hfill \\ \hfill & +{\beta }_{1K}{x}_{T1}{x}_{MK}+{\beta }_{2K}{x}_{T2}{x}_{MK}.\hfill \end{array}$$

Due to the nature of the study, we are concerned with the identification of important biomarkers, which are either prognostic or predictive. A biomarker is considered prognostic if the marker’s main effect is statistically significant, whereas a biomarker is considered predictive if the interaction between the marker and a treatment is significant. Toward this goal, we propose a Bayesian two-step Lasso strategy with the first step of biomarker group selection and the second step of individual biomarker selection. In the first step, we group all of the covariates by markers such that each group contains only one marker, including the marker main effect and its interactions with the two experimental treatments. The treatment main effects do not participate in variable selection and they always stay in the model. We use the Bayesian group Lasso to screen out the groups of model parameters corresponding to unimportant markers. In other words, the unit of variable selection in the first step is the entire group associated with each marker, which includes the marker’s main effect and the marker–treatment interactions. If the group is not important, we remove the whole group. In the second step, we take a step-down procedure to further examine each individual marker and its interactions with the two treatments. To obtain consistent estimates for the model parameters, we use adaptive versions of the Bayesian group Lasso and the Bayesian Lasso to provide differentiating penalties to parameters based on some initial point estimation. The detail of the Bayesian two-step Lasso strategy is described as follows.

Step 1

We group each biomarker’s main effect and the corresponding two biomarker–treatment interactions together,

$$\begin{array}{cc}\hfill {\mathrm{X}}^T\beta & ={\beta }_{T1}{x}_{T1}+{\beta }_{T2}{x}_{T2}\hfill \\ \hfill & +({\beta }_{M1}{x}_{M1}+{\beta }_{11}{x}_{T1}{x}_{M1}+{\beta }_{21}{x}_{T1}{x}_{T1}{x}_{M1})\mathrm{Group}1\hfill \\ \hfill & ⋮\hfill \\ \hfill & +({\beta }_{MK}{x}_{MK}+{\beta }_{1K}{x}_{T1}{x}_{T1}{x}_{MK})\mathrm{Group}K.\hfill \end{array}$$

Let β_k = (β_Mk , β_1k , β_2k)^T, k = 1, … , K; and for group variable selection, the shrinkage priors for β_k are given by

$$\begin{array}{cc}\hfill {\beta }_k\mid {\sigma }^2,\tau & ~N_{mk}(0,{\sigma }^2{{\tau }_k}^2{\mathrm{I}}_k),\hfill \\ \hfill {{\tau }_k}^2& ~\mathrm{Gmma}\left(\frac{m_k+1}{2},\frac{{\lambda }^2}{2\Vert {\tilde{\beta }}_k{\Vert }^2}\right),\hfill \\ \hfill {\lambda }^2& ~\mathrm{Gemma}(a,b),\hfill \\ \hfill \pi {\sigma }^2& \propto 1∕{\sigma }^2,\hfill \end{array}$$

where ${\tilde{\beta }}_k$ is an initial posterior estimate of β_k under noninformative prior distributions. The use of ${\tilde{\beta }}_k$ in the prior distribution of ${{\tau }_k}^2$ enables different penalties for different groups of variables, an idea similar to the Bayesian adaptive Lasso.

Let ${{\beta }_k}^{\left(1\right)},\cdots ,{{\beta }_k}^{\left(m\right)}$ denote the m posterior samples of β_k, and let ${\stackrel{‒}{\beta }}_k=m^{-1}{\sum }_{i=1}^m{{\beta }_k}^{\left(i\right)}$ denote the corresponding posterior mean. We can construct a distance measure from ${{\beta }_k}^{\left(i\right)}$ to ${\stackrel{‒}{\beta }}_k$

$${d_k}^{\left(i\right)}={({{\beta }_k}^{\left(i\right)}-{\stackrel{‒}{\beta }}_k)}^T{{\mathrm{W}}_k}^{-1}-({{\stackrel{‒}{\beta }}_k}^{\left(i\right)}-{\stackrel{‒}{\beta }}_k),i=1\cdots ,m,$$

where W_k is the posterior sample variance–covariance matrix. We denote the empirical cumulative distribution function of ${d_k}^{\left(i\right)}as{F}_k\left(d\right)=m^{-1}{\sum }_{i=1}^{m}I\left({d_k}^{\left(i\right)}<d\right)$, and then the kth biomarker group will be selected if

$${{\stackrel{‒}{\beta }}_k}^{-T}{{\mathrm{W}}_k}^{-1}{\stackrel{‒}{\beta }}_k>{F_k}^{-1}\left({\delta }_1\right),$$

where ${F_k}^{-1}(\cdot )$ is the empirical quantile function and δ₁ is a tuning parameter between 0 and 1.

Step 2

We apply the Bayesian version of the adaptive Lasso for finer variable selection after the relevant groups are selected in the first step. Let S be the set of model parameters for the selected marker groups, including the marker main effects and marker–treatment interactions. The prior for β_j in the Bayesian adaptive Lasso of the second step is

$$\pi ({\beta }_i\mid \lambda )\propto \exp \left(-\lambda \sum _{j∊s}\frac{\mid {\beta }_j\mid }{\mid {\tilde{\beta }}_j\mid }\right).$$

Using the exponential mixture of normal distributions, we have

$$\begin{array}{cc}\hfill {\beta }_j\mid {\sigma }^2,{{\tau }_j}^2& ~N(0,{\sigma }^2{{\tau }_j}^2),\hfill \\ \hfill {{\tau }_j}^2\mid {\lambda }^2& {~}^{i.i.d.}\mathrm{Exponential}\left(\frac{{\lambda }^2}{{{\tilde{\beta }}_j}^2}\right),\hfill \\ \hfill {\lambda }^2& ~\mathrm{Gemma}(a,b),\hfill \\ \hfill \pi \left({\sigma }^2\right)& \propto 1∕{\sigma }^2,\hfill \end{array}$$

where ${\tilde{\beta }}_j$ is an initial posterior mean estimate of β_j under noninformative prior distributions. At the end of the second step, the markers’ main effects and the marker–treatment interactions are selected individually based on the posterior distribution of each parameter. For example, a particular marker main effect or marker–treatment interaction will be selected if the δ posterior credible interval does not include zero, where δ₂ is another tuning parameter between 0 and 1.

The values of δ₁ and δ₂ can be calibrated to achieve desirable frequentist properties for variable selection. In the general clinical trial setting for targeted therapy development, the clinical study team needs to propose a null study case and an alternative study case based on available medical information. Usually, drug development is not going to be viable even if the pre-assumed treatment effect for the null case is true. Based on the available data, the alternative case should be the most likely case that can provide patients with meaningful treatment improvement. The null and alternative study cases can be used to tune δ₁ and δ₂ in the simulations to control the error rates. In clinical trials for targeted therapy development, hypothesis testing is typically conducted for treatment effects in both the overall patient population and certain predefined patient subgroups. When all the null hypotheses are true, the probability of rejecting at least one hypothesis is defined as the family-wise error rate. Since our main goal is variable selection, the strong control of the family-wise error rate is too stringent and not the best measure for evaluating the methods.

Instead, in our simulations, we tune the values of δ₁ and δ₂ based on the mean error rate of variable selection. In particular, all the parameters are set to be zero in the null case. For each parameter, we can calculate the probability of being erroneously chosen by our Bayesian two-step Lasso method over a large number of simulations. The mean error rate of variable selection is the average selection probability of all parameters under the null case. Within the sets of δ₁ and δ₂ values that meet our error rate control criterion, the set that maximizes the power of variable selection is chosen for trial conduct. Here, power is defined as the average selection probabilities of all non-zero parameters under the alternative case.

The goal of the Bayesian group Lasso in the first step is to screen out unimportant biomarkers, so that more efficient variable selection can be achieved in the second step on a reduced parameter space. We take a loose or more lenient selection criterion in the first step to minimize the chance of important biomarkers being excluded, and at the same time the goal of reducing the parameter dimension for the second variable selection can still be achieved. The screening of variables before applying a formal variable selection procedure has been used in practice, for which Fan and Lv (2008) provided a formal justification based on sure independence screening. Instead of screening each variable individually, we use a Bayesian group Lasso to screen all variables simultaneously.

3 Simulation Study

3.1 Model Setups

The primary goal of targeted therapy development is to identify prognostic or predictive biomarkers that can guide the molecular diagnosis and personalized treatment optimization for patients. Following this plan, we conducted simulations to evaluate the variable selection procedure using our Bayesian two-step Lasso strategy. We investigated 50 biomarkers including both prognostic and predictive markers, among which odd-numbered biomarkers were binary and even-numbered biomarkers were continuous. All biomarker values were generated from a multivariate normal distribution, and binary biomarkers were obtained by dichotomization with a fixed marker-positive percentage at 50%.

The true values of covariate effects are given in Table 1 for the null Model, alternative model 1, and alternative model 2, where the first row represents the marker main effects, and the remaining two rows correspond to the marker–treatment interactions. Fifty markers are used in the simulations for the null and alternative model 1, and 15 markers are used for alternative model 2. Fifty markers yield a total of 152 model parameters related to marker and treatment effects. To save space, the true parameter values related to the first 15 markers are shown in Table 1, and those not shown are all zero. We set the treatment main effects to be zero for both experimental treatments, and focused on the identification of important biomarkers. For alternative model 1, one can see that marker 1 (odd-numbered markers are binary) is a prognostic marker as patients with positive status of marker 1 would have improved survival regardless of their treatments. Similarly, marker 2 (even-numbered markers are continuous) is also prognostic for better survival. Markers 3 and 4 are prognostic for worse survival, and markers 5 through 12 are all predictive markers with small prognostic effects. All markers in alternative model 2 are binary.

Table 1.

True parameter values under the Cox proportional hazards model with the marker main effects (Main) of markers 1 to 15 (M1–M15), the marker and treatment 1 interaction (MT1), and the marker and treatment 2 interaction (MT2).

	Ml	M2	M3	M4	M5	M6	M7	M8	M9	MIO	M11	M12	M13	M14	M15
	Null Model
Main	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
MTl	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
MT2	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	Alternative Model 1
Main	−0.50	−0.50	0.50	0.50	−0.30	−0.30	0.30	0.30	−0.30	−0.30	0.30	0.30	0.00	0.00	0.00
MTl	0.00	0.00	0.00	0.00	−0.70	−0.70	0.70	0.70	0.00	0.00	0.00	0.00	0.00	0.00	0.00
MT2	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	−0.70	−0.70	0.70	0.70	0.00	0.00	0.00
	Alternative Model 2
Main	−1.00	0.00	0.00	−0.25	−0.25	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
MTl	0.00	−1.00	0.00	−1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
MT2	0.00	0.00	−1.00	0.00	−1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00

To mimic the common setup of a phase II exploratory trial in oncology, our simulation study involved a total sample size of 150, with an accrual period of four years and one additional year of follow-up. Patients’ survival times were generated from the proportional hazards model by assuming an exponential survival distribution. In particular, we assumed that T_i, the survival time for the ith patient, follows an exponential distribution with rate parameter λ₀ exp $\left({{\mathrm{X}}_i}^T\beta \right)$, where the baseline hazard rate λ₀ = 0.02 and X_i is the covariate vector of the ith patient. The censoring time, C_i, was generated from a uniform distribution on (0, c_max), where c_max is a constant that was adjusted to control the censoring rate at 7% and 15% for the null and alternative cases, respectively. The observed data were i.i.d. copies of (Z_i, Δ_i, X_i), where Z_i = min{T_i, C_i} Δ_i = I(T_i ≥ C_i), and I(·) is the indicator function.

In the gamma process prior for the baseline hazard rate, we used the hyperparameters of r = 0.01 and c = 0.001 in (3). We specified a Gamma(1, 10) as the prior distribution of λ², with mean 10 and variance 100. The point estimates of parameters depend on the number of time segments for modeling the baseline hazard in the Cox proportional hazards model. In our simulations, we used 30 segments to model the baseline cumulative hazard function.

3.2 Simulation Results

As discussed previously, the values of the tuning parameters δ₁ and δ₂ are determined by the mean error rate of variable selection. We conducted 1000 simulations for different combinations of δ₁ and δ₂ under both the null and alternative cases, and chose the values of δ₁ and δ₂ that can control the mean error rate of variable selection under the null case and maximize the mean selection probability of non-zero parameters under the alternative case.

Figure 1 shows the mean selection probabilities of parameters at different values of δ₁ and δ₂. The x-axis represents the average selection probabilities of all parameters under the null case, and the y-axis exhibits the average selection probabilities of non-zero parameters under the alternative case. Three values of δ₂ = (0.7, 0.8, 0.9) are shown, and the results for the same value of δ₂ are plotted on the same curve. For illustration, the values of δ₁ are given by the data points on the first curve (δ₂ = 0.7). The curves labeled as “Group.Adapt” are results from our Bayesian two-step Lasso with the Bayesian group Lasso in the first step and adaptive Lasso in the second step. On the other hand, those curves labeled as “Adapt.Adapt” are results from the two-step Lasso with the Bayesian adaptive Lasso in both steps.

Figure 1.

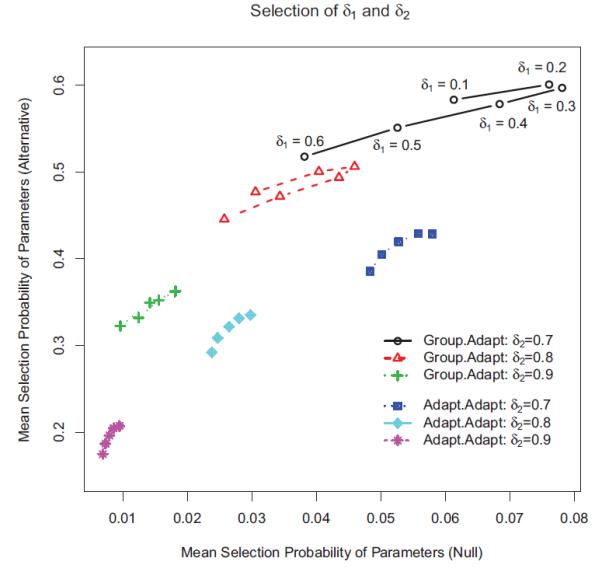
Mean selection probabilities of parameters at different values of δ₁ and δ₂. The x-axis gives the mean selection probabilities of all parameters under the null case, and the y-axis gives the selection probabilities of non-zero parameters under the alternative case. Three values of δ₂ = (0.7, 0.8, 0.9) are plotted, and the results for the same value of δ₂ are shown on the same curve.

Each data point in Figure 1 corresponds to one pair of δ₁ and δ₂ values, which can be used to choose the optimal combination of δ₁ and δ₂. For example, if the target value for the mean error rate of variable selection under the null case is about 0.08, the pair of δ₁ = 0.2 and δ₂ = 0.7 would give the highest mean selection probability of non-zero parameters under the alternative case. On the other hand, if we would like to control the mean error rate under the null case to within 0.05, we can choose δ₁ = 0.8 and δ₂ = 0.2. Figure 1 shows that “Group.Adapt” is always better than “Adapt.Adapt” when the mean error rate is controlled at the same level.

Table 2 shows that the mean bias using the “Group.Adapt” is smaller than that using the “Adapt.Adapt” procedure. The mean bias is calculated by averaging over all relevant parameters under either the null case or the alternative case. The point estimation of our Bayesian two-step Lasso method is also compared with the frequentist one-step adaptive Lasso, which has the mean biases of 0.00081 and −0.00141 under the null and alternative cases, respectively. The result shows that the posterior mean of our Bayesian two-step Lasso method is comparable and slightly better than the frequentis one-step adaptive Lasso in terms of estimation bias. The average mean squared errors of parameters are shown in the lower panel of the Table 2. The “Group.Adapt” procedure still performs slightly better than “Adapt.Adapt”. For the frequentist one-step adaptive Lasso, the average mean squared errors are 0.02238 and 0.07149 for the null and alternative model 1, separately.

Table 2.

Comparison of mean point estimation bias between two different Bayesian two-step Lasso methods: “Group.Adapt” implements the Bayesian group Lasso in the first step of variable seleciton, and “Adapt.Adapt” uses the Bayesian adaptive Lasso in both the first and second steps. The parameter δ₂ is fixed at 0.7.

	δ1 = 0.1	δ1 = 0.2	δ1 = 0.3	δ1 = 0.4	δ1 = 0.5	δ1 = 0.6
Average Bias Estimation
	“Group.Adapt”
Null	0.00063	0.00056	0.00045	0.00042	0.00016	0.00014
Alternative	−0.00118	−0.00113	−0.00110	−0.00065	−0.00088	−0.00087
	“Adapt.Adapt”
Null	0.02643	0.02114	0.01638	0.01234	0.01234	0.00890
Alternative	0.03556	0.03029	0.02529	0.02053	0.02053	0.01606
Average MSE Estimation
	“Group.Adapt”
Null	0.01281	0.01372	0.01286	0.01070	0.00790	0.00555
Alternative	0.02309	0.02384	0.02352	0.02260	0.02243	0.02244
	“Adapt.Adapt”
Null	0.01761	0.01585	0.01442	0.01331	0.01331	0.01243
Alternative	0.03413	0.03291	0.03231	0.03228	0.03228	0.03259

Based on the results in Figure 1, δ₁ = 0.2 and δ₂ = 0.7 were chosen to control the mean error rate under the null case at 0.08. The point estimates and the marginal selection probabilities of the model parameters in both the null case and the alternative case are shown in Table 3. Under the null case, the posterior means for all parameters are all close to zero. The selection probabilities for all parameters are generally under 0.10 with a maximum of 0.12. Under the alternative case, the parameters are reasonably well estimated but the estimation biases of parameters for binary markers are generally larger than those for continuous mark- ers. Important continuous biomarkers have substantially higher selection probabilities than their binary counterparts.

Table 3.

Simulation results of the Bayesian two-step Lasso with δ₁ = 0.2 and δ₂ = 0.7: posterior means, and selection probabilities of marker main effects and marker-treatment interactions (Main: marker main effect, MT1: marker and treatment 1 interaction, and MT2: marker and treatment 2 interaction).

	M1	M2	M3	M4	M5	M6	M7	M8	M9	M10	M11	M12	M13	M14	M15
	Null Model
Posterior Mean
Main	0.007	−0.002	0.004	−0.001	0.002	0.002	−0.006	0.001	−0.001	0.002	−0.009	0.002	−0.005	0.003	−0.001
MT1	−0.002	−0.000	0.008	0.001	0.008	0.000	−0.005	0.000	0.006	0.000	−0.003	0.007	0.007	−0.001	0.002
MT2	−0.001	−0.000	0.010	−0.003	−0.003	−0.005	0.000	0.005	−0.002	0.005	0.008	−0.002	0.003	−0.002	−0.006
Selection Probability
Main	0.108	0.089	0.109	0.081	0.084	0.073	0.108	0.085	0.096	0.067	0.101	0.098	0.102	0.090	0.103
MT1	0.054	0.098	0.050	0.089	0.059	0.077	0.055	0.088	0.058	0.083	0.047	0.082	0.053	0.065	0.062
MT2	0.062	0.094	0.055	0.084	0.043	0.079	0.050	0.090	0.041	0.081	0.052	0.076	0.054	0.118	0.056
	Alternative Model 1
Posterior Mean
Main	−0.340	−0.464	0.353	0.451	−0.289	−0.305	0.288	0.318	−0.301	−0.307	0.281	0.310	−0.005	−0.001	0.001
MT1	−0.057	−0.053	0.062	0.060	−0.463	−0.671	0.407	0.658	−0.013	−0.020	0.009	0.023	−0.003	−0.004	0.002
MT2	−0.064	−0.055	0.062	0.055	−0.017	−0.023	0.001	0.025	−0.467	−0.666	0.420	0.665	0.004	0.001	−0.001
Selection Probability
Main	0.485	0.953	0.490	0.930	0.377	0.697	0.380	0.722	0.404	0.730	0.345	0.703	0.082	0.067	0.072
MT1	0.055	0.092	0.051	0.107	0.393	0.846	0.331	0.837	0.049	0.064	0.059	0.088	0.045	0.058	0.040
MT2	0.078	0.102	0.066	0.089	0.034	0.061	0.030	0.086	0.376	0.837	0.330	0.855	0.046	0.069	0.037

Furthermore, we performed additional simulation studies to compare the operating characteristics of our Bayesian two-step Lasso strategy versus the one-step method under alternative model 2 in Table 1. For this simulation, we assumed all 15 markers to be binary with a fixed marker-positive percentage of 50%, and δ₂ = 0.8 was used for the one-step method, and δ₁ = 0.2 and δ₂ = 0.8 for the two-step method. For each method, the first panel represents the estimation bias of the posterior mean, the the second panel shows the posterior standard deviations, and the last panel gives the marginal selection probability of each parameter. For ease of exposition, the bias is multiplied by 100. The overall performance of point estimation of the Bayesian one-step and two-step Lasso methods are similar for parameters with true values of zero, while the biases of the two-step method are much smaller for parameters that are truly non-zero. A further comparison of the standard deviations in Table 4 shows that the two-step strategy generally results in more variations for parameter estimates compared with the one-step method. The powers of different methods can be compared by the selection probabilities of truly non-zero parameters, and the type I error rates are characterized by the selection probabilities of the parameters with true zero values. The two methods have similar type I errors, i.e., similar selection probabilities for zero-valued parameters. For the power of variable selection, the two-step method outperforms the one-step method, as the selection probabilities for non-zero parameters are better using the two-step method than those using the one-step method.

Table 4.

Simulation results under the alternative model 2 using the Bayesian two-step Lasso (δ₁ = 0.2, δ₂ = 0.8) and the one-step Bayesian adaptive Lasso (2 = 0.8). Bias is multiplied by 100, Main: marker main effect, MTl: marker and treatment 1 interaction, MT2: marker and treatment 2 interaction).

	Ml	M2	M3	M4	M5	M6	M7	M8	M9	M10
Two-Step Method
Bias of Posterior Mean
Main	−0.050	−0.111	−0.086	−0.060	−0.045	0.006	0.008	0.008	0.012	0.013
MTl	−0.176	0.254	0.028	0.091	−0.025	−0.011	−0.024	−0.023	−0.019	−0.006
MT2	−0.170	0.026	0.223	−0.016	0.072	−0.008	−0.010	−0.010	−0.006	−0.012
Standard Deviation of Posterior Mean
Main	0.318	0.166	0.159	0.247	0.248	0.106	0.113	0.119	0.115	0.121
MT1	0.272	0.472	0.188	0.501	0.215	0.122	0.134	0.140	0.149	0.135
MT2	0.269	0.188	0.461	0.188	0.515	0.137	0.120	0.133	0.125	0.145
Marginal Selection Probability
Main	0.987	0.143	0.144	0.425	0.398	0.047	0.053	0.065	0.057	0.070
MTl	0.135	0.634	0.102	0.724	0.102	0.034	0.038	0.039	0.041	0.031
MT2	0.127	0.093	0.659	0.080	0.720	0.040	0.027	0.041	0.026	0.040
One-Step Method
Bias of Posterior Mean
Main	0.148	−0.080	−0.070	0.014	0.026	0.007	0.004	0.006	0.009	0.006
MTl	−0.103	0.511	−0.001	0.356	−0.033	−0.016	−0.022	−0.024	−0.020	−0.014
MT2	−0.095	−0.008	0.480	−0.025	0.347	−0.016	−0.018	−0.016	−0.017	−0.020
Standard Deviation of Posterior Mean
Main	0.269	0.121	0.111	0.204	0.200	0.080	0.086	0.095	0.086	0.093
MTl	0.197	0.365	0.099	0.404	0.116	0.097	0.107	0.107	0.108	0.105
MT2	0.189	0.104	0.365	0.110	0.410	0.103	0.093	0.098	0.093	0.110
Marginal Selection Probability
Main	0.984	0.081	0.063	0.371	0.341	0.026	0.034	0.037	0.029	0.034
MTl	0.049	0.485	0.006	0.642	0.012	0.010	0.012	0.010	0.010	0.010
MT2	0.038	0.006	0.526	0.011	0.618	0.014	0.006	0.010	0.007	0.010

4 Discussion

Our Bayesian two-stage Lasso strategy is motivated by the need in the trial design for targeted therapy development for patients with non-small cell lung cancer at MD Anderson Cancer Center. Due to the exploratory nature of these trials, both learning information and treating patients effectively are important contributing factors for success. Therefore, such trials are typically divided into two stages. The primary objective of the first stage is to find biomarkers with prognostic or predictive values for use in the adaptive randomization of patients in the second stage of the trial. According to the FDA guidelines, biomarkers used in adaptive randomization must be CLIA certified (e.g, they must meet the requirements of the Clinical Laboratory Improvement Amendments—CLIA), which places a limit on the number of biomarkers that may be used in the adaptive stage. Therefore, the selection of biomarkers in the first stage is essential to the success of the adaptive randomization in the second stage. Since usually multiple experimental treatments are compared with the control treatment in trials for targeted therapy development, a biomarker is deemed important if it is marginally important or if it is important for at least one experimental treatment. Our Bayesian two-step Lasso strategy fulfills this requirement by bridging the Bayesian group Lasso and adaptive Lasso. The simulation results indicate that the Bayesian two-step Lasso strategy improves upon the one-step procedure. Foremost, using the group Lasso in the first step screens out biomarkers that are not important prognostically or predictively for any of the treatments. Then, as evidenced by the simulation results, using the adaptive Lasso in the second step of our strategy leads to better variable selection. The Bayesian group Lasso in the first step not only serves as an initial screening step to reduce the parameter space for the second step, it also possesses the similar spirit as the strong heredity principle of variable selection (Chipman, 1996). The parameters used in making decisions can be tuned using different frequentist operating characteristics of our method. The error rates of variable selection can be controlled numerically through simulations, which is especially applicable to trial designs in the exploratory phase of drug development.

Other stepwise Lasso strategies are also available for variable selection. For example, the relaxed Lasso is a two-step method, with the first Lasso to achieve model selection, and the second Lasso to achieve parameter estimation with a smaller penalty parameter (Meinshausen, 2007). Our two-step strategy is better suited to the Bayesian framework implemented in the design of BATTLE-type trials, where biomarker information is collected in the first stage and adaptive randomization kicks in during the second stage. The Bayesian two-step method can be easily implemented in trial designs for other targeted agents that are characterized by multiple treatments and multiple biomarker with a goal of identifying both prognostic and predictive markers.